Motor variability within a multi-effector system: experimental and analytical studies of multi-finger production of quick force pulses

Abstract

The purpose of the study was to develop a model of force variability for a fast action performed by a multi-effector system and to verify it for multi-finger quick force production. The experiments involved quick isometric contractions to different target force levels using different finger combinations. Force variance calculated over sets of trials for a multi-finger force production task showed non-monotonic single-peak profiles of force variance with a peak at a time between the times of the maxima of the force rate and of the total force. When analyzed in the four-dimensional space of finger forces, the variance peak was mostly expressed in the direction of the force rate, and was absent in the directions orthogonal to it. The non-monotonic time profile of the force variance could be reproduced by a model of force production, which assumes that each finger force profile is based on a template function scaled in duration and magnitude with two parameters assigned prior to each trial with some variability. The model allows decomposition of the force variance into two fractions related to variability in setting the magnitude and duration scaling parameters. The former fraction changes monotonically with time, while the latter shows a transient peak in the middle of the action. The model was able to reproduce experimental variance time profiles across conditions with the total error of under 8%. The results demonstrate, in particular, that fast multi-finger actions may show transient changes in motor variability in certain directions of the finger force space, particularly in the direction of the first force derivative, without any task-specific coordinating action by the controller. These findings require a reconsideration of some of the conclusions drawn in recent studies on the structure of motor variability in redundant multi-effector systems.

Introduction

A number of experimental studies have described linear relations between the magnitude of force produced by a person and its standard deviation (force/force variability, Newell et al. 1984; Newell and Carlton 1988), although in a more recent study an exponential relationship has been described (Slifkin and Newell 2000). These studies typically addressed force generation by a single effector and computed indices of force variability across repeated attempts at a task, commonly during a steady-state force production.

Further studies of quick motor actions has led to the emergence of a number of formal models for patterns of motor variability observed during the production of fast discrete movements or force pulses by a single effector (Newell and Carlton 1988; Plamondon and Alimi 1997; Jones et al. 2002). The main purpose of the current study has been to develop a model for the production of forces by a redundant motor system based on an earlier model of motor variability during single-joint actions (Gutman and Gottlieb 1992; Gutman et al. 1993; Latash and Gutman 1993). The original model by Gutman (Goodman) and colleagues (we will refer to it as the G-model) has been based on an assumption that patterns of motor variability are primarily defined by processes at the stage of motor planning (Gordon et al. 1994; Messier and Kalaska 1999; although see Van Beers et al. 2004). It suggests that patterns of variability are defined by imprecise setting of two scaling parameters related to the planned duration and amplitude of the motor output. This idea has recently been invoked in interpreting data obtained during multi-finger cyclic and discrete force production (Latash et al. 2002b).

The main goal of the study has been to investigate variance of the finger forces in different directions of the finger force space over time during quick force pulses and develop the G-model for multi-finger quick force production tasks. This choice was dictated by a couple of factors. First, a number of studies of motor variability during finger action have been published recently (Slifkin and Newell 2000; Rabin and Gordon 2004). Besides, over the last years, our group has accumulated substantial experience in studies of the production of forces by sets of fingers (reviewed in Latash et al. 2002a, 2003; Zatsiorsky and Latash 2004). In addition to model development, the current manuscript also presents results of an experimental study of patterns of finger force covariance during multi-finger quick force pulse production. The purpose of the experiment was to provide a description of patterns of force variability in multi-finger tasks, to verify model predictions, and to define certain model parameters. We have decided to study the production of very fast force pulses to minimize the possibility of on-line corrections of the force pulses (cf. Khan et al. 2003).

A formal analysis of force variability during multi-finger force production has been also dictated by recent studies within the framework of the uncontrolled manifold (UCM) hypothesis (Scholz and Schoner 1999; reviewed in Latash et al. 2002a, 2003). The hypothesis states that, during multi-element motor action, the controller acts in the state space of elemental variables and selects in this space a subspace (a UCM) corresponding to a desired set of values of particular performance variables. Then, the controller organizes covariation of elemental variables to keep most of their variability across repetitions at the task within the UCM. Certain non-uniform distributions of motor variance in the space of elemental variables have been interpreted as pointing at particular control strategies used by the central nervous system (Latash et al. 2002a; Shim et al. 2003). Typically, analysis within the UCM hypothesis has been performed over arrays of data points measured in different trials at particular phases of the task execution. As such, the analysis did not take into account possible effects of time changes of the variables on observed patterns of their covariation. We hypothesize in this study that quick multi-finger actions may show transient non-monotonic changes in motor variability in certain directions of the finger force space without any task-specific coordinating action by the controller.

Methods

Experiment

Subjects

Five male (age 25.6±3.2 yrs, weight 73.3±4.6 kg, height 1.78±0.069 m, hand length 0.2±0.012 m, and hand width 0.092±0.005 m) and four female (age 25.3±2.6 yrs, weight 59.8±5.2 kg, height 1.666±0.041 m, hand-length 0.184±0.012 m, hand-width 0.078±0.006 m) students took part in the experiments as subjects. The hand length was measured between the middle fingertip and the distal crease of the wrist with the hand extended and the hand width was measured between the lateral aspects of the index and little finger MCP joints. All the subjects were healthy and right-handed according to their preferential use of the hand during daily activities such as writing, drawing, and eating. None of the subjects had a history of long-term involvement in hand or finger activities such as typing and playing musical instruments. All the subjects gave informed consent according to the procedures approved by the Office for Regulatory Compliance of the Pennsylvania State University.

Apparatus

Four unidirectional piezoelectric sensors (model 208 C01; Piezotronic) were used for force measurement. Analog output signals from the sensors were amplified by AC/DC conditioners. Cotton covers were attached to the upper surface of the sensors to increase friction and prevent the influence of finger skin temperature on the measurements. The sensors were medio-laterally distributed 30 mm apart. The anterio-posterior position of the sensors could be adjusted within a 60-mm range to fit individual subject’s hand anatomy. The sensors were placed inside the groove in a wooden board so that the subject could place his or her fingers comfortably on the sensors (for a detailed description of the setup, see Li et al. 1998).

The subject sat in a chair facing the testing table with his/her right upper arm at approximately 45° of abduction in the frontal plane and 45° of flexion in the sagittal plane, the elbows at approximately 135°. A wooden board supported the wrist and the forearm and a wooden piece shaped to fit comfortably under the subject’s palm helped maintain a constant configuration of the hand and fingers. The metacarpophalangeal and interphalangeal joints were all about 20° into flexion, so that the hand formed a dome. The subject selected a comfortable position of the thumb. A computer monitor was located about 0.8 m away in front of the subject; it presented tasks and actual forces, as described later. A customized LabView program was used for data acquisition, and a MatLab program was written for data processing. The data were recorded at the sampling frequency of 1000 Hz with 16-bit resolution.

Procedure

Subjects sat relaxed with the fingers of the right hand on the sensors. During tests with maximum force production (maximum voluntary contraction—MVC), the subjects were required to press on the sensors as strongly as possible with a set of explicitly involved (master) finger(s). Master finger combinations were I, M, R, L, IM, IMR, and IMRL (I—index, M—middle, R—ring, and L—little fingers). The sum of the forces of the master fingers was displayed on-line on the screen, and the subjects were required to reach a maximum force level with the master fingers within 5 s after a trial had started. The subjects were instructed to pay no attention to possible force production by other, uninstructed fingers (slave fingers) as long as they were not lifted off the sensors and the master fingers produced maximum force. The subjects performed three trials, and the trial with the highest peak force by the master fingers was selected to set further experiments. The intervals between the trials were 1.5 min and the intervals between MVC tasks were 5 min. The order of MVC tasks was balanced across the subjects.

During quick force pulse production tests, three horizontal lines were shown on the screen, which matched each subject’s 10, 20, and 30% of the MVC for a given combination of master fingers. The computer generated two beeps (get ready), and then the line started moving over the screen showing the subject the summed force of the master fingers. The subjects were required to produce at any time over a 5 s time interval a quick force pulse as fast and accurately as possible to a pre-specified target force level. As soon as the subject reached the force of 0.5 N, the force trace on the monitor disappeared for 0.5 s to minimize possibility of vision based corrections. Then the force trace appeared again showing the subjects their final force level. The subjects were instructed to maintain the force level up to the end of the trial even if it had a large discrepancy with the target force level. The order of the 10%, 20%, and 30% of MVC conditions and the order of master finger combinations were balanced across the subjects. Subjects performed series of 12 consecutive trials with each master finger combination to each target force level. The intervals between the trials within a series were 8 s. The intervals between two series were 1 min.

Data processing

All the trials within a series at a particular task were aligned by the initiation of the total force produced by the master fingers. This time was defined as the moment when the force reached 1% of its peak value in that particular trial.

The four finger forces were considered a vector function f(t)=[f_I(t), f_M(t), f_R(t), f_L(t)]^T , where t stands for time, the subscripts I, M, R and L signify the index, middle, ring and little finger, respectively, and superscript T denotes transpose. The force rate vector f′ (t) was estimated from f(t) after filtering the data with a 40 Hz low-pass, fourth-order Butterworth filter. Since the data were digitized at 1000 Hz for 6 s, we consider t=nΔt, Δt=1 ms, n=0, 1, …, (6×10³−1). f′(t) was estimated at as f′(nΔt)=(f((n+1)Δt)−f(nΔt))/Δt (the last value of the force rate at n=6×10³−1 was assumed to be equal to the previous value). The vector-function f(t) defines a one-dimensional manifold (a line) in the space of finger forces R⁴. For each subject s, the mean vector f_s(t) was computed across the twelve trials at each task. Thus, a component of f_s(t) represents an average force of a given finger in a given task at an instant nΔt, where n is data sample, for the subject s. An inter-finger force covariance matrix Cov_s(f(t)) was computed for each subject and task:

$${\mathbf{\text{Cov}}}_s(\mathbf{f}(t))=\frac{1}{K-1}{\displaystyle \sum _{k=1}^K({\mathbf{f}}_{ks}(t){\mathbf{f}}_{ks}^{\mathrm{T}}(t)-{\overline{\mathbf{f}}}_s(t){\overline{\mathbf{f}}}_s^{\mathrm{T}}(t))}$$ (1)

where K is the number of trials, K=12, s=1, …, S, S=9 subjects. The main goal of this study can be reformulated as an investigation of variance of the finger forces in different directions of R⁴ over time t during quick force pulses.

Variability over time

For a direction k in R⁴, let f̄_k(t) and ${\mathit{f̄}}_k^{\prime }(t)$ be means of force and force rate across trials, and Var(f_k(t)) be the force variance time profile. We limit analysis to comparing force variances at three selected instants of time: T_maxR, T_maxV, and T_maxF when the functions f̄_k(t), ${\mathit{f̄}}_k^{\prime }(t)$, and Var(f_k(t)), respectively, reach their maxima. At these moments, we calculated values of variances Var(f_k(T_maxR)), Var(f_k(T_maxV)), and Var(f_k(T_maxR)). Maxima of variance Var(f_k(T_maxV)) were typically observed within the time interval between the force rate maximum T_maxR and the force maximum T_maxF. We will address this phenomenon as a V-peak. A V-peak is present in Var(f_k(t)) if the following two inequalities are met:

$$T_{\text{maxR}}<T_{\text{maxV}}\text{and}{T}_{\text{maxV}}<T_{\text{maxF}}$$ (2)

V-peaks were analyzed for the forces produced by all master fingers, by individual master fingers, and by slave fingers. The relative magnitude of a V-peak was estimated as:

$${\text{RM}}_{\text{V-peak}}(\text{Var}(f_k))=\text{Var}(f_k(T_{\text{maxV}}))/\text{Var}(f_k(T_{\text{maxF}}))$$ (3)

Variability in different directions in R⁴

To calculate variance of a vector in any desired direction in R⁴, we utilized the Rayleigh fraction. Variance of a set of K vectors {x_i} in space R^P in a direction of vector v is the variance of their projections on this direction. The length of a projection of vector x on vector v is v^Tx/(v^Tv)^0.5 ; its squared value can be written as v^Txx^Tv/v^Tv. For a demeaned set of vectors {x_i}, the variance in the direction of v is ${\mathbf{v}}^{\mathrm{T}}{\displaystyle \sum _{i=1}^K{\mathbf{x}}_i{\mathbf{x}}_i^{\mathrm{T}}\mathbf{v}/(K-1){\mathbf{v}}^{\mathrm{T}}\mathbf{v}}$. This formula can be rewritten as v^TCov(x)v/v^Tv, which is the Rayleigh fraction with vector v and covariance matrix of the vector set {x_i}. In our case, the force covariance matrix depends on time, so we calculated the force variance time profile in direction v as:

$$\text{Var}(f(t)){|}_{\mathrm{v}}=\frac{{\mathbf{v}}^{\mathrm{T}}\mathbf{Cov}(\mathbf{f}(t))\mathbf{v}}{{\mathbf{v}}^{\mathrm{T}}\mathbf{v}}$$ (4)

The variances along certain directions in R⁴ were computed: (a) variance in index finger force Var(f_I(t)); (b) variance in middle finger force Var(f_M(t)); (c) variance in the direction of force rate f′(t); and (d) variance of the orthogonal complement to vector f′(t) in space R^P (per dimension). The variances (a) and (b) were extracted from the diagonal of matrix Cov(f(t)), variance (c) was computed using Eq. (4), and variance (d) was computed as:

$$\begin{array}{c}\text{Var}(f(t)){|}_{\text{orth}\text{to}\mathbf{v}}=\frac{1}{P-1}{\displaystyle \sum _{i=1}^{P-1}\frac{{\mathbf{y}}_i^{\mathrm{T}}\mathbf{Cov}(\mathbf{f}(t)){\mathbf{y}}_i}{{\mathbf{y}}_i^{\mathrm{T}}{\mathbf{y}}_i}}\hfill \\ =\frac{\text{tr}(\mathbf{Cov}(\mathbf{f}(t)))-\text{Var}(f(t)){|}_{\mathbf{v}}}{P-1}\hfill \end{array}$$ (5)

where {y_n} are the basis vectors of an orthogonal complement to v, and tr(Cov(f(t)) is the trace of the covariance matrix.

Statistics

The inequalities describing the presence of V-peaks (Eq. 2) have been tested for each subject for all tasks and target force levels, separately for the slave and master fingers and for the total force produced by the master fingers. Two-way mixed-effects ANOVA with factors Maximum (3 levels, max-of-force-rate, max-of-force-variance, max-of-force) and Finger (3 levels, master, slave, and all), with appropriate post-hocs, was used to analyze differences among T_maxR , T_maxV, and T_maxF. To test the existence of differences in V-peak magnitudes (Eq. 3) in the four selected directions in R⁴, we used two-way repeated-measures ANOVA with factors Direction (4 levels; in the directions of the index finger force vector (f_I=[1,0,0,0]), of the middle finger force vector (f_M=[0,1,0,0]), of the force rate vector f′(t), and of vectors orthogonal to the vector of force rate), and Force levels (3 levels, 10%, 20%, and 30% of the MVC), with contrasts.

The model

An analytical form of a two-parametric force control considered in this work is:

$$f_{kn}(t)=b_{kn}{u}_n(t/{\tau }_{kn})$$ (6)

where f_kn(t) is the actual force-time profile of finger n (n∈{I,M,R,L}) in trial k. This equation is a generalization of a model developed for single-joint movements (Gutman and Gottlieb 1995; Latash and Gutman 1996). According to the model, the template force-time profile u_n(t) is modified by two scaling parameters, b_kn and τ_kn, assigned prior to each trial k with some variability. The assumptions of the model are:

1. Scaling parameters b_kn and τ_kn are random variables with means b̄_n and τ̄_n and standard deviations SD(b_n) and SD(τ_n).

2. There is a non-zero covariance between scaling parameters assigned to different fingers n and m: Cov(b_n,b_m) ≠ 0, Cov(τ_n,τ_m) ≠ 0 (n,m∈{I,M,R,L}), but not between the magnitude and duration scaling parameters, Cov(b_n,τ_m)=0.

3. Force templates {u_n(t)} are assumed to be deterministic functions in a sense that their contribution into the force variability is small as compared to the contribution of variability of b and τ.

4. No on-line correction is assumed during the production of quick force pulses.

Covariance matrix of the model and its connection to experimental covariance matrix

As follows from Appendix A (Eq. 10), the entries of the covariance matrix of our model (Eq. 6) are:

$$\text{Cov}(f_n(t),f_m(t))=\overline{f_n(t)f_m(t)}{x}_{nm}+t^2\overline{f_n^{\prime }(t)f_m^{\prime }(t)}{y}_{nm}$$ (7)

Here, x_nm=CV(b_n)CV(b_m)r(b_n, b_m), y_nm=CV(τ_n) CV(τ_m)r(τ_n, τ_m) (where CVs are coefficients of variation of scaling parameters b_n and τ_n, CV(b_n)=SD(b_n)/b̄_n, CV(τ_n)=SD(τ_n)/τ̄_n; the horizontal lines over the symbols signify averaging), and f′(t)is the derivative of f(t) with respect to time. In the experiments, neither {u_n(t)}, nor {b_n} and {τ_n} are observable; only their coefficients of variation (CVs) can be assessed.

The model covariance Cov(f_n(t), f_m(t)) may be viewed as the sum of an experimental covariance (further denoted as Cov_exp(f_n(t),f_m(t))) and an error ϑ_nm(t):

$$\begin{array}{c}{\text{Cov}}_{\text{exp}}(f_n(t),f_m(t))=\mathit{\text{Cov}}(f_n(t),f_m(t))+{\vartheta }_{nm}(t)\hfill \\ =\overline{f_n(t)f_m(t)}{x}_{nm}+t^2\overline{f_n^{\prime }(t)f_m^{\prime }(t)}{y}_{nm}+{\vartheta }_{mm}(t)\hfill \end{array}$$ (8)

This expression can be considered an equation of linear regression of Cov(f_n(t), f_m(t)) on functions $\overline{f_n(t)f_m(t)}$ and $t^2\overline{f_n^{\prime }(t)f_m^{\prime }(t)}$ with unknown coefficients x_nm and y_nm. Equation (8) can be written for each moment of time along a trial resulting in a set of equations. The coefficients can be calculated from this set of equations using the mean least square error criterion. Hence, Eq. (8) fits the model force variance to the experimental one. Later, we describe the results of calculating CV(b_n) and CV(τ_n) and estimating the accuracy of the model.

The matrix form of Eq. (8) is:

$$\begin{array}{cc}{\text{Cov}}_{\text{exp}}(\mathbf{f}(t))\hfill & =\text{Cov}(\mathbf{f}(t))+\vartheta (t)\hfill \\ \hfill & =\mathbf{D}(\overline{\mathbf{f}(t)})\mathbf{XD}(\overline{\mathbf{f}(t)})+t^2\mathbf{D}(\overline{\mathbf{f}(t)})\mathbf{YD}(\overline{\mathbf{f}(t)})\hfill \\ \hfill & +\vartheta (t)\hfill \end{array}$$ (9)

where ϑ(t) is matrix of residuals.

To calculate the model time profiles Var(f(t))|_f‘(t) in the direction of the force rate vector, we applied Rayleigh fraction (Eq. 4). Variance per coordinate in directions orthogonal to the force rate vector was calculated with Eq. (5).

Results

Force and force rate time profiles

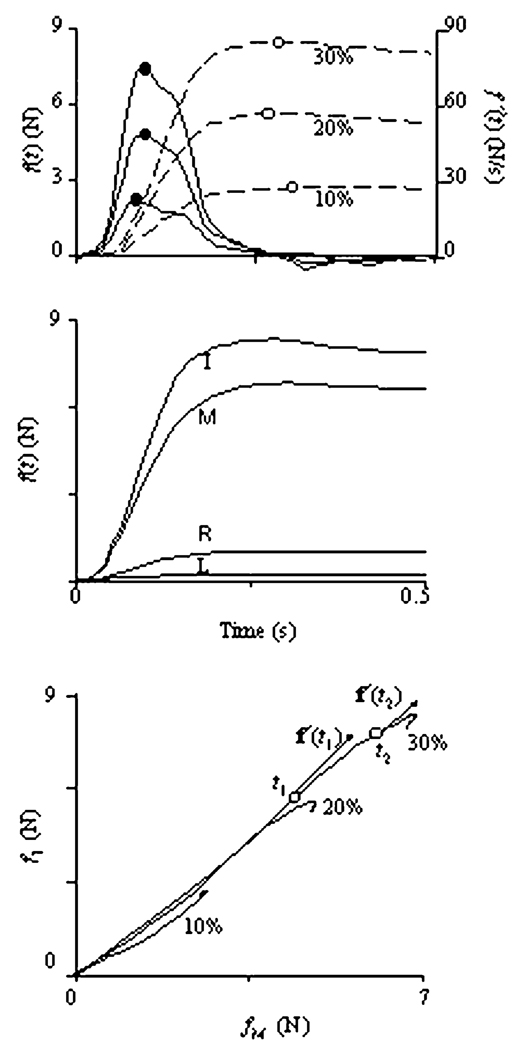
Typical force—time profiles for a representative subject performing tasks of force production over different magnitudes with the index finger are shown in the upper panel of Fig. 1. Averaged across twelve trials force time profiles are shown with dashed lines, while force rate time profiles are shown with solid lines. The force curves commonly showed a temporary overshoot of the target level (at the moment T_maxF). The f′(t) functions reached their peaks at about 0.1 s after the initiation of the force production (T_maxR). The middle panel of Fig. 1 shows force-time profiles for all four fingers in a two-finger task with the index and middle fingers as the master fingers (IM), averaged over 12 trials. Note the force production by the slave fingers, R and L. Lower panel of Fig. 1 shows finger force profiles in a two-dimensional subspace of the force space R⁴ with the axes corresponding to the forces produced by the index and middle fingers, f_I and f_M. Three traces correspond to the three target force levels. Vectors of force rate direction f′(t₁) and f′(t₂) are shown at two arbitrarily chosen moments of time t₁ and t₂.

Fig. 1.

A–C A Force f(t) (dashed lines) and force rate f′(t) (solid lines) time profiles during single-finger tasks performed by the index finger. The curves show averages over 12 trials performed by a representative subject. Target force levels were 10%, 20%, and 30% of the MVC. Empty circles and filled circles correspond to peaks of force and force rate, respectively. B Time profiles of the master (I and M) and slave (R and L) finger forces in a two-finger task (IM) at 30% of MVC. C. Force–force trajectories for a two-finger task (IM) at three target force levels. The directions of the force rate vectors f′(t₁) and f′(t₂) are shown for two arbitrarily selected times, t₁ and t₂

Force variance time profile: Location of peaks of variance (V-peaks) in time

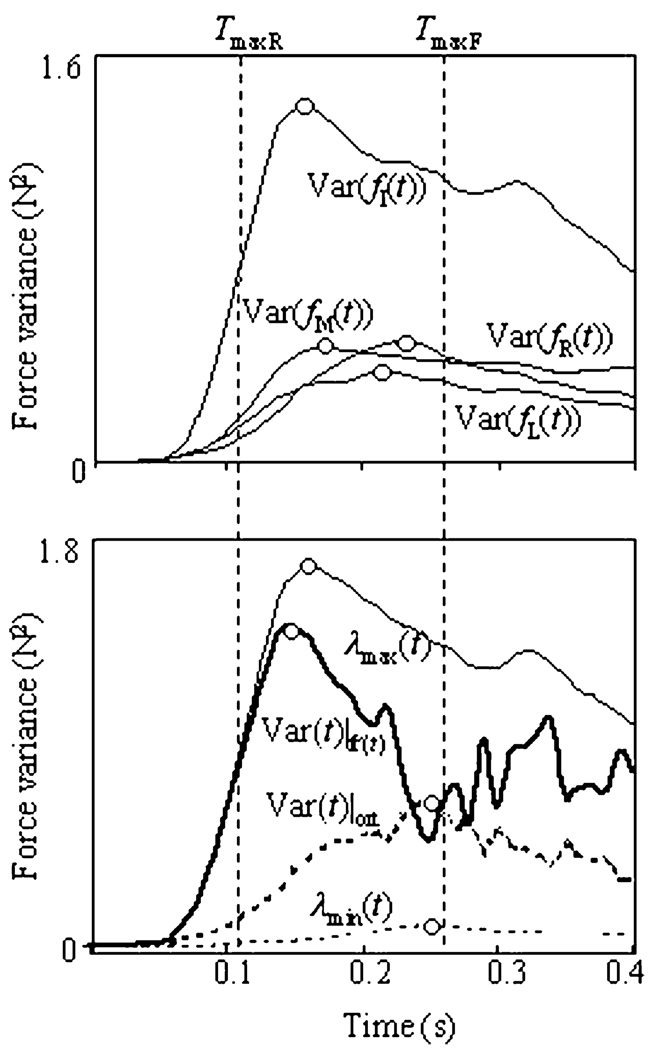
The upper panel of Fig. 2 shows examples of finger force variances (diagonal entries of the covariance matrix) as functions of time. The force variance time profiles have a characteristic non-monotonic shape with peaks (V-peaks) at about 0.2 s after the force initiation. Even though the V-peaks of different curves are differently expressed and slightly shifted with respect to each other, all of them occur between the maxima of force and force rate, as reflected by inequalities Eq. (4).

Fig. 2.

Upper panel: time profiles of finger force variances (Var(f_I(t)), Var(f_M(t)), Var(f_R(t)), and Var(f_L(t))) computed across 12 trials at the four-finger (IMRL) task to the target force of 30% of the MVC. Lower panel: Force variance time profiles in different directions of R⁴. λ_max(t) (thin solid line) and λ_min(t) (thin dotted line) correspond to directions of the first and forth principal axes of the covariance matrix Cov(f(t)), Var(f(t))|_f′(t) is in the direction of the vector of force rate f′(t) (thick solid line), variance Var(f(t))|_ort is averaged across directions orthogonal to f′(t) (thick dotted line). Vertical dotted lines show the times of force rate and force peaks (T_maxR and T_maxF ). Note transient peaks (empty circles) in all the variance profiles between T_maxR and T_maxF. The peak was mostly expressed in the direction of force rate f′(t)

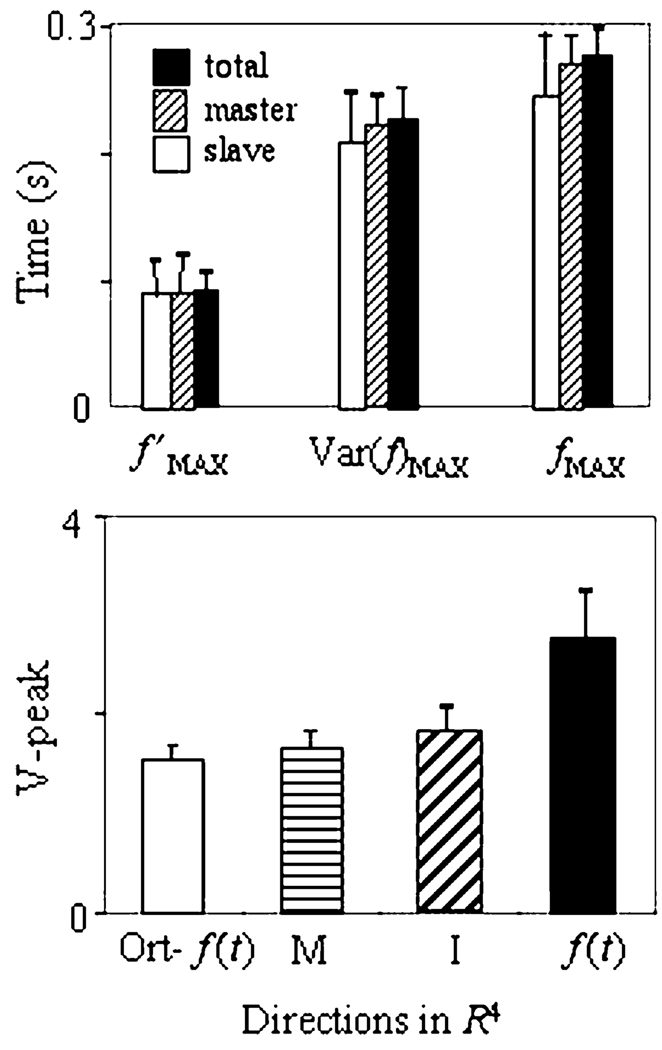
To test these inequalities statistically, values of T_maxR, T_maxV, and T_maxF were defined from the variance time histories of forces of individual fingers, for each subject, each of the seven tasks, and the three force target levels. The values were averaged across time profiles of force of master fingers, slave fingers, and of total force. Two-way, repeated-measures ANOVA with factors Maximum (3 levels, max-of-force-rate, max-of-force-variance, max-of-force) and Finger (3 levels, master, slave, and all) was applied to this data. There was a significant main effect of Maximum (F_(6,2) > 20, P < 0.005), no effect of Finger, and no interaction. Pair-wise contrasts showed a significant difference within the pairs T_maxR < T_maxV (P < 0.01) and T_maxV < T_maxF (P < 0.05) (see the mean plot on the upper panel of Fig. 3). Therefore, Fig. 2 shows a typical case with the maximum of variance between the maxima of force rate and of force.

Fig. 3.

Upper panel: Mean values of the times of the maxima of the force rate, force variance, and force are shown separately for force time profiles of the master fingers, slave fingers, and all the fingers (with standard error bars). Note that the peaks of variance (V-peak) occurred between the peaks of force rate and force. Lower panel: Relative magnitude of the V-peak (Eq. 3) and its 95% confidence interval (bars) for different directions in the finger force space R⁴ (I—index finger force, M—middle finger force, f′(t)—force rate, and ORT-f′(t)—directions orthogonal to f′(t)). V-peak is maximum in the direction of f′(t), and minimum in directions orthogonal to f′(t)

Force variance time profile: peaks of variance in different directions in R⁴

In this section, we are going to explore the dependences of the V-peak magnitude on the direction in the finger force space R⁴. The lower panel of Fig. 2 shows examples of time profiles of the force variance in the directions of the first and fourth principal vectors of the force covariance matrix Cov(f(t)) (eigenvalues λ_min(t) and λ_max(t)), in the direction of the force rate f′(t) (Var(f(t))|_f′(t), calculated according Eq. 4), and in directions orthogonal to it, per coordinate (Var(f(t))|_orth, calculated according to Eq. 5). All these variances show V-peaks of different magnitude (Fig. 3).

The relative magnitudes of the V-peaks in different directions in R⁴ (RM_V-peak, Eq. 3) were compared for the four-finger task (IMRL). For statistical comparisons, we have chosen directions of the index finger force vector (f_I=[1,0,0,0]), of the middle finger force vector (f_M=[0,1,0,0]), of the force rate vector f′(t), and of vectors orthogonal to the vector of force rate.

Two-way, repeated-measures ANOVA with the factors Direction (4 levels) and Force level (3 levels) showed a significant main effect on Direction (F_(6,3)=9, P < 0.05), but not of Force level. Pairwise contrasts have confirmed a significantly larger magnitude of the V-peak in the direction of the force rate as compared to directions orthogonal to the force rate (P < 0.001). This result is illustrated by Fig. 3, the lower panel, which shows the relative mean values of magnitude of V-peaks and their 95% confidence intervals. So, we can conclude that the relative magnitude of the V-peak depends on the direction in the finger force space R⁴.

Accuracy of model approximation of the experimental finger force variance

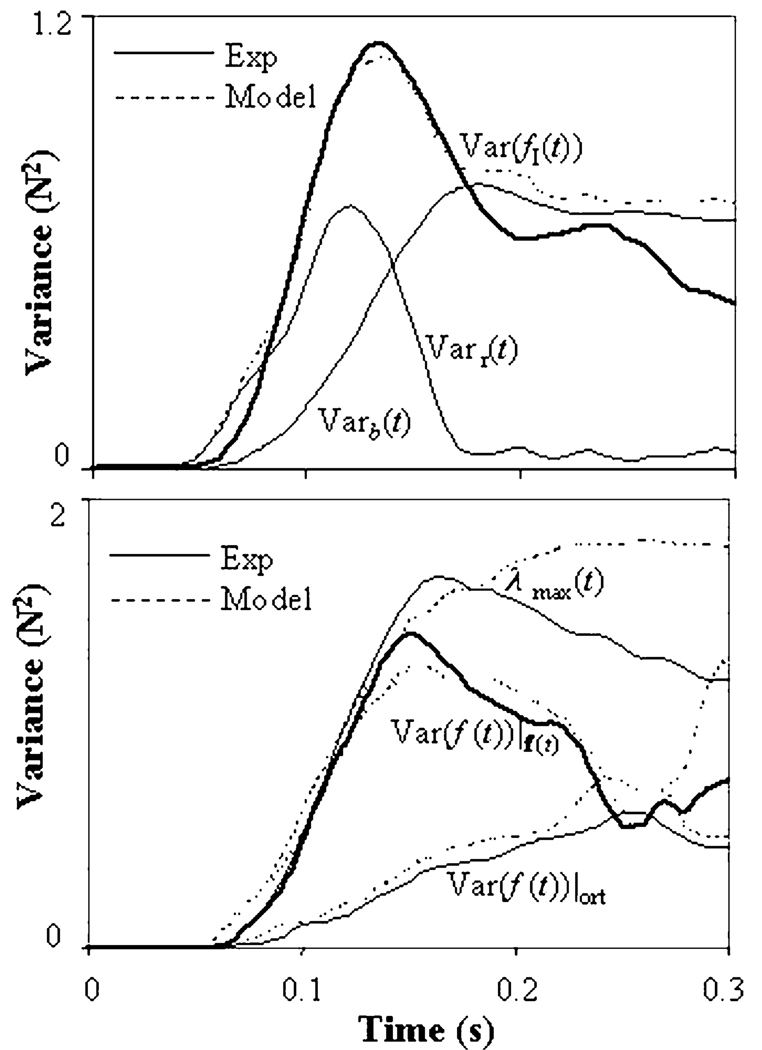
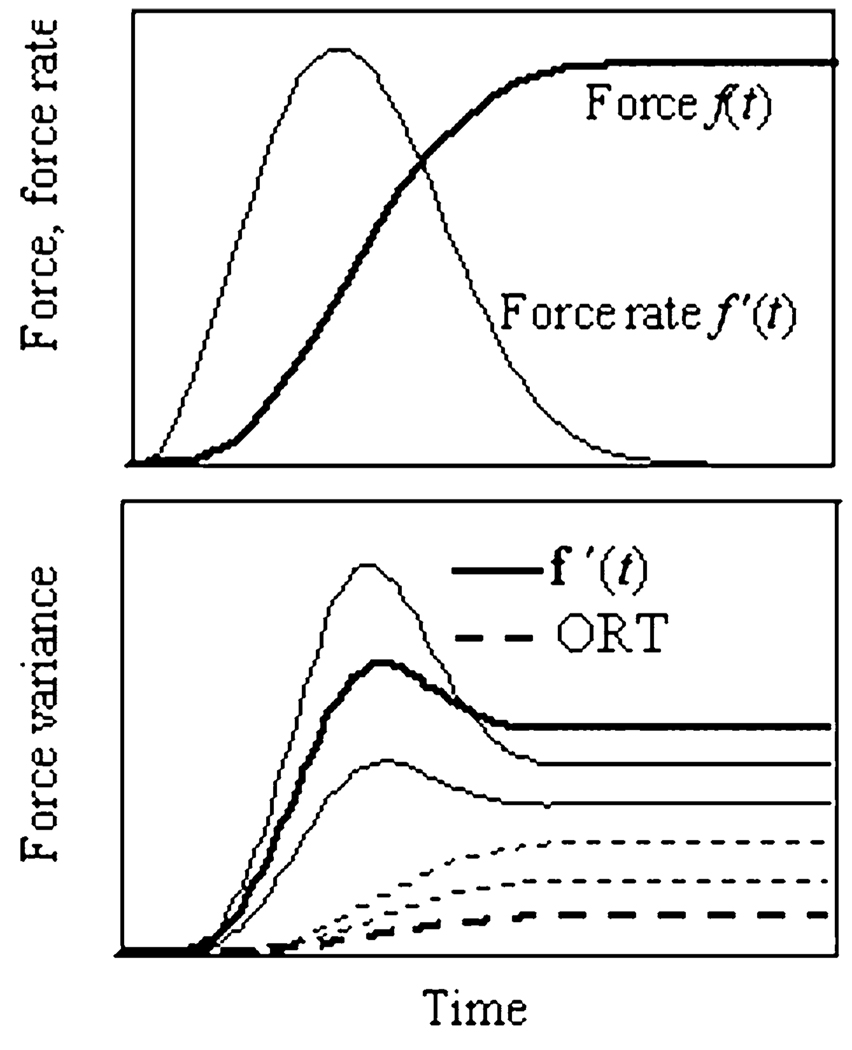
The experimental finger force covariance matrix Cov_exp(f(t)) was calculated according to Eq. (1). The model covariance matrix Cov(f(t)) consists of two matrix summands (Eq. 9). The experimental covariance differs from the model one on matrix of residuals ϑ(t). The upper panel of Fig. 4 shows entries Cov_exp(f₁₁(t)) (solid thick line) and Cov(f₁₁(t)) (dotted line) of these matrices as function of time. Cov_exp(f₁₁(t)) is the variances of the index finger force, while Cov(f₁₁(t)) is its model estimation, while the difference between them is the residual ϑ₁₁(t). The accuracy of the model covariance estimation was estimated by relative integral error (RIE) on the interval of time (t′, t″):

$$\text{RIE}=\frac{{\displaystyle \underset{t\prime }{\overset{t″}{\int }}{\displaystyle \sum _{mn}^4{\displaystyle \sum _{n=1}^4{\vartheta }_{nm}^2(t)dt}}}}{{\displaystyle \underset{t\prime }{\overset{t″}{\int }}{\displaystyle \sum _{mn}^4{\displaystyle \sum _{n=1}^4{\mathrm{\text{Cov}}}_{\text{exp}}^2(f_n(t),f_m(t))dt}}}}$$ (10)

Fig. 4.

Upper panel: Var_b(t) and Var_τ(t) are components of the index finger force variance, Var(f_I(t)). Lower panel: Examples of model fitting of force variance in different directions in the force space R⁴: In the direction of the main eigenvector of the covariance matrix, λ_max(t), in the direction of the force rate vector, Var(f(t))|_f′(t), and in directions orthogonal to it, Var(f (t))|_ort) per degree-of-freedom. Solid lines—experimental curves for a representative subject, dotted lines—model curves

The moments t′ and t″ have been chosen for the following reasons. Figure 4 shows that the discrepancy between the experimental and model variance is relatively large during the first 20 ms, possibly related to the relatively high noise of the low amplitude signal. Hence, we took t′=0.02 s. The model has been designed to describe the transient part of the force-time profile, but not steady-state force production. Therefore, for each subject, target force, and task, we took:t″ = T_{max F} = arg(max (f̄_tot(t))).

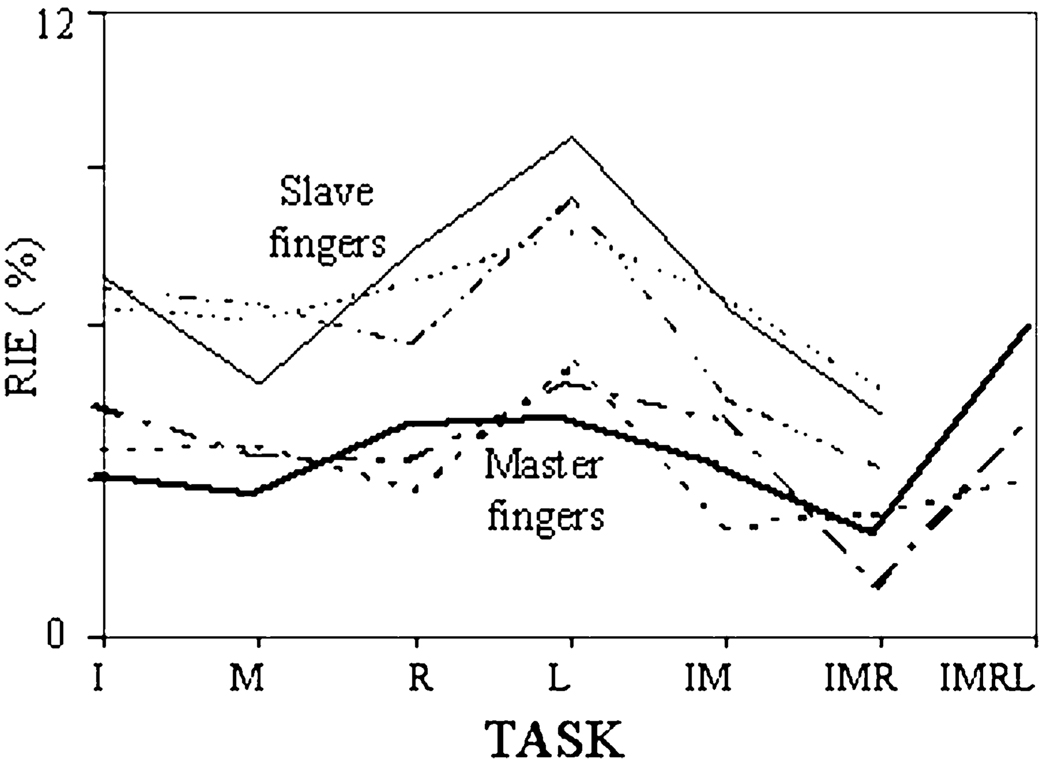
Within the (t′,t″) interval, RIE was calculated for all nine subjects, three target force levels, and seven tasks. The 95% confidence interval for RIE was (0.068, 0.08). So, on average, the model represents experimental covariance matrix with the error of about 8%. RIE for the master and slave fingers in different tasks, averaged across subjects and force values, is shown in Fig. 5. While the errors in the model prediction are somewhat higher for the slave fingers, they remain under 10% for both master and slave fingers.

Fig. 5.

Errors of the model representation of the experimental variance time profiles (RIE, in %; Eq. 10) for different master finger combinations (I—index finger, IM—index and middle fingers, etc.). Thin lines—slave fingers, thick lines—master fingers. The target force was 10% (dotted lines), 20% (dashed-dotted lines), and 30% (solid lines) of the MVC

Properties of the model variance time profile

Some of the features of the force covariance time profiles observed in the experiment (Fig. 2 and Fig. 4) can be reproduced by the model. In particular, the model time profiles of force variance and covariance show peaks between the moments of peak force and peak force rate, and the magnitude of this peak (V-peak) is higher in the direction of the force rate vector while it all but vanishes in the orthogonal directions (Fig. 4). An analytical proof of the presence of the V-peak and its dependence upon directions in R⁴ is given in Appendix C. As shown in the Appendix, Var_τ(t) drops to zero in directions orthogonal to the force rate vector, such that the force variance in these directions is defined only by Var_b(t). In our experiments, Var_b(t) was monotonic; hence, the V-peak was not (or barely) expressed (Fig. 1, the lower panel).

Computer simulation of finger force variance

According to the model, force variability can be represented as a linear combination of functions $\overline{f_n(t)f_m(t)}$ and $t^2\overline{f_n^{\prime }(t)f_m^{\prime }(t)}$ with coefficients {x_nm} and {y_nm} (Eq. 7). Assuming that a force time profile is given by a sigmoid function f(t)=b(1−exp(−(t/τ)^2.5)), the power of t defines the degree of asymmetry of the force rate time profile. To model results in an experiment with two master fingers, assume b̄ = 1 and τ̄ = 0.1. The model force and force rate time profiles are shown in the upper panel of Fig. 6. The lower panel of Fig. 6 shows examples of force variance time profiles corresponding to different values of {x_nm} and {y_nm}. The solid lines represent variance in the direction of force rate; the dashed lines show variance in the direction orthogonal to the force rate. The thick lines show the variances computed using {x_nm} and {y_nm} equal to averaged across subjects values found in the experiments; for fingers I and M, they are:

$$\begin{array}{c}\{x_{nm}\}=[\begin{array}{cc}0.029& 0.014\hfill \\ 0.014\hfill & 0.028\end{array}],\hfill \\ \{y_{nm}\}=[\begin{array}{cc}0.019& 0.017\\ 0.017\hfill & 0.021\hfill \end{array}]\hfill \end{array}$$

Fig. 6.

Upper panel: Force (thick line) and force rate (thin line) during a force pulse with a sigmoid time profile, f(t)=b(1− exp (−(t/τ)^2.5)). Lower panel: Typical force variance time profiles, parameterized by values of {x_nm} and {y_nm}. Solid lines: variance in the direction of the force rate; dashed lines: variance in direction orthogonal to the force rate. Y-axes are dimensionless

The model variance time profiles show features similar to those obtained in the experiments (compare with Fig. 2 and Fig. 4). In particular, there is a peak of the variance between the peaks of force and force rate, expressed mostly in the direction of the force rate and absent in directions orthogonal to the force rate.

Discussion

The experiments have shown reproducible patterns of force variance with a number of non-trivial features. In particular, a transient increase (V-peak) of the force variance between the times of peak force and peak force rate was seen across all subjects and all target forces. It is of interest that both explicitly involved (master) and non-involved (slave) fingers showed similar properties of the profiles of the force variance (e.g. Fig. 3). The V-peak resembles results from earlier studies of kinematic variability during fast single-joint movements, which showed a transient increase in the joint angle variability just after the time of the peak velocity (Darling and Cooke 1987; Van der Meulen et al. 1990). In the current study, however, we could also ask a question of whether this transient peak is expressed similarly in different directions of the multi-effector (four-finger) force space, R⁴. The quite dramatic differences among the different directions in R⁴ came as a surprise—in the direction of the force rate, the V-peak was strongly expressed while in orthogonal directions the peak was not seen. An explanation for these findings has been found in the generalized version of the G-model (Eq. 6; see also Appendices). The shape of the force variance time profile in an arbitrary direction in R⁴ was expressed analytically (Eq. 11), and the phenomenon of peak disappearance in directions orthogonal to the force rate has been proven formally (Appendix C). The average error of the model representation of experimental variance has been under 8%, which may be viewed as reasonably high accuracy.

In the following sections, we will try to put the model into a historical perspective. We will also consider implications of the current findings for the uncontrolled manifold hypothesis and analyze possible sources of the (relatively minor) discrepancies between the model and the experiment.

From earlier models of force variability to the current model

It is possible to track the historical roots of the current model back to studies of linear relationships between force and force variability (Newell 1991; Newell et al. 1984; Newell and Carlton 1988) mentioned in the Introduction. The earlier model of Gutman and his colleagues (the G-model, Gutman and Gottlieb 1992; Latash and Gutman 1993) suggested an approach that explicitly combined effects of errors in planning magnitude and duration of an action by a single effector. It assumed that much of the observed motor variability reflects processes of motor planning (e.g. Gordon et al. 1994; Messier and Kalaska 1999). The G-model has been able to show that a transient increase in the variability of the joint position during fast single-joint movements (Darling and Cooke 1987; Van der Meulen et al. 1990) could emerge from relationships between variabilities in setting time and amplitude scaling parameters (b and τ). Such a mechanism could induce non-motonic changes in positional variability by itself or in combination with a corrective action by a neural controller during the second phase of fast actions (cf. Van der Meulen et al. 1990).

Recently, the uncontrolled manifold (UCM) hypothesis has been formulated (Schöner 1995; reviewed in Latash et al. 2003) that suggests that coordination of a multi-effector system is associated with structuring variability of its elements in such a way that it has little effect on an important performance variable. As such, the UCM hypothesis opened an issue of a relationship between variability of a performance variable produced by a multi-element system and variability of the outputs of its elements. During multi-finger force production, the covariance matrix Cov(f) reflects this relationship. However, applications of the UCM hypothesis have been limited to analysis of patterns of variability within a set of elemental variables (e.g., joint rotations within a limb or forces produced by digits of a hand) either at selected times across repetitive trials at a motor task (reviewed in Latash et al. 2003) or across data points collected during a single realization of a task (Scholz et al. 2003). The UCM hypothesis has not addressed possible effects of timing errors across the elemental variables on the observed patterns of variability.

The current model unites the G-model and the general approach of the UCM hypothesis to offer analysis of variability of a multi-element system in both time and force domains as Cov(f(t)). From the G-model, it accepts the idea of two scaling parameters, b and τ, imprecisely set prior to each trial for each element, while from the UCM hypothesis, it borrows the idea of the importance of covariation among the outputs of the elements.

Implications for the UCM hypothesis

Results of the current study shed a new light on some of the findings in earlier studies of multi-finger force production within the framework of the UCM hypothesis. In particular, the UCM hypothesis was used to analyze covariation of force modes (hypothetical independent elemental variables that lead to force generation by individual digits, Zatsiorsky et al. 1998; Scholz et al. 2002; Danion et al. 2003) with respect to two hypotheses:

1. that the covariation stabilized the total force produced by the fingers, a force-stabilization hypothesis; and

2. that the covariation stabilized the total pronation/supination moment produced by the fingers, a moment-stabilization hypothesis.

In the first study with the production of a sine-like rhythmic total force profile at 2 Hz, force modes have been shown to co-vary in a way that preferentially stabilized the total moment, while the total force did not show stabilization over most of the cycle and could even be destabilized over a substantial portion of the cycle (Latash et al. 2001). In a study of both cyclic and discrete (ramp) total force production tasks at different rates (Latash et al. 2002b), the force-control hypothesis was confirmed, but only at relatively high forces and relatively slow rates of force production. A component of the total variance in the force mode space that did not affect the average value of the total force (compensated variance, V_COMP) showed time profiles similar to the time profiles of the total force. The other component, representing uncompensated variance (V_UN) showed time profiles that looked similar to those of the force derivative. It has been concluded that the central nervous system has difficulties compensating for possible timing errors across the elements while it was efficient in compensating for errors in the magnitude of the elements’ outputs.

Note that both studies analyzed variance across trials for a certain phase of the task and then interpolated the results to obtain time profiles of the variance components. As such, they failed to consider possible contribution of timing errors to the observed variance profiles. One of the important results of the current study is the demonstration of a non-monotonic time profile of a component of the finger force variance in the direction of the total force rate (in the R⁴ space). This component is analogous to V_UN with respect to the force-control hypothesis since apparently its changes lead to changes in the total force. The component of the total variance orthogonal to the derivative of the total force in the R⁴ space was monotonic. That component apparently did not affect the total force and, as such, can be seen as equivalent to V_COMP. It is quite possible, therefore, that the results of the previous study (Latash et al. 2002b) reflected not peculiarities of multi-finger control but properties of the variance time profile defined to a large degree by the presence of variability in the time scaling factor τ.

In more recent studies with the slow multi-finger ramp force production, stabilization of the total force has been shown over most of the ramp with the exception of a brief initial period (Shim et al. 2003; Shinohara et al. 2004). Note, however, that there is a discontinuity of the force profile at the beginning of the ramp force production, which is likely to be associated with relatively high force rates. As shown in the current study, the apparent failure of the subjects to stabilize the total force could be related to this transient increase in the force rate.

Sources of discrepancy between experimental and model variance

As seen from Fig. 2 and Fig.4, there are errors in the model representation of experimental force variance time profiles. Despite the fact that the errors are relatively small (under 8%), we do not attribute it to “experimental noise” (cf. Jones et al. 2002; Van Beers et al. 2004). The discrepancy between the model and experimental data is reflected by the term ϑ(t) in Eq. (8) and may include the following sources:

1. The model described by Eqs (8) and (9) is based on an assumption of small deviations of scaling parameters {b_i} and {τ_i} from their mean values; in fact, the deviations may be not small, leading to components of variability of higher orders

2. Correction of scaling parameters {b_i} and {τ_i} in-between trials does not contradict the model, but corrections made within a trial based on proprioceptive or visual feedback do. During the production of very quick force pulses that lasted under 200 ms, there are reasons to expect no corrections based on visual information (Khan et al. 2003). On the other hand, it has been shown that patterns of variability change under tactile information without a change in average performance (Rabin and Gordon 2004); and

3. Only two scaling parameters, b and τ, for each finger are considered in the model, while there are probably more parameters that define the force variability, e.g., those related to variations of the symmetry of the force time profile (cf. Jaric et al. 1998).

Overall, however, the accuracy of the model may be viewed as adequate as compared to other models of finger force production (Zatsiorsky et al. 1998; Danion et al. 2003). The model can be viewed as a tool to complement the UCM-hypothesis and enrich its applications to fast actions by multi-effector systems.

Appendices

Appendix A. Model of parametric force control

The equation of parametrical multi-finger force control is f_kn(t)=g(b_kn,u_n, t,τ_kn)=b_knu_n(t/τ_kn) where f_kn(t) is the actual force time profile of the finger n∈{I,M,R,L} in the kth trial, u_n(t) is a template, and b_kn and τ_kn are scaling parameters. For small changes of the scaling parameters

$$\mathrm{\Delta }{f}_n(t)=\frac{\partial g_n(t)}{\partial b_n}\mathrm{\Delta }{b}_n+\frac{\partial g_n(t)}{\partial {\tau }_n}\mathrm{\Delta }{\tau }_n$$ (11)

where Δf_n(t), Δb_n, and Δτ_n are increments of the force and its scaling parameters, $\frac{\partial g_n(t)}{\partial b_n}$ and $\frac{\partial g_n(t)}{\partial {\tau }_n}$ are partial derivatives of the force with respect to the parameters. The two summands of the force increment are:

$$\begin{array}{c}\frac{\partial g_n(t)}{\partial b_n}\mathrm{\Delta }{b}_n=b_n{u}_n(t/{\tau }_n)\frac{\mathrm{\Delta }{b}_n}{b_n}=f_n(t)\frac{\mathrm{\Delta }{b}_n}{b_n}\hfill \\ \frac{\partial g_n(t)}{\partial {\tau }_n}\mathrm{\Delta }{\tau }_n=-\frac{t}{{\tau }_k}{b}_n{u}_n^{\prime }(t/{\tau }_n)\frac{\mathrm{\Delta }{\tau }_n}{{\tau }_n}=-t{f}_n^{\prime }(t)\frac{\mathrm{\Delta }{\tau }_n}{{\tau }_n}\hfill \end{array}$$

(because ${f\prime }_n(t)=\frac{1}{{\tau }_n}{b}_n{u\prime }_n(t/{\tau }_n)$). So, Eq. (11) can be written:

$$\mathrm{\Delta }{f}_n(t)=f_n(t)\frac{\mathrm{\Delta }{b}_n}{b_n}-t{f}_n^{\prime }(t)\frac{\mathrm{\Delta }{\tau }_n}{{\tau }_n}$$ (12)

(see also Gutman and Gottlieb 1992).

Appendix B. Two components of the model force variance

Assume that changes in the finger force time profile are defined by the variability of scaling parameters b_kn and τ_kn, which are random variables with means b̄_n and τ̄_n and variances Var(b_n) and Var(τ_n) (or standard deviations SD(b_n) and SD(τ_n)). Assume also that SD (b_n) < < b̄_n and SD(τ_n)) < < τ̄_n; covariances Cov(b_n, b_m) ≠ 0, Cov(τ_n, τ_m) ≠ 0, Cov(b_n,b_m)=0; and templates u_n(t) are deterministic functions. The covariance between forces of fingers n and m at a time t can be estimated as:

$$\text{Cov}(f_n(t),f_m(t))=\overline{\mathrm{\Delta }{f}_n(t)\mathrm{\Delta }{f}_m(t)}$$ (13)

Here and further, $\overline{(*)}$ is the sign of mean. Substituting the expression of $\overline{\mathrm{\Delta }{f}_n(t)\mathrm{\Delta }{f}_m(t)}$ via increments of the scaling parameters (Eq. 12) yields:

$$\begin{array}{c}\text{Cov}(f_n(t),f_m(t))\hfill \\ \hfill =\overline{f_n(t)f_m(t)}\frac{\text{SD}(b_n)}{{\overline{b}}_n}\frac{\text{SD}(b_m)}{{\overline{b}}_m}r(b_n,b_m)\\ \hfill +t^2\overline{f_n^{\prime }(t)f_m^{\prime }(t)}\frac{\text{SD}({\tau }_n)}{{\overline{\tau }}_n}\frac{\text{SD}({\tau }_m)}{{\overline{\tau }}_m}r({\tau }_n,{\tau }_m)\end{array}$$ (14)

where r is coefficient of correlation. According to Eq. (14), force covariance is the weighted sum of two functions, $\overline{f_n(t)f_m(t)}$ and $t^2\overline{f_n^{\prime }(t)f_m^{\prime }(t)}$, with weights $x_{nm}=\frac{\text{SD}(b_n)}{{\overline{b}}_n}\frac{\text{SD}(b_m)}{{\overline{b}}_m}r(b_n,b_m)$ and $y_{nm}=\frac{\text{SD}({\tau }_n)}{{\overline{\tau }}_n}\frac{\text{SD}({\tau }_m)}{{\overline{\tau }}_m}r({\tau }_n,{\tau }_m)$. Using CV for coefficient of variation, one gets:

$$\begin{array}{c}{x}_{nm}=\text{CV}(b_n)\text{CV}(b_m)r(b_n,b_m),\hfill \\ y_{nm}=\text{CV}({\tau }_n)\text{CV}({\tau }_m)r({\tau }_n,{\tau }_m).\hfill \end{array}$$ (15)

If force variability is small, approximately $\overline{f_n(t)f_m(t)}=\overline{f_n(t)}\overline{f_m(t)}$; assuming that force rate variability is also small, the scalar expressions for all n and m can be written as a matrix equation:

$$\mathbf{\text{Cov}}(\mathbf{f}(t))=\mathbf{D}(\overline{\mathbf{f}(t)})\mathbf{XD}(\overline{\mathbf{f}(t)})+t^2\mathbf{D}(\overline{\mathbf{f}\prime (t)})\mathbf{YD}(\overline{\mathbf{f}\prime (t)})$$ (16)

where $\mathbf{D}(\overline{\mathbf{f}(t)})$ and $\mathbf{D}(\overline{\mathbf{f}\prime (t)})$ are diagonal matrices, in which diagonal entries are mean force $\{\overline{f_n(t)}\}$ and force rate $\{\overline{f_n^{\prime }(t)}\}$ time profiles, and {x_mn} and {y_mn} from Eq. (15) are entries of the matrices X and Y. Thus, the covariance matrix consists of two terms, related to setting the magnitude and duration scaling parameters, respectively.

Appendix C. Dependence of force variance upon time and direction in force space

Values of CV(τ) estimated from experimental data differ for different fingers. However, for simplicity, consider a common timing scaling parameter for all fingers with CV(τ_n)=ξ_τ for all n, and r(τ_n, τ_m)=1 for all n and m. In this case, Y_ss=ξ_τE, where E is a matrix with unit entries.

The expression for force variance in the direction of a vector w via Rayleigh fraction with a covariance matrix Cov(f(t)) is:

$$\begin{array}{cc}{\mathbf{w}}^{\mathrm{T}}(t)\mathbf{Cov}(\mathbf{f}(t))\mathbf{w}(t)=\hfill & {\mathbf{w}}^{\mathrm{T}}(t)\mathbf{D}(\overline{\mathbf{f}(t)}){\mathbf{X}}_{ss}\mathbf{D}(\overline{\mathbf{f}(t)})\mathbf{w}(t)\hfill \\ & +t^2{\mathbf{w}}^{\mathrm{T}}(t)\mathbf{D}(\overline{\mathbf{f}\prime (t)}){\mathbf{Y}}_{ss}\mathbf{D}(\overline{\mathbf{f}\prime (t)})\mathbf{w}(t)\hfill \end{array}$$ (17)

Here, we assume w a vector with unit norm. Let v be orthogonal to the direction of the force rate vector $\overline{\mathbf{f}\prime (t)}$. The second term of the right side of Eq. (17), Var_τ(t) is:

$${\text{Var}}_{\tau }={\xi }_{\tau }{t}^2{\mathbf{v}}^{\mathrm{T}}(t)\mathbf{D}(\overline{\mathbf{f}\prime (t)})\mathbf{ED}(\overline{\mathbf{f}\prime (t)})\mathbf{v}(t)$$

The factor $\mathbf{D}(\overline{\mathbf{f}\prime (t)})\mathbf{v}$ is a vector:

$$\begin{array}{c}\mathbf{D}(\overline{\mathbf{f}\prime (t)})\mathbf{v}=(\overline{f_{\mathrm{I}}^{\prime }(t)}{\upsilon }_{\mathrm{I}}(t),\overline{f_{\mathrm{M}}^{\prime }(t)}{\upsilon }_{\mathrm{M}}(t),\overline{f_{\mathrm{R}}^{\prime }(t)}{\upsilon }_{\mathrm{R}}(t),\hfill \\ \overline{f_{\mathrm{L}}^{\prime }(t)}{\upsilon }_{\mathrm{L}}(t){)}^{\mathrm{T}}.\hfill \end{array}$$

$\mathbf{D}(\overline{\mathbf{f}\prime (t)})\mathbf{v}$ multiplied by E is a zero vector, because each of its components

$${\xi }_{\tau }(\overline{f_{\mathrm{I}}^{\prime }(t)}{\upsilon }_{\mathrm{I}}(t)+\overline{f_{\mathrm{M}}^{\prime }(t)}{\upsilon }_{\mathrm{M}}(t)+\overline{f_{\mathrm{R}}^{\prime }(t)}{\upsilon }_{\mathrm{R}}(t)+\overline{f_{\mathrm{L}}^{\prime }(t)}{\upsilon }_{\mathrm{L}}(t))=0$$

is a scalar product of orthogonal vectors $\overline{\mathbf{f}\prime (t)}$ and v(t). Therefore, Var_τ(t) is zero. This means, that variance time profile in directions orthogonal to the direction of the force rate vector is defined only by the other term of Eq. (17). In our case, this term is monotonic, and hence the force variance time profile is not expected to show transient peaks (such as the V-peak).