Application of the T-matrix method to determine the structure of spheroidal cell nuclei with angle-resolved light scattering

Abstract

We demonstrate an inverse light-scattering analysis procedure based on using the T-matrix method as a light-scattering model. We measure light scattered by in vitro cell monolayers using angle-resolved low-coherence interferometry (a/LCI) and compare the data to predictions of the T-matrix theory. The comparison yields measurements of the equal volume diameter and aspect ratio of the spheroid cell nuclei with accuracy comparable to quantitative image analysis of fixed and stained samples. These improvements represent a significant upgrade for the a/LCI technique, expanding both the range of tissue in which it is applicable and potentially increasing its value as a diagnostic tool.

Angle-resolved low-coherence interferometry (a/LCI) has emerged as a promising means of distinguishing precancerous tissue from healthy tissue by measuring differences in average cell nuclei size [1,2]. The technique uses low-coherence interferometry to obtain a depth-resolved measurement of scattered light intensity over a range of angles near the backscatter angle. These measurements are then inverted to obtain the average nuclear size for a localized group of cells by comparison to a light-scattering model such as Mie theory, a model of scattering from spheres [3].

Mie theory can provide accurate measurements of size from substantially aspherical scatterers, and under some circumstances recover the spheroidal aspect ratio by combining multiple measurements using different orientations and polarizations [4,5]. While this method extends the applicability of Mie theory to a wide variety of common nuclear geometries, it requires considerable a priori knowledge about scatterer orientation and multiple measurements to yield the spheroidal aspect ratio. Additionally, with this approach, some uncertainty remains regarding which axis of a spheroid is actually measured. In this Letter, we present the results of a new inversion method based on the simulation of light-scattering using the T-matrix method [6] that allows for simultaneous measurement of both nuclear equal volume diameter (EVD) (defined in terms of the diameter of an equal volume sphere) as well as spheroidal aspect ratio.

Similar to Mie theory, the T-matrix method is a solution to Maxwell’s equations for scatterers of a size of the order of the illuminating wavelength. However, unlike Mie theory it can compute scattering from a variety of geometries including spheroids, Chebyshev particles, cylinders, etc. The method uses an infinite expansion of vector spherical wave functions that are evaluated numerically and then truncated when converged to a sufficient accuracy. The resulting matrix is a complete solution to Maxwell’s equations over the entire scatterer geometry and provides the scattered field over the entire solid angle for both polarizations. In principle, the method is applicable to any particle geometry, but in practice at least one axis of symmetry is usually required for efficient computation. Furthermore, particles much larger than the wavelength, or that are highly aspherical, may accumulate excessive rounding error that prevents convergence. An overview of the T-matrix computation is provided by Mishchenko et al. [7].

Biological applications of the T-matrix method were suggested by Nilsson, who used the method to model scattering from red blood cells [8]. The applicability of the T-matrix method to light-scattering from cell nuclei was explored by Keener et al., who showed that the approach provides an accurate model for scatterers with biologically relevant structures [9], and by Mourant et al., who explored its applications to small scatterers [10]. The T-matrix method was also considered by Duncan and Thomas, who showed that it could in principle be used for inverting depolarization rates from spheroidal scatterers [11]. Unfortunately, the T-matrix incurs a substantially higher computational cost versus Mie theory, which has prevented previous efforts from extending the technique to the actual inverse light-scattering problem in biological applications. However, the problem of constructing a scattering database is intrinsically parallel and allows for easy adaptation to distributed computing across many PCs. Furthermore, the method has the added advantage of yielding all possible orientations at negligible additional cost. To this end, we have implemented a massively parallel system for computing very large light-scattering databases that allows exploration of the T-matrix method for inverse analysis.

A T-matrix database was generated using public domain extended (128 bit) precision Fortran codes provided by Mishchenko et al. [6,7] with modifications to accommodate parallel computation. The database simulated scatterers for a 830 nm illumination from 7.5 to 12.5 μm diameter in increments of 40 nm, spheroidal aspect ratio from 0.56 to 1 (prolate to spherical) in increments of 0.01, background index of refraction 1.35 and 1.36, and scatterer index of refraction 1.42 and 1.43, all with a 10% standard deviation normal size distribution. Profiles consisted of 48 points beginning with the backscatter angle and moving forward in steps of 0.0103 rad. The parameters were chosen in accordance with the range of values known to be typical of MCF7 cell cultures [as determined by quantitative image analysis (QIA)] and for the a/LCI system used for these experiments.

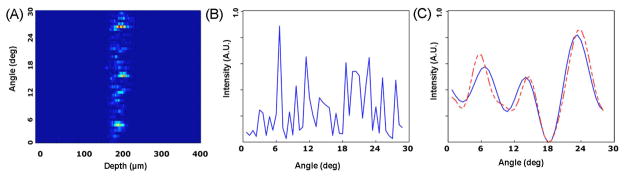
The T-matrix database was substituted into the Mie-theory-based analysis procedure presented by Pyhtila et al. [3]. Briefly, for each angle-resolved measurement and each simulated particle, a second-order polynomial was subtracted to detrend the data. This step is essential because cells contain many small scatterers that produce slowly varying oscillations that obscure the higher frequency, oscillatory component of scattering due to the nucleus. Detrending both the simulated and experimental data therefore isolates scattering from the nucleus. Next, the measured data were low pass filtered to remove high-frequency oscillations from long-range correlations (>12 μm) due to tissue scale structures. Finally the processed measurement was compared to the de-trended database and the best fit selected using a least-squares fitting (χ²) model that minimized the difference between the measurement and model (see Fig. 1).

Fig. 1.

(Color online) (A) a/LCI measurement showing depth-resolved angular scattering for a MCF7 cell monolayer with angles given relative to the backscatter angle. (B) Unprocessed angular scattering profile extracted by summing over depth in (A). (C) Processed scattering profile compared to best fit T-matrix model after detrending and low-pass filtering to isolate nuclear scattering.

The inversion process becomes less well conditioned as additional geometric parameters are included in the search space, leading to an increase in the likelihood that two different particles could yield similar scattering distributions. In either event, we require that the best fit score be at least 10% better than the score from all fits differing in EVD by at least one half-wavelength (±415 nm) or aspect ratio by ±0.03.

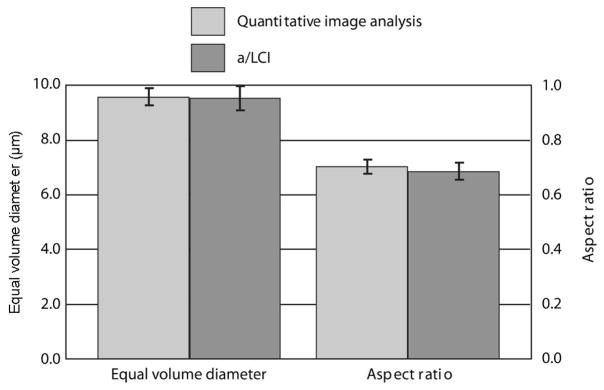
To test the T-matrix method, seven samples of MCF7 breast cancer cells (Fig. 2) were prepared on glass coverslips and 43 measurements recorded with the a/LCI system, six of which were subsequently rejected due to the lack of a database match according to the fitting criteria described above. These measurements likely yielded poor fits due to a weak signal arising from sparse cell culture in the probed region. After measurement, the samples were fixed and stained with DAPI in preparation for QIA. A total of 70 cells were randomly selected, and cells’ nuclear EVD and spheroidal aspect ratio were measured by QIA. The a/LCI measurements were analyzed with the T-matrix method compared to the results from QIA (Fig. 3). Both methods measured a nearly identical mean nuclear equal volume diameter, with QIA yielding an EVD of 9.52 μm with a 95% standard error of 0.44 μm, and a/LCI with T-matrix determining an EVD of 9.51 μm±0.34 μm. The results for the aspect ratio are also nearly identical, with a spheroidal aspect ratio of 0.70±0.026 determined by QIA and 0.69±0.032 determined by a/LCI. As a further comparison, we executed traditional a/LCI analysis of these experimental data using a Mie theory database that obtained a structural measurement of 9.47±0.34 μm in good agreement with the EVD of the T-matrix and QIA results. However, the Mie theory data cannot make a determination of the spheroidal aspect ratio.

Fig. 2.

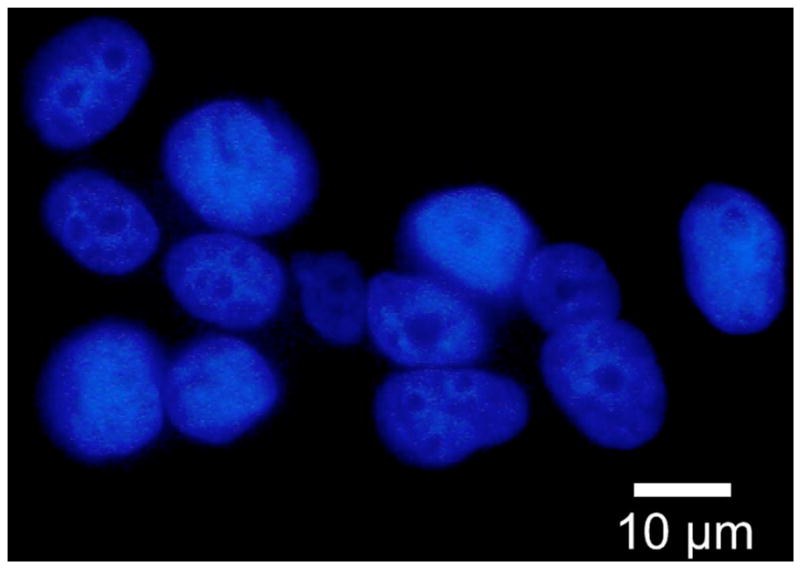
(Color online) Fluorescence microscopy image of MCF7 nuclei using DAPI. Nuclei are approximately spheroidal and randomly aligned.

Fig. 3.

Measurements of equal volume diameter and spheriodial aspect ratio by QIA using DAPI stain, and a/LCI using live cells. Error bars are standard error at 95% confidence.

The T-matrix method offers several improvements over Mie theory for a/LCI. First, the improved model resolves the ambiguity between the short and long axes observed for highly aspherical particles [4]. This advantage potentially allows analysis of new tissue types where the a/LCI probe beam does not align with the axis of symmetry for the cell nuclei. Second, the ability to model aspherical scatterers improves performance in situations where Mie theory may be a poor model, such as significantly aspherical, nonrandomly oriented particles. Finally, measuring scatterer shape through the aspect ratio provides a diagnostically and scientifically relevant parameter about tissue health at no additional cost in data acquisition time or instrument complexity. Thus both the quantity and quality of nuclear information provided by a/LCI can be improved by the T-matrix method.

The additional cell shape information provided by T-matrix modeling is a substantial improvement to the a/LCI technique. The value of nuclear shape as a diagnostic indicator of the cell status, particularly with regard to dysplastic development, has been recognized for over a century. This parameter is widely used in histological analysis as a marker for the genetic and epigenetic changes leading to cancer [12]. The ability to measure changes of nuclear shape in thick tissues with a/LCI has great potential to enhance clinical sensitivity and specificity of the approach. Furthermore, changes in nuclear shape have also been used to explore nuclear mechanics in response to external stress [5].

The additional power of the T-matrix method comes at the price of a substantial increase in complexity. While a single PC could easily compute an entire database of scatterers using Mie theory, computation of T-matrix databases with their larger parameter spaces and more complicated modeling can require tens of thousands of CPU hours. Furthermore, for significantly aspherical spheroid scatterers, even 128 bit extended precision variables may be insufficient to avoid excessive round off-error. In these cases, great care is needed to pick model parameters that minimize rounding error. The design and processing of a complete T-matrix database is a nontrivial task that requires further investigation. We intend to publish a detailed overview of the computation challenges, potential optimizations, and source code in a future work to enable further use of the method in a variety of remote sensing applications.

In conclusion, we have shown that the T-matrix method provides an effective model for inverse light-scattering analysis based on a/LCI measurements. This approach recovers both the average scatterer size and average scatterer spheroidal aspect ratio of cell nuclei within living MCF7 cell cultures with an accuracy comparable to histological analysis.