When to Promote, and When to Avoid, a Population Perspective

Abstract

Demography’s population perspective, and the sampling methods that help produce it, are powerful but underutilized research tools. The first half of this article makes the case for more vigorous promotion of a population perspective throughout the sciences. It briefly reviews the basic elements of population sampling and then provides examples from both developed and developing countries of how population sampling can enrich random-assignment policy experiments, multisite studies, and qualitative research. At the same time, an ill-considered application of a population perspective to the problem of causal inference can hinder social and behavioral science. The second half of the article describes the “slippery slope” by which some demographic studies slide from providing a highly useful description about the population to using regressions to estimate causal models for that population. It then suggests that causal modeling is sometimes well served by a highly selective look at small subsets of a population with interesting variability in independent variables of interest. A robust understanding of causal effects, however, rests on convergence between selective and population-wide perspectives.

My own perspective on population research was forged during the 25 years I spent at the University of Michigan’s Survey Research Center (SRC). Demography was for me less an academic exercise than a motion picture of turbulent family changes played out year after year. In the longitudinal study that I worked on for nearly a quarter century—the Panel Study of Income Dynamics (PSID)—we found that more than one in five sample families changed composition in some way every year! At first we regarded these changes as annoying—how could we track the economic fortunes of families if they changed so much? But we soon came to realize that demographic changes themselves were key to understanding family income dynamics. This forced me to become more of a demographer than I might have wished.

James Morgan was my primary mentor in my early years, but much of my learning occurred at the morning communal coffee table, which was frequented by the likes of sampling statistician Leslie Kish and economist Tom Juster, and visited occasionally by other SRC legends such as Angus Campbell and George Katona. Disciplinary distinctions were inconsequential at SRC; there was too much to learn.

When I moved to Northwestern University, I became even more involved with inter-disciplinary research collaborations and networks made up of demographers, sociologists, economists, and developmental psychologists.1 Some employed quantitative methods using survey- and census-based data, while others were ardent advocates of qualitative, experimental, or observational approaches. Some insisted on population representation; others had not given the issue much thought. These experiences prompt me to use the opportunity of this presidential address to explore the role of a population perspective in research.

My main message is that demography’s population perspective and tools are under-utilized in social, behavioral, and biomedical research. I will review the elements of population sampling and then provide examples of how population methods can enrich random-assignment experiments, multisite clinical and observational research, and qualitative studies. Many of my examples come from the United States, but several of the most innovative are drawn from developing countries. My fundamental argument is that demographers should be much more aggressive in promoting their population perspective throughout the sciences.

At the same time, however, I argue that an ill-considered application of a population perspective to the problem of causal inference can hinder social and behavioral science. Here I describe the “slippery slope” that causes some demographic studies to devolve from highly useful population description to problematic regression-based attempts to estimate causal models. I then suggest that causal modeling is sometimes well served by a highly selective look at small subsets of a population with interesting variability in independent variables of interest. In the end, though, a population-wide perspective on causal effects is a worthy and perhaps even sometimes attainable goal.

PROMOTING A POPULATION PERSPECTIVE

By population perspective, I mean descriptions (means, distributions, rates) and relationships (e.g., correlations) found in the population at large. Population perspective is most easily attained using data from censuses of an entire population, but also, through modern sampling methods, by looking at well-chosen samples drawn from the general population.

Population research has long profited from complete population enumerations provided by censuses and vital statistics. The remarkable power of a small (e.g., 1,000–2,000) but randomly chosen population sample to describe population characteristics was demonstrated by Laplace in France in the eighteenth century, but probability sampling did not become common practice until after World War II (Hansen 1987).

Modern population sampling employs random selection, but also stratification, clustering, and, in some cases, differential selection probabilities to maximize the statistical power, relative to the data collection costs, of the sample for inferences of interest (Cochran 1977). That demographers should promote their much broader application—in experimental, clinical, and even qualitative studies—is the key theme that I want to develop in the first half of this article.

Population Perspectives in Experimental Research

Random-assignment experiments have long been considered the gold standard in medical and laboratory-based psychological research. But subjects for these experiments are often recruited for reasons of convenience (e.g., from patient pools or undergraduate psychology classes) rather than for population representation. A striking example of the dangers of these practices in psychological research comes from Nisbett and Cohen’s (1996) study of the psychology of violence in the South and other U.S. regions. Their experiments show that Southerners’ cognitive, psychological, physiological, and behavioral reactions to insults are very different from the reactions of Northerners.

Beginning in the 1960s, but with increasing momentum in the 1980s and 1990s, the United States mounted a number of ambitious experiments testing policy impacts of income transfers, training and welfare-to-work programs, and a residential mobility program. In nearly every case, the experiments were limited to a single site or to no more than a handful of sites, raising the question of how program impacts drawn from these studies correspond to impacts that might result if the program were scaled up and offered more generally.2

In psychology, this is known as the problem of external validity or generalizability (Shadish, Cook, and Campbell 2002). Why not strive for an experimental or evaluation design that provides impact estimates for the entire population?

The issue of population representation was a prominent part of the discussions held by the Advisory Committee on Head Start Research and Evaluation, which was constituted in response to a 1998 Congressional mandate to the U.S. Department of Health and Human Services to conduct a national study of the impacts of its Head Start programs.3

The committee first established the feasibility of randomly assigning the Head Start program “treatment.” Demand for Head Start typically exceeded the supply of available slots, making it ethical and feasible to use lotteries to decide which children were selected for the final open slots. But which centers to enroll in the study?

I had the pleasure of serving on the committee and came to realize that the national Head Start program provided a nearly perfect setting for a population sampling approach in a policy experiment. With 35 years of operation, Head Start was a fully “mature” program overseen by the Head Start Bureau in the U.S. Department of Health and Human Services. The Bureau had access to a complete list of Head Start centers, the ideal starting point for drawing a probability sample. Moreover, sufficient information was available on each center to permit stratification, clustering, and the option of differential sampling fractions.

A lively debate ensued between those of us advocating a national probability sampling approach and those in favor of selecting a geographically diverse but not formally representative set of centers whose directors volunteered for the random-assignment impact assessment. Advocates of the volunteer approach worried about bias from noncooperation and felt that the goals of center diversity could be met by judicious recruitment of diverse centers. Their best guess was that only about 20% of centers selected in a national probability sample would agree to cooperate—a costly inefficiency.

The Committee’s report (Advisory Committee on Head Start Research and Evaluation 1999) endorsed the sampling approach, and a national-sample experiment was launched shortly thereafter. As it turned out, nearly 85%, not 20%, of centers falling into the sample agreed to cooperate (U.S. Department of Health and Human Services 2005). Thanks to the sampling approach, coupled with the high response rate, the evaluation was able to provide Congress and the public with representative national estimates of Head Start’s effectiveness. Moreover, the national probability sample of centers could also be used to provide representative impact estimates for important subgroups of Head Start children. For the most part, the experimental evaluation showed noteworthy positive impacts on literacy, math skills, and classroom behavior for children attending Head Start relative to their control-group counterparts.4

An alternative approach to population representation for policy experiments is to embed them into representative household samples. A good example is the Indonesian Work and Iron Status Evaluation (WISE), which randomly assigned a weekly iron supplementation treatment in a household sample drawn to be representative of the population of Central Java.5 Both treatment and control households will be repeatedly reinterviewed in order to assess program impacts on health, cognition, and the economic and social prosperity of the individual, family, and community.

Population Perspectives in Multisite Studies

A common method for conducting biomedical, developmental, and behavioral research on diverse populations is to form consortia of participating researchers or institutions. In clinical studies, this often takes the form of a network of biomedical researchers in medical centers who recruit volunteer research subjects from their patient pools. In the case of the National Institute of Child Health and Human Development (NICHD) Study of Early Child Care and Youth Development, the network consisted of developmental psychologists, each of whom was affiliated with a cooperating maternity hospital (NICHD Early Child Care Research Network 1994). In the case of the Fragile Families birth cohort study, study direction was centralized, and research staff recruited a multistate network of maternity hospitals (Reichman et al. 2001).

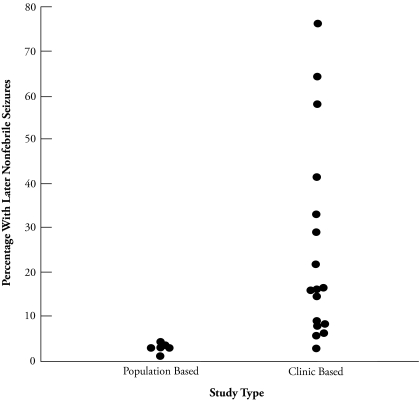
If studying diverse populations is a research goal, why not employ samplers’ tools and draw a fully representative population sample? The value of population data in health research has been repeatedly established. For example, while hormone replacement therapy appeared to reduce heart attack risk in a longitudinal study of nurses, the reverse proved to be the case for the general population (Million Women Study Collaborators 2003). And the prevalence of HIV was substantially overestimated using a sentinel system that relied on data from neonatal clinics rather than population samples (Boerma, Ghys, and Walker 2003). More than 25 years ago, Ellenberg and Nelson (1980) compiled evidence on the likelihood that children with fever-related seizures would have subsequent nonfebrile seizures (see Figure 1). Clinic-based studies, shown on the right in Figure 1, dominated the early literature and led to therapies that presumed a high risk of additional seizures. Population-based studies, shown on the left, indicated that the risk was much lower.

Figure 1.

Risk of Nonfebrile Seizures Following Febrile Seizures

Source: Ellenberg and Nelson (1980).

Fragile Families. In some cases, researchers simply fail to realize that population representation is a feasible option. An example is the Fragile Families Study, an ambitious longitudinal birth cohort survey focused on understanding couple and parenting dynamics surrounding a nonmarital birth (available online at http://www.fragilefamilies.princeton.edu). With the U.S. nonmarital birth rate at 37% and 42% of children in female-headed families poor,6 the task of understanding couple relations, child development, and contextual influences such as welfare reform among families with nonmarital births are high research and policy priorities.

Preliminary work suggested that it would be possible to recruit both mothers and fathers involved in nonmarital births in hospitals shortly after the birth occurred. Indeed, this seemed to be a “magic moment” in which couples were devoted to each other and quite willing to consent to a Fragile Families interview.

Despite the inherently demographic focus of the study, initial plans for the Fragile Families sample did not include population representation. Rather, the plan was to recruit cooperative hospitals in a number of large U.S. cities chosen for diversity with respect to economic conditions and state welfare and child support policies. Apart from this planned environmental diversity, which would provide the needed variation in policy variables of interest, little thought was given to designing the sample so that it would be representative of births in large U.S. cities.

I played the role of matchmaker between Fragile Families staff and Steven Heeringa, a sampling statistician at the University of Michigan. He showed that the judicious application of random but differential selection probabilities (by nonmarital/marital birth and state policy regime) and clustering (within hospitals) produced, at little additional cost, a representative sample of nonmarital births in U.S. cities with populations of 200,000 or more (Reichman et al. 2001).7 The first round of Fragile Families interviewing successfully recruited 4,898 families, including 3,712 unmarried couples and 1,186 married couples. With 87% and 77% response rates among nonmarital mothers and fathers, respectively, the quality of the data is quite high (Bendheim-Thoman Center for Research on Child Wellbeing 2005). Follow-up interviews were conducted when this representative set of children were ages 1, 3, and 5.

The National Children’s Study. A much more contentious example of the pros and cons of population sampling in multisite studies involves subject selection for the National Children’s Study (NCS; Michael and O’Muircheartaigh 2008). The NCS aims to recruit prospective mothers of 100,000 live births and follow children through their 21st birthdays to study the environmental, genetic, and psychosocial determinants of child health and well-being (see http://www.nationalchildrensstudy.gov). A key design decision for subject selection was whether to choose a national network of medical centers that would recruit pregnant women who volunteered to participate or instead a national probability sample of women at risk of becoming pregnant.8

Arguments against national probability sampling took two forms (Michael and O’Muircheartaigh 2008). Most often, concern was voiced over longitudinal response rates, which were thought to be much lower in a probability sample than in a patient-volunteer sample.9 But there were also analytical arguments that minimized the importance of population sampling for estimating behavioral models of interest (Deming 1953).

The sampling debate may seem strange to most demographers. Population estimates are the raison d’être for most demographic work. If a study like the NCS is going to the trouble and expense of obtaining high-quality measurements of environmental exposure, diseases, and genes for 100,000 babies, isn’t it crucial to gather data that could be used to estimate unbiased prevalence rates for the U.S. population of babies? Even if one wants to identify a more complicated statistic, such as the effects of an exposure on subsequent disease onset, why not collect data that would enable one to estimate that relationship as it exists in the overall U.S. population?

A vast gulf separates the research communities with model-based and population perspectives, and for good reason: their very bases for inference differ dramatically. The “model-based” view of inference begins with the specification of some behavioral model of interest. To take a concrete example related to the NCS, suppose we believe that child i’s IQ is a linear and additive function of ambient lead in the child’s dwelling, a set of other determinants (Z) of IQ, and an error term:

$$I{Q}_i={\beta }_0+{\beta }_{1}Lea{d}_i+{\beta }_2{Z}_i+e_i.$$ (1)

In this case, variability in estimates of the key parameter β₁ is generated by the model’s error term e_i. Data from a population sample could be used to generate estimates of β₁, but the “real” (behavioral) population of interest is conceived of as a “superpopulation”—a hypothetical infinite population from which the finite population (e.g., the U.S. population in 2000) is itself a sample (Deming and Stephan 1941). A properly drawn probability sample from a finite population can be used to estimate the parameters of Model (1), but provided that Model (1) is properly specified, so can data drawn in much less systematic ways—for example, from the collection of collaborating sites in a multisite study and their patient-volunteer samples.

Indeed, if Model (1) is a reasonably correct specification,10 and all of the Z controls are measured and included in the regression, then almost any convenience sample drawn from children with varying levels of lead in their environments will produce an unbiased estimate of the key β₁ causal effects parameter.11 Data from a representative sample impart no advantages over convenience-sample data, and probably cost more to collect.

In contrast, the “population-bound” (Kish 1987) or, as it is often called, “design-based” perspective for inference relies on randomization produced by probability sampling. The sampling distributions for survey-based estimators are generated by repeated sampling from the same population, and the goal is to infer the mean, regression coefficient, or other statistical parameters of interest that one would obtain from a population census.

Hypothesis testing of regression-type behavioral relationships does not fit comfortably within this population-bound framework. For example, testing whether a regression coefficient is different from zero makes little sense, since running the regression on data from a population census would never produce a coefficient that was exactly zero. Regression coefficients in a population-bound perspective have valuable uses, for example in describing population-average relationships and generating predictions within the population, but they do not relate directly to parameters of a behavioral model.

Proponents of a population perspective worry that Eq. (1) may not be quite right. Suppose, they might argue, that the effect of lead on IQ is larger for low- than for high-income children, perhaps because of a low-income parent’s inability to shield a child from the deleterious effects of ambient lead. Estimating (1) with a population sample provides a population-average value for β₁, which would differ from the β₁ estimated from a convenience sample that did not contain the same proportion of high- and low-income families as in the population.

In response, model-based proponents would point out that the problem can easily be remedied if Model (1) is reformulated to include a Lead × Income interaction term. With this correct model specification, convenience-sample data could again be used to provide unbiased estimates of β₁ and the coefficient on the Lead × Income interaction.

The argument for a model-based approach to case selection is strongest when (1) population description is of no value; (2) the research goal is to test a small number of very well specified behavioral models; and (3) key variables are difficult or expensive to measure in a probability survey. A key element of “well specified” is that variation in behavioral parameters across population subgroups is either known in advance or confidently assumed away.

In fact, neither of the first two conditions is likely to hold for the NCS or almost any other large-scale data collection. Despite the NCS’s efforts to specify its key hypotheses in advance, the data will no doubt be used to test literally thousands of research hypotheses over its life, and biomedical or social science theory can almost never specify behavioral parameters across population subgroups in advance or confidently assume them away.12

In the end, the proponents of population sampling prevailed, led initially by Rod Little and Robert Michael. The NCS currently plans to draw a representative sample of women at risk of becoming pregnant, follow them for up to four years until they become pregnant, and, with their cooperation, enroll them and their babies in the study. Sampling rates will be set to match the overall goal of recruiting 100,000 mothers and their babies.

Population Perspectives in Qualitative Research

Qualitative researchers rarely employ probability sampling for either “setting” or case selection. Such methods are difficult in the beginning stages of participant observation studies, in which investigators gather rich data over a sustained period in social settings of interest, in order both to frame and to answer basic research questions (Lofland and Lofland 1995).

Glaser and Strauss (1967) coined the term “theoretical sampling” in qualitative research to describe the process by which settings or cases are selected to provide theoretically interesting contrasts for participant observation studies. For example, theory building might suggest the need for selecting cases across cells of a design matrix based on combinations of certain attributes (e.g., economic status, race, and neighborhood type; Bernard 1995; Johnson 1990; Pelto and Pelto 1978). Despite the “sampling” terminology, studies rarely employ random case selection once theoretically interesting settings or groups have been identified.13

An alternative to participant observation studies is gathering information from a number of individuals or families through “semi-structured” interviewing (in which an interviewer guides a free-flowing conversation on a largely predetermined set of topics) or directed observation of individuals. Whom to interview or observe in those cases? Explications of qualitative methodology sometimes detail the utility of “key informants” and design matrices for interesting groups, but almost never discuss the systematic selection of cases within groups (Glaser and Strauss 1967; Patton 2002; Pelto and Pelto 1978).

My discussion of the potential for employing probability-sampling methods for case selection in qualitative studies is based on my experience with two such studies. The first is the New Hope Ethnographic Study, which selected 23 families at random from both the treatment and the control groups in the Milwaukee New Hope program evaluation. The larger study enrolled a total of 1,357 potential New Hope participants and randomly assigned half to receive New Hope services and the other half to a control group.14 The second study is the Time, Love, and Cash in Couples with Children (TLC3) study, which drew a stratified random sample of 75 cases in three cities from the larger Fragile Families study sample described earlier.15

I argue that drawing a probability sample from a larger population of interest for a qualitative study (1) ensures that cases represent both expected and unexpected situations of interest and (2) can often provide a useful basis for statistical inference. Although the second feature requires the selection of several dozen cases, the first advantage of a population approach applies equally well to large- and small-case qualitative studies.

Case selection in the New Hope qualitative study. Researchers designing the New Hope Ethnographic Study (NHES) debated at length the wisdom of random versus purposive case selection (Gibson and Duncan 2005). Because a complete list of program and control families was readily available, it was easy to generate a simple random sample of cases from each group. But some members of the research team argued that since an n = 46 sample was too small to allow for the detection of program impacts, and since the experiences of New Hope experimental families were so much more interesting than the experiences of control families, the NHES sample should consist only of families in the experimental group.

Moreover, there were arguments favoring nonrandom selection of “exemplar” cases—participants whom New Hope staff or preliminary survey data analyses could readily identify as embodying exactly the kinds of experiences that program designers either hoped for or feared. The ethnographic study’s repeated open-ended conversations with exemplar cases, it was argued, would provide much more useful information about the New Hope program than would potentially “uninteresting” cases selected at random. In the end, we opted for a stratified random sample of 46 cases drawn in equal numbers from treatment and control groups, plus three exemplar families.16

Experience repeatedly confirmed the wisdom of the random-sampling decision (Gibson and Duncan 2005). A priori theoretical or program-staff-based expectations about “interesting” and “uninteresting” situations proved depressingly inaccurate; subsequent analysis of both quantitative and qualitative data revealed truly interesting and relevant situations for understanding New Hope program impacts. And while control cases did not receive New Hope services, we were impressed with the comprehensive set of alternative Milwaukee-area services they managed to line up for themselves, which helped us gain a more complete understanding of the nature of the treatment-control contrast afforded by the experiment. For the most part, random case selection helped to identify false assumptions by ensuring that the cases we examined more closely were representative.

Statistical inference from randomly selected qualitative samples. Despite their relatively small numbers of cases, some qualitative studies offer enough statistical power for useful inference, provided that probability sampling methods are employed. And since their open-ended nature allows researchers to glean rich data on sensitive topics (e.g., sexual infidelity in the TLC3 study; Hill 2007), qualitative studies based on random samples can provide useful population estimates for data on sensitive topics that are impossible to secure through surveys.

What is the inferential power of an n = 75 sample like the one drawn for the TLC3 qualitative study? In the case of a relatively rare proportion (e.g., of mothers holding college degrees, .12), the standard deviation of the estimates is about .04, which provides substantial power to reject priors that the condition or event is quite prevalent in the population. In the case of a more evenly split proportion (say, of mothers with at least some college, .31), the standard deviation of the estimates is larger, at .05. But even here, the implied confidence interval is small enough to be quite informative of population proportions.

A hard-to-measure variable obtained in a random-sample qualitative study such as TLC3 may also be used as a right-hand-side variable in regression-based behavior models estimated with the larger Fragile Families Study data. To take a concrete example, suppose that we are interested in estimating the impact of domestic violence during pregnancy on the quality of a couple’s relationship following the birth of their child. Suppose further that all regression variables are measured for the TLC3 subsample, and all but domestic violence are measured in the larger Fragile Families sample. In this case, the TLC3 data on domestic violence can be treated as a kind of missing data problem. Given the random process generating the TLC3 cases, the missing data approximate a “missing completely at random” design. A host of methods (e.g., least squares on imputed data, maximum likelihood, Bayesian; see Little [1992] for a review) have been proposed to deal with these kinds of missing data estimation problems.

Embedding intensive qualitative substudies within larger, population-based surveys is not without potential problems. A particular concern is that intensive contact might somehow change respondents’ attitudes or behaviors, or the added burden might cause them to drop out of the study altogether. Provided that qualitative-study subjects continue to participate in the surveys, the first concern can be tested with the survey data. In the worst-case scenario, the survey data associated with the cases sampled for intensive study might be unusable.

Taken together, these examples suggest that our colleagues engaging in experimental, clinical, and other site-based studies and in qualitative research would profit from demography’s population-based perspective as well as the sampling methods that help produce it. The research world needs this perspective and our expertise in gaining it.

POPULATION PERSPECTIVES ON CAUSAL MODELING

I turn now to the cautionary part of my story and describe ways in which a traditional demographic approach can be misleading. My focus is on causal modeling in population research using data from censuses and large-sample population surveys. I conclude that causal modeling is (1) rarely convincing when based on population-wide regressions involving standard demographic control variables; and (2) often facilitated by eschewing full population representation in favor of an examination of an exceedingly small but strategically selected portion of a general population with the “right kind” of variation in the key independent variable of interest. In the end, though, a population-based understanding of causal effects should be our principal goal.

The Slippery Slope

Demographers are unmatched in their ability to describe population characteristics and processes such as fertility, union formation, and migration. There is good reason for the old joke that demographers are “broken down by age and sex”—they like to describe population phenomena across subgroups that are defined by a multitude of population traits. Thick demographic description often provides the key “stylized facts” about population phenomena that should precede causal modeling.

Troubles begin to arise when demographic research moves from tabular breakdowns by demographic characteristics to regressions that control for those characteristics. A regression coefficient on, say, education predicting fertility is properly described as education’s “regression-adjusted association” with fertility. But too often, fertility is termed an “effect” of education. Worse, the concluding sections of papers often include thoughts about policy recommendations based on the education “effects” estimated in the demographic regression. Under what circumstances is a demographic regression likely to produce a causal impact estimate for the independent variable of interest?

Causal analysis. To focus the discussion, let me return to the Head Start “effects” estimation problem that led to the large random-assignment policy study of Head Start described earlier. Although Head Start enrollment is not a typical demographic variable of interest, the argument I develop applies equally well across a variety of demographic independent variables of interest, such as maternal education or family size.

At its heart, the Head Start causal analysis problem is to estimate the difference in an outcome—for example, reading achievement—between a child who has attended Head Start and that same child if he or she had not participated in Head Start. When trying to determine the causal effect of, say, a mother’s education on her fertility, the problem is to estimate the difference in fertility between a woman with, say, a college degree and that same woman if she had only a high school diploma. Stated this way, reflecting what has become a widely accepted definition (Holland 1986; Neyman, Iwaszkiewicz, and St. Kolodziejczyk 1935; Rubin 1974), causation is specific to an individual and impossible to observe: a child either attends Head Start or does not; at any point, each woman has but one level of completed schooling.17

Others have pointed out that one solution to this problem is portrayed in Frank Capra’s 1946 movie It’s a Wonderful Life. A despondent George Bailey, played by Jimmy Stewart, is visited by an angel who shows him what a terrible place his beloved town would be if he had not lived. Bailey can thus confidently attribute any difference between this vision and what is actually happening to the town and its people to the causal effect of George Bailey.

Lacking angels, social scientists resort to the next best thing: random assignment experiments and, most often for demographers, multiple regression.18 In the regression case, the regression model—Model (2)—may take a form akin to Eq. (1):

$$Ac{h}_i={\beta }_0+{\beta }_{1}Head Star{t}_i+{\beta }_2{Z}_i+e_i$$ (2)

In Eq. (2), Ach_i is child i’s reading achievement; Head Start_i is a dichotomous indicator of whether child i attended Head Start; Z is a set of other determinants of child achievement; and e is an error term. Replacing Ach with fertility and Head Start with education produces the regression model for the fertility example. As with our lead-exposure and child IQ example, Eq. (2) should produce an unbiased estimate of β₁, the causal impact of Head Start, provided that Model (2) is properly specified, Head Start attendance is well measured, and relevant Zs are included.

Population variation in treatment effects. There are two potentially serious problems in attempting to estimate causal impacts in Eq. (2) with nonexperimental data. First, it is very unlikely that the effects of Head Start (the β₁s) are identical across individuals and even groups of individuals. Early childhood education programs appear to be most effective among relatively less advantaged children (Brooks-Gunn et al. 1992; Magnuson et al. 2004). In the education/fertility example, education “effects” may well differ across ethnic or geographically defined subgroups. Since variation in causal effects of interest is likely to be pervasive, it is often useful to recast the goal of a causal policy analysis as one of identifying “local area treatment effects” (Imbens and Angrist 1994).

The task of translating causal modeling into policy analysis is all the more difficult because groups that are affected by real-world policies are often idiosyncratic. An expansion of the Head Start program might target children with incomes just above the poverty line. A community college subsidy program might target low-income single mothers living in a single state. Groups for whom policy effects are unusually large or small may be quite different from groups to which real-world policies are targeted.

As with the lead and IQ model presented earlier, estimating Model (2) with all of the proper interactions would help to address these treatment heterogeneity problems. But it is a formidable task to identify them on the basis of often weak theory and to estimate them without undue data mining.

Omitted-variable bias. A second and pervasive problem with regression-based approaches to inferring causation, which was not considered in our discussion of the lead and child IQ Model (1), is that controlling for all of the relevant Z factors is exceedingly difficult. Failure to do so may impart serious bias to the estimate of β₁.

The possibility of omitted-variable bias is a huge concern. Consider some of the commonly used explanatory variables in demographic research: being reared by a highly educated parent, by a working mother, or in a large family; divorce; neighborhood location; peers; and child care arrangements. All are, at least in part, determined or influenced by the actions of the individuals whose outcomes are being studied. Spurious correlations between outcomes of interest and these demographic variables may in fact arise from difficult-to-measure characteristics of the individuals themselves or their parents (Duncan, Magnuson, and Ludwig 2004; Moffitt 2005). Such correlations are the source of omitted-variable bias in the estimation of β₁.

Population representation does not solve the omitted-variable bias problem. Indeed, since widely used population data collections like censuses or labor force surveys often cannot afford the time and expense of high-quality measurement of key Z variables that drive the selection process behind key independent variables of interest, they may produce a more biased estimate of β₁ than would more extensive and higher-quality measurement taken from a convenience sample!

How serious a problem is omitted-variable bias? It varies, but regrettably in ways that are difficult to predict. Consider the nonexperimental literature on the effects of Head Start. Currie and Thomas (1995) used the NLSY to contrast picture vocabulary (PPVT) test scores for children who attended Head Start with those of children who did not. Garces, Thomas, and Currie (2002) used PSID data for corresponding contrasts for high school completion (see Table 1). Uncontrolled ordinary least squares (OLS) regressions produced some perverse negative estimates of Head Start impacts in both studies. Extensive regression controls19 produced a uniformly null set of impact estimates. But when both studies focused on variation within families by relating sibling differences in outcomes to sibling differences in Head Start attendance, the Head Start impact estimates for white children became positive and statistically significant; they were smaller and remained statistically insignificant for black children.

Table 1.

OLS and Sibling Difference Estimates of the Effect of Head Start on Child Outcomes

Outcome	OLS Regression, No Controls	OLS Regression, Extensive Controls	Sibling Difference
PPVT Test Score
White	−5.6* (1.6)	−0.4 (1.4)	5.9* (1.5)
Black	1.0 (1.2)	0.7 (1.1)	0.3 (1.4)
Completed High School
All	−0.08* (0.03)	0.01 (0.03)	0.04 (0.05)
White			0.20* (0.10)
Black			−0.02 (0.07)

Source: Currie and Thomas (1995: Table 4) for PPVT results; Garces et al. (2002: Table 2) for high school completion results.

^*p < .05

Recent sophisticated studies of the effects of family size on child outcomes (reviewed later in this article) have shown few of the detrimental effects found in conventional demographic regression approaches. Experimental studies of dropout (Agodini and Dynarski 2004) and class size programs (Wilde and Hollister 2002) have shown that a “population regression” approach sometimes comes close to experimental estimates, but it often produces quite different results. In general, then, biases using conventional regression techniques can be quite serious, but there is no “in general” way of predicting when this will be the case.

Securing Less Biased Causal Estimates

What to do about the omitted-variable problem? One potential solution is through measurement—that is, measure as many of the important Z selection factors as possible and include them in the regression analysis. This requires careful conceptualization of the processes that determine the key independent variables of interest (in our examples, decisions regarding Head Start enrollment, maternal schooling, neighborhood conditions, and completed family size) and including measures that characterize that process in the population regression.

This conceptualization and measurement work is rarely done in survey research, in part because paying attention to measuring the selection process places yet more demands on the scarce time interviewers are able to spend with respondents, time that the various proponents of favored dependent and independent variables are typically fighting to claim. As mentioned above, data from the decennial census or large sample surveys such as the U.S. Current Population Survey will almost never provide the measures needed to control adequately for the selection process behind key independent variables.

A wide variety of alternative approaches have been proposed. Manski (1990) took a minimalist approach to assumptions about model specification and argued for the utility of estimating lower and upper bounds on the causal effects of interest. Propensity score methods (Rosenbaum and Rubin 1983) attempt to isolate the most relevant comparison groups but still depend on the adequacy of measured control variables.20 Fixed-effects models approach the bias problem by differencing out the possible effects of selection factors. In the case of sibling fixed-effects models, such as those employed by Currie and Thomas (1995) and Garces et al. (2002) and cited earlier, the influence of selection factors—both measured and unmeasured—that are common to siblings is differenced out, but potential biases from individual-specific selection factors remain.21

Robert Moffitt’s (2005) excellent Demography article detailed the strengths and weaknesses of a number of these methods, some of which are based on so-called “natural experiments.” Most attempt to solve the omitted-variable problem by focusing on a narrow subset of the overall population in which variation in key independent variables of interest is arguably beyond the control of the individuals involved.

I would like to argue for the virtues of these very narrow but judiciously selected population approaches. Working with natural experiments often requires the expertise of demographers, while at the same time, it avoids some of the possible biases in population regressions. The key in natural experiments is to focus on situations in which variation in a central independent variable of interest is unaffected by the process typically involved in the variable’s selection.

Natural experiments are pervasive (Duncan et al. 2004; Meyer 1995). One demographic example is the Angrist, Lavy, and Schlosser (2005) investigation of the effects of family size on child outcomes. Since larger families differ from smaller families in many ways that are difficult to capture with measured variables, the potential for omitted-variable bias is substantial. Angrist et al. (2005) capitalized on the fact that both twin births and same-sex sibling pairs are often associated with larger total family sizes. Family size impact estimates driven exclusively by twin- and same-sex sibling sources of variation show no indication of the kind of negative “impacts” of larger family size estimated in typical demographic regressions.22

A highly creative, population-based assessment of the impact of natural disasters on mortality, family disruption, and relocation is the Study of the Tsunami Aftermath and Recovery in Sumatra. It draws pre-tsunami data from a large-scale, nationally representative socioeconomic survey (SUSENAS), which is collected annually by Indonesia’s Central Bureau of Statistics. Special mortality follow-ups and data collections over the post-tsunami recovery period are being conducted with households in both affected and comparison districts in order to isolate the changes that can be attributed to the tsunami and its aftermath.23

A Head Start example. The logic and procedures behind natural experiments are illustrated by Ludwig and Miller’s (2007) research on Head Start program effects, which took advantage of a little-known policy change in the early years of the program. By the mid-1960s, the Office of Economic Opportunity (OEO)—the U.S. antipoverty agency in those days—was concerned that very few of the nation’s poorest counties were applying for Head Start funding. Children in these areas clearly needed help, but the counties lacked the expertise to apply for this program. In response, the OEO sent White House interns to the 300 poorest U.S. counties to assist local officials in developing proposals. This situation provided Ludwig and Miller (2007) with an opportunity for a comparison (based in part on census data) between the long-run outcomes of children living in counties just below the 300-county cutoff, many of whom were provided with the chance to attend Head Start, and those of children living in counties with poverty rates that placed them just above the 300-county cutoff.

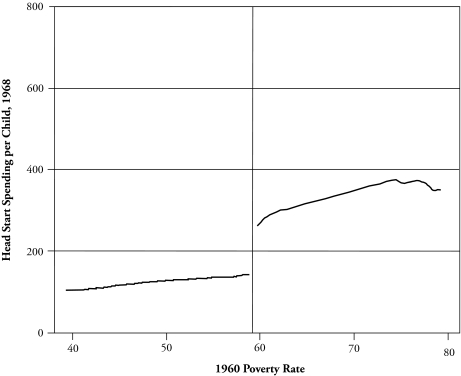
Ludwig and Miller (2007) first established that Head Start spending was indeed higher among counties targeted by OEO’s efforts to increase applications. Figure 2 shows per-child county spending on Head Start in 1968, with counties ranked according to their poverty rates in the 1960 census.24 The sharp drop in Head Start spending at a poverty rate of around 59% corresponds precisely to the 59.20% poverty rate distinguishing the poorest 300 counties. An estimate of the drop at the point of the regression discontinuity is $134—a statistically significant difference (see Table 2).25 Head Start enrollment, as measured in the NELS:88 survey, was 15 percentage points higher just below the cutoff point than just above it.

Figure 2.

Head Start Spending per 4-Year-Old in 1968

Table 2.

Estimated Effects for Eligible Versus Non-eligible Counties in the Ludwig and Miller (2005) Analysis of Head Start

	Difference for Eligible Counties
1972 Federal Head Start Spending per 4-Year-Old Child ($)	134*
Head Start Enrollment (from NELS:88) (%)	15*
Compare: 1972 Other Social Spending per Capita ($)	14
College Attendance
Eligible cohorts: 18- to 24-year-olds in 1990 census (%)	5.1*
Compare: Parents’ college attendance in 1970 (%)	0.0
Compare: 25- to 34-year-olds in 1990 census (%)	0.1

^*p < .05

As a falsification test, Ludwig and Miller investigated whether something else about the social spending in these poorest counties might advantage the children growing up in them. Federal per capita social spending does not experience the same jump as Head Start spending, a fact confirmed in a more formal regression analysis (Table 2).26

Ludwig and Miller next turned to possible “discontinuities” in an assortment of child outcomes. For example, if Head Start promotes school achievement, then we might expect to see a discontinuity in county-level college enrollment in the 1990 census for individuals whose preschool years coincided with the increase in Head Start spending. Sure enough, there was a statistically significant 5.1-percentage-point jump in college attendance in 1990 in counties that just made the 300-county cutoff compared with counties just on the other side of the line (Table 2). More generally, Ludwig and Miller (2007) found favorable regression-discontinuity jumps in mortality rates for children from causes that could be affected by Head Start and in a number of education-related outcomes.

Falsification tests are possible here as well: there was no jump in college enrollment among children too old to have profited from the increased Head Start funding (i.e., the 25-to 34-year-olds in the 1990 census), nor in the 1970 college attendance rates of the parents of cohort-eligible children. Taken together, the historical evidence gleaned from census and administrative sources, but concentrated on counties just above and below the 300-county OEO cutoff, points to an assortment of benefits that likely more than outweighed the costs of the program (Ludwig and Miller 2007).

A PLACE FOR A POPULATION PERSPECTIVE IN CAUSAL RESEARCH

Ludwig and Miller may have produced an elegant estimate of Head Start impacts, but it is hardly a general one: the exogenous variation in Head Start spending they exploited applies to Head Start centers operating more than 30 years ago, in counties with poverty rates just above or below 59%. Whether their estimated impacts hold true in more affluent areas, or in more recent years, is a matter of considerable speculation.

More generally, the highly selective nature of natural experiments, sibling fixed effects, instrumental variables, and similar approaches may reduce bias, but they suffer from a damaging loss in external validity. By burrowing deep within population data, these techniques sacrifice their population-wide perspective on causal effects. As promising as natural experiments may be, therefore, they do not begin to provide a full population perspective on causal impacts. What to do?

Stepping back, we see that the holy grail of a population perspective on causation needs to solve three disparate problems:

1. Population-wide data have the potential to provide causal estimates for whole populations and their policy-relevant subgroups, but population regressions typically fail to provide unbiased estimates of causal impacts.

2. “Natural experiments” may generate arguably unbiased causal estimates, but often only for small and idiosyncratic subgroups of the population, such as twins or, in the case of Ludwig and Miller (2007), individuals residing in counties with poverty rates around 59%.

3. Real-world policies are typically implemented among narrowly defined population subgroups, such as immigrant children or children living in families with near-poverty income. Regrettably, research-based natural experimental subgroups often overlap little with policy-relevant subgroups.

Rehabilitating the Population Regression

Approaches to grappling with these contradictory elements have filled volumes (Lee 2005; Morgan and Winship 2007; Pearl 2000; Spirtes, Glymour, and Scheines 2000). I would like to concentrate on one question: is there a place in the pantheon of causal approaches for the population regression approach?

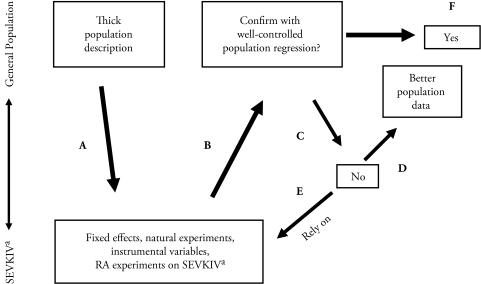
For causal analysis, it is useful to think of two population levels rather than just one. At the top of Figure 3 is the familiar general population level—the fountain for the data that keep demographers young. At the bottom are what I call SEVKIVs—subgroups with exogeneous variability on key independent variables.

Figure 3.

Steps for Causal Modeling

^aSEVKIV = subgroups with exogenous variability in key independent variables.

In the Ludwig and Miller work, these subgroups were children growing up in counties just above and below the 59% poverty cutoff. In the tsunami study, they are Sumatran districts devastated and little-affected by the disaster. Identical twins or siblings who differ on key independent variables are another example. In a nutshell, I am recommending that demographers go beyond breaking down by age and sex at the general population level and consider engaging in collaborations that lead to breakdowns by SEVKIVs as well.

It is important to begin with thick description at the general population level. Demographers have developed a highly creative and sophisticated set of tools, including multiple regression, for describing and forecasting population characteristics and dynamic processes. None of my remarks should be construed as detracting from these accomplishments—they are vital, and their continuing development should be encouraged and supported.

For the purposes of causal modeling, I am suggesting moving to the second population level—the SEVKIVs (path A in Figure 3). Here, the challenge is to think of events, policies, or accidents of geography that provide exogenous variation in key independent variables of interest and to organize data collections around that subset of the population. Random-assignment policy experiments are even better. The more SEVKIVs the better, since they show us how robust causal estimates are across various subsets of the population.

Once we have some confidence that SEVKIVs have produced a reasonably convincing collection of causal estimates, we can proceed to an investigation of whether a well-controlled population-level regression can reproduce key results from the SEVKIV analyses (path B). Here, we need to devote considerable mental and measurement effort to understanding and statistically controlling for the process by which individuals come to have certain values on the key policy-relevant independent variables of interest.27

If a SEVKIV analysis yields a convincing causal estimate for a well-defined population subgroup, can a well-controlled population regression run on that subgroup match it? Suppose, for example, that the national Head Start experiment were to show strongly positive impacts for girls but not for boys. Does that pattern emerge in a well-controlled population regression run on similar cohorts? The more precisely a well-controlled population-based regression can reproduce the collection of patterns found in more specialized studies, the more confidence we can have in its estimates.

Population-based regressions should probably be judged guilty of potentially serious bias until proven innocent. If the population regression approach fails to come close to the SEVKIV estimates (path C), then one option is to secure data with better measurement of the selection process behind key independent variables (path D) and a reanalysis of whether population regressions reproduce SEVKIV patterns. Failing that, it is probably best to rely on estimates from the SEVKIV analysis, despite the problems with their external validity (path E).28

If a well-controlled population regression can reproduce SEVKIV results (path F), then we have a blissful state of affairs—a population perspective on causal effects. In this case, the population-based data could be used to provide estimates of causal effects both for the overall population and for the population subgroups most likely to be affected by actual policies.

This is not a hopeless agenda. Consider the exceedingly well-researched problem of estimating the causal impact of completed schooling on lifetime earnings. David Card’s (1999) masterly review covers approaches that employ population regressions as well as a host of more sophisticated techniques, such as twin differences and instrumental variables. By and large, the population regressions produce estimates of the impacts of education on earnings that are consistently but only modestly below those of studies employing more sophisticated estimation methods, and there are reasons to suspect that the differences are smaller than they appear.29

Moreover, even if population-based regressions contain some possible bias, variation in causal estimates across population subgroups may still be quite useful. Card and Krueger (1992) have shown that the economic returns to schooling vary systematically by state of birth as well as by the quality of the state’s schools. At least in the case of education and earnings, a population-based regression approach can be quite informative.

SUMMARY

I fear that the complications of causal analysis may have obscured the very upbeat message I hope to convey: a population perspective, and the sampling tools that help to produce it, are much too important and powerful to be kept hidden away from our colleagues in the fields of experimental, clinical, and qualitative research. As a group, demographers must surely rank in the top tier among academics in terms of professionalism and collegiality, but also in terms of modesty—traits that have made it a true pleasure to organize the 2008 PAA’s annual meeting and an honor to promote PAA’s research priorities in Washington and beyond. But our modesty prevents us from being as aggressive as we should be in promoting our population perspective. More often than not, a population-based research perspective is ruled out simply because it is unfamiliar. And when it is considered, it often triggers misplaced fears of lower data quality or higher costs. Demographers should not hesitate to promote the use of sampling tools and their population perspective in these other research settings.

In the context of causal analysis, a population perspective, if not population-wide regressions, is also essential. Demographers should avoid the “slippery slope” of assuming that the standard set of demographic control variables will be capable of controlling for omitted-variable bias. A productive alternative is to look within a population to find subgroups for which “natural experiments” have produced variation in key independent variables of interest.

But since the generalizability of natural experiments is often quite limited, it is also worth returning to a well-controlled population-based regression. Careful thought and considerable interviewing time will surely be needed to capture the process by which the key independent variables take on their values. Even after this conceptualization and measurement is completed, confidence in a population regression approach requires evidence that its estimated effects agree with those obtained with alternative methods. This process is laborious but worthwhile; a population perspective on causal effects is a worthy goal for future generations of population scientists.