Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2010 Jun 1.
Published in final edited form as: J Comput Neurosci. 2008 Oct 8;26(3):331–338. doi: 10.1007/s10827-008-0115-5

Relationship between temperature and stimulation frequency in conduction block of amphibian myelinated axon

Changfeng Tai 1, Jicheng Wang 1, James R Roppolo 2, William C de Groat 2
PMCID: PMC2834478  NIHMSID: NIHMS175504  PMID: 18839298

Abstract

The temperature-frequency relationship in nerve conduction block induced by high-frequency, biphasic electrical current was investigated by computer simulation using an amphibian myelinated axon model based on Frankenhaeuser-Huxley (FH) equations. For an axon of diameter 10 µm, the minimal blocking frequency was changed from 6 kHz to 3 kHz as the temperature was decreased from 37 °C to 15 °C. The maximal blocking temperature below which the axon could be blocked was increased from 22 °C to 37 °C as the stimulation frequency was increased from 4 kHz to 8 kHz. The maximal blocking temperature was not influenced by axon diameter. Simulation analysis also revealed that activation of potassium channels might determine the temperature-frequency relationship. This study indicates that temperature might be one of the factors that cause the frequency discrepancy as reported in previous animal studies.

Keywords: Nerve block, Axonal conduction, High-frequency, Stimulation, Temperature

Introduction

A reversible nerve blocking method using biphasic, charge-balanced, electrical current could have many potential clinical applications, especially in the development of a neural prosthesis for the people with neurological disorders (Bhadra et al., 2006; Tai et al., 2004; 2005c; 2008). Previous studies using animals (Bowman and McNeal, 1986; Reboul and Rosenblueth, 1939; Rosenblueth and Reboul, 1939; Tanner, 1962) have shown that high-frequency, biphasic, electrical current applied to peripheral nerves can block nerve conduction. This conduction block is quickly reversible once the stimulation is terminated. In chronic applications a nerve blocking method employing biphasic, charge-balanced, electrical current will cause less damage to the nerve due to electro-chemical reactions than using uniphasic electrical current (Agnew and McCreery, 1990). Therefore, recently attention has been focused on the axonal conduction block induced by high-frequency, biphasic, charge-balanced electrical current (Bhadra et al., 2007; Liu et al., 2008; Tai et al., 2005a; 2005b; 2008; Wang et al, 2008; Zhang et al., 2006a; 2006b).

However, the minimal stimulation frequency required to induce the nerve block has varied significantly in reports from different investigators. The minimal stimulation frequency of 4–5 kHz was reported in studies using cat sciatic nerves when the temperature varied between 25 °C and 35 °C (Reboul and Rosenblueth, 1939; Rosenblueth and Reboul, 1939), or was undefined (presumably at room temperature 20–25 °C) (Bowman and McNeal, 1986). Our studies (Tai et al., 2004; 2005c; 2008) on the pudendal nerve of cat indicated that a minimal stimulation frequency of 6 kHz is required at 37 °C. Studies using sciatic nerve of rats (Bhadra and Kilgore, 2005; Williamson and Andrews, 2005) have shown that the stimulation frequency has to be higher than 10 kHz. In a recent study using frog sciatic nerve (Kilgore and Bhadra, 2004) it was shown that nerve conduction could be most efficiently blocked at a stimulation frequency as low as 3–5 kHz at room temperature. The different nerves used by different investigators might contribute to the frequency differences, since they are from different species (frog, rat, or cat). However, other experimental conditions may also play a role, including electrode geometry, experimental temperature, etc. Currently the frequency discrepancy has not been explained.

Our simulation studies (Liu, et al., 2008; Wang, et al., 2008) using mammalian myelinated axon models indicated that both slow and fast potassium channels could play an important role in the nerve conduction block induced by high-frequency biphasic electrical current and the temperature could be one of the factors that influence the minimal blocking frequency. Our recent animal experiments using mammalian myelinated nerve (i.e. cat pudendal nerve) further showed that the minimal blocking frequency was reduced from 6 kHz to 4 kHz as the temperature was decreased from 37 °C to 15 °C (Tai, et al., 2008). However, amphibian myelinated axon is different from mammalian myelinated axon. The slow potassium current is dominant in mammalian myelinated axon, but the amphibian myelinated axon only has fast potassium channels without slow potassium channels. It is not clear whether the temperature could also influence the minimal blocking frequency in amphibian myelinated axons, although animal experiments using frog sciatic nerve (Kilgore and Bhadra, 2004) indicated the most efficient minimal blocking frequency changed between 3 kHz and 5 kHz at room temperature. Although the results from amphibian myelinated axon might not directly applicable to the development of neural prosthesis involving mammalian myelinated axon, they will certainly help to further understand the frequency discrepancy reported in previous studies using both mammalian and amphibian myelinated axons. Therefore, in this study the relationship between temperature and stimulation frequency was investigated using a model of amphibian myelinated axon.

Methods

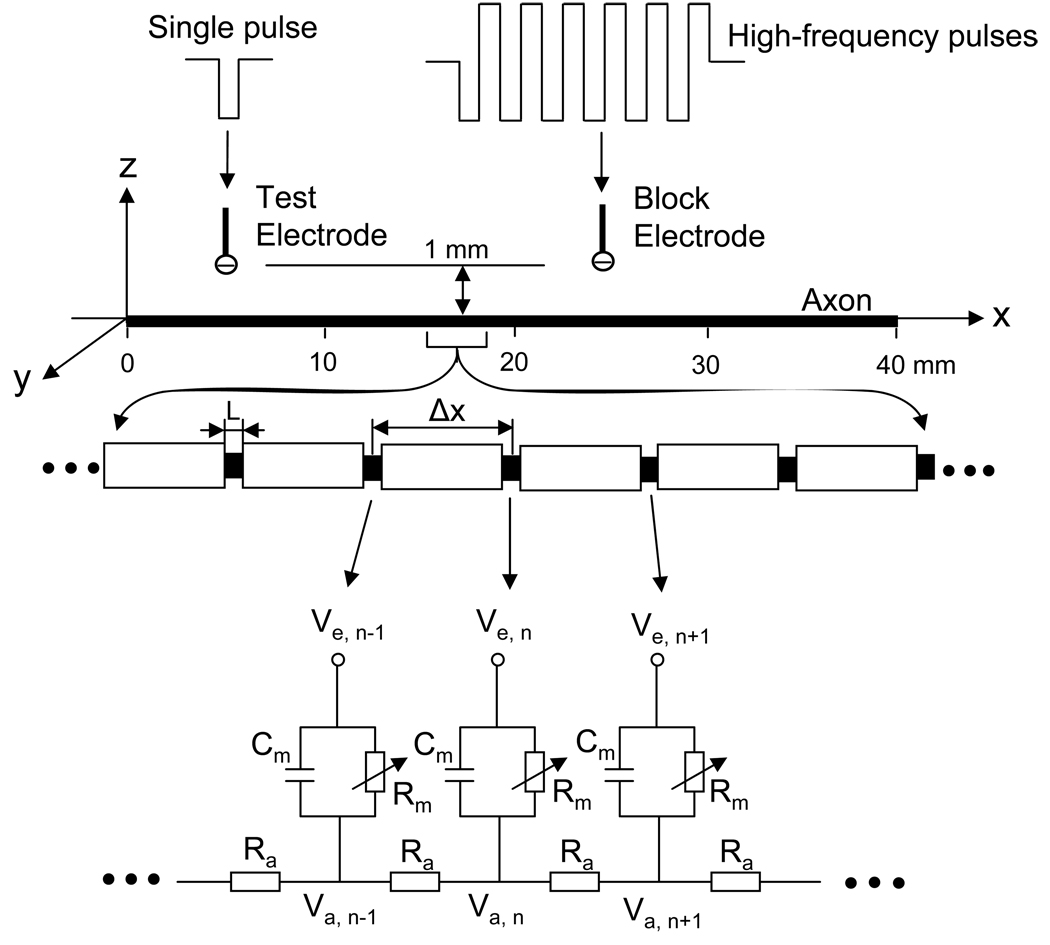
The amphibian axonal model used in this study to analyze the relationship between temperature and stimulation frequency is shown in Fig.1. A 40 mm long axon is modeled with the inter-node length Δx = 100d (where d is the axon diameter). Each node (nodal length L = 2.5 µm) is modeled by a membrane capacitance (cm) and a variable membrane resistance (Rm). The ionic currents passing through the variable membrane resistance are described by FH equations that were derived from frog sciatic nerves (Frankenhaeuser and Huxley, 1964; Rattay and Aberham, 1993). Two monopolar point electrodes (with the indifferent electrode at infinity) are placed at 1 mm distance from the axon (Fig.1). One is the block electrode at the 25 mm location along the axon, where the high-frequency, biphasic, continuous rectangular wave (as shown in Fig.1) will be delivered. The other is the test electrode at the 5 mm location, which delivers a uniphasic single pulse (pulse width 0.1 ms at variable intensities ranging from 0.5 mA to 2 mA) to evoke an action potential and to test whether this action potential can propagate through the site of the block electrode. The test electrode will always be a cathode (negative pulse), and the block electrode will always deliver biphasic pulses with the cathodal phase first.

Fig.1.

Fig.1

Open in a new tab

Amphibian myelinated axon model to simulate conduction block induced by high-frequency biphasic rectangular pulses. The inter-node length Δx = 100d; d is the axon diameter. L is the nodal length. Each node is modeled by a resistance-capacity circuit based on the FH model. Ra: axoplasm resistance; Rm: membrane resistance; Cm: membrane capacitance; Va: intracellular potential; Ve: extracellular potential.

We assume that the axon is in an infinite homogeneous medium (resistivity ρe= 300 Ωcm). After neglecting the small influence induced by the presence of the axon in the homogeneous medium, the extracellular potential Ve,n at the nth node along the axon can be calculated by:

Ve,n(t)=ρe4π[Iblock(t)(nΔx−x0)2+z02+Itest(t)(nΔx−x1)2+z12]

where Iblock(t) is the high-frequency, biphasic pulse current delivered to the block electrode (at location x0 = 25 mm, z0 = 1 mm); Itest(t) is the single test pulse delivered to the test electrode (at location x1 = 5 mm, z1 = 1 mm).

The change of the membrane potential Vn at the nth node is described by:

dVndt=[dΔx4ρiL(Vn−1−2Vn+Vn+1Δx2+Ve,n−1−2Ve,n+Ve,n+1Δx2)−Ii,n]/cm

where Vn = Va,n –Ve,n–Vrest; Va,n is the intracellular potential at the nth node; Ve,n is the extracellular potential at the nth node; Vrest is the resting membrane potential (−70 mV); ρi is the resistivity of axoplasm (100 Ωcm); cm is the capacity of the membrane (2 µF/cm2); Ii,n is the ionic current at the nth node described by FH equations. See appendix for more detail about the FH equations (Frankenhaeuser and Huxley, 1964; Rattay and Aberham, 1993; Zhang et al, 2006b).

The model was solved by Runge-Kutta method with a time step of 0.001 ms (Boyce and Diprima, 1997). The simulation always started at initial condition Vn = 0. The membrane potentials at the two end nodes of the modeled axon were always equal to the membrane potentials of their closest neighbors, which implemented the sealed boundary conditions (no longitudinal currents) at the two ends of the modeled axon. In order to analyze the relationship between temperature and stimulation frequency, the simulation was performed at different temperatures (37, 27, 20 and 15 °C). The stimulation intensity threshold was determined with a resolution of ±0.1 mA. The temperature threshold was determined with a resolution of ±1 °C.

Results

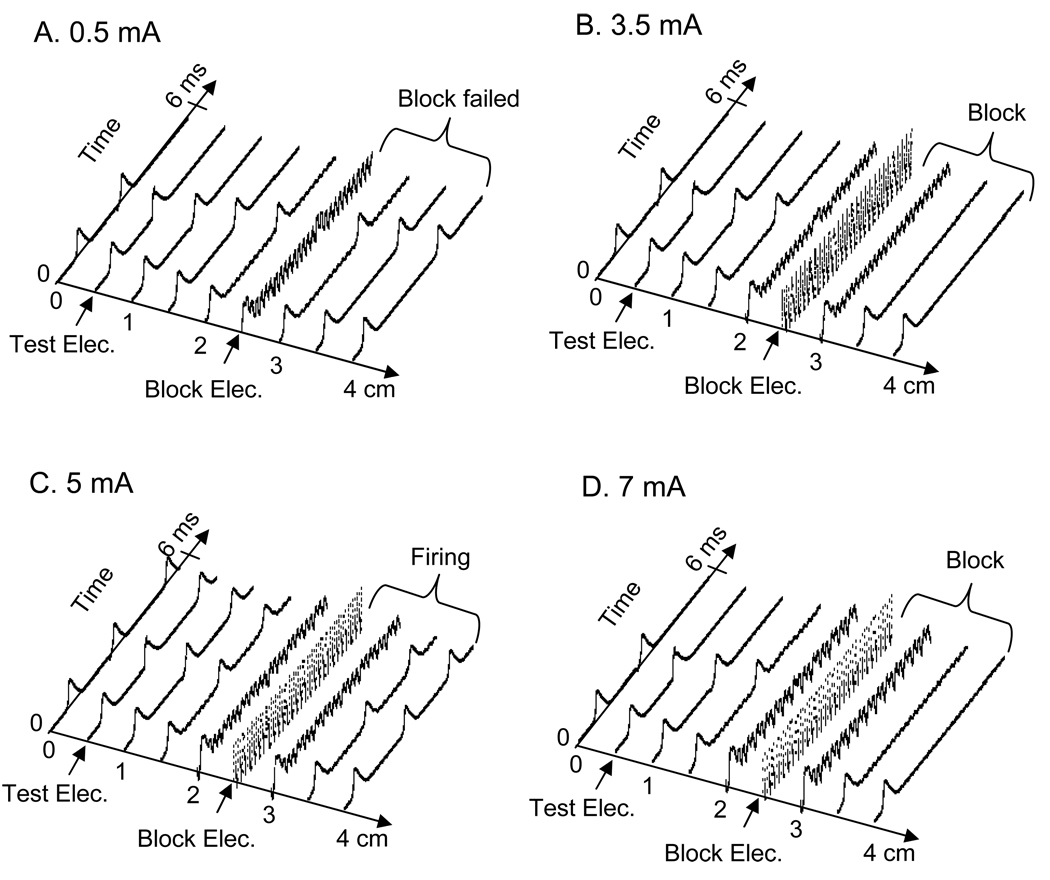
Using the amphibian myelinated axon model shown in Fig.1, we successfully simulated the nerve conduction block. The simulation analysis mainly focused on the relationship between temperature and stimulation frequency. Fig.2 shows a typical nerve firing pattern and conduction block at a temperature of 27 °C induced by stimulation of 5 kHz at different stimulation intensities in an axon of 10 µm diameter. The test pulse at the test electrode was applied at 2.5 ms after the start of the high-frequency, biphasic stimulation in Fig.2 A, B, and D, but was not applied in Fig.2 C. It generated an action potential propagating toward the block electrode. At a stimulation intensity of 0.5 mA (Fig.2 A) the high-frequency, biphasic stimulation (5 kHz) generated an initial action potential and failed to block the propagation of the action potential induced by the test electrode; whereas at a higher intensity (3.5 mA, Fig.2 B) it successfully blocked the nerve conduction. However, further increasing the intensity of the high-frequency stimulation caused repetitive firing as shown in Fig.2 C (5 mA), although only an initial action potential was induced at other intensities (Fig.2 A, B and D). This repetitive firing disappeared and nerve conduction could be blocked again after the stimulation intensity increased further (7 mA, Fig.2 D).

Fig.2.

Fig.2

Open in a new tab

Propagation of action potentials along the axon induced by high-frequency biphasic stimulation at different intensities. A. 0.5 mA; B. 3.5 mA; C. 5 mA; D. 7 mA. In A, B and D, the high-frequency biphasic stimulation only induced an initial action potential, but in C it caused repetitive firing. A second action potential was also initiated after a 2.5 ms delay by the test electrode in A, B and D, but not in C. This action potential was propagating towards the block electrode, and was blocked by the block electrode in B and D, but not in A. The short arrows mark the locations of test and block electrodes. Stimulation: 5 kHz. Axon diameter: 10 µm. Temperature: 27 °C.

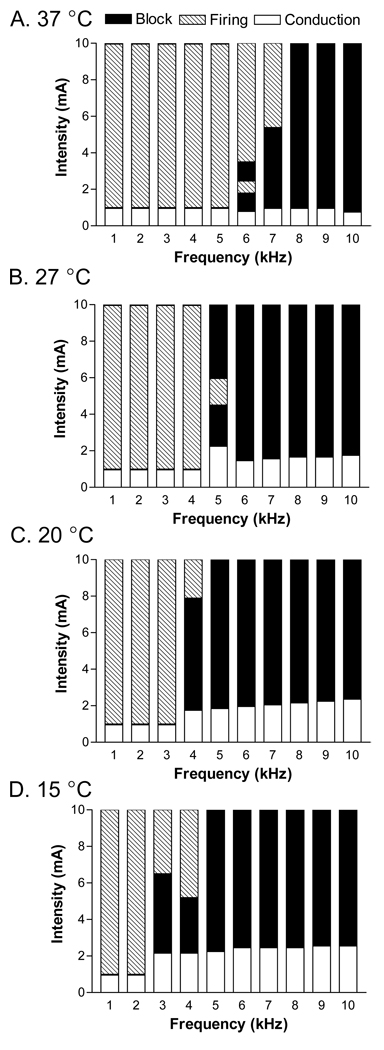
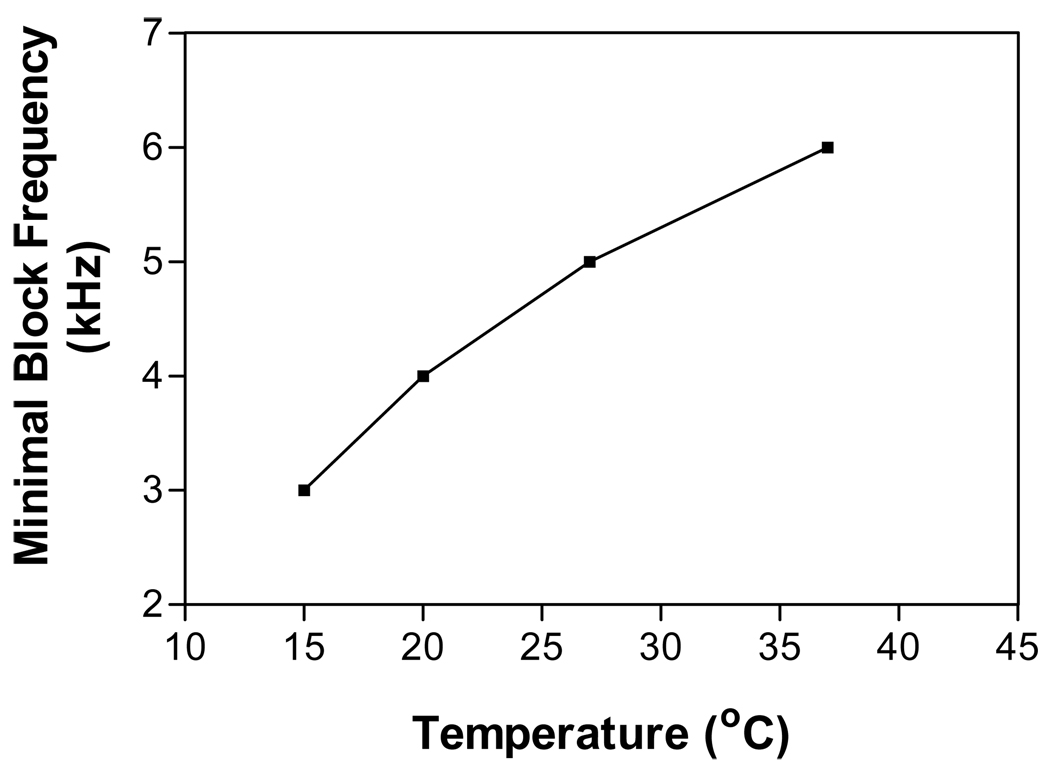
Fig.3 shows the pattern of nerve block or repetitive firing at different stimulation frequencies (1–10 kHz), intensities (0–10 mA), and temperatures (15, 20, 27, and 37 °C) in an axon of 10 µm diameter. At a temperature of 37 °C (Fig.3 A), the minimal stimulation frequency required to produce nerve conduction block is 6 kHz. This minimal blocking frequency is reduced to 5 kHz at a temperature of 27 °C (Fig.3 B), and can be reduced to 4 kHz or 3 kHz if the temperature is decreased to 20 °C or 15 °C respectively (Fig.3 C and D). At the minimal blocking frequency, the nerve block can only occur at a certain range of stimulation intensity. This means that once the stimulation frequency reaches the minimal frequency, nerve block can always be achieved by adjusting the stimulation intensity. The minimal frequencies required to observe nerve block in an axon of diameter 10 µm are plotted against the corresponding temperature in Fig.4. The minimal blocking frequency changes from 3 kHz to 6 kHz as the temperature increases from 15 °C to 37 °C.

Fig.3.

Fig.3

Open in a new tab

Pattern of nerve block and repetitive firing induced by different stimulation intensities and frequencies at temperatures of 37 °C (A), 27 °C (B), 20 °C (C), and 15 °C (D). The dark areas represent the stimulation intensity ranges causing nerve block as shown in Fig. 2 B or D. The hatched areas represent the repetitive firing as shown in Fig. 2 C. The white areas represent normal conduction as shown in Fig.2 A. Axon diameter: 10 µm.

Fig.4.

Fig.4

Open in a new tab

The minimal stimulation frequency required to block the axonal conduction changes with temperature. Stimulation intensities are at the blocking thresholds. Axon diameter: 10 µm.

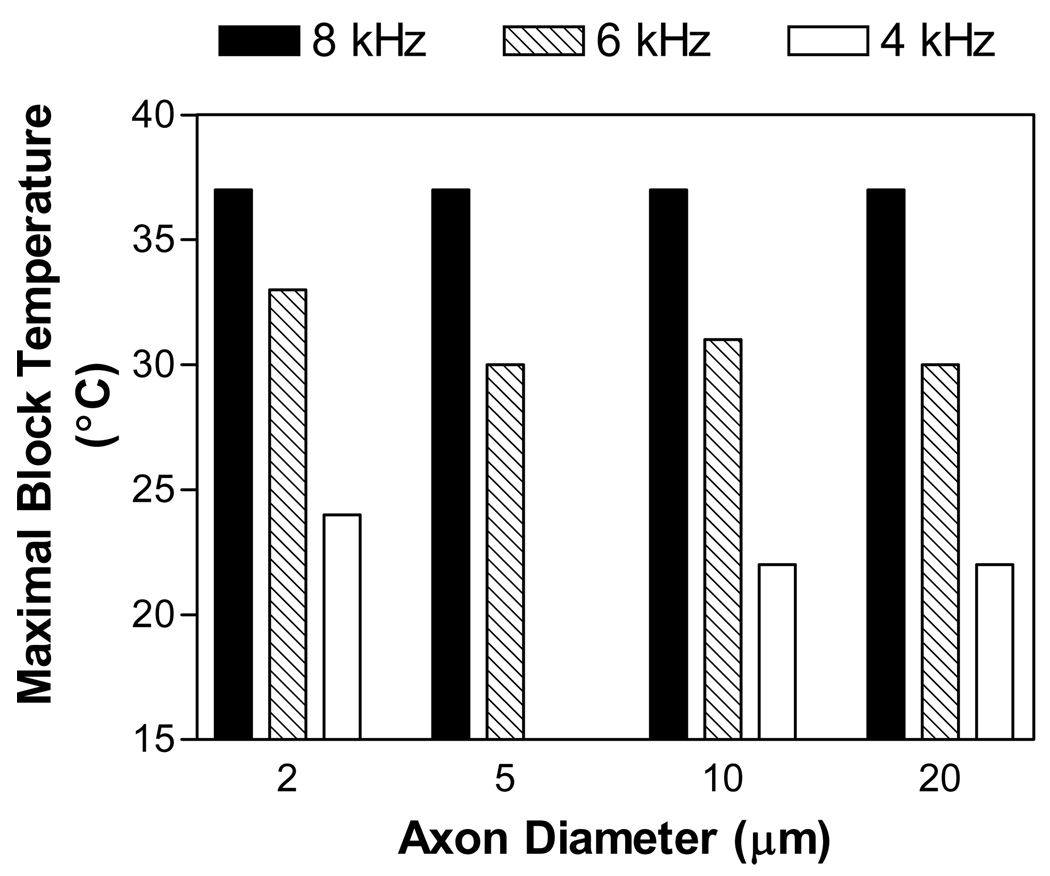
For a certain stimulation frequency, nerve block can only occur when the temperature is below a maximal value. Fig.5 shows the maximal temperatures below which axons of different diameters (2, 5, 10, or 20 µm) can be blocked by a 5 mA stimulation at different frequencies (4, 6, or 8 kHz). Although the maximal blocking temperatures for an axon of certain diameter decrease as the stimulation frequency is reduced, they are almost same for different diameter axons at a certain stimulation frequency. However, at a stimulation frequency of 4 kHz the small axon of 5 µm diameter can not be blocked at temperatures above 15 °C due to repetitive firing (see Fig.2 C). Our previous study (Zhang et al., 2006a) using amphibian myelinated axon model has shown that the repetitive firing occurs in a larger range of stimulation intensity in small axons (2–5 µm) than in large axons (10–20 µm). Although the repetitive firing is dependent on axon diameter, the maximal temperature for nerve block seems independent on axon diameter (Fig.5). Therefore, the relationship between maximal blocking temperature and stimulation frequency is not influenced by axon diameter as long as the nerve block is not interrupted by the repetitive firing.

Fig.5.

Fig.5

Open in a new tab

Influences of axonal diameter and stimulation frequency on the maximal temperature below which the axon can be blocked. Stimulation intensity: 5 mA.

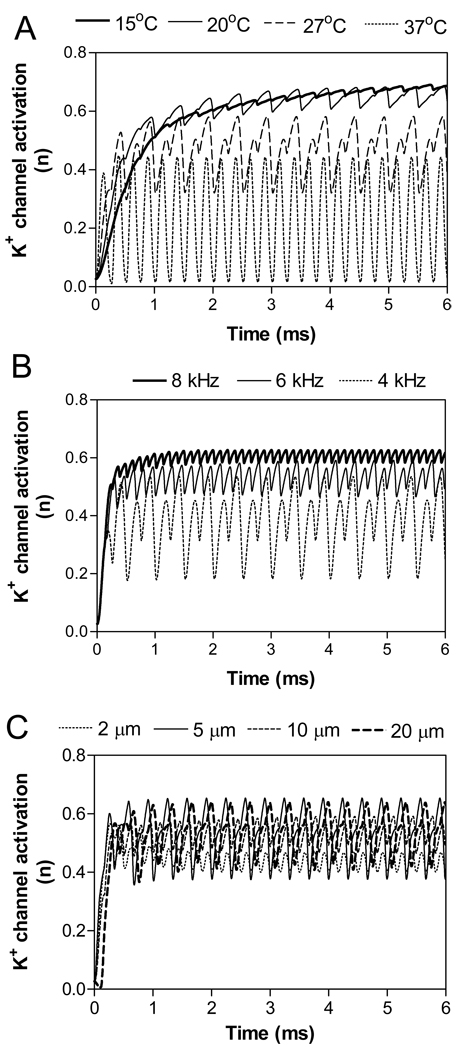
Our previous simulation studies using both myelinated and unmyelinated axon models (Liu et al., 2008; Tai et al., 2005a; 2005b; Wang et al., 2008; Zhang et al., 2006a; 2006b) have revealed that the high-frequency, biphasic electrical stimulation constantly activates the potassium channels in axonal membrane, causing the failure for action potentials to propagate through the region where the block electrode is located. Although this mechanism still needs to be verified by further animal experiments, the activation of potassium channels under the block electrode can very well explain the relationship between the stimulation frequency and the maximal blocking temperature. Fig.6 A shows how the activation (n) of potassium channels changes with temperature at a stimulation frequency of 4 kHz. When the temperature changes from 37 °C to 15 °C, the activation (n) of potassium channels changes from oscillation to constant activation at a higher level (around 0.6). At temperatures of 15 °C or 20 °C, nerve conduction block can be observed due to the strong activation (n) of potassium channels. This explains why at a frequency of 4 kHz the temperature has to be lower than 24 °C in order to block the nerve conduction (Fig.5).

Fig.6.

Fig.6

Open in a new tab

Influences of temperature (A), stimulation frequency (B), and axon diameter on potassium channel activation (n) in the axonal node under blocking electrode. A: Stimulation of 4 kHz frequency, 5 mA intensity in a 10 µm diameter axon. At 37 °C each stimulus evokes a transient K+ channel activation; whereas at 15 °C and 20 °C the K+ channel is tonically activated. B: Stimulation of 5 mA intensity in a 10 µm diameter axon at 30 °C. C: Stimulation of 6 kHz and 5 mA at 30 °C.

Fig.6 B shows how the activation of potassium channels under the block electrode changes with stimulation frequency at a temperature of 30 °C. As the frequency increases from 4 kHz to 8 kHz, the activation of potassium channels changes from oscillation to constant activation at a higher level (around 0.6). At frequencies of 6 kHz or 8 kHz, nerve conduction block can be observed due to the strong activation of potassium channels. This explains why at a certain temperature the stimulation frequency has to be high enough in order to block the nerve conduction (Fig.3–Fig.4).

Fig.6 C shows that the activation of potassium channels under the block electrode is not significantly influenced by axon diameter. At 30 °C, the stimulation of 6 kHz and 5 mA induced an activation of potassium channels oscillating around 0.5 (between 0.4 and 0.6) for axons of different diameters (2–20 µm). This explains why the maximal temperature as shown in Fig.5 is not influenced by the axon diameter.

Discussion

In this study we investigated the relationship between temperature and stimulation frequency in the conduction block of amphibian myelinated axon. The minimal frequency required to block nerve conduction increases as the temperature increases (Fig. 3–Fig.4). The maximal temperature below which the nerve block can be induced decreases as the stimulation frequency decreases (Fig.5). Axon diameter does not influence the maximal blocking temperature (Fig.5). The activation of potassium channels under the block electrode correlates well with the temperature-frequency relationship (Fig.6).

It has been known for more than 60 years (Reboul and Rosenblueth, 1939; Rosenblueth and Reboul, 1939) that the high-frequency alternating currents could block nerve conduction. However, the minimal stimulation frequency required to block the nerve varied considerably in reports from different investigators (Bhadra and Kilgore, 2005; Bowman and McNeal, 1986; Reboul and Rosenblueth, 1939; Tai et al., 2004; 2005c; Tanner, 1962; Williamson and Andrews, 2005). Our previous studies by both computer simulation (Wang, et al., 2008) and animal experiment (Tai, et al., 2008) have shown that the temperature could be one of the factors causing the frequency discrepancy in mammalian myelinated axons. The results presented in this study further indicated that the temperature could also be a factor in amphibian myelinated axons. A recent study using isolated frog sciatic nerve (Kilgore and Bhadra, 2004) reported that more effective or consistent block could be achieved at a lowest frequency between 3 kHz and 5 kHz at room temperature. It is unfortunate that the specific room temperature was not defined. If we assume that the room temperature was between 15 °C and 27 °C, the minimal blocking frequency of 3–5 kHz obtained in animal experiments using frog sciatic nerve agrees very well with our simulation results (Fig. 3–Fig. 4). It is worthy noting that the temperature influence could only partially explain the discrepancy of minimal blocking frequency (1–10 kHz) presented in previous animal studies, since it only caused the minimal blocking frequency changing from 6 kHz to 3 kHz in the temperature range of 15–37 °C based on the results from this study. Other factors causing the frequency discrepancy might include electrode geometry (bipolar or tripolar), different types of nerves (sciatic nerve or pudendal nerve), or different species (frog, rat, or cat). Simulation studies using axon models, for example, incorporating stochastic gating mechanism of ion channels (Adair, 2003), may further resolve the freqeucny discrepancy in nerve conduction block.

Our previous simulation studies using both myelinated and unmyelinated axon models (Liu et al., 2008; Tai et al., 2005a; 2005b; Wang et al., 2008; Zhang et al., 2006a; 2006b) have indicated that the constant activation of potassium channels under the block electrode is a possible mechanism underlying the nerve conduction block, although the other study suggested a dynamic steady-state depolarization under the block electrode as a possible mechanism (Kilgore and Bhadra, 2004; Bhadra et al., 2007). In this study, the activation of potassium channels also explains very well the relationship between temperature and minimal blocking frequency (Fig.3–Fig.4 and Fig.6B) and the relationship between stimulation frequency and maximal blocking temperature (Fig.5 and Fig.6A). When the temperature decreases, the kinetics of the potassium channel becomes slower such that the channels remain open between stimulus pulses. This allows the potassium channel activation to increase with each stimulus pulse and eventually reach a plateau (Fig.6A). Therefore, as the temperature decreases the activation of potassium channels changes from an oscillatory pattern to constant activation for a certain stimulation frequency (Fig.6A). This explains why there is a maximal blocking temperature for a certain stimulation frequency. At a certain temperature where the kinetics of the potassium channels remain constant, an increase of stimulation frequency will eventually keep the potassium channels open between stimulus pulses and allow the potassium channel activation to gradually increase to a plateau level (Fig.6B). Therefore, as the frequency increases the activation of potassium channels changes from oscillation to constant activation (Fig.6B). This explains why there is a minimal blocking frequency for a certain temperature. The blocking mechanism suggested by our previous studies, i.e. the constant activation of potassium channels, could also explain why the maximal blocking temperature is not influenced by axon diameter (Fig.5). As shown in the appendix, the axon diameter does not determine the kinetics of potassium channels, which is reflected in Fig.6 C as a very similar level of potassium channel activation for all axons (2–20 µm diameters). This explains why the axon diameter has no influence on the relationship between maximal blocking temperature and stimulation frequency (Fig.5).

This study investigated the temperature-frequency relationship in nerve conduction block using an amphibian myelinated axon model. Although clinical application involves mammalian myelinated axon, the results from amphibian myelinated axon could help to further understand the frequency discrepancy reported in previous studies using both mammalian and amphibian myelinated axons. Resolving the frequency discrepancy will certainly help to determine the minimal stimulation frequency to be used in clinical application. Although the mechanism underlying the nerve conduction block is still not completely understood, our data presented in this study further indicates a role of potassium channels. Understanding the relationship between temperature and stimulation frequency and the possible mechanisms underlying the nerve conduction block will further promote the application of this nerve blocking method in the design of neural prosthetic devices for people with neurological disorders (Bhadra et al., 2006; Kilgore and Bhadra, 2004; Tai et al., 2004; 2005c; 2008).

Acknowledgments

This work is supported by the NIH grants R01-DK-068566 and R56-DK-068566.

Appendix

The ionic current Ii,n at nth node is described as:

Ii,n=iNa+iK+iP+iLiNa=PNam2hEF2RT[Na]0−[Na]i,eEF/RT1−eEF/RTiK=PKn2EF2RT[K]0−[K]i,eEF/RT1−eEF/RTip=PPp2EF2RT[Na]0−[Na]i,eEF/RT1−eEF/RTiL=gL(Vn−VL)E=Vn+Vrest

where PNa (0.008 cm/s), PK (0.0012 cm/s) and PP (0.00054 cm/s) are the ionic permeabilities for sodium, potassium and nonspecific currents respectively; gL (30.3 kΩ−1 cm−2) is the maximum conductance for leakage current. VL (0.026 mV) is reduced equilibrium membrane potential for leakage ions, in which the resting membrane potential Vrest (−70 mV) has been subtracted. [Na]i (13.7 mmole/l) and [Na]o (114.5 mmole/l) are sodium concentrations inside and outside the axon membrane. [K]i (120 mmole/l) and [K]o (2.5 mmole/l) are potassium concentrations inside and outside the axon membrane. F (96485 c/mole) is Faraday constant. R (8314.4 mJ/K/mole) is gas constant. m, h, n and p are dimensionless variables, whose values always change between 0 and 1. m and h represent activation and inactivation of sodium channels, whereas n represents activation of potassium channels. p represents activation of non-specific ion channels. The evolution equations for m, h, n and p are the following

dm/dt=[αm(1−m)−βmm]kmdh/dt=[αh(1−h)−βhh]kdn/dt=[αn(1−n)−βnn]kdp/dt=[αp(1−p)−βpp]k

and

αm=0.36(Vn−22)1−exp(22−Vn3)βm=0.4(13−Vn)1−exp(Vn−1320)αh=−0.1(Vn+10)1−exp(Vn+106)βh=4.51+exp(45−Vn10)αn=0.02(Vn−35)1−exp(35−Vn10)βn=0.05(10−Vn)1−exp(Vn−1010)αp=0.006(Vn−40)1−exp(40−Vn10)βp=−0.09(Vn+25)1−exp(Vn+2520)km=1.8(T−293)/10k=3(T−293)/10

where T is the temperature in °Kelvin. The initial values for m, h, n and p (when Vn = 0 mV) are 0.0005, 0.0268, 0.8249 and 0.0049 respectively.

References

  1. Adair RK. Noise and stochastic resonance in voltage-gated ion channels. PNAS. 2003;100:12099–12104. doi: 10.1073/pnas.2034447100. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Agnew WF, McCreery DH. Neural Prostheses: Fundamental Studies. Englewood Cliffs, NJ: Prentice Hall; 1990. [Google Scholar]
  3. Bhadra N, Bhadra N, Kilgore K, Gustafson KJ. High frequency electrical conduction block of pudendal nerve. J Neural Eng. 2006;3:180–187. doi: 10.1088/1741-2560/3/2/012. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Bhadra N, Lahowetz EA, Foldes ST, Kilgore KL. Simulation of high-frequency sinusoidal electrical block of mammalian myelinated axons. J Comput Neurosci. 2007;22:313–326. doi: 10.1007/s10827-006-0015-5. [DOI] [PubMed] [Google Scholar]
  5. Bhadra N, Kilgore KL. High-frequency electrical conduction block of mammalian peripheral motor nerve. Muscle Nerve. 2005;32:782–790. doi: 10.1002/mus.20428. [DOI] [PubMed] [Google Scholar]
  6. Bowman BR, McNeal DR. Response of single alpha motoneurons to high-frequency pulse train: firing behavior and conduction block phenomenon. Appl Neurophysiol. 1986;49:121–138. doi: 10.1159/000100137. [DOI] [PubMed] [Google Scholar]
  7. Boyce WE, Diprima RC. Elementary Differential Equations and Boundary Value Problems. 6th ed. John Wiley & Sons, Inc.; 1997. pp. 436–457. [Google Scholar]
  8. Frankenhaeuser B, Huxley AF. The action potential in the myelinated nerve fibre of Xenopus Laevis as computed on the basis of voltage clamp data. J Physiol (Lond) 1964;171:302–315. doi: 10.1113/jphysiol.1964.sp007378. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Kilgore KL, Bhadra N. Nerve conduction block utilising high-frequency alternating current. Med Biol Eng Comput. 2004;42:394–406. doi: 10.1007/BF02344716. [DOI] [PubMed] [Google Scholar]
  10. Liu H, Roppolo JR, de Groat WC, Tai C. The role of slow potassium current in nerve conduction block induced by high-frequency biphasic electrical current. IEEE Trans Biomed Eng. 2008 doi: 10.1109/TBME.2008.2006013. in press. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Rattay F, Aberham M. Modeling axon membranes for functional electrical stimulation. IEEE Trans Biomed Eng. 1993;40:1201–1209. doi: 10.1109/10.250575. [DOI] [PubMed] [Google Scholar]
  12. Reboul J, Rosenblueth A. The action of alternating currents upon the electrical excitability of nerve. Am J Physiol. 1939;125:205–215. [Google Scholar]
  13. Rosenblueth A, Reboul J. The blocking and deblocking effects of alternating currents on nerve. Am J Physiol. 1939;125:251–264. [Google Scholar]
  14. Tai C, de Groat WC, Roppolo JR. Simulation analysis of conduction block in unmyelinated axons induced by high-frequency biphasic electrical currents. IEEE Trans Biomed Eng. 2005a;52:1323–1332. doi: 10.1109/tbme.2005.847561. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Tai C, de Groat WC, Roppolo JR. Simulation of nerve block by high-frequency sinusoidal electrical current based on the Hodgkin-Huxley model. IEEE Trans Neural Syst Rehab Eng. 2005b;13:415–422. doi: 10.1109/TNSRE.2005.847356. [DOI] [PubMed] [Google Scholar]
  16. Tai C, Roppolo JR, de Groat WC. Block of external urethral sphincter contraction by high frequency electrical stimulation of pudendal nerve. J Urol. 2004;172:2069–2072. doi: 10.1097/01.ju.0000140709.71932.f0. [DOI] [PubMed] [Google Scholar]
  17. Tai C, Roppolo JR, de Groat WC. Response of external urethral sphincter to high frequency biphasic electrical stimulation of pudendal nerve. J Urol. 2005c;174:782–786. doi: 10.1097/01.ju.0000164728.25074.36. [DOI] [PubMed] [Google Scholar]
  18. Tai C, Wang J, Chancellor MB, Roppolo JR, de Groat WC. Influence of temperature on pudendal nerve block induced by high frequency biphasic electrical current. J Urol. 2008;180:1173–1178. doi: 10.1016/j.juro.2008.04.138. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Tanner JA. Reversible blocking of nerve conduction by alternating-current excitation. Nature. 1962;195:712–713. doi: 10.1038/195712b0. [DOI] [PubMed] [Google Scholar]
  20. Wang J, Shen B, Roppolo JR, de Groat WC, Tai C. Influence of frequency and temperature on the mechanisms of nerve conduction block induced by high-frequency biphasic electrical current. J Comput Neurosci. 2008;24:195–206. doi: 10.1007/s10827-007-0050-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Williamson RP, Andrews BJ. Localized electrical nerve blocking. IEEE Trans Biomed Eng. 2005;52:362–370. doi: 10.1109/TBME.2004.842790. [DOI] [PubMed] [Google Scholar]
  22. Zhang X, Roppolo JR, de Groat WC, Tai C. Simulation analysis of conduction block in myelinated axons induced by high-frequency biphasic rectangular pulses. IEEE Trans Biomed Eng. 2006a;53:1433–1436. doi: 10.1109/tbme.2006.873689. [DOI] [PubMed] [Google Scholar]
  23. Zhang X, Roppolo JR, de Groat WC, Tai C. Mechanism of nerve conduction block induced by high-frequency biphasic electrical currents. IEEE Trans Biomed Eng. 2006b;53:2445–2454. doi: 10.1109/TBME.2006.884640. [DOI] [PMC free article] [PubMed] [Google Scholar]

RESOURCES