Large Deviations for Random Trees and the Branching of RNA Secondary Structures

Abstract

We give a Large Deviation Principle (LDP) with explicit rate function for the distribution of vertex degrees in plane trees, a combinatorial model of RNA secondary structures. We calculate the typical degree distributions based on nearest neighbor free energies, and compare our results with the branching configurations found in two sets of large RNA secondary structures. We find substantial agreement overall, with some interesting deviations which merit further study.

1 Introduction

In this paper we give a Large Deviation Principle (LDP) for a combinatorial model of RNA secondary structures. This mathematical result allows us to make quantitative statements about the expected or “typical” branching configurations for our model of RNA folding. We are motivated by the question of identifying “unusual” substructures in large RNA molecules, which is a crucial aspect of searching for putative functional motifs. This is a challenging biological question since the accuracy of RNA secondary structure prediction methods by free energy minimization decreases with sequence length [6, 8, 13, 15, 26, 27]. We address one aspect of this problem by adopting a statistical mechanics approach to investigate the asymptotic branching degrees of large random trees under distributions which reflect the thermodynamics of RNA base pairing. Our goal is not to predict base pairs for a particular RNA sequence, but to analyze what a typical branching distribution might be for an arbitrary large RNA secondary structure.

Previous combinatorial results [10] on plane trees suggest that the degree of loop branching is correlated with thermodynamic stability and functional significance. We refine this analysis of the branching degree in RNA secondary structures by considering Gibbs distributions based on the nearest neighbor free energy parameters. We are particularly interested in the interplay between the energy term, which has dominated previous analyses, and the impact of entropy considerations in determining “unusual” configurations. Our mathematical results are given as an LDP for the distribution of vertex degrees among plane trees with N vertices. To the best of our knowledge, no studies of Gibbs distributions on random trees have been published, and our analysis of the energy-entropy competition for these random trees model appears to be new. We also compare our expected configurations as N → ∞ with the branching degrees found in two sets of RNA secondary structures: large subunit 23S ribosomal structures derived by comparative sequence analysis from the Gutell Lab at UT Austin and picornaviral structures predicted by free energy minimization from the Palmenberg Lab at UW Madison. We find substantial agreement overall between our asymptotic results for large random trees and the branching distributions found in the RNA secondary structures. This supports our statistical mechanics approach to developing a reasonable and mathematically tractable model of large RNA molecules. Conversely, deviations from our predictions indicate an aspect of RNA folding which is not well covered by the model and which merits further study.

2 Overview

A single-stranded RNA sequence encodes molecular structure and function in a hierarchical way [22], from primary sequence through secondary structure¹ to the tertiary interactions that determine the three-dimensional structure. Since the primary structure of an RNA molecule is a nucleotide sequence much like DNA, experimental sequencing techniques can easily determine its base composition, and there are ever-increasing numbers of known RNA sequences. RNA molecules also resemble proteins though, since unlike the canonical DNA double helix, different RNA sequences fold into a variety of three-dimensional structures. However, there are still only a few hundred solved RNA structures, largely small molecules or molecular fragments, in contrast to the thousands of known protein structures. Thus, understanding the relationship between an RNA sequence and the base pairings of its secondary structure is an essential step in understanding the RNA structure-function hierarchy. Beyond the computational problem of RNA secondary structure determination, there is the question of evaluating the significance of the base pairings. In particular, identifying “unusual” substructures in large RNA molecules is a crucial aspect of searching for putative functional motifs.

We begin addressing this problem by investigating the typical branching configurations of large RNA molecules using a statistical mechanics approach with a combinatorial model of RNA folding. As detailed in [10, 11], trees are widely used to represent nested RNA secondary structures, and as described in Section 3 we model the folding of RNA sequences using plane trees – ordered, rooted trees [21] which nicely abstract the different substructures in RNA folding. In Section 4 we consider the set of all plane trees on N vertices and define a Gibbs distribution on that set using energy functions from the nearest neighbor free energy model for RNA folding. We analyze these distributions as N → ∞, and give an LDP with explicit rate function.

Informally, an LDP with nonnegative rate function I for random variables X_N taking values in a set ℳ means that for all p ∈ ℳ and large N, we have

$$\text{P}\{X_N\approx p\}\approx e^{-NI(p)}.$$

In particular, when the minimal value 0 is attained by I at a unique point p^* ∈ ℳ, then for any neighborhood O of p^*, the probability P{X_N ∉O} decays exponentially in N. This can also be restated as a Law of Large Numbers with exponential convergence in probability to the limit point p^*.

As a consequence of this Law of Large Numbers, it makes sense to call a random tree from our model “typical” if the distribution of its branching degrees is close to p^*. More precisely, the LDP for our model tells us that there is a distribution p^* of branching degrees such that the distribution for a random tree is close to p^* with probability approaching 1 as the size of the tree grows to infinity. Therefore, it also makes sense to consider any tree with a branching degree distribution considerably deviating from p^* to be exotic. In Section 5 we compute p^*, the asymptotically most probable branching sequences for our model. An immediate implication is that it is unlikely (in the framework of our model) to observe a large RNA secondary structure with branching degree distribution that significantly differs from p^*. However, if such conformation is observed, the analysis of that conformation should result in some new insights.

Under the nearest neighbor thermodynamic model for RNA folding, the free energy of an RNA secondary structure is assumed to be the independent sum of the substructure free energies. In our model of RNA branching configurations, this corresponds to an assumption that the free energy of the entire tree is equal to the sum of free energies associated with each vertex. However, it is known from statistical mechanics that free energy is additive if all the subconfigurations are statistically independent of each other. If this requirement is not satisfied then additional entropy corrections related to the interdependencies or interactions between the subsystems or subconfigurations should appear.

We show that this is indeed the case for the systems that we consider. The combinatorial structure of the trees imposes certain restrictions on branching degrees that lead to their mutual statistical dependence which in turn induces certain entropy corrections. Due to this interplay between energy and entropy, the typical trees minimize the free energy corrected by the extra entropy term resulting from the combinatorics of plane trees, and do not minimize the energy plainly understood as sum of the energies of all the vertices. Therefore, the entropy correction is an important factor in determining the branching of typical large trees, which have a broader distribution of loop degrees than the exotic energy-minimizing configurations.

Based on our results, we have that the percentage of high degree vertices in a typical large tree is exponentially decreasing, but positive. As we discuss, the exact rate of decay depends on the specific thermodynamic parameters, and there are interesting differences in the behavior of our model under the two sets of energy values considered. In Section 6, we compare these asymptotic degree distributions with the branching found in a set of ribosomal and a set of picornaviral RNA secondary structures. There are definite qualitative similarities between our predictions and the secondary structure data, as well as various differences which suggest areas for future investigations.

3 Modeling RNA folding by trees

As pictured in Figure 1, RNA secondary structures can be modeled as trees by collapsing each single-stranded loop into a point and replacing the stacked base pairs by an edge connecting two such points. The tree is rooted at the vertex corresponding to the external loop, which contains the 5′ and 3′ ends of the sequence, and by imposing a linear ordering on the vertices of the tree, we maintain the 5′ to 3′ orientation of the RNA molecule. Such an ordered, rooted tree, known as a plane tree [21], gives a “low-resolution” model of RNA folding; it preserves information about the basic arrangement of loops and helices in an RNA secondary structure, and also captures certain essential elements of the free energy thermodynamic model. The free energy of a particular RNA secondary structure is calculated as the independent sum over the energies of well-defined substructures [28], namely the helices and different classes of loop structures. The primary loop classification is according to the number of base pairs, that is according to the branching degree (the number of children) of the corresponding vertex. Since we consider only the branching degree of the vertices in our rooted trees, we will frequently refer to the number of children simply as the degree of the vertex. Hence, there are three basic types of loops which we consider with the associated free energies given in Table 1. For our purposes, we consider bulge loops to be a special type of internal/degree 1 loop, loops with degree ≥ 2 are called “branching” loops rather than “multiloops”, and the exceptional energy function for the external loop is disregarded.

Figure 1.

The secondary structure, generated by the mfold Web Server available through http://frontend.bioinfo.rpi.edu/zukerm/home.html, for a 79 base fragment from the 3′ UTR of the 7440 nucleotide RNA virus poliovirus 1-Mahoney, Genbank Accession No. J0228140 [19]. The structure has two hairpin loops, two internal loops (one of which is a bulge loop of size 2), one branching (multi) loop, and an external loop. The adjacent plane tree (rooted at the bottom) models the configuration of the RNA secondary structure, preserving information about the basic arrangement of loops/vertices and helices/edges.

Table 1.

Loop structures and associated free energies at 37° [15, 25].

Name	Branching degree	dG 2.3	dG 3.0
Hairpin	0	3.5	4.10
Internal	1	3.0	2.3
Branching	d ≥ 2	4.6 - 0.2 (d + 1)	3.4 - 1.5 (d + 1)

Here, we consider two possible energy values for each type of loop structure, corresponding to the current standard known as dG 3.0 and the former standard dG 2.3. (See “Version 3.0 free energy parameters for RNA folding at 37°” and “Version 2.3 free energy parameters for RNA folding at 37°” available through the mfold website.) The energy of a loop is a function of the number of single-stranded bases and the number of base pairs, with an additional dependency for the stacking interactions [28]. For the purposes of our model, we have chosen a specific energy value from the unbounded set of possibilities for each of the three types of loops. These values correspond to loops where any enclosed base pairs are G – C, the closing base pair is C – G, and the single-stranded segments are A⁴. These loops occur in the combinatorial model of RNA folding previously considered in [10], and the dG 3.0 thermodynamic values were used in the results on RNA branching degrees given there. Clearly, there are many other possible choices and it may be interesting to investigate the impact of different thermodynamic values – energy minimizing versus maximizing, average against frequent, etc. – on the behavior of the model. We note that the dG 2.3 parameters were originally included in our analysis because the picornaviral secondary structures from [19] which are analyzed in Section 6 were determined using those values. In doing so, though, we noticed interesting changes in the evolution of the free energy model.

The free energy model is evolving in two significant ways. One type of development is extending and refining the experimental determination of thermodynamic values for the entropy and enthalpy of specific base interactions [14, 15]. While this has improved the accuracy of RNA secondary structure prediction, it has also greatly increased the complexity of the thermodynamic calculations; the free energy model now includes more than 10,000 parameters, nearly all of which pertain to small internal loops. The other evolving component is changes in the estimation of free energy functions which have not, or worse cannot, be measured directly. The loop destabilizing energies are the most notable instance of this, and the major source of change between the previous energy parameters (dG 2.3) and those currently used (dG 3.0). Through our mathematical results given in the next two sections, though, we can assess the impact of these changes and the importance of the entropy correction on the likely configurations of large RNA secondary structures without getting lost in the thousands of detailed thermodynamic parameters.

4 The Large Deviation Principle

As described above, we consider plane trees as our combinatorial model of RNA folding. Now, we introduce a family of Gibbs distributions on the trees, and state our main mathematical results.

We fix a number D ∈ ℕ and for each N ∈ ℕ consider the set 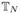(D) of plane trees on N ∈ ℕ vertices such that the number of children of each vertex (the branching degree) does not exceed D. We restrict ourselves to the trees with bounded degrees to simplify the mathematical treatment. However, if D is suitably large, this does not impose any significant restrictions since, although the degree of branching in RNA loops is theoretically unbounded, in practice it is necessarily limited by physical constraints. Moreover, as we shall see in the next section, the properties of the model stabilize as D → ∞.

To define Gibbs distributions on 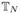(D) we associate an energy with each plane tree. In our model of RNA branching configurations, we assume that the energy associated with each vertex depends only on its branching degree and is given by a function c: {0, 1, …, D} → ℝ. To a first approximation, this is consistent with the thermodynamics of RNA folding. The energy of a tree T ∈ 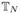(D) is then given by

$$H(T)=\sum _{j=1}^{N}c(d_j(T))=\sum _{k=0}^{D}c(k){\chi }_k(T),$$ (1)

where d_j denotes the branching degree of vertex j, and χ_k(T) is the number of vertices with k children in T. Now the Gibbs probability measure on 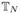(D) associated with H is given by

$$P_N\{T\}=\frac{e^{-\beta H(T)}}{Z_N},T\in {\mathbb{T}}_N(D),$$

where β > 0 is the inverse temperature parameter and Z_N is a normalizing constant known as the partition function:

$$Z_N=\sum _{T\in {\mathbb{T}}_N(D)}{e}^{-\beta H(T)}.$$

There are several interesting questions one could ask about the asymptotic behavior of measures P_N as N → ∞. Here we would like to study the frequencies of branching degrees, so for each N we introduce a probability measure ν_N on [0, 1]^D+1 defined as the distribution of the random vector $\frac{1}{N}({\chi }_0(T),{\chi }_1(T),\dots ,{\chi }_D(T))$ under P_N. Our main result is an LDP for ν_N.

Let us recall that a sequence of probability measures (μ_N)_N∈ℕ on a compact metric space (E, ρ) satisfies an LDP with a nonnegative lower-semicontinuous rate function I: E → ℝ if

$$\underset{N\to \infty }{limsup}\frac{1}{N}ln{\mu }_N(C)\le -I(C),\text{for}\text{any}\text{closed}\text{set}C\subset E,$$

and

$$\underset{N\to \infty }{liminf}\frac{1}{N}ln{\mu }_N(O)\ge -I(O),\text{for}\text{any}\text{open}\text{set}O\subset E,$$

where for a set O, we denote I(O) = inf_p∈O I(p), see [7, Section II.3] or [5, Section 1.2].

Informally, an LDP means that if we consider random variables X_N with distribution μ_N, then for all p and large N we have

$$\text{P}\{X_N\approx p\}\approx e^{-NI(p)}.$$

In particular, if the minimal value 0 is attained by I at a unique point p^*, then for any neighborhood O of p^*, μ_N (O^c) = P{X ∉ O} decays exponentially in N. This can be restated as a Law of Large Numbers with exponential convergence in probability to the limit point p^*.

For our model, it is natural to formulate the LDP for ν_N on the set

$$\mathcal{M}=\left\{p\in {[0,1]}^{D+1}:\sum _{k=0}^D{p}_k=1,\sum _{k=0}^D{kp}_k=1\right\}$$

equipped with Euclidean distance. Though the random vector $\frac{1}{N}({\chi }_0,\dots ,{\chi }_D)$ does not belong to ℳ, it is asymptotically close to ℳ:

$$\sum _{k=0}^D\frac{{\chi }_k}{N}=1,\sum _{k=0}^{D}k\frac{{\chi }_k}{N}=1-\frac{1}{N}.$$

So instead of formulating an LDP for the sequence of random vectors $\frac{1}{N}({\chi }_0,\dots ,{\chi }_D)$ we shall formulate an LDP for a sequence of random vectors that is close to it and belongs to ℳ.

Let us introduce J: ℳ → ℝ via

$$J(p)=\beta E(p)-h(p),$$

where

$$h(p)=-\sum _{k=0}^D{p}_{k}ln{p}_k$$ (2)

is the entropy of the probability vector p = (p₀, …, p_D), and

$$E(p)=\sum _{k=0}^D{p}_{k}c(k)$$

is the energy associated with p ∈ ℳ.

The function J is strictly convex, and attains its minimum on ℳ at a unique point p^*. Let

$$I(p)=J(p)-J(p^{\ast }).$$ (3)

For a measure Q on [0, 1]^D+1 × ℳ we define Q⁽¹⁾ and Q⁽²⁾ as the marginal distributions of Q on [0, 1]^D+1 and ℳ respectively.

Theorem 1

There is a sequence of probability measures (Q_N)_N∈ℕ defined on [0, 1]^D+1 × ℳ with the following properties.

1. For each N, we have $Q_N^{(1)}={\nu }_N$.

2. For each N,

   $$Q_N\left\{(x,y)\in {[0,1]}^{D+1}\times \mathcal{M}:\sum _{k=0}^D\mid x_k-y_k\mid >\frac{1}{N}\right\}=0.$$

3. The sequence ${(Q_N^{(2)})}_{N\in \mathbb{N}}$ satisfies LDP on ℳ with the rate function I defined in (3).

Remark 1

This theorem says that though the random vector χ/N does not belong to ℳ, one can find another random vector that is, on the one hand, very close to χ/N and on the other hand belongs to ℳ and satisfies the LDP.

An immediate consequence is the following Law of Large Numbers:

Corollary 1

As N → ∞,

$$\left(\frac{{\chi }_0}{N},\frac{{\chi }_1}{N},\dots ,\frac{{\chi }_D}{N}\right)\to p^{\ast }$$

in probability.

Remark 2

The statements above show that with high probability the degree frequencies are close to p^*. Note that in most cases p^* is not the minimizer of the energy E on ℳ.

We shall now give a sketch of the proof of Theorem 1. The proof is based on the fact that trees with equal branching degree sequences have equal energy. Therefore,

$$P_N\{\chi (T)=n\}=\frac{e^{-\beta E(n)}C(N,n)}{Z_N},$$ (4)

where n = (n₀, …, n_D) and C(N, n) is the number of plane trees of order N with n_k nodes of branching degree k:

$$C(N,n)=\frac{1}{N}\left(\begin{array}{c}N\\ n_0,n_1,n_2\dots \end{array}\right)=\frac{1}{N}\frac{N!}{n_0!n_1!n_2!\dots }$$

if n₁ + 2n₂ + … = N − 1, and 0 otherwise (see e.g. Theorem 5.3.10 in [21]). One can apply the formula

$$\begin{array}{l}C(N,n)=exp\left\{N\left(-\sum _{k=0}^D\frac{n_k}{N}ln\frac{n_k}{N}+O\left(\frac{lnN}{N}\right)\right)\right\},\\ =exp\left\{Nh\left(\frac{n}{N}\right)+O(lnN)\right\},\text{as}N\to \infty .\end{array}$$

which holds true uniformly in n, see e.g. [7, Lemma I.4.4].

Plugging this into (4), we get

$$\begin{array}{l}{P}_N\left\{\frac{\chi (T)}{N}=\frac{n}{N}\right\}=\frac{e^{-N[\beta E\left(\frac{n}{N}\right)-h\left(\frac{n}{N}\right)]+O(lnN)}}{Z_n},\\ =\frac{e^{-NJ\left(\frac{n}{N}\right)+O(lnN)}}{Z_N},\end{array}$$

which is the desired asymptotics. In fact, the LDP that we claim is a stronger statement and requires extra work to complete this argument rigorously. The complete proof along with other random tree models will appear in detail elsewhere [1].

5 Applications to RNA secondary structure

In this section we compute the asymptotically most probable branching sequences for our model under an additional requirement that the coefficients c(m) are given by

$$c(m)=\{\begin{array}{ll}{A}_1,\hfill & m=0,\hfill \\ A_2,\hfill & m=1,\hfill \\ A_3-A_{4}m,\hfill & m\ge 2,\hfill \end{array}$$

for some numbers A₁, A₂, A₃, A₄. Both the dG 2.3 and dG 3.0 thermodynamic values in Table 1 satisfy this requirement, and we shall address these models in detail in the end of this section.

For this choice of c(m) we have

$$\beta E(p)=a_1{p}_0+a_2{p}_1+\sum _{m=2}^D(a_3-a_{4}m)p_m,$$

where

$$a_i=\beta A_i=\frac{A_i}{kT},i=1,2,3,4,$$

k = 1.99 Cal/mole·K being the Boltzmann constant, and T the temperature.

Corollary 1 implies that a typical conformation will have degree frequencies close to the solution of

$$S(p)\to min,p\in \mathcal{M},$$

where

$$S(p)=\sum _{m=0}^D{p}_{m}ln{p}_m+a_1{p}_0+a_2{p}_1+\sum _{m=2}^D(a_3-a_{4}m)p_m.$$

It is easy to see that, since the function x ↦ x ln x has infinite negative derivative at zero, the minimal value of S(p) cannot be attained at the boundary of ℳ. Moreover, S is strictly convex, so that there is a unique minimizer. Therefore we can solve this problem by the method of Lagrange multipliers. We set

$$S(p,\lambda )=S(p)+{\lambda }_0\left(\sum _{m=0}^D{p}_m-1\right)+{\lambda }_1\left(\sum _{m=0}^D{mp}_m-1\right).$$

The optimal vector (p*, λ) must satisfy

$$0=\frac{\partial }{\partial p_m}S(p^{\ast },\lambda )=\{\begin{array}{ll}{a}_1+ln{p}_0^{\ast }+1+{\lambda }_0,\hfill & m=0,\hfill \\ a_2+ln{p}_1^{\ast }+1+{\lambda }_0+{\lambda }_1,\hfill & m=1,\hfill \\ a_3-a_{4}m+ln{p}_m^{\ast }+1+{\lambda }_0+m{\lambda }_1,\hfill & m\ge 2.\hfill \end{array}$$

We rewrite this as

$$\{\begin{array}{l}{p}_0^{\ast }=b_1^{-1}\mu ,\hfill \\ p_1^{\ast }=b_2^{-1}\mu \nu ,\hfill \\ p_m^{\ast }=b_3^{-1}\mu {(b_4\nu )}^m,m\ge 2,\hfill \end{array}$$ (5)

where μ = e^−λ₀−1, ν = e^−λ₁ and b_i = e^a_i, i = 1, …, 4. We notice that

$$\begin{array}{l}1=\sum _{m=0}^D{p}_m^{\ast }=\mu \left(b_1^{-1}+b_2^{-1}\nu +b_3^{-1}\sum _{m=2}^D{(b_4\nu )}^m\right),\\ 1=\sum _{m=0}^D{mp}_m^{\ast }=\mu \left(b_2^{-1}\nu +b_3^{-1}\sum _{m=2}^{D}m{(b_4\nu )}^m\right).\end{array}$$

Instead of solving this system explicitly, let us consider the case of D ≫ 1, i.e., rewrite the limiting system for D → ∞:

$$\begin{array}{l}1=\mu \left(b_1^{-1}+b_2^{-1}\nu +b_3^{-1}\frac{b_4^2{\nu }^2}{1-b_4\nu }\right),\\ 1=\mu \left(b_2^{-1}\nu +b_3^{-1}\frac{2b_4^2{\nu }^2-b_4^3{\nu }^3}{{(1-b_4\nu )}^2}\right).\end{array}$$

Excluding μ we get a quadratic equation on ν and among the two roots we choose

$$\nu =\frac{\sqrt{b_3}}{b_4(\sqrt{b_1}+\sqrt{b_3})}$$

that satisfies 0 < b₄ν < 1.

Now we can express μ as

$$\mu =\frac{(-b_1+\sqrt{b_3{b}_1})b_4(-b_3+b_1)b_2{b}_1}{-b_2{b}_4{b}_3\sqrt{b_3{b}_1}-2{b_1}^2{b}_2{b}_4+3b_2{b}_4{b}_1\sqrt{b_3{b}_1}+2b_3{b_1}^2-b_3{b}_1\sqrt{b_3{b}_1}-{b_1}^2\sqrt{b_3{b}_1}}.$$

For the dG 3.0 model, we have A₁ = 4.1 KCal/mole, A₂ = 2.3 KCal/mole, A₃ = 1.9 KCal/mole, A₄ = 1.5 KCal/mole at T = 273 + 37 = 310 K. Then the solution given above, yields

$$\nu \approx 0.013,\mu \approx \mathrm{368.3.}$$

Likewise, for the dG 2.3 model, we have A₁ = 3.5 KCal/mole, A₂ = 3.0 KCal/mole, A₃ = 4.4 KCal/mole, A₄ = 0.2 KCal/mole at T = 273 + 37 = 310 K. Then the solution given above, yields

$$\nu \approx 0.46,\mu \approx \mathrm{121.3.}$$

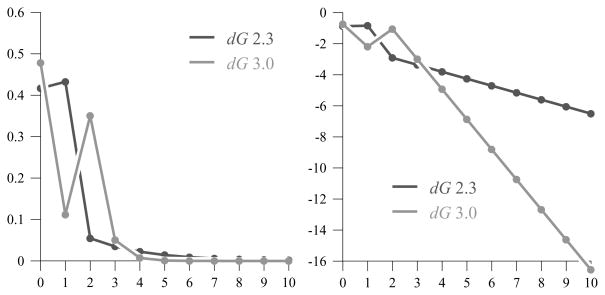
The first several values of p_m in both cases are displayed in Figure 2.

Figure 2.

The first 11 values of p_m for both the dG 3.0 model and the dG 2.3 model, where the right-hand graph shows the logarithm of the values.

The LDP for our model implies that, typically, the frequency of the loops of degree k decreases exponentially in k. However, the relative frequency for the first three terms and the exact rate of decay depends on the specific thermodynamic parameters. We know from previous results [10] that the trees which minimize the associated free energies in the dG 3.0 model maximize the number of vertices of degree 2. We see a similar behavior in the asymptotic distribution of vertex degrees under our LDP with the dG 3.0 thermodynamic values; in a typical large tree, 47.8% of the vertices would have degree 0 and 35.1% would have degree 2. Because of the impact of the entropy term correction, though, 11.2% of the vertices would have degree 1, and a vanishingly small but still nonzero percentage would be likely to have some degree ≥ 3. Thus, under the dG 3.0 model, the frequency of branching degrees in a typical large tree is a refined, and certainly more reasonable, distribution which still resembles our original calculation of the energy-minimizing configurations.

In contrast, the relative frequency among the vertices with degree 0, degree 1, and degree ≥ 2 is significantly different for the distribution calculated with the dG 2.3 values. Now, in a typical large tree, while 41.7% of the vertices would still have degree 0, only 5.5% would have degree 2, and 43.2% would have degree 1. Furthermore, although the percentage of loops with degree ≥ 3 still decreases exponentially, the rate is significantly lower than it was with the dG 3.0 values. The differences in the thermodynamic values are primarily a result of changes in the loop destabilizing energies for the hairpin and internal loops as well as more significant changes in the offset, free base penalty, and helix penalty for the multibranched loop energy function. In particular, the dG 2.3 values for the offset, free base penalty, and helix penalty are 4.60, 0.40, and 0.10 respectively, while the dG 3.0 values are 3.40, 0.0, .40. Intuitively, branching is significantly more favorable, energetically speaking, under the dG 3.0 thermodynamic model than it was in the dG 2.3 version. These changes then have a significant impact on the distribution among loops of small degrees as well as on the decay rate for the tail of the distribution.

In our model, we are able to assess the impact of these changes on the distribution of branching degrees for a typical large tree. However, our low-resolution model of RNA folding does not permit any assessment of the correctness of the two thermodynamic models, as was done in a recent analysis [6]. As we shall see, though, it is the dG 2.3 distribution, and not the dG 3.0 model, which more closely resembles the frequency of branching degrees in both the large subunit 23S ribosomal and the picornaviral RNA secondary structures.

6 Ribosomal and picornaviral branching degrees

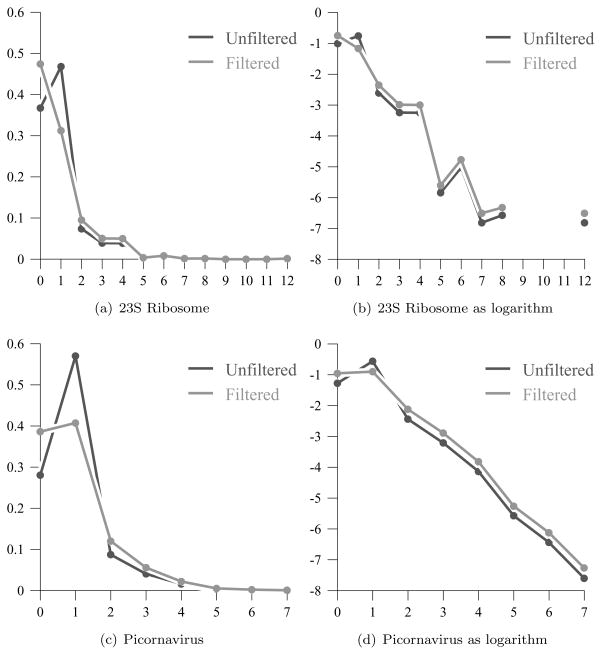
We analyze the branching degrees found in two different sets of RNA secondary structures, and compare them with the typical branching sequences for our large random trees. Our findings are summarized here in Figure 3 and in the discussion, while more details are given in Appendix A. Overall, the branching of these secondary structures agrees with the results for our model, although there are deviations which suggest interesting avenues for further investigation. Our comparisons are qualitative, rather than quantitative, since it would be unrealistic to expect precise agreement between our “low-resolution” model of RNA folding and the branching configurations of large ribosomal and picornaviral secondary structures. Still, we find some striking similarities between the predictions based on our model and the data for real RNA sequences.

Figure 3.

The distribution of loop degrees as fractions of the total. Each graph shows both the averages over the data set, as given in Tables 4 and 10, and the filtered averages, as given in Tables 7 and 14, after the smallest internal loops have been removed.

The first set of results, found in Appendix A.1, is for the large subunit 23S ribosomal RNA secondary structures determined through comparative sequence analysis by the Gutell Lab. We give results for 20 of the 77 pseudoknot-free sequences available online through their Comparative RNA Web (CRW) Site and Project [2]. The chosen sequences were also used in the analyses of [8] and are representative of the whole set. As seen in Table 2, the average sequence length is 2756.2 nucleotides, although there is certainly variability among the different types of ribosomal sequences. Since our results are asymptotic, we disregard the particular energy function for the external loop, and the degrees of the external loops are listed separately in Table 2.

In Tables 3 and 4, we give the distribution of loop degrees, where the degree of a loop is one less than the number of base pairs contained in the loop. We see that the most prevalent loops (46.81% overall) are the internal loops with degree 1, followed by the hairpin structures with degree 0. Most of the branching loops have degree 2, which agrees with the previous combinatorial analysis [10], although there is a distribution extending out to branching loops of degree 12. We note that the distribution of branching loops tails off much as we expected, although there is an interesting peak of degree 6 loops as well as smaller peaks at 4, 8, and of course 12. We find this correlation between loop parity and frequency interesting, although since ribosomal structure is highly conserved across various organisms, the distribution of loop degrees for these 23S RNA secondary structures are by no means independent.

As we do for the picornaviral sequences, discussed below, we investigate in more detail the distribution of sizes among the internal loops. As we see from Table 5, with only a few exceptions, the internal loops contain fewer than 16 unpaired bases, and a substantial fraction (48.36% on average) contain at most 2. It is reasonable [27] to consider two helices which are interrupted by an internal loop of fewer than 3 bases as one contiguous stem. When we adjust the count of loop degrees accordingly, by excluding internal/degree 1 loops with at most 2 unpaired bases as in Tables 6 and 7, then we see a distribution with different relative numbers of hairpin/degree 0, internal/degree 1, and branching/degree ≥ 2 loops. For these 23S ribosomal secondary structures, our prediction branching distributions for dG 2.3 are closer to the original unfiltered distribution, although the opposite will be true for the picornaviral secondary structures.

The second set of results is found in Appendix A.2. We consider the 11 picornaviral sequences analyzed in [19], which are available online from the Palmenberg Lab through http://www.virology.wisc.edu/acp/RNAFolds. The predicted secondary structures were computed by the mfold program v2.2, using the default values [19]. The average length for these sequences, as seen from Table 8, is 7566.27 bases – considerably longer than the large subunit 23S ribosomal sequences. We also list the external loop degrees separately in Table 8, since this special energy function is not considered in our asymptotic results.

Again, the most prevalent loops have degree 1, as seen in Tables 9 and 10, and the most common type of internal loops (48.14% on average) are those containing at most 2 unpaired bases. However, the relative number of hairpin/degree 0, internal/degree 1, and branching/degree ≥ 2 loops given in Tables 9 and 10 differs significantly from the LDP distribution. A large part of this deviation is resolved after further investigation into the distribution of internal loop sizes. As seen in Tables 11 and 12, there is a much broader distribution for the sizes of internal loops. While most contain fewer than 16 unpaired bases, the number of “large” internal loops does not drop off as sharply for the picornaviral secondary structures as it did for the 23S ribosomal ones. When we filter the data by excluding the smallest internal loops, as in Tables 13 and 14, then we see a distribution that agrees even more closely with our LDP probabilities. In this case, though, we have nearly equal numbers of hairpin/degree 0 loops and internal/degree 1 loops, while the numbers of branching/degree ≥ 2 loops drop off almost by a factor of 2. Thus, the predicted picornaviral configurations are less extensively branched than the ribosomal secondary structures, and the degree of branching more closely agrees with our LDP probabilities for the dG 2.3 model.

7 Discussion of related results

We adopt here a statistical mechanics approach, not to predict base pairs for a particular RNA sequence, but to analyze what a typical branching distribution might be for an arbitrary large RNA secondary structure. This work joins a growing body of results which analyze different general characteristics of RNA secondary structures, both theoretically [4, 12, 17, 18] and computationally [3, 9, 16, 20, 23, 24]. The qualities investigated have been the free energy and molecular stability [3, 16, 20, 23, 24] as well as the number and type of different substructural elements [4, 9, 12, 17, 18]. Asymptotics of the expected maximum number of base pairs are studied in [4], but the overall molecular configurations are not addressed.

Statistics for different structural elements are computed for short RNA sequences ≤ 100 bases in [9]. The unfiltered distribution of picornaviral degrees agrees closely with their statistical reference probability densities, whereas the distribution of the 23S ribosomal degrees resembles their “natural” sequence distribution by having slightly more hairpin/degree 0 loops and fewer internal/degree 1 loops. The statistics of average branching degree given in [9] reflect the fact that for large RNA sequences the size N of the associated tree is, typically, also large. Therefore, the average branching degree is close to 1 due to the identity

$$\sum _{k=0}^{D}k\frac{{\chi }_k}{N}=1-\frac{1}{N}.$$

This also agrees with the theoretical limit given in [12]; the asymptotic average branching degree of 1 was derived for non-root vertices using a model of RNA secondary structures at the base level and complicated recursion formulae depending on n, the number of bases in the sequence. We have not yet investigated the other characteristics analyzed in [9] and [12], however it may be possible to extend our low-resolution model of RNA folding and this statistical mechanics approach to other properties of RNA secondary structures.

In [17], the typical configuration of large subunit ribosomal RNA is investigated using a approach based on generating functions and stochastic context-free grammars. This approach yields explicit formulas for the frequency of different structural elements as a function of the sequence length n. Using the average sequences lengths for the 23S ribosomal and picornaviral secondary structures as n₁ and n₂, we computed the predicted number of hairpin, internal, and branching loops as well as the average degree of a branching loop. As in [17], we compare the averages from the RNA secondary structures and the predicted frequencies, and find reasonably good agreement for the 23S ribosomal structures. The relative differences for the predicted frequencies from the unfiltered 23S ribosomal averages are: −3.28% for hairpin loops, −13.05% for internal loops, 1.09% for branching loops, −6.35% for the total number of loops, and 1.84% for the average branching degree. In contrast, the comparisons for the picornaviral secondary structures are not as good. The relative differences for the predicted frequencies from the unfiltered picornaviral averages are: 21.67% for hairpin loops, −31.46% for internal loops, 6.94% for branching loops, −10.52% for the total number of loops, and 19.42% for the average branching degree. Since the equations in [17] were derived by training the grammar on a database of large subunit ribosomal RNA, it is perhaps not surprising that the predictions of the model do not correspond as well to the picornaviral secondary structures. The paper [18] provides related results by considering a model of RNA folding where two bases pair with probability p and investigates different properties of the RNA secondary structures, but not does not include an analysis of branching degrees.

8 Conclusions

We considered Gibbs distributions for our plane tree model of RNA folding based on the nearest neighbor thermodynamics. An important feature of our model is that we can describe the typical branching configurations of the trees by calculating the asymptotic degree sequences via a Large Deviation Principle (LDP). As discussed, this has at least two implications for the branching of large RNA secondary structures, such as the large subunit 23S ribosomal molecules or RNA viral genomes like picornaviruses.

One implication concerns the asymptotic distribution of vertex degrees in a large random tree from our model. The LDP for our model implies that, typically, the frequency of the loops of degree k decreases exponentially in k. The exact rate of decay depends on the specific thermodynamic parameters, however, and we considered two sets of energy values, the current standard dG 3.0 and the former standard dG 2.3. Surprisingly, we find that the typical distribution based on the dG 2.3 parameters corresponds more closely to the branching degrees of both the picornaviral and ribosomal RNA secondary structures. The differences in the thermodynamic values are primarily a result of changes in the loop destabilizing energies for the hairpin and internal loops as well as more significant changes in the offset, free base penalty, and helix penalty for the multibranched loop energy function. These changes then have a significant impact on the distribution among loops of small degrees as well as on the decay rate for the tail of the distribution. To be able to distinguish unusual substructures against the background of a typical configuration, we will need to understand better the impact of different thermodynamic values on the behavior of the model.

A second implication to emerge from our current analysis is that combinatorial constraints lead to important entropy considerations in determining the most likely branching distributions in large random trees. The nontrivial combinatorics of the plane trees implies that typical trees are minimizers of the free energy corrected by an extra entropy term. Thus, although the typical trees in the dG 3.0 model are structurally, and therefore energetically, related to the trees which have minimal energy, a typical large tree will not be a minimizer of the free energy understood as the sum of the energies of individual loops. In fact, the LDP tells us that, in our combinatorial model of RNA folding, the energy-minimizing trees are extremely improbable. Thus, when modeling the folding of large RNA molecules, it is important to include entropy considerations which distinguish the most likely configurations from those which simply minimize the additive free energy.

A Analysis of RNA Branching Degrees

A.1 23S Ribosomal RNA

Table 2.

Sequence information, including the degree of the external loop, for 20 of the 77 pseudoknot-free 23S ribosomal RNA secondary structures from the CRW [2]. The 20 selected were also used in the analyses of [8], and are representative of the whole set. The different types of sequences are (a) Archae, (b) Eubacteria, (c) Choloroplast, (m) Mitochondria, and (e) Eucarya.

Index	Type	Organism Name	GenBank Accession #	Length	Degree
1	a	Haloarcula marismortui	X13738	2925	1
2	a	Thermococcus celer	M67497	3029	1
3	b	Thermotoga maritima	M67498	3023	1
4	b	Thermus thermophilus	X12612	2915	1
5	b	Borrelia burgdorferi	M88330	2926	1
6	b	Escherichia coli	J01695	2904	1
7	b	Pseudomonas aeruginosa	Y00432	2893	1
8	b	Bacillus subtilis	K00637 AF008220 Z99119	2927	1
9	b	Mycobacterium leprae	X56657	3122	1
10	c	Chlamydomonas reinhardtii	X15727	2902	1
11	c	Zea mays	Z00028	2985	1
12	m	Chlamydomonas eugametos	AF008237	1915	13
13	m	Saccharomyces cerevisiae	J01527	3273	1
14	m	Zea mays	K01868	3514	6
15	m	Caenorhabditis elegans	X54252	953	8
16	m	Drosophila melanogaster	X53506	1335	9
17	m	Xenopus laevis	M10217	1640	12
18	e	Giardia intestinalis	X52949	2850	10
19	e	Saccharomyces cerevisiae	U53879	3554	7
20	e	Arabidopsis thaliana	X52320	3539	12

Table 3.

Degree distributions of loops.

Index	sum	0	1	2	3	4	5	6	7	8	9	10	11	12
1	197	70	93	14	9	9		2
2	191	73	88	13	7	6	1	1		1				1
3	201	72	94	15	9	9		1	1
4	192	72	91	12	7	6	1	1		1				1
5	201	71	95	15	9	9		2
6	199	70	95	14	10	8		1	1
7	199	70	95	14	10	8		1	1
8	207	71	102	14	9	9		1	1
9	205	74	100	14	7	6	1	1		1				1
10	202	70	98	14	9	9		2
11	206	71	100	15	9	9		2
12	115	49	50	6	3	5	1	1
13	157	59	73	12	6	3	1	2						1
14	180	65	85	15	6	6	1	2
15	49	23	18	4	1	3
16	77	33	33	4	1	6
17	101	41	46	6	3	3	2
18	190	74	82	17	7	8	1	1
19	221	80	102	21	8	8		1		1
20	218	80	102	20	7	6	1	1		1
total	3508	1288	1642	259	137	136	10	23	4	5	0	0	0	4

Table 4.

Degree distributions of loops as percentages.

Index	0	1	2	3	4	5	6	7	8	9	10	11	12
1	35.5	47.2	7.1	4.6	4.6		1.0
2	38.2	46.1	6.8	3.7	3.1	0.5	0.5		0.5				0.5
3	35.8	46.8	7.5	4.5	4.5		0.5	0.5
4	37.5	47.4	6.2	3.6	3.1	0.5	0.5		0.5				0.5
5	35.3	47.3	7.5	4.5	4.5		1.0
6	35.2	47.7	7.0	5.0	4.0		0.5	0.5
7	35.2	47.7	7.0	5.0	4.0		0.5	0.5
8	34.3	49.3	6.8	4.3	4.3		0.5	0.5
9	36.1	48.8	6.8	3.4	2.9	0.5	0.5		0.5				0.5
10	34.7	48.5	6.9	4.5	4.5		1.0
11	34.5	48.5	7.3	4.4	4.4		1.0
12	42.6	43.5	5.2	2.6	4.3	0.9	0.9
13	37.6	46.5	7.6	3.8	1.9	0.6	1.3						0.6
14	36.1	47.2	8.3	3.3	3.3	0.6	1.1
15	46.9	36.7	8.2	2.0	6.1
16	42.9	42.9	5.2	1.3	7.8
17	40.6	45.5	5.9	3.0	3.0	2.0
18	38.9	43.2	8.9	3.7	4.2	0.5	0.5
19	36.2	46.2	9.5	3.6	3.6		0.5		0.5
20	36.7	46.8	9.2	3.2	2.8	0.5	0.5		0.5
total	36.72	46.81	7.38	3.91	3.88	0.29	0.66	0.11	0.14	0	0	0	0.11

Table 5.

Number of internal loops of different sizes, given as the distribution of loops with at most 15 unpaired bases and as a list of large internal loop sizes with multiplicity.

Index	Number of internal loops with 1 ≤ size ≤ 15															List of large loop sizes
	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
1	27	13	6	7	4	7	4	6	10	4	1	1	1	1		37
2	26	15	2	8	5	6	5	6	9	2	1	1		1		35
3	24	17	4	10	4	10	7	4	6	4	2			1		31
4	27	17	4	11	6	8	4	3	5	2	2			1		31
5	26	18	4	10	7	8	5	4	7	2	1	1		1		30
6	24	19	3	11	8	7	3	5	9	2	2			1		30
7	26	17	5	11	6	8	5	4	7	2	2			1		31
8	32	18	4	10	7	9	5	4	6	2	2			1	1	30
9	29	19	3	10	8	9	6	3	5	3	2			1	1	31
10	29	19	3	9	6	10	4	4	7	2	2			1		29, 41
11	28	18	6	10	7	6	7	5	7	1	2			1		20, 29
12	15	9	4	4	1	4	2	1	2	3	1				1	18, 20, 27
13	27	12	4	6	3	5		4	4		2		1	1		28, 36, 50, 64
14	26	16	4	9	3	5	5	4	7	2	1	1		1		31
15	4	8	2	1	1				2
16	10	9	3	3		1		1	4							17, 20
17	15	9	5	4	2	3		1	2	1			1			18, 33, 47
18	27	14	4	9	2	5	5	5	3	3	1	1		1		25, 27
19	34	19	3	11	5	7	7	4	5	3	1	1		1		36
20	35	17	4	9	5	7	7	3	5	3	1	1		3		16, 37

Table 6.

Degree distributions of loops with contiguous stems.

Index	sum	0	1	2	3	4	5	6	7	8	9	10	11	12
1	157	70	53	14	9	9		2
2	150	73	47	13	7	6	1	1		1				1
3	160	72	53	15	9	9		1	1
4	148	72	47	12	7	6	1	1		1				1
5	157	71	51	15	9	9		2
6	156	70	52	14	10	8		1	1
7	156	70	52	14	10	8		1	1
8	157	71	52	14	9	9		1	1
9	157	74	52	14	7	6	1	1		1				1
10	154	70	50	14	9	9		2
11	160	71	54	15	9	9		2
12	91	49	26	6	3	5	1	1
13	118	59	34	12	6	3	1	2						1
14	138	65	43	15	6	6	1	2
15	37	23	6	4	1	3
16	58	33	14	4	1	6
17	77	41	22	6	3	3	2
18	149	74	41	17	7	8	1	1
19	168	80	49	21	8	8		1		1
20	166	80	50	20	7	6	1	1		1
total	2714	1288	848	259	137	136	10	23	4	5	0	0	0	4

Table 7.

Degree distributions of loops as percentages with contiguous stems.

Index	0	1	2	3	4	5	6	7	8	9	10	11	12
1	39.3	29.8	7.9	5.1	5.1		1.1
2	41.2	26.6	7.3	4.0	3.4	0.6	0.6		0.6				0.6
3	40.7	29.9	8.5	5.1	5.1		0.6	0.6
4	41.4	27.0	6.9	4.0	3.4	0.6	0.6		0.6				0.6
5	40.8	29.3	8.6	5.2	5.2		1.1
6	40.0	29.7	8.0	5.7	4.6		0.6	0.6
7	40.0	29.7	8.0	5.7	4.6		0.6	0.6
8	42.3	31.0	8.3	5.4	5.4		0.6	0.6
9	43.5	30.6	8.2	4.1	3.5	0.6	0.6		0.6				0.6
10	41.2	29.4	8.2	5.3	5.3		1.2
11	41.3	31.4	8.7	5.2	5.2		1.2
12	25.3	13.4	3.1	1.5	2.6	0.5	0.5
13	33.0	19.0	6.7	3.4	1.7	0.6	1.1						0.6
14	36.9	24.4	8.5	3.4	3.4	0.6	1.1
15	11.2	2.9	1.9	0.5	1.5
16	16.6	7.0	2.0	0.5	3.0
17	21.1	11.3	3.1	1.5	1.5	1.0
18	41.8	23.2	9.6	4.0	4.5	0.6	0.6
19	48.5	29.7	12.7	4.8	4.8		0.6		0.6
20	48.2	30.1	12.0	4.2	3.6	0.6	0.6		0.6
total	47.46	31.25	9.54	5.05	5.01	0.37	0.85	0.15	0.18	0	0	0	0.15

A.2 Picornaviral RNA

Table 8.

Sequence information, including the degree of the external loop, for the 11 picornaviral sequences analyzed in [19], available online through http://www.virology.wisc.edu/acp/RNAFolds.

Index	Virus Name	GenBank Acc. #	Length	Degree
1	coxsackievirus B3	M33854	7396	13
2	ECHO virus-22	L02971	7339	17
3	encephalomyocarditis virus-A	M81861	7735	25
4	foot-and-mouth disease virus-A12	M10975	8214	1
5	hepatitis A virus-Hml75	M14707	7478	20
6	rhinovirus-14	K02121	7212	16
7	rhinovirus-16	L24917	7124	11
8	Mengovirus-M	L22089	7761	26
9	poliovirus 1-Mahoney	J0228140	7440	20
10	poliovirus 3-Sabin	X00596	7432	22
11	Theiler’s murine encephalomyelitis virus-Bean	M16020	8098	37

Table 9.

Degree distributions of loops.

Index	sum	0	1	2	3	4	5	6	7
1	499	142	281	41	20	12	3
2	478	130	275	42	23	7	1
3	530	138	320	44	16	11	1
4	594	167	337	45	25	14	3	1	2
5	482	136	267	58	12	4	3	2
6	454	126	259	37	25	5	2
7	456	140	237	46	23	6	1	3
8	494	130	300	37	17	8	1	1
9	485	143	267	43	21	8	2		1
10	507	137	293	50	20	4	2	1
11	537	157	309	38	21	9	2	1
total	5516	1546	3145	481	223	88	21	9	3

Table 10.

Degree distributions of loops as percentages.

Index	0	1	2	3	4	5	6	7
1	26.4	52.3	7.6	3.7	2.2	0.6
2	24.2	51.2	7.8	4.3	1.3	0.2
3	25.7	59.6	8.2	3.0	2.0	0.2
4	31.1	62.8	8.4	4.7	2.6	0.6	0.2	0.4
5	25.3	49.7	10.8	2.2	0.7	0.6	0.4
6	23.5	48.2	6.9	4.7	0.9	0.4
7	26.1	44.1	8.6	4.3	1.1	0.2	0.6
8	24.2	55.9	6.9	3.2	1.5	0.2	0.2
9	26.6	49.7	8.0	3.9	1.5	0.4		0.2
10	25.5	54.6	9.3	3.7	0.7	0.4	0.2
11	29.2	57.5	7.1	3.9	1.7	0.4	0.2
total	28.03	57.02	8.72	4.04	1.60	0.38	0.16	0.05

Table 11.

Distribution of internal loops with at most 15 unpaired bases.

Index	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
1	68	65	45	29	9	9	9	3	6	6	8	4	3	7	2
2	68	60	33	26	15	11	8	5	9	11	3	1	4	4	1
3	83	66	52	32	20	8	9	5	9	5	5	5	4	7	2
4	99	90	48	26	16	13	9	7	6	6	2	3	3	3	2
5	51	90	34	23	10	12	6	5	7	7	8	3	2	4	1
6	67	59	33	19	12	15	4	3	6	3	4	5	6	1	6
7	49	66	21	30	12	8	7	3	5	2	3	2	2	2	4
8	63	68	38	25	29	14	6	10	10	10	3	2	4	1	5
9	55	69	36	20	14	7	12	5	12	4	2	4	3	2	4
10	68	65	34	35	15	9	10	9	13	8	4	5	3	4	1
11	79	66	42	32	20	8	10	9	6	6	5	4	4	2	1

Table 12.

Distribution of large (≥ 15 unpaired bases) internal loop sizes.

Index	16	17	18	19	20	21	22	23	24	25	26	27	28	29	30
1			1			4	3
2	2	2	2	3	1	1	1	1	1	1		1
3	3	1	1		1			1						1
4	3								1
5				1			2						1
6		2	1	3	3	1	2	1			1			1	1
7	3	1	5	2	2		1	3	1		1	2
8	1	4	1	1	1			2	1						1
9	5	3	5	2	1		1	1
10	3	2	1		1				1				1		1
11	2	3		2	3		1			1				2	1

Table 13.

Degree distributions of loops with contiguous stems.

Index	sum	0	1	2	3	4	5	6	7
1	366	142	148	41	20	12	3
2	350	130	147	42	23	7	1
3	381	138	171	44	16	11	1
4	405	167	148	45	25	14	3	1	2
5	341	136	126	58	12	4	3	2
6	328	126	133	37	25	5	2
7	341	140	122	46	23	6	1	3
8	363	130	169	37	17	8	1	1
9	361	143	143	43	21	8	2		1
10	374	137	160	50	20	4	2	1
11	392	157	164	38	21	9	2	1
total	4002	1546	1631	481	223	88	21	9	3

Table 14.

Degree distributions of loops as percentages with contiguous stems.

Index	0	1	2	3	4	5	6	7
1	35.1	36.6	10.1	5.0	3.0	0.7
2	31.8	35.9	10.3	5.6	1.7	0.2
3	35.6	44.1	11.3	4.1	2.8	0.3
4	48.0	42.5	12.9	7.2	4.0	0.9	0.3	0.6
5	34.3	31.8	14.6	3.0	1.0	0.8	0.5
6	30.7	32.4	9.0	6.1	1.2	0.5
7	33.2	28.9	10.9	5.5	1.4	0.2	0.7
8	32.0	41.6	9.1	4.2	2.0	0.2	0.2
9	34.6	34.6	10.4	5.1	1.9	0.5		0.2
10	33.9	39.6	12.4	5.0	1.0	0.5	0.2
11	40.1	41.8	9.7	5.4	2.3	0.5	0.3
total	38.63	40.75	12.02	5.57	2.20	0.52	0.22	0.07