Rhythmicity without Synchrony in the Electrically Uncoupled Inferior Olive

Abstract

Neurons of the inferior olivary nucleus (IO) form the climbing fibers that excite Purkinje cells of the cerebellar cortex. IO neurons are electrically coupled through gap junctions, and they generate synchronous, subthreshold oscillations of membrane potential at ∼5–10 Hz. Experimental and theoretical studies have suggested that both the rhythmicity and synchrony of IO neurons require electrical coupling. We recorded from pairs of IO neurons in slices of mouse brainstem in vitro. Most pairs of neurons from wild-type (WT) mice were electrically coupled, but coupling was rare and weak between neurons of knock-out (KO) mice for connexin36, a neuronal gap junction protein. IO cells in both WT and KO mice generated rhythmic membrane fluctuations of similar frequency and amplitude. Oscillations in neighboring pairs of WT neurons were strongly synchronized, whereas the oscillations of KO pairs were uncorrelated. Spontaneous oscillations in KO neurons were not blocked by tetrodotoxin. Spontaneously oscillating neurons of both WT and KO mice generated occasional action potentials in phase with their membrane rhythms, but only the action potentials of WT neuron pairs were synchronous. Harmaline, a β-carboline derivative thought to induce tremor by facilitating rhythmogenesis in the IO, was injected systemically into WT and KO mice. Harmaline-induced tremors were robust and indistinguishable in the two genotypes, suggesting that gap junction-mediated synchrony does not play a role in harmaline-induced tremor. We conclude that electrical coupling is not necessary for the generation of spontaneous subthreshold oscillations in single IO neurons, but that coupling can serve to synchronize rhythmic activity among IO neurons.

Many neurons in the CNS generate rhythmic, synchronized activity, using mechanisms that are poorly understood. One of the most dramatically rhythmic brain structures is the inferior olive (IO). Its neurons are the origin of the climbing fibers, which provide strong synaptic excitation to the Purkinje cells of the cerebellum; every action potential in a climbing fiber evokes a complex spike in all of its postsynaptic Purkinje cells (Eccles et al., 1966, 1967). IO neurons have several distinctive physiological characteristics (Crill, 1970; Llinás and Yarom, 1981a,b), including a strong tendency to generate spontaneous subthreshold oscillations of their membrane potential (Benardo and Foster, 1986;Llinás and Yarom, 1986). IO cells fire action potentials at frequencies from 1 to 10 Hz (Armstrong et al., 1968). The subthreshold membrane oscillations of IO cells determine the precise timing of IO action potentials and thus also the timing of the complex spikes of Purkinje cells (Llinás, 1991; Lampl and Yarom, 1993). The firing of complex spikes in multiple Purkinje cells, and by inference the spiking of multiple IO neurons, often occurs with a significant degree of synchrony that may play an important role in the coordination and timing of motor control (Bell and Kawasaki, 1972; Sasaki et al., 1989;Llinás, 1991; Welsh et al., 1995).

A variety of mechanisms have been proposed to explain the rhythmicity and synchrony of IO neurons. Subthreshold membrane oscillations seem to involve the interaction of several types of voltage-dependent ion channels in IO cell membranes, most notably low-threshold calcium channels, hyperpolarization-activated cation channels, and perhaps the NMDA subtype of glutamate-gated channels (Llinás and Yarom, 1981a,b, 1986; Benardo and Foster, 1986; Yarom and Llinás, 1987;Bal and McCormick, 1997; Placantonakis and Welsh, 2001). Synchronous firing is presumed to require gap junctions, which interconnect IO neurons and mediate direct electrical coupling (Llinás et al., 1974; Sotelo et al., 1974; Llinás and Yarom, 1981b; Benardo and Foster, 1986). However, several lines of evidence have inspired the hypothesis that electrical coupling not only mediates synchrony but also is essential for generating the subthreshold oscillations themselves (Llinás, 1991; Yarom, 1991; Sherman and Rinzel, 1992;Lampl and Yarom, 1997; Manor et al., 2000). However, this hypothesis has never been directly tested.

Here we describe studies of IO neurons in a mouse with a null mutation for the gene encoding connexin36 (Cx36), the protein most prevalent in neuronal gap junctions of the mammalian brain (Condorelli et al., 2000; Rash et al., 2000). Previous work on Cx36knock-out (KO) mice showed that electrical coupling is almost entirely absent between certain inhibitory neurons of the neocortex (Deans et al., 2001), the hippocampus (Hormuzdi et al., 2001), and the reticular nucleus of the thalamus (Landisman et al., 2002), all of which are frequently coupled in wild-type (WT) animals. We show here that both the incidence and strength of electrical coupling between IO neurons are also greatly reduced in the Cx36 KO mouse compared with WT controls. The uncoupled IO network in the KO mice continues to generate subthreshold membrane oscillations, but they are asynchronous. Surprisingly, a type of drug-induced tremor that is thought to depend on synchronized discharges in the olivocerebellar system was just as vigorous in the KO mice as in the WT mice.

MATERIALS AND METHODS

Longitudinal (parasagittal) slices (300 μm thick) were prepared as described previously (Llinás and Yarom, 1981b; Gibson et al., 1999) from Cx36 WT or KO littermate mice [postnatal day 14 (P14) to P17]. The construction of the mice and β-galactosidase histochemistry have been described in detail previously (Deans et al., 2001). Briefly, mice were intracardially perfused with 5–10 ml of an ice-cold solution containing (in mm): 124 sucrose, 3 KCl, 1.25 NaH₂PO₄, 2 MgSO₄, 26 NaHCO₃, 10 dextrose, and 2 CaCl₂. The brain was then rapidly removed, and slices were made with a vibratome (Campden Instruments, Lafayette, IN). Slices were incubated for 45 min at 32°C and then kept at room temperature in a holding chamber until they were transferred to a submersion-style recording chamber held at 32°C. The incubation solution contained (in mm): 126 NaCl, 3 KCl, 1.25 NaH₂PO₄, 2 MgSO₄, 26 NaHCO₃, 10 dextrose, and 2 CaCl₂, saturated with 95% O₂/5% CO₂; the recording solution was the same, except for reduced divalent ion levels (1 MgSO₄ and 1 CaCl₂) and a slight increase in potassium (3.5 KCl). Micropipettes were filled with (in mm): 135 potassium gluconate, 4 KCl, 2 NaCl, 10 HEPES, 0.2 EGTA, 4 ATP-Mg, 0.3 GTP-Tris, and 7 phosphocreatine-Tris, pH 7.25 (280 mOsm). All recordings were made in current-clamp mode using matched amplifiers (Axoprobe; Axon Instruments, Foster City, CA), and cells were visualized under IR-differential interference contrast (DIC) optics using a Zeiss (Thornwood, NY) Axioskop and a Hamamatsu (Bridgewater, NJ) CCD camera.

Data were digitized, collected, and analyzed with auto- and cross-correlograms and power spectra using Labview (National Instruments, Austin, TX) routines written by Jay R. Gibson (University of Texas Southwestern Medical Center, Dallas, TX), as described previously (Beierlein et al., 2000). Subthreshold membrane potentials were band-pass filtered (1–70 Hz) before analysis. The correlograms were first averaged and then normalized by the product of the SD of the signal in each recording: Normalized correlation (t) = [Average(A[t′] × B[t′− t])]/[SD(A[t′]) × SD(B[t′])], whereA[t′] and B[t′] represent the two voltage records, t′ is the time variable for the actual traces, and t is the time variable for the correlation. For each neuron pair, we report the average cross-correlation derived from five 10 sec epochs of activity. Shuffled controls were obtained by phase-shifting spontaneous oscillations from 10 WT cell pairs by regular intervals, multiple times, and then calculating the cross-correlation at time 0 for each shuffled epoch. The correlations from all phase-shifted samples were averaged (mean, 0.03), and the 95% confidence interval was estimated from the variance. Action potential correlations were calculated as described previously (Beierlein et al., 2000).

For the tremor experiments, age-matched (P14–P31) groups of WT and KO mice were tested with the experimenter blind as to genotype. Each mouse was injected intraperitoneally with harmaline (10–15 mg/kg). Immediately after injection, mice were placed in a small ventilated chamber suspended from a transducer that measured vertical force. Harmaline-induced tremor patterns were continuously monitored, recorded on a computer, and quantified offline. Power spectra for each mouse were calculated from the average of three robust, representative 5 sec epochs of tremor obtained while animals were not locomoting.

Data are reported as mean ± SD unless specified otherwise.

RESULTS

Electrical coupling requires Cx36

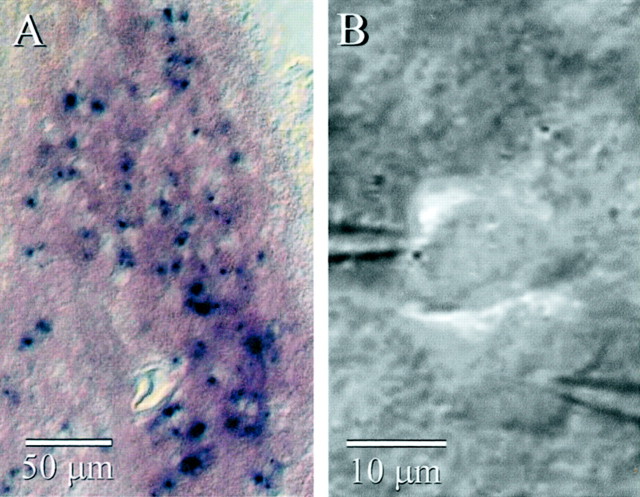
β-galactosidase histochemistry of Cx36 KO tissue showed cellular staining distributed throughout the IO (Fig.1A). The intensity of staining varied widely across neurons, and some were not stained at all; the absence of stain might indicate lack of gene expression, or it could reflect a technical problem, such as poor reagent penetrance. Regardless, the β-galactosidase staining is consistent with previous evidence that Cx36 is widely expressed in the neurons of the IO (Condorelli et al., 2000; Rash et al., 2000).

Fig. 1.

IO neurons from KO mice. A, β-Galactosidase histochemistry of a parasagittal section from aCx36 KO mouse shows many strongly stained cells in the IO nucleus. B, IR-DIC image of two very closely spaced neurons during paired whole-cell recordings from the IO of a KO mouse. Despite their proximity, these cells were not electrically coupled to each other.

We recorded from neurons along the full rostrocaudal extent of the inferior olive. Most cells generate spontaneous subthreshold oscillations of membrane potential (Fig.2A) (see below). The intrinsic spiking properties of IO cells (Table1) were similar to those described previously (Llinás and Yarom, 1981b). Each action potential displayed a rapid, overshooting spike of ∼100 mV, followed by a smaller (∼50 mV) but prolonged plateau phase (Fig.2A,B,D) that had several voltage “ripples” across it (see Fig. 6A–C, spikes). The action potentials of IO neurons from WT and Cx36 KO mice did not differ in amplitude, duration, spontaneous frequency, or the number of plateau ripples (Table 1). Input resistances, measured with −100 pA hyperpolarizing steps, were ∼30% higher in KO neurons than in WT neurons. Resting membrane potentials (defined as the mean membrane potential in spontaneously oscillating cells in the absence of holding current) did not differ between WT and KO cells.

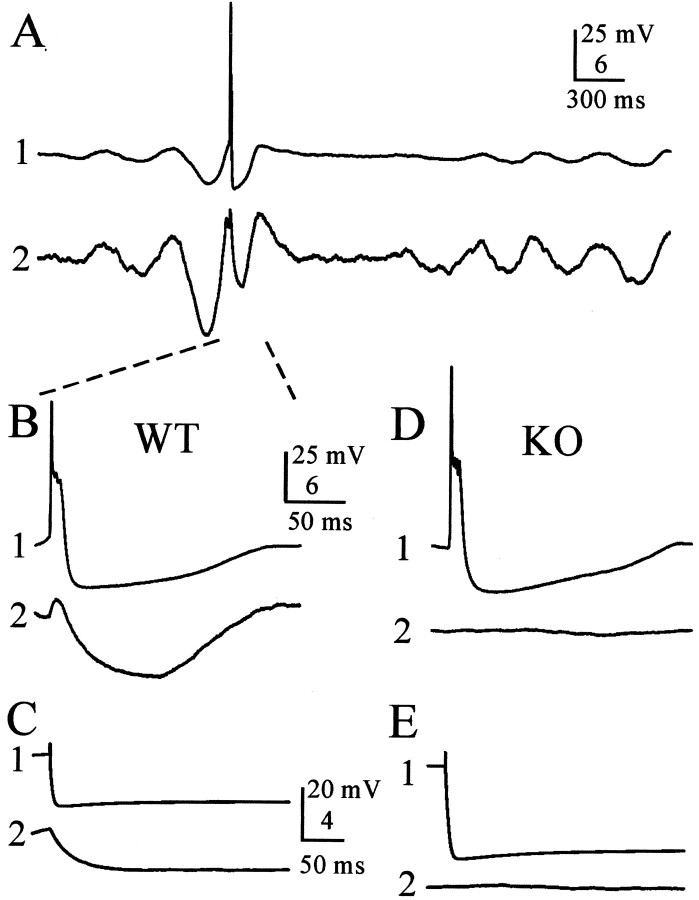
Fig. 2.

Electrical coupling is greatly diminished in theCx36 KO mouse. A, Paired whole-cell recordings from coupled WT cells show synchronized subthreshold oscillations, occasional action potentials in cell 1, and correlated electrical coupling potentials in cell 2. Note that the gain for cell 2 is higher than that from cell 1. B, Expanded view of a spontaneous action potential in cell 1 and its associated electrotonically propagated spikelet in cell 2 (same recordings shown in A). Dashed lines show where traces inA are expanded in B. C, Electrical coupling in a pair of WT neurons. A hyperpolarizing current step (−1 nA) injected into cell 1 induced an electrotonically propagated hyperpolarization in cell 2. D, E, Electrical coupling was absent in a representative pair of IO cells from a Cx36KO mouse. To remove the effects of spontaneous membrane oscillations, voltage traces in C–E are the averages of 10 trials, with the exception of the representative action potential in the KO cell shown in D.

Table 1.

Physiological properties of inferior olivary neurons^1-a

	WT	KO
Input resistance (MΩ)*	69  ± 32 (30)	91  ± 36 (18)
Time constant (msec)	11.3  ± 4.3 (30)	13.2  ± 4.3 (18)
Resting potential (mV)	−50  ± 3 (24)	−50  ± 3 (30)
Action potential duration (msec)	11.5  ± 4.1 (10)	11.3  ± 3.6 (10)
Action potential amplitude, peak (mV)	103.8  ± 8.6 (10)	103.0  ± 7.7 (10)
Action potential amplitude, plateau (mV)	50.9  ± 6.4 (10)	51.7  ± 3.7 (10)
Action potential plateau, number of ripples	3.2  ± 1.2 (10)	3.7  ± 1.8 (10)
Electrical coupling, prevalence1-160	74% (29)	10% (32)
Electrical coupling coefficient1-165	0.038  ± 0.027 (23)	0.010  ± 0.002 (3)
Subthreshold oscillations, prevalence	82% (60)	79% (63)
Subthreshold oscillations, frequency (Hz)	4.2  ± 1.7 (49)	4.5  ± 1.6 (50)
Subthreshold oscillations, amplitude (mV)*	12.4  ± 6.9 (49)	15.6  ± 7.2 (50)

^F1-aData are mean ± SD (number of neurons or neuron pairs).

^*p < 0.05 (Student's ttest).

F1-160: p < 0.001 (Fisher's exact test).

F1-165: p < 0.0001 (Student's ttest).

Fig. 6.

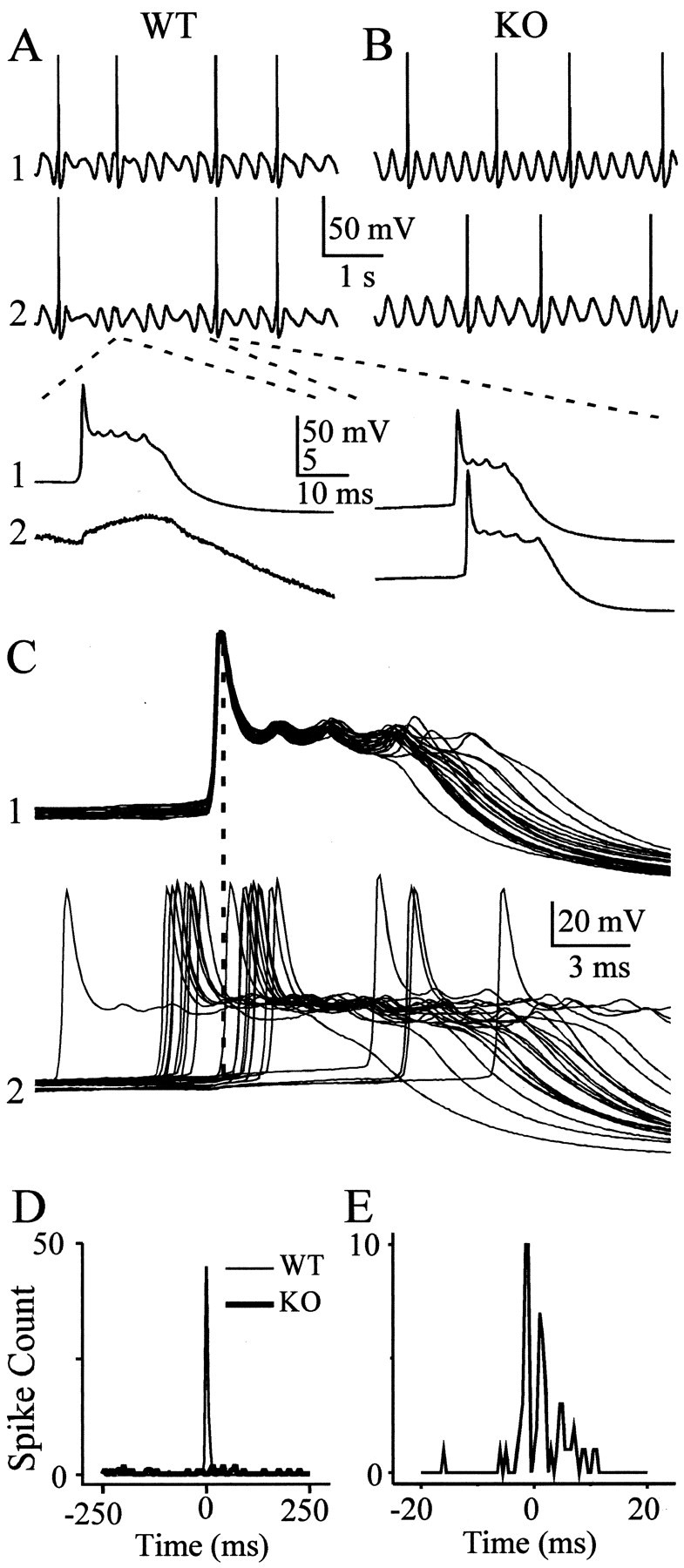
Action potentials are synchronized by electrical coupling. A, Spontaneous spiking from two WT neurons during a 4-sec-long epoch of spontaneous subthreshold rhythms shows simultaneous spiking. The traces below show magnified views of an action potential in the top cell, a subthreshold spikelet in the bottom cell (left), and two nearly simultaneous spikes (right). Dashed lines show wheretop traces are expanded in bottom traces.B, A similar 4 sec epoch of rhythmic activity in two KO neurons shows only asynchronous spiking. C, When 22 spiking epochs from the WT pair are aligned on the spikes of one cell, it is evident that spikes in the second cell most often occur with a brief lag or lead. Dashed line is aligned with peaks of spikes in cell 1. D, Spike cross-correlogram (5 msec bin width) taken from 200 sec of spontaneous spiking from the pairs illustrated above. WT cells show a strong peak at 0 msec, whereas spikes from KO cells were uncorrelated. E, When the same WT spiking data were cross-correlated with finer temporal resolution (0.5 msec bin width), it is clear that the periods of highest spiking probability occurred before and after spikes in the reference neuron.

Electrical coupling is common between IO neurons (Llinás et al., 1974). To assay coupling prevalence and strength, we recorded simultaneously from closely spaced neuron pairs (<25 μm between somata; for the majority, spacing was <5 μm) (Fig.1B). To quantify the strength of coupling, 10–50 strong (−1 nA) hyperpolarizing current steps (600 msec) were applied to each IO cell in turn (Fig. 2C,E). The voltage responses to the current steps in the injected and neighboring cells were each averaged. Values for the coupling coefficient (defined as ΔV_{neighboring cell}/ΔV_{injected cell}) were estimated for both directions of current flow. Coupling coefficients did not depend significantly on direction, and reported values are the averages of estimates from both directions. Cell pairs were considered electrically coupled if they had an average coupling coefficient of >0.008, which was just above our detection limit. In the WT mice, 79% of sampled IO neuron pairs were electrically coupled, with a mean coupling coefficient of 0.038 (Table 1). In contrast, only 9% of pairs from KO mice were coupled (p < 0.001; Fisher's exact test). The electrical coupling between pairs from the WT was, on average, approximately four times stronger than that between the few coupled pairs observed in KO slices (Table 1) (p < 0.001; t test). Thus, considering both prevalence and strength, KO neurons had only ∼3% of the electrical coupling observed in WT neurons. In most coupled pairs of WT neurons (14 of 17), action potentials in one neuron evoked prominent spikelets (electrotonically conducted action potentials) in the neuron coupled to it (Fig. 2B) (mean spikelet amplitude, 1.51 ± 1.23 mV; range, 0.47–4.7 mV). Each spikelet was followed by relatively strong, prolonged hyperpolarization (Fig.2B, cell 2) that reflects the electrotonically conducted afterhyperpolarization of the presynaptic cell (coupling potentials in fast-spiking interneurons of neocortex) (Galarreta and Hestrin, 1999; Gibson et al., 1999) and perhaps also some contribution generated by spontaneous oscillations in neighboring coupled cells. KO pairs never generated electrically coupled spikelets (Fig.2D).

In a recent report, Devor and Yarom (2002b) demonstrated that electrical coupling between IO neurons depends strongly on cell spacing. To be sure we were maximizing the detectability of coupling, we recorded a subset of neuronal pairs in which somata were <5 μm apart (many were nominally touching, as in Fig. 1B). Among this subset, all six WT pairs were coupled (coupling coefficient, 0.03 ± 0.008), whereas only one of 11 KO pairs was coupled, very weakly (coupling coefficient, ∼0.008).

Spontaneous subthreshold oscillations do not require electrical coupling

Many IO neurons generate spontaneous subthreshold oscillations of their membrane potentials when recorded under control conditions (Fig.2A) (Benardo and Foster, 1986; Llinás and Yarom, 1986). Experimental data and theoretical analyses have suggested that these oscillations may be an emergent property of the electrically coupled network of IO neurons, and that coupling is required for the maintenance of rhythms (Manor et al., 2000; Loewenstein et al., 2001). We found, however, that spontaneous rhythms occurred in ∼80% of IO neurons from both WT and Cx36 KO mice (Fig.3A,B). They ranged in amplitude from 2 to 30 mV peak-to-peak and had frequencies of ∼1–8 Hz (Table 1). The prevalence and frequency of subthreshold rhythms in WT and KO cells were not different, and those from KO neurons were slightly but significantly larger than those from WT neurons. To eliminate the possibility that subthreshold rhythms of KO neurons were being driven by afferents from an extrinsic source, we bathed the slices in TTX to block action potentials. Nine of 10 KO cells bathed in TTX were spontaneously rhythmic, with amplitudes and frequencies indistinguishable from cells recorded without TTX. These results suggest that electrical coupling is not important for subthreshold rhythmogenesis in the IO.

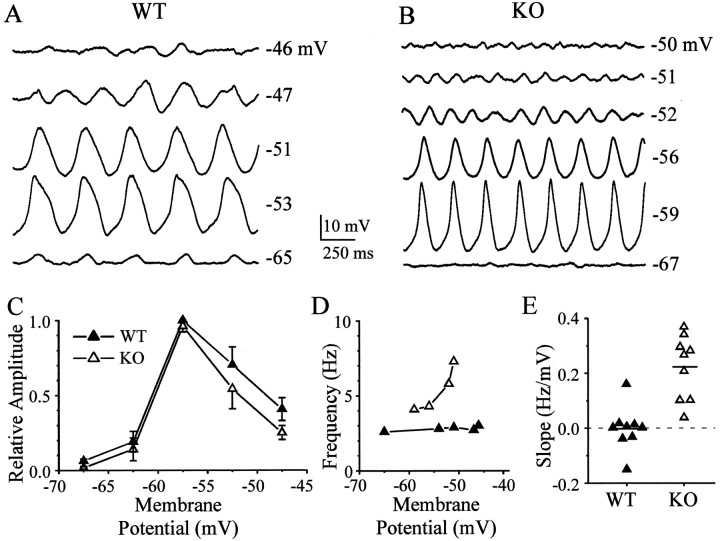
Fig. 3.

The frequency of spontaneous subthreshold oscillations in WT cells is determined by the electrically coupled network. Membrane potentials were altered by injecting steady currents, either hyperpolarizing or depolarizing, into WT (A) and KO (B) cells.C, Amplitudes of subthreshold oscillations were a strong function of membrane potential in both WT and KO neurons: summary of data from nine WT and nine KO cells. Mean amplitudes at various membrane potentials were scaled to largest responses and summed across 5-mV-wide bins, along with SE bars. The only significant difference was at the most hyperpolarized level (−66 to −70 mV), where the WT response was greater than the KO response (p< 0.05; t test). D, Oscillation frequency was a strong function of membrane polarization in neurons from the KO but was invariant with membrane potential in WT neurons. The graph shows data obtained from cells illustrated inA (WT) and B (KO). E, To summarize the voltage dependence of oscillation frequency, the best-fit line was calculated for each set of data points (as inD) (9 WT and 9 KO cells). The graph in Eplots the slopes of the linear fits, in Hertz per millivolts.Dashed line shows slope of zero.

The frequency of subthreshold rhythms in a single IO neuron tends to be independent of its mean membrane potential, which suggests that the activity of each neuron is strongly influenced by input from the electrically coupled local network (Benardo and Foster, 1986; Lampl and Yarom, 1997). We confirmed this in neurons from WT mice (Fig.3A) (n = 9). When steady currents were injected into spontaneously rhythmic cells, the amplitudes of subthreshold oscillations were largest near resting potential or slightly negative to it and greatly decreased at potentials 10–15 mV more hyperpolarized or depolarized (Fig. 3A,C); the fundamental oscillation frequency, however, did not change with polarization in the WT (Fig. 3D). Current injections into KO neurons also strongly modulated the amplitude of subthreshold oscillations, with a voltage dependence similar to that of WT cells (Fig. 3B,C) (n = 9). The oscillation frequency of KO cells, however, increased to almost twice its baseline level as membrane potential was depolarized by 10–15 mV (Fig.3B,D). In general, the oscillation frequency of WT cells was invariant with membrane potential (Fig. 3E) (mean slope, 0 ± 0.08 Hz/mV), whereas the frequency of most KO cells increased as the membrane was depolarized (mean slope, 0.22 ± 0.11 Hz/mV) (WT and KO means were different; p < 0.0005;t test).

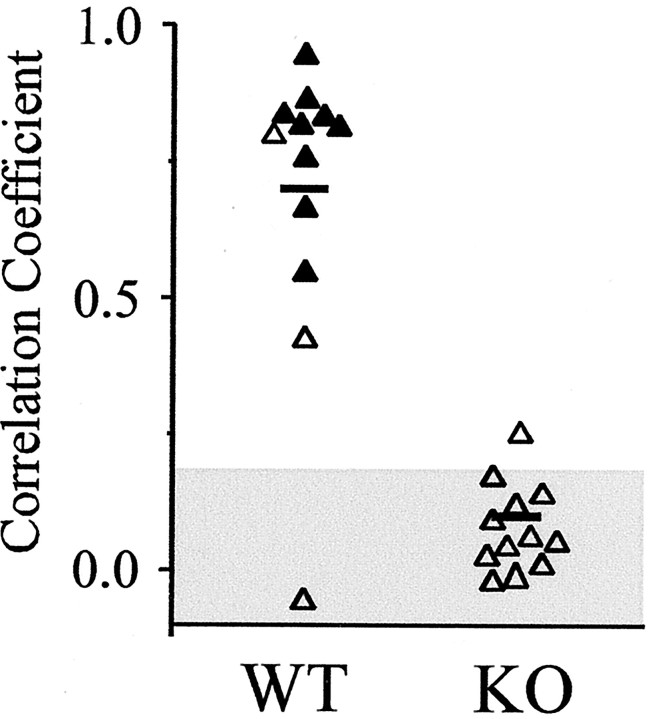
Paired recordings from neighboring IO neurons were used to measure the synchrony of their subthreshold and spiking activities. Figure4 shows representative recordings from a WT pair and a KO pair. Subthreshold oscillations of neighboring WT neurons were usually well correlated (Fig. 4A,left), whereas IO pairs from the KO were almost always uncorrelated (Fig. 4A, right). These differences were evident from plots of the membrane potential of one cell against another (Fig. 4B) and from cross-correlograms (Fig. 4C). When the mean frequencies of subthreshold oscillations in simultaneously recorded WT neurons were compared, they were indistinguishable from each other (Fig.4D, left) (mean difference in peak frequencies between paired cells was 0.14 ± 0.28 Hz;n = 20 pairs). However, the frequencies of paired KO neurons were always at least slightly different from each other (Fig.4D, right) (mean difference in frequency between paired cells was 0.8 ± 0.8 Hz; n = 19 pairs). The disparity between frequencies of recorded pairs was significantly greater in the KO than in the WT (p < 0.005; t test). Almost all sampled WT pairs showed significantly correlated rhythms, whereas correlations in the KO pairs were all very weak (Fig.5), and the two groups were significantly different (p < 0.000005; Student'st test). In the IO of WT mice, two pairs that were not measurably coupled to one another nevertheless had well correlated subthreshold oscillations (Fig. 5).

Fig. 4.

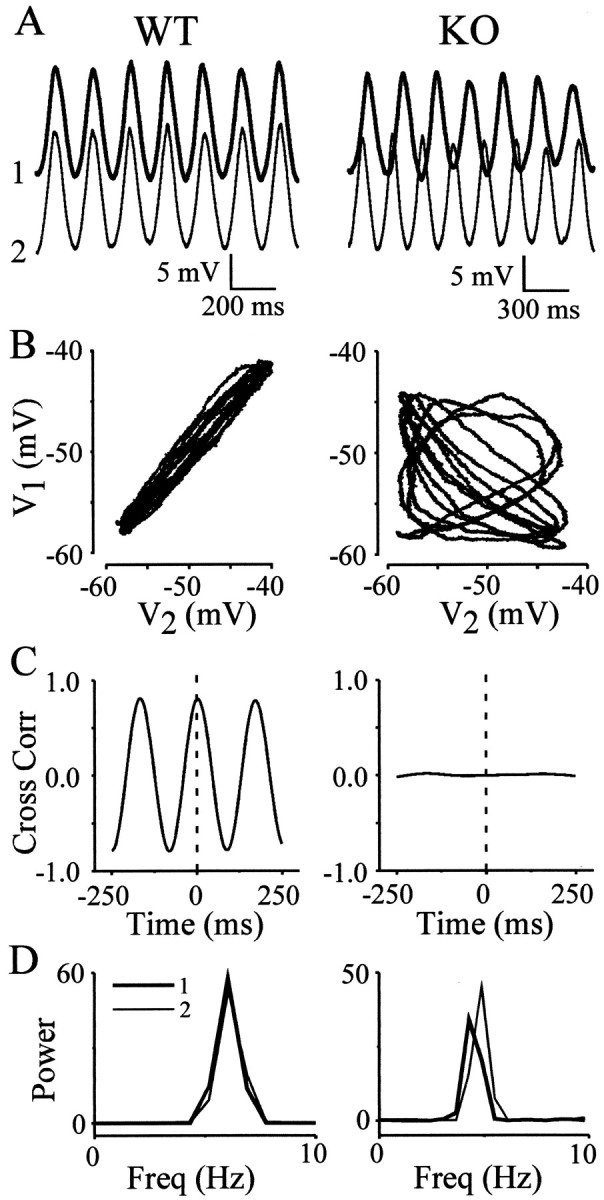
Electrical synapses are required for synchrony of spontaneous rhythms. Left, Data derived from one WT pair; right, data derived from one KO pair.A, Rhythms recorded simultaneously from two closely spaced WT (left) and KO (right) neurons appear similar in amplitude and frequency, although the phase of the two KO recordings obviously varies. B, Data from the same cell pairs are shown in Lissajous figures, which plot the membrane potential of IO₁ versus IO₂. Recordings from the WT neurons are nearly identical (left), but those from KO neurons show no correlation (right).C, Cross-correlograms (Cross Corr) of both pairs derived from >60 sec of data quantify the high degree of rhythmic correlation between WT cells (left) and the absence of correlation between KO cells (right).Dashed lines mark zero time. D, Power spectra calculated from the same data show that the frequencies (Freq) of paired WT neurons were identical, whereas KO cell frequencies differed.

Fig. 5.

Rhythms of electrically uncoupled IO neurons are asynchronous. The graph plots the peak correlations obtained from cross-correlograms of 12 WT and KO neuron pairs, obtained as described in Figure 3C. Filled triangles are from cell pairs that were measurably, electrically coupled; open triangles are from pairs that were not coupled.Horizontal lines are mean values. The shaded area shows the 95% confidence interval, derived from shuffled data of 10 WT neurons.

Synchronous spiking requires electrical coupling

The action potentials of IO neurons are usually triggered near the peaks of their subthreshold oscillations (Lampl and Yarom, 1993). Because the oscillations are temporally correlated in normal animals, action potentials should also tend to be correlated. Many of the WT and KO cells generated occasional spikes approximately once every 5–15 subthreshold cycles, when their membranes were spontaneously oscillating (Fig.6A,B). These action potentials arose from the depolarizing crest of the subthreshold oscillations. When pairs of WT neurons were recorded, action potentials were indeed temporally correlated (Fig. 6A,C,D). Pairs of KO neurons, however, generated similar frequencies of action potentials but were uncorrelated (n = 4 pairs each from WT and KO) (Fig. 6B). Cross-correlograms generated from 200 sec epochs of spontaneous spiking (5 msec bin widths) of WT pairs showed a strong central peak near 0 msec, but correlograms from KO pairs were inevitably flat (Fig. 6D).

To characterize the behavior of WT neurons at finer temporal resolution, correlograms of spiking activity were calculated with 0.5 msec bin widths. These revealed that the probability of spiking peaked on either side of the zero time point, at approximately +2 msec and −2 msec, with almost no correlated spikes in precise synchrony (Fig.6C,E). All four tested pairs of spiking WT neurons had peaks offset from zero time. The most straightforward explanation of this result is that each relatively rare spike in one neuron tends to enhance the probability of spiking in its neighboring neuron, with an average lag of ∼2 msec. The mechanism of this triggering is very likely to be the electrical synapse that interconnects the two cells. A broad IO action potential in one neuron generates a relatively prolonged electrotonic spikelet in the coupled neuron (Fig.6A,C), and that spikelet often triggers an action potential with a lag determined by the kinetics of the coupling transform. The symmetry of the correlogram peaks in Figure6E suggests that each neuron of this pair was approximately equally capable of triggering a spike in the other.

Harmaline-induced tremor does not require IO synchrony

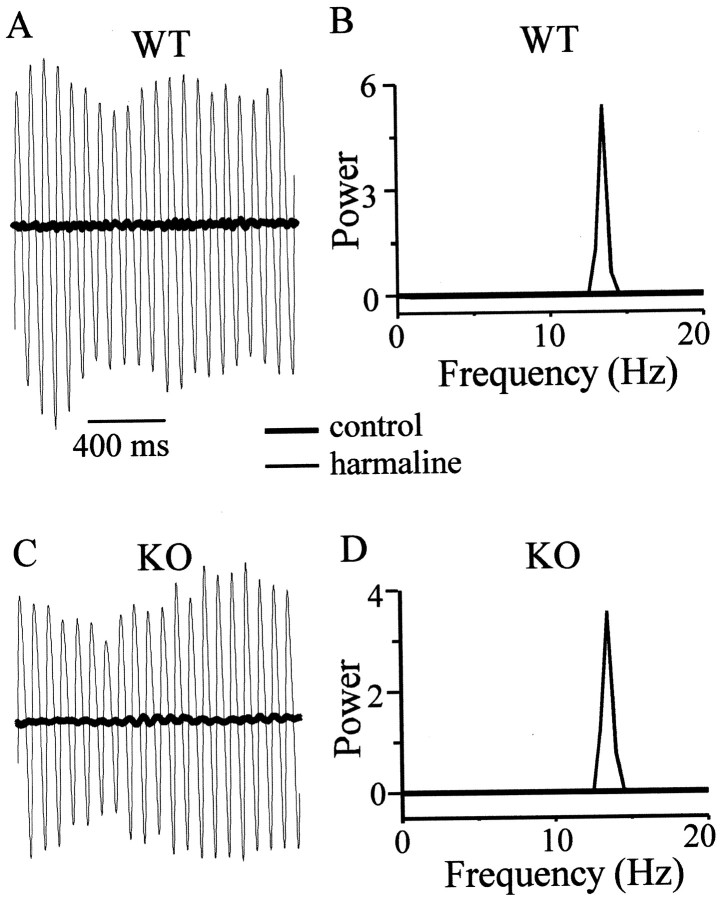
Harmaline, a β-carboline derivative, causes 8–14 Hz tremor in mice (Fowler et al., 2001). Harmaline-induced tremor requires an inferior olivary nucleus in other species (Llinás and Volkind, 1973), and the drug is assumed to act by modulating the rhythm-generating ionic currents of IO cells (Llinás and Yarom, 1986; Llinás, 1991). To test the functional impact of electrical coupling and the IO synchrony that it mediates, we measured harmaline-induced tremor in both WT and KO mice. Prominent harmaline-induced tremors with a peak frequency of ∼13–14 Hz typically began 5–10 min after systemic administration of the drug (Fig. 7A,C). Tremor was indistinguishable in WT and KO animals. No genotype-related differences were seen in the frequency (Fig. 7B,D), peak amplitude, average onset time, or integrated power of the tremors (Table2), nor were any differences detected across genotypes when juvenile (P14–P17) and young adult (P31) mice were compared separately.

Fig. 7.

Harmaline-induced tremor does not require electrical coupling in IO. A, Force transducer output from representative spontaneous tremor in a WT mouse before (thick line) and after (thin line) harmaline administration. Transducer output units are arbitrary but fixed across all measurements. B, Power spectra from force measurements in control (thick) and harmaline (thin) states; harmaline tremor is evident as a sharp, strong peak at ∼14 Hz. C, Similar force measurements in a representative KO mouse before and after harmaline (same scale as in A). D, The power spectrum from the KO mouse tremor is similar to that of the WT mouse.

Table 2.

Harmaline-induced tremor^2-a

	WT (n = 4)	KO (n = 8)
Peak tremor frequency (Hz)	13.0  ± 0.3	13.8  ± 0.9
Onset of tremor (sec)	317  ± 121	429  ± 230
Peak power (arbitrary units)	2.0  ± 1.4	1.9  ± 1.9
Integrated power (arbitrary units)	0.85  ± 0.48	0.98  ± 1.27

^F2-aData are mean ± SD.

DISCUSSION

Our results demonstrate that IO neurons are electrically coupled by Cx36-dependent gap junctions. This is consistent with in situ hybridization results (Condorelli et al., 2000) and ultrastructural labeling studies (Rash et al., 2000), which show an abundance of Cx36 mRNA and protein in the IO. IO coupling is similar in strength, prevalence, and Cx36 dependence to the coupling between inhibitory neurons in the neocortex (Galarreta and Hestrin, 1999; Gibson et al., 1999; Deans et al., 2001), hippocampus (Hormuzdi et al., 2001), and thalamic reticular nucleus (Landisman et al., 2002). Cx36 may not be the only connexin subtype that is functional in IO neurons, because we did observe a small amount of residual coupling in KO tissue, but Cx36 does seem to be required for the large majority of the coupling. Interestingly, KO mice do not compensate for the loss of Cx36 by expressing large amounts of some other type of connexin in neurons of the neocortex (Deans et al., 2001), thalamic reticular nucleus (Landisman et al., 2002), or inferior olive (this study).

By comparing our results from WT and KO neurons, it is clear that electrical coupling can synchronize the activity of IO neurons and that it is not necessary for the generation of spontaneous subthreshold oscillations in IO. Surprisingly, the harmaline-induced tremor was unaffected by a strong reduction of coupling between IO neurons. These results are consistent with some long-standing hypotheses about the cellular mechanisms of inferior olivary function, but they contradict certain others.

Each action potential in an IO neuron triggers powerful climbing fiber synapses that evoke complex spikes in cerebellar Purkinje cells (Eccles et al., 1966). Synchrony in this system is evident from both the correlated complex spikes of Purkinje cells (Lang et al., 1999) and the synchronized rhythms of IO neurons (Leznik et al., 2002). One compelling view is that synchrony in the olivocerebellar system is critical to its role in motor control (Llinás et al., 1975;Llinás, 1991). Synchrony of IO neurons has long been attributed to the fact that they are electrically coupled by gap junctions (Llinás et al., 1974; Sotelo et al., 1974; Llinás and Yarom, 1981b), although the dependence of synchrony on coupling had not been demonstrated directly. In our study of the Cx36 KO mouse, we found that electrical coupling between IO cells, synchrony of spontaneous subthreshold oscillations, and correlations between spikes are nearly abolished. These results strongly support the classical view that electrical coupling can synchronize the activity of IO neurons and thereby coordinate the firing of ensembles of Purkinje cells.

IO neurons are also intrinsically rhythmic, and this rhythmicity has a strong effect on the timing of their action potentials (Lampl and Yarom, 1993). The mechanism of subthreshold oscillations clearly involves particular ionic currents in IO membranes (Llinás and Yarom, 1981a,b; Benardo and Foster, 1986; Bal and McCormick, 1997). However, a variety of indirect experimental results (Llinás and Yarom, 1986; Yarom, 1991; Bleasel and Pettigrew, 1992; Lampl and Yarom, 1997) and theoretical studies (Manor et al., 1997; Loewenstein et al., 2001) have inspired the hypothesis that single IO neurons cannot generate spontaneous, ongoing oscillations, but that rhythmicity occurs as an emergent property of the electrically coupled network of IO neurons. Our data challenge this idea. IO neurons of theCx36 KO were electrically uncoupled, yet just as strongly rhythmic as IO neurons of WT mice. The two most probable explanations for this result are that: (1) single IO neurons of normal mice are indeed intrinsically rhythmic, because of their voltage- and time-dependent ion channels, or (2) IO neurons of theCx36-null mutant express a different complement of ion channels compared with their WT siblings. Although it cannot be ruled out, the latter possibility seems less likely. Most of the intrinsic membrane properties of the KO cells, including resting potentials, action potential mechanisms, and subthreshold oscillation frequency, were similar to those of the WT cells (Table 1). An exception was input resistance, which was somewhat higher in KO neurons. However, higher input resistance in the uncoupled KO cells is predicted if gap junctional conductance is a significant fraction of the input conductance of each WT neuron (Deans et al., 2001). In coupled networks of neocortical interneurons, for example, calculations suggest each cell is coupled to tens of other cells, and approximately half of the input conductance of each cell is attributable to summed gap junctional conductances (Amitai et al., 2002). The higher input resistance of KO neurons may account for the modestly larger amplitude of their oscillations compared with WT cells. These results suggest that a substantial change in olivary ion channel types or density is not part of the Cx36 KO phenotype, although it is possible that small compensatory changes occur. It is also unlikely that the weak residual coupling we observed in KO neurons caused their spontaneous oscillations; theories predicting a rhythmogenic role for coupling also predict synchrony among the oscillating cells (Manor et al., 1997;Loewenstein et al., 2001), and our paired KO recordings did not reveal any synchrony. We suggest that single IO neurons are intrinsically capable of generating spontaneous subthreshold oscillations. This is not to say that electrical coupling has no effect on subthreshold oscillations. The different voltage dependencies of WT and KO oscillations (Fig. 3C) suggest that the electrically coupled network of WT neurons sustains oscillations of single IO cells over a range of membrane potentials that tends to inactivate the conductances that generate the oscillations of uncoupled KO cells.

Perhaps the most surprising result of our study is that KO mice, which have a profound deficit in electrical coupling and spontaneous spike synchrony in their IO, nevertheless have normal harmaline-induced tremors. There is extensive evidence implicating the IO in the origins of harmaline tremors (Llinás and Volkind, 1973; de Montigny and Lamarre, 1973). It seems natural to assume that the electrical coupling of IO neurons plays a role in coordinating strong volleys of afferent excitation to the cerebellum, which in turn lead to synchronous tremor-inducing output to motor structures (Loewenstein, 2002). Indeed, that is what we expected. However, the robust tremor of the KO animals and its close similarity to that of WT animals demands another explanation.

If the IO is indeed an essential component of the pacemaker for harmaline-induced tremors, then there must be some gap junction-independent mechanism that allows IO neurons to synchronize at ∼14 Hz in vivo. There are several possibilities. Within the IO, complex synaptic clusters called glomeruli contain closely apposed, gap junction-coupled dendrites; these dendrites are also postsynaptic to numerous GABAergic inhibitory synapses (Sotelo et al., 1974; De Zeeuw et al., 1990). Blocking IO inhibition in rats apparently enhances the synchrony of its climbing fiber output (Llinás and Sasaki, 1989; Lang et al., 1996), but it is possible that the IO inhibitory circuits also serve as the substrate for synchrony in the absence of electrical coupling. The IO has a system of recurrent inhibition (Armstrong et al., 1968; Crill, 1970; Llinás et al., 1974), although there is little evidence for inhibitory interneurons within the IO (De Zeeuw et al., 1998). It is possible that when intrinsic rhythmicity is enhanced by harmaline, spike discharges by IO neurons could be synchronized by a divergent set of inhibitory feedback connections. Such inhibitory feedback could come from internuclear connections. Olivocerebellar axons excite the cerebellar nuclei, and the nuclear cells return a GABAergic feedback projection to the IO (Sotelo et al., 1986; De Zeeuw et al., 1997). This reciprocal excitatory–inhibitory circuit could in principle generate a high degree of synchronous, rhythmic activity under the proper conditions. Cerebellar nuclear neurons have many of the same intrinsic membrane currents prominent in IO cells, including low-threshold calcium currents (Llinás and Mühlethaler, 1988; Aizenman and Linden, 1999). Harmaline may facilitate the rhythmicity of nuclear cells just as it does IO cells (Llinás and Yarom, 1986). Collaterals of the nuclear cells would then deliver this synchronized, rhythmic inhibition to downstream motor circuits.

Our data suggest that gap junction-mediated synchrony does not play a major role in pathological forms of tremors, such as essential tremor, which the effects of harmaline may mimic. This does not necessarily imply, however, that electrical coupling in IO is irrelevant to olivocerebellar function. More sensitive tests of tremor patterns across time and body segments may yet reveal differences between the WT and KO phenotype. Recent work using voltage-sensitive dyes to image activity in IO slices revealed spatially distinct domains, consisting of hundreds of neurons, that generate highly synchronized rhythms (Devor and Yarom, 2002a; Leznik et al., 2002). Modeling results suggest that the size of the rhythmic domains may be determined by the strength of electrical coupling (Leznik et al., 2002). Clusters of synchronized IO neurons drive synchronized complex spiking in spatially discrete groups of Purkinje cells (Welsh et al., 1995; Lang et al., 1999). Our results lead to the prediction that the Cx36 KO mouse should have disruptions in the spatiotemporal patterns of complex spiking in the cerebellar cortex. If such patterns are indeed important for the control of movement, then the KO animals should also exhibit specific deficits of motor control.