Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2011 Mar 22.
Published in final edited form as: J Biomech. 2009 Dec 14;43(5):994–997. doi: 10.1016/j.jbiomech.2009.11.014

Using Relative Velocity Vectors to Reveal Axial Rotation About the Medial and Lateral Compartment of the Knee

William J Anderst a,*, Scott Tashman a
PMCID: PMC2834859  NIHMSID: NIHMS160848  PMID: 20006336

Abstract

A new technique is presented that utilizes relative velocity vectors between articulating surfaces to characterize the internal/external rotation of the tibio-femoral joint during dynamic loading. Precise tibio-femoral motion was determined by tracking the movement of implanted tantalum beads in high-speed biplane x-rays. Three-dimensional, subject-specific CT reconstructions of the femur and tibia, consisting of triangular mesh elements, were positioned in each analyzed frame. The minimum distance between subchondral bone surfaces was recorded for each mesh element comprising each bone surface, and the relative velocity between these opposing closest surface elements was determined each frame. Internal/external rotation was visualized by superimposing tangential relative velocity vectors onto bone surfaces at each instant. Rotation about medial and lateral compartments was quantified by calculating the angle between these tangential relative vectors within each compartment. Results acquired from 68 test sessions involving 23 dogs indicated a consistent pattern of sequential rotation about the lateral condyle (approximately 60 ms after paw strike) followed by rotation about the medial condyle (approximately 100 ms after paw strike). These results imply that axial knee rotation follows a repeatable pattern within and among subjects. This pattern involves rotation about both the lateral and medial compartments. The technique described can be easily applied to study human knee internal/external rotation during a variety of activities. This information may be useful to define normal and pathologic conditions, to confirm post-surgical restoration of knee mechanics, and to design more realistic prosthetic devices. Furthermore, analysis of joint arthrokinematics, such as those described, may identify changes in joint mechanics associated with joint degeneration.

Keywords: knee kinematics, arthrokinematics, helical axis, x-ray

1. Introduction

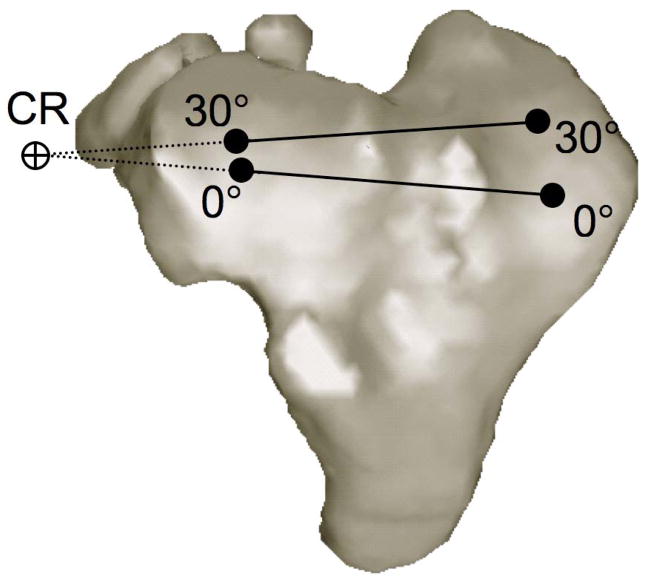
Studies that have measured in vivo bone kinematics during walking and running have reported internal rotation of the tibia relative to the femur accompanying knee flexion (Lafortune et al., 1992; Levens and Blosser, 1948; Reinschmidt et al., 1997; Tashman et al., 2007). The axis of this internal/external rotation between the femur and tibia has been approximated by projecting flexion facet centers onto the tibia or by measuring cartilage contact points on the tibia surface at different flexion angles (Freeman and Pinskerova, 2005; Karrholm et al., 2000; Koo and Andriacchi, 2008; Li et al., 2005; Scarvell et al, 2004). The intersection of lines created by connecting these estimated contact point locations on the medial and lateral tibia surfaces during various angles of flexion approximates the center of rotation in the transverse plane (Figure 1). The majority of research using this technique has concluded that the internal tibial rotation accompanying flexion occurs about an axis passing through the medial condyle (DeFrate et al., 2004; Freeman and Pinskerova, 2005; Komistek, et al., 2003). However these results may be activity dependent, as recent reports concluded pivoting occurs about both the medial and lateral sides of the knee during walking, with the average center of rotation on the lateral side (Koo and Andriacchi and 2008). It is well-known that inaccuracies exist in determining axial center of rotation using this and other techniques such as the helical axis method (Reuleaux, 1875; Panjabi, 1979; Woltring et al., 1985]. These errors increase when the rotation angle decreases (as during pure translation) and when distances between initial and final points decrease (as occurs with high sampling frequency).

Figure 1.

Figure 1

Open in a new tab

Calculating center of rotation about the transverse plane using contact point locations. The center of rotation (CR) is determined by the intersection of the lines connecting the medial and lateral contact points at 0° and 30° of knee flexion.

We have developed methods to precisely measure dynamic bone motion in vivo (Anderst et al., 2009; Tashman and Anderst and 2003) and to use this precise kinematic input to reveal articular surface interactions using three-dimensional reconstructions of subject-specific bone models (Anderst and Tashman, 2003). An advantage of collecting precise dynamic (rather than static) in vivo data is the ability to calculate relative velocity between subchondral bone surfaces. Visualizing the relative velocity between femur and tibia medial and lateral bone surfaces reveals internal/external rotation information that cannot be acquired from static data. Specifically, instantaneous axial rotation about the medial and lateral compartments can be visualized and quantified during functional, dynamic loading. This information cannot be obtained with a small number of contact point measurements acquired at fixed flexion angles.

We have previously reported external rotation of the tibia relative to the femur during loaded flexion in canine knees (Tashman, et al., 2004). The current study presents a technique to partition the instantaneous internal/external rotation into separate rotational motions about the medial and lateral compartments. It was hypothesized that the external rotation would occur exclusively about an axis passing through the medial compartment.

2. Methods

Subjects were 23 foxhounds. Following IACUC approval, each dog had at least three 1.6 mm tantalum beads implanted into both the right distal femur and right proximal tibia. Testing consisted of running on a treadmill (1.5 m/s) within a stereoradiographic imaging system that collected X-ray images at 250 Hz. Paw strike timing was detected using an accelerometer attached to the right tibia for all trials. Data was collected 10 times for each dog, once with the knees intact (pre-surgery) and 9 times following CCL-transection (or sham, for the controls) surgery. The data presented in this study includes all 10 test dates from the control group (n=5), and the pre-surgery data for the entire CCL-deficient group (n=18), resulting in a total of 68 test sessions. Three trials were collected at each test session, and all valid trials for each dog were ensemble averaged for the peak loading phase of running (paw strike to 200 ms after paw strike).

Implanted beads were identified in each stereoradiographic image and 2D bead coordinates were input to a commercial software package for tracking and 3D reconstruction (EVa, Motion Analysis Inc.). Three-dimensional bead coordinates were smoothed using a fourth-order zero-lag Butterworth low-pass filter with a cutoff frequency of 20 Hz. Bead locations were also identified in subject-specific CT scans (0.488 mm × 0.488 ×1.0 mm voxels). Subchondral bone surface models, composed of triangular mesh elements, were reconstructed from the 2D CT scan slices 19. Bead motion (determined by 3D tracking of radiographic images) served as input to drive the movement of the subject-specific bone models. Anatomical coordinate systems were defined in the femur and tibia, as described previously (Tashman, et al., 2004). Joint kinematics were determined using ordered rotations (Kane, 1983) of the anatomical coordinate systems attached to each bone (Grood and Suntay, 1983). Group average internal/external rotation versus time for all analyzed trials was calculated.

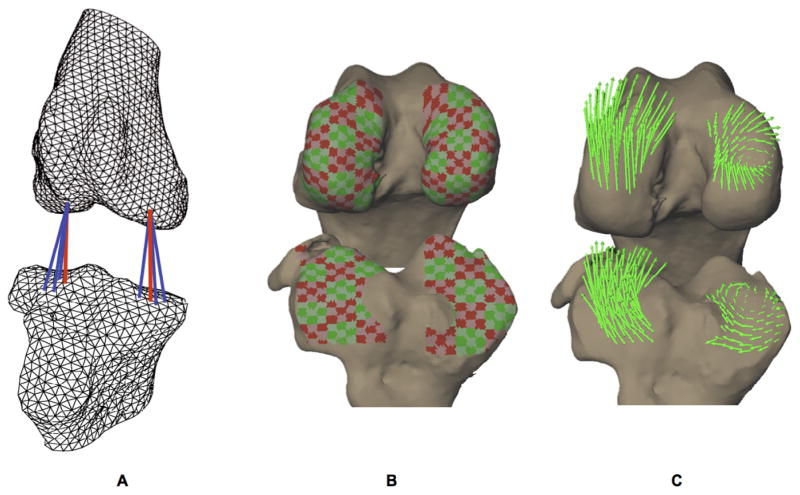
The minimum distance from each triangular mesh element centroid on the femur to the tibial surface was calculated and vice versa (Figure 2A). The velocity of each mesh element centroid was also calculated for each frame of data. The relative velocity between these femur and tibia surface elements was calculated. Only mesh elements within close proximity to the opposing subchondral bone (all elements within 3 mm of the opposing bone surface) were included in this analysis. These relative velocity vectors were partitioned into components parallel and perpendicular to the face of the mesh element, to determine tangent and perpendicular velocities, respectively.

Figure 2. Calculating relative velocity between subchondral bone surfaces.

Figure 2

Open in a new tab

A) Subchondral bone surfaces were reconstructed using a fine triangular mesh (< 1 mm2 per triangle). The minimum distance from each mesh element on the femur to the tibia was calculated and vice versa every 0.004 s (indicated by red lines).

B) Adjacent mesh elements were grouped into subregions on each articulating surface with areas approximately 3 to 5 mm2.

C) The velocity of each subchondral bone surface mesh element was calculated for each frame of data. The relative velocity between each mesh element and its nearest neighbor on the opposing surface was calculated if the surfaces were within 3 mm of each other. The relative velocity vector was partitioned into components parallel (tangent velocity) and perpendicular (perpendicular velocity) to the mesh element. The average tangential relative velocity of mesh elements within each subregion was calculated (green arrows).

Velocity data was reduced by grouping adjacent mesh elements to define subregions on each articulating surface, with surface areas of approximately 3 to 5 mm2 (Figure 2B). The average tangential relative velocities were calculated for each subregion, and visualized on the subchondral bone surfaces (Figure 2C). The average angle between these relative velocity vectors was calculated within each compartment (medial and lateral) as follows. First, for each subregion within the compartment, the average angle between the relative velocity vector and the relative velocity vectors for all other subregions in the same compartment were calculated. The mean of all of these average angles was then determined, representing the mean angle between all of the relative velocity vectors for that compartment. In this way, an “inter-velocity vector angle” was determined for each instant within each compartment. Small inter-velocity vector angles (parallel velocity vectors) indicated relative linear translation between opposing surfaces, while large inter-velocity vector angles indicated a rotation or pivot between opposing surfaces. Among-day variability was determined by calculating the control group standard deviation in inter-velocity vector angle at each instant in time over the 10 test sessions. All calculations were performed on femur relative velocity vectors for the present analysis. Time-synchronized average inter-velocity vector angles at each instant were determined using data from all dogs on all 68 test sessions.

3. Results

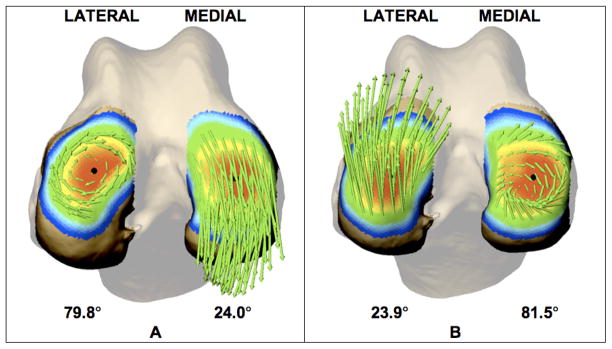
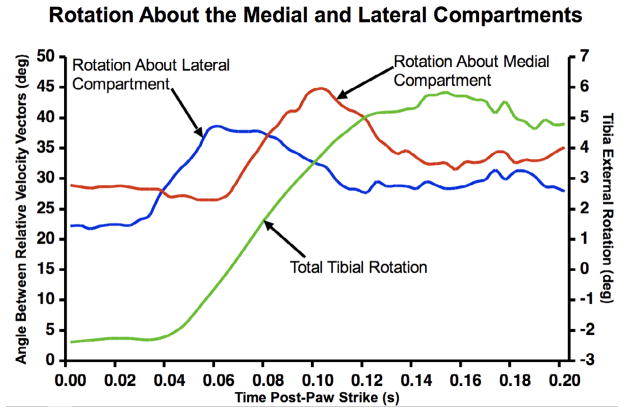
Approximately 60 ms after paw strike, relative velocity vectors indicated a pivot about the lateral compartment (Figure 3A). A pivot about the medial compartment followed, approximately 100 ms after paw strike (Figure 3B). This pattern of a changing axis of external rotation of the tibia relative to femur was evident in the group average curves (Figure 4). The average variability in inter-velocity vector angle was 8.1° and 8.8° for the lateral and medial femur, respectively.

Figure 3.

Figure 3

Open in a new tab

Femur articulating surface 60 ms (A) and 100 ms (B) after paw strike. Bone surfaces are color-coded to indicate distance from femur to tibia (0–6 mm scale from red to blue). Green arrows represent relative velocity vectors tangent to each subregion. Relative velocity vectors indicate an initial rotation about the lateral condyle (A) followed by rotation about the medial condyle (B). Average angle between relative velocity vectors within each compartment at this instant is indicated below the bone surface. In each case, the center of rotation is near the center of closest contact (black circle).

Figure 4.

Figure 4

Open in a new tab

Relationship between average angle between tangent velocity vectors within each compartment and tibia external rotation for 23 dogs over 68 test sessions. Larger values on the left vertical axis indicate more rotation about the lateral (blue) and medial (red) compartment. Right vertical axis indicates tibia external rotation (green). Paw-strike occurred at time 0.00s and maximum extension occurred at time 0.06s. This figure reveals how rotations about the lateral and medial compartments combine to produce the total tibial rotation.

4. Discussion

Following paw strike, the external rotation of the tibia relative to the femur occurred by pivoting in sequence about the lateral then the medial compartment. Therefore, the hypothesis that rotation occurs exclusively about an axis passing through the medial compartment was not supported. Visualizing velocity vectors tangent to articulating bone surfaces provides information regarding internal/external rotation beyond that which can be obtained through traditional joint kinematics or helical axis measurements. For instance, traditional kinematic measurements may reveal tibial internal rotation of 15 degrees following foot strike. However, this information alone does not indicate whether this rotation occurred about the medial compartment, lateral compartment, the geometric center of the joint, or a combination of these. Additionally, traditional joint kinematics do not reveal information specific to the interactions between articulating surfaces. Because pathological joint degeneration is focal (Radin, 1982), and analysis of joint arthrokinematics reveals information regarding the interaction between articulating surfaces, it may be more advantageous to investigate joint arthrokinematics, rather than kinematics, to identify mechanisms leading to cartilage deterioration. Arthrokinematic analysis of dynamic loading may be particularly informative when applied to joint models that include subject-specific soft tissue in addition to the bones. The lack of soft tissue in the canine knee models is a limitation of the study. However, with the femur and tibia cartilage less than 2 mm in thickness combined (Kiviranta, et al., 1987), inclusion of cartilage in the models would likely result in minimal change in magnitude and direction of the relative velocity between femur and tibia closest contact points. In any case, the method presented here can be easily applied using relative velocity between cartilage models in addition to or in place of bone models when the cartilage geometry is known. An additional benefit of the technique described here is that it does not restrict analysis to large movements between instants of analysis, as is the case when performing finite helical axis measurements (Sheehan, 2007).

It is not yet known if this sequential rotation about the lateral then medial compartment exists in human knees during dynamic loading activities such as walking and running. Future research applying the technique described above will address this question. This information may be beneficial when investigating the etiology of knee osteoarthritis, evaluating recovery from surgical procedures, and in designing artificial joints.

Acknowledgments

National Institutes of Health Grant AR43860 funded this study. The study sponsor had no role in the study design, in collection, analysis and interpretation of data, in the writing of the manuscript, and in the decision to submit the manuscript for publication.

Visualization software for this project was designed by Roger Zauel. Data collection for this project occurred at the Motion Analysis Lab at Henry Ford Hospital in Detroit, MI, USA.

Footnotes

Conflict of Interest Statement

The authors have no personal relationships with other people or organizations that could inappropriately influence (bias) their work.

Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.

References

  1. Anderst W, Zauel R, Bishop J, Demps E, et al. Validation of three-dimensional model-based tibio-femoral tracking during running. Med Eng Phys. 2009;31(1):10–6. doi: 10.1016/j.medengphy.2008.03.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Anderst WJ, Tashman S. A method to estimate in vivo dynamic articular surface interaction. J Biomech. 2003;36(9):1291–9. doi: 10.1016/s0021-9290(03)00157-x. [DOI] [PubMed] [Google Scholar]
  3. DeFrate LE, Sun H, Gill TJ, Rubash HE, et al. In vivo tibiofemoral contact analysis using 3D MRI-based knee models. J Biomech. 2004;37(10):1499–504. doi: 10.1016/j.jbiomech.2004.01.012. [DOI] [PubMed] [Google Scholar]
  4. Freeman MA, Pinskerova V. The movement of the normal tibio-femoral joint. J Biomech. 2005;38(2):197–208. doi: 10.1016/j.jbiomech.2004.02.006. [DOI] [PubMed] [Google Scholar]
  5. Grood ES, Suntay WJ. A joint coordinate system for the clinical description of three-dimensional motions: application to the knee. J Biomech Eng. 1983;105(2):136–44. doi: 10.1115/1.3138397. [DOI] [PubMed] [Google Scholar]
  6. Kane TLP, Leivseth G. Spacecraft dynamics. New York: McGraw-Hill; 1983. [Google Scholar]
  7. Karrholm J, Brandsson S, Freeman MA. Tibiofemoral movement 4: changes of axial tibial rotation caused by forced rotation at the weight-bearing knee studied by RSA. J Bone Joint Surg BR. 2000;82(8):1201–3. doi: 10.1302/0301-620x.82b8.10715. [DOI] [PubMed] [Google Scholar]
  8. Kiviranta I, Tammi M, Jurvelin J, et al. Topographical variation of glycosaminoglycan content and cartilage thickness in canine knee (stifle) joint cartilage. Application of the microspectrophotometric method. J Anat. 1987;150:265–276. [PMC free article] [PubMed] [Google Scholar]
  9. Komistek RD, Dennis DA, Mahfouz M. In vivo fluoroscopic analysis of the normal human knee. Clin Orthop Relat Res. 2003;410:69–81. doi: 10.1097/01.blo.0000062384.79828.3b. [DOI] [PubMed] [Google Scholar]
  10. Koo S, Andriacchi TP. The knee joint center of rotation is predominantly on the lateral side during normal walking. J Biomech. 2008;41(6):1269–73. doi: 10.1016/j.jbiomech.2008.01.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Lafortune MA, Cavanagh PR, Sommer HJ, 3rd, Kalenak A. Three-dimensional kinematics of the human knee during walking. J Biomech. 1992;25(4):347–57. doi: 10.1016/0021-9290(92)90254-x. [DOI] [PubMed] [Google Scholar]
  12. Levens AS, IV, Blosser JA. Transverse rotation of the segments of the lower extremity in locomotion. Journal of Bone and Joint Surgery. 1948;30A:859–872. [PubMed] [Google Scholar]
  13. Li G, DeFrate LE, Park SE, Gill TJ, et al. In vivo articular cartilage contact kinematics of the knee: an investigation using dual-orthogonal fluoroscopy and magnetic resonance image-based computer models. Am J Sports Med. 2005;33(1):102–7. doi: 10.1177/0363546504265577. [DOI] [PubMed] [Google Scholar]
  14. Panjabi MM. Centers and angles of rotation of body joints: a study of errors and optimization. J Biomech. 1979;12(12):911–20. doi: 10.1016/0021-9290(79)90059-9. [DOI] [PubMed] [Google Scholar]
  15. Radin EL. Mechanical factors in the casuation of osteoarthritis. Rheumatology. 1982;7:46–52. [Google Scholar]
  16. Reinschmidt C, van den Bogert AJ, Nigg BM, Lundberg A, et al. Effect of skin movement on the analysis of skeletal knee joint motion during running. J Biomech. 1997;30(7):729–32. doi: 10.1016/s0021-9290(97)00001-8. [DOI] [PubMed] [Google Scholar]
  17. Reuleaux F. The Kinematics of Machinery: Outline of a Theory of Machines. New York: Dover; 1963. pp. 56–70. [Google Scholar]
  18. Scarvell JM, Smith PN, Refshauge KM, Galloway HR, et al. Comparison of kinematic analysis by mapping tibiofemoral contact with movement of the femoral condylar centres in healthy and anterior cruciate ligament injured knees. J Orthop Res. 2004;22(5):955–62. doi: 10.1016/j.orthres.2003.12.016. [DOI] [PubMed] [Google Scholar]
  19. Sheehan FT. The finite helical axis of the knee joint (a non-invasive in vivo study using fast-PC MRI) J Biomech. 2007;40(5):1038–47. doi: 10.1016/j.jbiomech.2006.04.006. [DOI] [PubMed] [Google Scholar]
  20. Tashman S, Anderst W. In-vivo measurement of dynamic joint motion using high speed biplane radiography and CT: application to canine ACL deficiency. J Biomech Eng. 2003;125(2):238–45. doi: 10.1115/1.1559896. [DOI] [PubMed] [Google Scholar]
  21. Tashman S, Anderst W, Kolowich P, Havstad S, et al. Kinematics of the ACL-deficient canine knee during gait: serial changes over two years. J Orthop Res. 2004;22 (5):931–41. doi: 10.1016/j.orthres.2004.01.008. [DOI] [PubMed] [Google Scholar]
  22. Tashman S, Kolowich P, Collon D, Anderson K, et al. Dynamic function of the ACL-reconstructed knee during running. Clin Orthop Relat Res. 2007;454:66–73. doi: 10.1097/BLO.0b013e31802bab3e. [DOI] [PubMed] [Google Scholar]
  23. Woltring HJ, Huiskes R, de Lange A, Veldpaus FE. Finite centroid and helical axis estimation from noisy landmark measurements in the study of human joint kinematics. J Biomech. 1985;18(5):379–89. doi: 10.1016/0021-9290(85)90293-3. [DOI] [PubMed] [Google Scholar]

RESOURCES