Abstract
Various methods have been used to quantify the kinematic variability or stability of the human spine. However, each of these methods evaluates dynamic behavior within the stable region of state space. In contrast, our goal was to determine the extent of the stable region. A 2D mathematical model was developed for a human sitting on an unstable seat apparatus (i.e., the “wobble chair”). Forward dynamic simulations were used to compute trajectories based on the initial state. From these trajectories, a scalar field of trajectory divergence was calculated, specifically a finite time Lyapunov exponent (FTLE) field. Theoretically, ridges of local maxima within this field are expected to partition the state space into regions of qualitatively different behavior. We found that ridges formed at the boundary between regions of stability and failure (i.e., falling). The location of the basin of stability found using the FTLE field matched well with the basin of stability determined by an alternative method. In addition, an equilibrium manifold was found, which describes a set of equilibrium configurations that act as a low dimensional attractor in the controlled system. These simulations are a first step in developing a method to locate state space boundaries for torso stability. Identifying these boundaries may provide a framework for assessing factors that contribute to health risks associated with spinal injury and poor balance recovery (e.g., age, fatigue, load/weight and distribution). Furthermore, an approach is presented that can be adapted to find state space boundaries in other biomechanical applications.
1. Introduction
Spinal instability is often associated with low back pain (Bergmark, 1989; Granata and Orishimo, 2001; McGill, 2001; Dieën et al., 2003; Brown and McGill, 2005; Reeves et al., 2007). Experiments using an unstable seat apparatus isolate motion of the lumbar spine and are used to quantify torso stability (Cholewicki et al., 2000; Reeves et al., 2006; Tanaka and Granata, 2007; Lee and Granata, 2008). Kinematic variability methods such as RMS distance, ellipse area, and path velocity (Lee and Granata, 2008) as well as dynamic stability methods such as stability diffusion (Cholewicki et al., 2000) and Lyapunov stability (Tanaka and Granata, 2007; Lee and Granata, 2008) have been utilized. All of these methods have a common attribute; each evaluates dynamic behavior within the stable region of state space. For unstable sitting, the stable region of state space includes all possible configurations and velocities where the person is able to maintain balance without falling over (i.e., the basin of stability). In some cases, the amount of kinematic variability may be unimportant as long as the state of the system remains within the basin of stability (Tanaka et al., 2009). The location and relative movement of segments may be less important than whether movements remain within a safe envelope, thereby avoiding excessive tissue strain. Since low back injury may be caused by relatively extreme conditions associated with a loss of stability, a better understanding of the basin of stability for the human spine and the neuromuscular control parameters that determine its extent may lead to improved treatment and prevention of this debilitating medical condition.
In this paper, methods previously developed to determine the basin of stability in a single degree of freedom mechanical model (Tanaka and Ross, 2009) are extended to higher degrees of freedom. These methods are applied to a mathematical model of the “wobble chair”, a nonlinear system that exhibits complex behavior due to strong coupling between two rigid segments. Using this model, the basin of stability in the four-dimensional state space is estimated.
2. Methods
2.1 Anthropometric Parameters
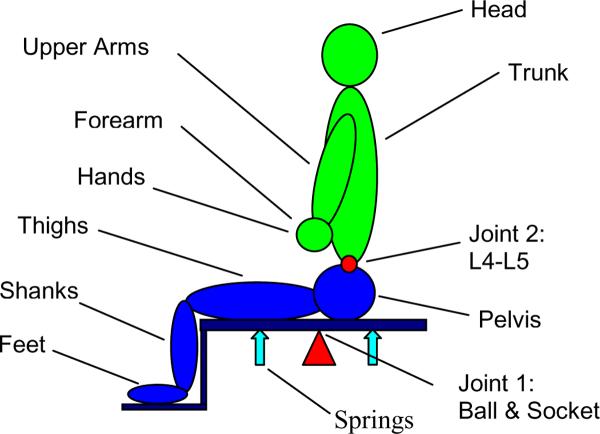
The wobble chair (Figure 1) was modeled as a double inverted pendulum, with all motion restricted to the sagittal plane. The lower body and chair formed the first segment, while the second segment consisted of the head, arms, and torso. A pivot joint between the two segments was located between the fourth and fifth lumbar vertebrae (Dieën et al., 2003). A segmented model was developed to estimate the locations of the two segment centers of mass (COM) and the intervening joint for an average human female. Individual body segments were modeled using existing data (de Leva, 1996) for segment masses, COM locations, and radii of gyration. Respective components of the lower and upper body were assumed to be rigidly fused resulting in a composite COM and moment of inertia for each (parameters listed in Table 1).
Figure 1.
Model of a person sitting on the wobble chair. Components of the lower body contribute to segment one, while components of the upper body make up segment two.
Table 1.
Model Parameters
| Parameter | Value | Description |
|---|---|---|
| m1 | 27.4 kg | Lower body mass |
| m2 | 31.8 kg | Upper body mass |
| I1 | 2.35 kg·m2 | Lower body mass moment of inertia |
| I2 | 4.86 kg·m2 | Upper body mass moment of inertia |
| L1x | 0.1272 m | Lower body segment vector – horizontal |
| L1y | 0.1580 m | Lower body segment vector – vertical |
| L2x | 0.000 m | Upper body segment vector – horizontal |
| L2y | 0.7179 m | Upper body segment vector – vertical |
| c1x | −0.1771 m | Lower body COM vector – horizontal |
| c1y | 0.0780 m | Lower body COM vector – vertical |
| c2x | 0.000 m | Upper body COM vector – horizontal |
| c2y | 0.2736 m | Upper body COM vector – vertical |
| g | 9.81 m/s2 | Acceleration of gravity |
| k1 | 10,900 N/m | Wobble chair linear spring constant |
| d | 10.35 cm | Distance from ball joint to springs |
| k2 | 100 Nm | Torsional stiffness of the spine |
| k3 | 0.1 Nm·s | Torsional damping of the spine |
| Gd | 200 Nm/(rad/s) | Derivative gain |
| Gp | 3×105 Nm/rad | Proportional gain |
| τpmax | 8×104 Nm | Maximum proportional gain |
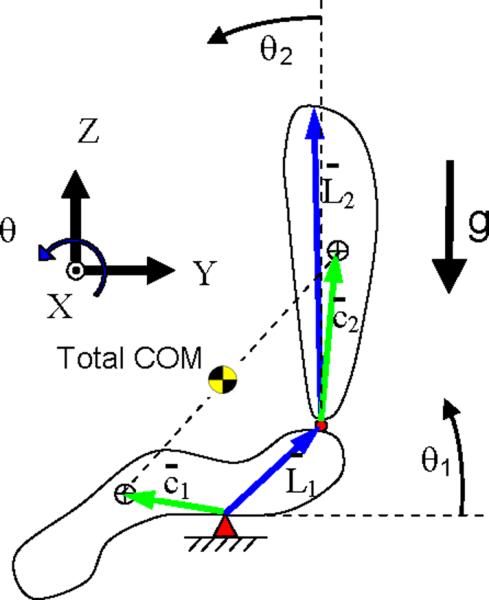
These two segments represent a reduced-order model suitable for dynamical system analysis (Figure 2). Since the model is planar, it has two mechanical degrees of freedom (θ1 and θ2) and therefore its state space has dimension four (i.e., twice the number of degrees of freedom). Given the definitions of θ1 and θ2 (Figure 2), (θ1 = 0, θ2 = 0) indicates a balanced configuration. But, this is just one of many points in a larger set of balanced configurations known as the equilibrium manifold, as discussed below.
Figure 2.
Simplified model of a person sitting on the wobble chair. Position vectors, and , show the connectivity of the model. Vectors and are from the joint to the center of mass of each segment. In the initial balanced configuration shown, segment angles θ1 and θ2 are set to zero.
2.2 Mathematical Model
A Lagrangian approach was used to determine the equation of motion for the wobble chair:
| (1) |
where θ, , and are the rotation angle, angular velocity, and angular acceleration vectors, respectively. The matrices M, C, and G are defined below.
| (2) |
| (3) |
| (4) |
| (5,6) |
where mi is the segment mass, is the vector from the joint to the segment center of mass, is the segment position vector, Ii is the segment moment of inertia, g is the acceleration of gravity, and τi is the torque. The subscript i indicates the segment number, 1 or 2. Parameters R'θi and R”θi are the first and second time derivatives of the rotation matrix:
| (7) |
.
As in the actual wobble chair apparatus (Lee and Granata, 2008; Tanaka et al., 2009), compression springs (k1) at distance d1 were included in the model to provide a stabilizing torque (τSpr = k1d2sinθ1). Also included were passive torques at the lumbar spine due to elastic stiffness (k2: with θsk = k2(θ2−θ1)) and viscous damping (k3: with ). An actuator was employed between the two segments to represent the muscles that flex or extend the spine. Proportional-derivative (PD) control of this actuator was used to maintain stability. No control torque was applied between the base and the chair to simulate the presence of the ball joint. Direct control of each segment is not possible because the system is under-actuated (Spong, 1995), having fewer actuators than degrees of freedom. Stabilizing control was achieved by causing flexion at the joint between the two segments when the overall center of mass was posterior to the point of equilibrium and extension when the overall COM was anterior to equilibrium. Although these configuration changes did not affect the location of the combined COM, they did change the seat angle and the torque provided by the stabilizing springs. Thus, flexion and extension between the two segments was able to alter the external moment applied to the combined segments.
Individual torques were combined mathematically to generate a net joint torque vector,
| (8) |
The torque provided by the proportional-derivative controller, CPD, is
| (9) |
where, Gd is the derivative gain constant, θcr = τpmax/Gp is the smallest angle at which the maximum gain is achieved, Gp is the proportional gain constant, and τpmax is the maximum value of proportional torque. Physiologically, τpmax represents the fact that muscle strength is limited.
2.3 Equilibrium Manifold
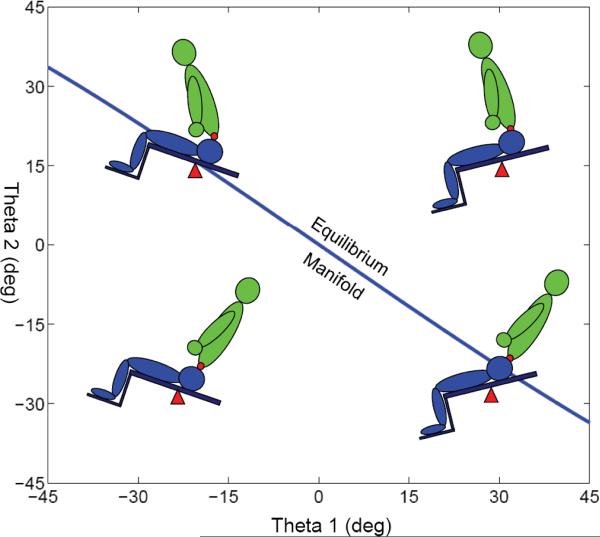
An equilibrium manifold was known to exist based on the wobble chair's topological equivalence to the Acrobot, a robotic double inverted pendulum system resembling an acrobat (Murray and Hauser, 1991; Spong, 1995). The equilibrium manifold describes a set of configurations where the system can maintain static equilibrium given appropriate torque between segments. Similar to a point attractor, this manifold attracts nearby trajectories in the controlled system, but is a one-dimensional curve instead of a point (see Figure 4). The location of the equilibrium manifold for the wobble chair model was calculated by generating a smooth curve between a series of equilibrium points. For each angle of segment one, equilibrium points were found by determining the angle of the second segment needed for the sum of the moments about the free pin joint to equal zero (Figure 2). Individual points were combined to estimate the location of the equilibrium manifold. In actual wobble chair experiments which have previously been performed, participants were constrained by the equipment to remain close to the origin of the graph, within ± 15 degrees (Lee et al., 2008; Slota et al., 2008; Tanaka et al., 2009).
Figure 4.
Equilibrium manifold for the wobble chair in the zero velocity plane . The box indicates the region that is attainable in wobble chair experiments.
2.4 Forward Dynamic Simulations and Trajectory Evolution
The equation of motion (1) above is deterministic, therefore there is a unique trajectory in the four-dimensional state space of (θ1, , θ2, ) for any set of initial conditions. Numerical simulation is straightforward and was done using MATLAB® software (MathWorks; Natick, MA). To obtain an estimate of the region of stability, two approaches were used: (a) a “brute force” numerical technique that simply recorded the long-term fate of an initial condition; and (b) an alternative technique that used local information to obtain the boundary of the stable region. The brute-force or direct method followed trajectories as they evolved over time to determine if the initial state space location is stable (Soliman and Thompson, 1991), i.e. the trajectory stays within a predetermined bounded region over a finite time (Derrick and Grossman, 1987). For this method, trajectories that remained bounded over the length of the simulation (30 s) were considered stable and marked with circles at their initial state space location. In preliminary simulations it was observed that initial conditions that became unstable diverged greatly from the central equilibrium configuration. Unbounded trajectories were defined as those trajectories for which θ1 or θ2 departed from (0,0) by an arbitrarily large angle (± 300°). To improve simulation speed, trajectories that exceeded this criterion were considered to have departed from the stable region without chance for recovery and trajectory tracking was discontinued at this point. These trajectories were defined as unbounded and their initial state space locations marked with crosses.
2.5 Use of Lagrangian Coherent Structures to find Basins of Stability
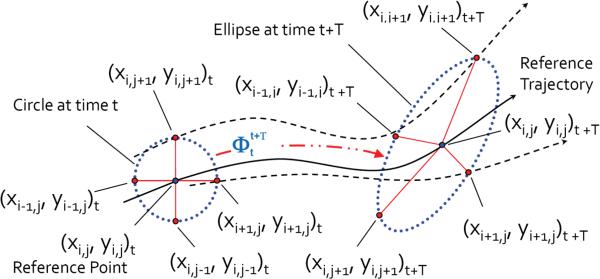
The second method was based on Lagrangian coherent structures (LCS), which evaluates the tendency for the system dynamics to attract or repel a trajectory from a location in state space (akin to a local state space gradient). For the system considered here, the LCS corresponds to a repelling boundary separating stable states from unstable ones. Numerical implementation was as follows: 1) the state transition matrix method was employed to generate a finite-time Lyapunov exponent (FTLE) field; 2) ridges in this field correspond to LCS (Tanaka and Ross, 2009). Briefly, the state transition matrix, Φ, is a linear map (Figure 3) that describes how perturbations from a reference trajectory evolve over time (Appendix A). The state transition matrix is calculated for each point on a rectilinear grid in the state space, revealing how an initial spherical distribution of perturbations deforms.
Figure 3.
The state transition matrix was calculated by first forming a basis about the reference point using nearly orthogonal vectors, then tracking the trajectories forward in time (T) and determining the changes in the basis vectors. For simplicity of illustration, the two-dimensional version is shown.
The state transition matrix can be interpreted as describing the local stretching at each point in state space and can therefore be used to calculate the largest rate of stretching at each point, termed here the finite time Lyapunov exponent (FTLE),
| (10) |
where T is the evolution time over which stretching is evaluated, λmax is the maximum eigenvalue, and Φ* is the transpose of Φ. The FTLE field σ T is developed by associating each FTLE with its initial location in state space. Since the FTLE is calculated for each point on a regular grid, a full field can be developed using this method. LCS are defined as the ridges in the FTLE field, a connected set of local maxima (Shadden et al., 2005; Lekien et al., 2007). They represent a boundary in state space that separates qualitatively different dynamical behaviors. As a boundary, they have one dimension less than the state space. In this case, the LCS defines the three-dimensional edge of the four-dimensional basin of stability. On one side of the LCS motion is stable (over a finite time), while on the other side motion is unstable (falling).
It is useful to use a regular grid when performing forward dynamic simulations and the equations of motion for the system are known. However, if only sparse data are available, such as time series data collected from experiments, there may not be a data point in the exact location where the neighboring trajectory should begin. In this case, a variation of the method may be used: nearest neighbors to the ideal state space locations can be found and their trajectory tracked to estimate the state transition matrix (Tanaka and Ross, 2009).
3. Results
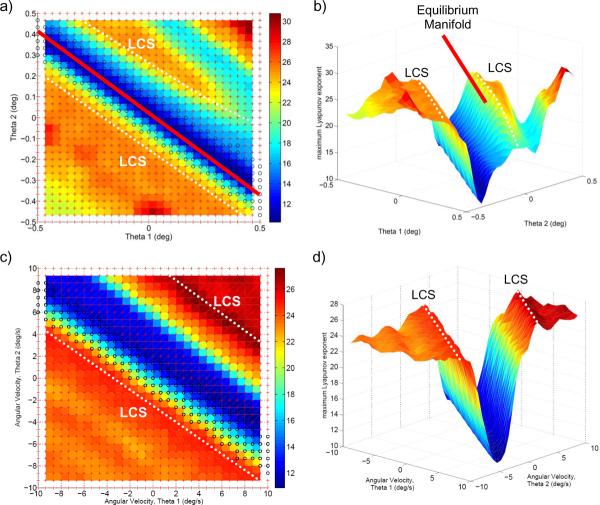
A unique equilibrium configuration could be achieved for any value of torso flexion/extension. Evaluating these configurations over a continuous range torso flexion/extension angles resulted in a one-dimensional curve in the zero velocity plane of state space. Over the range of ±30°, the equilibrium manifold was almost linear (Figure 4).
The FTLE field was generated using forward dynamics simulations for a time T = 0.5 s based on a regular grid of initial conditions (Figure 5). Recall that the planar wobble chair model has two mechanical degrees of freedom (θ1 and θ2) and therefore a four-dimensional state space (θ1, , θ2, ). Since the LCS is a three dimensional surface separating the 4D state space into two distinct regions (stable and unstable), it is easier to view planar sections of state space rather than the entire 4D hyper volume. Figure 5a and 5b show the slice of configuration space when the velocities are both zero in 2D and 3D, respectively. The location of the equilibrium manifold (solid line) was found to align well with the trough of the FTLE field. In addition, the basin of stability found through the evolution of trajectories (circles) correlated well with the LCS (ridges). Within the slice of velocity space where configuration angles are zero (Figure 5c and 5d), the stable trajectories generally aligned with the valley in the FTLE field and are well within the basin of stability boundaries as delimited by the LCS curves.
Figure 5.
LCS are visible in the FTLE field when viewed in configuration space (a and b), . The equilibrium manifold (solid line), LCS (ridges, dashed line), and stable trajectory evolutions (circles) were all observed to correlate well. A valley representing the stable region of state space is also present in the tangent space (c and d), . The evolution time was 0.5 seconds.
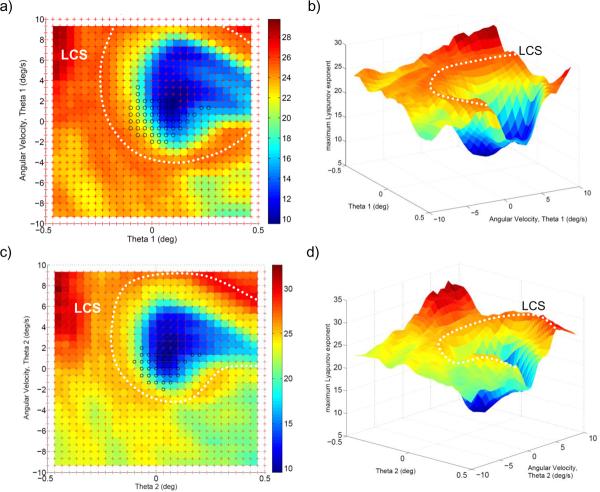
In other slices of state space (Figure 6), a basin of stability was also found using both trajectory evolution and LCS. Similar to the results found for the velocity space, the basins of stability found through evolution of trajectories lay inside of those found using the LCS method.
Figure 6.
In the θ1 phase plane (a and b), , a depression in the FTLE field is observed to the upper right of the origin. In the θ2 phase plane (c and d), , a depression in the FTLE field is observed slightly closer to the origin. The evolution time T was 0.5 seconds.
4. Discussion
The boundary of the basin of stability obtained using the regular grid LCS method was generated in high resolution. As expected, ridges in the FTLE field were formed at the boundary between the stable and unstable regions as found using the direct method. When plotted in configuration space, the two methods yielded similar results. In the other two projections (Figure 6), the size of the basin of stability was roughly the same using both methods, but in general the LCS method overestimated the basin size. These differences may result from inherent differences in the way each method determines the basin of stability. The direct method allows states of the system to evolve over a relatively long time (up to 30 s) and evaluates directly whether or not large angles are achieved. If large angles are achieved, instability is inferred. On the other hand, the LCS method locates state space boundaries using a much shorter evolution time (0.5 s), inferring instability from short-time trajectory divergence. Essentially the LCS method uses the non-uniform rate of local trajectory divergence to predict future behavior without actually following any single trajectory for a long time. If the evolution time were increased from 0.5 s to 30 s, we may see greater agreement in the two basin estimates, but the LCS method might then lose its appeal from the point of view of computational efficiency.
The BoS for the wobble chair represent the states of the system in which balance may be achieved. This may be used as a surrogate to better understand the BoS of the torso, which cannot be measured experimentally without risk of injury to the participant.
The wobble chair model seems to be less tolerant to perturbations in the posterior than the anterior direction. This effect was observed as a shift in the location of the basin of stability towards the upper right corner of the phase plane plots (Figure 6). This shift makes the edge of the basin of stability closer to the equilibrium manifold in the negative direction, implying that it is easier to fall backwards than forwards. A similar trend was also observed in actual wobble chair experiments (Tanaka, 2008). However, we do not know the reason for this difference. It may be due to geometrical asymmetry between the upper and lower body. Another possibility is that small errors in centering of the combined center of mass over the pivot point may be causing this behavior. It may also be that a person has better control of their combined center of mass in flexion than extension. Further investigation is needed to determine if this trend is indicative of real system behavior.
It is interesting to note the similarity in results when varying initial angles with zero velocity (Figure 5a and 5b) and varying initial velocities with a horizontal seat and vertical torso (Figure 5c and 5d). This similarity results from the generally conservative nature of the system. To better illustrate this concept, consider the following scenario: a person sits on the wobble chair with the seat horizontal (θ1=0), the torso vertical (θ2=0), backward seat velocity , and forward torso velocity . After a short evolution time, the person may achieve the state of a backward rotated seat (θ1=−δk), forward torso angle (θ2=δl), and zero velocity , which is essentially a redistribution of kinetic energy aided by the controller. In this example, the second state is on the same trajectory as the first state, so its evolution over a short time (FTLE) or long time (direct method) will yield similar results. When the first state, (0,0,−δi, δj), is plotted in velocity space, its 2D location is (−δi,, δj). This is similar to the second state, (−δk, δl, 0,0), when plotted in zero velocity, 2D configuration space (−δk, δl). Such correspondence exemplifies why an apparent equilibrium manifold also appears in the velocity plot. There exists a set of initial velocities of the two segments that will evolve into a configuration that lies on the equilibrium manifold.
Similar to other biomechanical models (Morasso and Schieppati, 1999; Soetanto et al., 2001; Lo and Ashton-Miller, 2008), neuromuscular control was simulated here using a PD controller. However, the actual control scheme applied by the nervous system is expected to be more effective due to its high complexity and nonlinearity. Although neuromuscular control has a time delay that retards performance, this effect is compensated for by anticipatory control (Morasso and Schieppati, 1999). Considering these factors, it is possible that the basin of stability will be larger for actual human balance control. Note, however, that the purpose of this study was not to give the most accurate model of torso dynamics, but instead to use a simple model and controller to demonstrate that the basin of stability could be computed, thus providing a foundation for future work.
The type of controller selected may have had an influence on the shape of the BoS. Although the BoS was broad in the direction of the equilibrium manifold where the values of θ1 and θ2 were balanced, the width was quite narrow when θ1 and θ2 were imbalanced. This general trend was expected since imbalance indicates a shift in the overall center of mass away from the equilibrium configuration. However, it is likely that larger deviations from the equilibrium manifold may be achieved in actual human experiments because the performance of neuromuscular control system is expected to be superior to that of the simple PD control used in this simulation.
A deterministic model was used, which simplified the calculations but made it less representative of real biological systems where stochastic processes are always present. In unstable sitting, system noise includes random force perturbations caused by muscle twitches, inaccurate motor unit activation, involuntary movements, or external environmental forces (Collins and De Luca, 1993) and afferent feedback errors leading to inappropriate motor control (McIlroy et al., 2003). Although LCS are generally insensitive to noise (Haller, 2001; Haller, 2002; Tanaka and Ross, 2009), this noise may weaken the strength of the LCS, making it easier for trajectories to cross. Yet, if the noise levels are small, the underlying deterministic behavior will still dominate.
In summary, the LCS method was effective in finding the basin of stability of the equilibrium manifold for the wobble chair scenario. These simulations are a first step toward determining the location of state space boundaries for torso stability from experiments. Future work could incorporate experimental data to calibrate the controller and thereby better approximate actual human performance. More complex controllers could also be evaluated to investigate their robustness, where robustness can be interpreted as basin of stability size. Finally, this paper presents an approach that can be adapted to find state space boundaries in other biomechanical applications.
Acknowledgements
Support for this work was provided by Cooperative Agreement Number R01 OH 008504 (to Dr. Kevin Granata and MAN) from the CDC-NIOSH, grant R21 HD046628-01A2 from NCMRR - NICHD (to Dr. Deborah Givens), and from the Kevin P. Granata Occupational Safety and Health Pilot Research Program of Virginia Tech's Center for Innovation in Construction Safety and Health (to SDR). Its contents are solely the responsibility of the authors and do not necessarily represent the official views of the sponsor. The authors would also like to express their sincere gratitude to Dr. Kevin P. Granata for his contributions and guidance during the early portions of this research.
Appendix A
In this paper, the two-dimensional state transition matrix (Shadden et al., 2005; Tanaka and Ross, 2009) was expanded to four dimensions,
| (A1) |
where . The partial derivatives in equation (A1) are obtained by central finite differencing of neighboring trajectories,
| (A2) |
where indices i, j, k, and l represent the grid location of the reference point in the x, y, z, and w direction respectively. The state transition matrix describes the magnitude of local deformation in each direction of state space (as in Figure 3), which may be used to calculate finite time Lyapunov exponents.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Conflict of Interest The authors declare that there are no conflicts of interest associated with this research.
References
- Bergmark A. Stability of the lumbar spine. A study in mechanical engineering. Acta Orthop Scand. 1989;(Suppl 230):1–54. doi: 10.3109/17453678909154177. [DOI] [PubMed] [Google Scholar]
- Brown SH, McGill SM. Clin Biomech. 9. Vol. 20. Bristol, Avon: 2005. Muscle force-stiffness characteristics influence joint stability: a spine example; pp. 917–22. [DOI] [PubMed] [Google Scholar]
- Cholewicki J, Polzhofer GK, Radebold A. Postural control of trunk during unstable sitting. J Biomech. 2000;33(12):1733–7. doi: 10.1016/s0021-9290(00)00126-3. [DOI] [PubMed] [Google Scholar]
- Collins JJ, De Luca CJ. Open-loop and closed-loop control of posture: a random-walk analysis of center-of-pressure trajectories. Exp Brain Res. 1993;95(2):308–18. doi: 10.1007/BF00229788. [DOI] [PubMed] [Google Scholar]
- de Leva P. Adjustments to Zatsiorsky-Seluyanov's segment inertia parameters. Journal of Biomechanics. 1996;29(9):1223–1230. doi: 10.1016/0021-9290(95)00178-6. [DOI] [PubMed] [Google Scholar]
- Derrick WR, Grossman SI. Introduction to Differential Equations With Boundary Value Problems. West Publishing Company; St. Paul: 1987. [Google Scholar]
- Dieën JHV, Cholewicki J, Radebold A. Trunk muscle recruitment patterns in patients with low back pain enhance the stability of the lumbar spine. Spine. 2003;28(8):834–41. [PubMed] [Google Scholar]
- Granata KP, Orishimo KF. Response of trunk muscle coactivation to changes in spinal stability. J Biomech. 2001;34(9):1117–23. doi: 10.1016/s0021-9290(01)00081-1. [DOI] [PubMed] [Google Scholar]
- Haller G. Distinguished material surfaces and coherent structures in three-dimensional fluid flows. Physica D. 2001;149(4):248–277. [Google Scholar]
- Haller G. Lagrangian coherent structures from approximate velocity data. Physics of Fluids. 2002;14(6):1851–1861. [Google Scholar]
- Lee H, Granata KP. Clin Biomech. 6. Vol. 23. Bristol, Avon: 2008. Process stationarity and reliability of trunk postural stability; pp. 735–42. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee H, Granata KP, Madigan ML. Clin Biomech. 5. Vol. 23. Bristol, Avon: 2008. Effects of trunk exertion force and direction on postural control of the trunk during unstable sitting; pp. 505–9. [DOI] [PubMed] [Google Scholar]
- Lekien F, Shadden SC, Marsden JE. Lagrangian coherent structures in n-dimensional systems. Journal of Mathematical Physics. 2007;48(6) [Google Scholar]
- Lo J, Ashton-Miller JA. Effect of upper and lower extremity control strategies on predicted injury risk during simulated forward falls: a study in healthy young adults. J Biomech Eng. 2008;130(4):041015. doi: 10.1115/1.2947275. [DOI] [PubMed] [Google Scholar]
- McGill SM. Low back stability: from formal description to issues for performance and rehabilitation. Exerc Sport Sci Rev. 2001;29(1):26–31. doi: 10.1097/00003677-200101000-00006. [DOI] [PubMed] [Google Scholar]
- McIlroy WE, Bishop DC, Staines WR, Nelson AJ, Maki BE, Brooke JD. Modulation of afferent inflow during the control of balancing tasks using the lower limbs. Brain Res. 2003;961(1):73–80. doi: 10.1016/s0006-8993(02)03845-3. [DOI] [PubMed] [Google Scholar]
- Morasso PG, Schieppati M. Can muscle stiffness alone stabilize upright standing? J Neurophysiol. 1999;82(3):1622–6. doi: 10.1152/jn.1999.82.3.1622. [DOI] [PubMed] [Google Scholar]
- Murray R, Hauser J. A Case Study on Approximate Linearization: The Acrobot Example. Electronics Research Loaboatory, College of Engineering, University of California, Berkeley; Berkeley, California: 1991. pp. 1–43. [Google Scholar]
- Reeves NP, Everding VQ, Cholewicki J, Morrisette DC. The effects of trunk stiffness on postural control during unstable seated balance. Exp Brain Res. 2006;174(4):694–700. doi: 10.1007/s00221-006-0516-5. [DOI] [PubMed] [Google Scholar]
- Reeves NP, Narendra KS, Cholewicki J. Clin Biomech. 3. Vol. 22. Bristol, Avon: 2007. Spine stability: the six blind men and the elephant; pp. 266–74. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shadden SC, Lekien F, Marsden JE. Definition and properties of Lagrangian coherent structures from finite-time Lyapunov exponents in two-dimensional aperiodic flows. Physica D-Nonlinear Phenomena. 2005;212(3–4):271–304. [Google Scholar]
- Slota GP, Granata KP, Madigan ML. Clin Biomech. 4. Vol. 23. Bristol, Avon: 2008. Effects of seated whole-body vibration on postural control of the trunk during unstable seated balance; pp. 381–6. [DOI] [PubMed] [Google Scholar]
- Soetanto D, Kuo CY, Babic D. Stabilization of human standing posture using functional neuromuscular stimulation. J Biomech. 2001;34(12):1589–97. doi: 10.1016/s0021-9290(01)00144-0. [DOI] [PubMed] [Google Scholar]
- Soliman MS, Thompson JMT. Transient and Steady-State Analysis of Capsize Phenomena. Applied Ocean Research. 1991;13(2):82–92. [Google Scholar]
- Spong MW. The Swing up Control Problem for the Acrobot. Ieee Control Systems Magazine. 1995;15(1):49–55. [Google Scholar]
- Tanaka ML. Biodynamic Analysis of Human Torso Stability using Finite Time Lyapunov Exponents. Virginia Tech - Wake Forest University School of Biomedical Engineering. Virginia Polytechnic Institute and State University (Virginia Tech); Blacksburg: 2008. Ph.D. [Google Scholar]
- Tanaka ML, Granata KP. Methods & Nonlinear Analysis for Measuring Torso Stability. ASCE 18th Engineering Mechanics Division Conference; Blacksburg, VA. 2007. [Google Scholar]
- Tanaka ML, Nussbaum MA, Ross SD. Evaluation of the threshold of stability for the human spine. J Biomech. 2009;42(8):1017–1022. doi: 10.1016/j.jbiomech.2009.02.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tanaka ML, Ross SD. Separatrices and basins of stability from time series data: an application to biodynamics. Nonlinear Dynamics. 2009;58(1):1–21. [Google Scholar]