Relationship between the oxidation potential and electron spin density of the primary electron donor in reaction centers from Rhodobacter sphaeroides

Abstract

The primary electron donor in bacterial reaction centers is a dimer of bacteriochlorophyll a molecules, labeled L or M based on their proximity to the symmetry-related protein subunits. The electronic structure of the bacteriochlorophyll dimer was probed by introducing small systematic variations in the bacteriochlorophyll–protein interactions by a series of site-directed mutations that replaced residue Leu M160 with histidine, tyrosine, glutamic acid, glutamine, aspartic acid, asparagine, lysine, and serine. The midpoint potentials for oxidation of the dimer in the mutants showed an almost continuous increase up to ≈60 mV compared with wild type. The spin density distribution of the unpaired electron in the cation radical state of the dimer was determined by electron–nuclear–nuclear triple resonance spectroscopy in solution. The ratio of the spin density on the L side of the dimer to the M side varied from ≈2:1 to ≈5:1 in the mutants compared with ≈2:1 for wild type. The correlation between the midpoint potential and spin density distribution was described using a simple molecular orbital model, in which the major effect of the mutations is assumed to be a change in the energy of the M half of the dimer, providing estimates for the coupling and energy levels of the orbitals in the dimer. These results demonstrate that the midpoint potential can be fine-tuned by electrostatic interactions with amino acids near the dimer and show that the properties of the electronic structure of a donor or acceptor in a protein complex can be directly related to functional properties such as the oxidation–reduction midpoint potential.

The reaction center is the site of the primary process in photosynthesis, which is the conversion of light energy into a charge-separated state (for reviews, see ref. 1). The electron transfer process in the reaction center has the remarkable aspect that the quantum yield is near unity, that is, for every photon absorbed, one electron is transferred. The reaction center isolated from the purple bacterium Rhodobacter sphaeroides is particularly useful for the study of electron transfer because this complex has been well characterized biochemically and spectroscopically, and the three-dimensional structure has been determined by x-ray diffraction (2–5). The reaction center has two core subunits, L and M, that form the binding sites for the cofactors and are related by an ≈2-fold symmetry axis. The primary electron donor (P) consists of two symmetry-related bacteriochlorophyll (BChl) a molecules labeled P_L and P_M that overlap at the ring I position and are separated by ≈3.5 Å (Fig. 1). Light absorption causes the excitation of P, and within 3.5 ps, an electron is transferred to a bacteriopheophytin acceptor. Electron transfer proceeds to the primary quinone acceptor, Q_A, in ≈200 ps and to the secondary quinone, Q_B, in ≈200 μs. After reduction of the donor by cytochrome c₂, absorption of a second photon leads to the transfer of a second electron to Q_B, which then leaves the protein carrying the electrons and associated protons to the cytochrome bc₁ complex.

Figure 1.

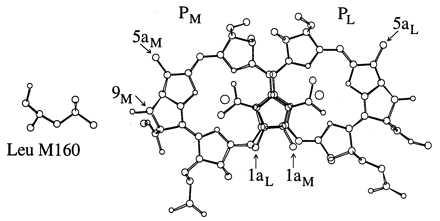
View of the BChl dimer and residue Leu M160. Substitution of residues at this position may result in the formation of a hydrogen bond with the 9_M-keto carbonyl. The protons on the 1a and 5a methyl groups exhibit large hfcs characteristic of the spin density of the conjugated system. Coordinates are from file 4RCR of the Protein DataBank, Biology Department, Brookhaven National Laboratory, Upton, NY.

The midpoint potential is one of the physical properties of the primary electron donor that plays a key role in the energetics of electron transfer. Oxidation of the BChl a dimer is monitored by bleaching of the Q_y absorption band and occurs at a potential several hundred millivolts below that of BChl a in solution (reviewed in ref. 6). Modification of the midpoint potential of the BChl dimer has been associated with changes in hydrogen bonding interactions in bacterial reaction centers (7–9). The BChl dimer has four groups, the keto group on ring V and the acetyl group on ring I of each side, that are part of the conjugated π electronic system and are possible proton acceptors for hydrogen bonds. In the wild-type R. sphaeroides structure, only one of the four possible hydrogen bond interactions is observed, between His L168 and the acetyl group of P_L. The gain or loss of histidine residues in a series of previously described mutants alters the hydrogen bonding arrangement of P (reviewed in ref. 10).

Another physical property of the dimer that is determined by its electronic structure is the electron spin density distribution. Because the dimer is an electronically coupled system, the unpaired electron in the P^+⋅ state is distributed over both halves. The spin density distribution can be obtained from the ratios of the hyperfine coupling constants (hfcs), as measured by electron nuclear double resonance (ENDOR) spectroscopy. Measurements on wild-type reaction centers reveal an asymmetric spin density distribution (11), and this distribution can be altered by mutations such as those in the histidine hydrogen bond mutants (12). On the basis of a simple Hückel molecular orbital model of the dimer (13, 14), the spin density distribution can be related to two parameters of the electronic structure, the energy difference (Δα) and the coupling (β_D) between the two halves of the dimer. The alterations in the spin density distribution observed in mutant reaction centers with hydrogen bonds from histidine residues to the 9-keto positions of the dimer are consistent with changes in the ratio Δα/β_D.

In this work, a set of mutant reaction centers with the substitutions Ser, Lys, Asn, Asp, Gln, Glu, Tyr, and His at residue Leu M160 (Fig. 1) were characterized. Comparison of different substitutions should allow identification of the properties of nearby amino acid residues that contribute to the electronic structure of the dimer. Because these changes are all at the same position, they should introduce small systematic variations in the parameters of the molecular orbital model, enabling a fit of the data to the model. The results should be useful in understanding the relationships that govern the electronic structure and electron transfer in the reaction center.

METHODS

Strain Construction and Protein Isolation.

Oligonucleotide-directed mutagenesis was performed either by using polymerase III holoenzyme (Stratagene) or by using the method of Barik (15) with Vent DNA polymerase (New England Biolabs). After DNA sequencing, the XhoI–BamHI fragment containing the mutation was transferred into the shuttle vector pRKSCHSp (16). The mutated genes were expressed in the R. sphaeroides pufLM deletion strain ΔLM1.1, which is derived from the wild-type 2.4.1 strain (17). The construction of the LH(M160) mutant has been described (8). The wild-type reaction centers were those isolated from the ΔLM1.1 deletion strain complemented with wild-type genes. Cells were grown semiaerobically under nonphotosynthetic conditions, and reaction centers were isolated from all strains by published procedures (8, 12, 16). Isolated reaction centers were prepared in 15 mM Tris⋅HCl buffer (pH 8), 0.025% lauryldimethylamine N-oxide, and 1 mM EDTA.

Optical Spectroscopy.

Optical absorption spectra of the isolated reaction centers were measured using a Cary 5 spectrophotometer (Varian). The transient absorption changes at 295 K and pH 8 after excitation of the sample at 532 nm with a 5-ns laser pulse were measured using a kinetic spectrophotometer of local design (18). The P⁺Q_A⁻ recombination rate was determined from single exponential fits of the change in absorption of the Q_y transition at 865 nm in reaction center samples (A₈₀₂^{1 cm} = 1) with 0.5 mM terbutryn added to block electron transfer to the secondary quinone.

Oxidation–Reduction Titrations.

The P/P⁺ midpoint potential was determined from oxidation–reduction titrations of isolated reaction centers. The amplitude of the Q_y dimer band, at 865 nm in wild type, was monitored while titrating the sample either chemically with potassium ferricyanide and sodium ascorbate (8, 19) or by electrochemical methods (20–22). Each titration was performed in both the oxidative and reductive direction to ensure that the absorption changes observed were reversible. The relative amount of reduced P as a function of the ambient potential was fit according to the Nernst equation (n = 1) using the measured absorption data combined from oxidative and reductive titrations as described (21).

Magnetic Resonance Spectroscopy.

EPR, ENDOR, and electron–nuclear–nuclear triple resonance (special TRIPLE) spectra were recorded with a Bruker ESP 300E spectrometer (Billerica, MA) as described (23), using ENDOR accessories and an ENDOR TM110 cavity of local design (24). The cation radical of the BChl dimer was generated in the cavity by continuous wave illumination with a tungsten halogen lamp (100 W, 700–950 nm using filters) (23). The hfcs were determined by fits of the spectra (25), and the spin density distribution was calculated from the ratios of the methyl hfcs assigned to each half of the dimer as described below.

RESULTS

Optical Absorption Spectra.

Room temperature (295 K) optical absorption spectra of the mutant reaction centers were all similar to that of wild type (data not shown). For all mutants, the peak position of the Q_y band due to the P/P* transition was within 4 nm of the 865 nm position for wild type. No systematic correlations were evident between the peak position of this band and the other properties of the mutants, consistent with the observation that P* is insensitive to these types of mutations (discussed in refs. 8 and 22).

Charge Recombination Rate.

The P⁺Q_A⁻ charge recombination time ranged between 70 and 115 ms compared with 100 ms for wild type (Table 1). The relationship between the charge recombination rate and midpoint potential is similar to that modeled previously for the histidine hydrogen bond mutants (21). The extent of bleaching in the mutants was similar to that of wild type.

Table 1.

P^+⋅ EPR linewidths, ¹H hfcs and spin densities, P/P⁺ midpoint potentials, and P⁺ Q_A⁻ charge recombination times for reaction centers with mutations at residue Leu M160

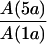
Strain	M160	ΔB, mT	A, MHz						ΣA	ρL	ΔρL		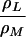Em, mV	ΔEm, mV	ΔEm(2), mV	τ, ms
			5aL	1aL	5aM	1aM	L	M
Wild type	Leu	0.96	5.75	3.98	3.24	1.38	1.44	2.35	14.35	0.68		2.11	506  ±  5			100
LK(M160)	Lys	0.95	5.49	3.89	3.44	1.45	1.41	2.37	14.27	0.66	−0.02	1.92	511  ±  4	5	16	98
LS(M160)	Ser	0.96	5.69	4.02	3.30	1.30	1.42	2.54	14.31	0.68	0.00	2.11	514  ±  3	8	8	115
LN(M160)	Asn	0.98	5.85	4.10	3.10	1.20	1.42	2.58	14.25	0.70	0.02	2.31	527  ±  4	21	24	94
LD(M160)	Asp	0.99	6.24	4.43	2.75	1.10	1.41	2.50	14.52	0.74	0.06	2.77	539  ±  3	33	35	85
LQ(M160)	Gln	1.03	6.55	4.77	2.25	0.85	1.37	2.65	14.42	0.79	0.11	3.65	544  ±  9	38	38	80
LE(M160)	Glu	1.04	6.70	4.75	2.15	0.85	1.41	2.53	14.45	0.79	0.11	3.82	546  ±  2	40	44	81
LY(M160)	Tyr	1.08	6.90	5.10	1.75	0.80	1.35	2.19	14.55	0.82	0.14	4.71	558  ±  7	52	45	71
LH(M160)	His	1.09	6.95	5.15	1.70	0.75	1.35	2.27	14.55	0.83	0.15	4.94	563  ±  10	57	50	71

ΔB is the peak-to-peak Gaussian envelope EPR line width. The error in the hfcs (A) for the 1a and 5a methyl protons is ±20 kHz. ρ_L is the fraction of spin density on P_L as measured by [A(1a_L) + A(5a_L)]/[A(1a_L) + A(5a_L) + A(1a_M) + A(5a_M)]. Δρ_L is ρ_L (wild type) − ρ_L (mutant). The ratio ρ_L/ρ_M is derived from the respective hfcs using [A(1a_L) + A(5a_L)]/[A(1a_M) + A(5a_M)]. E_m is the P/P⁺ midpoint potential as measured by electrochemical titrations. ΔE_m is E_m (wild type) − E_m (mutant). ΔE_m(2) is the change in midpoint potential based on chemical titrations with an average error of 8 mV. τ is the P⁺Q_A⁻ charge recombination time with an estimated error of ±5%. 

Oxidation Potential.

The P/P⁺ midpoint potentials of the mutants were determined from both electrochemical and chemical titrations (data not shown). The midpoint potentials for the mutants were either similar to or higher than those of the wild type (Table 1). The values from the electrochemical titrations were larger than those for the chemical titrations by an average difference of 19 mV. The higher values for the electrochemical titrations probably were caused in part by the higher ionic strength of the buffer as has been discussed (21). After allowing for this average difference, then the two sets of measurements agreed within experimental error. The values for the wild type and the LH(M160) mutant agreed with previously determined values (8, 21).

Spin Density Distribution.

The ¹H Special TRIPLE spectra of wild type and the set of mutants showed variations in the line positions that correspond to one half of the respective hfcs (Fig. 2). The largest line shifts compared with wild type were observed for the LH(M160) mutant. The assignment of the methyl proton hfcs for the 1a and 5a positions in P_L and P_M (Table 1) was based on the characteristic ratios of A(5a)/A(1a) for the L and M halves of the dimer (26) that have been determined unambiguously from crystals in wild type (11, 27), with the assumption that these ratios are not significantly changed in the mutants. As has been observed in other mutants, the variations in these ratios in the mutants are smaller than the difference in the ratio between P_L and P_M (12). The difference in the ratio A(5a)/A(1a) for P_L and P_M (Table 1) arises from differences in the structures of P_L and P_M and in the interactions with the surrounding protein (23, 26). In addition, the sum of the values for the proton hfcs of all four methyl groups is approximately constant, indicating that there is no significant redistribution of spin density within each BChl. Assuming that the spin density at the methyl protons is changing in the same way as the spin density over the entire BChl macrocycle, the fraction of spin density on P_L is calculated as the ratio of the sum of the methyl proton hfcs of P_L divided by the sum of all four methyl hfc values. The hfcs for the β-protons were not used in this analysis because their values are very sensitive to small structural changes in the macrocycle geometry (12). No signal is assigned to a proton shared in a hydrogen bond between P and the protein because the corresponding hfc is expected to be small and has never been identified in the spectrum of wild type or any mutants (12, 23). The changes observed in the hfcs are consistent with changes in the line width of the EPR signal (Table 1), which is an independent measure that reflects the values of the hfcs and the number of contributing nuclei to each hfc.

Figure 2.

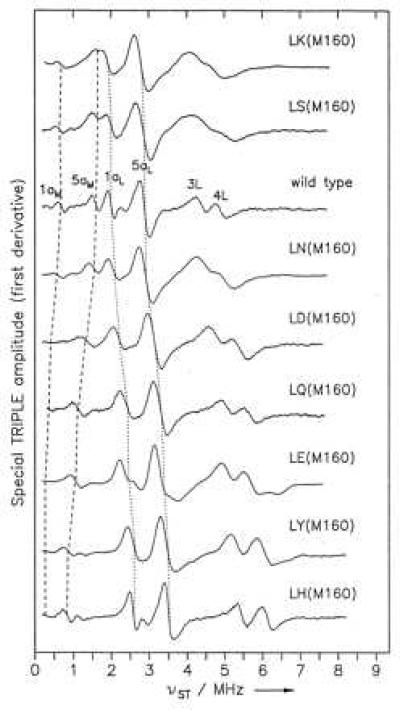
¹H Special TRIPLE spectra of P^+⋅ in reaction centers isolated from wild type and mutants with substitutions at residue M160. The line positions for the methyl protons of the 1a and 5a groups of P_M and P_L are indicated by dashed and dotted lines, respectively. The assignment of the hfcs is summarized in Table 1. In addition to the four spectral lines for the 1a and 5a methyl groups, lines are also evident from the β proton hfcs at ring II and ring IV. The lines corresponding to the β hfcs of the 3L and 4L positions of wild type at 8.75 and 9.75 MHz, respectively, are labeled.

DISCUSSION

A distribution of values for both the oxidation potential and the relative spin density of the BChl dimer was found for a set of mutants with different amino acid substitutions at residue M160 of the reaction center (Table 1). The small systematic changes in these measured values relative to those of wild type indicate that the system as a whole has only been minimally perturbed and that no large structural changes have occurred. The similarity in the optical absorption spectra indicate that the P/P* energy difference is not significantly altered. The correlation between the midpoint potential and charge recombination rate is consistent with the interpretation that the change in midpoint potential causes a parallel change in the energy of the charge-separated states as discussed previously (21). Given these properties of the mutants, the data can be interpreted in terms of changes in the parameters that describe the energy levels of the dimer.

Model for the Relationship Between Oxidation Potential and Spin Density Distribution.

Molecular orbital models have been developed to describe both the optical transitions and ENDOR spectra of the BChl dimer in wild-type reaction centers (13, 14, 28, 29). In the simplest model, a Hückel approximation for conjugated molecules is used, with P simplified as an ethylene dimer with four π centers. The energy of the highest occupied molecular orbital of P_L is assumed to be higher by the amount Δα than that of P_M because of the different interactions with the surrounding protein for the two BChls (Fig. 3A). The interaction of the two BChls results in two molecular orbitals with a difference in energy, ΔE, that is determined by Δα and the resonance integral β_D:

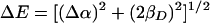1

An expression for the spin density distribution of the two halves of the dimer can also be derived from this model in the weak coupling limit (14):

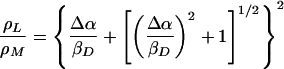2

This model can be used to estimate the energy changes of the molecular orbitals of the mutants compared with wild type without specifying the nature of the interactions that cause the changes. The simplest application of this model to the mutants assumes that there is no change as a result of the mutations in either the coupling between the two BChls, given by the parameter β_D, or the energy of P_L relative to the continuum, given by the parameter E_L. In this framework, the oxidation potential of the dimer E_m corresponds to the energy required to remove an electron from the highest occupied molecular orbital of the dimer to the continuum. This orbital is at an energy ɛ above the highest occupied molecular orbital of P_L such that:

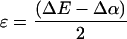3

The oxidation potential is given by:

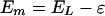4

Qualitatively, this model predicts that mutations that stabilize P_M will increase E_m as well as increase the spin density asymmetry caused by the increase in Δα.

Figure 3.

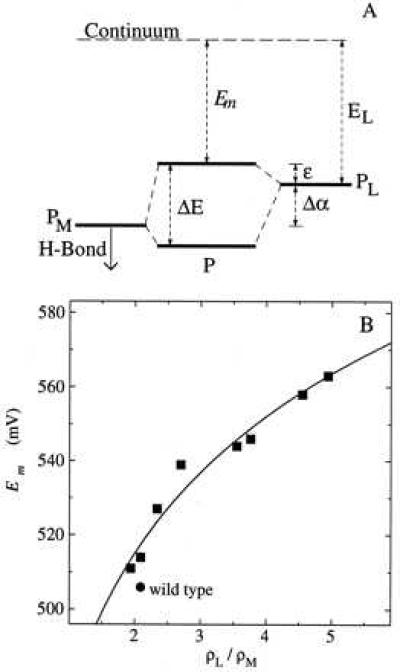
(A) Molecular orbital model for the BChl dimer of the reaction center. The energy splitting ΔE of the molecular orbitals of P is determined by the energy difference Δα and the interaction energy β_D between the two BChls P_L and P_M. In the cation radical, the upper dimer energy level is singly occupied. The mutations at M160 that introduce a hydrogen bond to the 9-keto carbonyl of P_M are expected to stabilize the energy of the P_M half of the dimer, resulting in changes in the energy levels of the molecular orbitals of the dimer and consequent changes in the P/P⁺ midpoint potential E_m and the spin density distribution in P^+⋅. (B) Fit of data to molecular orbital model. The midpoint potential and spin density distribution measured for the M160 mutants and wild type were fit to Eq. 5. Least squares fits yielded values of 260 and 210 meV (with estimated errors of 30 meV) for β_D and 730 and 690 meV (with estimated errors of 20 meV) for E_L from the electrochemical and chemical data, respectively.

The molecular orbital model provides an analytical expression for relating the measured values of the midpoint potential and the electron spin density distribution with two free parameters, E_L and β_D. This dependence can be obtained by rewriting Eq. 4 using Eqs. 1–3. In the regime in which Δα is positive, the appropriate expression is:

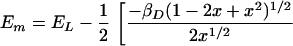5

where x = ρ_L/ρ_M. The data for the M160 mutants can be well fitted using this relation with a value of 240 ± 40 meV for β_D and 710 ± 20 meV for E_L (Fig. 3B).

The relationship given by Eq. 5 assumes that only the energy of the highest occupied molecular orbital of P_M is altered by the mutations. It is very well possible that mutations at M160 also alter the energy of the highest occupied molecular orbital of P_L, but at a significantly reduced level, because otherwise a very weak or inverse dependence is predicted. An accurate determination of the relative contribution of changes in the energy of the highest occupied molecular orbital of P_L requires the introduction of new parameters that are not well constrained; however, assuming that this contribution is small (20% or less) and independent of ρ_L/ρ_M, the value of β_D is estimated to decrease up to 170 meV. Using Eq. 2 with ρ_L/ρ_M = 2.1 and β_D = 170 to 240 meV, the value of Δα for wild type can be estimated to be 60–85 meV.

The fit shows that this relatively simple model adequately describes the observed correlation between the midpoint potential and spin density distribution. The more asymmetric spin density distribution observed in the mutants indicates that the mutations stabilize P_M relative to wild type. The assumption that the coupling term β_D is not significantly altered by the mutations is consistent with the observation that the spin density distribution within each BChl of the dimer is essentially unchanged by the mutations. A change in β_D would not be expected for these mutations because the M160 position is not near the ring I overlap region, which is critical to the coupling of the two BChls. An alternative assumption that β_D and not Δα changes as a result of the mutations does not describe the data and yields unrealistic values for the parameters.

Comparison to Other Results.

When the energy of P_M relative to the continuum increases significantly, then the model predicts that ɛ becomes small and the midpoint potential becomes approximately equal to E_L. Such a situation probably occurs in the heterodimer mutant in which replacement of His M202, the ligand to the Mg of P_M, with Leu results in the replacement of the BChl at P_M with a bacteriopheophytin, which is significantly more difficult to oxidize (30). The estimate of 710 meV for E_L based on the data from the M160 mutants is thus in good agreement with the measured midpoint potential of 640–660 mV for reaction centers with M202 heterodimer mutation (22, 31, 32).

A very broad optical absorption band centered near 2600 cm⁻¹ in wild type and 2800 cm⁻¹ in the LH(M160) mutant (33) has been proposed to correspond to a transition between the two highest occupied molecular orbitals of P⁺ (13). In the simplest model, the energy difference for this transition ΔE is related to β_D and Δα by Eq. 1. To explain the large line width of this IR band, the Hückel model has been modified to include the contributions of vibrational modes (28, 29). In these modified models, there is considerable uncertainty in the values of the parameters because of the lack of knowledge concerning the coupled modes. However, both the spectral features of the IR band and the 2:1 spin density ratio for wild type can be modeled using β_D = 140 meV (29), in good agreement with the lower limit of the present study, and the basic dependence given by Eq. 5 remains valid.

The ratio Δα/β_D has been estimated from ENDOR data of mutations at other sites near the dimer. These data also can be interpreted in terms of the present molecular orbital model, in particular for the mutation Leu to His at L131. Because this site is symmetry-related to M160, the major effect should be on the energy of the highest occupied molecular orbital of P_L, but the dependence will be different. For L-side mutations, an increase of E_m corresponds with a decrease of ρ_L/ρ_M. The molecular orbital model predicts that mutations that change the energy of the highest occupied molecular orbital of P_L relative to the continuum will have a larger change in midpoint potential relative to wild type than mutations that affect the highest occupied molecular orbital of P_M, consistent with the observation that the LH(L131) mutation results in an increase in midpoint potential of ≈80 mV compared with ≈60 mV for the LH(M160) mutation (8). A series of mutations at L131 that are similar to those at M160 should allow an improvement in the quality of the estimates for the model parameters and provide a test for the extent to which the mutations affect both sides of the dimer. Using expressions that describe the relationship between the midpoint potential and spin density distribution for mutations on either side would yield the energies of the highest occupied molecular orbitals of both P_L and P_M relative to the continuum; hence, the parameter Δα could be directly obtained from a fit of the data from both sets of mutants.

Mutations also have been made at residues L168 and M197, which are near the ring I overlap of the BChl dimer. It is likely that these mutations affect the energies of both sides of the dimer, resulting in a larger midpoint potential change relative to the change in spin density distribution than is seen with mutations that primarily affect one side of the dimer. Mutations at His L168, which forms a hydrogen bond with the 2-acetyl group in wild type, appear to have an additional energetic contribution, probably caused by rotation of the acetyl group (12).

The Nature of the Interaction Between the BChl Dimer and Amino Acid Residue M160.

Comparison of the changes in midpoint potential with the properties of the amino acid residues substituted at M160 reveals several trends that are consistent with an electrostatic interaction, in which the increase in the midpoint potential observed in most of the mutants results from a partial positive charge contributed by the substituted residues. In general, the substitutions that gave larger changes in midpoint potential were amino acid residues with longer side chains, such as Gln compared with Asn. Assuming that the position of the backbone does not change for these mutations, the longer side chain found in Gln compared with Asn would correspond to a smaller distance between the proton-donating atom and the 9-keto carbonyl of P_M and hence a stronger electrostatic interaction. A weaker tendency is found by comparison of the proton-donating group for residues that would be anticipated to have identical configurations, such as Asn and Asp. In this case, the larger midpoint potential increase is correlated with the residue with the more electronegative proton-donating atom, e.g., oxygen, compared with nitrogen. For the Glu and Asp substitutions, the side chains are probably protonated because a negative charge would be expected to stabilize P⁺ and hence decrease the P/P⁺ midpoint potential, and the very small changes observed for the Lys substitution make it unlikely that its side chain is ionized. This indicates that, in the hydrophobic environment of this position in a transmembrane helix near the dimer, these residues apparently have highly shifted pK_a values that favor the uncharged state. All of the mutations at M160 in this series introduce a residue whose side chain could act as a proton donor in a hydrogen bond with the 9-keto carbonyl of P_M, and shifts observed in the vibrational frequency of the 9-keto carbonyl are consistent with the formation of a hydrogen bond for most of the mutants, including Glu and Asp (ref. 34 and A. Ivancich, K.A., J.C.W., J.P.A., and T. A. Mattioli, unpublished work).

The correlation observed between the spin density distribution and the P/P⁺ midpoint potential is qualitatively consistent with an electrostatic interaction. The presence of the proton-donating group near P_M would draw electron density toward P_M and increase the partial positive charge on P_L. The energy needed to redistribute the electrons in the dimer would correspond to the change in midpoint potential. This predicts that the relationship between the change in midpoint potential and the change in spin density is linear for small changes in spin density:

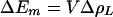6

where V is the potential required to move an electron from P_L to P_M. For the M160 mutants, a linear relationship was observed, with V = 280 ± 40 meV (Fig. 4). This value of V is consistent with an approximate value that can be estimated based on the structure of the reaction center. The distances from the proton donor at M160 to the center of P_M and P_L are ≈10 and 20 Å, respectively. For a simple point charge model, V is inversely proportional to the effective dielectric constant and the difference in these distances. Using an effective dielectric constant of 2, the fitted value of V agrees approximately with the calculated value of 360 meV. Although these estimates could be more accurately made by using partial charges for the system, they demonstrate that the observed changes are consistent with a simple electrostatic relationship.

Figure 4.

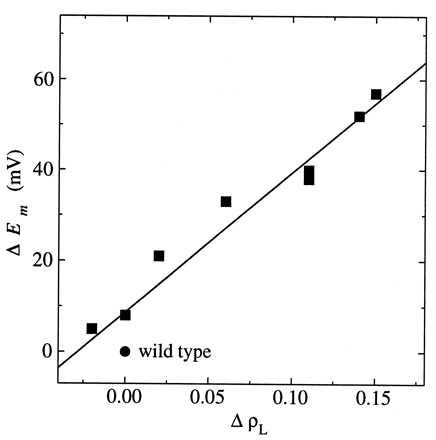
The change in midpoint potential (ΔE_m) as a function of the change in spin density on the L half of the dimer (Δρ_L) for each mutant compared with wild type. A least squares fit of the data to a straight line with a slope of 310 mV and an offset of 9 mV is shown. The SD of the slope is 30 mV. A fit using the midpoint potentials determined from the chemical titrations yields a slope of 250 ± 40 mV.

CONCLUSIONS

A relationship has been established between the electronic structure of P and a key factor in its electron transfer properties, namely the oxidation–reduction midpoint potential. This relationship should hold for any mutation that changes only the energy levels of the dimer, regardless of the nature of the interaction between the amino acid residue and the dimer. For the M160 mutants, the changes in energy can be specifically interpreted in terms of electrostatic interactions. Similarly, any mutation that changes electrostatic interactions should have a characteristic effect on the spin density distribution and midpoint potential that will depend on the position of the mutation, which determines the distance to the two halves. The molecular orbital model and the electrostatic interpretation offer complementary descriptions for the change in energy due to these mutations. The molecular orbital model emphasizes changes in the orbitals of the coupled dimer whereas the electrostatic interpretation accounts for changes in the energies of the individual halves.

Changes in midpoint potentials due to alterations that do not involve metal ligands in other biological systems, such as cytochromes (reviewed in ref. 35), have been difficult to model on a molecular level. In principle, the relationships provided by the molecular orbital model will hold for all interactions between amino acid residues and oxidized or reduced cofactors. Thus, even in systems in which detailed structural information is lacking, it should be possible to estimate parameters describing the electronic structure of the electron donors and acceptors by similarly modeling the correlations between observable physical properties in altered proteins. Understanding the nature of the BChl dimer in reaction centers will be useful for any electron or energy transfer reaction involving chlorophyll molecules, which are often found as oligomeric complexes in proteins. For example, the coupling is a critical parameter for understanding light harvesting systems, in which energy is highly delocalized among the pigments. Furthermore, these results suggest that the ability to distribute electrons between coupled molecules in an electron donor allows the energy levels of the associated charge-separated states to be exquisitely sensitive to interactions with the surrounding protein.