Base pair analogs in the gas phase

Abstract

A rotationally resolved electronic spectrum of the gas-phase dimer 2-aminopyridine·2-pyridone, an analog of the adenine·thymine base pair, has been observed and assigned, leading to precise measurements of its moments of inertia and preliminary determinations of its structure. A Watson–Crick configuration results, with N···H—N and N—H···O hydrogen bond lengths of 2.898 and 2.810 Å, respectively. The two bases are found not to be coplanar; a dihedral angle of 6.1° between the base planes is also estimated from the measured moments of inertia. Possible chemical and biological implications of these results are discussed.

Fifty years have elapsed since x-ray diffraction photographs of fibers pulled from concentrated solutions of DNA revealed that its structure is a double-stranded helix held together by hydrogen bonds between the complementary base pairs adenine (A) and thymine (T), and guanine (G) and cytosine (C) (1–3), providing a molecular-level explanation of heredity (4). Despite this passage of time, the structure of an isolated A·T or G·C base pair in the absence of solvent and/or a surrounding medium has yet to be determined. Only the average structure of the base pairs in the condensed phase can be determined from fiber-diffraction patterns of DNA. To be sure, we now know that many different kinds of DNA exist and that, although they share many common features, they can differ significantly in detail. These differences include the number of residues per turn, the translation per residue, the angle between the base planes and the helix axis, and the dihedral angle between base planes (5). We also know that these features may be functionally important, both in gene expression and in the construction of the cell (6), but we do not know the extent to which the differences in DNA structures are a consequence of the condensed-phase environment in which they are found. Gas-phase studies are needed not only to provide benchmark structures but also to quantify the relative importance of intra- and intermolecular interactions in molecular biology.

Toward this end, we report here a preliminary determination of the structure of the base-pair mimic 2-aminopyridine·2-pyridone (2AP·2PY) by using the technique of rotationally resolved electronic spectroscopy in the gas phase. 2AP·2PY is found to be held together by two N···H—N and N—H···O hydrogen bonds, identical with those found in the A·T base pair itself. As will be seen, understanding the nature of these interactions provides insight into the structure, stability, and electronic properties of the bonds that hold DNA together.

Methods

Our experiments were performed in the collision-free environment of a molecular beam (7). Approximately 1 g of 2AP was placed in a quartz sample container at nearly 200°C and entrained in 41 kPa (6 psig) of He. After equilibrium was established, ≈2 g of 2PY was added to the sample container, and the spectrum of the 2AP·2PY dimer appeared shortly thereafter. During this time, the mixture was expanded through a 280-μm quartz nozzle held at 150°C into a vacuum chamber, skimmed about 2 cm downstream of the nozzle before entering a second differentially pumped chamber, and probed 10 cm downstream of the nozzle with a high-resolution laser (full width at half-maximum ≈ 1 MHz in the UV region). The excitation source was an argon-ion-pumped continuous-wave single-frequency, tunable, ring dye laser operating with 4-dicyanmethylene-2-methyl-b-(p-dimethylaminostyryl)-4H-pyran (DCM) and frequency doubled by an intracavity LiIO₃ crystal. Typical powers used were 400 μW in the UV region. The spectra were acquired at an acquisition rate of 50 Hz over a 2,000-s scan (step size, ≈0.5 MHz). Four signals were collected. The photomultiplier tube-detected fluorescence signal was collected with spatially selective optics by using photon counting and stored on a data-acquisition computer. A signal from a near-confocal interferometer having a mode-matched free spectral range of 599.5040 ± 0.005 MHz in the UV region was collected to perform relative-frequency calibration. The absorption spectrum of I₂ was collected to determine the absolute transition frequencies, which are accurate to ±18 MHz. Finally, the power signal was collected to normalize the photomultiplier-tube signal.

Supplementing the experimental work, ab initio calculations at ground-state B3LYP/6–31G+(d,p) and excited-state CIS/6–31G levels were performed by using the gaussian 98 (8) suite of electronic structure programs on personal computers.

Results

Previous studies of this type on isolated nucleic acid bases, albeit at significantly lower resolution, have faced serious obstacles. The pyrimidine bases C and T exhibit broad absorption bands and a near-total absence of fluorescence, even at low temperature or in supersonic jets (9–11), apparently because of rapid nonradiative decay of the excited S₁ state (12). But vibrationally resolved UV spectra have recently been measured for A, G, and the G·G and G·C dimers in the gas phase, by using resonant two-photon ionization (R2PI) detection techniques in supersonic jets (13–15). And Müller et al. (16) have recently used both R2PI and fluorescence-based methods to detect S₁–S₀ vibronic spectra of the 2AP·2PY base-pair analog described here.

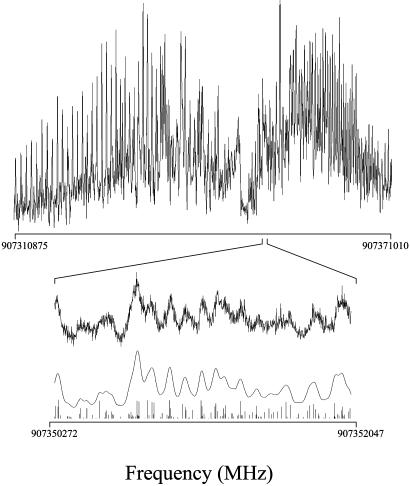
The high-resolution fluorescence excitation spectrum of the presumed S₁–S₀ electronic origin of the 2AP·2PY dimer is shown in Fig. 1. This spectrum was both frequency- and intensity-fit, with an observed-minus-calculated standard deviation of 3.5 MHz. It was obtained at a relatively high temperature (≈7 K) and therefore contains >15,000 transitions. Because of this congestion, one peak corresponding to a single rovibronic transition could not be identified within the spectrum. However, the intensity fit reveals a Lorentzian linewidth of 38 ± 3 MHz, corresponding to a fluorescence lifetime of 4.2 ± 0.3 ns. The frequency fit of the spectrum yields rotational constants that are conservatively estimated to be accurate to one-tenth of this width or 0.4 MHz. These constants are listed in Table 1, together with the calculated [B3LYP/6–31G+(d,p)] rotational constants of the 2AP·2PY dimer. The theoretical values for 2AP·2PY are all within 3% of the experimental ones, confirming its structure. 2AP·2PY has the Watson–Crick configuration, with two N···H—N and N—H···O hydrogen bonds joining the monomer units together, exactly as in the A·T base pair found in naturally occurring DNA.

Fig. 1.

The central ≈2-cm^–1 portion of the rotationally resolved fluorescence excitation spectrum of the origin band in the S₁–S₀ electronic spectrum of the 2AP·2PY dimer at 330.3947 nm, recorded in the collision-free environment of a molecular beam by using a high-resolution laser. Three scale expansions below illustrate a simulated spectrum at full resolution (1 MHz) and fits of the experimental spectrum at the experimental resolution of 38 MHz.

Table 1. Inertial parameters of the zero-point vibrational levels of the ground (S₀) and first excited (S₁) singlet states of the A·T base-pair mimic 2AP·2PY, based on a fit of its fluorescence excitation spectrum at ≈ 330 nm (the band origin is at 30,266.83 ± 0.02 cm^-1).

	Experimental		Theoretical*
Parameter	S0 state	S1 state	S0 state
A, MHz	1,602.8 (4)	1,596.9 (4)	1,602.1
B, MHz	341.0 (4)	336.9 (4)	332.6
C, MHz	281.5 (4)	278.5 (4)	275.8
ΔI, amu·Å2	-2.11	-2.19
κ	-0.910	-0.911

A, B, C, ΔI, and κ are the three rotational constants, inertial defect_r and asymmetry parameter, respectively. amu, Atomic mass units.

^*B3LYP/6-31G+(d,p) values.

The intensity fit of the spectrum in Fig. 1 also shows that the S₁–S₀ electronic transition moment (TM) makes an angle of ±62 ± 3° with the a axis of the dimer. Because the ratio of a-type intensity and b-type intensity depends on the square of the TM, only its relative orientation can be determined experimentally. However, if the TM of the 2PY monomer (17) is placed within the inertial axis frame of the dimer, one of the two possible TM orientations is found to coincide to within 8° of that of the monomer. Thus, we conclude that TM orientation in the dimer is rotated by 62° in a counterclockwise direction, away from its a axis, and that its S₁–S₀ transition is highly localized on the 2PY “side” of the molecule. In agreement with this, the electronic origin of 2AP·2PY is shifted by only ≈400 cm^–1 with respect to that of 2PY itself (17).

Still, the fact that the TMs of 2PY and 2AP·2PY are not exactly aligned suggests some rearrangement of electrons on dimer formation. Ab initio calculations support this view. The B3LYP/6–31G+(d,p) and CIS/6–31G calculations show that only the highest occupied and lowest unoccupied molecular orbitals of 2PY·2AP play a significant role in its S₁–S₀ transition. These two molecular orbitals are largely localized on 2PY, but both are partially delocalized onto the 2AP side of the molecule. Covalent interactions between the two monomer units is one possible explanation of this behavior (18). Another is state mixing; vibronic coupling of the S₁ state (localized on 2PY) and the S₂ state (localized on 2AP) could lead to the observed rotation of the TM.

Discussion

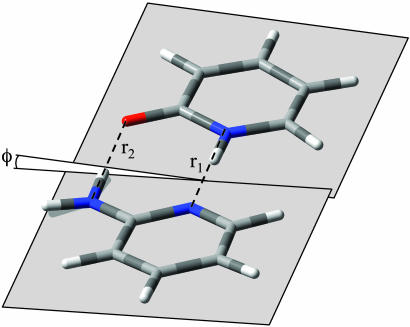
Three rotational constants are clearly inadequate to determine the structure of a large molecule like 2AP·2PY in either electronic state. However, these constants are primarily sensitive to the separation of the two monomer units and to the dihedral angle between the two base planes; they are only secondarily sensitive to the detailed geometry of the two rings. The rotational constants of the two monomer units have been determined by both microwave (19, 20) and high-resolution UV methods (21), and these are well reproduced by ab initio calculations. Therefore, we base our preliminary determination of the ground-state geometry of 2AP·2PY on the [B3LYP/6–31G+(d,p)] theoretical structures of 2AP and 2PY and on the further assumption that these are unchanged on complex formation. A coordinate system was then defined that represents the approach of the two monomer units along the N···H—N direction, as shown in Fig. 2. r₁ is the (heavy-atom) distance between the two nitrogen atoms, r₂ is the analogous distance between the amino nitrogen and oxygen atoms, and ϕ is the torsional (or C—N—N—C dihedral) angle between the two planes. Unique values of these three parameters were then obtained by varying them until the calculated values of A, B, and C matched the observed ones, within experimental error. This analysis yields the hydrogen bond lengths r₁ (N···H—N) = 2.898 ± 0.002 Å and r₂ (N—H···O) = 2.810 ± 0.004 Å and the dihedral angle ϕ = 6.1 ± 0.2°.

Fig. 2.

Model structure of the 2AP·2PY dimer illustrating the Watson–Crick configuration found experimentally and geometrical parameters derived from the fit of the spectrum in Fig. 1. r₁ and r₂ are the hydrogen bond distances N···H—N and N—H···O, and ϕ is the (nonzero) dihedral angle.

Table 2 compares the experimental values of the hydrogen bond lengths in ground-state 2AP·2PY with theoretical estimates (16) and with experimental values for the 2AP dimer (22), the 2PY dimer (23), and the Watson–Crick A·T base pair found in sodium adenylyl-3′,5′-uridine (SAU) by Seeman et al. (24). The latter experimental values are based on x-ray diffraction studies of crystals. Theory gives a good account of the properties of the hydrogen bonds in 2AP·2PY. At the B3LYP/6–311++G(2d,2p) level (16), the two (heavy-atom) distances are quite different, as observed in the gas phase. The theoretical values of r₁ and r₂ are 0.04 and 0.07 Å longer, respectively. [Symmetry (or the lack thereof) seems to play an important role in those interactions, because the “asymmetric” dimer 2-hydroxypyridone·2PY also has N···H—N and O—H···O bonds of significantly different lengths (2.86 and 2.45 Å, respectively) (ref. 25; unpublished data).] Experimentally, the N···H—N bond in 2AP·2PY is found to be 0.17 Å shorter than that in 2AP·2AP, but 0.08 Å longer than that in SAU. The N—H···O bond in 2AP·2PY is 0.05 Å longer than that in 2PY·2PY but 0.14 Å shorter than that in SAU. These data suggest that crystal-packing effects on hydrogen bond lengths are significant.

Table 2. Hydrogen bond lengths, in Å, in 2AP·2PY and related systems.

	2AP·2PY		2AP·2AP Cryst (22)	2PY·2PY Cryst (23)	SAU Cryst (24)
Bond	Gas phase	Calc (16)
N···H—N	2.90	2.94	3.07	—	2.82
N—H···O	2.81	2.88	—	2.76	2.95

Calc, calculated; Cryst, crystal; SAU, sodium adenylyl-3′,5′-uridine.

A survey of 88 crystal structures with similar hydrogen-bonding motifs in the Cambridge Structural Database (26) reveals average bond lengths of r₁ (N···H—N) = 2.92 ± 0.10 Å and r₂ (N—H···O) = 3.00 ± 0.09 Å. The gas-phase value of r₁ (2.90 Å) lies well within the distribution of x-ray values, but the gas-phase value of r₂ (2.81 Å) lies well outside this distribution.

More surprising, perhaps, is the experimental finding [supported by theory (16)] that 2AP·2PY is not a planar molecule in either electronic state. Most models of DNA assume that the complementary base pairs occupy a common plane. But, in 2AP·2PY, at least, this is not the case, as is immediately apparent from the inertial defects (ΔI = I_c – I_a – I_b) that are derived from the fit of its high-resolution spectrum. Both electronic states of 2AP·2PY have ΔI values on the order of –2 μÅ2^, indicating a significant deviation from planarity. (Values of ΔI ≈ 0 are expected for a planar molecule.) The calculated ground-state structure of 2AP·2PY has ΔI ≈ –2.17 μÅ2^. Examination of this structure suggests that the source of the nonplanarity is the NH₂ group of 2AP. Ground-state 2AP has ΔI ≈ –0.26 μŲ (21), supporting this view. Indeed, aniline itself is a nonplanar molecule (27). Recent measurements of the vibrational TM angles in adenine suggest that it, too, is nonplanar in the gas phase with the NH₂ group tilted, 20°, out-of-plane (28). Thus, the statement that “clear, direct experimental evidence about the nonplanarity of isolated bases is still missing due to the (lack of) resolution of the available experimental techniques” (ref. 29, p. 3256) is now moot.

The biological consequences of this nonplanarity may be significant. Some interstrand NH₂-group contacts in B-DNA crystal structures appear to be stabilized by NH₂-group pyramidalization and interstrand bifurcated hydrogen bonds (29). In 2AP itself, Kydd and Mills (20) established that the angle between the plane made by the NH₂ group and the ring is nearly 32° in the gas phase. In the crystal structure (22), this angle is reduced to ≈15°. This difference indicates that the geometry of the NH₂ group highly depends on the local environment of the molecule. The flexibility offered by the NH₂ group is advantageous for the dimer, because the NH₂ group will most likely deform in such a way that the N—H···O bond is linear, creating an overall structure that is bound by two linear hydrogen bonds by an induced fit.

More globally, an incipient chirality apparently is created when a planar base connects to a nonplanar one, giving the base pair a right- or left-handed sense, on its own. It is believed that helices form when a series of subunits bind to each other in a regular way to take advantage of a π-stacking of the bases. Is it possible that the direction of the helix twist can be traced to the nonplanar character of the purine bases? Could the degrees of this nonplanarity (and twist) be influenced by an attached solvent molecule or other environmental factors? And are the properties of the real A·T base pair similar to those of the mimic described here? Further experiments and calculations will be necessary to answer these intriguing questions.