Abstract
Efficient detection of multiple inter-related surfaces representing the boundaries of objects of interest in d-D images (d ≥ 3) is important and remains challenging in many medical image analysis applications. In this paper, we study several layered net surface (LNS) problems captured by an interesting type of geometric graphs called ordered multi-column graphs in the d-D discrete space (d ≥ 3 is any constant integer). The LNS problems model the simultaneous detection of multiple mutually related surfaces in three or higher dimensional medical images. Although we prove that the d-D LNS problem (d ≥ 3) on a general ordered multi-column graph is NP-hard, the (special) ordered multi-column graphs that model medical image segmentation have the self-closure structures and thus admit polynomial time exact algorithms for solving the LNS problems. Our techniques also solve the related net surface volume (NSV) problems of computing well-shaped geometric regions of an optimal total volume in a d-D weighted voxel grid. The NSV problems find applications in medical image segmentation and data mining. Our techniques yield the first polynomial time exact algorithms for several high dimensional medical image segmentation problems. Experiments and comparisons based on real medical data showed that our LNS algorithms and software are computationally efficient and produce highly accurate and consistent segmentation results.
Keywords: Surface detection, ordered multi-column graphs, minimum-cost closed sets, geometric optimization, medical image segmentation
1. Introduction
In this paper, we study the layered net surface (LNS) problems and their extensions in discrete geometry in the d-D space (d ≥ 3 is any constant integer). These problems arise in d-D medical image segmentation and other applications.
Image segmentation, a central problem in medical image analysis, aims to define accurate boundaries for the objects of interest captured by image data. 3-D image segmentation for improved medical diagnosis promises to revolutionize the current medical imaging practice which is inherently 2-D. Although intensive research has been done on 2-D image segmentation in several decades, efficient and effective 3-D image segmentation still poses one of the major challenges in image understanding. In common practice, to identify surfaces representing the boundaries of the sought 3-D objects, first 2-D image slices are more or less analyzed independently; then the 2-D results are stacked together to form the 3-D segmentation output. This approach has some inherent limitations — the most fundamental one stems from the lack of contextual slice-to-slice information when analyzing a sequence of consecutive 2-D images. Performing the segmentation directly on a 3-D image can produce a more consistent segmentation result, yielding 3-D surfaces for object boundaries instead of a set of individual 2-D contours. However, most 2-D image segmentation approaches are difficult to extend to a direct 3-D segmentation, not to mention higher dimensional cases (e.g., a time-series of 3-D images).
We present novel techniques for the LNS problems, i.e., for a simultaneous segmentation of multiple inter-related surfaces in three and higher dimensional medical images. This is an important step towards achieving a practical 3-D surface detection tool since many surfaces in medical images appear in mutual relations. A number of medical imaging problems can benefit from an efficient method for simultaneous detection of multiple inter-related 3-D surfaces.11,18,23,24,25,35,19
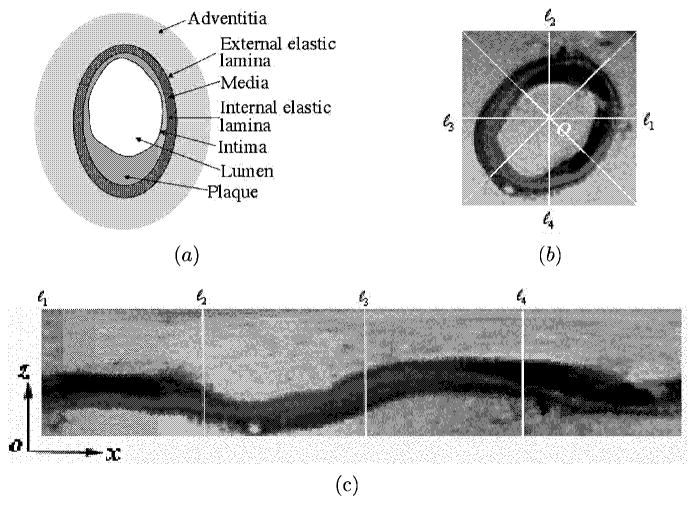
We use vascular MR images of femoral arteries to exemplify the segmentation of multiple inter-related surfaces and the underlying constraints. Figure 1(a) is a schematic cross-sectional anatomy of a diseased artery, and Figure 1(b) shows a 2-D cross-sectional vascular MR image of a human femoral artery specimen. A 3-D MR artery image consists of a sequence of such 2-D cross-sections. To detect the vascular layer structures shown in Figure 1(a), we first perform a polar resampling in each 2-D slice along the centerline of the vessel (see Figure 1(b)), and then embed the resampled 2-D geometric space into a 3-D grid ℐ(x, y, z), as in Figure 1(c). This process is called “unfolding”.22 Each of the sought surfaces in ℐ(x, y, z) for the object boundaries (e.g., lumen, internal and external elastic lamina, etc) then contains exactly one voxel in every column of ℐ(x, y, z) that is parallel to the z-axis. Finally, the “unfolded” surfaces in ℐ(x, y, z) are segmented. Some geometric constraints on these surfaces should be satisfied by the segmentation. In this example, pairs of the sought surfaces must be non-crossing and within a given range of distances apart. Since many anatomical structures are smooth, the segmented surfaces must be sufficiently “smooth”. Generally speaking, the smoothness is related to the surface curvature and means that an object boundary cannot change abruptly.
Fig. 1.
Illustrating the “unfolding” operations on the transversal cross-sections of vascular MR images of a human femoral artery specimen. (a) A schematic cross-sectional anatomy of a diseased artery. (b) Performing a polar resampling. (c) Each transversal cross-section is embedded as an xz-slice in the 3-D xyz-space.
The simultaneous detection of multiple inter-related surfaces has been studied by the medical image analysis community for a long time. For the 2-D case, there are several satisfactory results.23,22,25,2,29 However, little work has been done on the three and higher dimensional cases. Previous attempts26,27,8 on extending graph-search based segmentation methods for the 2-D case to identifying even a single optimal surface in 3-D medical images either made the methods computationally intractable or traded their ability to achieve global optima for computational efficiency. Motivated by this segmentation problem, Wu and Chen30 introduced the optimal net surface problems and presented efficient polynomial time exact algorithms for them. But, the algorithms in the paper30 can detect only one optimal surface in 3-D. An implementation of their algorithms and experimental validation based on real 3-D medical images were presented in the paper.15 More recently, Li et al.16 extended the approach15 to segmenting multiple inter-related surfaces in 3-D. However, their new method does not incorporate the very important region information (e.g., homogeneity) for the surface detection.
Modeling the simultaneous detection of multiple inter-related surfaces in high dimensional medical images, we introduce the layered net surface (LNS) problems on an interesting type of geometric graphs, called ordered multi-column graphs, embedded in the d-D discrete space for d ≥ 3 (to be defined in Section 2). We further extend the LNS problems to a more general ordered multi-column graph. Motivated by segmenting anatomical structures with a relatively regular geometric shape, such as the left ventricles, kidneys, livers, and lungs, we also study several net surface volume (NSV) problems, which aim to find well-shaped regions of an optimal “volume” in a d-D weighted voxel grid. These well-shaped geometric regions are closely related to monotonicity and convexity in d-D discrete spaces (Section 6). Our main results in this paper are summarized as follows.
We develop an efficient algorithm for solving the LNS problem on an interesting type of ordered multi-column graphs in polynomial time, by formulating it as computing a minimum-cost closed set in a vertex-weighted directed graph.
We prove that the LNS problem on a general ordered multi-column graph is NP-hard. However, the (special) ordered multi-column graphs that model medical image segmentation applications have additional properties, and the LNS problem on such graphs is polynomially solvable.
We extend our LNS technique to solving the NSV problems of computing several classes of optimal well-shaped geometric regions in a d-D weighted voxel grid. These NSV problems arise in data mining,9,7 image segmentation,2 and data visualization.1 The classes of regions that we study can be viewed as generalizations of some of the pyramid structures in the paper.7
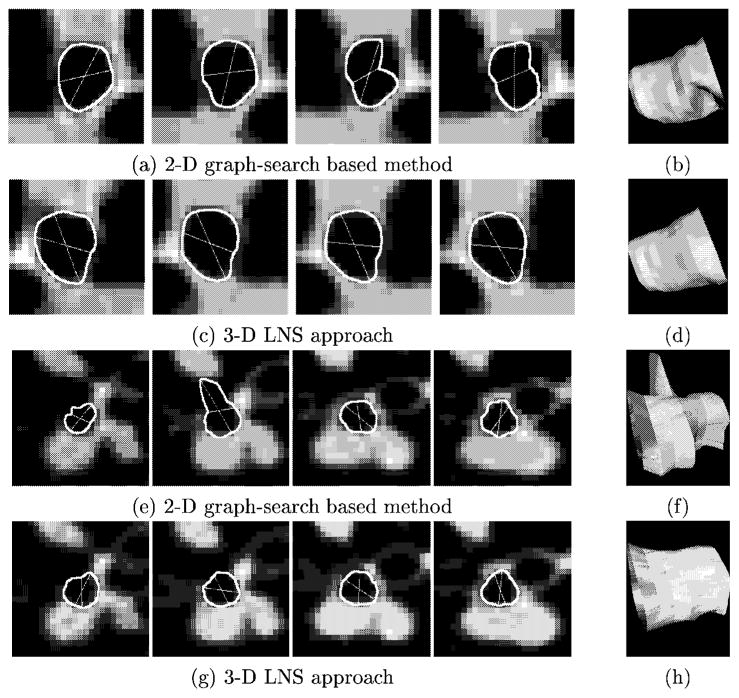
We apply our polynomial time LNS algorithms to segmenting multiple inter-related object boundaries in 3-D medical images. Our method can be easily extended to higher dimensional image segmentation. We also show implementation and experimental results of our algorithms.
Our LNS approach was inspired by Wu and Chen’s algorithms30 for solving the optimal net surface problems. However, instead of searching for a single optimal surface as in the paper,30 our algorithms concurrently identify multiple optimal inter-related surfaces. Our approach is based on a characterization of the self-closure structures of the underlying graphs and a sophisticated graph transformation scheme, in order to enforce the constraints of the LNS problems and to ensure the optimality of the solutions. The extension of our LNS approach to the NSV problems is quite elegant. To compute a sought optimal d-D region, we exploit the monotonicity property of the target region and transform in a nontrivial fashion the NSV problem to the LNS problem.
The rest of the paper is organized as follows. In Section 2, we formally define the layered net surface (LNS) problems. The modeling of medical image segmentation as our optimal LNS problems are discussed in Section 3. Our algorithm for solving the LNS problem is presented in Section 4. We prove the NP-hardness of the LNS problem on a general ordered multi-column graph in Section 5 and show the problem on a special ordered multi-column graph is polynominal-time solvable. Section 6 gives extensions of our LNS techniques to solving the NSV problems. Finally, our implementation and experimental results are shown in Section 7.
2. The Layered Net Surface (LNS) Problems
A multi-column graph G = (V, E) embedded in the d-D discrete space is defined as follows. For a given undirected graph B = (VB, EB) embedded in (d − 1)-D (called the net model) and an integer κ > 0, G is an undirected graph in d-D generated by B and κ. For each vertex v = (x0, x1, …, xd−2) ∈ VB, there is a sequence Col(v) of κ vertices in G corresponding to v; Col(v) = {(x0, x1, …, xd−2, k) | k = 0, 1, …, κ−1}, called the v-column of G. We denote the vertex (x0, x1, …, xd−2, k) of Col(v) by vk. If an edge (v, u) ∈ EB, then we say that the v-column and u-column in G are adjacent to each other. For each vertex vk ∈ Col(v), vk has edges in G to a non-empty list of consecutive vertices in every adjacent u-column Col(u) of Col(v), say uk′, uk′+1, …, uk′+s (s ≥ 0); we call (uk′, uk′+1, …, uk′+s), in this order, the edge interval of vk on Col(u), denoted by I(vk, u). For an edge interval I, we denote by Bottom(I) (resp., Top(I)) the d-th coordinate of the first (resp., last) vertex in I (e.g., Bottom(I(vk, u)) = k′ and Top(I(vk, u)) = k′ + s in the above example).
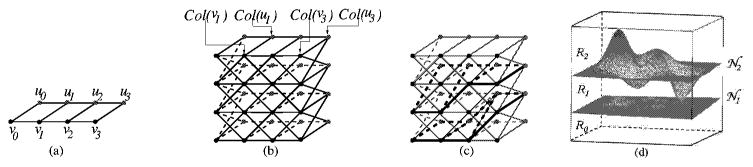
Two adjacent columns Col(v) and Col(u) in G are said to be in proper order if for any two vertices vk and vk+1 in Col(v), Bottom(I(vk, u)) ≤ Bottom(I(vk+1, u)) and Top(I(vk, u)) ≤ Top(I(vk+1, u)), and if the same holds for any two vertices uk and uk+1 of Col(u) on Col(v). The corresponding edge (v, u) ∈ EB is called a proper edge. If all pairs of adjacent columns in G are in proper order, then we call G a properly ordered multi-column graph (briefly, a properly ordered graph). Figures 2(a)–2(b) show a net model and a properly ordered graph.
Fig. 2.
(a) A 2-D net model B. (b) A 3-D properly ordered multi-column graph G generated by B and κ = 4 (the edges between Col(ui) and Col(ui+1), i = 0,1, 2, are symmetric to those between Col(vi) and Col(vi+1), and the edges between Col(vj) and Col(uj), j = 1, 2, are symmetric to those between Col(v3) and Col(u3); all these edges are omitted for a better readability). (c) Two (l, 2)-separate net surfaces in G marked by heavy edges. (d) Two net surfaces divide the vertex set of G into three disjoint vertex subsets.
Note that in medical image segmentation, the boundaries of the target objects (e.g., organs) are often sufficiently “smooth”. The smoothness constraint on the sought surfaces is modeled by the proper ordering of the edges in a multi-column graph G, that is, the edges connecting each vertex vk in G to every adjacent column Col(u) of Col(v) form a vertex interval on Col(u), and such vertex intervals for any two adjacent columns of G are in proper order.
A net surface in G (also called a net) is a subgraph of G defined by a function  : VB → {0,1, …, κ − 1}, such that for every edge (v, u) ∈ EB, (vk′, Uk″), with k′ =
: VB → {0,1, …, κ − 1}, such that for every edge (v, u) ∈ EB, (vk′, Uk″), with k′ =  (v) and k″ =
(v) and k″ =  (u), is also an edge in E. For simplicity, we denote a net by its function
(u), is also an edge in E. For simplicity, we denote a net by its function  . Intuitively, a net
. Intuitively, a net  in G is a special mapping of the (d − 1)-D net model B to the d-D space, such that
in G is a special mapping of the (d − 1)-D net model B to the d-D space, such that  “intersects” each v-column of G at exactly one vertex and
“intersects” each v-column of G at exactly one vertex and  preserves all topologies of B.
preserves all topologies of B.  can be viewed as a functional “surface” of B in d-D defined on the (d − 1)-D space in which B is embedded.
can be viewed as a functional “surface” of B in d-D defined on the (d − 1)-D space in which B is embedded.
Given two integers L and U, 0 < L < U, two nets  and
and  of a properly ordered graph G are said to be (L, U)-separate if L ≤
of a properly ordered graph G are said to be (L, U)-separate if L ≤  (v) −
(v) −  (v) ≤ U for every vertex v ∈ VB. Roughly speaking,
(v) ≤ U for every vertex v ∈ VB. Roughly speaking,  and
and  do not cross each other and are within a specified range of distance to each other. Figure 2(c) shows two net surfaces. For a given set of l − 1 integer parameter pairs {(Li, Ui) | 0 < Li < Ui, 1 ≤ i < l}, l ≥ 2, we consider l net surfaces
do not cross each other and are within a specified range of distance to each other. Figure 2(c) shows two net surfaces. For a given set of l − 1 integer parameter pairs {(Li, Ui) | 0 < Li < Ui, 1 ≤ i < l}, l ≥ 2, we consider l net surfaces 
 = {
= { ,
,  , …,
, …,  } in G such that
} in G such that  is “on top” of
is “on top” of  (i.e., ∀ v ∈ VB,
(i.e., ∀ v ∈ VB,  (v) >
(v) >  (v)), and
(v)), and  and
and  are (Li, Ui)-separate (i = 1,2, …, l − 1). Then, these l net surfaces partition the vertex set V of G into l + 1 disjoint subsets Ri, with R0 = {vk | v ∈ VB, 0 ≤ k ≤
are (Li, Ui)-separate (i = 1,2, …, l − 1). Then, these l net surfaces partition the vertex set V of G into l + 1 disjoint subsets Ri, with R0 = {vk | v ∈ VB, 0 ≤ k ≤  (v)}, Ri; = {vk | v ∈ VB,
(v)}, Ri; = {vk | v ∈ VB,  (v) < k ≤
(v) < k ≤  (v)} for i = 1,2, …, l −1, and Rl = {vk | v ∈ VB,
(v)} for i = 1,2, …, l −1, and Rl = {vk | v ∈ VB,  (v) < k ≤ κ} (see Figure 2(d)).
(v) < k ≤ κ} (see Figure 2(d)).
Motivated by medical image segmentation,22,5,6,36,19 we assign costs to every vertex of G as follows. Each vertex Vk ∈ V has an on-surface cost b(vk), which is an arbitrary real value. For each region Ri (i = 0,1, …, l), every vertex vk ∈ Ri ⊆ V is assigned a real-valued in-region cost ci(vk). The on-surface cost of each vertex in G is inversely related to the likelihood that it may appear on a desired net surface, while the in-region costs Ci(·) (i = 0,1, …, l) measure the inverse likelihood of a given vertex preserving the expected regional properties of the partition {R0, R1, …, Rl}. Both the on-surface and in-region costs for image segmentation can be determined by using simple low-level image features.22,36,33,19
The layered net surface (LNS) problem seeks l net surfaces 
 = {
= { ,
,  , …,
, …,  } in G such that the total cost α(
} in G such that the total cost α(
 ) induced by the l net surfaces in
) induced by the l net surfaces in 
 , with
, with
is minimized, where V(H) denotes the vertex set of a graph H.
In fact, our algorithmic framework is general enough for the cases in which each vertex has only an on-surface cost, only in-region costs, or both. We illustrate our unified approach as an example for the case where each vertex has both the on-surface and in-region costs.
In this paper, we also consider the layered net surface problem on a more general ordered multi-column graph, defined as follows. Note that any two adjacent columns of a properly ordered multi-column graph are in proper order. We now define the reverse order on two adjacent columns Col(v) and Col(u) in a d-D multi-column graph G = (V, E) generated by a (d − 1)-D net model B = (VB, EB): If for any two vertices Vk and Vk+1 in Col(v), Bottom(I(vk, u)) ≥ Bottom(I(vk+1, u)) and Top(I(vk, u)) ≥ Top(I(vk+1, u)), and if the same holds for any two vertices uk and uk+1 of Col(u) on Col(v), then we say that Col(u) and Col(v) are in reverse order. The corresponding edge (v, u) ∈ EB is called a reverse edge. If every two adjacent columns in G are in either proper order or reverse order, then we call G a d-D ordered multi-column graph. Further, for two (L, U)-separate nets  and
and  in G, if two adjacent columns Col(v) and Col(u) are in reverse order, then L ≤
in G, if two adjacent columns Col(v) and Col(u) are in reverse order, then L ≤  (v) −
(v) −  (v) ≤ U and L ≤
(v) ≤ U and L ≤  (u) −
(u) −  (u) ≤ U. We prove that the LNS problem on a general d-D ordered multi-column graph (d ≥ 3) is NP-hard (see Section 5).
(u) ≤ U. We prove that the LNS problem on a general d-D ordered multi-column graph (d ≥ 3) is NP-hard (see Section 5).
Interestingly, if the ordered multi-column graph is generated by a special net model, which also models key medical image segmentation problems(see Section 3), the LNS problem is polynomially solvable. The special net model B = (VB, EB) is defined in the following way. First, remove from B all reverse edges; the remaining B is a set 
 of connected components with proper edges only. Then, contract each connected component of
of connected components with proper edges only. Then, contract each connected component of 
 into a single vertex. Finally, for each (removed) reverse edge (v, u) ∈ EB, say, v in C′ ∈
into a single vertex. Finally, for each (removed) reverse edge (v, u) ∈ EB, say, v in C′ ∈ 
 and u in C″ ∈
and u in C″ ∈ 
 (C′ = C″ is possible), add an edge between the contracted vertices of C′ and C″. The resulting graph is called the p-contracted graph of B. The bipartite LNS (BLNS) problem is defined on a d-D ordered multi-column graph with a net model B whose p-contracted graph is bipartite. For the BLNS problem, we naturally assume that each vertex in G has only an on-surface cost.
(C′ = C″ is possible), add an edge between the contracted vertices of C′ and C″. The resulting graph is called the p-contracted graph of B. The bipartite LNS (BLNS) problem is defined on a d-D ordered multi-column graph with a net model B whose p-contracted graph is bipartite. For the BLNS problem, we naturally assume that each vertex in G has only an on-surface cost.
3. Modeling Medical Image Segmentation
This section discusses the modeling of medical image segmentation problems. Numerous medical applications can benefit from simultaneous detection of multiple optimal interacting surfaces representing terrain-like or tubular structures, which can be modeled as our optimal LNS problems. If we also consider the motion of these anatomical structures, then we have a time-series of 3-D images, forming a 4-D image.
It is easy to embed a 3-D image with a terrain-like object into the 3-D space. Let ℐ(x, y, z) = {(x, y, z) | 0 ≤ x < X, 0 ≤ y < Y, 0 ≤ z < Z} be a 3-D image of size X × Y × Z, where X, Y, and Z denote the image size in the x, y, and z dimensions, respectively. Each desired terrain-like boundary surface contains exactly one voxel ℐ(x, y, z) in each column of ℐ(x, y, z) that is parallel to the z-axis. Since many anatomical structures are smooth, one may expect the resulting surfaces to be sufficiently “smooth”. The smoothness constraints guarantee the surface continuity in 3-D. Specifically, we use two smoothness parameters, Δx and Δy, to specify the maximum allowed change in the z-coordinate of a feasible surface along each unit distance change in the x and y directions, respectively. Note that here we assume a 4-neighbor adjacency (the modeling described below can be easily extended to other adjacency settings). In addition, assume that we are looking for l boundary surfaces and any two adjacent desired surfaces 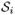 and
and 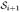 are within a certain range of distances apart (e.g., for all 0 ≤ x < X and 0 ≤ y < Y,
). A cost c(x, y, z) is assigned to each voxel ℐ(x, y, z) such that the cost is inversely related to the likelihood that a desired surface would contain the voxel, which is usually determined by using simple low-level image features.22 The multiple surface detection problem seeks l feasible surfaces in ℐ whose total sum of voxel costs is minimized.
are within a certain range of distances apart (e.g., for all 0 ≤ x < X and 0 ≤ y < Y,
). A cost c(x, y, z) is assigned to each voxel ℐ(x, y, z) such that the cost is inversely related to the likelihood that a desired surface would contain the voxel, which is usually determined by using simple low-level image features.22 The multiple surface detection problem seeks l feasible surfaces in ℐ whose total sum of voxel costs is minimized.
This (terrain-like) surface detection problem can be modeled as a layered net surface problem on a properly ordered graph G = (V, E), as follows. The net model of G is a 2-D X × Y grid B. Each voxel ℐ(x, y, z) corresponds to exactly one vertex v(x, y, z) in G. Thus, any grid point (x, y) in B is associated with a column Col(x, y) of Z vertices of G, i.e., Col(x, y) = {v(x, y, z)|z = 0,1, …, Z − 1}. Then, for every vertex v(x, y, z) ∈ V with x < X − 1 (resp., y < Y − 1), there is an edge to vertex v(x + 1, y, z′) (resp., v(x, y + l, z′)) for any z′ such that 0 ≤ z′ < Z and |z′ − z| ≤ Δx (resp., |z′ − z| ≤ Δy). These edges are used to enforce the smoothness constraint of the target surfaces along the x-dimension (resp., y-dimension). Each vertex v(x, y, z) has an on-surface cost equal to the cost c(x, y, z) of the corresponding voxel ℐ(x, y, z). It is straightforward to show that G is a properly ordered graph defined on the net model B. We are then looking for l net surfaces { ,
,  …,
…, 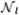 } in G such that
} in G such that  , and
, and  are (
)-separate for i = 1,2, …, l − 1. Hence, this surface detection problem is modeled as a layered net surface problem on the properly ordered graph G. Note that in this application, we do not consider the region-based information for the segmentation though it is easy to be incorporated into G.
are (
)-separate for i = 1,2, …, l − 1. Hence, this surface detection problem is modeled as a layered net surface problem on the properly ordered graph G. Note that in this application, we do not consider the region-based information for the segmentation though it is easy to be incorporated into G.
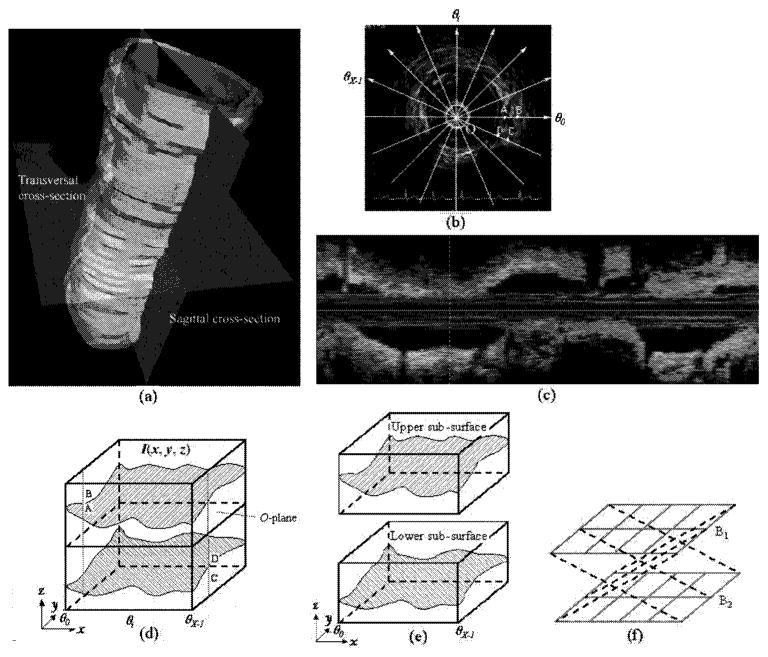
To segment a tubular structure in a 3-D image 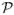 , we need to first “unfold” it, and then embed it into the 3-D xyz-space to obtain an image ℐ(x, y, z). In common medical practice, there are two useful unfolding approaches: One is based on the transversal cross-sections (TCS) of the tubular object; the other is based on the sagittal cross-sections (SCS) (see Figure 3(a)).
, we need to first “unfold” it, and then embed it into the 3-D xyz-space to obtain an image ℐ(x, y, z). In common medical practice, there are two useful unfolding approaches: One is based on the transversal cross-sections (TCS) of the tubular object; the other is based on the sagittal cross-sections (SCS) (see Figure 3(a)).
Fig. 3.
Illustrating the sagittal cross-section based unfolding method, (a) The sagittal and transversal cross-sections of a tubular object, (b) A transversal cross-section of a 3-D intravascular ultrasound vessel image. Resampling is performed at each angle for all transversal cross-sections to form a sagittal cross-section, (c) A sagittal cross-section of a 3-D intravascular ultrasound image at an angle θi. (d) A schematic unfolded 3-D image ℐ(x, y, z). Each sagittal cross-section at an angle θi is embedded as a yz-slice of ℐ at x = θi. (e) Splitting ℐ into two sub-images 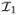 and
and 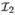 . (f) The net model B for ℐ.
. (f) The net model B for ℐ.
In the TCS-based approach, as illustrated in Figure 1, each transversal cross-section is unfolded by performing a polar resampling with respect to the center point O, and is embedded into an xz-plane, called an xz-slice of ℐ. Hence, any two adjacent columns on a same xz-slice satisfy the smoothness constraints. Note that on each xz-slice, the last column is treated as being adjacent to the first column, thus satisfying the smoothness constraints as well. Additionally, the corresponding columns on any two adjacent xz-slices also need to meet the smoothness constraints in the y-direction. Next, by applying the same modeling to ℐ(x,y,z) as for the terrain-like object, we transform this problem into that of computing multiple optimal interacting net surfaces in a properly ordered graph G, whose net model B is a 2-D grid with a wraparound in the x-dimension.
In the SCS-based method, each sagittal cross-section of the tubular structure, which consists of a sequence of profiles from all transversal cross-sections at the same angle, corresponds to a yz-slice of ℐ. Figure 3(b) shows a transversal cross-section of a 3-D intravascular ultrasound vessel image, in which each angle defines a sagittal cross-section. The sagittal cross-section corresponding to angle θi in Figure 3(b) is illustrated in Figure 3(c) and is embedded as a yz-slice of ℐ at x = θi (see Figure 3(d)). Note that the centerline of the tubular object is on every sagittal cross-section, thus forming the so-called O-plane in ℐ. The O-plane splits a desired tubular surface in the original image 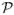 into two sub-surfaces, the upper sub-surface and lower sub-surface, as shown in Figure 3(d). To model this problem, we decompose the image ℐ along the O-plane into two sub-images
into two sub-surfaces, the upper sub-surface and lower sub-surface, as shown in Figure 3(d). To model this problem, we decompose the image ℐ along the O-plane into two sub-images 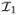 and
and 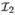 (see Figure 3(e)), each of which is used for searching the upper sub-surfaces and the lower sub-surfaces, respectively. One may search for the upper sub-surfaces and the lower sub-surfaces in
(see Figure 3(e)), each of which is used for searching the upper sub-surfaces and the lower sub-surfaces, respectively. One may search for the upper sub-surfaces and the lower sub-surfaces in 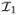 and
and 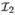 separately, by using our algorithm for the LNS problem. The net models B1 and B2 for
separately, by using our algorithm for the LNS problem. The net models B1 and B2 for 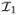 and
and 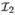 , respectively, are a 2-D grid with only proper edges. However, the upper (resp., lower) surface on the last sagittal cross-section (i.e., at x = θX−1 in Figure 3(e)) needs to be smoothly connected with the lower (resp., upper) surface on the first sagittal cross-section (i.e., at x = θ0 in Figure 3(e)). To enforce this smoothness constraint, we introduce a reverse edge between the corresponding vertices on the last column of B1 (resp., B2) and the first column of B2 (resp., B1) (see Figure 3(f)), thus forming a net model B. Obviously, the p-contracted graph of B is bipartite. Hence, we model this segmentation problem as solving a BLNS problem.
, respectively, are a 2-D grid with only proper edges. However, the upper (resp., lower) surface on the last sagittal cross-section (i.e., at x = θX−1 in Figure 3(e)) needs to be smoothly connected with the lower (resp., upper) surface on the first sagittal cross-section (i.e., at x = θ0 in Figure 3(e)). To enforce this smoothness constraint, we introduce a reverse edge between the corresponding vertices on the last column of B1 (resp., B2) and the first column of B2 (resp., B1) (see Figure 3(f)), thus forming a net model B. Obviously, the p-contracted graph of B is bipartite. Hence, we model this segmentation problem as solving a BLNS problem.
4. Algorithm for the Layered Net Surface (LNS) Problem
This section gives our polynomial time algorithm for the layered net surface problem on a d-D properly ordered graph G = (V, E). We first exploit the self-closure structure of the LNS problem, and then model it as a minimum-cost closed set problem based on a nontrivial graph transformation scheme.
A closed set  in a directed graph with arbitrary vertex costs w(·) is a subset of vertices such that all successors of any vertex in
in a directed graph with arbitrary vertex costs w(·) is a subset of vertices such that all successors of any vertex in  are also contained in
are also contained in  .20,14 The cost of a closed set
.20,14 The cost of a closed set  , denoted by w(
, denoted by w( ), is the total cost of all vertices in
), is the total cost of all vertices in  . Note that a closed set can be empty (with a cost zero). The minimum-cost closed set problem seeks a closed set in the graph whose cost is minimized.
. Note that a closed set can be empty (with a cost zero). The minimum-cost closed set problem seeks a closed set in the graph whose cost is minimized.
4.1. Overview of the LNS algorithm
Our LNS algorithm is based on a sophisticated graph transformation scheme, which enables us to simultaneously identify l > 1 optimal inter-related net surfaces as a whole by computing a minimum closed set in a weighted directed graph G′ that we transform from G. The algorithm uses the following three main steps.
Step 1: Graph Construction
Build a vertex-weighted directed graph G′ = (V′, E′), which contains l vertex-disjoint subgraphs . Each subgraph is used to search for the i-th net surface in ℐ. The separation constraints of the net surfaces are enforced by introducing a subset of directed edges between any two adjacent subgraphs, and (i = 1,2,…, l−1). The construction of the graph G (see Section 4.3) hinges on the self-closure structure exploited in Section 4.2.
Step 2: Computing a Minimum-cost Closed Set
Compute a minimum-cost non-empty closed set  *in G′, which can be done by formulating it as computing a minimum s-t cut in an edge-weighted directed graph transformed from G′.
*in G′, which can be done by formulating it as computing a minimum s-t cut in an edge-weighted directed graph transformed from G′.
Step 3: Net Surfaces Reconstruction
The set of l optimal net surfaces is reconstructed from the minimum-cost closed set  * with each net surface being specified by
.
* with each net surface being specified by
.
4.2. The self-closure property of the LNS problem
Our algorithm for the LNS problem hinges on the following observations about the self-closure structure of any feasible LNS solution. Recall that in a set of l feasible net surfaces 
 = {
= { ,
,  , …,
, …, 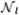 } in G,
} in G,  is “on top” of
is “on top” of  , for each i = 1,2,…,l−1.
, for each i = 1,2,…,l−1.
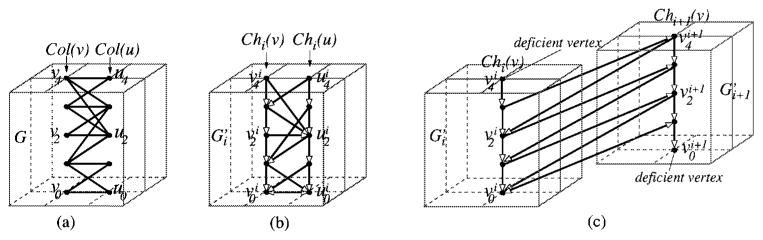
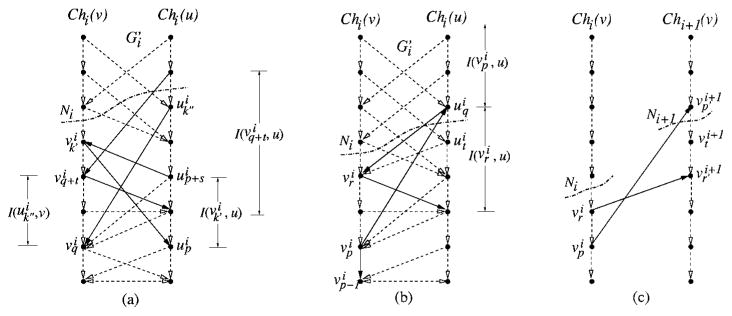
For a vertex vk ∈ V (i.e., v ∈ VB and 0 ≤ k < κ) and each adjacent column Col(u) of Col(v) (i.e., (v,u) ∈ EB), the lowest-neighbor of vk on Col(u) is the vertex in Col(u) with the smallest d-th coordinate that has an edge to vk in G (i.e., the vertex in Col(u) with the smallest d-th coordinate that can possibly appear together with vk on a same feasible net surface in G). In Figure 4(a), the lowest-neighbor of v2 (resp., u2) on Col(u) (resp., Col(v)) is u2 (resp., v1).
Fig. 4.
(a) Illustrating the proper ordering of the edges in G. (b) Constructing a subgraph from G. (c) Incorporating the surface separation constraints into the construction of and (with Li = 1 and Ui = 2).
Given the surface separation constraints, we define below the upstream and downstream vertices of any vertex in G, to help characterize the spatial relations between feasible net surfaces in G. For every vertex vk ∈ V and 1 ≤ i < l (resp., 1 < i ≤ l), the i-th upstream (resp., downstream) vertex of vk is vk+Li (resp., vmax{0,k−Ui−1}) if k + Li < κ (resp., k − Li−1 ≥ 0). Intuitively, if vk ∈  , then the i-th upstream (resp., downstream) vertex of vk is the vertex in Col(v) with the smallest d-th coordinate that can be on
, then the i-th upstream (resp., downstream) vertex of vk is the vertex in Col(v) with the smallest d-th coordinate that can be on  (resp.,
(resp., 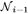 ).
).
We say that a vertex vk is below (resp., above) a net surface  if
if  (v) > k (resp.,
(v) > k (resp.,  (v) < k), and denote by LO(
(v) < k), and denote by LO( ) the subset of all vertices of G that are on or below
) the subset of all vertices of G that are on or below  . For every vertex vk ∈ LO(
. For every vertex vk ∈ LO( ), consider its lowest-neighbor uk′ on any adjacent Col(u) of Col(v). Let r =
), consider its lowest-neighbor uk′ on any adjacent Col(u) of Col(v). Let r =  (v) and uk″ be the lowest-neighbor of vr on Col(u) (vr ∈ Col(v) is on
(v) and uk″ be the lowest-neighbor of vr on Col(u) (vr ∈ Col(v) is on  ). Then by the definition of net surfaces, k″ ≤
). Then by the definition of net surfaces, k″ ≤  (u). Since k ≤
(u). Since k ≤  (v), we have k′ ≤ k″ due to the proper ordering. Thus, k′ ≤
(v), we have k′ ≤ k″ due to the proper ordering. Thus, k′ ≤  (u), and further, uk′ ∈ LO(
(u), and further, uk′ ∈ LO( ). Hence, we have the following observation.
). Hence, we have the following observation.
Observation 1
For any feasible net surface  in G, if a vertex vk is in LO(
in G, if a vertex vk is in LO( ), then every lowest-neighbor of vk is also in LO(
), then every lowest-neighbor of vk is also in LO( ).
).
Observation 1 characterizes the self-closure property of every set LO( ). However, our task is more involved since the l net surfaces in
). However, our task is more involved since the l net surfaces in 
 are inter-related. We thus need to further examine the closure structure between the LO(
are inter-related. We thus need to further examine the closure structure between the LO( )’S. Consider any vertex vk ∈ LO(
)’S. Consider any vertex vk ∈ LO( ). Since k ≤
). Since k ≤  (v), the i-th upstream vertex of
(v), the i-th upstream vertex of 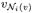 is “above” the i-th upstream vertex of vk (i.e.,
is “above” the i-th upstream vertex of vk (i.e.,  (v) + Li ≥ k + Li). In the meanwhile,
(v) + Li ≥ k + Li). In the meanwhile,  (v) ≥
(v) ≥  (v) + Li (by the definition of the i-th upstream vertex). Hence, the i-th upstream vertex of vk, vk+Li, is in LO(
(v) + Li (by the definition of the i-th upstream vertex). Hence, the i-th upstream vertex of vk, vk+Li, is in LO( ). Using a similar argument, the i-th downstream vertex of vk, vmax{0,k−Ui−1} is in LO(
). Using a similar argument, the i-th downstream vertex of vk, vmax{0,k−Ui−1} is in LO(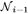 ). Thus, the observation below follows.
). Thus, the observation below follows.
Observation 2
Given any set 
 = {
= { ,
,  ,…
,… 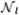 } of l feasible net surfaces in G, the i-th upstream (resp., downstream) vertex of each vertex in LO(
} of l feasible net surfaces in G, the i-th upstream (resp., downstream) vertex of each vertex in LO( ) is in LO(
) is in LO( ) (resp., LO(
) (resp., LO(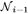 )), for every 1 ≤ i < l (resp., 1 < i ≤ l).
)), for every 1 ≤ i < l (resp., 1 < i ≤ l).
Observations 1 and 2 show an important self-closure structure of the LNS problem, which is crucial to our LNS algorithm and suggests a connection between our target problem and the minimum-cost closed set problem.20,14 In our LNS approach, instead of directly searching for an optimal set of l net surfaces, , we look for l optimal subsets of vertices in G, , such that each uniquely defines the net surface .
4.3. The graph transformation scheme
This section presents the construction of the vertex-weighted directed graph G′ = (V′, E′) from the d-D properly ordered graph G = (V, E), which enables us to simultaneously identify l > 1 optimal inter-related net surfaces as a whole by computing a minimum closed set. This construction crucially relies on the self-closure structure shown in Section 4.2.
The graph G′ contains l vertex-disjoint subgraphs
; each
is for the search of the i-th net surface  .
and
. The surface separation constraints between any two consecutive net surfaces
.
and
. The surface separation constraints between any two consecutive net surfaces  and
and  are enforced in G′ by a subset of edges in
, which connect the corresponding subgraphs
and
.
are enforced in G′ by a subset of edges in
, which connect the corresponding subgraphs
and
.
We first show the construction of every
(i = 1,2, …,l) from G. For
, each vertex vk in G corresponds to exactly one vertex
. Note that
is used for the search of LO( ) that defines the i-th net surface
) that defines the i-th net surface  . If vertex vk ∈ Col(v) appears on
. If vertex vk ∈ Col(v) appears on  , then all vertices of Col(v) “below” vk (i.e., those vertices of Col(v) whose d-th coordinate is ≤ k) are in LO(
, then all vertices of Col(v) “below” vk (i.e., those vertices of Col(v) whose d-th coordinate is ≤ k) are in LO( ). Thus, for each v ∈ VB of the net model B and k = 1,2,…,κ − 1, vertex
has a directed edge (
), forming a chain
in
for Col(v), denoted by Chi(v). These chains help capture the closure property of LO(
). Thus, for each v ∈ VB of the net model B and k = 1,2,…,κ − 1, vertex
has a directed edge (
), forming a chain
in
for Col(v), denoted by Chi(v). These chains help capture the closure property of LO( ). Two chains Chi(v) and Chi(u) in
are said to be adjacent if their corresponding columns Col(v) and Col(u) in G are adjacent. Next, we put directed edges between any two adjacent chains in
to ensure the feasibility of the net surface
). Two chains Chi(v) and Chi(u) in
are said to be adjacent if their corresponding columns Col(v) and Col(u) in G are adjacent. Next, we put directed edges between any two adjacent chains in
to ensure the feasibility of the net surface  . For every vertex vk of each Col(v) in G and its lowest-neighbor uk′ on each adjacent Col(u) of Col(v), we put into
a directed edge from
to
. The role of this edge is to ensure that if vk ∈
. For every vertex vk of each Col(v) in G and its lowest-neighbor uk′ on each adjacent Col(u) of Col(v), we put into
a directed edge from
to
. The role of this edge is to ensure that if vk ∈  , then
, then  must contain a vertex in Col(u) that is no “lower” than uk′ (i.e.,
must contain a vertex in Col(u) that is no “lower” than uk′ (i.e.,  (u) ≥ k′). This is because a feasible
(u) ≥ k′). This is because a feasible  containing vk can only contain a vertex in the edge interval I(vk,u) of vk on Col(u), i.e., I(vk,u) = (uk′, uk′+1, …, uk′+s) (s ≥0). It might appear that adding this edge to
might not do the job. But, based on the proper ordering in G, we are able to prove that our graph transformation well enforces the feasibility of the net surfaces (see Lemmas 4 and 5). Figure 4(a) shows the part of the graph G associated with an edge (v,u) ∈ EB, and Figure 4(b) illustrates the corresponding construction in
. This completes the construction of each
.
containing vk can only contain a vertex in the edge interval I(vk,u) of vk on Col(u), i.e., I(vk,u) = (uk′, uk′+1, …, uk′+s) (s ≥0). It might appear that adding this edge to
might not do the job. But, based on the proper ordering in G, we are able to prove that our graph transformation well enforces the feasibility of the net surfaces (see Lemmas 4 and 5). Figure 4(a) shows the part of the graph G associated with an edge (v,u) ∈ EB, and Figure 4(b) illustrates the corresponding construction in
. This completes the construction of each
.
We now put directed edges into
between
and
, to enforce the surface separation constraints. Based on Observation 2, if vertex vk ∈  , then its i-th upstream vertex vk+Li must be on or below the net surface
, then its i-th upstream vertex vk+Li must be on or below the net surface  (i.e., vk+Li ∈ LO(
(i.e., vk+Li ∈ LO( )). Thus, for each vertex
with k < κ − Li on the chain Chi(v) in
, a directed edge is put in
from
to
on Chi+1(v) in
(see Figure 4(c)). Intuitively, these edges ensure that the net surface
)). Thus, for each vertex
with k < κ − Li on the chain Chi(v) in
, a directed edge is put in
from
to
on Chi+1(v) in
(see Figure 4(c)). Intuitively, these edges ensure that the net surface  must be at a distance of at least Li “above”
must be at a distance of at least Li “above”  (i.e., for each v ∈ VB,
(i.e., for each v ∈ VB,  (v) −
(v) −  (v) ≥ Li). On the other hand, each vertex
with k ≥ Li on Chi+1(v) has a directed edge in
to
on Chi(v) with k′ = max{0, k − Ui} (note that vk′ in G is the (i + 1)-th downstream vertex of vk), making sure that
(v) ≥ Li). On the other hand, each vertex
with k ≥ Li on Chi+1(v) has a directed edge in
to
on Chi(v) with k′ = max{0, k − Ui} (note that vk′ in G is the (i + 1)-th downstream vertex of vk), making sure that  must be at a distance of no larger than Ui “above”
must be at a distance of no larger than Ui “above”  (i.e., for each v ∈ VB,
(i.e., for each v ∈ VB,  (v) −
(v) −  (v) ≤ Ui). Note that in this construction, any vertex
with k ≥ κ − Li has no edge to any vertex on Chi+1(v), forming the upper deficient vertex segment udvi(v) of Chi(v), and any vertex
with k < Li has no edge to any vertex on Chi(v), forming the lower deficient vertex segment ldvi+1 (v) of Chi+1(v). Each of these vertices of G′ is called a deficient vertices. This construction is applied to every pair of the corresponding chains of any two subgraphs
and
, for i = 1, 2, …, l −1.
(v) ≤ Ui). Note that in this construction, any vertex
with k ≥ κ − Li has no edge to any vertex on Chi+1(v), forming the upper deficient vertex segment udvi(v) of Chi(v), and any vertex
with k < Li has no edge to any vertex on Chi(v), forming the lower deficient vertex segment ldvi+1 (v) of Chi+1(v). Each of these vertices of G′ is called a deficient vertices. This construction is applied to every pair of the corresponding chains of any two subgraphs
and
, for i = 1, 2, …, l −1.
Recall that we aim to compute a minimum-cost non-empty closed set in G′, which can specify l optimal net surfaces in G. However, the graph G′ constructed up to this point does not yet work for this purpose. When a closed set  in G′ includes only deficient vertices of a chain in G′, which is possible, it does not correspond to l feasible net surfaces. The reader may notice that for any deficient vertex in G′, the corresponding vertex in G cannot lie on a feasible net surface. Hence, it might seem safe to remove all deficient vertices from G′. However, this removal of deficient vertices may in turn cause other vertices in G′ to become deficient. (A vertex
on Chi(v) is said to be deficient if either no vertex in
or
connects with it, or there exists an edge (v, u) ∈ EB but no vertex on Chi(u) of
is adjacent to it.) Moreover, we cannot simply delete all edges incident with the deficient vertices.
in G′ includes only deficient vertices of a chain in G′, which is possible, it does not correspond to l feasible net surfaces. The reader may notice that for any deficient vertex in G′, the corresponding vertex in G cannot lie on a feasible net surface. Hence, it might seem safe to remove all deficient vertices from G′. However, this removal of deficient vertices may in turn cause other vertices in G′ to become deficient. (A vertex
on Chi(v) is said to be deficient if either no vertex in
or
connects with it, or there exists an edge (v, u) ∈ EB but no vertex on Chi(u) of
is adjacent to it.) Moreover, we cannot simply delete all edges incident with the deficient vertices.
By utilizing the proper order of graph G, we develop a deficient vertex pruning scheme, as follows. Instead of removing the deficient vertices one by one, we grow the deficient vertex segments until no further changes can occur, and then safely remove all deficient vertex segments and their edges. We first consider the lower deficient vertex segment ldvi(v) of each chain Chi(v) in G′. A key observation here is that when pruning the lower deficient vertex segments, if a vertex on Chi(v) is deficient, then all vertices on Chi(v) “below” (i.e., with k′ ≤ k) are also deficient. Hence, the deficient vertices on every Chi(v) always form a continuous segment and it is sufficient to consider the “topmost” deficient vertex on ldvi(v) (i.e., , k ≤ t). For each column Col(u) adjacent to Col(v), recall that I(vt, u) denotes the edge interval of vt on Col(u) in G. If I(vt, u) ⊆ ldvi(u), then the removal of ldvi(v) does not cause additional deficient vertices on Chi(u). Otherwise, consider the edge interval I(vt+1, u) of vt+1 on Col(u). Let q be the smallest d-th coordinate of the vertices in I(vt+1, u). Due to the proper order of G, no vertices vk with k > t have an edge connecting with uq−1 ∈ Col(u). Thus, the vertex is deficient since the edge (v, u) ∈ EB but the removal of all incident edges of the vertices in ldvi(v) leaves no edge connecting with any vertex on Chi(v) in . Let be the topmost deficient vertex on ldvi(u). If q − 1 > t′, then the lower deficient vertex segment ldvi(u) now grows up to . Note that for each vertex with k ≥ q and uk ∈ I(vt, u), if uk is on a feasible surface, then the vertex of Col(v) on that surface must be no lower than vt+1; in fact, the edge (vt+1, uk) is in G. Thus, a directed edge from to is put in to enforce this relation. This pruning procedure is also applied to Chi(v) with respect to Chi+1(v) and Chi−1 (v). When no further changes are needed on the lower deficient vertex segments of G′, we just remove all these segments and their incident edges. Actually, we can maintain a queue to keep the chains of G′ with a changed lower deficient vertex segment. When eventually the queue is empty, it means that no lower deficient vertex segments will be further changed. The upper deficient vertex segments in G′ are handled in a similar way. It is not hard to see that the following lemma holds.
Lemma 1
The deficient vertex pruning scheme runs in O(|E′|) time on G′ = (V′, E′).
We simply denote the graph thus resulted also by G′. Note that in G′ if any chain Chi (v) =  , then there is no feasible solution to the LNS problem. In the rest of this section, we assume that the LNS problem has feasible solutions. Then, for every v ∈ VB and i = 1, 2, …, l, let μi(v) and κi(v) be the smallest and largest d-th coordinates of the vertices on the chain Chi(v) of
, respectively. We denote by Z0 the set of the “lowest” vertices (i.e., with the smallest d-th coordinate) on every chains of G′ and by H0 the induced subgraph of Z0 in G′. Our above construction of G′ ensures the following lemma.
, then there is no feasible solution to the LNS problem. In the rest of this section, we assume that the LNS problem has feasible solutions. Then, for every v ∈ VB and i = 1, 2, …, l, let μi(v) and κi(v) be the smallest and largest d-th coordinates of the vertices on the chain Chi(v) of
, respectively. We denote by Z0 the set of the “lowest” vertices (i.e., with the smallest d-th coordinate) on every chains of G′ and by H0 the induced subgraph of Z0 in G′. Our above construction of G′ ensures the following lemma.
Lemma 2
(1) H0 is a strongly connected component of G′. (2) Z0 is a closed set in G′. (3) For any non-empty closed set  in G′, Z0 ⊆
in G′, Z0 ⊆  .
.
Up to this point, the graph construction establishes the connection between a closed set in G′ and l feasible net surfaces in G. Our goal is to compute a non-empty minimum-cost closed set in G′, which can specify l optimal nets in G. Thus, we need to further assign a cost w(·) to each vertex in G′.
Note that the cost of 
 is
, where Ri’s are the disjoint subsets of V partitioned by the nets in
is
, where Ri’s are the disjoint subsets of V partitioned by the nets in 
 . Further, recall that we are looking for LO(
. Further, recall that we are looking for LO( ) instead of
) instead of  directly, by using the subgraph
. Thus, we want to find a way to assign vertex costs to
, so that for any feasible
directly, by using the subgraph
. Thus, we want to find a way to assign vertex costs to
, so that for any feasible  in G, the cost b(
in G, the cost b( ) can be “distributed” to those vertices of
corresponding to LO(
) can be “distributed” to those vertices of
corresponding to LO( ) (i.e.,
). We may go one step further to require that for any vertex vr ∈ Col(v) in G, the total cost of the vertices
on Chi(v) of
with k ≤ r (i.e.,
) be equal to the cost of vr. In addition, note that R0 = LO(
) (i.e.,
). We may go one step further to require that for any vertex vr ∈ Col(v) in G, the total cost of the vertices
on Chi(v) of
with k ≤ r (i.e.,
) be equal to the cost of vr. In addition, note that R0 = LO( ), Ri =LO(
), Ri =LO( ) − LO(
) − LO( ) (i = 1, 2, …, l − 1), and Rl = V − LO(
) (i = 1, 2, …, l − 1), and Rl = V − LO(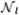 ), and consider the removal of the deficient vertices as well. Thus, we have the following vertex-cost assignment scheme for each subgraph
(i = 1, 2, …, l): For every v ∈ VB,
), and consider the removal of the deficient vertices as well. Thus, we have the following vertex-cost assignment scheme for each subgraph
(i = 1, 2, …, l): For every v ∈ VB,
| (1) |
This completes the construction of G′.
4.4. Computing optimal layered net surfaces for the LNS problem
The graph G′ thus constructed allows us to find l optimal net surfaces in G, by computing a non-empty minimum-cost closed set in G′. In order to do that, below we prove the following facts: (1) Any closed set  ≠
≠  in G′ defines l feasible net surfaces in G whose total cost differs from that of
in G′ defines l feasible net surfaces in G whose total cost differs from that of  by a fixed value; (2) any set
by a fixed value; (2) any set 
 of l feasible net surfaces in G corresponds to a closed set
of l feasible net surfaces in G corresponds to a closed set  ≠
≠  in G′ whose cost differs from that of
in G′ whose cost differs from that of 
 by a fixed value. Consequently, a non-empty closed set in G′ with the minimum cost can specify l optimal net surfaces in G.
by a fixed value. Consequently, a non-empty closed set in G′ with the minimum cost can specify l optimal net surfaces in G.
Given any closed set  ≠
≠  in G′, we define l feasible net surfaces,
in G′, we define l feasible net surfaces, 
 = {
= { ,
,  ,…,
,…, 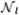 }, in G, as follows. Recall that we search for each net
}, in G, as follows. Recall that we search for each net  , in the subgraph
. Let
. For each vertex v ∈ VB, denote by
, in the subgraph
. Let
. For each vertex v ∈ VB, denote by 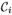 (v) the set of vertices of
(v) the set of vertices of 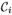 on the chain Chi(v) of
. Based on the construction of
, it is not hard to show that
on the chain Chi(v) of
. Based on the construction of
, it is not hard to show that 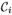 (v) ≠
(v) ≠  . Let ri(v) be the largest d-th coordinate of the vertices in
. Let ri(v) be the largest d-th coordinate of the vertices in 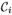 (v). Define the function
(v). Define the function  as
as  (v) = ri(v) for every v ∈ VB.
(v) = ri(v) for every v ∈ VB.
First, we show that 
 thus defined in G indeed consists of l feasible net surfaces. Lemmas 3 and 4 summarize the fact.
thus defined in G indeed consists of l feasible net surfaces. Lemmas 3 and 4 summarize the fact.
Lemma 3
Each  defined by
defined by 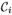 is a feasible net surface in G.
is a feasible net surface in G.
Proof
For each edge (v, u) ∈ EB, let k′ =  (v) and k″ =
(v) and k″ =  (u). We need to prove that (vk′, uk″) is an edge in G. In G, let the edge interval I(vk′, u) of vk′ on Col(u) be (up, up+1,…, up+s) and the edge interval I(uk″, v) of uk″ on Col(v) be (vq, vq+1,…, vq+t) (see Figure 5(a)). If vertex uk″ is in the edge interval I(vk′, u), then we are done. Otherwise, either p > k″ or p + s < k″. Consider the case with p > k″. By the observation that
(u). We need to prove that (vk′, uk″) is an edge in G. In G, let the edge interval I(vk′, u) of vk′ on Col(u) be (up, up+1,…, up+s) and the edge interval I(uk″, v) of uk″ on Col(v) be (vq, vq+1,…, vq+t) (see Figure 5(a)). If vertex uk″ is in the edge interval I(vk′, u), then we are done. Otherwise, either p > k″ or p + s < k″. Consider the case with p > k″. By the observation that 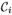 , ≠
, ≠  is a closed set in
and the construction of
, vertex
, which contradicts to the fact that k″ is the largest d-th coordinate of the vertices in
is a closed set in
and the construction of
, vertex
, which contradicts to the fact that k″ is the largest d-th coordinate of the vertices in 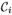 (u). Thus, we only need to consider the case with p + s < k″ (see Figure 5(a)). By a similar argument, we have q + t < k′. Since there is an edge between vertices vq+t and uk″ in G (vq+t ∈ I(uk″, v)), vertex uk″ thus is in the edge interval I(vq+t, u) of vq+t on Col(u). Hence, we have the largest d-th coordinate Top(I(vq+t, u)) of vertices in I(vq+t, u) is no less than k″. Note that k″ > p + s and p + s is the largest d-th coordinate Top(I(vk′, u)) of vertices in I(vk′, u). Thus, Top(I(vq+t, u)) > Top(I(vk′, u)), contradicting with the proper ordering of the graph G (since k′ > q + t). Hence, the lemma follows.
(u). Thus, we only need to consider the case with p + s < k″ (see Figure 5(a)). By a similar argument, we have q + t < k′. Since there is an edge between vertices vq+t and uk″ in G (vq+t ∈ I(uk″, v)), vertex uk″ thus is in the edge interval I(vq+t, u) of vq+t on Col(u). Hence, we have the largest d-th coordinate Top(I(vq+t, u)) of vertices in I(vq+t, u) is no less than k″. Note that k″ > p + s and p + s is the largest d-th coordinate Top(I(vk′, u)) of vertices in I(vk′, u). Thus, Top(I(vq+t, u)) > Top(I(vk′, u)), contradicting with the proper ordering of the graph G (since k′ > q + t). Hence, the lemma follows.
Fig. 5.
(a) Illustrating the proof of Lemma 3. (b) Illustrating Case (2) in the proof of Lemma 6. (c) Illustrating Case (3) in the proof of Lemma 6.
Lemma 4
Any two adjacent net surfaces  and
and  in G (i = 1, 2,…, l − 1) defined by a closed set
in G (i = 1, 2,…, l − 1) defined by a closed set  ≠
≠  in G′ are (Li, Ui)-separate.
in G′ are (Li, Ui)-separate.
Proof
For each vertex v ∈ VB, we need to prove that Li <  (v) −
(v) −  (v) ≤ Ui. Let k′ =
(v) ≤ Ui. Let k′ =  (v) and k″ =
(v) and k″ = (v). Denote by vp the i-th upstream vertex of vk′ By the construction of G′, there is a directed edge from
to
, which indicates that
is in
(v). Denote by vp the i-th upstream vertex of vk′ By the construction of G′, there is a directed edge from
to
, which indicates that
is in 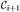 (v) ⊂
(v) ⊂  . Note that k″ is the largest d-th coordinate of vertices in
. Note that k″ is the largest d-th coordinate of vertices in 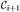 (v). Thus, we have p ≤ k″ and k″ − k′ ≥ p − k′ ≥ Li (the definition of the upstream vertices). On the other hand, let vq denote the i + 1-st downstream vertex of vk″. Then, vertex
has a directed edge to
. Similarly, q ≤ k′. From the definition of the downstream vertices, k″ − q ≤ Ui. Hence, k″ − k′ ≤ k″ − q ≤ Ui. This proves the lemma.
(v). Thus, we have p ≤ k″ and k″ − k′ ≥ p − k′ ≥ Li (the definition of the upstream vertices). On the other hand, let vq denote the i + 1-st downstream vertex of vk″. Then, vertex
has a directed edge to
. Similarly, q ≤ k′. From the definition of the downstream vertices, k″ − q ≤ Ui. Hence, k″ − k′ ≤ k″ − q ≤ Ui. This proves the lemma.
Then, we show that the cost α(
 ) of
) of 
 thus defined by
thus defined by  differs by a fixed value from the total vertex cost w(
differs by a fixed value from the total vertex cost w( ) of
) of  . Note that in
, if a vertex
, then all vertices in {
, k ≤ q} are also in
. Note that in
, if a vertex
, then all vertices in {
, k ≤ q} are also in 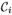 (v). Hence, the total vertex cost of
(v). Hence, the total vertex cost of 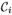 (v) is
. Thus, we have
(v) is
. Thus, we have
| (2) |
Note that the term , denoted by cl(V), is fixed and is the total sum of the l-th in-region costs of all vertices in G. From Lemmas 3 and 4 and Equation (2), the following lemma holds.
Lemma 5
Any closed set  ≠
≠  in G′ specifies l feasible net surfaces in G whose total cost differs from that of
in G′ specifies l feasible net surfaces in G whose total cost differs from that of  by a fixed value cl(V).
by a fixed value cl(V).
Next, we argue that any l feasible net surfaces, 
 = {
= { ,
,  , …,
, …, 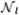 } in G correspond to a closed set
} in G correspond to a closed set  ≠
≠  in G′. Based on the construction of G′, every vertex vk on the net
in G′. Based on the construction of G′, every vertex vk on the net  corresponds to a vertex
in
(
is not a deficient vertex). We construct a closed set
corresponds to a vertex
in
(
is not a deficient vertex). We construct a closed set 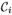 ≠
≠  in
for each net
in
for each net  , as follows. Initially, let
, as follows. Initially, let 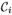 =
=  . For each vertex v ∈ VB, we add to
. For each vertex v ∈ VB, we add to 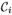 , the subset
of vertices on Chi(v) of
. Let
. We prove that
, the subset
of vertices on Chi(v) of
. Let
. We prove that  is a closed set in G′.
is a closed set in G′.
Lemma 6
Any l feasible net surfaces, 
 = {
= { ,
,  ,…,
,…, 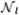 }, in G define a closed set
}, in G define a closed set  in G′.
in G′.
Proof
For each vertex , due to the construction of the graph G′, the only successors of are: (1) (if p ≥ μi(v)) on the same chain Chi(v); (2) one vertex on every adjacent chain Chi(u) of Chi(v) in ;(3) one vertex on the chain Chi+1(v) in (if i < 1); and (4) one vertex on the chain Chi−1(v) in (if i > 1).
Case (1)
Obviously,
due to the construction of  .
.
Case (2)
Consider each adjacent chain Chi(u) of Chi(v) in
. Let r =  (v) and t =
(v) and t =  (u). We have r ≥ p since r is the largest d-th coordinate of vertices of Chi(v) that we put in
(u). We have r ≥ p since r is the largest d-th coordinate of vertices of Chi(v) that we put in 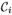 . Since all vertices
with μi(u) ≤ k ≤ t are in
. Since all vertices
with μi(u) ≤ k ≤ t are in 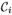 , if q ≤ t, then we are done. Hence, we assume that q > t (see Figure 5(b)). Since
is a successor of
, the smallest d-th coordinate Bottom(I(vp, u)) of the vertices in the edge interval I(vp, u) of vp on Col(u) is q (i.e., Bottom(I(vp, u)) = q). Note that the edge (vr, ut) is on the net surface
, if q ≤ t, then we are done. Hence, we assume that q > t (see Figure 5(b)). Since
is a successor of
, the smallest d-th coordinate Bottom(I(vp, u)) of the vertices in the edge interval I(vp, u) of vp on Col(u) is q (i.e., Bottom(I(vp, u)) = q). Note that the edge (vr, ut) is on the net surface  . Thus, ut ∈ I(vr, u) and Bottom(I(vr, u)) ≤ t. Hence, we have Bottom(I(vp, u)) = q > t ≥ Bottom(I(vr, u)), a contradiction to the proper ordering property of the graph G (since r ≥ p). Consequently, q ≤ t and
.
. Thus, ut ∈ I(vr, u) and Bottom(I(vr, u)) ≤ t. Hence, we have Bottom(I(vp, u)) = q > t ≥ Bottom(I(vr, u)), a contradiction to the proper ordering property of the graph G (since r ≥ p). Consequently, q ≤ t and
.
Case (3)
Let r =  (v) and t =
(v) and t =  (v). Then, r ≥ p. We need to prove t ≥ p′. Since the successor of
on Chi+1(v) is
, vp′ is the vertex in Col(v) with the smallest d-th coordinate that can be on
(v). Then, r ≥ p. We need to prove t ≥ p′. Since the successor of
on Chi+1(v) is
, vp′ is the vertex in Col(v) with the smallest d-th coordinate that can be on  (vp is on the net
(vp is on the net  ). Note that p′ − p ≥ Li, but p′ may not equal to p + Li due to the deficient vertex pruning operations. Now assume that the successor of
on Chi+1(v) is
. We conclude that r′ ≥ p′. Otherwise, since r′ − r ≥ Li and r ≥ p, we have p′ − p > r′ − p ≥ r′ − r ≥ Li (see Figure 5(c)). Hence, vertex vr′ is the vertex in Col(v) with the smallest d-th coordinate that can be on
). Note that p′ − p ≥ Li, but p′ may not equal to p + Li due to the deficient vertex pruning operations. Now assume that the successor of
on Chi+1(v) is
. We conclude that r′ ≥ p′. Otherwise, since r′ − r ≥ Li and r ≥ p, we have p′ − p > r′ − p ≥ r′ − r ≥ Li (see Figure 5(c)). Hence, vertex vr′ is the vertex in Col(v) with the smallest d-th coordinate that can be on  , a contradiction. Thus, r′ ≥ p′. Since vr ∈
, a contradiction. Thus, r′ ≥ p′. Since vr ∈  and vt ∈
and vt ∈  , t ≥ r′. This indicates that t ≥ p′.
, t ≥ r′. This indicates that t ≥ p′.
Case (4)
A similar argument as for Case (3) can be applied, which proves that .
In conclusion, for each vertex
, all successors of
are in  . Thus, the lemma holds.
. Thus, the lemma holds.
Using a similar argument as in Equation (2), we can show that w( ) = α(
) = α( 
 ) − cl(V). Together with Lemma 6, the following lemma follows.
) − cl(V). Together with Lemma 6, the following lemma follows.
Lemma 7
Any set 
 of l feasible net surfaces in G defines a closed set
of l feasible net surfaces in G defines a closed set  ≠ ∅ in G′ whose cost differs from that of
≠ ∅ in G′ whose cost differs from that of 
 by a fixed value.
by a fixed value.
By Lemmas 5 and 7, we compute a minimum-cost closed set  * ≠
* ≠  in G′, which specifies l optimal net surfaces in G. However, the minimum closed set
in G′, which specifies l optimal net surfaces in G. However, the minimum closed set  * in G′ can be empty (with a weight zero), and when this is the case,
* in G′ can be empty (with a weight zero), and when this is the case,  * =
* =  gives little useful information on G′. Fortunately, our careful construction of G′ still enables us to overcome this difficulty. If the minimum closed set in G′ is empty, then it implies that the weight of every non-empty closed set in G′ is non-negative. To obtain a minimum non-empty closed set in G′, we do the following: Let M be the total weight of vertices in Z0; pick an arbitrary vertex u ∈ Z0 and assign a new weight w(u) − M − 1 to u. We call this a translation operation on G′. From Lemma 2, Z0 ≠
gives little useful information on G′. Fortunately, our careful construction of G′ still enables us to overcome this difficulty. If the minimum closed set in G′ is empty, then it implies that the weight of every non-empty closed set in G′ is non-negative. To obtain a minimum non-empty closed set in G′, we do the following: Let M be the total weight of vertices in Z0; pick an arbitrary vertex u ∈ Z0 and assign a new weight w(u) − M − 1 to u. We call this a translation operation on G′. From Lemma 2, Z0 ≠  is a closed set in G′ and is a subset of any non-empty closed set in G′. Further, observe that the total weight of vertices in the closed set Z0 (after a translation operation on G′) is negative. This implies that any minimum closed set in G′ (after a translation operation on G′) cannot be empty. Also based on Lemma 2, we have the following lemma.
is a closed set in G′ and is a subset of any non-empty closed set in G′. Further, observe that the total weight of vertices in the closed set Z0 (after a translation operation on G′) is negative. This implies that any minimum closed set in G′ (after a translation operation on G′) cannot be empty. Also based on Lemma 2, we have the following lemma.
Lemma 8
For a non-empty closed set  in G′, let w(
in G′, let w( ) denote the total weight of
) denote the total weight of  before any translation operation on G′. Then after a translation operation, the weight of
before any translation operation on G′. Then after a translation operation, the weight of  is w(
is w( ) − M − 1.
) − M − 1.
Now, we can simply find a minimum closed set  * in G′ after performing a translation operation on G′. Based on Lemma 8,
* in G′ after performing a translation operation on G′. Based on Lemma 8,  * is a minimum non-empty closed set in G′ before the translation.
* is a minimum non-empty closed set in G′ before the translation.
As in the paper,20,14,30 we find a minimum closed set  * ≠
* ≠  in G′ by formulating it as computing a minimum s-t cut in a weighted directed graph G″ transformed from G′, with |G″| = O(|G′|). Note that G′ has O(l · n) vertices and
edges, where n = |V| is the number of vertices in G, and nB = |VB| and mB = |EB| for the net model B. The deficient vertex pruning procedure takes
time. By using the minimum s-t cut algorithm in the paper,12 we obtain the following result.
in G′ by formulating it as computing a minimum s-t cut in a weighted directed graph G″ transformed from G′, with |G″| = O(|G′|). Note that G′ has O(l · n) vertices and
edges, where n = |V| is the number of vertices in G, and nB = |VB| and mB = |EB| for the net model B. The deficient vertex pruning procedure takes
time. By using the minimum s-t cut algorithm in the paper,12 we obtain the following result.
Theorem 1
The LNS problem can be solved in time.
5. Algorithm for the Bipartite LNS (BLNS) Problem
In this section, we consider the layered net surface problem on a d-D (d ≥ 3) ordered multi-column graph. We prove that the LNS problem on such a multi-column graph is NP-hard and give a polynomial time algorithm for solving the BLNS problem. Recall that the BLNS problem is defined on an ordered multi-column graph such that the p-contracted graph of its net model B is bipartite.
Theorem 2
The optimal LNS problem on a d-D ordered multi-column graph (d ≥ 3) is NP-hard.
Proof
We can prove that the LNS problem on a general d-D ordered multi-column graph is NP-hard, by reducing to it the minimum vertex cover problem that is known to be NP-complete.10
Given an undirected graph B = (VB, EB), the minimum vertex cover problem seeks a vertex cover V′ ⊆ VB such that for each edge (v, u) ∈ EB, at least one of v and u is in V′ and |V′| is minimized. This problem is reduced to the optimal LNS problem, as follows. First, embed the graph B into the 2-D space. Next, a 3-D ordered multi-column graph G = (V, E) is constructed. For each vertex v = (x, y) ∈ VB, there are two corresponding vertices in V, v0 = (x, y, 0) and v1 = (x, y, l). Assign a cost 0 to v0 and a cost 1 to v1. For every edge (v, u) ∈ EB, v0 connects with u1 in G and v1 connects with both u0 and u1. Obviously, the graph G thus generated is an ordered multi-column graph. Actually, any two adjacent columns in G are in reverse order. We simply assume l = 1. Note that a vertex v ∈ VB is in a vertex cover V′ of B if and only if v1 ∈ V is on a net surface in G, and the cost of the net surface equals the cardinality of the vertex cover. Hence, Theorem 2 holds.
The NP-hardness proof of the LNS problem actually shows that on a d-D ordered multi-column graph (d ≥ 3) generated by a net model with only reverse edges, the LNS problem is NP-hard. On the other hand, Section 4 shows that on any d-D ordered multi-column graph generated by a net model whose edges are all proper, the LNS problem is polynomially solvable. Hence, it is desirable to examine net models in order to explore the polynomial solvability of the LNS problem. We next consider the LNS problem on a d-D ordered multi-column graph G = (V, E) with a special net model B = (VB, EB) whose p-contracted graph is bipartite.
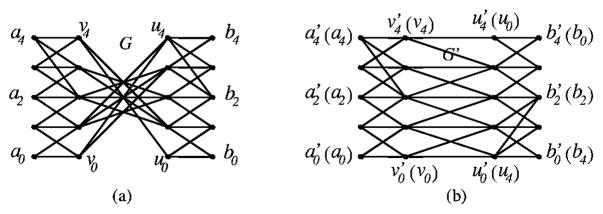
Observe that if the p-contracted graph of the net model B = (VB, EB) is a bipartite one, then essentially, we can partition VB into two disjoint subsets Q and Q̄ (VB = Q ∪ Q̄), such that each reverse edge of B connects one vertex in Q with one in Q̄, but both vertices of each proper edge of B are either in Q or in Q̄. Based on this observation, we can construct a properly ordered graph G ′ = (V′, E′) such that the optimal solution to the LNS problem in G′ defines an optimal solution to the BLNS problem in G.
Each vertex in G defines one and exactly one vertex in G′. For every vertex vk in G, if v ∈ Q, then it corresponds to vertex in G′; otherwise, if v ∈ Q̄, then it corresponds to vertex in G′ (see Figure 6). The cost of each vertex in G′ is equal to the on-surface cost of its corresponding vertex in G. We denote by Col(v′) the column of κ vertices in G′ that are associated with v ∈ VB. Then, edges in G′ are introduced. For each edge (vk, uj) in G, there are three cases: (1) if both v and u are in Q, then put in G′ an edge ( ); (2) if both v and u are in Q̄, then add in G′ an edge ( ); and (3) if v ∈ Q and u ∈ Q̄, then introduce in G′ an edge ( ). Figure 6(b) illustrates the construction of the properly ordered graph G′ from the ordered graph G in Figure 4(a).
Fig. 6.
(a) Illustrating the reverse ordering of G. Columns Col(v) and Col(u) are in reverse order, (b) Constructing a properly ordered graph G′ from G (assume that a, v ∈ Q, u, b ∈ Q̄, and Q ∪ Q̄ = VB). Each vertex in a parenthesis is a corresponding vertex in G.
Lemma 9
The graph G′ = (V′, E′) constructed from G is a properly ordered multi-column graph.
Proof
Consider any edge (v, u) ∈ EB of the net model B. If (v, u) is a proper edge, obviously, the columns Col(v′) and Col(u′) in G′ are in proper order. We thus only investigate the case that (v, u) is a reverse edge. Without loss of generality (WLOG), assume v ∈ Q and u ∈ Q̄. In G, each vertex Vk has an edge interval I(vk, u) = {up, up−1, …, up−s} (s ≥ 0) on Col(u). From the construction of G′, vertex connects with an interval of vertices on Col(u′), that is, { }.
We now consider the edge intervals of two adjacent vertices and on Col(u′). Let (s ≥ 0) and (t ≥ 0). This indicates that the edge interval I(vk, u) of vk on Col(u) is {uκ−1−p, uκ−p, …, uκ−1−p+s} and the edge interval I(vk+1, u) of vk+1 on Col(u) is {uκ−1−q, uκ−q, …, uκ−1−q+t}. Since Col(v) and Col(u) are in reverse order, we have κ − 1 − p ≥ κ − 1 − q and κ − 1 − p + s ≥ κ − 1 − q + t. Alternatively, p ≤ q and p − s ≤ q − t, that is, and .
On the other hand, consider any two adjacent vertices and , and their edge intervals on Col(v′). Let( (s ≥ 0) and (t ≥ 0). Note that vertex (resp., ) in G′ corresponds to uκ−1−k (resp., uκ−2−k) in G. The edge interval of uκ−1−k on Col(v) is {vp, vp−1, …, vp−s} and the edge interval of uκ−2−k on Col(v) is {vq, vq−1, …, vq−t}. Due to the inverse order between Col(v) and Col(u), we have p ≤ q and p − s ≤ q − t, that is, and .
Hence, Col(v′) and Col(u′) are in proper order. This proves the lemma.
We show in the following that the optimal solution to the LNS problem in G′ defines an optimal solution to the BLNS problem in G.
Lemma 10
Any l feasible net surfaces in G′ specify l feasible net surfaces in G with the same total cost, and vice versa.
Proof
By Lemma 9, G′ is a properly ordered graph. Let
be a feasible solution to the LNS problem in G′. For each net surface
, we define a function  in G, as follows. Consider every vertex v ∈ VB. If v ∈ Q, then
; otherwise, if v ∈ Q̄, then
. The construction of G′ from G immediately indicates that each
in G, as follows. Consider every vertex v ∈ VB. If v ∈ Q, then
; otherwise, if v ∈ Q̄, then
. The construction of G′ from G immediately indicates that each  is a feasible net surface in G and any two adjacent net surfaces
is a feasible net surface in G and any two adjacent net surfaces  and
and  satisfy the separation constraints. Furthermore, the total cost of
satisfy the separation constraints. Furthermore, the total cost of  equals to the total cost of
. Hence,
equals to the total cost of
. Hence, 
 = {
= { ,
,  ,…,
,…, 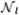 } is a feasible solution to the BLNS problem in G, and α (
} is a feasible solution to the BLNS problem in G, and α (
 ) = α(
) = α(
 ′). A similar argument can show that any l feasible nets in G define l feasible net surfaces in G′ with the same total cost.
′). A similar argument can show that any l feasible nets in G define l feasible net surfaces in G′ with the same total cost.
Note that G′ has the same size as G (i.e., |V′| = |V|and |E′| = |E|), and by Theorem 1 an optimal set of l nets in G′ can be computed in time. Based on Lemma 10, Theorem 3 follows.
Theorem 3
The general BLNS problem can be solved in time, where l is the number of sought net surfaces, n = |V|, mB = |EB|, and nB = |VB|.
6. Algorithms for the Net Surface Volume (NSV) Problems
This section presents our algorithms for several optimal net surface volume (NSV) problems. Specifically, instead of looking for multiple inter-related net surfaces as in Section 4, for a given d-D voxel grid Γ = [0..N − 1]d of n = Nd cells, with each cell x(x0, x1,…, xd−1) ∈ Γ having an arbitrary real “volume” value vol(x), we seek multiple surfaces that enclose a well-shaped region R ⊆ Γ, such that the volume vol(R) of R, vol(R) = Σx ∈Rvol(x), is minimized (or maximized). Note that even the case of the NSV problem on finding an optimal simple polygon in a weighted 2-D grid is in general NP-hard.2,28 The NSV problems in higher dimensions are so under-explored that few known methods actually address them. Interestingly, our LNS approach can be generalized to solving the optimal NSV problems on several nontrivial and useful classes of geometric regions in polynomial time. Recently, Chen et al.7 studied certain more restricted classes of regions than our classes.
6.1. The weakly watershed-monotone regions and watershed-monotone shells
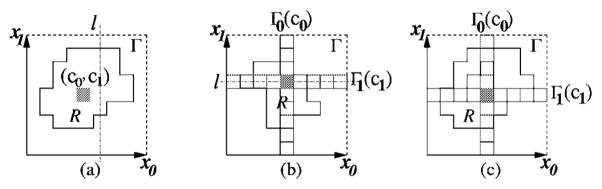
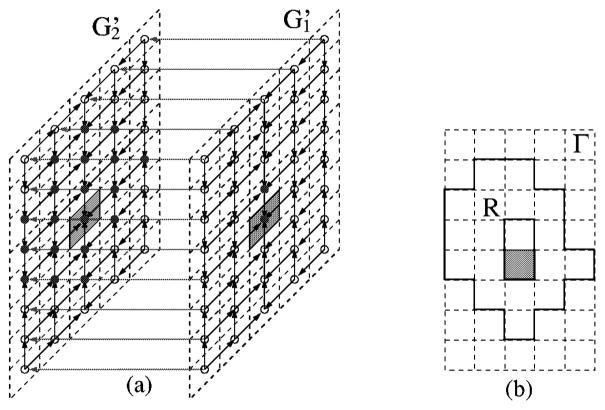
We consider two classes of regions, called weakly watershed-monotone regions and watershed-monotone shells, defined as follows. For any integers 0 ≤ i < d and 0 ≤ c < N, let Γi (c) denote the hyperplane xi = c in the domain of Γ, i.e., Γi (c) is orthogonal to the xi-axis and consists of all voxels of Γ whose xi-coordinate is c. A region R in Γ is said to be xi-monotone if for any line l parallel to the xi-axis, the intersection R ∩ l is either empty or a continuous segment. Further, we say that R is watershed-monotone with respect to Γi (c) if (1) R is xi-monotone, and (2) for any line l orthogonal to Γi (c), if the intersection R∩l ne;  , then R∩l intersects a voxel of R ∩ Γi (c). (Intuitively, the intersection of R and ΓI(c) is equal to the projection of R onto Γi (c), and is like a “watershed” of R.) If for every i = 0,1,…, d − 1, R is watershed-monotone to a Γi (ci) for an integer 0 ≤ ci < N, then we say that R is watershed-monotone. In Figure 7(a), the region R is watershed-monotone to both Γ0 (c0) and Γ1 (c1), and thus R is watershed-monotone. A region R ⊆ Γ is weakly watershed-monotone if R is watershed-monotone to every axis in a set of d − 1 axes of Γ and is monotone (but need not be watershed-monotone) to the remaining axis (e.g., see Figure 7(b)). Clearly, watershed-monotone regions are a subclass of weakly watershed-monotone regions.
, then R∩l intersects a voxel of R ∩ Γi (c). (Intuitively, the intersection of R and ΓI(c) is equal to the projection of R onto Γi (c), and is like a “watershed” of R.) If for every i = 0,1,…, d − 1, R is watershed-monotone to a Γi (ci) for an integer 0 ≤ ci < N, then we say that R is watershed-monotone. In Figure 7(a), the region R is watershed-monotone to both Γ0 (c0) and Γ1 (c1), and thus R is watershed-monotone. A region R ⊆ Γ is weakly watershed-monotone if R is watershed-monotone to every axis in a set of d − 1 axes of Γ and is monotone (but need not be watershed-monotone) to the remaining axis (e.g., see Figure 7(b)). Clearly, watershed-monotone regions are a subclass of weakly watershed-monotone regions.
Fig. 7.
(a) A watershed-monotone region, (b) A weakly watershed-monotone region which is not watershed-monotone to any Γ1(c). (c) A watershed-monotone shell. (For a better readability, a 2-D pixel grid Γ is used.)
Suppose R is watershed-monotone with respect to some Γi (ci), for each i = 0,1,…, d − 1; then it is easy to see that . A voxel in is called a kernel voxel of R. Our second region class is called the watershed-monotone shells. For any two watershed-monotone regions R1 and R2 such that R1 and R2 have a common kernel voxel c and R2 ⊆ R1, the region R in Γ bounded between R1 and R2, i.e., R = R1−R2, is a watershed-monotone shell (e.g., see Figure 7(c)).
6.2. Modeling the optimal NSV problem for weakly watershed-monotone regions
In this section, we extend our approach for the LNS problem to solving the optimal NSV problem on weakly watershed-monotone regions. WLOG, we assume that a voxel c(c0, c1,…, cd−2, cd−1) ∈ Γ is given and the target weakly watershed-monotone region R is xd−1-monotone (but not necessarily watershed-monotone to any Γd−1(c)) and is watershed-monotone to Γi(ci)for each i ∈ {0,1,…, d − 2}.
Denote by  the projection of Γ onto the first d −1 dimensions, i.e.,
the projection of Γ onto the first d −1 dimensions, i.e.,  = [0..N − 1]d − 1. A surface S′ in Γ is said to be xi-monotone if for any line l parallel to the xi-axis, the intersection of S′ and l either is empty or is in one single voxel. Observe that the boundary surface S of a weakly watershed-monotone region R in Γ can be split into two surface pieces, the “upper” boundary surface Su and the “lower” boundary surface Sl, both being xd−1-monotone. We let Su consist of the voxels forming the upper boundary of R (Su ⊆ R), and Sl consist of the voxels that are immediately below the voxels on the lower boundary of R (Sl
= [0..N − 1]d − 1. A surface S′ in Γ is said to be xi-monotone if for any line l parallel to the xi-axis, the intersection of S′ and l either is empty or is in one single voxel. Observe that the boundary surface S of a weakly watershed-monotone region R in Γ can be split into two surface pieces, the “upper” boundary surface Su and the “lower” boundary surface Sl, both being xd−1-monotone. We let Su consist of the voxels forming the upper boundary of R (Su ⊆ R), and Sl consist of the voxels that are immediately below the voxels on the lower boundary of R (Sl  R), with respect to Γd−1(0). Obviously, the domain of Su and Sl may be only a subset of
R), with respect to Γd−1(0). Obviously, the domain of Su and Sl may be only a subset of  , denoted by
, denoted by  . To obtain R, it is sufficient to compute Su and Sl. Note that we may view
. To obtain R, it is sufficient to compute Su and Sl. Note that we may view  as an implicit net model and Γ as an implicit ordered multi-column graph.
as an implicit net model and Γ as an implicit ordered multi-column graph.
Our approach in Section 4 can simultaneously identify multiple inter-related net surfaces that are defined on the entire domain  . However, the domain
. However, the domain  of Su and Sl may just be a proper subset of
of Su and Sl may just be a proper subset of  . Besides, here we optimize a different “volume” criterion. We overcome these difficulties as follows. First, we “extend” (or “spread”) each of Su and Sl to become an xd − 1 -monotone surface defined on the entire
. Besides, here we optimize a different “volume” criterion. We overcome these difficulties as follows. First, we “extend” (or “spread”) each of Su and Sl to become an xd − 1 -monotone surface defined on the entire  , denoted by
and
, respectively (e.g., Figures 8(a) and 8(b)). Interestingly, based on the monotonicity of R, we can manage to extend Su and Sl in such a way that
. This implies that for any voxel x ∈
, denoted by
and
, respectively (e.g., Figures 8(a) and 8(b)). Interestingly, based on the monotonicity of R, we can manage to extend Su and Sl in such a way that
. This implies that for any voxel x ∈  −
−  , the voxel of
defined on x must be the same as the voxel of
defined on x. (Recall that LO(S′) denote the region in Γ consisting of all voxels on or below a (net) surface S′.) Then, the volume vol(R) of the sought region R is equal to
. Hence, we look for two such extended surfaces
and
with
minimized; further, both
and
must be of a “good” shape to form a weakly watershed-monotone region.
, the voxel of
defined on x must be the same as the voxel of
defined on x. (Recall that LO(S′) denote the region in Γ consisting of all voxels on or below a (net) surface S′.) Then, the volume vol(R) of the sought region R is equal to
. Hence, we look for two such extended surfaces
and
with
minimized; further, both
and
must be of a “good” shape to form a weakly watershed-monotone region.
Fig. 8.
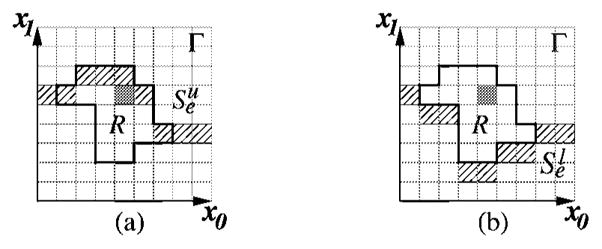
(a) The extended “upper” boundary surface of a weakly watershed-monotone region R (consisting of the shaded pixels). (b) The extended “lower” boundary surface of R.
Next, we construct two properly ordered graphs G1= (V1, E1) and G2 = (V2, E2), which are for searching for
and
, respectively.
and
are both defined on the following net model B = (VB, EB). Each voxel x ∈ 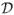 corresponds to exactly one vertex ux ∈ VB of B. For every two adjacent voxels of
corresponds to exactly one vertex ux ∈ VB of B. For every two adjacent voxels of  , x = (x0, x1,…, xd − 2) and y = (y0, y1, …, yd − 2), along any dimension (i.e.,
), we put an edge (ux, uy) in B.
, x = (x0, x1,…, xd − 2) and y = (y0, y1, …, yd − 2), along any dimension (i.e.,
), we put an edge (ux, uy) in B.
Before we start constructing G1 and G2 to incorporate the watershed-monotonicity, we need to introduce some notation. For a voxel x(x0, x1,…, xd − 1) ∈ Γ, let x(i, val) denote the voxel in Γ whose i-th coordinate is val and the remaining coordinate values are the same as those of voxel x. The i-th column Col(x, i) of voxel x consists of all voxels {x(i, k) | k = 0,1,…, N − 1} in Γ. Two columns Col(x, d − 1) and Col(y, d − 1) are said to be adjacent in the p-th dimension (p = 0,1,…, d−2), if xi = yi for every i ∉ {p, d − 1} and |xp − yp| = 1.
We first construct graph G1 = (V1, E1). Each voxel x ∈ Γ defines exactly one vertex in G1 (if the voxel in Γ is denoted by x(i, val), we then denote by the corresponding vertex in G1). Each vertex is assigned a cost . We next introduce edges into G1. For each dimension i (i = 0,1,…, d − 2), consider every pair of (d − 1)-st columns Col(x, d − 1) and Col(y, d − 1) adjacent in the i-th dimension. WOLG, we assume that yi = xi + 1. Recall that we want to compute a weakly watershed-monotone region R with respect to a given voxel c(c0, c1, … ci,…, cd − 1) in Γ. Two cases are distinguished. (1) xi < Ci: Note that for any two voxels x(d − 1, k′) and y(d − 1, k″) on , we have k′ ≥ k″. Thus, for every 0 ≤ k < N, let vertex connect with each vertex with k′ ≤ k. (2) xi ≥ ci: For any two voxels x(d − 1, k′) and y(d − 1, k″) on , we have k′ ≤ k″. Hence, for every 0 ≤ k < N, we connect vertex with each vertex with k′ ≤ k. The construction of G2 is similar to that of G1. But the ways of putting edges and assigning vertex costs in G2 are different. Every vertex in G2 connects vertices with k′ ≤ k if ’s corresponding vertex in G1 connects vertices with k″ ≥ k in G1; and vice versa. In addition, each vertex in G2 is assigned a cost . Lemma 11 immediately follows from the graph constructions.
Lemma 11
The graphs G1 and G2 thus obtained are both properly ordered graphs on the net model B.
Suppose we are given any two feasible net surfaces  in G1 and
in G1 and  in G2, with
in G2, with  “above”
“above”  (i.e., ∀ux ∈ VB,
(i.e., ∀ux ∈ VB,  (ux) ≥
(ux) ≥  (ux)). We can specify a region R in Γ using
(ux)). We can specify a region R in Γ using  and
and  , which actually correspond to
and
respectively in Γ, as follows. Initially, R =
, which actually correspond to
and
respectively in Γ, as follows. Initially, R =  . For every voxel x ∈
. For every voxel x ∈  , if
, if  (ux) >
(ux) >  (ux), then we put in R all voxels x(d − 1, k) with
(ux), then we put in R all voxels x(d − 1, k) with  (ux) ≥ k >
(ux) ≥ k >  (ux). The next lemma shows that the region R thus obtained is aweakly watershed-monotone in Γ.
(ux). The next lemma shows that the region R thus obtained is aweakly watershed-monotone in Γ.
Lemma 12
Any feasible net surfaces  in G1 and
in G1 and  in G2 with
in G2 with  above
above  define a weakly watershed-monotone region R in Γ with vol(R) = c(LO(
define a weakly watershed-monotone region R in Γ with vol(R) = c(LO( )) + c(LO(
)) + c(LO( )).
)).
Proof
First, by the construction of R, it is easy to see that R is xd − 1-monotone. Hence, below we show that R is watershed-monotone to every Γi (ci) for i = 0, 1, …, d − 2, i.e., R is xi-monotone and the intersection of R with Γi (ci) equals the projection of R to Γ i(ci). We prove this by contradiction.
Assume that there exists an h ∈ {0,1,…, d − 2} such that R is not xh-monotone. Then, there is a voxel a(a0,…, ah − 1, ch, ah+1,…, ad − 1) ∈ Γh (ch) such that the intersection of R with the h-th column Col (a, h) of a has at least two disconnected voxel segments, denoted by I0, I1,…, Iq along the h-th dimension, in this order. Let a (h, lej) and a(h, rej) be the two end voxels of segment Ij. For any two segments Ij and Ij+1, the gap segment Ig consists of all voxels a (h, k) in between Ij and Ij+1 with rej < k < lej+1. Considering the possible position of Ig in Γ, Ig can be “above”
(i.e.,
), or
; further, Ig can be to the “left” (i.e., lej+1 ≤ ch), the “right” (i.e., rej ≥ ch) of Γ h(ch), or intersect Γ h(ch) (i.e., rej < ch < lej+1). Hence, there are six cases for the possible position of Ig. In one such case, for instance, Ig is to the left of Γh (ch) and is a subset of
. The voxel a(h,rej) ∈ R implies that the vertex
. Due to the construction of G2, all vertices
in G2 with rej < k ≤ ch are in LO( ), that is,
. Hence, the only possibility for which Ig
), that is,
. Hence, the only possibility for which Ig 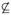 R is when
, implying that the vertex
which corresponds to voxel a(h, rej + 1) ∈ Ig is in LO(
R is when
, implying that the vertex
which corresponds to voxel a(h, rej + 1) ∈ Ig is in LO( ). By the construction of G1, all vertices
with rej ≥ k ≥ 0 are in LO(
). By the construction of G1, all vertices
with rej ≥ k ≥ 0 are in LO( ). Hence, the voxel segment Ij is not in R, a contradiction. The other five cases can be handled similarly. Therefore, for every i = 0, 1, …, d − 2, R is monotone to Γi (ci).
). Hence, the voxel segment Ij is not in R, a contradiction. The other five cases can be handled similarly. Therefore, for every i = 0, 1, …, d − 2, R is monotone to Γi (ci).
Then, we argue that for each i = 0,1,…, d − 2, the intersection of R with Γi (ci) equals the projection of R to Γ i(ci). Assume otherwise, i.e., there exists a voxel a ∈ R whose projection a(h, ch) on Γ h (ch) is not in R. Note that a ∈ R indicates that its corresponding vertex
is in LO( ), and its corresponding vertex
is not in LO(
), and its corresponding vertex
is not in LO( ). Thus, the vertex
of G2 is also included in LO(
). Thus, the vertex
of G2 is also included in LO( ) based on the construction of G2. But,
and a(h, ch) ∉ R imply that the vertex
of G1 is in LO(
) based on the construction of G2. But,
and a(h, ch) ∉ R imply that the vertex
of G1 is in LO( ). Hence, all vertices
with 0 ≤ k < N are in LO(
). Hence, all vertices
with 0 ≤ k < N are in LO( ), which means a ∉ R, a contradiction. Thus, R is watershed-monotone to every Γi(ci) for i = 0,1,…, d − 2.
), which means a ∉ R, a contradiction. Thus, R is watershed-monotone to every Γi(ci) for i = 0,1,…, d − 2.
Finally, we calculate the volume vol(R) of the region R.
This proves the lemma.
6.3. Computing a weakly watershed-monotone region of minimum total volume
Based on Lemma 12, we need to compute two such net surfaces and with the total cost minimized. As in Section 4, we formulate this problem as computing a minimum-cost closed set in a vertex-weighted directed graph G′ constructed from G1and G2.
The directed graph G′ = (V′, E′) contains two vertex-disjoint subgraphs and , which are used to search for and , respectively. (resp., ) is constructed from G1(resp., G2) using the same approach as that in Section 4.3 for building from G. The cost w(·) of each vertex in (resp., ) is set to be the cost of its corresponding vertex in G1 (resp., G2). Further, note that must be above . To ensure this, a set of directed edges connecting each vertex in to the corresponding vertex in is introduced. Thus, and (see Figure 9 for an example).
Fig. 9.
Computing an optimal weakly watershed-monotone region R. For a better readability, a 2-D pixel grid Γ is used, (a) Illustrating the construction of the graph G′. The shaded pixel is the given weak watershed kernel pixel c. Only a portion of the directed edges from
to
is shown. The solid vertices shown make up of a closed set in G′. (b) The extended “upper” surface
defined by the vertices of
in
in G′. (b) The extended “upper” surface
defined by the vertices of
in  . (c) The extended “lower” surface
defined by the vertices of
in
. (c) The extended “lower” surface
defined by the vertices of
in  . (d) A weakly watershed-monotone region R corresponding to the closed set
. (d) A weakly watershed-monotone region R corresponding to the closed set  .
.
Then, given any non-empty closed set  in G′, we can define two net surfaces
in G′, we can define two net surfaces  and
and  in G1 and G2, as in Section 4.4.
in G1 and G2, as in Section 4.4.  and
and  have the following property.
have the following property.
Lemma 13
Any non-empty closed set  in G′ specifies two net surfaces
in G′ specifies two net surfaces  in G1 and
in G1 and  in G2 such that
in G2 such that  is above
is above  and the cost w(
and the cost w( ) of
) of  is equal to c(LO(
is equal to c(LO( )) + c(LO(
)) + c(LO( )).
)).
By Lemmas 12 and 13, we have the following fact.
Lemma 14
Any non-empty closed set  in G′ specifies a feasible weakly watershed-monotone region R ⊆ Γ whose total volume is equal to the total cost of
in G′ specifies a feasible weakly watershed-monotone region R ⊆ Γ whose total volume is equal to the total cost of  .
.
Now we show how to construct a closed set  in G′ with the same total cost from a given weakly watershed-monotone region R of Γ. For simplicity, we use x(val) to denote a voxel x(d − 1, val) in Γ and
to denote the corresponding vertex of x(d − 1, val) in
.
in G′ with the same total cost from a given weakly watershed-monotone region R of Γ. For simplicity, we use x(val) to denote a voxel x(d − 1, val) in Γ and
to denote the corresponding vertex of x(d − 1, val) in
.
Lemma 15
For any weakly watershed-monotone region R of Γ, there is a corresponding closed set  in G′ with its cost w(
in G′ with its cost w( ) = vol(R).
) = vol(R).
Proof
For a given weakly watershed-monotone region R ⊆ Γ, we define a closed set  in G′, as follows. First, we let
in G′, as follows. First, we let 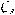 =
=  . For each x ∈
. For each x ∈ 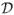 , if the intersection of R and the voxel set (x(0), x(1),…, x(N − 1)} (also denote by Col(x, d− 1)) is not empty, say, consisting of voxels x(lw), x(lw + 1), …, x(up), with 0 ≤ lw ≤ up < N, then we put into
, if the intersection of R and the voxel set (x(0), x(1),…, x(N − 1)} (also denote by Col(x, d− 1)) is not empty, say, consisting of voxels x(lw), x(lw + 1), …, x(up), with 0 ≤ lw ≤ up < N, then we put into 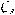 the vertex
of
and the vertex
of
if lw > 0. The sought closed set
the vertex
of
and the vertex
of
if lw > 0. The sought closed set  is the closure in G′ generated by
is the closure in G′ generated by 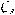 . We next prove the cost w(
. We next prove the cost w( ) equals vol(R).
) equals vol(R).
For each x ∈ 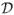 , we distinguish two cases: Col(x, d − 1) ∩ R ≠
, we distinguish two cases: Col(x, d − 1) ∩ R ≠  and Col(x, d − 1) ∩ R =
and Col(x, d − 1) ∩ R =  .
.
Case (1)
Col(x, d − 1) ∩ R ≠  . In this case, all vertices
of
with 0 ≤ k ≤ up and
of
with 0 ≤ k ≤ lw are included in
. In this case, all vertices
of
with 0 ≤ k ≤ up and
of
with 0 ≤ k ≤ lw are included in  . Let Ch1(x) (resp., Ch2(x)) denote the vertices in
(resp.,
) corresponding to voxels in Col(x, d − 1). Next, we will show that no vertices
with up < k < N and
with lw ≤ k < N are in
. Let Ch1(x) (resp., Ch2(x)) denote the vertices in
(resp.,
) corresponding to voxels in Col(x, d − 1). Next, we will show that no vertices
with up < k < N and
with lw ≤ k < N are in  . Otherwise, assume that
is the “top” vertex of Ch2(a) in
. Otherwise, assume that
is the “top” vertex of Ch2(a) in  (i.e., for any vertex
, k ≤ t) and t > up. The constructions of G′ and
(i.e., for any vertex
, k ≤ t) and t > up. The constructions of G′ and  s indicate that there is no path from any vertex of
in
s indicate that there is no path from any vertex of
in 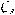 to a vertex in
whose corresponding voxel is in R. Thus, there must be a vertex
of
in
to a vertex in
whose corresponding voxel is in R. Thus, there must be a vertex
of
in  s, from which
is reachable in
(i.e., there is a directed path in
from
to
) and the (d − 1)-th coordinate bd − 1 of the voxel b is ≥ t. By characterizing of the property of G′, we then can claim that P: v′(b0, b1,…, bd−2, bd−1) → v′(a0, b1, …, bd−2, bd−1) → v′(a0, a1, b2, …, bd−2, bd−1) → · · · → v′(a0, a1, …, ad−2, bd−1) → v′(a0, a1, …, ad−2, t) is a path from
to
in
. Moreover, due to the watershed-monotonicity, all corresponding voxels of the vertices on the path P, except the last one (a0, a1, …, ad−2, t) (since R is not necessarily watershed-monotone to Γd−1(cd−1)), are in R. Thus, a(bd−1) = (a0, a1, …, ad−2, bd−1) ∈ R, a(up) = (a0, a1, …, ad−2, up) ∈ R, and the voxel a(t) = (a0, a1, …, ad−2, t) is in between a(bd−1) and a(up) (i.e., bd−1 ≥ t> up). Since R is monotone to xd−1-axis, a(t) ∈ R, a contradiction. Hence, no vertices
with up < k < N are in
s, from which
is reachable in
(i.e., there is a directed path in
from
to
) and the (d − 1)-th coordinate bd − 1 of the voxel b is ≥ t. By characterizing of the property of G′, we then can claim that P: v′(b0, b1,…, bd−2, bd−1) → v′(a0, b1, …, bd−2, bd−1) → v′(a0, a1, b2, …, bd−2, bd−1) → · · · → v′(a0, a1, …, ad−2, bd−1) → v′(a0, a1, …, ad−2, t) is a path from
to
in
. Moreover, due to the watershed-monotonicity, all corresponding voxels of the vertices on the path P, except the last one (a0, a1, …, ad−2, t) (since R is not necessarily watershed-monotone to Γd−1(cd−1)), are in R. Thus, a(bd−1) = (a0, a1, …, ad−2, bd−1) ∈ R, a(up) = (a0, a1, …, ad−2, up) ∈ R, and the voxel a(t) = (a0, a1, …, ad−2, t) is in between a(bd−1) and a(up) (i.e., bd−1 ≥ t> up). Since R is monotone to xd−1-axis, a(t) ∈ R, a contradiction. Hence, no vertices
with up < k < N are in  . Using a similar argument, we can show that no vertices
of
with lw ≤ k < N are in
. Using a similar argument, we can show that no vertices
of
with lw ≤ k < N are in  . Hence, we have w(Ch2(x) ∩
. Hence, we have w(Ch2(x) ∩  ) + w(Ch1(x) ∩
) + w(Ch1(x) ∩  ) = vol(Col(x, d − 1) ∩ R).
) = vol(Col(x, d − 1) ∩ R).
Case (2)
Col(x, d − 1) ∩ R =  . Let vertex
be the “top” vertex in (Ch1(x)∩
. Let vertex
be the “top” vertex in (Ch1(x)∩ ) (i.e., for any
, k ≤ lw). Then, the vertex
of
is in
) (i.e., for any
, k ≤ lw). Then, the vertex
of
is in  . We want to show that for any vertex
of Ch2(x) in
. We want to show that for any vertex
of Ch2(x) in  , k ≤ lw. Assume that in
, k ≤ lw. Assume that in  there exists a vertex
of Ch2(x) with t > lw. Since Col(x, d− 1) ∩ R =
there exists a vertex
of Ch2(x) with t > lw. Since Col(x, d− 1) ∩ R =  , no vertex of
in
, no vertex of
in 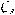 can reach
. Hence, there must exist a path in G′ from a certain vertex
(with the (d − 1)-th coordinate ad−1 of the voxel a being ≥ t) of
in
can reach
. Hence, there must exist a path in G′ from a certain vertex
(with the (d − 1)-th coordinate ad−1 of the voxel a being ≥ t) of
in 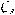 to
. But this implies that the vertex
is also in
to
. But this implies that the vertex
is also in  , a contradiction. Thus, we have w(Ch2(x) ∩
, a contradiction. Thus, we have w(Ch2(x) ∩  ) + w(Ch1(x) ∩
) + w(Ch1(x) ∩  ) = vol(Col(x, d − 1) ∩ R) = 0.
) = vol(Col(x, d − 1) ∩ R) = 0.
Therefore, w( ) = Σx∈
) = Σx∈ w(Ch2(x)∩
w(Ch2(x)∩ ) + w(Ch1(x)∩
) + w(Ch1(x)∩ ) = Σx∈
) = Σx∈ vol (Col(x, d − 1) ∩ R) = vol(R). Thus, the lemma follows.
vol (Col(x, d − 1) ∩ R) = vol(R). Thus, the lemma follows.
Hence, we compute a minimum-cost non-empty closed set  * in G′, which is used to specify a weakly watershed-monotone region R* in Γ with the minimum volume. Note that |V′| = O(n) and |E′| = O(d · n). By using the minimum s-t cut algorithm in the paper,12 we have the following result.
* in G′, which is used to specify a weakly watershed-monotone region R* in Γ with the minimum volume. Note that |V′| = O(n) and |E′| = O(d · n). By using the minimum s-t cut algorithm in the paper,12 we have the following result.
Theorem 4
The optimal weakly watershed-monotone region problem is solvable in time.
6.4. Algorithm for computing an optimal watershed-monotone shell
This section presents our algorithm for solving the d-D optimal watershed-monotone shell problem (d ≥ 3). We solve this problem by using the same framework as the one for the optimal weakly watershed-monotone region problem. However, the construction of the graph G′ = (V′, E′), which is directly constructed from Γ, is in a slightly different way to incorporate the “shell” structure of the target region R.
The graph G′ for this problem contains two disjoint subgraphs and , which are used to search for the inner and outer boundaries, SI and SO, of R, respectively. Note that in our algorithm for the optimal weakly watershed-monotone region problem, each subgraph is employed for searching one of the two pieces of the boundary surface of the target region. The geometric constraints between SO and SI are enforced by a set of edges between and .
We first show the construction of . Each voxel x ∈ Γ corresponds to exactly one vertex with a cost of −vol(x). For a given watershed kernel voxel c(c0, c1, …, cd−1) the directed edges are introduced as follows. Consider every voxel x on each hyperplane xi = ci = 0,1, …, d − 1). The i-th column Col(x,i), as defined in Section 6.2, is divided into two sub-columns Coll(x,i) and Colu(x,i), such that Coll(x,i) (resp., Colu(x,i)) consists of all voxels in Col(x,i) whose i-th coordinates are no bigger (resp., smaller) than ci. Then, for every k = N − 1, N − 2, …, ci + 1 (i.e., x(i,k) ∈ Colu(x,i)), the vertex has a directed edge to in ; for every k = 0,1,…, ci − 1 (i.e., x(i,k) ∈ Coll(x,i)), the vertex has a directed edge to , as illustrated in Figure 10(a).
Fig. 10.
Computing an optimal watershed-monotone shell. For a better readability, a 2-D pixel grid Γ is used, (a) Illustrating the construction of the graph G′. The shaded pixel is the given watershed kernel pixel c. Only a portion of the edges from to is shown, (b) A watershed-monotone shell R corresponding to the closed set in G′ consisting of all the solid vertices in (a).
The construction of is similar to that of . The only difference is the vertex-cost assignment scheme. In , each vertex associated with a voxel x ∈ Γ has a cost of vol(x). Then, for every voxel x ∈ Γ, we put a directed edge from the vertex of to the vertex in .
We then compute a minimum-cost closed set  * ≠
* ≠  in G′. An optimal watershed-monotone shell in Γ can be specified using R*, as follows. Initially, let R* = ∅. For each voxel x ∈ Γ, if the vertex
of
is in
in G′. An optimal watershed-monotone shell in Γ can be specified using R*, as follows. Initially, let R* = ∅. For each voxel x ∈ Γ, if the vertex
of
is in  *, but
of
is not, then put x into R* (see Figure 10(b)). The correctness of our algorithm for this problem follows from a similar argument for the optimal weakly watershed-monotone region problem.
*, but
of
is not, then put x into R* (see Figure 10(b)). The correctness of our algorithm for this problem follows from a similar argument for the optimal weakly watershed-monotone region problem.
Lemma 16
(1) Any watershed-monotone shell R ≠ ∅ in Γ corresponds to a non-empty closed set  in G′ whose cost is equal to the volume of R. (2) Any non-empty closed set
in G′ whose cost is equal to the volume of R. (2) Any non-empty closed set  in G′ defines a watershed-monotone shell R ≠ ∅ in Γ whose volume is equal to the cost of
in G′ defines a watershed-monotone shell R ≠ ∅ in Γ whose volume is equal to the cost of  .
.
Note that the graph G′ thus constructed has 2|Γ| = 2n vertices and O(dn) edges. By using the minimum s-t cut algorithm in the paper,12 we have the following theorem.
Theorem 5
An optimal watershed-monotone shell in a d-D voxel grid Γ (d ≥ 3) can be computed in time.
7. Implementation and Experiments
To further examine the behavior and performance of our LNS algorithm, we implemented it in standard C++ templates. After the implementation, we extensively experimented with 3-D images on physical phantoms, human pulmonary CT data, vascular MR data, and intravascular ultrasound data, and compared with a previously validated slice-by-slice 2-D segmentation approach based on graph search techniques.32 Over the years, graph search techniques have become one of the best understood and most utilized 2-D medical image segmentation tools.22 Our LNS program was tested on an AMD Athlon MP 2000+ Dual CPU workstation with 3.5GB memory running MS Windows XP. In our implementation, we only consider the on-surface cost of voxels.
The experiments showed that our LNS algorithm and software are computationally efficient and produce highly accurate and consistent segmentation results. The average execution times of our simultaneous l-surface (l = 2,3) detection algorithm on images of various sizes are shown in Table 1.
Table 1.
Average execution times (in seconds). Here (l denotes the number of sought surfaces.
| Image Size | 602×40 | 802×40 | 1002×40 | 1402×40 | 2002×40 |
|---|---|---|---|---|---|
| l = 2 | 3.3 | 6.1 | 16.2 | 85.8 | 376.1 |
| l = 3 | 4.8 | 9.4 | 22.3 | 96.1 | 401.3 |
An accuracy assessment on images of physical phantom tubes revealed that the overall signed errors for the inner and outer diameters derived from the tube boundaries were (mean ± standard deviation) −0.36 ± 2.47% and −0.08 ± 1.35%, respectively. Figure 11 presents the segmentation results by single surface detection methods versus our LNS algorithm. The synthesized image consists of 3 identical slices stacked together to form a 3-D image. Our LNS approach outperforms both the single surface detection algorithm30,15 and the 2-D MetaMorphs method.13 In comparison, the current MetaMorphs implementation is unable to segment the outer contour.
Fig. 11.
Single-surface methods versus our inter-related surface method, (a) Cross-section of the original synthesized image. (b) Single surface detection30,15 using a standard edge-based cost function, (c) MetaMorphs method13 segmenting the inner border in 2-D. (d) Double-surface segmentation obtained by our LNS approach.
Our LNS approach was tested on segmenting both the inner and outer airway wall surfaces in CT images, in which outer wall surfaces are very difficult to detect due to their blurred and discontinuous appearance and the presence of adjacent blood vessels. The CT images had a nearly isotropic resolution of 0.7 × 0.7 × 0.6mm3 and consisted of 500 – 600 image slices, with 512 × 512 pixels per slice. The currently used 2-D dynamic programming method works reasonably well for the inner wall segmentation but is unsuitable for the segmentation of the outer airway wall. Our new approach produces good segmentation results for both airway wall surfaces in a robust manner. Comparing to manual tracing on 39 randomly selected slices, our LNS technique yielded signed border positioning errors of −0.01 ± 0.15mm and 0.01 ± 0.17mm for the inner and outer wall surfaces, respectively. Figure 12 gives the comparisons on some airway wall segmentation results with a previous slice-by-slice 2-D graph-search based approach.32 Typically, by taking advantage of the 3-D coherence information, our LNS method can follow the 3-D airway wall structures correctly even among small and blurred airway segments, while the 2-D method exhibits large perturbations, and is even completely lost on some image slices.
Fig. 12.
Comparisons on airway wall segmentation results. For a better readability of the 3-D surface renderings, only the single luminal surface results are shown. (a), (b), (e), and (f) are the results yielded by the slice-by-slice 2-D graph-search based approach on two different airway segments. Four consecutive slices and the 3-D surface rendering are shown for each airway segment (10 slices). (c), (d), (g), and (h) are the walls segmented by our 3-D LNS approach.
Our algorithm was also used to simultaneously identify four vascular wall surfaces — the lumen–intima surface, internal elastic lamina (IEL), external elastic lamina (EEL), and adventitia in 3-D MR image data (see Figures 1(a) and 13). Our method successfully identified the four specified surfaces in 44 out of all 48 image slices. In comparison with manual tracing, the mean signed surface positioning errors for the lumen, IEL, and EEL boundaries were (mean ± standard deviation) 0.44 ± 0.37 pixel, −0.29 ± 0.34 pixel, and 0.11 ± 0.31 pixel. Comparing to the results obtained by the 2-D graph-search based approach,32 our method showed higher accuracy and 3-D consistency. Besides, the 2-D approach constantly requires the user to interactively define boundary points for guiding the border detection in difficult locations.
Fig. 13.
Results on MR vascular wall surface segmentation. (a) Four consecutive slices from the original image data. (b) Manually identified lumen, IEL, and EEL surfaces. The outermost adventitia surfaces are not shown. (c) Results produced by the program for our LNS algorithm.
Our 3-D LNS method for intravascular ultrasound (IVUS) image segmentation demonstrated lower surface positioning errors as well as more robust performance indicated by the success rate in comparison to the 2-D graph-search based approach.32 The IVUS images consisted of 1581 image frames approximately 0.5mm apart, with 384 × 384 pixels per frame and in-plane resolution of 0.3 × 0.3mm2/pixel. Some results are given in Table 2.
Table 2.
Comparison results on intravascular ultrasound image segmentation between our 3-D LNS technique and the 2-D graph search approach32.
| Method | Success Rate | Positioning Error | Maximum Error |
|---|---|---|---|
| 2-D graph search | 68% | 0.13±0.08mm | 2.1mm |
| 3-D LNS | 82% | 0.09±0.03mm | 1.9mm |
We have shown that our LNS technique provides a powerful tool for medical image segmentation. However, with the resolution of medical imaging scanners continuously increasing at a rapid pace, the time complexity of our LNS algorithm may constrain its feasibility in segmentation of large image data sets. As future work, we can apply a hierarchical refinement method to alleviate this problem in practice. Several recent works 4,3,21,34,17,31 have demonstrated that multi-scale image segmentation using graph cuts can produce impressive segmentation results. We first solves the LNS problem on the coarsest level graph and then solve the problem at successive higher resolution but on a narrow banded graph derived from the optimal solution found at the previous coarser graph. This multi-scale approach makes it possible to achieve high quality segmentation results on large data sets with faster speed, thus allowing our LNS technique to be used in a wider range of medical applications.
Footnotes
This research was supported in part by an NIH-NIBIB research grant R01-EB004640. A preliminary version of this paper was presented at the 16th Annual International Symposium on Algorithms and Computation (ISAAC), 2005.
Contributor Information
XIAODONG WU, Dept. of Electrical and Computer Engineering, Dept. of Radiation Oncology, University of Iowa, Iowa City, Iowa 52242, USA, xiaodong-wu@uiowa.edu.
DANNY Z. CHEN, Department of Computer Science and Engineering, University of Notre Dame, Notre Dame, IN 46556, USA, chen@cse.nd.edu.
KANG LI, Dept. of Electrical and Computer Engineering, Carnegie Mellon University, Pittsburgh, PA 15213, USA, kangl@cmu.edu.
MILAN SONKA, Dept. of Electrical and Computer Engineering, University of Iowa, Iowa City, IA 52242-1595, USA, sonka@engineering.uiowa.edu.
References
- 1.Amir A, Kashi R, Netanyalm NS. Analyzing quantitative databases: Image is everything. Proc. 27th Int. Conf. Very Large Data Bases (VLDB),; Rome, Italy. 2001. pp. 89–98. [Google Scholar]
- 2.Asano T, Chen DZ, Katoh N, Tokuyama T. Efficient algorithms for optimization-based image segmentation. Int J Comput Geom Appl. 2001;11(2):145–166. [Google Scholar]
- 3.Barbu A, Zhu S. Graph partition by Swendsen–Wang cuts. Proc. Int. Conf. Computer Vision; Nice, France. 2003. pp. 320–327. [Google Scholar]
- 4.Benezit F, Cour T, Shi J. Spectral segmentation with multi-scale graph decomposition. Proc. IEEE Computer Society Conf. Computer Vision and Pattern Recognition (CVPR); Jun, 2005. pp. 1124–1131. [Google Scholar]
- 5.Boykov Y, Kolmogorov V. Computing geodesics and minimal surfaces via graph cuts. Proc. Int. Conf. Computer Vision (ICCV); Nice, France. Oct, 2003. pp. 26–33. [Google Scholar]
- 6.Chakraborty A, Staib H, Duncan J. Deformable boundary finding in medical images by integrating gradient and region information. IEEE Trans Med Imag. 1996;15(6):859–870. doi: 10.1109/42.544503. [DOI] [PubMed] [Google Scholar]
- 7.Chen DZ, Chun J, Katoh N, Tokuyama T. Efficient algorithms for approximating a multi-dimensional voxel terrain by a unimodal terrain. Proc. 10th Ann. Int. Computing and Combinatorics Conf; Jeju Island, Korea. 2004. pp. 238–248. [Google Scholar]
- 8.Frank RJ, McPherson DD, Chandran KB, Dove EL. Computers in Cardiology. IEEE; Los Alamitos: 1996. Optimal surface detection in intravascular ultrasound using multi-dimensional graph search; pp. 45–48. [Google Scholar]
- 9.Fukuda T, Morimoto Y, Morishita S, Tokuyama T. Data mining with optimized two-dimensional association rules. ACM Trans Datab Syst. 2001;26:179–213. [Google Scholar]
- 10.Carey MR, Johnson DS. Computers and Intractability: A Guide to the Theory of NP-Completeness. Freeman; San Francisco, CA: 1979. [Google Scholar]
- 11.Goldenberg R, Kimmel R, Rivlin E, Rudzsky M. Cortex segmentation: A fast variational geometric approach. IEEE Trans Med Imag. 2002;21(2):1544–1551. doi: 10.1109/TMI.2002.806594. [DOI] [PubMed] [Google Scholar]
- 12.Goldberg AV, Tarjan RE. A new approach to the maximum-flow problem. J Assoc Comput Mach. 1988;35:921–940. [Google Scholar]
- 13.Huang X, Metaxas D, Chen T. MetaMorphs: Deformable shape and texture models. Proc. IEEE Computer Society Conf. Computer Vision and Pattern Recognition (CVPR); Jun, 2004. pp. 496–503. [Google Scholar]
- 14.Hochbaum DS. A new-old algorithm for minimum-cut and maximum-flow in closure graphs. Networks. 2001;37(4):171–193. [Google Scholar]
- 15.Li K, Wu X, Chen DZ, Sonka M. Efficient optimal surface detection: Theory, implementation and experimental validation. Proc. SPIE’s Int. Symp. Medical Imaging: Imaging Processing; San Diego, CA. 2004. pp. 620–627. [Google Scholar]
- 16.Li K, Wu X, Chen DZ, Sonka M. Globally optimal segmentation of interacting surfaces with geometric constraints. Proc. IEEE Computer Society Conf. Computer Vision and Pattern Recognition (CVPR); Jun, 2004. pp. 394–399. [Google Scholar]
- 17.Lombaert H, Sun Y, Grady L, Xu C. A multilevel banded graph cuts method for fast image segmentation. Proc. 10th IEEE Int. Conf. Computer Vision; Oct, 2005. [Google Scholar]
- 18.MacDonald D, Kabani N, Avis D, Evans AC. Automated 3-D extraction of inner and outer surfaces of cerebral cortex from MRI. NeuroImage. 2000;12(3):340–356. doi: 10.1006/nimg.1999.0534. [DOI] [PubMed] [Google Scholar]
- 19.Paragios N. A variational approach for the segmentation of the left ventricle in cardiac image analysis. Int J Comput Vis. 2002;46(3):223–247. [Google Scholar]
- 20.Picard JC. Maximal closure of a graph and applications to combinatorial problems. Manag Sci. 1976;22:1268–1272. [Google Scholar]
- 21.Sharon E, Brandt A, Basri R. Fast multiscale image segmentation. Proc. IEEE Computer Society Conf. Computer Vision and Pattern Recognition (CVPR); Jun, 2000. pp. 70–77. [Google Scholar]
- 22.Sonka M, Hlavac V, Boyle R. Image Processing, Analysis, and Machine Vision. 2. Brooks/Cole Publishing Company; Pacific Grove, CA: 1999. [Google Scholar]
- 23.Sonka M, Winniford MD, Collins SM. Robust simultaneous detection of coronary borders in complex images. IEEE Trans Medi Imag. 1995;14(1):151–161. doi: 10.1109/42.370412. [DOI] [PubMed] [Google Scholar]
- 24.Sonka M, Zhang X, Siebs M, Bissing MS, DeJong S, Collins SM, McKay CR. Segmentation of intravascular ultrasound images: A knowledge-based approach. IEEE Trans Med Imag. 1995;14(4):719–732. doi: 10.1109/42.476113. [DOI] [PubMed] [Google Scholar]
- 25.Spreeuwers L, Breeuwer M. Detection of left ventricular epi- and endocardial borders using coupled active contours. Computer Assisted Radiology and Surgery. 2003 [Google Scholar]
- 26.Thedens DR, Skorton DJ, Fleagle SR. A three-dimensional graph searching technique for cardiac border detection in sequential images and its application to magnetic resonance image data. Computers in Cardiology. 1990:57–60. [Google Scholar]
- 27.Thedens DR, Skorton DJ, Fleagle SR. Methods of graph searching for border detection in image sequences with applications to cardiac magnetic resonance imaging. IEEE Trans Med Imag. 1995;14(1):42–55. doi: 10.1109/42.370401. [DOI] [PubMed] [Google Scholar]
- 28.Woeginger GJ. Computing maximum valued region. Acta Cybernetica. 1992;10:303–315. [Google Scholar]
- 29.Wu X. Segmenting doughnut-shaped objects in medical images. Proc. 14th Ann. Int. Symp. Algorithms and Computation; 2003. pp. 375–384. [Google Scholar]
- 30.Wu X, Chen DZ. Optimal net surface problems with applications. Proc. 29th Int. Colloq. Automata, Languages and Programming (ICALP); 2002. pp. 1029–1042. [Google Scholar]
- 31.Xu N, Bansal R, Ahuja N. Object segmentation using graph cuts based active contours. Proc. IEEE Computer Society Conf. Computer Vision and Pattern Recognition (CVPR); Jun, 2003. pp. 46–53. [Google Scholar]
- 32.Yang F, Holzapfel G, Schulze-Bauer C, Stollberger R, Thedens D, Bolinger L, Stolpen A, Sonka M. Segmentation of wall and plaque in in-vitro vascular MR image. Int J Cardiovasc Imag. 2003;19(5):419–428. doi: 10.1023/a:1025829232098. [DOI] [PubMed] [Google Scholar]
- 33.Yezzi A, Tsai A, Willsky A. A statistical approach to snakes for bimodal and trimodal imagery. Proc. IEEE Int. Conf. Computer Vision; Corfu, Greece. 1999. pp. 898–903. [Google Scholar]
- 34.Yu SX. Segmentation using multiscale cues. Proc. IEEE Computer Society Conf. Computer Vision and Pattern Recognition (CVPR); Jun, 2004. pp. 70–77. [Google Scholar]
- 35.Zeng X, Staib LH, Schultz RT, Duncan JS. Segmentation and measurement of the cortex from 3-D MR images using coupled surfaces propagation. IEEE Trans Med Imag. 1999;18:927–937. doi: 10.1109/42.811276. [DOI] [PubMed] [Google Scholar]
- 36.Zhu S, Yuille A. Region competition: Unifying snakes, region growing, and Bayes/MDL for multiband images segmentation. IEEE Trans Patt Anal Mach Intell. 1996;18:884–900. [Google Scholar]