Redesigning the monovalent cation specificity of an enzyme

Abstract

Monovalent-cation-activated enzymes are abundantly represented in plants and in the animal world. Most of these enzymes are specifically activated by K⁺, whereas a few of them show preferential activation by Na⁺. The monovalent cation specificity of these enzymes remains elusive in molecular terms and has not been reengineered by site-directed mutagenesis. Here we demonstrate that thrombin, a Na⁺-activated allosteric enzyme involved in vertebrate blood clotting, can be converted into a K⁺-specific enzyme by redesigning a loop that shapes the entrance to the cation-binding site. The conversion, however, does not result into a K⁺-activated enzyme.

Since the discovery of the activating effect of K⁺ on pyruvate kinase, over 60 years ago (1), enzymes activated by monovalent cations have been identified abundantly in both the animal world and plants (2, 3). The list of such enzymes continues to grow (4–11) and encompasses members of the RNA world, such as ribozymes (12) and the ribosome itself (13, 14). Monovalent-cation-binding sites have been identified structurally in several enzymes, e.g., dialkylglycine decarboxylase (15), pyruvate kinase (16), thrombin (17), the molecular chaperone Hsc70 (18), fructose-1,6-bisphosphatase (19), S-adenosylmethionine synthetase (20), tryptophan synthase (21), coagulation factor Xa (22), methylamine dehydrogenase (23), Haemophilus influenzae HslV protein (24), and activated protein C (25). A compilation of x-ray structures of Na⁺- and K⁺-binding sites in proteins has been offered recently (26). The monovalent-cation-binding site of a catalytic RNA has also been described by x-ray crystallography (12). Monovalent cations activate enzymes in essentially two ways (3), either by forming a ternary complex with enzyme and substrate or allosterically. The two mechanisms are easily distinguishable. In the former case, the presence of the cation is absolutely required for catalytic activity, whereas, in the latter case, the cation significantly increases the activity from a finite basal value. Monovalent-cation-activated enzymes typically express optimal catalytic activity in the presence of K⁺, with the smaller cations Li⁺ and Na⁺ being less effective (3). An interesting correlation exists between the preference for K⁺ and the intracellular localization of such enzymes.

The discovery of monovalent-cation-activated enzymes has long raised questions on the molecular basis of the observed effects and, in particular, on the origin of the cation selectivity that resembles the selectivity found in ion channels (27, 28). Emphasis has been put on the differences in ionic radius and hydration energy among different monovalent cations, coupled to the electrostatic properties of the protein (27, 28). Studies on the basis of cation specificity in these enzymes have typically focused on the kinetic aspects of the activation, with relatively little attention paid to the thermodynamic components of cation binding (29). Furthermore, the monovalent cation preference of an enzyme has not been redesigned by site-directed mutagenesis.

The clotting enzyme thrombin is activated by Na⁺ in an allosteric fashion, with the smaller cation Li⁺ and the larger cation K⁺ being less effective (30). The preference for Na⁺ rather than K⁺ is unusual among monovalent-cation-activated enzymes, but it correlates well with the extracellular localization of thrombin in the blood. The Na⁺ effect on thrombin activity plays a significant role in blood coagulation and explains the phenotypes associated with mutations of the prothrombin gene and the coagulopathies secondary to hypernatremia or hyponatremia (31). The Na⁺-binding properties of thrombin have been studied in great detail, both kinetically and thermodynamically (29), and key structural determinants of Na⁺ binding and allosteric activation have been identified by x-ray crystallographic studies (32, 33). Here, we exploit this wealth of information to redesign the monovalent cation specificity of this important enzyme.

Materials and Methods

Site-directed mutagenesis of human thrombin was carried out in a HPC4-modified pNUT expression vector (34) by using the QuikChange Site-Directed Mutagenesis Kit from Stratagene. Expression of thrombin mutants was carried out in baby hamster kidney cells. Mutants were activated with the prothrombinase complex between 40 to 60 min at 37°C. Enzymes used in the activation were supplied by Enzyme Research Laboratories (South Bend, IN). Mutants were purified to homogeneity by FPLC by using Resource Q and S columns with a linear gradient from 0.05 to 0.5 M choline chloride/5 mM Mes (pH 6) at room temperature. Active-site concentrations were determined by titration with hirudin. The chromogenic substrate H-d-Phe-Pro-Arg-p-nitroanilide (FPR) was obtained from Midwest Biotech (Carmel, IN).

Equilibrium dissociation constants for monovalent cation (M⁺) binding were determined by fluorescence titration with a Spex FluoroMax-3 spectrophotometer (Jobin-Yvon, Edison, NJ). Fluorescence titrations took place under experimental conditions of 5 mM Tris, 0.1% polyethylene glycol (PEG) 8000, 800 mM ionic strength (pH 8.0) in the temperature range 2–45°C. Titrations were carried out by adding aliquots of thrombin in a solution containing [M⁺] = 800 mM Cl^– salt to a solution containing the enzyme in 800 mM choline chloride. In this experiment, the ionic strength (800 mM), enzyme concentration (20 nM), and [Cl^–] (800 mM) of the solution were held constant, whereas [M⁺] was varied. Excitation was at 295 nm, and emission was measured at 333 nm. The value of thrombin intrinsic fluorescence, F, as a function of [M⁺] was fit according to the equation (30)

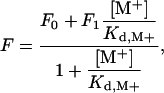[1]

where F₀ and F₁ are the values of F in the absence of and under saturating monovalent cation concentration, and K_d,M+ is the equilibrium dissociation constant for M⁺ binding.

The temperature dependence of K_d,M+ was used to derive the thermodynamic parameters pertaining to Na⁺ or K⁺ binding to thrombin, according to the equation (29)

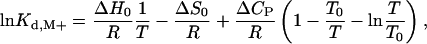[2]

where ΔH₀ and ΔS₀ are the enthalpy and entropy changes due to cation binding at the reference temperature T₀ = 298.15 K, ΔC_P is the heat-capacity change associated with cation binding, R is the gas constant, and T is the absolute temperature. The van't Hoff plot of ln K_d,M+ vs. 1/T is linear when ΔC_P = 0 and curves upward when ΔC_P < 0.

The equilibrium dissociation constant for Na⁺ or K⁺ binding was alternatively determined from the linkage between the k_cat/K for FPR hydrolysis and [M⁺], under conditions of 5 mM Tris/0.1% PEG8000 (pH 8.0) at 25°C. The value of s = k_cat/K_m was calculated from the individual K_m and k_cat values derived from analysis of progress curves run at different substrate concentrations (from 5 to 30 μM) and was fit according to the equation (29, 30)

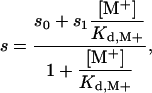[3]

where s₀ and s₁ are the values of k_cat/K_m in the absence of and under saturating [M⁺]. The value of s₀ is derived in the presence of the inert cation choline, which mimics the Na⁺-free form of the enzyme, whereas the value of s₁ refers to the extrapolation [M⁺] → ∞. The three parameters s₀, s₁, and K_d,M+ are independent, which means that the magnitude of cation activation (s₁/s₀) is not necessarily linked to the strength of cation binding (K_d,M+).

Results

In thrombin, Na⁺ is coordinated octahedrally by the backbone O atoms of residues Arg-221a and Lys-224 and four buried water molecules (17, 22, 32). One of these water molecules connects Na⁺ with the Oδ2 atom of Asp-189, which defines the primary specificity of the enzyme (32). When Na⁺ is released from its site, the side chain of Asp-189 reorients, and the perturbation extends up to the catalytic Ser-195 (33). Although key structural determinants responsible for Na⁺ binding to thrombin have been identified, together with the mechanism that transduces Na⁺ binding into enhanced catalytic activity (33), the factors that influence the Na⁺ vs. K⁺ preference of this enzyme are not known.

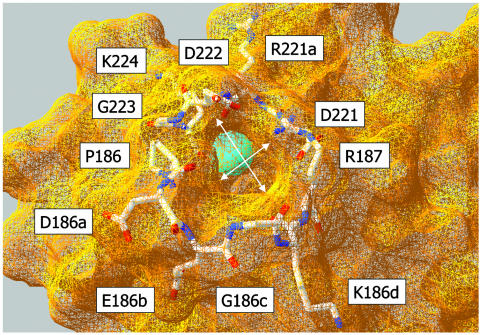
The 220- and 186-loops of thrombin define an aperture at the bottom of the molecule that presumably serves as the entrance to the Na⁺-binding site (Fig. 1). A comparison of these loops among serine proteases shows that the 220-loop is quite rigid, and its backbone architecture is highly conserved even among proteases that do not bind Na⁺. The 186-loop, on the other hand, shows a conspicuous variability in both composition and length. In thrombin, the 186-loop contains a four-residue insertion (186a–d) relative to chymotrypsin and trypsin. The insertion has been retained in its length, but not in composition, from hagfish to human. We therefore surmised that the 186-loop of thrombin plays an important role in cation specificity and that its length may be more important than its chemical composition. To this end, we made Ala substitutions at positions P186, D186a, E186b, K186d, and R187. To reduce the length of the loop, we deleted the four-residue insertion 186a–d. Alternatively, the length of the loop was increased with Ala insertions upstream of each residue in the 186a–d stretch.

Fig. 1.

Architecture of the pore of entry to the Na⁺-binding site of thrombin, shown from the water-accessible surface by using the coordinates of Protein Data Bank ID code 2THF (32). The bound Na⁺ is represented as a cyan ball, buried inside the protein. The shape of the pore is pseudoelliptical, with a longer axis of 7.3 Å and a shorter axis of 5.1 Å (arrows). The pore is lined by residues of the 220-loop (above) and 186-loop (below) shown as Corey–Pauling–Koltun models. The size of the pore requires significant dehydration of Na⁺ (ionic radius, 0.9 Å) or K⁺ (ionic radius, 1.3 Å) before binding. The atomic radius of a water molecule is ≈1.4 Å.

The Ala substitutions of Pro-186, Asp-186a, Glu-186b, and Lys-186d had a modest effect on the activity of the enzyme (Table 1). The k_cat and K_m for FPR hydrolysis changed marginally compared with wild type and so did the affinity for Na⁺ and K⁺. The preferential binding of Na⁺ vs. K⁺ was retained in all cases. This finding confirmed that the exact chemical composition of the 186-loop is largely inconsequential to catalytic function and cation specificity, as predicted by the lack of sequence conservation in thrombins from different species. Mutation of Arg-187 to Ala produced a more marked perturbation of FPR hydrolysis and reduced the catalytic parameters to the values observed in the absence of Na⁺ (30). Indeed, replacement of Arg-187 with Ala decreased the Na⁺ affinity drastically and brought the affinity for K⁺ to a value too low to be measured. Arg-187 stabilizes the Na⁺-binding site by its ion-pair interactions with Asp-221 and Asp-222. The naturally occurring mutant prothrombin Greenville carries the R187Q substitution and is associated with a bleeding phenotype (35). The loss of catalytic activity of the R187A mutant explains this phenotype in terms of a loss of Na⁺ binding that stabilizes thrombin in the Na⁺-free anticoagulant slow form (31).

Table 1. Kinetic rate constants for FPR hydrolysis (in the presence of Na⁺) and monovalent cation-binding affinities for wild-type and mutant thrombins.

	Sequence 186-187	s, μM-1·s-1	kcat, s-1	Km, μM	Kd,Na+, mM	Kd,K+, mM	R*
Wild type	PDEGKR	77 ± 5	28 ± 1	0.36 ± 0.03	14 ± 1	160 ± 10	11 ± 1
P186A	ADEGKR	69 ± 3	32 ± 1	0.45 ± 0.04	10 ± 1	190 ± 20	19 ± 2
D186aA	PAEGKR	35 ± 2	27 ± 1	0.77 ± 0.07	19 ± 1	150 ± 10	7.6 ± 0.8
E186bA	PDAGKR	27 ± 1	29 ± 1	1.1 ± 0.1	14 ± 1	110 ± 10	7.9 ± 0.8
K186dA	PDEGAR	43 ± 2	22 ± 1	0.50 ± 0.05	15 ± 1	102 ± 9	6.8 ± 0.7
R187A	PDEGKA	6.2 ± 0.3	22 ± 1	3.5 ± 0.3	210 ± 20	>1,000	ND
del186a-d	P----R	0.021 ± 0.001	7.2 ± 0.2	340 ± 30	100 ± 10	700 ± 70	7.0 ± 0.7
D186aA′	PADEGKR	31 ± 1	28 ± 1	0.91 ± 0.09	46 ± 5	100 ± 10	2.2 ± 0.3
E186bA′	PDAEGKR	24 ± 1	24 ± 1	1.0 ± 0.1	40 ± 4	87 ± 9	2.2 ± 0.3
G186cA′	PDEAGKR	31 ± 1	21 ± 1	0.68 ± 0.07	57 ± 6	83 ± 9	1.5 ± 0.2
K186dA′	PDEGAKR	17 ± 1	21 ± 1	1.2 ± 0.1	61 ± 6	91 ± 9	1.5 ± 0.2
QuadA′	PADAEAGAKR	5.4 ± 0.3	21 ± 1	3.7 ± 0.4	110 ± 10	14 ± 1	0.13 ± 0.02

Kinetic parameters refer to 5 mM Tris/0.1% PEG8000/200 mM NaCl (pH 8.0) at 25°C. Equilibrium dissociation constants for Na⁺ and K⁺ were calculated under experimental conditions of 5 mM Tris/0.1% PEG8000 (pH 8.0) at 10°C, I = 800 mM. ND, value could not be determined with confidence because of the weak K⁺ affinity.

^*Binding specificity ratio between Na⁺ and K⁺.

Reduction of the length of the 186-loop insertion led to more drastic perturbations of function. The mutation weakened both Na⁺ and K⁺ binding, almost to the same extent, and brought about a loss of catalytic activity well beyond that expected from the reduction in Na⁺ affinity (30). Deletion of the entire insertion may have caused deleterious changes in the primary specificity pocket of the enzyme around Asp-189. Because a shorter 186-loop weakened the Na⁺ affinity but did not produce a change in cation specificity, we examined the effects of increasing the length of the loop with single Ala insertions in the 186a–d region. The insertions had little effect on catalytic activity, but significantly decreased the Na⁺ vs. K⁺ discrimination by reducing the affinity for Na⁺ and increasing the affinity for K⁺. Intrigued by the trend shown in the Ala-insertion mutants, we constructed a quadruple mutant by combining the four individual insertions. The resulting mutant, quadA′, showed a reduction of catalytic activity toward FPR partially attributable to impaired Na⁺ binding, but it also featured a complete reversal of monovalent cation specificity compared with wild type.

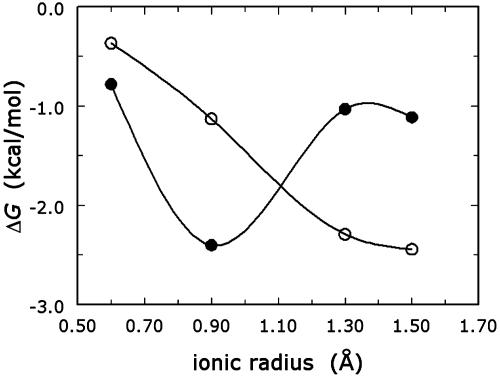
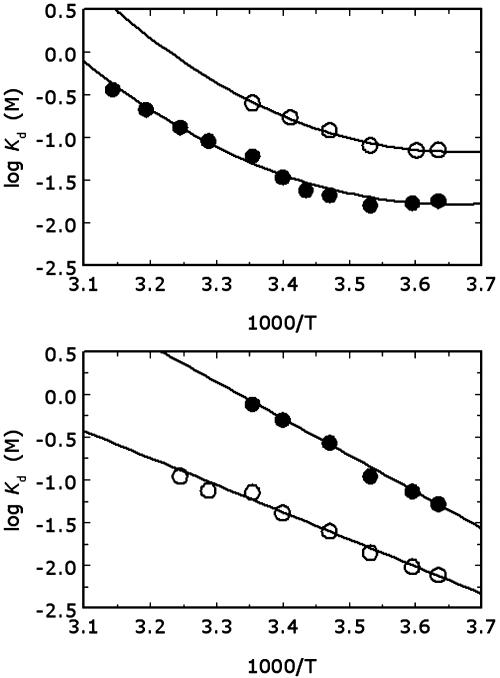
QuadA′ binds K⁺ with an affinity almost 10-fold higher than Na⁺, and its cation-binding profile has a minimum shifted toward larger ionic radii compared with wild type (Fig. 2). The K⁺ vs. Na⁺ preference is seen over the entire temperature range from 2 to 45°C (Fig. 3) and is linked to noteworthy thermodynamic signatures. Na⁺ binding to wild-type thrombin produces a large heat-capacity change (29), the structural origin of which remains unknown. Binding of K⁺ to wild type is characterized by a lower affinity than Na⁺, but by an equally large heat-capacity change (Fig. 3), although Na⁺ and K⁺ have significant differences in ionic radius, charge density, and hydration energy. The reduced mobility of buried water molecules around the bound Na⁺, engaged in the formation of water-binding sites connecting strands and loops of the Na⁺ site, may be at the origin of the large negative change in heat capacity. This role for buried water molecules was originally proposed to explain the large heat-capacity change observed in the tryptophan repressor–operator interaction (36). The standard enthalpy and entropy of binding, calculated at the reference temperature of 25°C, show that the Na⁺ vs. K⁺ preference in the wild type is entropic in nature. A possible explanation for this entropic effect is that more water molecules are released when thrombin interacts with Na⁺ than with K⁺. The smaller ionic radius of Na⁺ than K⁺ increases the hydration energy and hence the average number of water molecules bound to the cation. If binding to thrombin selects for a fixed number of water molecules absorbed to the hydration shell of the cation, then, on the average, more water molecules are released for binding Na⁺ than K⁺. Hence, when the cation is forced to partially dehydrate before binding to the protein, the binding affinity is higher for the smaller cation, which is consistent with the conclusions drawn in discussions of monovalent cation selectivity (27, 28). The crucial role of hydration has also been stressed recently in the interpretation of the enhanced activation of pyruvate kinase by Na⁺ and K⁺ under reduced water conditions (37).

Fig. 2.

Monovalent cation specificity profile for wild-type thrombin (•) and the mutant quadA′ (○). Shown are the values of the binding free energy ΔG = RT ln K_d,M+ determined for Li⁺, Na⁺, K⁺, and Rb⁺ by fluorescence titrations under experimental conditions of 5 mM Tris/0.1% PEG8000 (pH 8.0) at 10°C; I = 800 mM. Note how the specificity of quadA′ is shifted toward cations of larger ionic radius compared with wild type. Continuous curves are spline interpolations of the data.

Fig. 3.

van't Hoff plots for Na⁺ (•) and K⁺ (○) binding to wild-type thrombin (Upper) and the mutant quadA′ (Lower) in the temperature range from 2 to 45°C. The plots are curved in the case of wild type, signaling the presence of a large heat-capacity change. This change is not seen in the quadA′ mutant, for which the van't Hoff plot is linear. Note how the cation specificity of this mutant is completely reversed compared with wild type. Continuous lines were drawn according to Eq. 2 by using best-fit parameter values. Wild type: ΔH₀ = –14.6 ± 0.6 kcal·mol^–1 (1 cal = 4.184 J), ΔS₀ = –43 ± 2 cal·mol^–1·K^–1, ΔC_P =–580 ± 90 cal·mol^–1·K^–1 (•); ΔH₀ =–17.5 ± 0.9 kcal·mol^–1, ΔS₀ = –56 ± 3 cal·mol^–1·K^–1, ΔC_P = –680 ± 80 cal·mol^–1·K^–1 (○). quadA′: ΔH₀ = –19.5 ± 0.9 kcal·mol^–1, ΔS₀ = –65 ± 3 cal·mol^–1·K^–1, ΔC_P = 0 cal·mol¹·K^–1 (•); ΔH₀ = –14.5 ± 0.6 kcal·mol^–1, ΔS₀ = –43 ± 2 cal·mol^–1·K^–1 ΔC_P = 0 cal·mol^–1·K^–1 (○). Experimental conditions are 5 mM Tris/0.1% PEG8000 (pH 8.0) and I = 800 mM.

Two important changes take place when the length of the 186-loop insertion is increased in the quadA′ mutant: (i) K⁺ is bound preferentially over Na⁺, and (ii) either cation is bound without a large heat-capacity change. The length of the 186-loop insertion holds the key to understanding cation specificity and the origin of the large heat-capacity change observed when Na⁺ or K⁺ bind to wild type. At 25°C, the entropic and enthalpic components of K⁺ binding to quadA′ are very similar to those of Na⁺ binding to wild type. The K⁺ vs. Na⁺ preference of quadA′ is also entropic in origin, suggesting that the enlarged pore in quadA′ can admit a more hydrated Na⁺, thereby shifting the entropic gain from water release in favor of K⁺ that dehydrates more easily due to its lower hydration energy (27, 28). Hence, when the size of the pore is such that dehydration of Na⁺ is not forced, then the larger cation featuring a lower hydration energy is bound preferentially, again consistent with the conclusions of previous discussions (27, 28). The lack of heat-capacity change in the quadA′ mutant may be due to the enlarged size of the pore and the weakening of the water bridges within the Na⁺ site, leading to increased mobility of the entire cation-binding environment. This conclusion would again be consistent with the scenario invoked to explain the origin of large heat-capacity changes in the tryptophan repressor–operator interaction (36).

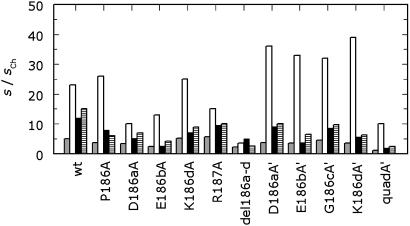
The reversal of cation specificity for the quadA′ mutant is supported by independent measurements of Na⁺ and K⁺ binding by using the linkage between cation binding and FPR hydrolysis in Eq. 3. The values of K_d for Na⁺ and K⁺ binding derived from kinetic linkage analysis are consistent with those determined by fluorescence titration (Fig. 3) throughout the temperature range studied. Na⁺ and K⁺ were found to compete for binding by both kinetic and fluorescence measurements (data not shown), just as in the case of wild type (30). The k_cat/K_m of the enzyme remains higher in the presence of Na⁺ because of the larger activation observed in the presence of this cation (Fig. 4). The monovalent-cation-activation effect on enzyme activity depends on the strength of monovalent cation binding (K_d,M+ in Eq. 3) and the transduction of this binding interaction into enhanced catalytic activity (s₁/s₀ in Eq. 3). Because these two processes are not necessarily linked and are described by thermodynamically independent parameters in Eq. 3, no a priori correlation exists between the strength of cation binding and the magnitude of enhancement of catalytic activity. In the case of wild type and all the thrombin mutants reported here, except quadA′, Na⁺ binds with the highest affinity among monovalent cations and also produces the highest degree of enhancement of k_cat/K_m (Fig. 4). This effect, however, does not correlate with the strength of Na⁺ binding (Table 1). QuadA′ binds K⁺ with higher affinity than Na⁺, but it is nonetheless significantly more active in the presence of Na⁺ than K⁺. The catalytic activity of quadA′ was also measured toward an array of chromogenic substrates other than FPR and toward physiologic substrates, and the presence of Na⁺ consistently resulted in the highest values of k_cat/K_m (data not shown). Hence, quadA′ is an enzyme more specific for K⁺ than Na⁺, but it is not a K⁺-activated enzyme.

Fig. 4.

Monovalent cation activation profile for wild-type and mutant thrombins. Shown are the values of s = k_cat/K_m for the hydrolysis of FPR in the presence of different monovalent cations, expressed in units of the value calculated in choline chloride (34), to approximate the ratio s₁/s₀ in Eq. 3. Experimental conditions are 5 mM Tris/0.1% PEG8000 (pH 8.0) at 25°C. The salt concentration is 200 mM LiCl (gray), NaCl (white), KCl (black), or RbCl (hatched). Note how the activation is maximal in the presence of Na⁺ in all cases and it does not correlate with the strength of Na⁺ binding (Table 1).

Discussion

The ability of certain proteins to discriminate between Na⁺ and K⁺ is central to many processes of biological relevance. The need for the cell to store K⁺ and exclude Na⁺ provides a driving force for selecting proteins and nucleic acids that interact preferentially with K⁺. Indeed, the majority of monovalent-cation-activated enzymes are activated by K⁺ and are intracellular enzymes (2, 3). On the other hand, extracellular enzymes activated by monovalent cations show a preference for Na⁺. How monovalent-cation-activated enzymes distinguish so efficiently between Na⁺ and K⁺ has long been a subject of considerable debate (2, 3, 27). Some of the most interesting ideas in this area have emphasized hydration and electrostatic effects and have been borrowed from discussions on the origin of cation selectivity in ion channels (27), with which monovalent-cation-activated enzymes share striking analogies of ion-binding selectivity and affinity. Spectacular progress has recently been made in the elucidation of the cation selectivity of ion channels (38, 39). The x-ray structure of the K⁺ channel (38) has revealed how the selectivity filter accommodates K⁺ in a cage of backbone O atoms perfectly disposed in space to mimic the hydration shell of the cation in solution. Because of this cage, a Na⁺ ion would not enjoy a similar tight fit and would not be transferred effectively through the channel like the larger cation K⁺. Hence, the K⁺ channel has evolved to achieve optimal fit of the size and hydration properties of K⁺, mainly through a steric fit produced by the cage of O atoms in the selectivity filter. The architecture of the cage also optimizes the electrostatic coupling between the protein and the bound cation (40).

Ion channels have also been studied extensively in terms of mutagenesis experiments aimed at altering their cation specificity. These studies largely support the view that ion size, hydration, and electrostatic coupling set the rules for cation specificity (27), as revealed eloquently by the recent structural work of MacKinnon and colleagues (38–40). Ligand-gated ion channels are either cation- or anion-selective and their selectivity can be reengineered by few amino acid substitutions. For example, neutralization of glutamate residues converts the nicotinic acetylcholine receptor (41) and the 5-hydroxytryptamine receptor (42) from cationic to anionic, whereas the converse mutations convert the glycine receptor from anionic to cationic (43, 44). In this particular case, the diameter of the ion channel contributed significantly to the cationic/anionic selectivity. The selectivity of a K⁺ channel in Drosophila can be shifted to cations of larger ionic radius like Rb⁺ and 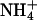by single amino acid substitutions (45). Similar findings have been reported for a K⁺ channel in Arabidopsis thaliana (46). Likewise, mutagenesis work carried out on Na⁺ channels has shown that the selectivity can be shifted to cations of larger ionic radius like K⁺ and 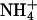(47, 48), or even to divalent cations like Ca²⁺, when the net negative charge at the site is increased (49).

Although the analogies between ion channels and monovalent-cation-activated enzymes are numerous and striking, the latter group of proteins has received considerably less attention as a platform to explore and redesign monovalent cation specificity. We have shown that the monovalent cation preference of thrombin can be shifted from Na⁺ to K⁺ by altering the size of the 186-loop and enlarging the pore of entry of the cation to its site. A short 186-loop selects Na⁺ over K⁺, whereas a long enough loop has reversed cation specificity. The length of the 186-loop in the wild-type enzyme has the optimal shape to ensure high Na⁺ affinity coupled with good selectivity over K⁺. Because K⁺ has a larger ionic radius than Na⁺, it dehydrates preferentially and can be bound with higher affinity by a protein (27). However, in the presence of a strong electrostatic field, Na⁺ and K⁺ can be dehydrated to the same extent, and the smaller cation, Na⁺, may bind with higher affinity (27). The size of the pore in Fig. 1 suggests that Na⁺ or K⁺ must dehydrate significantly before binding to thrombin, and, indeed, a strong electrostatic field is generated around the pore whose role has never been fully explained (50). It is likely that this field is responsible for dehydrating Na⁺ to enable optimal penetration of the pore in the wild type. When the length of the 186-loop is increased as in the quadA′ mutant, the electrostatic field may be weakened, and the enzyme acquires preference for K⁺ over Na⁺ because of the lower cost of dehydrating the larger cation. This scenario strongly suggests that cation specificity in thrombin depends on the hydration properties of the cation and the electrostatic properties of the protein, just as found in ion channels (27, 38–40).

The increased affinity toward K⁺ in the quadA′ mutant is not translated into a preferential activation of thrombin in the presence of this cation. The quadA′ mutant retains optimal catalytic activity in the presence of Na⁺. This finding is not surprising because cation binding and enhancement of catalytic activity are distinct processes not necessarily linked thermodynamically. In enzymes activated by monovalent cations no correlation exists between strength of cation binding and enzyme activation. In fact, the two processes can be decoupled completely. Mutants of tyrosine phenol-lyase (51) and trypsin-digested tryptophan indole-lyase (52) retain K⁺ binding but have practically lost the activation effect. In these cases, the determinants responsible for transduction of cation binding into enhanced catalytic activity have been selectively affected by the mutation. Cation binding can also be mimicked by the ε-amino group of a Lys side chain in pyruvate kinase (53), Hsp70 (54), or thrombin (55), but in no case does the mimicry translate into enhanced catalytic activity. Reengineering cation specificity into a monovalent-cation-activated enzyme should not be expected to produce a protein that has optimal activity in the presence of the most specific cation. Hence, the relation we presently observe between cation selectivity and optimal catalytic activity in enzymes like pyruvate kinase or thrombin is the result of a long evolutionary optimization of the linkage between cation binding and allosteric activation. Further mutagenesis work involving residues important for allosteric transduction in thrombin (33) will help design a K⁺-activated mutant by using quadA′ as an important starting point.