Deblurring of Class-Averaged Images in Single-Particle Electron Microscopy

Abstract

This paper proposes a method for deblurring of class-averaged images in single-particle electron microscopy (EM). Since EM images of biological samples are very noisy, the images which are nominally identical projection images are often grouped, aligned and averaged in order to cancel or reduce the background noise. However, the noise in the individual EM images generates errors in the alignment process, which creates an inherent limit on the accuracy of the resulting class averages. This inaccurate class average due to the alignment errors can be viewed as the result of a convolution of an underlying clear image with a blurring function. In this work, we develop a deconvolution method that gives an estimate for the underlying clear image from a blurred class-averaged image using precomputed statistics of misalignment. Since this convolution is over the group of rigid body motions of the plane, SE(2), we use the Fourier transform for SE(2) in order to convert the convolution into a matrix multiplication in the corresponding Fourier space. For practical implementation we use a Hermite-function-based image modeling technique, because Hermite expansions enable lossless Cartesian-polar coordinate conversion using the Laguerre-Fourier expansions, and Hermite expansion and Laguerre-Fourier expansion retain their structures under the Fourier transform. Based on these mathematical properties, we can obtain the deconvolution of the blurred class average using simple matrix multiplication. Tests of the proposed deconvolution method using synthetic and experimental EM images confirm the performance of our method.

1 Introduction

In single-particle electron microscopy (EM), the goal is to reconstruct the 3D structure of biomolecular complexes from 2D projection data. In practice, a large number of essentially identical copies of the complex of interest are embedded in a thin support layer (vitreous ice or negative stain) in a number of orientations. The micrographs taken by the electron microscopes contain the projections of a number of essentially identical biological samples in various orientations. There are several widely used algorithms that reconstruct the 3D structure using these projection EM images (e.g. EMAN [17], SPIDER [31], IMAGIC [36], and XMIPP [33]).

Single-particle EM is fundamentally contrast limited. Image formation and specimen damage occur in parallel, hence the maintenance of sample integrity imposes strict limits on the electron dose. This, in turn, can restrict the experimentally achievable signal-to-noise ratios to very low values [7, 9]. One way to deal with the noisy images is to apply denoising methods. There exist many denoising methods for EM including the use of a “bilateral filter” [11] or sinograms [24] on the individual micrographs.

In our work, instead of considering denoising of individual electron micrographs, we consider groups of images as a whole. Projections corresponding to the same (or fairly similar) projection directions are grouped together, aligned, and averaged. During the averaging process, the random noise of the background has a tendency to cancel, and the features of interest in the projections reinforce each other as the number of superimposed projections becomes large [7]. This class averaging technique is useful for the analysis of classes of 2D electron micrographs as well as in 3D reconstruction for cryo-EM [18,19,39].

One difficulty with this approach is that the accuracy of the superposition of images is affected by noise. This results in a blurry image relative to the true underlying image of interest. This effect can be modeled via the use of SE(2), the special Euclidean group (in two dimensions), defined as the group of rigid body motions (translation and rotation) on the plane. SE(2) is a noncommutative and noncompact Lie group. An element g ∈ SE(2) can be written as g = g(b₁, b₂, θ) where (b₁, b₂) ∈ ℝ² and θ ∈ [0, 2π) and for x = (x₁, x₂) ∈ ℝ²

$$g·\mathbf{x}=(x_{1}cos\theta -x_{2}sin\theta +b_1,x_{1}sin\theta +x_{2}cos\theta +b_2)$$

defines the action of SE(2) on ℝ². In this setting, the image model for individual EM images can be represented as

$$\psi (\mathbf{x},t)=\rho (g_t^{-1}·\mathbf{x})+n(\mathbf{x},t).$$ (1)

ρ(x) is the underlying clear image, gt is the homogeneous transformation in SE(2), n is the Gaussian noise, x ∈ ℝ² is the planar position of points in each image, and t ∈ ℝ⁺ is an artificial time variable used to order the images.

If there were no noise term, the appropriate matching of two images, ψ(x, t_i) and ψ(x, t_j), would occur at gt_i = gt_j and the average would be $(\psi (\mathbf{x},t_i)+\psi (\mathbf{x},t_j))/2=\rho (g_{t_i}^{-1}\mathbf{x})$. However, if noise is present in the images, then the matching of many data images produces various gt. The average will be of the form

$$\frac{1}{N}\sum _{i=1}^N\psi (\mathbf{x},t_i)\approx \frac{1}{N}\sum _{i=1}^N\rho (g_{t_i}^{-1}·\mathbf{x})+m={\int }_{\text{SE}(2)}\left(\frac{1}{N}\sum _{i=1}^N\delta (g_{t_i}^{-1}\circ g)\right)\rho (g^{-1}·\mathbf{x})dg+m,$$ (2)

where m is the mean of the noise. The first equality assumes that the noise term is approximately canceled out during the averaging process, and the second equality shows that this superposition is convolution over the group of rigid-body motions of the plane, SE(2). The integral term in (2) is essentially the blurred version of ρ(x) depending on the distribution of gt_i. Here we can let m = 0 without loss of generality. When m ≠ 0, we can consider the modified noisy image, ψ′(x, t) = ψ(x, t) − m. As long as we can estimate the mean of noise, this modification is quite simple. In fact, the mean of background noise can be simply estimated using samples from electron micrographs.

We therefore seek to solve the following inverse problem: Given a blurred image, γ(x), that describes the average of many optimally aligned experimentally-obtained projection images, and given an estimate of the probability density function describing the error distribution in the alignment of these superimposed images, f(g), we seek to find the deblurred image ρ(x). This is expressed as the solution to the problem:

$${\int }_{G}f(g)\rho (g^{-1}·\mathbf{x})dg=\gamma (\mathbf{x}).$$ (3)

Here G is the group of transformations involved in alignment, g · x denotes the group action of G on ℝ², and dg is the associated invariant integration measure for that group [5]. The instances of (i) G = SO(2) (the group of rotations in the plane) and (ii) G = ℝ² (the translation group in the plane) are also relevant, while the general problem uses (iii) G = SE(2). Explicitly, in these three cases we have

$${\int }_{-\infty }^{\infty }{\int }_{-\infty }^{\infty }{f}_1(y_1,y_2)\rho (x_1-y_1,x_2-y_2){dy}_1{dy}_2={\gamma }_1(x_1,x_2),$$ (4)

$${\int }_0^{2\pi }{f}_2(\theta )\rho (x_{1}cos\theta +x_{2}sin\theta ,-x_{1}sin\theta +x_{2}cos\theta )d\theta ={\gamma }_2(x_1,x_2),$$ (5)

$$\begin{array}{c}{\int }_{-\infty }^{\infty }{\int }_{-\infty }^{\infty }{\int }_0^{2\pi }{f}_3(y_1,y_2,\theta )\rho ((x_1-y_1)cos\theta +(x_2-y_2)sin\theta ,-(x_1-y_1)sin\theta +(x_2-y_2)cos\theta ){dy}_1{dy}_{2}d\theta \\ ={\gamma }_3(x_1,x_2).\end{array}$$ (6)

Cases (i) and (ii) can be solved using classical Fourier analysis. The noncommutative situation in the general case (iii) is more complicated and requires a relatively new way to look at the problem. For this case, theoretical solutions have been reported in the literature [15, 42, 43] using the Fourier transform for SE(2). Noncommutativity implies that in general the irreducible unitary representations are given by matrices instead of scalars and the Fourier transform converts the convolution on SE(2) to the multiplication of infinite-dimensional matrices in the Fourier space. Recall that in the commutative case the effect of the Fourier transform is to convert convolution to pointwise multiplication.

Regarding finding ρ from the observation ψ in (1), a similar work is found in [2]. While it develops the mathematical framework to estimate the statistics of “deformation” (equivalently alignment in this paper) and the reference template (equivalently underlying clear image in this paper), we focus on the practical implementation of deconvolution after averaging in order to find the underlying clear image. We note that the method in [2] focuses on compact Lie groups, but our method works on the non-compact Lie group SE(2).

The focus of this paper is both on the noncommutative framework for deblurring of the class averages and the practical implementation of this group-based approach. It is important to distinguish our contribution from the classical uses of deconvolution for image enhancement in microscopy. The general form of these problems is to first identify the point spread function (PSF) of the imaging system and then use the deconvolution algorithm to eliminate the effect of the PSF and obtain the estimate for the underlying true image. For instance, McNally et al. [22] use deconvolution to reduce the out-of-focus light in fluorescence microscopy for three-dimensional imaging. Manz et al. [21] apply widefield deconvolution fluorescence microscopy to single bacterial cells. In this form, deconvolution has also been applied to confocal microscopy for the enhancement of images [6, 34] and to electron microscopy [10,13].

In this paper, the problem which the deconvolution method is applied to is completely different. We assume that each micrograph is a projection of the biological samples with additive background noise, and observe that the averaging process, whose goal is to reduce the noise, produces a blurry average. More precisely, the blurring effect is caused by the computational process used in the alignment of the images. Based on the blurring functions whose estimation will be reviewed in Section 2, the development and the implementation of the deconvolution in the appropriate domain for the blurred class average will be the main topic of this paper.

2 Preliminary work

Previously we proposed a method of estimating the blurring function in the class averaging process [26]. In this section, we will briefly review that work.

Classification of single-particle EM projection images has been addressed by a number of approaches [7, 8, 17, 31]. Once images that have a nominally identical (or fairly similar) projection direction have been assigned to a class, they are aligned with respect to one another as a prerequisite for averaging. The alignment of two images, ρ₁(x) and ρ₂(x), can be achieved by solving the following minimization problem:

$$\underset{g\in \text{SE}(2)}{min}(\sum _i{\left|\right|{\rho }_1({\mathbf{x}}_i)-{\rho }_2(g^{-1}·{\mathbf{x}}_i)\left|\right|}^2),$$ (7)

where g is the homogeneous transformation in SE(2), x_i ∈ ℝ² is the planar position of pixels in images. Even though there are many mathematical and computational issues associated with solutions to (7) [12, 41], we use a simple method to align images; we match the mass center and the principal axis of the images [26]. To implement this alignment method, each image in a class is translated, rotated and clipped by a circular window so that the resulting image has its mass center at the geometric center of the circular window and has the diagonal inertia matrix. We apply this alignment method to the classified EM images, and then we take the average of the aligned class images. In the presence of the background noise, the alignment cannot be perfect. The misalignment leads to a blurry class average which can be modeled as (3).

In previous work we have shown that Gaussian distributions can be used as a model for the blurring functions in EM class averaging [26]. Let us consider the 1D Gaussian function:

$$f(x,t)=\frac{1}{2\sqrt{\pi t}}{e}^{-x^2/4t}.$$ (8)

The mean and the variance are 0 and 2t, respectively. Using this, we can define the blurring functions f_i for (4)–(6) as follows:

$$f_1(x_1,x_2,t_1)=f(x_1,t_1)f(x_2,t_1)=\frac{1}{4\pi t_1}{e}^{-(x_1^2+x_2^2)/4t_1}$$ (9)

$$f_2(\theta ,t_2)=\sum _{n=-\infty }^{\infty }f(\theta -2\pi n,t_2)=\frac{1}{2\pi }\sum _{k=-\infty }^{\infty }{e}^{-k^2{t}_2}{e}^{ik\theta }$$ (10)

and

$$f_3(x_1,x_2,\theta ;t_1,t_2)=f_1(x_1,x_2,t_1)f_2(\theta ,t_2)=\frac{1}{8{\pi }^2{t}_1}{e}^{-(x_1^2+x_2^2)/4t_1}\sum _{k=-\infty }^{\infty }{e}^{-k^2{t}_2}{e}^{ik\theta }$$ (11)

where the values of t₁ and t₂ can be chosen separately to describe different amounts of translational and rotational error, as well as to account for the fact that the units of measurement are different for translations and rotations. Here f₂(θ, t₂) is a Gaussian distribution on ℝ “wrapped around the circle” to result in a Gaussian on SO(2).

Explicitly, we estimate the two parameters as [26]

$$t_1=\frac{(1+4\nu ){\sigma }^2}{2M^2}\sum _i{x}_i^2$$

and

$$t_2=\frac{K}{2{({\lambda }_1-{\lambda }_2)}^2}\left(K\sum _i{x}_i^2\sum _j{y}_j^2+\sum _i{x}_i^2{y}_i^2\right),$$

where K = (1 + 4ν)σ²/M², σ² is the variance of the background noise, and ν is the correlation between noises at the adjacent pixels. M is defined by M = 〈Σ_i ψ(x_i, t)〉− mW, where 〈·〉 denotes the mean operator over t, ψ is the noisy image, m is the mean of the background noise and W is the number of pixel points enclosed by the circular window. The inertia matrix of the noisy image ψ(x, t) is computed as

$$J(t)=\frac{1}{M}\sum _i{\mathbf{x}}_i{\mathbf{x}}_i^T\psi ({\mathbf{x}}_i,t)=\left(\begin{array}{cc}{L}_1(t)& 0\\ 0& L_2(t)\end{array}\right).$$

Note that the noisy image ψ is aligned so as to have the diagonal inertia matrix. The term (λ₁ −λ₂) is defined as [26]

$$({\lambda }_1-{\lambda }_2)=\langle L_1(t)\rangle -\langle L_2(t)\rangle .$$

Again, it has been shown that the blurring function can be defined by Gaussian functions, and the mean and the variance of the Gaussian can be computed using the statistics of the background noise [26]. Now we will focus on developing a method for computing the underlying clear image ρ(x) using a given blurred image, γ(x) in (3).

One of the most widely used methods for alignment is the maximum likelihood method. For example, Sigworth [32] applied the maximum likelihood approach to alignment of two 2D images with the application to single-particle images. Based on this approach, the method to align and refine 2D EM images with multiple references was also introduced in [30]. This maximum likelihood approach uses an iterative process and the computation time ranges from 30 min [32] to several hours [30].

The alignment method in [26] is probably not the most powerful in the context of minimization of (7) and may produce somewhat larger alignment errors. However, the ultimate goal of this paper is the comparison of the deblurred result against the gold standards of the field. Our alignment method, while perhaps producing blurrier images than other alignment methods, can be easily modeled. This in turn allows us to generate high quality images after deblurring/deconvolution. This is not necessarily the case with other alignment methods since their blurring kernels may not be quantifiable.

3 Deconvolution of blurred images using Fourier transform

In this section we address how to solve each of the three deconvolution problems in (4)-(6) using the Fourier transform.

3.1 The 2-D Fourier transform for translational deconvolution

The natural tool to use to solve the deconvolution problem in (4) is the classical (Abelian or commutative) 2D Fourier transform. The Fourier transform of the probability density function, f₁(x₁, x₂, t₁) in (9) is $\widehat{f_1}(\omega )=e^{-({\omega }_1^2+{\omega }_2^2)t_1}$. The convolution theorem then converts (4) to a problem in Fourier space of the form

$$\widehat{f_1}(\omega )\widehat{\rho }(\omega )={\widehat{\gamma }}_1(\omega ),$$

which is inverted after regularization as

$$\widehat{\rho }(\omega )={\widehat{\gamma }}_1(\omega )\overline{\widehat{f_1}(\omega )}/(\epsilon +\mid \widehat{f_1}(\omega ){\mid }^2).$$ (12)

The regularization parameter, ε, is a very small positive number that is introduced to handle zeros of the Fourier transform. In fact, for the Gaussian distribution of interest in our problem, there are no zeros, but in both real and Fourier space the tails of the distribution can approach zero at points sufficiently far from the origin.

3.2 The 1-D Fourier transform for rotational deconvolution

If the image functions are defined on polar coordinates, (5) can be rewritten as

$${\int }_0^{2\pi }{f}_2(\theta )\rho (r,\phi -\theta )d\theta ={\gamma }_2(r,\phi ),$$

using x₁ = r cos φ and x₂ = r sin φ. If we fixed the value of r, (5) becomes the convolution of the two functions on a circle as

$${\int }_0^{2\pi }{f}_2(\theta ){\rho }^{(r)}(\phi -\theta )d\theta ={\gamma }_2^{(r)}(\phi ),$$ (13)

where ρ^(r) (φ − θ) = ρ (r, φ − θ) and ${\gamma }_2^{(r)}(\phi )={\gamma }_2(r,\phi )$.

In general, the Fourier series expansion of a function defined on a circle gives

$$h(\theta )=\frac{1}{2\pi }\sum _{-\infty }^{\infty }{h}_n{e}^{in\theta },$$

where

$$h_n={\int }_0^{2\pi }h(\theta )e^{-in\theta }d\theta .$$

The Fourier transform of the distribution function, f₂(θ, t₂) in (10) is ${(\widehat{f_2})}_n=e^{-n^2{t}_2}$.

The convolution theorem of Fourier series converts (13) to the problem in Fourier space of the form

$${(\widehat{f_2})}_n{({\widehat{\rho }}^{(r)})}_n={({\widehat{\gamma }}_2^{(r)})}_n.$$

As in the case of the translational deconvolution, the inversion with regularization is

$${({\widehat{\rho }}^{(r)})}_n={({\widehat{\gamma }}_2^{(r)})}_n\overline{{(\widehat{f_2})}_n}/(\epsilon +\mid {(\widehat{f_2})}_n{\mid }^2).$$ (14)

3.3 Deconvolution of combined translational and rotational blurring

In order to solve the full SE(2) deconvolution problem, the appropriate concept of Fourier transform is required. In particular, since f₃ in (11) is a function on the group of rigid-body motions of the plane, SE(2), and a function on ℝ² can be viewed as a function on SE(2) that is constant over the orientational variable, (6) can be treated as a convolution on SE(2). We review here the group SE(2) and the associated Fourier analysis [5,15].

3.3.1 Representation theory of the Euclidean motion group of the plane

Each element of SE(2) is parameterized in either rectangular or polar coordinates as:

$$g(a_1,a_2,\theta )=\left(\begin{array}{ccc}cos\theta & -sin\theta & a_1\\ sin\theta & cos\theta & a_2\\ 0& 0& 1\end{array}\right)$$

or

$$g(a,\phi ,\theta )=\left(\begin{array}{ccc}cos\theta & -sin\theta & acos\phi \\ sin\theta & cos\theta & asin\phi \\ 0& 0& 1\end{array}\right).$$

Irreducible unitary representations of SE(2) (see [5,35,38] for general definition) can be viewed as infinite-dimensional matrices, U(g, p) with elements expressed as

$$u_{mn}(g(a,\phi ,\theta ),p)=i^{n-m}{e}^{-i[n\theta +(m-n)\phi ]}{J}_{n-m}(pa)$$ (15)

where J_ν(x) is the ν’th order Bessel function and m and n range over all integer values. From this expression, and the fact that U(g, p) is a unitary representation, we have

$$u_{mn}(g^{-1}(a,\phi ,\theta ),p)=u_{mn}^{-1}(g(a,\phi ,\theta ),p)=\overline{u_{nm}(g(a,\phi ,\theta ),p)}=i^{n-m}{e}^{i[m\theta +(n-m)\phi ]}{J}_{m-n}(pa).$$ (16)

3.3.2 Fourier transform for the Euclidean motion group of the plane, SE(2)

The Fourier transform of a sufficiently well-behaved function on SE(2), and the corresponding inverse transform are defined as [5]

$$\mathcal{F}(f)=\widehat{f}(p)={\int }_{\text{SE}(2)}f(g)U(g^{-1},p)dg$$ (17)

and

$${\mathcal{F}}^{-1}(\widehat{f})=f(g)={\int }_0^{\infty }\text{trace}(\widehat{f}(p)U(g,p))\mathit{pdp}.$$

The matrix elements of the Fourier transform can be calculated using the matrix elements of U(g, p) defined in (15) as

$${\widehat{f}}_{mn}(p)={\int }_{\text{SE}(2)}f(g)u_{mn}(g^{-1},p)dg.$$ (18)

Likewise, the inverse transform can be written in terms of elements as

$$f(g)=\sum _{n,m\in Z}{\int }_0^{\infty }{\widehat{f}}_{mn}(p)u_{nm}(g,p)\mathit{pdp}.$$

3.3.3 Regularized deconvolution of deblurring in SE(2)

The convolution on the motion group in (6) can be converted to

$$\widehat{\rho }(p)\widehat{f_3}(p)={\widehat{\gamma }}_3(p),$$ (19)

where $\widehat{(·)}$ denotes the Fourier transform in SE(2). The functions ρ(x) and γ₃(x) are functions on the 2D Euclidean plane. Using the polar coordinates for the functions and the definition of the SE(2)-Fourier transform (18), the SE(2)-Fourier transform of a 2D function can be written as

$$\begin{array}{c}{\widehat{\rho }}_{mn}(p)={\int }_{\theta =0}^{2\pi }{\int }_{\phi =0}^{2\pi }{\int }_{r=0}^{\infty }\rho (r,\phi )i^{n-m}{e}^{i[m\theta +(n-m)\phi ]}{J}_{m-n}(pr)\mathit{rdrd}\phi d\theta \\ =2\pi {\delta }_{m,0}{\int }_{\phi =0}^{2\pi }{\int }_{r=0}^{\infty }\rho (r,\phi )i^n{e}^{in\phi }{J}_{-n}(pr)\mathit{rdrd}\phi .\end{array}$$

It is important to note that the matrices ρ̂(p) and γ̂₃(p) are essentially row vectors, since the elements at m ≠ 0 are zeros.

The direct solution using matrix inversion would be

$$\widehat{\rho }(p)={\widehat{\gamma }}_3(p){[\widehat{f_3}(p)]}^{-1}.$$ (20)

However, if the matrix $\widehat{f_3}(p)$ becomes singular, then this needs to be regularized. The procedure for doing this is explained in [4], and involves the computation of a weighted least-squares pseudo-inverse. Lesosky et al. [15] also proposed a theoretical approach to solve (19) using regularization.

For the blurring function that is induced by the noise model, we can compute the entries of $\widehat{f_3}(p)$ analytically. We can rewrite the function in (11) using polar coordinates as

$$f_3(r,\phi ,\theta ;t_1,t_2)=\frac{1}{8{\pi }^2{t}_1}{e}^{-r^2/4t_1}\sum _{k=-\infty }^{\infty }{e}^{-k^2{t}_2}{e}^{ik\theta }.$$ (21)

Computing the SE(2) Fourier transform of the distribution, we find

$${(\widehat{f_3})}_{mn}(p)=\frac{1}{2t_1}{\delta }_{mn}\left({\int }_0^{\infty }{e}^{-r^2/4t_1}{J}_0(pr)\mathit{rdr}\right)e^{-m^2{t}_2}={\delta }_{mn}{e}^{-p^2{t}_1}{e}^{-m^2{t}_2}.$$ (22)

The natural integration measure for SE(2) in (17) is expressed in coordinates as dg = rdrdφdθ. Note that $\widehat{f_3}(p)$ is diagonal. Its inversion is the simple inversion of scalar values and the inversion with the regularization parameter is the same as that in the previous two cases.

4 Deconvolution of blurred class-averaged images using Hermite and Laguerre functions

Even though the Fourier transform is a good way to solve the deconvolution problem, its implementation requires us to address some technical details related to the fact that the image is defined on a discrete grid, while the formulation is for a continuous domain. Although we can apply the discrete Fourier transform (DFT), sampling of the continuous blurring function is required for the transform. The grid for this sampling should be fine enough to avoid aliasing. At this level of granularity resampling of the image function is also required in order to match the resolution of the samplings of the image function and the blurring function. In addition, we need another resampling process in order to perform the Fourier transform in SE(2), since the image function on the polar grid is required.

To avoid this difficulty, we develop a deconvolution method combining the SE(2) Fourier method and the Hermite and Laguerre-Fourier expansions. We utilize special properties of these expansions associated with the Fourier transform and Cartesian-polar coordinate conversion.

The Hermite polynomial (of order n) is defined by the Rodrigues formula

$$H_n(x)={(-1)}^n{e}^{x^2}\frac{d^n}{{dx}^n}(e^{-x^2}).$$

and the Hermite function, h_n(x) is defined as

$$h_n(x)=\frac{1}{s_n}{H}_n(x)e^{-x^2/2},$$

where $s_n=\sqrt{2^{n}n!\sqrt{\pi }}$. The Hermite function is an eigenfunction for the Fourier transform and satisfies the relation

$${\int }_{-\infty }^{\infty }{h}_n(x)e^{-i\omega x}dx=\sqrt{2\pi }{(-i)}^n{h}_n(\omega ).$$ (23)

The associated Laguerre polynomials are generated by the Rodrigues formula,

$$L_n^k(x)=\frac{e^x{x}^{-k}}{n!}\frac{d^n}{d{x}^n}(e^{-x}{x}^{n+k}).$$

Using the Laguerre polynomials and Fourier basis, we can define a basis function in two-dimensional polar coordinates as follows [20,28].

$${\chi }_{m,n}(r,\phi )={(-1)}^{(m-\mid n\mid )/2}\sqrt{\frac{[(m-\mid n\mid )/2]!}{\pi [(m+\mid n\mid )/2]!}}{r}^{\mid n\mid }{L}_{(m-\mid n\mid )/2}^{\mid n\mid }(r^2)e^{-r^2/2}{e}^{-in\phi },$$

For convenience, we divide it into two parts as

$${\chi }_{m,n}(r,\phi )=y_{m,n}(r)z_n(\phi ),$$

where

$$\begin{array}{l}{y}_{m,n}(r)={(-1)}^{(m-\mid n\mid )/2}\sqrt{\frac{[(m-\mid n\mid )/2]!}{\pi [(m+\mid n\mid )/2]!}}{r}^{\mid n\mid }{L}_{(m-\mid n\mid )/2}^{\mid n\mid }(r^2)e^{-r^2/2},\\ z_n(\phi )=e^{-in\phi }.\end{array}$$

The function χ_m,n(r, φ) is suitable for expansion of a function defined on polar coordinates, while a function defined on Cartesian coordinates can be expanded using the Hermite functions. Mathematically, the two expansions (Laguerre-Fourier expansion and Hermite expansion) can be converted losslessly to each other with the same bandlimit [28].

We now will show how to solve the deconvolution problems combining these expansions and the SE(2) Fourier transform. The appropriate expansion will be chosen for the three cases.

4.1 Translational deconvolution using Hermite expansion

The Hermite expansion of an image function is

$$\rho (x_1,x_2)=\sum _{m=0}^{\infty }\sum _{n=0}^{\infty }{\check{\rho }}_{mn}{h}_m(x_1)h_n(x_2),$$

where the Hermite coefficients are given as

$${\check{\rho }}_{mn}={\int }_{{\mathbb{R}}^2}\rho (x_1,x_2)h_m(x_1)h_n(x_2)d{x}_{1}d{x}_2.$$

A bandlimited Hermite expansion with the bandlimit N is written as

$$\rho (x_1,x_2)=\sum _{m=0}^N\sum _{n=0}^{N-m}{\check{\rho }}_{mn}{h}_m(x_1)h_n(x_2).$$ (24)

When using the 2D bandlimited Hermite expansion to represent a 2D discrete image, it is important to determine an appropriate value for the bandlimit N. An extremely low value may cause oversmoothing for the data and an excessively high value may produce high frequency information that is not related to the original image. The bandlimit is chosen so that the bandlimit Hermite expansion best fits to the discrete image, while keeping the matrix used for computing Hermite coefficients invertible. The details of this method appears in [28].

Using (23), we compute the 2D Fourier transform of the image function as

$$\widehat{\rho }({\omega }_1,{\omega }_2)=\sum _{m=0}^N\sum _{n=0}^{N-m}{\check{\rho }}_{mn}(2\pi ){(-i)}^{m+n}{h}_m({\omega }_1)h_n({\omega }_2).$$

Since the 2D Fourier transform of f₁(x₁, x₂, t₁) in (9) is $\widehat{f_1}({\omega }_1,{\omega }_2)=e^{-({\omega }_1^2+{\omega }_2^2)t_1}$, the Fourier transform of the blurred image is written as

$${\widehat{\gamma }}_1({\omega }_1,{\omega }_2)=\sum _{m=0}^N\sum _{n=0}^{N-m}{\check{\rho }}_{mn}(2\pi ){(-i)}^{m+n}{h}_m({\omega }_1)h_n({\omega }_2)e^{-({\omega }_1^2+{\omega }_2^2)t_1}.$$ (25)

On the other hand, since H_m(x) is an m’th order polynomial, it can be rewritten as

$$H_m(x)=H_m(\frac{ax}{a})=\sum _{k=0}^m{\alpha }_{m,k}(a^{-1})H_k(ax),$$

where the α_m,k(a⁻¹) are the appropriate coefficients relating a Hermite polynomial and its scaled version. Using this expression, we can have

$$h_m(\omega )e^{-{\omega }^2{t}_1}=\sum _{k=0}^m{\alpha }_{m,k}(a^{-1})\frac{s_k}{s_m}{h}_k(a\omega ),$$

where $a=\sqrt{2t_1+1}$. Therefore, (25) can be rewritten as

$${\widehat{\gamma }}_1({\omega }_1,{\omega }_2)=\sum _{m=0}^N\sum _{n=0}^{N-m}{\check{\rho }}_{mn}(2\pi ){(-i)}^{m+n}\sum _{k=0}^m\sum _{l=0}^n{\alpha }_{m,k}(a^{-1}){\alpha }_{n,l}(a^{-1})\frac{s_k}{s_m}\frac{s_l}{s_n}{h}_k(a{\omega }_1)h_l(a{\omega }_2).$$

We can reorder the summations and have

$${\widehat{\gamma }}_1({\omega }_1,{\omega }_2)=\sum _{k=0}^N\sum _{l=0}^{N-k}\left(\sum _{m=k}^{N-l}\sum _{n=l}^{N-m}{\check{\rho }}_{mn}(2\pi ){(-i)}^{m+n}{\alpha }_{m,k}(a^{-1}){\alpha }_{n,l}(a^{-1})\frac{s_k}{s_m}\frac{s_l}{s_n}\right)h_k(a{\omega }_1)h_l(a{\omega }_2).$$ (26)

Its inverse Fourier transform is

$${\gamma }_1(x_1,x_2)=\sum _{k=0}^N\sum _{l=0}^{N-k}\left(\sum _{m=k}^{N-l}\sum _{n=l}^{N-m}{\check{\rho }}_{mn}(2\pi ){(-i)}^{m+n}{\alpha }_{m,k}(a^{-1}){\alpha }_{n,l}(a^{-1})\frac{s_k}{s_m}\frac{s_l}{s_n}\right)\frac{i^{k+l}}{2\pi a^2}{h}_k(x_1/a)h_l(x_2/a).$$

If we have a bandlimited Hermite expansion for a blurred image expressed as

$${\gamma }_1(x_1,x_2)=\sum _{k=0}^N\sum _{l=0}^{N-k}{\check{\gamma }}_{kl}{h}_k(x_1/a)h_l(x_2/a),$$ (27)

then its Fourier transform is

$${\widehat{\gamma }}_1({\omega }_1,{\omega }_2)=\sum _{k=0}^N\sum _{l=0}^{N-k}{\check{\gamma }}_{kl}\frac{2\pi a^2}{i^{k+1}}{h}_k(a{\omega }_1)h_l(a{\omega }_2).$$ (28)

Equating (25) and (28) on various samples on (ω^(p), ω^(q)) gives

$$(\mathit{EHU})R{(\mathit{EHU})}^T=H_a\times G\times H_a^T,$$

where E_m,n = δ_m,ne^{−t₁(ω(m))2} H_m,n = h_n−1(ω^(m)), (H_a)_m,n = h_n−1(aω^(m)), U_m,n = δ_m,n(−i)^m, R_m,n = ρ̌_m−1,n−1 and G_m,n = γ̌_m−1,n−1. The goal is to compute R which is the Hermite coefficients of the underlying clear image. In order to obtain R, we must examine the inversion of the matrices.

Inversion of U is given by $U_{m,n}^{-1}={\delta }_{m,n}{i}^m$. The pseudo-inverse of H is given by H⁺ = (H^TH)⁻¹H^T if the sampling points, ω^(p) are chosen appropriately as shown in [28]. Inverting E requires regularization because the inverse of e^{−t₁(ω(m))2} may be unstable for large values of ω^(m). Therefore, $E_{m,n}^{+}={\delta }_{m,n}(1/(e^{-t_1{({\omega }^{(m)})}^2}+\epsilon )$ with small ε. With this, we can write the deconvolution solution as

$$R=U^{-1}{H}^{+}{E}^{+}{H}_a\times G\times {(U^{-1}{H}^{+}{E}^{+}{H}_a)}^T.$$

4.2 Rotational deconvolution using Laguerre-Fourier expansion

Using the Laguerre-Fourier expansions, an image function defined on polar coordinates can be expressed as [28]

$$\rho (r,\phi )=\sum _{m=0}^{\infty }\underset{n=-m}{\overset{m}{{\sum }^{\prime }}}{\stackrel{\sim }{\rho }}_{mn}{\chi }_{mn}^{\ast }(r,\phi ),$$

where the Laguerre-Fourier coefficients are given as

$${\stackrel{\sim }{\rho }}_{mn}={\int }_{{\mathbb{R}}^2}\rho (r,\phi ){\chi }_{mn}(r,\phi )\mathit{rdrd}\phi ,$$

and ${\mathrm{\sum }}_n^{\prime }$ denotes the summation for the index n that is increased by multiples of 2.

A bandlimited Laguerre-Fourier expansion for an image function with the bandlimit N is written as

$$\rho (r,\phi )=\sum _{m=0}^N\underset{n=-m}{\overset{m}{{\sum }^{\prime }}}{\stackrel{\sim }{\rho }}_{mn}{\chi }_{mn}^{\ast }(r,\phi ).$$ (29)

If the image function in (5) is defined on polar coordinates, the convolution can be rewritten as

$${\int }_0^{2\pi }{f}_2(\theta )\rho (r,\phi -\theta )d\theta ={\gamma }_2(r,\phi ),$$ (30)

with the coordinate conversion, x₁ = r cos θ and x₂ = r sin θ. Using (10) and (29), (30) can be rewritten as

$${\int }_0^{2\pi }\frac{1}{2\pi }\sum _{k=-\infty }^{\infty }{e}^{-k^2{t}_2}{e}^{ik\theta }\sum _{m=0}^N\underset{n=-m}{\overset{m}{{\sum }^{\prime }}}{\stackrel{\sim }{\rho }}_{mn}{\chi }_{mn}^{\ast }(r,\phi -\theta )d\theta ={\gamma }_2(r,\phi ),$$

The left hand side can be computed as

$$\begin{array}{c}\frac{1}{2\pi }\sum _{k=-\infty }^{\infty }\sum _{m=0}^N\underset{n=-m}{\overset{m}{{\sum }^{\prime }}}{e}^{-k^2{t}_2}{\stackrel{\sim }{\rho }}_{mn}{y}_{mn}(r){\int }_0^{2\pi }{e}^{ik\theta }{e}^{in(\phi -\theta )}d\theta =\sum _{k=-\infty }^{\infty }\sum _{m=0}^N\underset{n=-m}{\overset{m}{{\sum }^{\prime }}}{e}^{-k^2{t}_2}{e}^{in\phi }{\stackrel{\sim }{\rho }}_{mn}{y}_{mn}(r){\delta }_{k,n}\\ =\sum _{m=0}^N\underset{n=-m}{\overset{m}{{\sum }^{\prime }}}\left({\stackrel{\sim }{\rho }}_{mn}{e}^{-n^2{t}_2}\right)y_{mn}(r)z_n^{\ast }(\phi )=\sum _{m=0}^N\underset{n=-m}{\overset{m}{{\sum }^{\prime }}}\left({\stackrel{\sim }{\rho }}_{mn}{e}^{-n^2{t}_2}\right){\chi }_{mn}^{\ast }(r,\phi )\end{array}$$

Therefore the blurred image is

$${\gamma }_2(r,\phi )=\sum _{m=0}^N\underset{n=-m}{\overset{m}{{\sum }^{\prime }}}{\stackrel{\sim }{\gamma }}_{mn}{\chi }_{mn}^{\ast }(r,\phi ),$$ (31)

where

$${\stackrel{\sim }{\gamma }}_{mn}={\stackrel{\sim }{\rho }}_{mn}{e}^{-n^2{t}_2}.$$

This means that the convolved (blurred) image of a bandlimited Laguerre-Fourier expansion with purely rotational blurring is also a bandlimited Laguerre-Fourier expansion with the same bandlimit. The only difference is that the coefficients are scaled. Once we compute the Laguerre-Fourier coefficients (γ̃_mn) of the blurred image, the Laguerre-Fourier coefficients of the deblurred image is given by

$${\stackrel{\sim }{\rho }}_{mn}={\stackrel{\sim }{\gamma }}_{mn}\{1/(e^{-n^2{t}_2}+\epsilon )\}$$ (32)

with regularization.

4.3 Translational and rotational deconvolution using Laguerre-Fourier expansion

In this section, we develop a method for deconvolution of an image blurred via translational and rotational blurring. We utilize the special property of the Laguerre-Fourier expansion in SE(2) Fourier transform.

4.3.1 Fourier transform of the Laguerre-Fourier expansion

If a function on polar coordinates ρ(r, φ) is defined as a bandlimited Laguerre-Fourier expansion as

$$\rho (r,\phi )=\sum _{k=0}^N\underset{l=-k}{\overset{k}{{\sum }^{\prime }}}{\stackrel{\sim }{\rho }}_{kl}{\chi }_{kl}^{\ast }(r,\phi ),$$

then its Fourier transform in SE(2) is

$$\begin{array}{c}{\widehat{\rho }}_{mn}(p)={\int }_{\theta =0}^{2\pi }{\int }_{\phi =0}^{2\pi }{\int }_{r=0}^{\infty }\rho (r,\phi )i^{n-m}{e}^{i[m\theta +(n-m)\phi ]}{J}_{m-n}(pr)\mathit{rdrd}\phi d\theta \\ =\sum _{k=0}^N\underset{l=-k}{\overset{k}{{\sum }^{\prime }}}{\stackrel{\sim }{\rho }}_{kl}{\int }_{\theta =0}^{2\pi }{\int }_{\phi =0}^{2\pi }{\int }_{r=0}^{\infty }{y}_{kl}(r)z_l^{\ast }(\phi )i^{n-m}{e}^{i[m\theta +(n-m)\phi ]}{J}_{m-n}(pr)\mathit{rdrd}\phi d\theta \\ =i^{n-m}\sum _{k=0}^N\underset{l=-k}{\overset{k}{{\sum }^{\prime }}}{\stackrel{\sim }{\rho }}_{kl}{\int }_{r=0}^{\infty }{y}_{kl}(r)J_{m-n}(pr)\mathit{rdr}{\int }_{\phi =0}^{2\pi }{e}^{il\phi }{e}^{i(n-m)\phi }d\phi {\int }_{\theta =0}^{2\pi }{e}^{im\theta }d\theta \\ =4{\pi }^2{i}^{n-m}\sum _{k=0}^N\underset{l=-k}{\overset{k}{{\sum }^{\prime }}}{\stackrel{\sim }{\rho }}_{kl}\left({\int }_{r=0}^{\infty }{y}_{kl}(r)J_{m-n}(pr)\mathit{rdr}\right){\delta }_{l,-n}{\delta }_{m,0}\\ =4{\pi }^2{i}^n\sum _{k=0}^N\underset{l=-k}{\overset{k}{{\sum }^{\prime }}}{\stackrel{\sim }{\rho }}_{kl}\left({\int }_{r=0}^{\infty }{y}_{kl}(r)J_l(pr)\mathit{rdr}\right){\delta }_{l,-n}{\delta }_{m,0}.\end{array}$$

On the other hand, we have the useful identity (see [3] and [5])

$${\int }_0^{\infty }{(\alpha r)}^m{L}_n^m({\alpha }^2{r}^2)e^{-{\alpha }^2{r}^2/2}{J}_m(kr)\mathit{rdr}={(-1)}^n{\alpha }^{-2}{(k/\alpha )}^m{L}_n^m(k^2/{\alpha }^2)e^{-k^2/2{\alpha }^2}.$$

Using this identity, we can compute

$$\begin{array}{c}{\int }_{r=0}^{\infty }{y}_{kl}(r)J_l(pr)\mathit{rdr}={(-1)}^{(k-\mid l\mid )/2}\sqrt{\frac{[(k-\mid l\mid )/2]!}{\pi [(k+\mid l\mid )/2]!}}{\int }_{r=0}^{\infty }{r}^{\mid l\mid }{L}_{(k-\mid l\mid )/2}^{\mid l\mid }(r^2)e^{-r^2/2}{J}_l(pr)\mathit{rdr}\\ ={(-1)}^{(k-\mid l\mid )/2}\sqrt{\frac{[(k-\mid l\mid )/2]!}{\pi [(k+\mid l\mid )/2]!}}{(-1)}^{(k-1)/2}{p}^{\mid l\mid }{L}_{(k-\mid l\mid )/2}^{\mid l\mid }(p^2)e^{-p^2/2}={(-1)}^{(k-l)/2}{y}_{k,l}(p).\end{array}$$

Therefore, the SE(2) Fourier transform ρ̂_mn(p) can be expressed using the Laguerre-Fourier coefficients ρ̃_kl:

$${\widehat{\rho }}_{mn}(p)=4{\pi }^2{i}^n\sum _{k=0}^N\underset{l=-k}{\overset{k}{{\sum }^{\prime }}}{\stackrel{\sim }{\rho }}_{kl}{(-1)}^{\frac{k-l}{2}}{y}_{k,l}(p){\delta }_{l,-n}{\delta }_{m,0}=4{\pi }^2{i}^n\underset{k=\mid n\mid }{\overset{2[\frac{N-n}{2}]+n}{{\sum }^{\prime }}}{\stackrel{\sim }{\rho }}_{k,-n}{(-1)}^{\frac{k+n}{2}}{y}_{k,-n}(p){\delta }_{m,0},$$ (33)

where [n/2] = n/2 if n is even and [n/2] = (n − 1)/2 if n is odd.

Note that ρ̂(p) in (33) is a row vector with (2N + 1) elements. This truncation comes naturally due to the use of the bandlimited Laguerre-Fourier expansion. From this observation, we can compare the bandlimit N in this paper and the truncation limit T in [15]. In [15], all of the functions are defined on SE(2) and the infinite size of SE(2)-Fourier matrix is truncated using T. Even though comparing the truncation size (2N +1 vs 2T +1) in the two approaches, we can see the relationship T = N, this relationship should not be overestimated. First of all, N is used to truncate the Laguerre-Fourier expansions (and simultaneously to truncate the Hermite expansions), while T is used to truncate the Fourier matrix directly. Therefore the methods to determine the limits would be different. Moreover, if we extend our method to handle the SE(2) functions by adding a φ-dependent term in the image expansion, the bandlimit for the Laguerre-Fourier expansion does not truncate the SE(2)-Fourier matrix into a square matrix.

4.3.2 Deconvolution using the Laguerre-Fourier expansion

In Section 4.1, we noticed that the translationally blurred version of (24) is (27). This scaling effect on the domain appears in the polar coordinates as follows: if the original image is given as

$$\rho (r,\phi )=\sum _{m=0}^N\underset{n=-m}{\overset{m}{{\sum }^{\prime }}}{\stackrel{\sim }{\rho }}_{mn}{\chi }_{mn}^{\ast }(r,\phi ),$$ (34)

then its translational blurring is

$$\gamma (r,\phi )=\sum _{m=0}^N\underset{n=-m}{\overset{m}{{\sum }^{\prime }}}{\stackrel{\sim }{\gamma }}_{mn}{\chi }_{mn}^{\ast }(\frac{r}{a},\phi ),$$ (35)

since the (34) and (24) are equivalent under the simple coordinate relation, r = cos φ and r = sin φ [28]. In Section 4.2, we noted that the rotationally blurred version of (29) retains the structure of the bandlimited Laguerre-Fourier expansion without scaling in the domain.

Therefore, we can conclude that the blurring in SE(2) of (34) has the structure of (35), because the blurring function f₃ in (11) can be decomposed into translation and rotation. See Appendix A for the details of the commutativity of the translational and rotational blurring functions.

The method for obtaining the Laguerre-Fourier expansion fitted to the discrete image function defined on a rectangular discrete grid appears in [28]. We first obtain the Hermite expansion fitted to the image function and then convert it to the Laguerre-Fourier expansion. More improved method for computing the Hermite expansion for discrete samples is also available in [27].

Using (22), (33) and the convolution theorem, we have

$${\widehat{\gamma }}_{m,n}(p)={\left(\widehat{\rho }(p)\widehat{f_3}(p)\right)}_{m,n}=4{\pi }^2{i}^n{\delta }_{m,0}\underset{k=\mid n\mid }{\overset{2[\frac{N-n}{2}]+n}{{\sum }^{\prime }}}{\stackrel{\sim }{\rho }}_{k,-n}{(-1)}^{\frac{k+n}{2}}{y}_{k,-n}(p)e^{-p^2{t}_1}{e}^{-n^2{t}_2}.$$ (36)

In addition, using (33) we can write the SE(2) Fourier transform of (35) directly as

$${\widehat{\gamma }}_{m,n}(p)=4{\pi }^2{i}^n{\delta }_{m,0}\underset{k=\mid n\mid }{\overset{2[\frac{N-n}{2}]+n}{{\sum }^{\prime }}}{\stackrel{\sim }{\gamma }}_{k,-n}{(-1)}^{\frac{k+n}{2}}{a}^2{y}_{k,-n}(ap).$$ (37)

Equating (36) and (37) gives

$$\underset{k=\mid n\mid }{\overset{2[\frac{N-n}{2}]+n}{{\sum }^{\prime }}}{\stackrel{\sim }{\rho }}_{k,-n}{(-1)}^{\frac{k}{2}}{y}_{k,n}(p)e^{-p^2{t}_1}{e}^{-n^2{t}_2}=\underset{k=\mid n\mid }{\overset{2[\frac{N-n}{2}]+n}{{\sum }^{\prime }}}{\stackrel{\sim }{\gamma }}_{k,-n}{(-1)}^{\frac{k}{2}}{a}^2{y}_{k,n}(ap)$$

because y_m,n = y_m,−n. Since this should hold for any choice of p with a fixed n, we have the following matrix factorization

$$\mathit{DYJ}\times r=a^2{Y}_{a}J\times g,$$

where D_k,l = δ_k,le^{−(p(k))2t₁}e^−n2t₂, $J_{k,l}={\delta }_{k,l}{(-1)}^{\frac{\mid n\mid }{2}+k-1}$,

$$\begin{array}{c}r={\left[\begin{array}{cccc}{\stackrel{\sim }{\rho }}_{\mid n\mid ,-n}& {\stackrel{\sim }{\rho }}_{\mid n\mid +2,-n}& \cdots & {\stackrel{\sim }{\rho }}_{2[\frac{N-n}{2}]+n,-n}\end{array}\right]}^T\\ g={\left[\begin{array}{cccc}{\stackrel{\sim }{\gamma }}_{\mid n\mid ,-n}& {\stackrel{\sim }{\gamma }}_{\mid n\mid +2,-n}& \cdots & {\stackrel{\sim }{\gamma }}_{2[\frac{N-n}{2}]+n,-n}\end{array}\right]}^T\\ Y=\left[\begin{array}{ccc}{y}_{\mid n\mid ,n}(p^{(1)})& y_{\mid n\mid +2,n}(p^{(1)})& ⋮\\ y_{\mid n\mid ,n}(p^{(2)})& \ddots & ⋮\\ \cdots & \cdots & y_{2[\frac{N-n}{2}]+n,n}(p^{(M)})\end{array}\right]\end{array}$$

and

$$Y_a=\left[\begin{array}{ccc}{y}_{\mid n\mid ,n}(a{p}^{(1)})& y_{\mid n\mid +2,n}(a{p}^{(1)})& ⋮\\ y_{\mid n\mid ,n}(a{p}^{(2)})& \ddots & ⋮\\ \cdots & \cdots & y_{2[\frac{N-n}{2}]+n,n}(a{p}^{(M)})\end{array}\right].$$

The goal is to compute r which is the Laguerre-Fourier coefficients of the underlying clear image. J⁻¹ = J and the pseudo-inverse of Y is given by Y ⁺ = (Y^TY)⁻¹Y^T if the sampling points, p’s are chosen appropriately as shown in [28]. This guarantees the stable inversion of Y. Since inverting D needs regularization, we compute

$$D_{k,l}^{+}={\delta }_{k,l}(1/(e^{-t_1{(p^{(k)})}^2}{e}^{-t_2{n}^2}+\epsilon )$$ (38)

with small ε. Now we have

$$r=a^{2}J{Y}^{+}{D}^{+}{Y}_{a}J\times g.$$

Note that this holds for a fixed value for n. Therefore, applying it for different n gives the full ρ̃_m,n that is the Laguerre-Fourier coefficients for the underlying clear image.

Theoretically the SE(2) deconvolution with the blurring function (11) can be achieved by consecutively applying the translational deconvolution and the rotational deconvolution, since the translational blurring and the rotational blurring can be separable in our case. However, actual implementation of deconvolution requires regularization and thus two regularization factors are engaged in the two consecutive deconvolutions. In contrast, the SE(2) deconvolution can be done with one regularization factor.

5 Examples

In this section, we first apply our deconvolution method to artificial noisy projection images to assess its effectiveness in the case when the underlying image is known. We then apply it to real experimental EM images. We use the deconvolution method derived in Section 4.3.

5.1 Tests with synthetic images

We generate artificial projection images and their class averages as follows. First we obtain a projection image of GroEL/ES (PDB code: 1AON) by assigning small three-dimensional Gaussian densities for all of the C_α atoms with standard deviation 2Å and then calculating a projection as shown in Fig. 1(a)¹ with the sampling rate = 1.76Å/pixel. Next, we add Gaussian noise over the image as shown in Fig. 1(b). By adding other noise samples taken from the same Gaussian distribution to the original test image, we generate many noisy images. Then for alignment, each image is translated, rotated and clipped by a circular window so that the resulting image has its mass center at the geometric center of the circular window and has a diagonal inertia matrix. The averaged image is shown in Fig. 1(c) which can be modeled as (2). Subtracting the mean intensity of the background noise from Fig. 1(c), we have Fig. 1(d) which can be seen as a convolution of the underlying clear image and the blurring function. Note that the original size of the images are 256 × 256 and they are cropped to 186 × 186 for better visualization as shown in Fig. 1.

Figure 1.

Test image preparation. (a) Clear projection of GroEL/ES (PDB code:1AON). This is a projection of small Gaussian functions (std=2Å) assigned at all C_α’s. (b) Addition of the Gaussian noise and (a). (c) Image obtained by aligning and averaging many noisy images clipped by a circular window. (d) Image obtained by subtracting the mean intensity of the background noise from (c).

Since the number of images in a class is finite, the background noise cannot be completely canceled, even though its intensity is effectively reduced by averaging. This residual noise may cause serious artifacts in the deconvolution process, because deconvolution magnifies the high frequency information. In order to reduce the residual noise, we can apply simple image processing techniques to the class-averaged images as follows.

If the variance of the additive Gaussian background noise in each EM image is σ², then the residual noise follows a normal distribution, $\mathcal{N}(0,\sigma /\sqrt{M})$, where M is the number of images in a class that are averaged. As proposed in [26], we assign zero to the pixels whose intensity is between ( $-s\sigma /\sqrt{M},s\sigma /\sqrt{M}$) where s is the scaling factor which is chosen to be s = 2.5. Using this processing, we can substantially remove the residual noise placed on the region unoccupied by the specimen.

In order to reduce the residual noise placed on the region where the specimen occupies, we use Wiener filters. If we observe an image y = x + n, where x is the true image and n is the additive noise, the Wiener filter, ŵ(ω), for noise reduction is defined as²

$$\widehat{w}(\mathit{\omega })=\frac{S_x(\mathit{\omega })}{S_x(\mathit{\omega })+S_n(\mathit{\omega })}$$ (39)

in the frequency domain, where ω ∈ ℝ² denotes the frequency, and S_x(ω) and S_n(ω) denote the power spectrums of the true image and the noise, respectively. Explicitly, the estimation of x is obtained by x̄ = w * y, where * denotes the convolution, or equivalently $\widehat{\overline{x}}=\widehat{w}\widehat{y}$, where $\widehat{(·)}$ denotes the 2D Fourier transform. Note that in this formulation, the noise, n, is the residual noise whose variance is σ²/M, where σ² is the variance of the additive background noise in each EM image and M is the number of images in a class that are averaged.

Theoretically S_n(ω) is the expectation of the power spectrum of the residual noise. If the noise is white Gaussian and spatially uncorrelated, then S_n(ω) is the variance of the noise regardless of the frequencies. However, if the residual noise is the average of correlated 2D noise, the expectation of the power spectrum of the residual noise is a function of frequency. For many sets of artificially generated 2D residual noise with the specific correlation and variance, the power spectrums of the residual noise are computed and averaged to estimate S_n(ω). The spatially correlated 2D noise can be obtained by a method that is explained in Appendix B.

Since we do not have the image, x, before applying the Wiener filter, we cannot directly compute S_x(ω). To estimate it, we first use the power spectrum of the observed image, y. Then we can compute a Wiener filter and obtain an estimate for the image, x. Using this restored image, we recompute S_x(ω). We repeat this iterative process until it converges.

Fig. 2 shows the test results using the artificial projection images shown in Fig. 1. Fig. 2(a) shows the class average that is obtained by aligning and averaging 500 noisy images. The noise is sampled from a normal distribution, 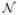(128, 16). Note that the mean of the noise is set at 128 which corresponds to the gray color shown in Fig. 1(c). This mean intensity is subtracted from the class average to produce the class average with the black background as shown in Fig. 2(a). Fig. 2(b) is denoised version of Fig. 2(a) using the Wiener filter. An iterative method is used for estimating the power spectrum of the denoised image and converges after two iterations. Fig. 2(c) shows the deconvolution result with the regularizing factor, ε = 0.2 for computing (38) and the bandlimit for the Hermite expansions, N = 210. This bandlimit is determined as described in Section 4.1 using the method developed in [28]. For the purpose of comparison with the deconvolution result, Fig. 2(d) shows the noise-free original projection which can be viewed as the perfect answer for the deconvolution. The tests are performed with the images whose size is 256 × 256 and they are cropped to 186×186 for better visualization in Fig. 2. In order to show the detailed features in the test results, Fig. 3 shows part of Fig. 2 after magnification. The Wiener filter reduces the residual noise (compare Fig. 3(a) and Fig. 3(b)), and the deconvolution process restores the high frequency information as shown in Fig. 3(c).

Figure 2.

An example of deblurring of a class average. (a) Class average. (b) Denoised class average by the Wiener filter. (c) Deblurred image. (d) Noise-free original projection image.

Figure 3.

Zoomed-in images of Fig. 2. (a) Class average. (b) Denoised class average by the Wiener filter. (c) Deblurred image. (d) Noise-free original projection image.

For more general tests, in Table 1 the standard deviation (SD) of the background Gaussian noise, the correlation of two adjacent noise samples are defined for four different cases. In addition, the signal-to-noise ratio that is the ratio of the variance of the signal to the variance of the noise is provided in Table 1. In all cases, the mean intensity of the noise is 128. In Table 2, the “Class average” row shows the normalized least squared errors (NLSEs) between the original projection image and the unmodified class average, and the ‘Deblurred image’ row shows the NLSEs between the original projection image and the deblurred class average which is the result of our deconvolution method. For the four cases with different numbers of test images that are averaged, the deblurred images consistently show smaller differences from the original projection image than the unmodified class averages.

Table 1.

Statistical parameters of the background noise and signal-to-noise ratios for four test cases.

	Case 1	Case 2	Case 3	Case 4
SD	16	16	32	32
Correlation	0	0.3	0	0.3
SNR	3.0625	3.0625	0.7656	0.7656

Table 2.

NLSEs between the class-averaged images/the deblurred images and the original projection image in the example of GroEL/ES.

Number of images		100	300	500
Case 1	Class average	0.0677	0.0517	0.0484
	Deblurred image	0.0447	0.0310	0.0295
Case 2	Class average	0.0952	0.0833	0.0849
	Deblurred image	0.0708	0.0533	0.0533
Case 3	Class average	0.1394	0.1115	0.1131
	Deblurred image	0.1019	0.0770	0.0775
Case 4	Class average	0.1935	0.1629	0.1615
	Deblurred image	0.1611	0.1291	0.1289

In addition to the NLSEs, Table 3 and 4 show the image differences measured in the Sobolev norm [25,40] and the relative entropy (Kullback-Leibler divergence) [1], respectively. Furthermore, in Table 5 we compute the cross correlation coefficients to measure the similarity between the original projection image and the test images (class average and debelurred class average). With the four measurement methods, the image differences are dropped and the image similarity is increased after the deblurring process is applied. The definition of the three measurement methods for the image difference appears in Appendix C.

Table 3.

Sobolev norms between the class-averaged images/the deblurred images and the original projection image in the example of GroEL/ES.

Number of images		100	300	500
Case 1	Class average	0.0046	0.0027	0.0023
	Deblurred image	0.0020	0.0010	0.0009
Case 2	Class average	0.0091	0.0069	0.0072
	Deblurred image	0.0050	0.0028	0.0028
Case 3	Class average	0.0194	0.0124	0.0128
	Deblurred image	0.0104	0.0059	0.0060
Case 4	Class average	0.0374	0.0265	0.0261
	Deblurred image	0.0259	0.0167	0.0166

Table 4.

Relative entropies (in thousands) between the class-averaged images/the deblurred images and the original projection image in the example of GroEL/ES.

Number of images		100	300	500
Case 1	Class average	2.0591	1.3392	1.0591
	Deblurred image	0.4943	0.5289	0.4668
Case 2	Class average	3.7560	2.7310	2.5515
	Deblurred image	1.9080	1.1564	0.9637
Case 3	Class average	7.1911	5.0762	4.9079
	Deblurred image	1.9191	2.3372	2.1738
Case 4	Class average	13.737	10.531	10.163
	Deblurred image	6.2620	5.7420	5.6620

Table 5.

Cross correlation coefficients between the class-averaged images/the deblurred images and the original projection image in the example of GroEL/ES.

Number of images		100	300	500
Case 1	Class average	0.9903	0.9938	0.9937
	Deblurred image	0.9948	0.9970	0.9970
Case 2	Class average	0.9812	0.9869	0.9871
	Deblurred image	0.9870	0.9916	0.9917
Case 3	Class average	0.9977	0.9987	0.9988
	Deblurred image	0.9990	0.9995	0.9996
Case 4	Class average	0.9955	0.9966	0.9965
	Deblurred image	0.9975	0.9986	0.9987

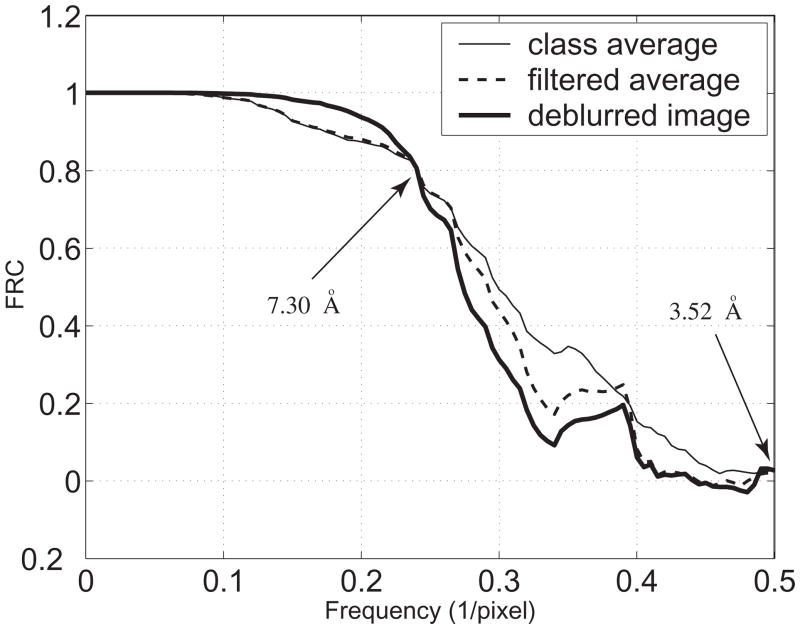
In order to assess image quality further, we compute the Fourier Ring Correlation (FRC). The FRC provides the normalized cross correlation coefficients over corresponding rings in Fourier domain [29,37]. The FRC for two images, ρ₁ and ρ₂, is defined as

$$\mathit{FRC}(r)=\frac{{\sum }_{{\mathbf{r}}_i\in r}\widehat{{\rho }_1}({\mathbf{r}}_i){\widehat{{\rho }_2}}^{\ast }({\mathbf{r}}_i)}{\sqrt{{\sum }_{{\mathbf{r}}_i\in r}\mid \widehat{{\rho }_1}({\mathbf{r}}_i){\mid }^2·{\sum }_{{\mathbf{r}}_i\in r}\mid \widehat{{\rho }_2}({\mathbf{r}}_i){\mid }^2}}$$

where ρ̂(r_i) is the complex structure factor at position r in Fourier space, and the * denotes complex conjugate. r_i is Fourier-space voxels that are contained in the ring with radius r.

Fig. 4 shows the FRC for the images from Fig. 2. The thin continuous curve is the FRC between the original reference image (Fig. 2(d)) and the class average (Fig. 2(a)). The dashed curve is the FRC between the original reference image and the Wiener-filtered class average (Fig. 2(b)). The thick continuous curve is the FRC between the original reference image and the deblurred image (Fig. 2(c)).

Figure 4.

The Fourier Ring Correlation with the images from Fig. 2.

As shown in Fig. 4, the Wiener filter acts as a low pass filter. The thick continuous curve indicates that the information at the frequency lower than 0.24 pixel⁻¹ is recovered after our deconvolution method is applied based on the sampling rate = 1.76 Å/pixel used to compute the 2D discrete projection image shown in Fig. 1(a). In order to avoid the unstable inversion in deconvolution induced by the high frequency noise, we applied the Wiener filter and used the regularization factor in deconvolution. This manipulation causes some loss of very high frequency information as seen in the FRC figure. However information at these frequencies is rarely included in single-particle analyses, and thus does not contribute to the 3D reconstruction in such cases. Furthermore, the metrics involving image differences (NLSE, Sobolev, and the relative entropy) and the image similarity (cross correlation coefficients) ensure that the deconvolution brings optimal information recovery over the resolution range of interest in spite of the information degradation in the higher frequency range.

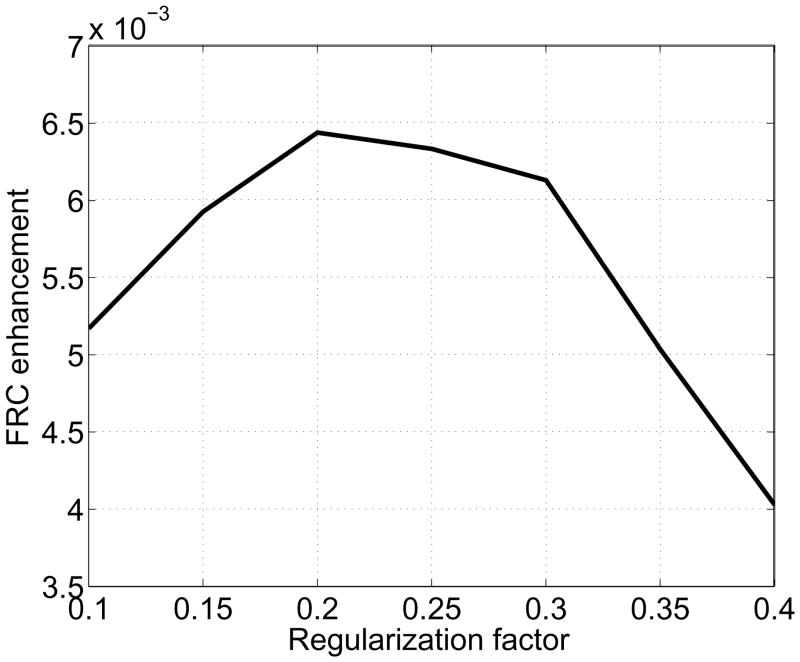
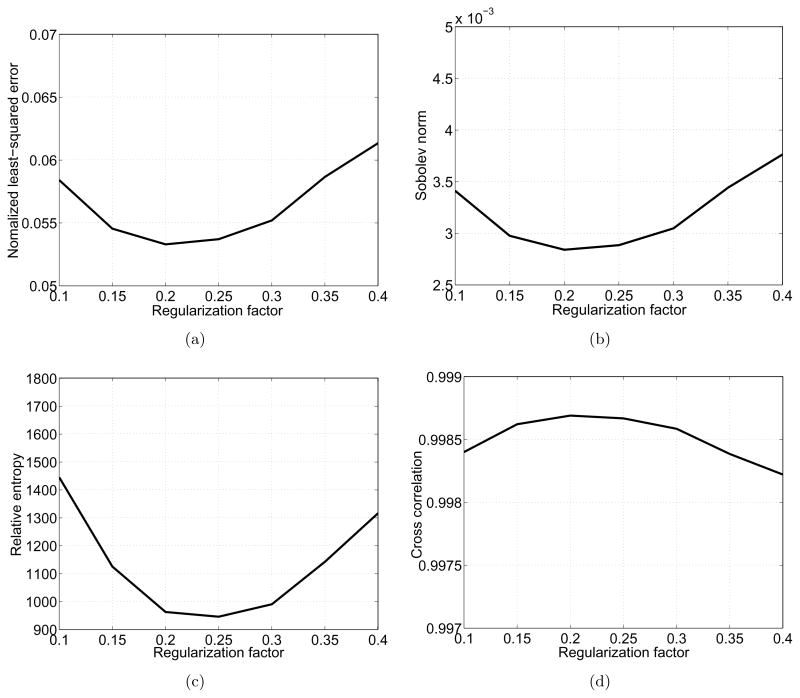
Using the FRC, we can quantify the image quality enhancement brought by the deconvolution. In Fig. 5, we compute the area enclosed by the thick and thin continuous curves at the frequency lower than the threshold 0.24 pixel⁻¹ (corresponding to 7.30 Å) and plot it as a function of the regularization factor, ε. The optimal value for ε that brings the maximum enhancement of image quality is 0.2. The four image comparison methods above also can be computed with various values for ε as shown in Fig. 6. All the graphs justify the choice of ε = 0.2, and show that the resulting images are not greatly sensitive to the regularization factor around 0.2.

Figure 5.

Image enhancement by deconvolution. The amount of enhancement is defined as the area enclosed by the curves at the frequency lower than the threshold 0.24(1/pixel) in Fig. 4.

Figure 6.

Image differences and similarity with various values for the regularization factor. (a) NLSEs, (b) Sobolev norms, (c) relative entropies, (d) cross correlation coefficients.

5.2 Tests with experimental data

We also report the test results using the experimental EM images of GluR. We use the same image data that we used in the previous work [26]. The preparation method of the specimen, the EM imaging process and postprocessing of the images are explained in Appendix D. Fig. 7 shows the test results for two class averages. The Wiener filter reduces the residual noise in the class averages and the deblurring method gives the improved representative images (Fig. 7(c) and 7(g)) for the classes compared to the blurry class averages (Fig. 7(b) and 7(f)). The tests are performed with the images whose size is 64 × 64 and they are cropped to 44 × 44 for better visualization in Fig. 7. In these examples, the bandlimit for the Hermite expansions is N = 50, which is determined by the method in [28] to capture the image information with stable computation of the Hermite coefficients. The number of class images for the two examples in Fig. 7 are 93 and 334, respectively.

Figure 7.

Class averages and their deblurring with GluR. (a) and (e) Two class averages after matching centers and principal axes. (b) and (f) Denoised version of (a) and (e) by the Wiener filter, respectively. (c) and (g) Deblurred images of (b) and (f), respectively. (d) and (h) Class averages obtained by EMAN.

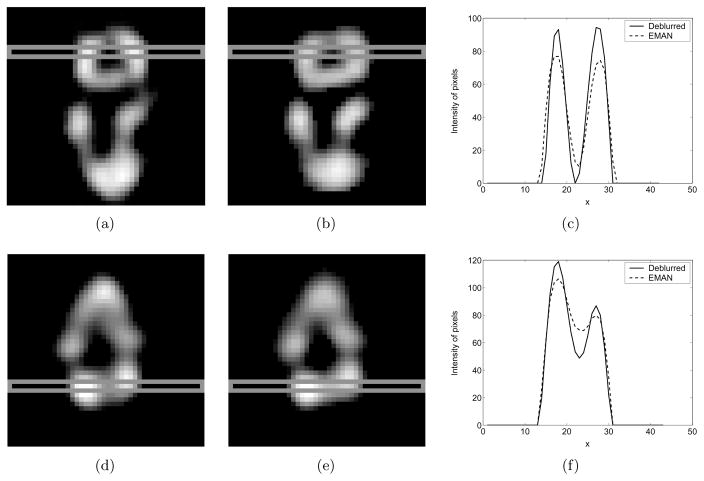
Unlike the case with the artificial projection images, there is no reference projection image that can be compared with the class averages computationally obtained using these experimental EM images. Therefore, it is hard to quantitatively compare the class averages obtained by our deconvolution method (Fig 7(c) and Fig 7(g)) and EMAN (Fig 7(d) and Fig 7(h)). However, we can observe qualitative improvement that our deconvolution method brings. In Fig. 8(a) and Fig. 8(b), intensities of pixels surrounded by thin gray boxes are taken from the class averages obtained by deconvolution and EMAN, respectively. The profiles of these pixel intensities in the slices are shown in Fig. 8(c). The class average obtained by our deconvolution method shows a sharper profile than the class average by EMAN. With the second example (Fig. 8(d) and Fig. 8(e)), we also observe a sharper profile in the class average obtained by our deconvolution method as shown in Fig. 8(f). Since EMAN is regarded as one of the well-established tools in the field, the improved sharpness provided by the deconvolution method developed in this paper is something that we will seek to integrate with the developers of the computational tools for single-particle EM such as EMAN, IMAGIC and SPIDER.

Figure 8.

Qualitative comparison between the class averages obtained by deconvolution and EMAN. (a) and (b) The pixel values in the slices surrounded by thin gray boxes are taken from the class averages obtained by deconvolution and EMAN, respectively. (c) The profiles for the pixel values from the slices. (d), (e) and (f) show the results for the second example.

We used a standard PC (Intel Core Duo processor 2.66GHz, 1GB memory) and Matlab programming. The computation times for deconvolution of 256 × 256 images in Fig. 2 and 64 × 64 images in Fig. 7 are 34.6(sec) and 1.5 (sec), respectively.

6 Conclusion

In this work, we developed a method to restore the 2D blurred images that are generated by translational and rotational misalignment during the class averaging process in single-particle electron microscopy. In our formulation, the blurring process is expressed as a convolution over SE(2) of an original clear image and a blurring function which can be estimated using the statistics of the background noise in electron micrographs. Since the convolution can be replaced with matrix multiplication in the Fourier space, the deconvolution (i.e., deblurring) is a simple inversion process in that space.

In order to easily estimate the blurring function, we used our alignment method whose advantage is that the statistics of the resulting alignment errors can be modeled simply. Using the statistics of the alignment errors, the deconvolution can be performed to obtain the deblurred class averages. If there is another alignment method that can be modeled as thoroughly as we have done for this simple method, in principle our deconvolution formulation can be applied on top. While the deconvolution in this paper is not strongly dependent on the alignment method, it does require that the blurring function be derivable from the alignment process. Ultimately, the quality of our final results relative to well-established approaches in the field justify the use of the alignment method that we chose.

Although the use of Fourier analysis (either commutative or noncommutative) possesses significant advantages associated with its behavior in convolution and deconvolution, its implementation requires a careful manipulation of the data due to the discrete nature of the image data and the continuous nature of the analysis. If the discrete Fourier transform is used, resampling of the image function on a finer grid is required and this requires interpolation. In addition, we need another resampling process in order to perform Fourier transform in SE(2), since in this case we require that the image function be re-expressed on polar coordinates.

To treat this, we proposed a method to implement the deconvolution in SE(2) using the Fourier transform and the Hermite and Laguerre-Fourier expansions. The interconversion between the Hermite and Laguerre-Fourier expansions is possible losslessly and it can be viewed as the coordinate interconversion between Cartesian and polar coordinates [28]. Therefore, once we have the Hermite expansion for an image, the corresponding expression on the polar coordinates, which is exactly the Laguerre-Fourier expansion, can be obtained easily. Since the two expansions retain their structure under the Fourier transform, the expansions enable the straightforward implementation of the deconvolution method. Consequently, once the 2D bandlimited Hermite expansion optimally fitted to the class average denoised by the Wiener filter is obtained, the deconvolution in SE(2) is achieved by the matrix inversion and multiplication.

We applied our method to the synthetic and experimental EM images to verify its performance. The deblurring method proposed here can be used as one of the important intermediate steps in single-particle electron microscopy. If the class averages are deblurred and then are used to update the 3D model in the iterative 3D reconstruction process, we can expect that we can reconstruct the 3D structure with higher accuracy in less time.

An ideal deblurring method would provide an optimal tradeoff between minimization of image blurriness and maximization of the Fourier ring correlation (FRC) over the frequency range of interest. In this paper our focus has been primarily on deblurring. In future work we plan to address methods with enhanced FRC performance using experimental data.

Appendix

A. Decomposition of the blurring kernel

Suppose that on a plane and on a circle, the Gaussian distribution densities are respectively given as

$$f_1(r,\phi )=\frac{1}{4\pi t_1}{e}^{-r^2/4t_1}\text{and}{f}_2(\theta )=\frac{1}{2\pi }\sum _{k=-\infty }^{\infty }{e}^{-k^2{t}_2}{e}^{ik\theta }.$$

Based on these function, we define the following functions on SE(2)

$$F_1(r,\phi ,\theta )=\frac{1}{4\pi t_1}{e}^{-r^2/4t_1}\delta (\theta )$$

and

$$F_2(r,\phi ,\theta )=\frac{1}{2\pi }\sum _{k=-\infty }^{\infty }{e}^{-k^2{t}_2}{e}^{ik\theta }\frac{\delta (r)}{2\pi r}\delta (\phi ).$$

We want to show that

$$(F_1\ast F_2)(g)=(F_2\ast F_1)(g)=f_1(g)f_2(g).$$

This allows us to decompose our blurring kernel into purely translational and purely rotational parts.

By definition, the two convolutions are written as

$$(F_1\ast F_2)(g)={\int }_{\text{SE}(2)}{F}_1(h)F_2(h^{-1}\circ g)dh$$

and

$$(F_2\ast F_1)(g)={\int }_{\text{SE}(2)}{F}_2(h)F_1(h^{-1}\circ g)dh.$$

By changing the variable k = h⁻¹ο g, we have

$$(F_1\ast F_2)(g)={\int }_{\text{SE}(2)}{F}_1(g\circ k^{-1})F_2(k)dk={\int }_{\text{SE}(2)}{F}_2(h)F_1(g\circ h^{-1})dh.$$

g and h can be parameterized as

$$g=g(r,\phi ,\theta )=\left(\begin{array}{ccc}cos\theta & -sin\theta & rcos\phi \\ sin\theta & cos\theta & rsin\phi \\ 0& 0& 1\end{array}\right)$$

and

$$h=h(R,\mathrm{\Phi },\mathrm{\Theta })=\left(\begin{array}{ccc}cos\mathrm{\Theta }& -sin\mathrm{\Theta }& Rcos\mathrm{\Phi }\\ sin\mathrm{\Theta }& cos\mathrm{\Theta }& Rsin\mathrm{\Phi }\\ 0& 0& 1\end{array}\right).$$

The multiplications are

$$h^{-1}\circ g=\left(\begin{array}{ccc}cos(\theta -\mathrm{\Theta })& -sin(\theta -\mathrm{\Theta })& rcos(\phi -\mathrm{\Theta })-Rcos(\mathrm{\Phi }-\mathrm{\Theta })\\ sin(\theta -\mathrm{\Theta })& cos(\theta -\mathrm{\Theta })& rsin(\phi -\mathrm{\Theta })-Rsin(\mathrm{\Phi }-\mathrm{\Theta }))\\ 0& 0& 1\end{array}\right)$$

and

$$g\circ h^{-1}=\left(\begin{array}{ccc}cos(\theta -\mathrm{\Theta })& -sin(\theta -\mathrm{\Theta })& rcos\phi -Rcos(\theta +\mathrm{\Phi }-\mathrm{\Theta })\\ sin(\theta -\mathrm{\Theta })& cos(\theta -\mathrm{\Theta })& rsin\phi -Rsin(\theta +\mathrm{\Phi }-\mathrm{\Theta })\\ 0& 0& 1\end{array}\right).$$

Therefore,

$$\begin{array}{c}(F_1\ast F_2)(g)=\int F_2(h)F_1(g\circ h^{-1})dh\\ ={\int }_{\text{SE}(2)}\left\{\frac{1}{2\pi }\sum _{k=-\infty }^{\infty }{e}^{-k^2{t}_2}{e}^{ik\mathrm{\Theta }}\frac{\delta (R)}{2\pi R}\delta (\mathrm{\Phi })\right\}\\ \times \left\{\frac{1}{4\pi t_1}{e}^{-(R^2+r^2-2\mathit{Rr}cos(\phi -\theta -\mathrm{\Phi }+\mathrm{\Theta }))/4t_1}\delta (\theta -\mathrm{\Theta })\right\}\mathit{RdRd}\mathrm{\Phi }d\mathrm{\Theta }.\end{array}$$

Integration over Θ gives

$$\begin{array}{c}=\int \left\{\frac{1}{2\pi }\sum _{k=-\infty }^{\infty }{e}^{-k^2{t}_2}{e}^{ik\theta }\frac{\delta (R)}{2\pi R}\delta (\mathrm{\Phi })\right\}\left\{\frac{1}{4\pi t_1}{e}^{-(R^2+r^2-2\mathit{Rr}cos(\phi -\mathrm{\Phi }))/4t_1}\right\}\mathit{RdRd}\mathrm{\Phi }\\ =\frac{1}{8{\pi }^2{t}_1}\sum _{k=-\infty }^{\infty }{e}^{-k^2{t}_2}{e}^{ik\theta }\int \left\{e^{-(R^2+r^2-2\mathit{Rr}cos(\phi -\mathrm{\Phi }))/4t_1}\frac{\delta (R)}{2\pi R}\delta (\mathrm{\Phi })\right\}\mathit{RdRd}\mathrm{\Phi }.\end{array}$$

Using the fact that the δ(R)=(2πR) is a special delta function on a polar coordinate at singularity (R = 0), we have

$$(F_1\ast F_2)(g)=\frac{1}{8{\pi }^2{t}_1}\sum _{k=-\infty }^{\infty }{e}^{-k^2{t}_2}{e}^{ik\theta }{e}^{-r^2/4t_1}.$$

Similarly, we compute

$$\begin{array}{c}(F_2\ast F_1)(g)=\int F_2(h)F_1(h^{-1}\circ g)dh\\ ={\int }_{\text{SE}(2)}\left\{\frac{1}{2\pi }\sum _{k=-\infty }^{\infty }{e}^{-k^2{t}_2}{e}^{ik\mathrm{\Theta }}\frac{\delta (R)}{2\pi R}\delta (\mathrm{\Phi })\right\}\\ \times \left\{\frac{1}{4\pi t_1}{e}^{-(R^2+r^2-2\mathit{Rr}cos(\phi -\mathrm{\Phi }))/4t_1}\delta (\theta -\mathrm{\Theta })\right\}\mathit{RdRd}\mathrm{\Phi }d\mathrm{\Theta }.\\ =\frac{1}{8{\pi }^2{t}_1}\sum _{k=-\infty }^{\infty }{e}^{-k^2{t}_2}{e}^{ik\theta }{e}^{-r^2/4t_1}.\end{array}$$

Therefore, we showed that

$$(F_1\ast F_2)(g)=(F_2\ast F_1)(g)=f_1(g)f_2(g)=\frac{1}{8{\pi }^2{t}_1}\sum _{k=-\infty }^{\infty }{e}^{-k^2{t}_2}{e}^{ik\theta }{e}^{-r^2/4t_1},$$

where

$$g=g(r,\phi ,\theta )=\left(\begin{array}{ccc}cos\theta & -sin\theta & rcos\phi \\ sin\theta & cos\theta & rsin\phi \\ 0& 0& 1\end{array}\right).$$

B. Generation of 2-D correlated noise

In this section, we generate the 2D correlated noise. The correlation between two adjacent noise samples is defined as ν. For N noise samples, each of which forms the Gaussian distribution, we can compute the N × N covariance matrix, Σ. This correlated noise samples can be generated by

$$\mathbf{y}=S\mathbf{x},$$

where y ∈ ℝ^N is N correlated samples, Σ = S² and x ∈ ℝ^N is N independent samplings from a Gaussian. If the size of N is large, it is not practical to compute S = Σ^1/2.

Alternatively, we generate the correlated noise as follows. It is natural to consider five independent random variables to define one pixel noise value, because one random variable contributes to generate one noise value and the other four adjacent noises. If each noise sample follows a normal distribution N(μ, σ) and the correlation between two adjacent noise samples is ν, then we can model the random variables at the position ‘1’ and ‘2’ in Fig. 9 as

Figure 9.

The pixel ‘1’ and ‘2’ are considered simultaneously. The correlation of two adjacent noise is ν.

$$P_1=\mu +\sigma (a{Z}_1+b{Z}_2+b{Z}_3+b{Z}_5+b{Z}_7)$$ (40)

$$P_2=\mu +\sigma (a{Z}_2+b{Z}_1+b{Z}_4+b{Z}_6+b{Z}_8)$$ (41)

where Z_i are independent random variables from a normal distribution N (0, 1).

Because the mean and variance of P₁ and P₂ are respectively μ and σ², we have a constraint, a² + 4b² = 1. Furthermore, since the covariance of P₁ and P₂ is νσ², we have another constraint as 2ab = ν. Using parametrization a = cos θ and 2b = sin θ, we simply have one solution to the constraints as

$$\begin{array}{c}\theta ={sin}^{-1}(2\nu )/2,\\ a=cos\theta \text{and}b=(sin\theta )/2.\end{array}$$

This method is also easy to implement. A 2D correlated noise can be generated by linear combination of five 2D uncorrelated Gaussian noise using (40).

C. Definition of measurement methods for image difference

The NLSE of the two images, R(m, n) and I(m, n), is defined as [16]

$$\text{NLSE}=\sqrt{\frac{{\sum }_{m=1}^N{\sum }_{n=1}^N{[R(m,n)-I(m,n)]}^2}{{\sum }_{m=1}^N{\sum }_{n=1}^N{[R(m,n)]}^2}}.$$

The Sobolev norm which is defined as [25,40]

$$\mathit{Sob}(f,g)={\left(\frac{1}{{(n(U))}^2}\sum _{u\in U}{(1+\mid {\eta }_u{\mid }^2)}^{\delta }\mid F(u)-G(u){\mid }^2\right)}^{1/2},$$

where f and g are image functions, and F and G are the discrete Fourier transforms of f and g, respectively. η_u is the two-dimensional frequency vector associated with u. U is the frequency domain which is a lattice of the same dimensions as the domain of the image functions. n(U) is the number of pixels of the lattice. We use δ = 1/2 in this paper. The Sobolev norm includes the difference between two images in terms of the derivatives.

Relative entropy (also known as Kullback-Leibler divergence) is an asymmetric measure of the discrepancy between two probability distributions [14]. It can also be used for measuring the difference between images. It is defined as [1]

$$D(p||\widehat{p})=\sum _{\mathbf{x}}p(\mathbf{x})log\frac{p(\mathbf{x})}{\widehat{p}(\mathbf{x})},$$

where p(x) and p̂(x) are two image functions. We let p̂(x) be the reference image and let p(x) be the test image.

D. Experimental EM images

In this section, we explain the process of obtaining experimental single-particle EM images of purified, recombinantly expressed amino-3-hydroxy-5-methyl-4-isoxazolepropionic acid (AMPA)-selective ionotropic glutamate receptor in negative stain [23]. These receptors were composed of four GluR2 subunits that contained a glutamine at the Q/R site (GluR2-Q). The intact receptor has a relative molar mass of approximately 400kDa and dimensions of 190Å × 115Å × 100Å [23]. Receptors were stained with 2% (w/v) uranyl acetate and visualized on Kodak SO-163 film under low-dose conditions (< 10e⁻/Ų) at a magnification of 48,600× on a JEOL JEM-1010 electron microscope in the Rippel EM Facility. Negatives with minimal drift/astigmatism were identified and digitized using a Nikon Coolscan 8000 at 4000dpi (effective pixel size, 1.31A). Particles were picked and processed using the EMAN package [17]. The individual images are 64×64 pixels with a pixel size of 5.24 Å. The images were high passed filtered at 250Å and low passed filtered at 10.5Å. The contrast transfer function of the microscope was corrected and the phase flipping was applied to the individual images as described in [23].