Differential hydrophobicity drives self-assembly in Huntington's disease

Abstract

Identifying the driving forces and the mechanism of association of huntingtin-exon1, a close marker for the progress of Huntington's disease, is an important prerequisite to finding potential drug targets and, ultimately, a cure. We introduce here a modeling framework based on a key analogy of the physicochemical properties of the exon1 fragment to block copolymers. We use a systematic mesoscale methodology, based on dissipative particle dynamics, which is capable of overcoming kinetic barriers, thus capturing the dynamics of significantly larger systems over longer times than considered before. Our results reveal that the relative hydrophobicity of the poly(glutamine) block as compared with the rest of the (proline-based) exon1 fragment, ignored to date, constitutes a major factor in the initiation of the self-assembly process. We find that the assembly is governed by both the concentration of exon1 and the length of the poly(glutamine) stretch, with a low-length threshold for association, even at the lowest volume fractions we considered. Moreover, this self-association occurs irrespective of whether the glutamine stretch is in random-coil or hairpin configuration, leading to spherical or cylindrical assemblies, respectively. We discuss the implications of these results for reinterpretation of existing research within this context, including that the routes toward aggregation of exon1 may be distinct from those of the widely studied homopolymeric poly(glutamine) peptides.

Neurodegenerative disorders are often linked with insoluble protein aggregates of fibrillar morphology, rich in β-structure content. In Huntington's disease, aggregates of N-terminal proteolytic fragments (exon1) of the protein huntingtin (1, 2) are found in the nuclei or the perinuclear cytoplasm of neurons (3, 4). Although a major thrust of research (5) is focused on the pathogenic role of huntingtin exon1 association, the underlying driving forces and mechanism of this process, which could ultimately provide a therapeutic approach toward overcoming Huntington's disease, remain to be established (6).

The age of onset of Huntington's disease is correlated with the expansion of the CAG trinucleotide repeat sequence that encodes for glutamine, with a pathogenic threshold of 34–41 consecutive glutamines [poly(Q)] (7). Because of this observation, previous research has predominantly focused on the propensity of long homopolymeric poly(Q)s to form hairpin or other β-sheet structures as a prerequisite and driving force for the formation of insoluble fibrillar aggregates (8). Perutz's influential proposal (7), that hydrogen bonding between the main chain and side-chain amides could lead to stabilized polar zipper structures only for poly(Q) lengths exceeding the threshold, shares among current models the emphasis on the length-dependent random coil to β-sheet structure transition of the single poly(Q) peptide chain.

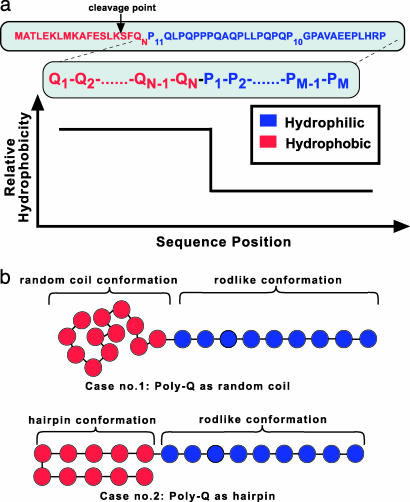
However, recent experiments have demonstrated instead that poly(Q) in solution is in a stable random-coil conformation irrespective of its length (9). Further studies have corroborated this finding for exon1 fragments over a broad length range of the poly(Q) stretch (10–13). Above a concentration threshold, exon1 aggregates form in vitro in a concentration-dependent process (14) and only after prolonged existence as prefibrillar globular-type suspensions. Given that the poly(Q) component at the pathogenic threshold forms less than half of the peptide fragment (see Fig. 1), it is surprising that only recently have biophysical studies addressed the aggregation properties of entire exon1 fragments.

Fig. 1.

(a) The huntingtin exon1 fragment is analogous to an amphipathic block copolymer, where homopolymeric blocks are covalently linked in series. The hydrophobicity profile of the exon1 fragment containing a poly(Q) stretch (hydrophobic block, in red) and a poly(proline) stretch (more hydrophilic block, in blue) is sketched at the top of the figure. It provides a driving force for the spontaneous formation of self-assembled clusters. Note that, experimentally, the exon1 fragment is cleaved by the proteolytic enzyme trypsin at the point indicated in the figure. Exon1 fragment hence refers to the sequence on the right of the arrow (10). (b) In the DPD simulations, the poly(proline) was modeled as a “rod” due to its high persistence length, whereas the poly(Q) stretch was modeled in the two most prominent conformations, as a random coil or as a hairpin. Each bead corresponds to approximately three residues. Simulations were run for N_Q = 9, 18, 27, 36, and 60 residues and for volume fractions 2.5%, 5%, 10%, 15%, 20%, and 40% in water, modeled explicitly, for poly(Q) in both random-coil and rod-like conformations.

The exon1 fragment sequence consists of a block of glutamines followed by a stretch of mainly proline residues, an arrangement that remarkably resembles diblock copolymers, where two homopolymeric blocks are covalently linked (Fig. 1). This key realization, particularly because proline is chemically very dissimilar to glutamine in water, coupled with the experimental findings above, leads us to draw an analogy to this class of systems. It is well known that block copolymers in solution will spontaneously self-assemble into complex mesoscopic morphologies (15). Their shape (16), size (17), stability and dynamical behavior (18), and possible geometrical transformations (19) intricately depend on several factors (15–19) whose relative contributions are still unfolding. These factors are (i) the effective interaction between monomers of each block, (ii) each block's affinity for the solvent, (iii) the length of each block, and (iv) their relative volume fraction (where conformation plays a role). A key implication for our system is that in a selective solvent (i.e., solvent that interacts differently with each block), spontaneous self-assembly into spherical or cylindrical structures is expected in dilute solutions, with the more hydrophobic part forming a core and the more hydrophilic part forming an outside corona. The critical condition for occurrence of this directed self-assembly depends on the concentration and the length of each block. To date, little attention has been paid to the implications of the block structure of exon1 and the difference in hydrophobicity of glutamine and proline residues as a driving force for the initiation of exon1 association. This connection is the focus of this article.

To explore the mechanism of self-association of the exon1 fragment theoretically as a function of concentration and chain length, it is crucial that the method can treat a large number of chains over long timescales without getting trapped in kinetic barriers. The solvent has both to be explicitly taken into account and also to exhibit the correct hydrodynamic behavior. This makes simulations extremely challenging: all-atom, or even coarse-grained molecular dynamics are prohibitive; Monte Carlo are less insightful and still difficult to equilibrate (20); and Brownian dynamics have also been shown to get trapped in metastable configurations (21). To overcome these limitations, we have used a recent off-lattice particle-based methodology, dissipative particle dynamics (DPD) (22), which has been shown to correctly lead to mesoscale structures in block copolymer melts (23) and cell membranes (24, 25). This is, to our knowledge, the first application of this method to peptides in solution. Simulations in this work are based on effective particles (beads) at the residue level. The solvent is explicitly modeled and preserves hydrodynamics. The relevant interactions are obtained through a systematic procedure based on a map to Flory– Huggins theory (26). As a result, the DPD method enables us to study the dynamics of systems at least 3 orders of magnitude bigger than previous protein-aggregation studies (27).

Equipped with these tools, our simulations reveal that spontaneous association of the diblock exon1 fragments occurs when the length of the poly(Q) segment, N_Q, is as low as 18 at volume fractions as low as 2.5%. Assemblies readily form irrespective of whether the poly(Q) segment is initially in a random-coil or hairpin configuration (Fig. 1b), with the assemblies being sphere- or cylinder-like, respectively, without any a priori assumption on shape. This self-assembly occurs without any explicit attractive interactions in the model. The implication is not only that β-structure is not a necessary condition for association, but also that this initial assembly route toward the insoluble fibrils may not be available to the poly(Q)-only peptides.

Methodology: DPD Fundamentals

The DPD method was originally proposed (22) to describe the hydrodynamics of atomic fluids. The effective radial forces acting on the unit particles, or “beads,” are pairwise additive and short-ranged and have no hard core. All forces are zero beyond a cutoff distance, R_c, which defines the only lengthscale in the system, and hence the size of the beads for a given bead-number density ρ. Taking the bead mass, m, as the unit of mass, the unit of time, τ, is then given by 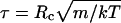. The total force on each bead, i, is given by a conservative, dissipative, and random component 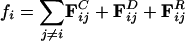, where the sum runs over all beads, j, within radial distance, R_c. The forces act along the bead centers and conserve linear and angular momentum. The dissipative forces arise from the lost internal degrees of freedom of the bead and are linear in relative velocity, whereas the random forces arise from their coupling to the environment. Subsequently, it has been shown that, if the magnitudes of the dissipative F^D = –γω^D (r̂_ij·v_ij)r̂_ij and random 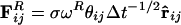components satisfy the fluctuation–dissipation theorem, the simulation obeys the canonical distribution and a constant temperature can be maintained (28). According to Groot and Warren (26), the arbitrary weight functions, ω^D and ω^R, are ω^D(r) = [ω^R(r)]² = (1 – r)² for r < R_c and 0 for r ≥ R_c. The noise amplitude (σ) and drag constant (γ) are related by σ² = 2γk_BT. r_ij is the distance between the centers of beads i and j, v_ij is their relative velocity, and r̂_ij the unit vector joining their centers. θ_ij(t) is a randomly fluctuating variable with Gaussian statistics. The conservative part of the force can encode physicochemical properties to the beads and is given by 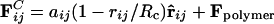for r_ij < R_c and 0 otherwise, where a_ij, the maximum repulsion between beads i and j, is obtained through an involved but systematic procedure (24, 26), and F_polymer describes the appropriate spring forces that create polymers from beads (26).

Modeling

Map for Coarse-Graining the Conservative Force. Although the detail of interatomic interactions is lost and indeed meaningless at lengthscales smaller than the bead size, beads still retain physicochemical properties through the magnitude of the repulsive conservative force parameters, a_ij, which have two components, a_ij = a + [Δa]_ij. For a given bead size (and, hence, bead density, ρ), the magnitude of the repulsion parameter, a, common to all beads, can be derived from the equation of state of the system to match the compressibility of the solvent (26), because we are in the dilute solution regime. In our system, using this approach self-consistently, we obtained a repulsion parameter a = 239 for density ρ = 5 and, hence, a bead size of 450 ų, which corresponds to ≈3 residues. This result is further justified when considering the conformations of each of the blocks (see Conformations). To model mixtures, the excess repulsion parameters for the interactions of unlike beads [Δa]_ij are obtained through a procedure (24, 26) by analogy to and in quantitative agreement with Flory–Huggins solution theory of immiscible polymers. The free energy of mixing within this theory is given in terms of the phenomenological parameter, χ, which accounts for the interactions between species (29). According to refs. 24 and 26, a relationship between χ and excess repulsion can be obtained, which for our system was found to be χ = 0.63 Δa. We note that this procedure remains valid only within the range where mean field is expected to hold or homogeneous mixing can be numerically achieved. This mapping opens the way to further exploration of relating microscopic information to mesoscopic lengthscales.

Quantifying χ. A distinct value of χ is required to model each pair of interactions in our system within Flory–Huggins theory, shown also to be applicable in biomolecular systems (30). Although χ can be measured by light-scattering or partition experiments, we could not identify such experiments in the literature either for poly(proline) or for poly(Q) in an aqueous solution. The relevance of these measurements motivates this experimental work. Deriving χ values from microscopic considerations for realistic systems is not established at present and is outside the scope of this work. We extracted the glutamine–proline interaction, χ_Q-P =–0.52, from the effective interresidue contact energies, which were obtained from averaging over crystal structures in protein banks with solvent molecules filling the voids (31). For the glutamine–water and proline–water interactions, we decided to focus on χ_Q-W = 2.26 and χ_P-W = 0.39 parameters as most suitable to reflect not only the enthalpic interactions (32) but also the capability of each monomer for hydrogen bonding with water and its packing and conformation (33). Taking only enthalpic considerations into account can lead to χ values that would imply that glutamine is considerably more hydrophilic than proline, whereas the solubility of each amino acid in water (154.5 g of proline per 100 g of water; 3.6 g of glutamine per 100 g of water), as an indicator of hydrophilicity, supports the opposite view. We have nevertheless explored an extensive series of other parameter combinations (see Results) and found that our conclusions do not depend qualitatively on the absolute magnitudes of these parameters but mainly on their relative differences.

Conformations. The glutamine–water interactions described above underscore the importance of polymer conformation and its behavior distinct from the monomer.

It is experimentally known that poly(proline) in aqueous solution adopts a relatively rigid α-helical structure with three residues per turn, stabilized by a hydrogen bond between every fourth residue (34). This conformation, consistent with the restrictive motion of the pentagon loop, exhibits a persistence length of 220 Å (or 70 residues) which is an order of magnitude higher than other homopolypeptides (typically 10–30 Å) (35). Thus, poly(proline) behaves as a rigid rod, which is the shape we adopt here. The interdispersed residues between prolines in the exon1 poly(proline) fragment that we have ignored would make the chain semiflexible at most and leave our conclusions and qualitative results unaffected (17). The rod-like helical conformation of the poly(proline) block was modeled by introducing an angle potential between consecutive proline beads.

The conformation of poly(Q) is still the subject of much debate in the literature. We use as the starting point the recent experimental evidence that the structure of poly(Q) in monomeric form is random coil (13). We also consider preformed hairpin conformations as a contrast to examine the effects of conformational variation on the mechanism and kinetics of aggregation. All conformations are modeled through an additional force component, F_polymer, to the conservative force. Individual beads are joined into a polymer chain by springs through the potential, U_spring(i, j) = (1/2)k_spring(r_ij – r_eq)², where the subscripts i and j indicate connectivity in the chain {j = i + 1 for linear chains or j = [i + 1, N_Q – (i – 1)] for hairpins}. The equilibrium bond distance, r_eq = 0.7, and bond force constant, k_spring = 40.0, are chosen such that the mean distance between connected beads equals the maximum of the pair correlation function of an equivalent system of unconnected beads (26). Angular harmonic potentials have been additionally used to model rod-like conformations for the poly(proline) block, with an equilibrium bond angle θ_eq = π and an angle force constant, k_angle = 20.

Results

We performed simulations of exon1 fragments in concentrations ranging from 2.5% to 40% (2.5%, 5%, 10%, 15%, 20%, and 40%) volume fraction in explicit water and for poly(Q) segments covering the whole range of healthy to very pathogenic lengths, from 9 to 60 residues (N_Q = 9, 18, 27, 36, and 60 residues). The proline blocks were in a rod-like conformation, whereas the glutamine blocks were modeled as both random coils and β-sheet hairpins.

Simulations were carried out in two different box sizes, 20 × 10 × 22 and 20 × 20 × 22. Periodic boundary conditions were used and in each case the bead-number density ρ was set to five beads per unit volume. Because each bead represents ≈3 residues or 15 water molecules, the DPD unit volume is equivalent to 2,250 ų and the unit length corresponds to 13.1 Å. Each polymer contained nine proline beads and, for each of the different lengths of glutamine repeats, 3–20 beads accordingly. For each length, we considered all volume fractions within the reported range. The box size was chosen to minimize finite-size effects. All simulations were at constant temperature, T = 300 K.

To safeguard against biased clustering, the chains were always singly dispersed in solution at random positions with random initial (coil) configurations. Each run included at least 1 × 10⁵ steps, with a maximum of 2 × 10⁵. Because of the nature of the soft potentials in the DPD, correlations are lost faster than in other methodologies. In our calculations, we have averaged over configurations separated by 1,000 time steps and typically only after excluding the first 80,000 steps. The leap-frog algorithm was used to propagate Newton's equations of motion, thereby maintaining time reversibility (36), and a time step of 0.02, checked for consistency within the stochastic differential equation, was used to maintain equilibrium within an 1% temperature range from approximately time step 1,000 onward.

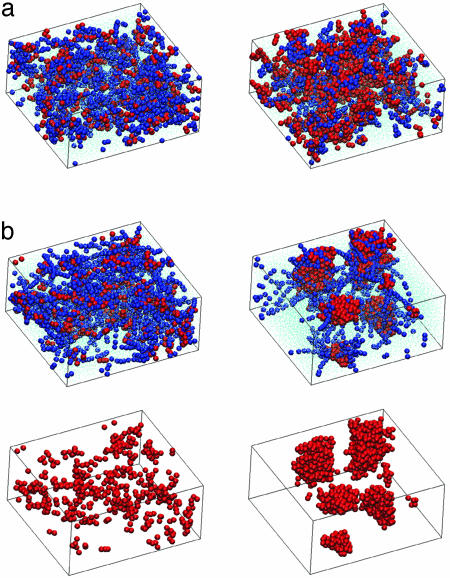
We have distilled the conclusions from our numerics in Figs. 2, 3, 4 and present the most representative rather than exhaustive results. Our results show that, at the concentrations considered, the poly(Q) length onset for assembly is very low. Only for N_Q = 9 did we observe chains remaining as monomers within the simulation time (Fig. 2a), in sharp contrast to all other cases where assemblies readily formed regardless of whether poly(Q) was in a coil or hairpin initial conformation. A representative example where self-assembly occurs is shown in Fig. 2 for N_Q = 36. The core of the assemblies is mainly formed by glutamine residues, with low-water content and the proline blocks sticking out toward the water (in all figures prolines are blue, glutamines are red). We consistently observed, for all lengths above the threshold, that random-coil poly(Q) segments formed sphere-like structures, whereas hairpins led to cylindrical-like shapes. In both cases, assemblies did not fuse at low concentrations and chains did not readily leave the assemblies due to their high hydrophobicity. For the highest packing volume of 40% we observed the fusing of these assemblies.

Fig. 2.

Threshold for self-assembly is low and depends on concentration and length. Snapshots at time steps 1 (a) and 1 × 10⁵ (b) for peptides with 9 (Left) and 36 (Right) glutamine residues at 10% concentration with the poly(Q) block modeled as a random coil. Glutamine beads are in red, proline beads are in blue, and water beads are represented as points; 22,000 beads were used for 1 × 10⁵ time steps. The snapshots of b are repeated without proline and water beads for clarity. No aggregation is obtained for N_Q = 9, but for N_Q = 36 several globular clusters are formed with the glutamine beads forming the inner core and the rod-like proline blocks sticking out. The proline blocks remain surrounded by water throughout the simulation, demonstrating little propensity to separate from water through clustering. Similar self-assembled structures are readily formed in all considered systems with glutamine stretches, N_Q = 18 and higher, for all volume fractions from as low as 2.5%. Note that initial configurations are always randomly chosen for dispersed chains in solution to avoid biased clustering. The methodology contains no explicit attractive interactions. Self-assembly is hence an outcome and not an input in the simulations. The procedures for deriving bead sizes and parameter interactions are outlined in the text. Here, we have used in DPD units: a = 239, a_pw = 239.61, a_gw = 242.59, a_pg = 238.17, σ = 3, γ = 4.5, T = 1, time step size = 0.02, ρ = 5, in-box dimensions = 20 × 10 × 22.

Fig. 3.

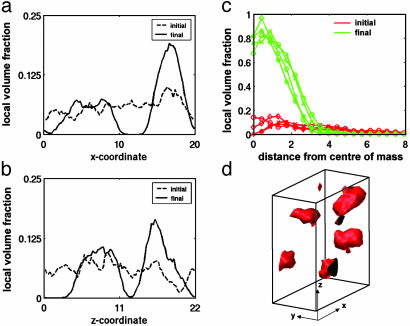
Assembly of exon1 fragments with poly(Q) stretches in random-coil conformation. The typical self-assembled formations for poly(Q)s of any length above the threshold are globular with the glutamine beads dominating the core of the globules as shown by the isosurface plots (d). Proline beads distributed around the Q core and water beads are not included in the plots for clarity. The figure corresponds to poly(Q) length N_Q = 36 at 10% volume fraction. Comparing pre- and postequilibration averaged density profiles in the x (a) and z (b) directions shows the transition from a relatively uniform density distribution to an inhomogeneous distribution exhibiting significant local-concentration fluctuations. The postequilibrium volume fraction (c) approaches 1.0 at the core of each of the clusters, demonstrating the relative-hydrophobicity-driven formation of the clusters.

Fig. 4.

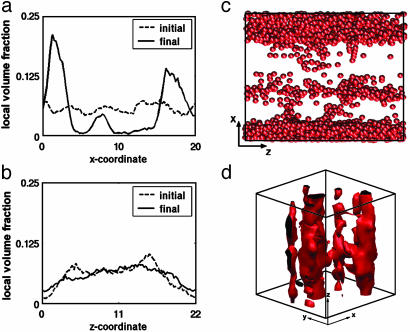
Assembly of exon1 fragments with poly(Q) stretches in hairpin conformation. In contrast to Fig. 3, typical structures of poly(Q) with preformed hairpins are rod-like (c). The postequilibrium density profiles (a and b) highlight the anisotropy of the structures in contrast with those in Fig. 3. The isosurface plot (d) (which has been translated 12 R_c along the x axis for visualization purposes) shows that the rod-like clusters are in fact interconnected, forming a single aggregate. Data shown are for same the poly(Q) length and volume fraction as in Fig. 3.

Although visually apparent, we quantified the formation and shape progression of the clusters by calculating averages of a radial-density distribution and a density profile along each of the three axes for the glutamine beads. Because the poly(proline) blocks do not form part of the core and their radial positions are largely determined by the last glutamine residue, they do not contribute additional information in describing the shape of these clusters. By using the final configuration of the simulation, and a specified bead center-to-center cutoff distance of 1.5, assemblies were defined according to standard procedure (37). Plots from the random-coil simulations of glutamine-bead density against radial distance from the center of mass of the assemblies were then produced by averaging over equilibrated time steps for each of the four assemblies formed for N_Q = 36 at 10% volume faction (Fig. 3c, in green). The beads are clustered around the centers of mass of the assemblies with local volume fraction approaching 1 at the core of the assemblies, demonstrating that little interpenetration of either proline or water beads occurs at the centers of the assemblies. In contrast to the initial positions of the chains (in red), the peaks clearly show the spherical symmetry of the formed assemblies. Equivalent results are obtained for all structures formed from randomcoil poly(Q)s.

Density profiles and isosurfaces were used to compare the structure of the assemblies formed when the glutamine blocks adopt random coil (Fig. 3 a, b, and d) and hairpin conformations (Fig. 4 a, b, and d). Assemblies appear as peaks in the density profiles along the x (Fig. 3a) and z axes (Fig. 3b) for the system shown also as an isosurface plot in Fig. 3d. The four assemblies are highlighted by the two peaks along both axes. By contrast, three elongated assemblies are formed in the hairpin simulation (Fig. 4c). The density profile on the x axis shows three clear peaks but the density does not reach zero between the peaks. The anisotropic shape of the assemblies is highlighted by the difference in the density profiles along x and z axes (Fig. 4 a and b). When the data are plotted as an isosurface (Fig. 4d), it appears that the elongated assemblies are in fact interconnected. These results hold for all formed assemblies from hairpin-containing exon1 fragments we considered.

The results we obtained were qualitatively robust for a broad series of additional parameter variations. We checked that the rod-like conformation of proline was a good approximation. We found clusters with inner cores of similar size and densities when the angle potential U_angle between proline beads was removed. The proline–glutamine strength interaction had a substantial effect only for packing of >40% volume, far from biological relevance. A similar effect was observed for the interaction strengths for poly(Q) and poly(proline) with water. We checked this through exploring diverse interaction variations from χ_GW = –0.34 to 2.26 and from χ_PW = 0.39 to 2.42. Finally, even when we exchanged the hydrophobicity of the segments, the principles remained the same but the structures changed, namely the rigid structure of the prolines formed the core, which led to cylindrical structures in both the random-coil and hairpin poly(Q).

Discussion

Although a wealth of information concerning the pathology and physiology of Huntington's disease exists, the underlying forces and mechanisms that govern the aggregation of the exon1 fragment of huntingtin remain unclear. The similarity of exon1, composed primarily by a poly(Q) block followed by proline-rich segments, to diblock copolymers, coupled with the well established fact that block copolymers will spontaneously self-assemble into complex mesoscopic morphologies in selective solvent, motivated us to apply a mesoscale methodology capable of capturing the dynamics of exon1 fragments. This approach of using DPD for simulating protein aggregation established that (i) the different hydrophobicities of the glutamine versus the nonglutamine segments are a major factor in the initiation of the assembly process; (ii) β-structure is not necessary for assembly to occur, although the processes of association for random coils and hairpins are distinct; and (iii) the onset for this spontaneous association is governed by both the concentration and the length of the poly(Q) stretch in the exon1 fragment.

The significance of differential or relative hydrophobicity for the initiation of assembly is that the physicochemical behavior of the exon1 fragment does not only depend on the poly(Q) properties, but also on the rest of the fragment. The difference in solvent affinity between the two blocks and its effect on the behavior of the exon1 fragments in solution has important implications for the interpretations of existing and future experimental work, because investigations on exon1 fragments should show differences from that of pure poly(Q) peptides. Although the latter exclude the relative hydrophobicity properties by default, our framework may unify the various models presently discussed in the research community (5). For instance, our findings are in agreement with recent studies focusing on solubilizing the normally insoluble poly(Q) blocks by attaching soluble peptides or proteins, which reveal similar poly(Q) length thresholds for the aggregation (3, 13, 14), and provide a microscopic explanation for the enhanced solubility. The notion of amphiphilicity-driven assembly of peptides has been put forward as an important concept for amyloid and PrP peptides, implicated in Alzheimer's disease and prion disease, respectively (38). Our findings underscore this reasoning.

Quantifying the relative hydrophobicities of poly(Q) and poly(proline), the major amino acids present in the exon1 fragment is challenging. A χ value that reflects the hydrophobicity of the two blocks more accurately would also enhance the quantitative accuracy of our results. However, it is now recognized that χ, which is a measure of solvent–solute interaction, includes entropic and enthalpic effects, and that it is composition-, pressure-, and temperature-dependent (32). Because the effective χ_eff varies as a function of conformation, it is clear that as a poly(Q) segment transforms from a random coil to elongated β-sheet during the aggregation process, its packing characteristics will vary and χ_eff will therefore deviate from its apparent value in the globular state (33). Hence, it appears that for poly(Q) in aqueous solution χ_eff is a dynamically evolving parameter. Additionally, hydrogen bonding modulates all these effects. Not only does the change from random-coil to a more elongated β-sheet conformation tend to increase χ_eff, but the reduction in available donor/acceptor sites for hydrogen bonding increases its value as well. This increase happens in a composition-dependent manner and may have the effect of stabilizing an aggregate further with increasing size. Thus, the hydrophobic character of poly(Q) stretches may be stronger with increasing intra- and intermolecular hydrogen bonding (38).

The second major finding of this work is that assembly is possible irrespective of whether the poly(Q) component is initially in random-coil or hairpin configuration. The implication is that work focused on single-chain properties of poly(Q)s may not be sufficient to describe all possible aggregation mechanisms of the disease. Although these investigations play an important role in characterizing the initial monomer behavior, the ensuing models allow only for the hairpin formation (or equivalent intramolecular conformational changes to β-sheet-containing structures) as a prerequisite for aggregation and neglect the role played by relative hydrophobicity in driving self-assembly. This difference is especially important because, above the critical condition for assembly, the timescale for the formation of the self-assembled clusters may be much faster than any β-sheet structure formation within a single chain. Which of the two (or both) will occur depends on the timescale of such structured formations of the single-chain exon1 fragments (which may itself depended on length). Recent experimental evidence suggests that the timescale for formation of the assemblies is in fact faster than that for the formation of β-content structures (14). From a theoretical point of view, the emerging picture is that, although the kinetics of random coils and hairpins are very distinct, the intermolecular and intramolecular degrees of freedom governing the thermodynamics and the kinetics of the system are coupled in nontrivial ways. For example, as the level of intra- and intermolecular hydrogen bonding increases, this increase may in turn increase the hydrophobicity of the aggregates by lowering the number of hydrogen bond donor/acceptor groups available to interact with the surrounding water molecules. This increased hydrophobicity makes further inter- and intramolecular hydrogen bonding more favorable because of the reduced local concentration of water molecules, resulting in a positive feedback loop driving the system toward complete phase separation.

Another important outcome derived from our simulations concerns the onset for the spontaneous assembly. Applying our framework revealed that this process is favored for poly(Q) component lengths in the fragment as low as 18, and possibly shorter, which is indeed what investigators have observed, thus additionally validating our approach. Dynamic light scattering and NMR monitoring of the aggregation of peptides with glutamine stretches as low as 20 and 22 revealed that aggregation is possible for such short poly(Q) segments (10, 13). It is also worth pointing out that our coarse-grained model contains no explicit attractive interactions among beads, so self-association is not an input but an outcome of the simulation. However, the lengths of the poly(Q) are to be taken with caution, partly because beads represent three residues, which results in an uncertainty of at least 3 Qs.

Finally, it is important to distinguish between the initial structures observed in our simulations, which may be stable or metastable, and the final precipitated or phase-separated fibrils. Further steps toward the precipitates may include conformational changes within the core of the formed clusters, where the possibility of glutamine-based hydrogen bonding increases, and/or fusion between clusters. In either case, hydrogen bonding within and between glutamine stretches inside the cores must play an important role and may eventually lead to Perutz's polar zippers and nanotube final fibrillar structures. Structural changes can now be interpreted within the context of preformed clusters and monitored initially within the solution. β-Sheet content formation should not just be thought of as occurring only in single chains, but also within many-chain clusters in solutions. Indeed, these soluble globular structures may have been inadvertently seen in the experiments of Scherzinger et al. (10). Recently work of Ross and coworkers (14) also emphasized the solubility of globular clusters. Using Fourier transform IR spectroscopy, they detected the appearance of progressively increasing secondary structures shortly after the formation of the globular oligomers. Crucially, however, a large increase in the band coincided with the appearance of fibers. This finding strongly supports the concept of oligomeric intermediates with limited hydrogen bonding acting as intermediate structures in the pathway to fibers with highly optimized hydrogen bonding networks or β-sheets.

In all the issues raised in Discussion, the length of the poly(Q) stretch plays a role because, as the more hydrophobic part of the exon1 fragment that readily forms the compact core of the clusters, it, rather then the hydrophilic block, mainly modulates all thermodynamic and kinetic interactions (39). Properties therefore become length-dependent in a progressive, rather in a switch-like manner. In conclusion, the finding that a contrasting hydrophobicity in stretches of amino acids initially induces spontaneous self-assembly should facilitate future research into extracting the complete aggregation pathways in Huntington's disease and other poly(Q)-related diseases (11).