Simulation of the folding equilibrium of α-helical peptides: A comparison of the generalized Born approximation with explicit solvent

Abstract

We compare simulations using the generalized Born/surface area (GB/SA) implicit solvent model with simulations using explicit solvent (transferable intermolecular potential 3 point, TIP3P) to test the GB/SA algorithm. We use the replica exchange molecular dynamics method to sample the conformational phase space of two α-helical peptides, A₂₁ and the F_s, by using two different classical potentials and both water models. We find that when using GB/SA: (i) A₂₁ is predicted to be more helical than the F_s peptide at all temperatures; (ii) the native structure of the F_s peptide is predicted to be a helical bundle instead of a single helix; and (iii) the persistence length and most probable end-to-end distance are too large in the unfolded state when compared against the explicit solvent simulations. We find that the potential of mean force in the ϕψ plane is markedly different in the two solvents, making the two simulated peptides respond differently when the backbone torsions are perturbed. A fit of the temperature melting curves obtained in these simulations to a Lifson–Roig model finds that the GB/SA model has an unphysically large nucleation parameter, whereas the explicit solvent model produces values similar to experiment.

Classical molecular dynamics (MD) is limited by the amount of real time that can be simulated with current methods and computers. Most of that time is usually spent computing the interactions among water atoms. This fact has provided a strong impetus to replace the explicitly represented water in simulations with implicit solvent. Implicit solvent models are continuum models that attempt to capture the average effect of the water on a solute.

The generalized Born/surface area (GB/SA) models (1) are implicit solvent models that are often used in biomolecular simulations. GB/SA models have been used in protein loop prediction algorithms (2), protein–protein docking (3, 4), pK_a shift calculations (5, 6), the refinement of NMR-derived structures (7), and MD simulations to sample limited regions of phase space in several different proteins, peptides, and nucleic acid structures (8–16). The GB and GB/SA implicit solvent models have also been used to study folding peptides (17–20), mini-proteins (21–23), and protein fragments (24, 25). Despite the widespread use of the GB/SA model, the effect that replacing explicit water with GB/SA implicit water has on the stability and structure of proteins and peptides is unclear. Other implicit solvent models have also been used to study peptide folding (26).

The use of enhanced sampling algorithm allows for the simulation of peptides in explicit solvent. The replica exchange MD (REMD) algorithm (27) has been used to study the structure and thermodynamics of peptides, using explicit solvent models, over a wide range of temperatures (28–32). The determination of the thermodynamics equilibrium without biasing the sampling provides a way to test the accuracy of force fields in describing the equilibrium between folded and unfolded states.

The GB/SA model estimates the free energy of solvation as the sum of two terms. The first term is a SA term to approximate the free energy of solvation of uncharged solutes (33, 34); the second term is an approximate solution (1, 35, 36) for the Poisson (or linearized Poisson–Boltzmann) energy, which approximates the free energy for charging the solute after it is immersed in solvent. Both approximations are uncontrolled, namely, the magnitude of the error in the energies and forces is unknown.

The best way to learn the limitations of the GB/SA solvent model is to compare a simulation in explicit solvent with a simulation in GB/SA solvent. Explicit solvent simulations are the most accurate way known to reproduce the effects of solvation on solute conformation. Also, comparing one simulation against another simulation guarantees that any differences are caused by the treatment of solvent alone and not by the particular choice of force field for the peptide. Although some of the aforementioned studies compare simulations in GB/SA against simulations in water, most of these studies are limited by incomplete sampling and biases caused by the choice of initial conditions.

The earliest study that compared the GB/SA model and explicit solvent and that included both unfolded and native states was a study of the β-sheet-forming peptide Betanova (17). This study used high-temperature simulations to generate points along an unfolding trajectory. Umbrella sampling was then used to sample windows around these points. Although the authors of that study found some differences between the GB/SA and explicit solvent simulations, they found qualitative similarities in the potentials of mean force (PMF) calculated with explicit solvent, GB/SA, and GB (without a SA term). Bursulaya and Brooks (17) concluded that “the GB solvation potential itself is sufficient to describe the PMF of Betanova.”

Recent attempts have been made to compare and contrast GB/SA and explicit solvent simulations on other β-sheet peptides (37). Zhou and Berne (37) sampled the C-terminal β-hairpin of protein G (GB1) by using both a GB/SA solvent model and explicit solvent via the REMD method (27). They found that the lowest free energy state with GB/SA was significantly different from the lowest free energy state in explicit solvent. In particular, incorrect salt bridges were formed at the core of thepeptide, at the expense of hydrophobic contacts. Zhou (38) extended this study on GB1 by examining several other force fields with the same system (GB1).

β-Sheet-forming peptides such as Betanova and GB1 may not be the ideal systems for characterizing the GB/SA model, because the structure and thermodynamic stability of the peptides are not well characterized. In addition, the time scale for relaxation in these peptides is an order of magnitude longer than for α-helical peptides, making simulations with β peptides more difficult (39, 40). Also, changes in sequence in β peptides are more likely to change the backbone structure or hydrophobic packing than in α-helices. α-Helical peptides have been widely studied and are well characterized structurally and thermodynamically (41–45).

In this study, we use two α-helical peptides for comparing GB/SA and explicit solvent: A₂₁, a polyalanine sequence, and F_s, a mixed alanine/arginine sequence known to form highly thermostable helices in water (46). We simulate these systems with two separate force fields and two solvent models: the GB/SA model of solvent and with explicit waters. We sample the conformational space of these peptides with the REMD method (27). It is of interest to compare these two peptides, because the stabilizing effect of the arginines in the F_s peptide is most probably caused by interactions between its charged side chain and the peptide backbone, which are not simply hydrophobic in character (30). This makes for a particularly stringent test of charge/solvent interactions in a model of water.

Methods

We simulate two peptides. The first is Ace-A₂₁-Nme (A₂₁). The second is Ace-A₅-(AAARA)₃-A-Nme (F_s). Ace is an acetyl group; Nme is an N-methyl group. Each peptide is simulated with two different force fields and two different solvents. One solvent is explicit transferable intermolecular potential 3 point (TIP3P) water (47), and the other is implicit GB/SA solvent as implemented by Tsui and Case (15) in the amber 6.0 suite of programs (48). The force fields are the force field of Cornell et al. (49) (parm94) and the modified force field (parm-mod) of Garcia and Sanbonmatsu (30), which was shown to greatly increase the agreement between the simulated and actual temperature melting (T_m) profiles for water-soluble helices.

amber 4.1 (50) and amber 6.0 (48) are used for the explicit solvent and implicit solvent simulations, respectively. These are modified to perform REMD (27) and use the Nose–Hoover temperature coupling algorithm (51). The GB/SA simulations all have 30 replicas exponentially spaced in temperature from 200 to 623.73 K. Replica exchanges are attempted between 30 randomly chosen pairs of replicas every 10 integration steps. Although our GB/SA simulations have attempted exchanges at 0.02-ps intervals (more frequent than our explicit solvent simulations), the overlap of energy histograms at neighboring temperatures resulting from the simulation is consistent with the canonical ensemble (52). The simulations in explicit solvent of A₂₁, A₂₁ with modified force field, F_s, and F_s with modified force field are performed, respectively, with 32, 46, 42, and 42 replicas distributed from 275–455 K, 278–487 K, 275–551 K, and 275–551 K. Each simulation is in a cubic box of 43.5, 43.5, 43.7, and 43.7 Å per side containing 2,640, 2,640, 2,660, and 2,660 TIP3P waters, respectively. The volumes are fixed at the final volume obtained after 100 ps of constant pressure simulation at 300 K and 1 atm on a single denatured peptide with the parm94 force field. Replica exchanges are attempted between all neighboring pairs of replicas at 250 integration step intervals.

All simulations are done by using a 2-fs time step. Bonds involving hydrogen are constrained in length with the algorithm shake (53) with a 0.0005-Å tolerance. settle (54) is used for constraining bond lengths in explicit waters. Electrostatic interactions in explicit solvent are calculated with the generalized reaction field method (55, 56) with an 8-Å cutoff. Van der Waals interactions between atoms separated by three bonds (namely, one to four nonbonded interactions) are not scaled; electrostatic interactions between these atoms are reduced by a factor of 1.2. Nonbonded pair lists are updated every 10 integration steps. The Berendsen thermostat (57) is used with a coupling time of 0.1 ps for all explicit solvent simulations. GB/SA simulations are made with a Nose–Hoover thermostat (51) with a 1-ps coupling time and fixed center of mass and zero angular momentum. For the GB/SA simulations, the intrinsic Born radii are taken from Tsui and Case (15). The water dielectric constant of water is 78.5, and for the peptide it is 4. The surface tension for a water-oil interface is 0.005 kcal/mol per Ų.

All of the GB/SA calculations are equilibrated for 3 ns per replica and have production runs of 4 ns per replica. All of the explicit solvent simulations have at least 4 ns of equilibration and 4 ns of production.

Lifson–Roig (58, 59) theory as described by Hong and Schellman (60) is used to analyze the thermal denaturation curves. For each sampled structure, we compute the ϕ and ψ values of each of the 21 residues; we count 21 residues because both ends have caps that can participate in hydrogen bonding. Each residue is then classified as either helix or coil based on its ϕ-ψ values: helix residues are those with –100⁰ ≤ Φ ≤ –30⁰ and –67⁰ ≤ ϕ –7⁰. Calculations of the helical content follow the Lifson—Roig model, where n (n > 3) consecutive helices make a helical segment of length n –2. The variation of w with temperature is fit to produce estimates of ΔH(300 K), ΔS(300 K), and ΔCv(300 K) for helix formation on a per-residue basis at 300 K from the function

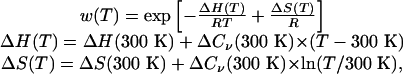where T is the temperature in Kelvin, R is the ideal gas constant (0.001986 kcal/mol per K), H is energy, S is entropy, and C_v is heat capacity at constant volume.

Results and Discussion

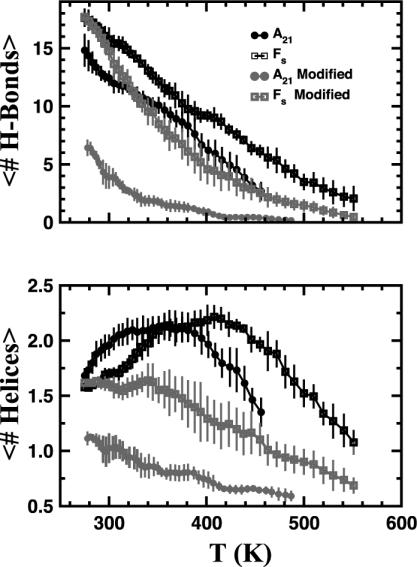
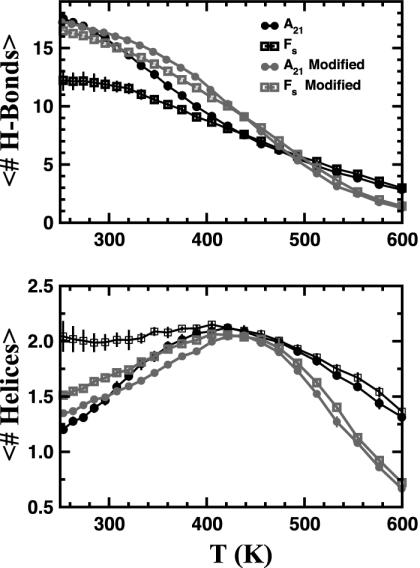
In Fig. 1 we show the heat denaturation curves for A₂₁ and F_s peptides in explicit solvent with both force fields (parm94 and parm-mod). The REMD explicit solvent simulations for A₂₁ and the F_s peptide have been reported by Garcia and Sanbonmatsu (30). The thermal denaturation curves obtained with the parm-mod force field were in agreement with experimental determination of the transition temperature, helix nucleation, and propagation parameters (46, 61). For this reason we consider the results for A₂₁ parm-mod to be good for comparison of explicit and implicit solvent models of solvation. Fig. 2 shows similar curves for the GB/SA simulations. There is a qualitative similarity between the explicit solvent and GB/SA simulations. Both show a weakly cooperative transition between disordered states at high temperature and helical structures at low temperature. The advantages of GB/SA are apparent. Not only do GB/SA simulations run faster than explicit solvent simulations, but the removal of the solvent friction in GB/SA decreases the correlation time and decreases the sampling error for the same amount of real time simulated.

Fig. 1.

Equilibrium thermal denaturation of A₂₁ and F_s peptides in explicit solvent by using the parm94 and parm-mod force fields. (Upper) The mean number of hydrogen bonds computed as the average number of w residues by using the classification described in Methods. (Lower) The average number of helices computed as the average number of unbroken stretches of w residues. Error bars are 65% confidence limits estimated by block averages. The F_s peptide is clearly more helical than A₂₁ under both force fields.

Fig. 2.

Equilibrium thermal denaturation of A₂₁ and F_s peptides in GB/SA by using the parm94 and parm-mod force fields. (Upper) The mean number of hydrogen bonds. (Lower) The average number of helices. The curves and error bars are computed as in Fig. 1. Unlike in explicit solvent (Fig. 1), at high temperatures the F_s peptide has the same helical content as A₂₁, and at lower temperatures with the parm94 force field it is less helical. The low-temperature behavior is caused by the experimentally incorrect formation of structures with multiple helices.

In Table 1 we show the T_ms, the temperatures at which half of the possible hydrogen bonds are formed, determined from the data in Figs. 1 and 2. Comparing the various T_ms shows two peculiarities. First, in all of the explicit solvent simulations, the F_s peptide is more helical than A₂₁; however, in all of the GB/SA simulations the F_s peptide is less helical than A₂₁. Second, changing force fields from the parm94 to parm-mod force field decreases the helical content in explicit solvent; however, the same change increases the helical content with GB/SA solvent. What are the origins of these differences?

Table 1. Some basic properties of the eight simulations.

System	Tm, K	v, 300 K	w, 300 K	ΔH, kcal/mol	ΔS, cal/mol per K	ΔCv, cal/mol per K
A21 in TIP3P (parm94)	361 (14)	0.30 (0.02)	1.68 (0.04)	-0.23 (0.21)	0.20 (0.5)	-10.9 (1.6)
Fs in TIP3P (parm94)	393 (20)	0.27 (0.05)	2.12 (0.18)	-0.72 (0.13)	-0.9 (0.4)	-4.0 (1.1)
A21 in TIP3P(parm-mod)	258	0.059 (0.006)	1.12 (0.01)	-0.58 (0.06)	-1.7 (0.2)	0.2 (1.0)
Fs in TIP3P (parm-mod)	342 (8)	0.13 (0.03)	1.67 (0.10)	-0.88 (0.15)	-2.0 (0.5)	1.2 (1.3)
A21 in GB/SA (parm94)	399 (6)	0.89 (0.02)	3.25 (0.03)	-1.39 (0.01)	-2.36 (0.03)	0.0 (0.1)
Fs in GB/SA (parm94)	380 (5)	0.79 (0.02)	2.20 (0.03)	-0.47 (0.01)	-0.02 (0.04)	-4.2 (0.3)
A21 in GB/SA (parm-mod)	432 (3)	1.63 (0.08)	4.63 (0.16)	-1.48 (0.01)	-0.02 (0.04)	-4.2 (0.3)
Fs in Gb/SA (parm-mod)	431 (2)	1.57 (0.07)	4.03 (0.12)	-1.23 (0.02)	-1.56 (0.04)	-4.5 (0.02)

T_m is the denaturation temperature measured as the temperature at which half of the possible native α-helical hydrogen bonds are formed. v is the Lifson—Roig helix nucleation parameter at 300 K (smaller values indicate a large nucleation penalty). w is the Lifson—Roig helix propagation parameter at 300 K. ΔH, ΔS, and ΔC_v are the energy, entropy, and heat capacity changes, respectively, for helix formation on a per-residue basis found by fitting the variation of w with temperature as described in Methods.

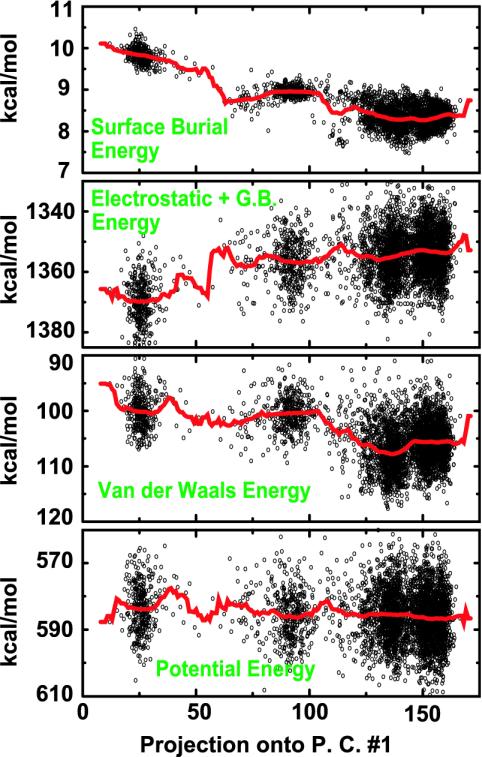
Examination of the low-temperature structures in these simulations shows that the dominant structures are single α-helices except for the F_s peptide in GB/SA solvent by using the parm94 force field. Visual examination shows that this peptide forms multiple helical structures at low temperatures. A good method to differentiate low-temperature structures is with principal component projections (62, 63). In this method, directions are chosen in the 3N conformational space of the peptide that best represent (in a least-squares sense) the ensemble of peptide conformations. Making projections of the 200-K population onto its two largest principal components shows several distinct conformational clusters. This projection, along with representative structures from the dominant clusters, is shown in Fig. 3. Simple counting based on this projection shows that <9% of the population has a single α-helical structure (first principal component <60 Å).

Fig. 3.

A projection of the 200-K ensemble of the F_s peptide in GB/SA (parm94) onto the two largest principal components; each structure in the ensemble corresponds to a single point in the plane. We show representative structures from the major clusters. The ribbon backbone is colored according to sequence position: red is N-terminal and blue is C-terminal. Fewer than 9% of the structures occur in the leftmost cluster, which corresponds to the physically correct single-helix structures. The 200-K ensemble is shown for clarity. Remnants of these major clusters persist above 350 K.

The multiple-helix structures melt out more rapidly with an increase in temperature than the single-helix structure (data not shown), which indicates that the multiple-helix structures have a lower energy than the single-helix structure. In Fig. 4, we show a breakdown of some of the primary energy components that stabilize these multiple-helix structures. They are less electrostatically stable. This is most probably because they have a smaller number of satisfied hydrogen bonds, a more desolvated helical core (in the parts that are helical), and several partially buried arginine residues, which are positively charged. This is offset by favorable intrapeptide van der Waals interactions and a large SA burial.

Fig. 4.

The variation of energetic factors along the largest principal component for the F_s peptide in GB/SA at 200 K. Each point corresponds to a structure in the 200-K ensemble. The principal component is the same as principal component 1 shown in Fig. 3. The leftmost cluster corresponds to structures that have a single helix as seen experimentally. The other clusters contain multiple helices. The red line is an average over structures with similar values for their largest principal component. The multiple helix structures have unfavorable electrostatic plus GB interactions (compared with a single helix) and favorable van der Waals and surface burial interactions.

The formation of these low-temperature, multiple-helix structures is the reason for the large number of apparent helices and relatively small number of hydrogen bonds at low temperature seen in Fig. 2; thus, the addition of arginine residues to a single polyalanine sequence reduces its helicity in GB/SA solvent by stabilizing structures alternate to the experimentally observed single helix.

The effects of arginine residues in polyalanine sequences in explicit solvent were analyzed via simulation by Garcia and Sanbonmatsu (30). It was found that an arginine residue at position i increases the helicity of residues at position i-2 by shielding the carbonyl group involved in the hydrogen bond between residues i-4 and i from attack by water molecules. To see whether a similar effect might be happening in the GB/SA simulations, we need to eliminate the interference of the multiple-helix structures. The simplest method is to raise the temperature to a point where almost no multiple-helix structures are populated. In Fig. 5, we show the average helicity as a function of residue position at high temperature (375 K). There is enhancement of helicity in explicit solvent at positions before arginine residues, but no enhancement (or very small enhancement) in GB/SA. Visual examination of the structures actually shows a significant amount of scavenging of the residue i-4 to residue i hydrogen bond by arginines, which would more plausibly destabilize an α-helix than stabilize it.

Fig. 5.

The fractional helicity as a function of residue index for the F_s peptide (parm94) in explicit solvent and in GB/SA. The temperature (375 K) is slightly below the denaturation temperature for both the explicit solvent and GB/SA denaturation temperatures (393 K and 380 K, respectively). The explicit solvent simulations have enhancement of the helicity at residue positions one and two positions toward the N terminus of arginine residues; no enhancement is seen in GB/SA simulations.

Another anomaly we seek to answer is the different effects of changing force fields from the parm94 to the parm-mod force field. This change lowers the T_m of both the A₂₁ and F_s peptides in explicit solvent by 103 K and 51 K, respectively (Table 1). At the same time, it raises the T_m of both the A₂₁ and F_s peptides in GB/SA by 33 K and 51 K, respectively. These results are particularly striking because the partial charges and van der Waals interactions are identical in parm94 and parm-mod; only the dihedral angles on the backbone are altered. The native (low-temperature) structures of A₂₁ are similar under all conditions of solvent and temperature we examined. This finding leads us to conclude that these opposing effects are produced because the unfolded (high-temperature) states are different under GB/SA and explicit solvent conditions.

In Fig. 6, we show the ϕ-ψ angle distribution for the central seven residues in A₂₁ (parm94) for both explicit and GB/SA solvents averaged over the population at 456 K. This temperature is at least 50 K above the T_ms of A₂₁ for both solvents, so this average is primarily seeing unfolded states. In explicit solvent there is a significant population of residues in the upper left hand quadrant of the Ramachandran map, but in GB/SA solvent most of the population is in the α-helical region of the map. This strong preference for one conformation creates a large persistence length in the unfolded state with GB/SA. Fig. 6 also shows the distribution of end-to-end lengths in the unfolded state. The peptide in GB/SA is more extended than the peptide in explicit solvent; its most probable end-to-end length is >30 Å, which is comparable to the native helix end-to-end distance.

Fig. 6.

The potential of mean force in the Φ–Ψ plane averaged over the central seven residues of A₂₁ in the unfolded state with explicit solvent (A) and GB/SA (B). Both are shown at a temperature ≈1.27 times the T_m (456 K and 513 K). Contours are in units of RT at each temperature. Notice that explicit solvent produces a much more diverse distribution of conformations including β, PPII, and left-handed α-helix, but the GB/SA simulation is largely restricted to the α-helical region. This restriction produces a large persistence length and a large mean end-to-end distance with GB/SA compared with explicit solvent. (C) The distribution of end-to-end distances for explicit solvent (red) and GB/SA (black).

The change in energy of a residue in moving from parm94 to parm-mod depends on its ϕ-ψ value. This change from parm94 to parm-mod stabilizes conformations with ψ near –120° and 120°. Because A₂₁ in explicit solvent has a large population with ψ values near 120°, this perturbation stabilizes this population relative to the α-helix population near –60°; however, in the GB/SA solvent there is no significant population with ψ values near 120°, so the dominant effect is to stabilize the α-helix population at –60° relative to the conformations with ψ values near 0°.

Conclusions

We have shown that the ensemble of conformations sampled with explicit solvent and with the implicit GB/SA model differ significantly in both the unfolded and folded state.

Of two peptides studied with the parm94 force field, we found that the native conformation was incorrectly predicted for one of them (F_s). Instead of being a single helix, this peptide formed many different types of helical bundles. At higher temperatures, these structures melt out, leaving a single helix in equilibrium with unfolded conformations; however, in contrast to the behavior in explicit solvent, the arginine residues in the F_s peptide provide no extra stability to the helical conformation and may even work to destabilize it by competing for hydrogen bonds.

Analysis of the unfolded conformations showed that the GB/SA unfolded states are vastly different from the unfolded states in explicit solvent. In particular, the GB/SA solvent produced highly rigid unfolded states with nearly all their residues in the α region of the Ramachandran map. The strong difference in the unfolded state makes the simulations behave quite differently under force field perturbations. It is also ref lected in the large nucleation parameters for helix formation.

These differences are enough to alter the T_ms, even under conditions where the native conformation has the approximately correct structure, by 100 K or more. They are also enough to eliminate many highly interesting effects like the stabilization of helices by the addition of charged residues (45).

Other simulations have found discrepancies between explicit solvent simulations and GB/SA simulations in the low-temperature structures of a peptide that forms a β hairpin (GB1) (37). In contrast to those results and our own, it has been claimed that the potentials of mean force surface of Betanova is qualitatively the same in explicit solvent and GB/SA solvent (17). In particular, this result found only a 2.2-Å deviation of Betanova from the NMR structure by using GB solvent (without a SA term), which is only slightly >1.9-Å deviation found by using explicit solvent. It has been suggested that the umbrella sampling method used in this study may improperly account for the entropic contribution to the free energy by limiting the peptide configurations sampled (64).

We see large differences in the stability and the unfolded states of α-helical peptides between explicit solvent and GB/SA. It should be considered whether these differences are important and if too much accuracy is being lost for the computational gains of GB/SA.