Joint Blind Source Separation by Multi-set Canonical Correlation Analysis

Abstract

In this work, we introduce a simple and effective scheme to achieve joint blind source separation (BSS) of multiple datasets using multi-set canonical correlation analysis (M-CCA) [1]. We first propose a generative model of joint BSS based on the correlation of latent sources within and between datasets. We specify source separability conditions, and show that, when the conditions are satisfied, the group of corresponding sources from each dataset can be jointly extracted by M-CCA through maximization of correlation among the extracted sources. We compare source separation performance of the M-CCA scheme with other joint BSS methods and demonstrate the superior performance of the M-CCA scheme in achieving joint BSS for a large number of datasets, group of corresponding sources with heterogeneous correlation values, and complex-valued sources with circular and non-circular distributions. We apply M-CCA to analysis of functional magnetic resonance imaging (fMRI) data from multiple subjects and show its utility in estimating meaningful brain activations from a visuomotor task.

I. Introduction

Blind source separation (BSS) has been successfully applied to a wide variety of applications such as the estimation of brain activations in fMRI data and speech enhancement for robust speech recognition. When multiple datasets are jointly analyzed as a group, e.g., when estimating brain activations in fMRI data from a group of subjects, or, when separating speech and audio signals in multiple frequency bands, BSS methods face the challenge of keeping the coherence of separated sources across different datasets. For instance, in group fMRI data analysis, the coherence among source estimates across different subjects is important for subsequent analysis stages such as group level inference and the study of inter-subject variability [2]. In speech or audio source separation in the frequency domain, the coherence among the source estimates across different frequency bands is crucial for reliable back-reconstruction of the source estimates to the temporal domain [3]. Therefore, a joint BSS scheme on multiple datasets is motivated for separating the latent sources from each dataset while keeping the correspondence of the source estimates across different dataset.

A number of methods have been proposed for achieving joint BSS. Group ICA [2] maintains the coherence of the source estimates by assuming a common signal subspace shared by all datasets and maximizes the statistical independence of the sources within the common signal subspace. Because ICA is performed in the common signal subspace, a group dimension reduction stage is required to aggregate the common features across the datasets while discarding the distinct features for their lesser contribution to the variance of aggregated data. After ICA, a disaggregation procedure has to be employed to back-reconstruct the source estimates for each individual subject. Tensorial ICA [4] specifies a similar common signal subspace model as Group ICA. In addition, each group of the corresponding mixing vectors is represented by a common mixing vector associated with a cross-subject variation vector using a rank-one approximation. In this way, the group datasets are decomposed into a three-way tensor product of the common sources, common mixing vectors, and the associated cross-subject variation vectors.

Independent vector analysis (IVA) models the corresponding sources from each dataset as an independent source vector with a dependent multivariate super-Gaussian distribution [3]. The source separation method is then developed as a generalization of Infomax ICA [5] by maximizing the mutual information between joint and factorized source vector distributions. In the derivation of IVA learning rule, the covariance matrix in the independent source vector distribution is assumed to be an identity matrix. Therefore, the group of corresponding sources within an independent source vector are assumed to be uncorrelated with each other. In [6], it is noted that the dependencies among those corresponding sources are implied in the higher order moments of the distribution function. However, even though, the development of IVA algorithm is simplified by the assumption of an identity covariance matrix, the performance of the algorithm might suffer when separating independent source vectors containing correlated source elements.

In this work, we introduce a joint BSS model for a group of datasets based on the correlation of latent sources within and between datasets. We show that joint BSS can be achieved by M-CCA. M-CCA is developed as an extension of canonical correlation analysis (CCA) to find linear transforms that simplify the correlation structure among a group of random vectors [1]. M-CCA algorithm takes multiple stages, where in each stage, a linear combination is found for each random vector such that correlation among the group of resulting variates, i.e. the canonical variates, is maximized. Motivated by M-CCA, we propose a generative model for joint BSS and study source separability conditions based on between-set source correlation values and eigenvalues of each group of corresponding sources. We show that, when the canonical variates obtained at different stages are constrained to be uncorrelated, M-CCA achieves joint BSS of the latent sources under the proposed generative model and derived separability conditions.

Through numerical simulation we show that, compared with Group ICA and IVA, M-CCA achieves better performance on joint BSS of (i) large number of datasets, (ii) group of corresponding sources with heterogeneous correlation values, and (iii) complex-valued sources with circular and non-circular distributions. We also apply M-CCA to jointly separate brain activations from group fMRI data and show that M-CCA estimates brain networks that exhibit higher cross-subject consistency.

In Section II, we introduce a generative model for joint BSS of group datasets and state source separability conditions based on (i) the distinction of between-set source correlation values and (ii) the maximum eigenvalue of each group of corresponding sources. We justify that joint BSS of sources in the generative model can be achieved by a multi-stage deflationary correlation maximization scheme. In Section III, we give a brief review of CCA and M-CCA, and outline the implementation of M-CCA for joint BSS. In section IV, we compare source separation performance of M-CCA with the existing methods on simulated data and group fMRI data. In the last section, we discuss several interesting aspects of M-CCA method to conclude the work.

II. Joint BSS by correlation maximization

In this section, we first introduce a generative model for group datasets based on within- and between-set source correlation structures. Next, we study two types of source separability conditions, (i) condition on between-set source correlation values and (ii) condition on eigenvalues of source correlation matrices, for achieving joint BSS by a multi-stage correlation maximization scheme.

A. Generative model for group dataset

We assume the following generative model:

1. For a group of M datasets, each dataset, ${\mathbf{x}}_m={[x_m^{(1)},x_m^{(2)},\dots ,x_m^{(K)}]}^T$, m = 1, 2, …, M contains linear mixtures of K sources given in the source vector ${\mathbf{s}}_m={[s_m^{(1)},s_m^{(2)},\dots ,s_m^{(K)}]}^T$, mixed by a nonsingular matrix, A_m, i.e.,

   $${\mathbf{x}}_m={\mathbf{A}}_m{\mathbf{s}}_m,$$ (1)

   where x_m, s_m ∈ ℂ^K are K-dimensional complex random vectors, whose samples form the mixture dataset and source dataset respectively, A_m ∈ ℂ^K×K is a non-singular complex square matrix;

2. Sources are uncorrelated within each dataset and have zero mean and unit variance, i.e.,

   $$E\{{\mathbf{s}}_m\}=\mathbf{0},m=1,2,\dots M$$

   and

   $$E\{{\mathbf{s}}_m{{\mathbf{s}}_m}^H\}=\mathbf{I},m=1,2,\dots M$$ (2)

   where (·)^H denotes the Hermitian transpose and I is the identity matrix;

3. Sources from any pair of datasets m ≠ n; m, n ∈ {1, 2, …, M} have nonzero correlation only on their corresponding indices. Without loss of generality, we assume that the magnitude of correlation between corresponding sources are in non-decreasing order, i.e.,

   $$\mid r_{m,n}^{(1)}\mid \ge \mid r_{m,n}^{(2)}\mid ,\dots ,\ge \mid r_{m,n}^{(K)}\mid ,$$

   where $r_{m,n}^{(k)}=E\{s_m^{(k)}{(s_n^{(k)})}^{\ast }\}$, (·)* represents complex conjugate, and |·| represents the magnitude of a complex quantity.

   Assumptions (ii) and (iii) can be written in a compact form in terms of the concatenated source vector $\mathbf{s}={[{\mathbf{s}}_1^T,{\mathbf{s}}_2^T,\dots ,{\mathbf{s}}_M^T]}^T$:

   $$E\{\mathbf{s}{\mathbf{s}}^H\}=\left[\begin{array}{cccc}\mathbf{I}& {\mathbf{\Lambda }}_{1,2}& \dots & {\mathbf{\Lambda }}_{1,M}\\ {\mathbf{\Lambda }}_{2,1}& \mathbf{I}& \dots & {\mathbf{\Lambda }}_{2,M}\\ \dots & & & \\ {\mathbf{\Lambda }}_{M,1}& {\mathbf{\Lambda }}_{M,2}& \dots & \mathbf{I}\end{array}\right]$$

   where ${\mathbf{\Lambda }}_{m,n}=\text{diag}([r_{m,n}^{(1)},r_{m,n}^{(2)},\dots ,r_{m,n}^{(K)}])$ for m, n ∈ {1, 2, …, M} is a diagonal matrix with the correlation values of the corresponding sources in s_m and s_n on its diagonal.

This assumed correlation pattern for latent sources in the generative model can be effectively used to construct a joint source separation scheme. In this scheme, the group of sources that have the maximal between-set correlation values are first extracted from the datasets. By removing the estimated sources from the datasets and repeating the correlation maximization procedure, subsequent procedures can extract groups of corresponding sources from each dataset in decreasing order of between-set correlation values.

B. Joint BSS by maximizing between-set source correlation values

In this section, we state the separability condition based on source correlation values, i.e., the entries in Λ_m,n and prove that, when the condition is satisfied, a joint BSS can be achieved by a multistage correlation maximization scheme. We study joint BSS on M = 2 datasets and joint BSS on M > 2 datasets as two comparative cases in order to highlight how the source separability condition is relaxed for joint BSS on multiple datasets compared to the case of two datasets.

1) Joint BSS of two datasets

Given two datasets x_m, m = 1, 2, following the generative model given in (i)–(iii) in Section II-A and

$$\mid r_{1,2}^{(1)}\mid \ne \mid r_{1,2}^{(2)}\mid ,$$ (3)

the first pair of corresponding sources, $s_1^{(1)}={({\mathbf{w}}_1^{(1)})}^H{\mathbf{x}}_1$ and $s_2^{(1)}={({\mathbf{w}}_2^{(1)})}^H{\mathbf{x}}_2$ can be jointly extracted, up to phase ambiguity, by two demixing vectors, ${\mathbf{w}}_1^{(1)}$ and ${\mathbf{w}}_2^{(1)}$, that maximize the magnitude of correlation coefficient between the two extracted sources, i.e.,

$$\{{\mathbf{w}}_1^{(1)},{\mathbf{w}}_2^{(1)}\}=arg\underset{\mathbf{w}}{max}\mid {\widehat{r}}_{1,2}^{(1)}\mid$$

where ${\widehat{r}}_{1,2}^{(1)}\triangleq \text{corr}({({\mathbf{w}}_1^{(1)})}^H{\mathbf{x}}_1,{({\mathbf{w}}_2^{(1)})}^H{\mathbf{x}}_2)$. In other words, (3) defines source separability condition by correlation maximization on two datasets.

To see this, suppose x₁ and x₂ are linear mixtures of sources from s₁ and s₂ respectively, i.e., $x_1={\sum }_{k=1}^K{\alpha }_k{s}_1^{(k)}$ and $x_2={\sum }_{k=1}^K{\beta }_k{s}_2^{(k)}$, where α_k, β_k, k = 1, 2, …, K, are complex-valued mixing coefficients. Without loss of generality, we assume that x₁ and x₂ have unit variance, the correlation between x₁ and x₂ can be written as

$${\overline{r}}_{1,2}\triangleq E\{x_1{x_2}^{\ast }\}=\sum _{k=1}^K{\alpha }_k{\beta }_k^{\ast }{r}_{1,2}^{(k)},$$

since $E\{s_1^{(k)}{(s_2^{(l)})}^{\ast }\}=0$, ∀k ≠ l.

We have

$$\mid {\overline{r}}_{1,2}\mid \le \sum _{k=1}^K\mid {\alpha }_k\mid \mid {\beta }_k\mid \mid r_{1,2}^{(k)}\mid$$ (4)

due to the triangle inequality.

The right side of inequality (4) can be written as an inner product of two vectors, z₁ and z₂, where

$${\mathbf{z}}_1={\left[\mid {\alpha }_1\mid \sqrt{\mid r_{1,2}^{(1)}\mid },\mid {\alpha }_2\mid \sqrt{\mid r_{1,2}^{(2)}\mid },\dots ,\mid {\alpha }_K\mid \sqrt{\mid r_{1,2}^{(K)}\mid }\right]}^T$$

and

$${\mathbf{z}}_2={\left[\mid {\beta }_1\mid \sqrt{\mid r_{1,2}^{(1)}\mid },\mid {\beta }_2\mid \sqrt{\mid r_{1,2}^{(2)}\mid },\dots ,\mid {\beta }_K\mid \sqrt{\mid r_{1,2}^{(K)}\mid }\right]}^T.$$

Noting that x₁ and x₂ have unit variance, the sources are assumed to have unit variance according to the generative model, we then have ${\sum }_{k=1}^K\mid {\alpha }_k{\mid }^2=1$ and ${\sum }_{k=1}^K\mid {\beta }_k{\mid }^2=1$. Therefore, vectors z₁ and z₂ are confined on a K-dimensional hyper-ellipsoid with semi-axes

$$\left\{\sqrt{\mid r_{1,2}^{(1)}\mid },\sqrt{\mid r_{1,2}^{(2)}\mid },\dots ,\sqrt{\mid r_{1,2}^{(K)}\mid }\right\}.$$

According to assumption (iii) in the generative model and the condition specified in (3), we have $\mid r_{1,2}^{(1)}\mid >\mid r_{1,2}^{(k)}\mid$, ∀k > 1, hence,

$$\langle {\mathbf{z}}_1,{\mathbf{z}}_2\rangle \le \mid \mid {\mathbf{z}}_1\mid \mid \mid \mid {\mathbf{z}}_2\mid \mid \le \mid r_{1,2}^{(1)}\mid ,$$ (5)

where the equality holds and the inner product is maximized if the angle between z₁ and z₂ is zero, i.e., z₁ and z₂ are parallel and point to the same direction, and $\mid \mid {\mathbf{z}}_1\mid \mid =\mid \mid {\mathbf{z}}_2\mid \mid =\sqrt{\mid r_{1,2}^{(1)}\mid }$. Fig. 1 illustrates maximization of 〈z₁, z₂〉 in two-dimensional plane.

Fig. 1.

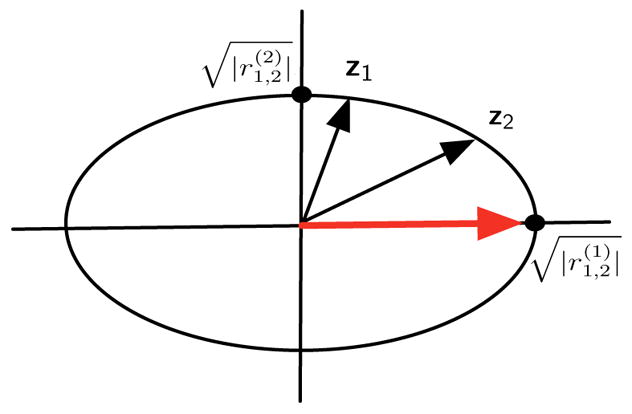
Illustration of the ellipsoid inequality in two-dimensional space, red arrow denotes the position of z₁ and z₂ achieving maximum of 〈z₁, z₂〉

By (4) and (5), |r̄_1,2| achieves its maximum, $\mid r_{1,2}^{(1)}\mid$, when $\mid {\alpha }_k\mid =\mid {\beta }_k\mid =\{\begin{array}{ll}1,\hfill & k=1\hfill \\ 0,\hfill & k\ne 1\hfill \end{array}$. Correspondingly, we have $\mid x_1\mid =\mid s_1^{(1)}\mid$ and $\mid x_2\mid =\mid s_2^{(1)}\mid$.

Therefore, if two demixing vectors ${\mathbf{w}}_1^{(1)}$ and ${\mathbf{w}}_2^{(1)}$ can be found to maximize the correlation between the extracted sources from each dataset, the extracted sources are the first pair of corresponding sources, up to phase ambiguity.

Now, suppose that the first pair of corresponding sources are extracted and removed from x₁ and x₂. By the same reasoning, the second pair of corresponding sources $s_1^{(2)}$ and $s_2^{(2)}$ can be jointly recovered by two demixing vectors that maximize the correlation coefficients if

$$\mid r_{1,2}^{(2)}\mid \ne \mid r_{1,2}^{(3)}\mid .$$

By induction, the kth pair of corresponding sources can be jointly recovered by correlation maximization if

$$\mid r_{1,2}^{(k)}\mid \ne \mid r_{1,2}^{(k+1)}\mid .$$

As a conclusion, all the K pairs of corresponding sources can be jointly recovered from x₁ and x₂ in this deflationary procedure if the following condition is satisfied

$$\mid r_{1,2}^{(k)}\mid \ne \mid r_{1,2}^{(l)}\mid ,1\le k<l\le K.$$ (6)

If each dataset is whitened before joint BSS, the demixing matrix for each dataset becomes an orthonormal matrix. In this case, removal of the extracted sources in the deflationary scheme can be converted to the constraint that the current demixing vector be orthogonal to the previously obtained ones. Compared with source removal, imposing orthogonality constraints on the demixing vectors has the advantage that each joint source extraction stage can be solved as a constrained optimization problem [1].

2) Joint BSS of more than two datasets

In case of joint BSS on M > 2 datasets, we notice that there are $\left(\begin{array}{l}M\hfill \\ 2\hfill \end{array}\right)=\frac{M!}{2!(M-2)!}$ correlation coefficients among the group of corresponding sources in M datasets. We define

$${\widehat{R}}^{(k)}\triangleq \sum _{m,n=1}^M\mid {\widehat{r}}_{m,n}^{(k)}\mid ,$$

i.e., the sum of correlation magnitudes, as the measure of overall correlation among the kth group of extracted sources. Since the maximum of R̂^(k) is achieved if and only if each element $\mid {\widehat{r}}_{m,n}^{(k)}\mid$ in the sum reaches its maximum, it is straightforward to extend condition (6) to M datasets as

$$\begin{array}{l}\forall m,n\in \{1,2,\dots ,M\},\\ \mid r_{m,n}^{(k)}\mid \ne \mid r_{m,n}^{(l)}\mid ,1\le k<l\le K\end{array}$$ (7)

and conclude that, when (7) is satisfied, joint BSS of K sources in M datasets can be achieved by maximizing R̂^(k), k = 1, 2, …, K, using a deflationary procedure.

However, the condition specified in (7) is not a necessary condition to achieve joint BSS on M datasets. To see this, we consider joint extraction of the first group of corresponding sources in M datasets by maximizing ${\widehat{R}}^{(1)}={\displaystyle \sum _{m,n=1}^M}\mid {\widehat{r}}_{m,n}^{(1)}\mid$. When R̂ ⁽¹⁾ is maximized, all $\mid {\widehat{r}}_{m,n}^{(1)}\mid$, ∀m, n ∈ {1, 2, …, M} reach their respective maximum. Apply source separability condition in (3) to the mth and nth datasets, we have that, when $\mid {\widehat{r}}_{m,n}^{(1)}\mid$ is maximized, the first source in these two datasets are jointly extracted if

$$\mid r_{m,n}^{(1)}\mid \ne \mid r_{m,n}^{(2)}\mid .$$ (8)

Therefore, to guarantee that the first source in all M datasets are extracted, we just need to find, for each m = 1, 2, …, M, an index n ∈ {1, 2, …, M}, n ≠ m, such that (8) is satisfied. Hence, the necessary condition to extract the first group of corresponding sources by maximization of R̂ ⁽¹⁾ can be stated as

$$\forall m\in \{1,\dots ,M\},\exists n\ne m,\text{such}\text{that}\mid r_{m,n}^{(1)}\mid \ne \mid r_{m,n}^{(2)}\mid .$$

Suppose R̂^(k), k = 1, 2, …, K, is sequentially maximized with the aforementioned deflationary scheme, the necessary condition for joint BSS of K sources in M dataset can be stated as

$$\begin{array}{l}\forall m\in \{1,\dots ,M\},\exists n\ne m,\text{such}\text{that}\\ \mid r_{m,n}^{(k)}\mid \ne \mid r_{m,n}^{(l)}\mid ,1\le k<l\le K\end{array}$$ (9)

It is important to note that: when M = 2, (9) reduces to (6); when M > 2, (9) is a more relaxed condition than (7) which is a direct extension of (6). The difference between (9) and (7) suggests that, with respect to the generative model introduced in Section II-A, joint BSS on a larger group of datasets is easier to be achieved than joint BSS on a smaller group of datasets.

C. Joint BSS by maximizing eigenvalue of source correlation matrix

In this section, we study source separability condition based on the maximum eigenvalues of source correlation matrices. We show that, according to the generative model, eigenvalues of the augmented source correlation matrix R_s are composed of eigenvalues of correlation matrices for each group of corresponding sources. Furthermore, eigenvector corresponding to the maximum eigenvalue for a group of corresponding sources directly indicates the separability condition of the group of sources.

To analyze R_s, we first notice that for a square matrix A and a permutation matrix P of the same size, A′ = PAP^T has the same eigenvalues as A and the corresponding eigenvectors has the relation x′= P^T x. Therefore, we can work on a permuted version of the augmented correlation matrix ${\mathbf{R}}_s^{\prime }=\mathbf{P}{\mathbf{R}}_s{\mathbf{P}}^T$ without losing generality.

We permute columns and rows of R_s such that the non-zero correlation values of the corresponding source groups are clustered to form submatrices on the main diagonal, as shown below.

Let:

$$\mathbf{P}=\left[\begin{array}{ccccccccccccc}1& 0& \dots & 0& 0& 0& \dots & 0& & 0& 0& \dots & 0\\ 0& 0& \dots & 0& 1& 0& \dots & 0& & 0& 0& \dots & 0\\ \dots & & & & \dots & & & & \cdots & \dots & & & \\ 0& 0& \dots & 0& 0& 0& \dots & 0& & 1& 0& \dots & 0\\ 0& 1& \dots & 0& 0& 0& \dots & 0& & 0& 0& \dots & 0\\ 0& 0& \dots & 0& 0& 1& \dots & 0& & 0& 0& \dots & 0\\ \dots & & & & \dots & & & & \cdots & \dots & & & \\ 0& 0& \dots & 0& 0& 0& \dots & 0& & 0& 1& \dots & 0\\ & & \dots & & & & & & & & & & \\ 0& 0& \dots & 1& 0& 0& \dots & 0& & 0& 0& \dots & 0\\ 0& 0& \dots & 0& 0& 0& \dots & 1& & 0& 0& \dots & 0\\ \dots & & & & \dots & & & & \cdots & \dots & & & \\ 0& 0& \dots & 0& 0& 0& \dots & 0& & 0& 0& \dots & 1\end{array}\right]$$

then, we have

$${\mathbf{R}}_s^{\prime }=\mathbf{P}{\mathbf{R}}_s{\mathbf{P}}^T=\left[\begin{array}{cccc}{\mathbf{R}}^{(1)}& 0& \dots & 0\\ 0& {\mathbf{R}}^{(2)}& \dots & 0\\ \dots & & & \\ 0& 0& \dots & {\mathbf{R}}^{(K)}\end{array}\right]$$

where R^(k) is the M×M source correlation matrix of the kth group of corresponding sources from each dataset.

Since ${\mathbf{R}}_s^{\prime }$ is block diagonal, its eigenvalues are the eigenvalues of R^(k), k = 1, 2 …, K. The eigenvectors of ${\mathbf{R}}_s^{\prime }$ are composed of the eigenvectors of R^(k), k = 1, 2 …, K, in its kth segment of length M and zeros elsewhere.

Based on the assumption in Section II-A, between-set source correlation values are non-increasing across different groups of corresponding sources. Given that all the diagonal elements of R^(k), k = 1, 2 …, K, are constrained to be one, R⁽¹⁾ is the closest to being singular and the maximum eigenvalue of R^(k) provides a measure on degree of singularity. Hence, when

$${\lambda }_{max}({\mathbf{R}}^{(1)})>max\{{\lambda }_{max}({\mathbf{R}}^{(2)}),\dots ,{\lambda }_{max}({\mathbf{R}}^{(K)})\},$$

the first group of corresponding sources can be extracted by the eigenvector of ${\mathbf{R}}_s^{\prime }$ associated with its largest eigenvalue.

Through a deflationary procedure described in Section II-B, the eigenvector associated with λ_max(R^(k)) extracts the kth group of corresponding sources when

$${\lambda }_{max}({\mathbf{R}}^{(k)})>max\{{\lambda }_{max}({\mathbf{R}}^{(k+1)}),\dots ,{\lambda }_{max}({\mathbf{R}}^{(K)})\}.$$

Therefore, the source separability condition can be stated as

$${\lambda }_{max}({\mathbf{R}}^{(1)})>{\lambda }_{max}({\mathbf{R}}^{(2)})>\dots >{\lambda }_{max}({\mathbf{R}}^{(K)}).$$ (10)

To provide insight into the ordering of λ_max(R^(k)), here we demonstrate an approximation of R^(k) with identical cross-correlation values as in [7] p. 478. The approximated R^(k) takes the following form:

$${\mathbf{R}}^{(k)}=\left[\begin{array}{cccc}1& {\rho }_k& \dots & {\rho }_k\\ {\rho }_k& 1& \dots & {\rho }_k\\ \dots & & & \\ {\rho }_k& {\rho }_k& \dots & 1\end{array}\right]$$

where ρ_k is a constant pairwise source correlation value.

Since R^(k) = (1 − ρ_k)I + ρ_k11^T, it can be shown that λ_max(R^(k)) = 1 + (M − 1) ρ_k, and λ_min(R^(k)) = 1 − ρ_k with multiplicity (M−1). Hence (10) is satisfied for ρ₁ > ρ₂ > … > ρ_K and each group of corresponding sources can be jointly extracted by the eigenvectors associated with λ_max(R^(k)), k = 1, 2, …, K.

In our framework, the demixing transformations obtained by M-CCA are constrained to be orthonormal. Due to invariance of eigenvalues to orthonormal transformation, source separability condition derived from source correlation matrix R_s is directly applicable to the mixture datasets.

III. Implementation of joint BSS by M-CCA

A. CCA and M-CCA

CCA is a statistical method that summarize the correlation structure between two random vectors by linear transformations [8]. Given two random vectors x₁ and x₂, CCA seeks two transformation vectors, a and b, such that the correlation between variables y₁ = a^T x₁ and y₂ = b^T x₂ is maximized. The variables y₁ and y₂ are defined as the first pair of canonical variates between x₁ and x₂. Similarly, the second pair of transformation vectors can be found such that the resulting canonical variates achieve maximum correlation and are uncorrelated to the previously obtained canonical variates. The process can continue and the total number of canonical variates is limited by the minimum dimension of x₁ and x₂. It is shown in [7] that all the transformation vectors of CCA can be obtained by solving an eigenvalue decomposition problem.

M-CCA extends the theory of CCA to more than two random vectors to identify canonical variates that summarize the correlation structure among multiple random vectors by linear transformations [1]. In contrast to CCA where correlation between two canonical variates is maximized, M-CCA optimizes a objective function of the correlation matrix of the canonical variates from multiple random vectors such that the canonical variates achieve maximum overall correlation. Furthermore, due to the consideration of multiple random vectors, M-CCA can not be solved by a simple eigenvalue decomposition problem as in the case of CCA. Instead, M-CCA takes multiple stages such that in each stage, one group of canonical variates are obtained by optimizing the objective function with respect to a set of transformation vectors. For the second stage and higher stages in M-CCA, the estimated canonical variates are constrained to be uncorrelated to the ones estimated in the previous stages. M-CCA reduces to CCA when the number of random vectors is two.

A recent advancement of M-CCA is the development of the signal processing network structure and the corresponding adaptive algorithm to achieve M-CCA on multiple datasets [9]. Although the adaptive implementation of M-CCA is important in many signal processing applications, in this work, we focus on batch mode M-CCA algorithms as they are typically used in BSS of fMRI data.

In summary, CCA and M-CCA find linear coordinates on which the within- and between-set correlation structures of multiple random vectors are simplified. That is, canonical variates obtained from the same random vector are uncorrelated with each other, and canonical variates obtained from different random vectors are correlated only on their corresponding indices.

B. Implementation of M-CCA to achieve joint BSS

The multi-stage deflationary correlation maximization scheme discussed in Section II can be implemented using the M-CCA algorithm [1]. To measure the overall correlation among canonical variates, five objective functions based on the correlation matrix of group canonical variates are proposed [1]. Two objective functions are, respectively, sum and sum of squares of all entries in the correlation matrix, i.e., SUMCOR and SSQCOR. The other three are based on the eigenvalues of the correlation matrix, i.e., MAXVAR, MINVAR, and GENVAR.

The five objective functions of M-CCA algorithm are closely related. Given that the eigenvalues of R^(k) sum up to M, the maximum of SSQCOR objective, i.e., $max{\sum }_i{\lambda }_i^2$ is dominated by λ_max; the minimum of GENVAR objective, i.e., min Π_i λ_i is dominated by λ_min. As for SUMCOR, i.e., max Σ_i,j r_ij, is similar to SSQCOR after proper sign correction on each source in the group. Therefore, the five M-CCA objective functions yield similar results on a group dataset.

In II-A, we have introduced a generative model for joint BSS where the latent sources have a similar correlation structure as the canonical variates in M-CCA. The justification of source separation is developed based on (i) sum over correlation magnitudes between all pairs of jointly extracted sources and (ii) maximum eigenvalues of the group of corresponding sources. Maximization of (i) can be achieved by the SSQCOR objective and maximization of (ii) is achieved directly achieved by the MAXVAR objective to optimize the demixing vectors for jointly extracting the sources.

As an example, we summarize the M-CCA procedure based on the SSQCOR objective as the following. Procedures based on other objective functions are similarly defined.

• Stage 1

  $$\{{\mathbf{w}}_1^{(1)},{\mathbf{w}}_2^{(1)},\dots ,{\mathbf{w}}_M^{(1)}\}=arg\underset{\mathbf{w}}{max}\left\{\sum _{m,n=1}^M\mid r_{m,n}^{(1)}{\mid }^2\right\}$$

• Stage 2 to K

  for k = 2:K

  $$\begin{array}{l}(\text{i})\{{\mathbf{w}}_1^{(k)},{\mathbf{w}}_2^{(k)},\dots ,{\mathbf{w}}_M^{(k)}\}=arg\underset{\mathbf{w}}{max}\left\{\sum _{m,n=1}^M\mid r_{m,n}^{(k)}{\mid }^2\right\}\\ \text{s}.\text{t}.{\mathbf{w}}_m^{(k)}\perp \{{\mathbf{w}}_m^{(1)},{\mathbf{w}}_m^{(2)},\dots ,{\mathbf{w}}_M^{(k-1)}\},m=1,2,\dots ,M\end{array}$$

  end

In [1], stage 1 is solved by first writing out the partial derivative function of the sum of squares objective with respect to each demixing vector and finding the stationary point by letting the partial derivative function equal to zero. Since the sum of squares objective is a quadratic form of each demixing vector, the partial derivative function is a linear function of each demixing vector. Therefore, closed form solution of the stationary point can be derived. Starting from an initial point, each demixing vector is updated in sequel to guarantee that the objective is increasing and a sweep through all the demixing vectors constitutes one step of the iterative maximization procedure. The iterations cease when the objective convergence criterion is met and the resulting demixing vectors are taken as the optimal solution. Stage 2 and higher stages are solved in a similar manner with the objective function replaced by a Lagrangian incorporating the orthogonality constraints on the demixing vectors. A Matlab implementation of the M-CCA algorithm is available at the web link: http://mlsp.umbc.edu/resources.

IV. Experiments

A. Joint BSS on simulated datasets

1) Generation of the group datasets

We generate K groups of sources with samples drawn randomly from a Laplacian distribution. Each group contains M sources. A positive definite matrix Σ_k is randomly generated for the kth group of sources. A linear transformation C_k is then applied to each group of sources to impose a correlation structure specified by Σ_k so that the sources form the group of corresponding sources. Specifically, we use ${\mathbf{C}}_k=\mathbf{E}\ast {\mathrm{\Lambda }}^{\frac{1}{2}}$ where E and Λ are eigenvector and eigenvalue matrices of Σ_k. Across different groups k = 1, 2, …, K, the entry values in the correlation matrix Σ_k are generated in decreasing order. One source from each group is picked out to form the set of K latent sources for one dataset. The K sources are then mixed by a randomly generated K × K nonsingular mixing matrix.

2) Factors related to the separation performance

We study the performance of joint BSS by M-CCA method with respect to the following three factors. (i) The number of datasets incorporated in the joint BSS, (ii) The homogeneity of correlation values within the group of corresponding sources, and (iii) Real valued sources and complex-valued sources with circular and non-circular distributions.

3) Measure of performance and comparison with reference methods

Ten Monte Carlo trials are performed with different realizations of the sources and mixing matrices in each trial. The performance of the BSS algorithm is evaluated using the normalized inter-symbol interference (ISI) [10]

$$\text{ISI}=\frac{1}{2K(K-1)}\left[\sum _{i=1}^K\left(\sum _{j=1}^K\frac{\mid g_{ij}\mid }{{max}_k\mid g_{ik}\mid }-1\right)+\sum _{j=1}^K\left(\sum _{i=1}^K\frac{\mid g_{ij}\mid }{{max}_k\mid g_{kj}\mid }-1\right)\right]$$

where G = {g_ij} is the global matrix, i.e., the product of estimated demixing matrix and true mixing matrix. In the case of joint BSS on multiple datasets, the coherence of the source separation among different datasets should also be taken into account. Therefore, we calculate ISI based on the average global matrix of all datasets. When the sources are jointly separated for all datasets, the estimated global matrices for all datasets should be close to an identity matrix up to the same permutation. Correspondingly, the ISI for a successful joint BSS is close to zero.

We compare the performance of Group ICA, IVA, and M-CCA in each simulated case.

4) Experimental results

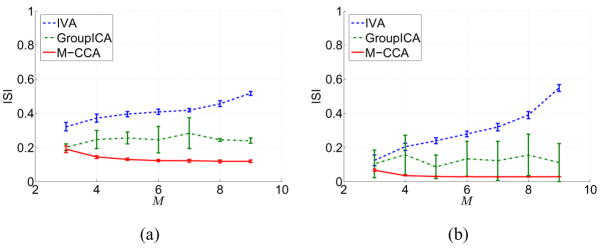
1. We test the estimation of different number of simulated datasets in a joint BSS scheme by the three algorithms and calculate ISI as shown in Fig. 2. It is observed that the performance of M-CCA improves as the number of datasets increases from M = 2 to M = 8 and saturates for M > 8. The observation agrees with the separability condition of M-CCA in that, when the number of datasets increases, the separability condition becomes more relaxed and the chance for a given dataset to have distinct source correlation values with at least one other dataset is increased. For large number of datasets, the separability condition is always easy to satisfy, therefore, the performance does not improve as the number of datasets further increases and the residual separation error is due to finite sample size effect.

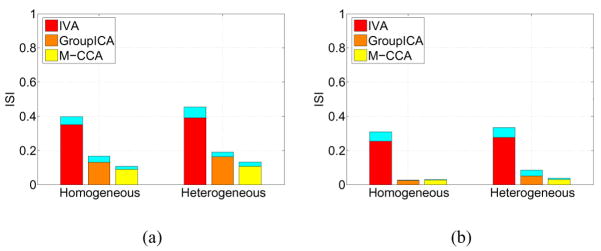
2. Although it is natural to expect the between-set correlation values to be similar within a group of corresponding sources, there might be correlation values that are significantly different for certain sources in the group due to, e.g., the existence of outliers. To test the performance of source separation in this more general case, we inject, within each group, a set of sources with correlation values significantly different from the other sources in the group so that the entries in the correlation matrix are distributed heterogeneously.

   Fig. 3 shows a performance comparison for joint separation of sources with homogeneous and heterogeneous correlation values. The performance of Group ICA degrades in the presence of heterogeneous source correlation values while the performance of M-CCA is not affected by the heterogeneous correlation values. In the first step of Group ICA, a set of common source factors representing each group of corresponding sources is found by performing group dimension reduction on concatenated data using PCA. In the second step, ICA is applied within the subspace of common source factors to maximize the independence. When there are outliers in the group of corresponding sources, Group ICA is not able to handle those outliers since group dimension reduction keeps only the dominating common factors while ignoring the outliers due to their insignificant contribution to the common factor. Therefore, it is reasonable to observe that the joint BSS performance of Group ICA degrades in the case of heterogeneous source correlation.

3. It is worth noting that Group ICA, IVA, and M-CCA are all capable of analyzing complex-valued data. This includes complex-valued sources, complex-valued mixing matrices, or both complex-valued sources and mixing matrices.

Fig. 2.

Source separation ISI of Group ICA, IVA, and M-CCA on different number of datasets M with K = 40 sources within each dataset and two sample size (a) N = 360 and (b) N = 3600

Fig. 3.

Source separation ISI of Group ICA, IVA, and M-CCA of group dataset containing sources with homogeneous and heterogeneous correlation values. Number of datasets M = 16, K = 20 sources within each dataset and two sample size (a) N = 360 and (b) N = 3600

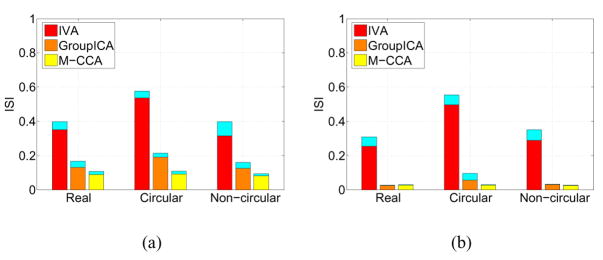
Since our implementation of Group ICA uses the Infomax (or maximum likelihood) ICA algorithm [5] to estimate group level sources, matching the nonlinearity to source distribution improves the performance. One important classification of complex source distribution is based on circularity. A complex source distribution is circular when its probability density is a function of only the source magnitude. Relation between nonlinear functions for Infomax ICA algorithm and complex-valued source distributions is studied in [11]. In our experiments, we use arctan(·) nonlinearity for Group ICA when the simulated complex-valued sources have non-circular distributions as it has been noted to provide robust separation performance. We use the nonlinear function proposed in [12] when the sources have circular distributions.

For IVA and M-CCA algorithms, on the other hand, no additional configuration is needed when processing the complex-valued data.

Fig. 4 shows the performance comparison for joint BSS on real, complex circular and complex non-circular sources. It is observed that M-CCA performance is robust to both real and complex-valued sources, as well as complex-valued sources with circular and non-circular distributions. The performance of Group ICA slightly degrades when the complex-valued sources are circular. The performance difference between M-CCA and Group ICA is more significant for small sample size N = 360, because M-CCA achieves joint BSS by second order statistics of the sources while Group ICA and IVA both implicitly use higher order statistics.

Fig. 4.

Source separation ISI of Group ICA, IVA, and M-CCA of group datasets containing real valued sources, complex circular sources, and complex non-circular sources. Number of datasets M = 16, K = 20 sources within each dataset and two sample size (a) N = 360 and (b) N = 3600

In all cases, the performance of IVA is poor on the simulated datasets. This is likely to be caused by the uncorrelatedness assumption on the group of corresponding sources in the IVA model. Figure 5 shows the 2D scatter plot of a pair of corresponding sources from the simulated datasets. It is observed that the pair of sources assume correlation whereas in IVA, the corresponding sources within an independent source vector are assumed to have a multivariate distribution with no second-order dependence [3]. Although higher-order dependence is a valid assumption, in this work, we focus on second-order dependence among the corresponding sources and use it to achieve joint BSS.

Fig. 5.

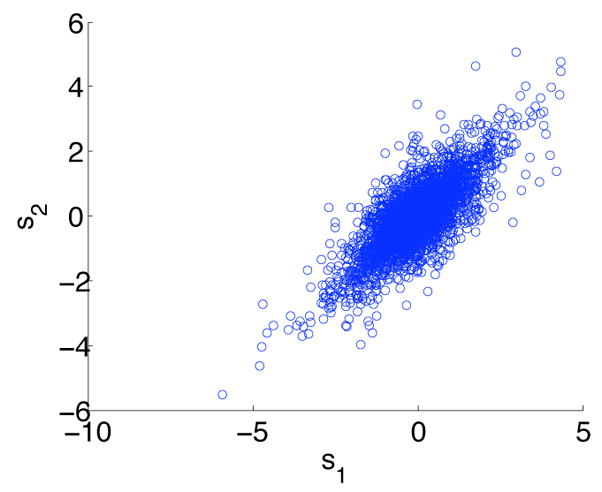
Two dimensional scatter plot of a pair of corresponding sources from the simulated dataset, sources have Laplacian distribution with sample size N = 3600

It is worth noting that correlation structure could be incorporated into the multivariate source vector distribution in IVA, at the expense of increased algorithm complexity. However, we would like to note that the correlation structure has to be either pre-specified or estimated by an algorithm such as M-CCA. This is an interesting topic by itself and worth further investigation.

B. Joint BSS on a group of fMRI datasets

1) fMRI data acquisition

Twelve right handed participants with normal vision – six females, six males, average age 30 years – participated in the study. Subjects performed a visuomotor task involving two identical but spatially offset, periodic, visual stimulus, shifted by 20 seconds from one another. The visual stimuli were projected via an LCD projector onto a rear-projection screen subtending approximately 25 degrees of visual field, visible via a mirror attached to the MRI head coil. The stimuli consisted of an 8 Hz reversing checkerboard pattern presented for 15 seconds in the right visual hemifield, followed by 5 seconds of an asterisk fixation, followed by 15 seconds of checkerboard presented to the left visual hemifield, followed by 20 seconds of asterisk fixation. The 55 second set of events was repeated four times for a total of 220 seconds. The motor stimuli consisted of participants touching their thumb to each of their four fingers sequentially, back and forth, at a self-paced rate using the hand on the same side on which the visual stimulus is presented.

Scans were acquired at the Olin Neuropsychiatry Research Center at the Institute of the Living on a Siemens Allegra 3T dedicated head scanner equipped with a 40mT/m gradients and a standard quadrature head coil. The functional scans were acquired using gradient-echo echo planar imaging with the following parameters: repeat time (TR) = 1.50s, echo time (TE) = 27 ms, field of view = 24 cm, acquisition matrix = 64 × 64, flip angle = 60 degrees, slice thickness = 4mm, gap = 1mm, 28 slices, ascending acquisition. Six ‘dummy’ scans were performed at the beginning to allow for longitudinal equilibrium, after which the paradigm was automatically triggered to start by the scanner.

A total number of twelve datasets are jointly analyzed. Each dataset is preprocessed according to typical fMRI analysis procedures consisting of slice timing correction, image registration, motion correction, smoothing, whitening, and dimension reduction [13]. Thirty-two normalized principal components are retained for each dataset and M-CCA is applied to the twelve sets of retained principal components.

We present two sources of interest from the M-CCA and Group ICA estimation results: (i) a source showing activation at inferior parietal lobule, posterior cingulate, and medial frontal gyrus (this set of regions is called the “default mode” network which tends to be less active during the performance of a task [14]), and (ii) the pre- and post-central gyrus (motor cortex) and occipital lobe (primary visual cortex).

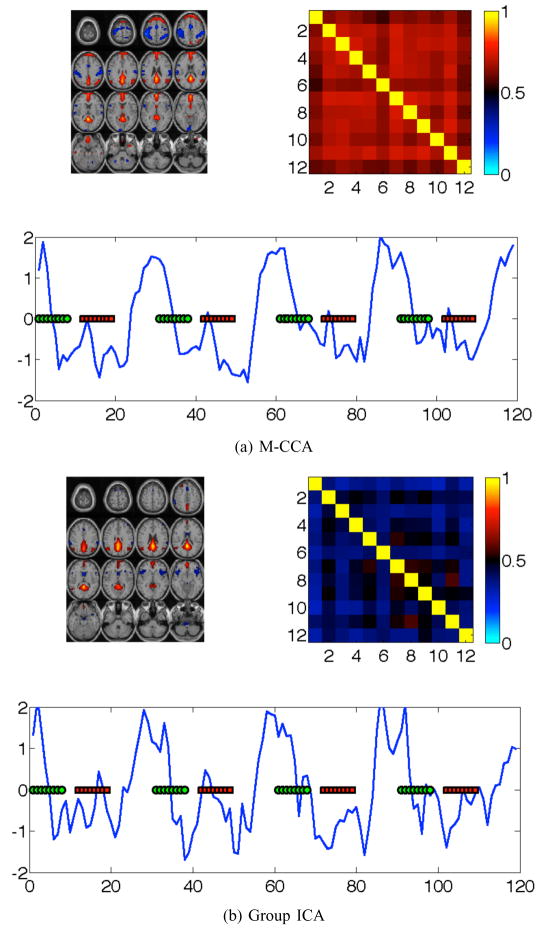
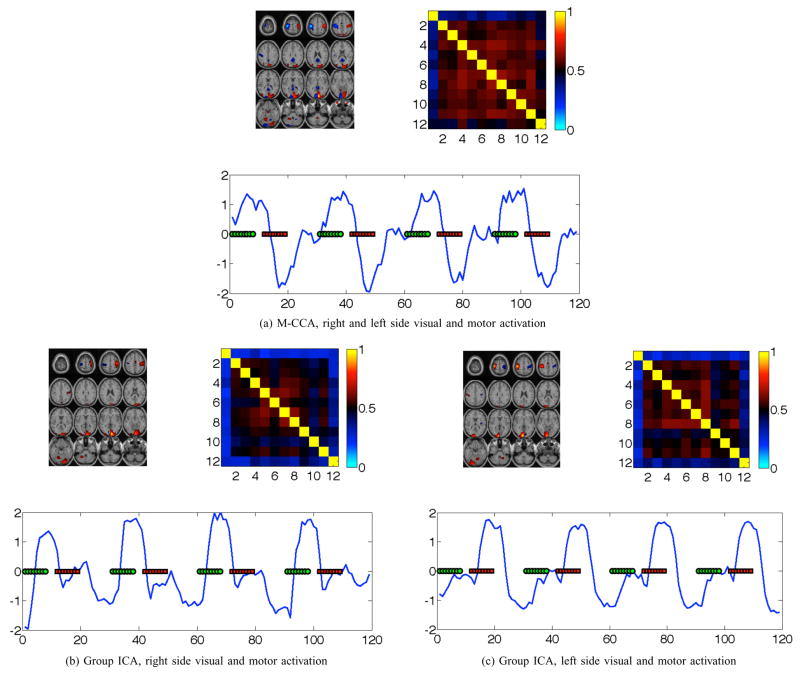
The estimated mean activation maps over all datasets, image of the cross-subject source correlation matrices, and the mean time course are displayed in Figures 6 and 7. The right and left side visuomotor task paradigm is overlaid onto the estimated time courses for reference. The results obtained by M-CCA are presented on the upper row and Group ICA on the lower row.

Fig. 6.

Estimated mean activation maps (top left), source correlation between subjects (top right), and time course (bottom) of the default mode by (a) M-CCA and (b) Group ICA. The right (Green circle) and left (Red block) visuomotor task paradigm is overlaid onto the estimated time courses for reference.

Fig. 7.

Estimated mean activation maps (top left), source correlation between subjects (top right), and time course (bottom) of visual and motor activation by (a) M-CCA and (b)–(c) Group ICA. The right (Green circle) and left (Red block) visuomotor task paradigm is overlaid onto the estimated time courses for reference.

For component (i), the estimated sources by M-CCA and Group ICA are shown in Figure 6. It is observed that the spatial map estimated by M-CCA shows higher cross-subject correlation level than Group ICA. The time courses of default mode estimated by M-CCA and Group ICA both show expected negative correlation against the onset of the visuomotor task. Furthermore, a multiple linear regression is performed on the estimated time course with the right (R) and left (L) visuomotor paradigm regressors. It is observed that time course estimated by M-CCA has more significant regression coefficients with the task paradigms, i.e., M-CCA (R): −0.52 with estimated confidence interval (CI): [−0.38,−0.65] and (L): −0.87 CI: [−0.74, −1.01]; Group ICA (R): −0.45 CI: [−0.28, −0.62] and (L) −0.60 CI:[−0.43, −0.77]. Hence M-CCA achieves higher consistency on spatial activation region and also the time courses show a higher correlation with the task paradigm.. The agreement on the spatial and temporal features suggests that default mode network is a common feature across all subjects that is driven by both left and right visuomotor task.

For component (ii), the estimated sources by M-CCA and Group ICA are shown in Figure 7. It is observed that the motor and visual activation on the right and left side of the cerebrum are estimated as one component by M-CCA, whereas in Group ICA, these activation regions are estimated as two independent components. ICA estimates sources with maximal non-Gaussian distributions, which is closely related to the sparsity of the identified regions in the brain activation map. Hence, the right and left side visual and motor activation regions are estimated by ICA as two separate components. On the other hand, M-CCA emphasizes consistency of the activation region across subjects. The sign of the right and left side activation regions are relative due to the sign ambiguity of BSS. Hence, the right and left side activation regions form a network that represent a consistent task-related feature of the group.

In summary, we present preliminary results of M-CCA as an alternative data-driven method for fMRI analysis and show that, in contrast to Group ICA, M-CCA emphasizes the similarity of components and thus estimates brain networks that are more consistently activated across subjects.

V. Discussion

In this work, we propose a joint BSS method using M-CCA. The method has the advantages that the source separation performance improves as the number of dataset increases. The method outperforms the existing group analysis methods in jointly separating group of corresponding sources with heterogeneous correlation values or, in case of complex-valued data, when sources have circular and non-circular distributions. The method is thus promising for application to signal processing problems where the coherence of the source estimates from multiple datasets is required.

Although the proposed method does not explicitly incorporate noise in the model, noise is addressed in the pre-processing step through a decomposition of each dataset into a signal subspace and a noise subspace [13]. Therefore, the joint BSS procedure is only applied within the signal subspace, as demonstrated in the analysis of the group fMRI data in IV-B.

In the following, we discuss several topics relevant to the M-CCA method.

A. Relation between M-CCA and “Carroll’s procedure”

PCA applied to the temporal concatenation of multiple datasets is implemented as a major step in Group ICA to obtain the subspace of common source factors. In [1] p441–442, this PCA scheme is called “Carroll’s procedure” and compared with the two eigenvalue-based M-CCA objective functions, MAXVAR and MINVAR. The eigenvectors obtained by PCA on the concatenated data can be segmented and normalized to obtain a set of transformation vectors that, when applied to each dataset, achieve a result similar to M-CCA.

When there are outliers in the group of corresponding source, multiple eigenvalues of R⁽¹⁾, …, R^(k−1) could be greater or equal to λ_max(R^(k)). Since “Carroll’s procedure” directly selects the first K largest eigenvalues of R_s and uses their associated eigenvectors to form the K groups of canonical transformations, the performance of group ICA is liable to degrade in presence of outlier sources.

In contrast, when separating the kth group of corresponding sources, the orthogonality constraints imposed in MAXVAR and MINVAR objective, i.e., $s_m^{(k)}\perp \{s_m^{(1)},s_m^{(2)},\dots ,s_m^{(k-1)}\}$, m = 1, 2, …, M exclude any eigenvector of R⁽¹⁾, …, R^(k−1) associated with an eigenvalue that is greater or equal to λ_max(R^(k)). Therefore, the performance of M-CCA is robust to the presence of outlier sources, which is observed in Section IV-A.4-(ii).

B. Comparison of M-CCA and CCA for joint BSS

When M-CCA and CCA are applied to joint BSS on datasets under the generative model in Section II-A, M-CCA has the advantage that the separability condition is relaxed as the number of datasets incorporated into the analysis is increased and correspondingly, the source separation performance is improved. This is observed in the results of the source separation experiments on simulated datasets in Section IV-A.4-(i).

On the other hand, the generative model and the separability condition together suggest that M-CCA can be decomposed into a set of CCA procedures on certain dataset pairs that satisfy the distinct correlation value condition. The estimates of the corresponding sources from all datasets can then be selected by matching and combining those pairwise CCA results. In practical data analysis, however, this idea is not feasible because the latent sources in the datasets may not strictly follow the generative model.

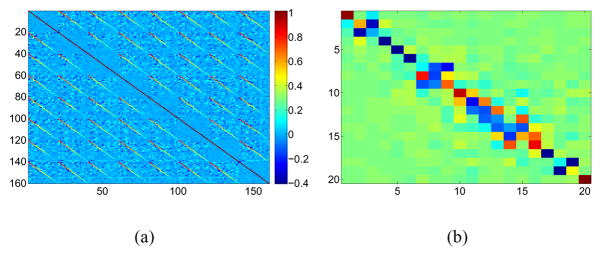
As an example, we generate M = 8 datasets with K = 20 sources in each dataset using the method described in IV-A.1. Fig. 8 shows joint BSS results on the generated datasets by M-CCA and multiple pairwise CCA. When the sources are not strictly uncorrelated across different indices, M-CCA keeps the coherence of the corresponding source estimates as it considers all the datasets during each correlation maximization stage, as shown in Fig. 8(a). On the other hand, pairwise CCA achieves exact diagonalization on the cross-correlation matrix of each specific dataset pair. Therefore, the sources from a dataset may have inconsistent estimates depending on the dataset it is paired with for the CCA procedure, as shown in Fig. 8(b).

Fig. 8.

(a) Correlation matrix of the all source estimates of all datasets by M-CCA, (b) Correlation matrix of the source estimates from x₁ by two different CCA procedures s₁ = CCA(x₁, x₂) vs. ${\mathbf{s}}_1^{\prime }=\text{CCA}({\mathbf{x}}_1,{\mathbf{x}}_3)$

C. Robustness of the M-CCA algorithm

There are five objective functions for M-CCA, MAXVAR, MINVAR, SUMCOR, SSQCOR, and GENVAR. Among these objective functions, MAXVAR and MINVAR lead to direct solutions. M-CCA algorithm based on the other three objective functions, SUMCOR, SSQCOR, and GENVAR utilizes iterative procedures to optimize the objective and hence the initial condition has an impact on the solution.

In order to test the robustness of the iterative M-CCA solutions to different initial conditions, we generate simulated group datasets and apply the iterative M-CCA algorithm based on SSQCOR as discussed in Section III-B. We perform multiple Monte Carlo trials of the algorithm on the same simulated datasets. In each trial, a random initialization is given to the demixing vectors to start the iterative optimization of the objective function. We calculate the Euclidean distance among the estimated demixing vectors for the same source at different trials.

It is observed that M-CCA solutions using SSQCOR objective is robust for both homogeneous and heterogeneous correlation structures, real and complex valued data types, as well as complex circular and non-circular distributions. The Matlab implementation of M-CCA mentioned in Section III-B is ready for this robustness test.

D. Relation between joint BSS by M-CCA and BSS based on secondorder statistics

The source separability conditions in this work are developed in a way similar to the BSS methods based on second-order statistics [15], where the distinction on autocorrelation structures of individual source signals is exploited to achieve BSS. In [15], sources in a dataset are simultaneously separated by one set of demixing vectors that approximately jointly diagonalize a group of covariance matrices at different time delays using the Jacobi technique. In our approach, on the other hand, multiple sets of demixing vectors are obtained by M-CCA to achieve approximate joint diagonalization on the cross-correlation matrices of all dataset pairs.

E. Other relevant works on CCA for BSS

CCA has been used for BSS on a single dataset by maximizing the auto-correlation of extracted sources [16], [17] and exploratory analysis of fMRI data [18]. The underlying assumption is that individual sources have higher autocorrelation values than their mixtures. A constrained CCA is applied to incorporate spatial information into fMRI analysis based on general linear model [19]. In our approach, the correlation is maximized among the corresponding sources extracted from multiple datasets and the autocorrelation of latent sources is not required.

M-CCA has been used in kernel-based methods to achieve ICA [20], which is known as kernel ICA and applied to analyze heterogeneous datasets [21]. In kernel ICA, M-CCA is used for finding the mutual information upper bound among multiple latent sources in a high dimensional feature space. A demixing matrix is then found for minimization of the mutual information upper bound. In this way, performing ICA in a maximum likelihood framework does not require any assumption on the distribution of the latent sources. It is important to note that in this method only the first group of canonical variates, i.e., the group of canonical variates with the maximum correlation, are obtained by M-CCA and utilized to optimize the ICA estimation. In our approach, on the other hand, multiple groups of canonical variates are estimated by M-CCA as the jointly extracted sources from multiple datasets.

CCA have been studied in terms of minimum MSE solution and applied in blind equalization of SIMO and MIMO systems [22],[23]. CCA is developed as an adaptive algorithm in [24],[25],[26]. CCA can be posed as generalized eigenvalue (GEV) decomposition [9] and the adaptive version of GEV decomposition is studied in [27],[28].

Motivated by the multivariate generalization of mutual information, in [29], dependence among multiple random variables is described by a graph structure and the separation of the dependent components is posed as a density estimation problem to form the method of dependent component analysis (DCA).

F. Summary

In this work, we propose a joint BSS scheme that achieves source separation based on latent source correlation structures across a group of datasets. We study the source separability conditions derived from two objective functions for M-CCA. We show that the proposed joint BSS scheme outperforms existing group analysis methods for large number of datasets, heterogeneous source correlation values, and processing of complex-valued data. The application to realistic fMRI group analysis shows promising results for estimating brain activations.