Abstract
The anterior and posterior commissures (AC and PC) typically form the reference points of the stereotactic coordinate system. Hence any discussion of target localization is limited by the variability of AC and PC selection. In an earlier study, which was performed using manual selections of AC and PC by 43 neurosurgeons, we showed that intersurgeon variability has a substantial impact on the localization of deep brain stimulation targets. We have developed and validated a fully automatic and robust AC and PC selection system that can be routinely used clinically. In this study, we show that this system is capable of localizing the AC and PC points with an accuracy that is better than that achieved clinically by manual selection, 0.65 mm (95% confidence interval: 0.56–0.79) versus 1.21 mm (95% confidence interval: 0.91–1.47) for AC and 0.56 mm (95% confidence interval: 0.46–0.66) versus 1.06 mm (95% confidence interval: 0.82–1.26) for PC.
Key Words: Anterior and posterior commissures, Automatic selection, Intersurgeon variability, Atlas, Nonrigid registration, Deep brain stimulation
Introduction
Functional neurosurgical procedures such as deep brain stimulation (DBS) require precise targeting of small areas deep inside the brain. Traditionally, this involves the preoperative selection of an approximate target location, followed by intraoperative adjustments using signal recordings and stimulations. Preoperative target selection is achieved by either direct or indirect localization. Direct selection of the targets can be done visually by the surgeon using the patient's MRI scan or by automated selection methods such as those presented in D'Haese et al. [1]. Indirect selection of various targets uses standardized coordinates from an anatomical atlas such as the Schaltenbrand-Wahren atlas. Indirect target selection is commonly used when targets are not reliably visible on MRI. The definition of a standard coordinate system is also necessary for effective communication of target locations. The anterior and posterior commissures (AC and PC) have become the reference points in the traditional stereotactic coordinate system. Based on the standard convention of the Schaltenbrand-Wahren atlas, AC and PC are defined as 2 points in the midsagittal plane with the shortest intraventricular distance between the commissures [3]. The midcommissure point (MC), or the center point on the AC-PC line, is often used as the origin of the AC-PC reference system. Even though some neurosurgeons continue to localize the AC and PC on ventriculograms, most neurosurgeons today rely on MRI. Therefore, any discussion of target localization is limited by the variability of AC and PC selection. In a 2008 study [2], we used data from 43 neurosurgeons to quantify errors that occur in selecting the DBS targets because of inaccuracies in the manual selection of AC and PC points. The findings suggested the need for automated and robust methods for the localization of these points of reference. To that end we proposed an atlas-based method to predict the position of AC and PC automatically [4]. A similar technique has been proposed recently by Anbazhagan et al. [5]. In this article, we present a validation of the method we described in Pallavaram et al. [4], and we show that it is more accurate than routine manual selection.
Dataset
With Institutional Review Board (Vanderbilt University IRB No. 060232) approval, a preoperative 3-dimensional MRI scan (TR = 12.2 ms, TE = 2.4 ms, 256 × 256 × 170 voxels, with typical voxel resolution of 1 × 1 × 1 mm3) was acquired for each patient using the Sense parallel imaging technique (T1-weighted/3-dimensional/turbo field echo) from Philips on a 3T scanner. These images were acquired with the patient anesthetized and the head taped to the table to minimize motion. The study presented herein includes 60 patients who underwent DBS surgery at our institution between December 2006 and January 2008.
Method
Atlas-Based Automatic AC and PC Predictions
An atlas-based method is used to predict automatically the position of AC and PC points. Atlas-based techniques require 2 main components: (1) reference image volumes in which points or structures of interest have been localized and (2) registration algorithms, which permit the spatial realignment of the reference volumes to other image volumes in which the structures or points of interest need to be localized. Reference volumes in which the points of interests have been localized will be referred to as atlases in the remainder of the text. In this work, automatic spatial realignment or registration between image volumes is achieved in 2 steps. First, the volumes are realigned using an affine transformation (rotation, translation and anisotropic scaling). This is followed by a nonrigid registration step. In this study, nonrigid registration is performed with the adaptive bases algorithm proposed by Rhode et al. [6]. Briefly, this algorithm computes a deformation field that is modeled as a linear combination of radial basis functions with finite support. This results in a transformation with several thousands of degrees of freedom. Two transformations (one from the atlas to the subject and the other from the subject to the atlas) are computed simultaneously and constrained to be inverses of each other. Both the rigid and nonrigid registration algorithms are mutual information-based [7, 8].
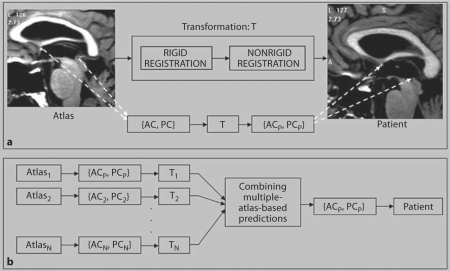
Using this method, AC and PC points selected on an atlas volume can be projected onto a patient's volume to predict these points on that particular patient. Figure 1a illustrates this concept for a given atlas. Atlas AC and PC are projected onto the patient using a transformation (T) which is the result of rigid and nonrigid registrations between the atlas and the patient. This leads to the automatic localization of the anterior and posterior commissures in the patient (ACP and PCP).
Fig. 1.
a Atlas-based automatic method for predicting the anterior and posterior commissures on a patient (ACP, PCP) by applying a transformation T (result of rigid and nonrigid registration between atlas and patient) to the atlas points (AC, PC). b Using multiple atlases to produce optimal AC and PC predictions by combining the individual-atlas-based predictions generated using the approach shown in a.
Multiple-Atlas-Based Automatic AC and PC Predictions
As others have observed (see for instance the work of Rohlfing et al. [9]), registration accuracy achievable by nonrigid registration may be influenced by morphological differences between the volumes to be registered. It is now relatively common to rely on outputs of several atlases to perform atlas-based segmentation [1, 9, 10]. To study the impact of the choice of an atlas on the process accuracy, we have used 4 MRI image volumes as atlases. Three of these were patient volumes, which differed in size and/or shape (both overall and at specific structures like the ventricles). The fourth one was a synthetic volume generated by averaging 20 patient volumes using the method proposed by Guimond et al. [11]. This is an iterative technique which starts with one of the volumes as a target and converges toward a volume that is representative of the population as a whole.
Figure 1b illustrates the extension of the single-atlas approach described in the previous section to a multiple-atlas approach. The AC and PC points selected on each of the N atlases (AC1 and PC1, AC2 and PC2, …, ACN and PCN) are projected onto the patient volume using the transformation between the respective atlas and the patient volume. These multiple predictions are then combined to produce the automatic prediction of the commissural points. The easiest way to combine the predictions from each atlas is to compute their average and use it as the optimal prediction. The drawback of this approach is that the predictions made by all the atlases are weighted equally, regardless of the quality of the registrations. In a 2005 study [12], we proposed an alternative approach in which the quality of the registration at a given location (subthalamic nucleus) was determined indirectly by estimating the quality of the segmentation of structures surrounding that location (thalamus, globus pallidus and putamen). The measure of the quality of the segmentation is given by the specificity and sensitivity of the segmentations obtained with each atlas on these structures. These are computed according to the Simultaneous Truth and Performance Level Estimation (STAPLE) algorithm proposed by Warfield et al. [10]. The specificity and sensitivity values are then used to weigh the contribution of each atlas to the optimal prediction while eliminating the contributions of atlases that produce low sensitivity values for the structures (i.e. atlases that lead to poor segmentation results for structures surrounding the location of interest).
Manual Localization of the Points on the Atlases
As shown in Pallavaram et al. [2], there is substantial intersurgeon variability in the manual selection of the AC and PC points, which complicates the creation of atlases. Indeed, errors in the localization of the AC and PC points in the atlases produce prediction errors independent of the registration accuracy. To minimize the effect of localization errors in the atlases, 2 neurosurgeons, coauthors P.E.K. and J.S.N., were asked to carefully select AC and PC on each of the atlases without any time constraints. For each atlas, the reference AC and PC points were computed as the average of the selections by the 2 neurosurgeons.
Evaluating Accuracy of Automatic AC and PC Predictions against Clinical Selections
We evaluated our automatic predictions of AC and PC points against clinical manual selections on 60 DBS patients. Thirty of these patients were operated on by one neurosurgeon and 30 by the other. The preoperative plans for these patients, which included clinical manual selection of AC and PC points, were generated by the neurosurgeon who performed the procedure. These clinical manual selections of the AC and PC points will be referred to as clinical selections. For each patient, using the preoperative MRI scan of the head, we generated automatic predictions of AC and PC using the individual- and the multiple-atlas-based methods described earlier. The accuracy of atlas-based automatic predictions (individual- as well as multiple-atlas-based) was evaluated by measuring the euclidian distance between the automatic predictions and clinical selections.
Need for a Standard to Evaluate AC and PC Prediction Accuracy
Planning for a DBS procedure is typically performed under time constraints. Thus, the clinical selections of AC and PC may not always be absolutely accurate. Consequently, measuring the distances between atlas-based predictions and clinical selections will not be conclusive in determining the accuracy of atlas-based predictions. To address this issue, a gold standard needs to be defined to which automatic AC and PC predictions and manual clinical selections can be compared.
Creation of the Gold Standard to Evaluate Prediction Accuracy
To create the AC and PC gold standards, the following method was applied. Due to the time-consuming nature of this technique, we selected 20 patients out of the 60 used in this study. First, 10 of the 30 patients operated on by one of the neurosurgeons and 10 of the 30 patients operated on by the other neurosurgeon were selected randomly. Each of these patients already had AC and PC selected clinically by the operating neurosurgeon at the time of surgical planning. On these 20 volumes, both neurosurgeons were asked to carefully select AC and PC points in the laboratory without time constraints, using the same software tool that served to create the atlases. Localization was performed independently by both neurosurgeons, and they did not have access to the points that were selected by them clinically. This experiment created 2 new sets of AC and PC selections (1 per neurosurgeon) on each of the 20 patients. These new selections can be considered to be the best achievable manual selections, henceforth referred to as the silver standards (SlvStd1 and SlvStd2). The average of the 2 silvers standards on a given patient is the gold standard for that patient.
Statistical Analysis
The accuracy of various selection methods was computed by comparing the distances between the selections and the corresponding reference points. Comparisons between these distances were conducted with a Wilcoxon signed-rank test to account for dependency between the values observed on the same patient. The Wilcoxon signed-rank test is a nonparametric statistical hypothesis test for the case of 2 related samples or repeated measurements on a single sample. It is used as an alternative to the paired Student t test when the population cannot be assumed to be normally distributed. The distances were summarized with the median and the lower and upper quartiles. R version 2.7.0 [13] was used for all statistical analyses.
Results
Comparing Single- and Multiple-Atlas-Based Predictions to Clinical Selections
The accuracy, with respect to clinical selections, of average multiple-atlas-based predictions and multiple-atlas-based predictions using STAPLE was compared. These 2 methods of combining predictions were not statistically different for AC (p = 0.48) and MC (p = 0.49). For PC the average method produced a smaller prediction error with respect to the clinical selection than the STAPLE method on 41 among the 60 patients (68%). This difference at PC was statistically significant (p < 0.001) based on a Wilcoxon signed-rank test, which takes into account the rank (1 or 2) within the pair (average and STAPLE) for each patient. The mean difference (STAPLE-based prediction errors – average-based prediction errors), however, is only 0.037 (95% confidence interval: 0.014–0.090), but the average method led to large errors in 1 patient because one of the atlases registered poorly to this image volume. In this patient, the error using the average method was 8.40 mm at AC and 2.16 mm at PC, while the error using the STAPLE for the same patient was 0.57 mm at AC and 0.93 mm at PC. Since the difference in accuracy between the STAPLE and the simple averaging method is very small and because the STAPLE approach is better at eliminating outliers, we have used it in the rest of this study.
Table 1 summarizes the prediction errors for individual- and for multiple-atlas-based prediction using STAPLE with respect to clinical selections on 60 patients. The median error with the lower and upper quartile values are provided. The p values comparing the prediction errors of individual atlas predictions with those of multiple- atlas-based predictions using STAPLE are also given. The superiority of the multiple-atlas-based method using STAPLE is highly statistically significant over atlas 1 for AC and MC, and over atlases 2, 3 and 4 for PC.
Table 1.
The prediction errors (millimeters) of individual-atlas and STAPLE-based multiple-atlas approaches with respect to clinical selections in 60 patient volumes are summarized with the medians (lower and upper quartile values in parentheses)
| Multiple-atlas-based prediction using STAPLE | Atlas-1-based prediction | Atlas-2-based prediction | Atlas-3-based prediction | Atlas-4-based prediction | |
|---|---|---|---|---|---|
| AC | 1.07 (0.70, 1.43) | 1.21 (1.02, 1.69) | 1.04 (0.69, 1.42) | 1.03 (0.68, 1.48) | 1.21 (0.70, 1.52) |
| p < 0.001 | p = 0.95 | p = 0.15 | p = 0.02 | ||
| PC | 0.94 (0.66, 1.21) | 1.02 (0.72, 1.39) | 1.03 (0.71, 1.38) | 1.10 (0.70, 1.58) | 1.11 (0.76, 1.39) |
| p = 0.52 | p = 0.008 | p = 0.008 | p < 0.001 | ||
| MC | 0.82 (0.55, 1.14) | 1.06 (0.78, 1.32) | 0.91 (0.55, 1.29) | 0.87 (0.55, 1.22) | 0.83 (0.64, 1.13) |
| p < 0.001 | p = 0.05 | p = 0.36 | p = 0.10 | ||
The p values of Wilcoxon signed-rank tests comparing the STAPLE-based prediction errors and individual-atlas-based prediction errors with respect to clinical selections are shown.
Comparison of the Atlas-Based Predictions and Clinical Selections against Silver Standards
Figure 2 shows representative results for the selection of AC. It illustrates the STAPLE-based atlas prediction (1), the gold standard (2) defined as the average between the careful selections by the 2 neurosurgeons (silver standards) (4) and the clinical selection (3), projected on the sagittal (left panel) and axial (right panel) slice passing through the gold standard point.
Fig. 2.
Representative AC selections. STAPLE-based prediction using multiple atlases (1), the gold standard (2), the clinical selection (3) and the careful selections by the 2 neurosurgeons (4) projected on the sagittal (left panel) and axial (right panel) slice passing through the gold standard point.
Table 2 summarizes the distances between pairwise combinations of multiple-atlas-based automatic predictions, clinical selections and the 2 silver standards. It reports, for AC, PC and MC, the median and the lower and upper quartiles of the euclidian distance in millimeters, between (a) the 2 silver standards (careful manual selections by the 2 surgeons); (b, c) the STAPLE-based atlas predictions and the silver standards, and (d, e) the clinical points and the 2 silver standards. The silver standards comparison (a) reflects the intersurgeon variability while carefully selecting the points manually. The p values comparing (a) with (b, c, d and e) using Wilcoxon signed-rank tests are also reported in table 2. The differences between clinical selections and the silver standards were statistically significant, thus indicating that the clinical selection is suboptimal. On the contrary, no statistical significance was found for the difference between the 2 silver standards (a) and that between STAPLE-based atlas predictions and silver standards (b and c). Although no conclusion can be drawn from large p values, based on these findings, we may conjecture that the atlas-based predictions are similar to an experienced neurosurgeon carefully selecting the points manually.
Table 2.
Median (lower and upper quartile values in parentheses) of the euclidian distances between various types of selections, silver standards (SlvStd1 and SlvStd2), multiple-atlas-based predictions using STAPLE (atlas) and clinical selections, of the AC, PC and MC points over 20 patient volumes
| SlvStd1 vs. SlvStd2 | SlvStd1 vs. atlas | SlvStd2 vs. atlas | SlvStd1 vs. clinical | SlvStd2 vs. clinical | |
|---|---|---|---|---|---|
| (a) | (b) | (c) | (d) | (e) | |
| AC | 0.56 (0.44, 0.87) | 0.82 (0.57, 0.92) | 0.59 (0.43, 0.92) | 1.19 (1.00, 1.57) | 1.29 (0.89, 1.60) |
| p = 0.048 | p = 0.220 | p < 0.001 | p = 0.001 | ||
| PC | 0.55 (0.38, 0.91) | 0.63 (0.45, 0.97) | 0.57 (0.42, 0.80) | 1.08 (0.97, 1.27) | 1.00 (0.79, 1.19) |
| p = 0.598 | p = 0.812 | p = 0.001 | p = 0.030 | ||
| MC | 0.51 (0.34, 0.58) | 0.43 (0.33, 0.50) | 0.52 (0.27, 0.64) | 0.72 (0.60, 1.14) | 0.98 (0.72, 1.30) |
| p = 0.890 | p = 0.667 | p < 0.001 | p < 0.001 | ||
Distances in columns (b–e) are compared to distances in (a) using Wilcoxon signed-rank tests, and the corresponding p values are shown.
Accuracy of Atlas-Based Predictions and Clinical Selections against Gold Standards
Table 3 summarizes the key findings of our study. It shows, for the 20 volumes for which the AC and PC gold standards were available, the median euclidean distances with the lower and upper quartiles, in millimeters, between (a) the automatic predictions and the gold standards, and (b) the clinical selections and the gold standards. These numbers are reported for the AC, PC and MC points. With respect to the gold standard, the median distances of atlas predictions are only about half of that of clinical selections. Highly statistically significant differences were found between the accuracies of atlas predictions and those of the clinical selections with respect to the gold standards for AC (p = 0.007), PC (p < 0.001) and MC (p < 0.001). The results also show that atlas-based predictions are significantly more accurate than clinical selections with respect to the gold standard. Finally, the 95% confidence intervals of the median accuracy of atlas-based predictions with respect to the gold standards are 0.56–0.79, 0.46–0.66 and 0.33–0.50 mm, respectively for the AC, PC and MC. For the accuracy of clinical selections with respect to gold standards the 95% confidence intervals are 0.91–1.47, 0.82–1.26 and 0.68–1.20 mm, respectively, for AC, PC and MC.
Table 3.
Median (lower quartile, upper quartile) of the Euclidian distances between gold standards, clinical selections (Clinical), and multiple atlases based predictions using STAPLE (Atlas) for AC, PC, and MC points over 20 patient volumes
| Atlas vs. Gold Standard | Clinical vs. Gold Standard | |
|---|---|---|
| (a) | (b) | |
| AC | 0.65 (0.53, 0.84) | 1.21 (0.74, 1.56) |
| p = 0.007 | ||
| PC | 0.56 (0.42, 0.70) | 1.06 (0.81, 1.25) |
| p < 0.001 | ||
| MC | 0.41 (0.29, 0.53) | 0.84 (0.62, 1.11) |
| p < 0.001 | ||
Distances shown in column (a) and (b) are compared using a Wilcoxon signed-rank tests, and the corresponding p values are given.
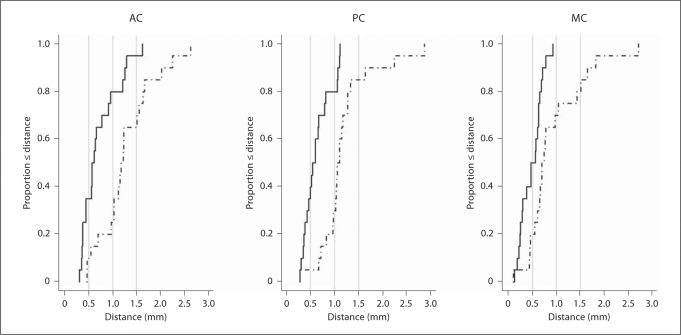
Figure 3 shows the cumulative distributions of the differences between atlas predictions and clinical selections with respect to the gold standard over the 20 volumes. The horizontal axis represents the distance in millimeters between the selections of a point (AC, PC or MC) using 2 different methods. The vertical axis represents the fraction of cases for whom the distance between the selections was less than or equal to the corresponding distance on the horizontal axis. Figure 3a shows that in about 80% of the cases the distance between atlas predictions and gold standard for AC is less than 1.0 mm; this is true in only 25% of the cases for the clinical selections. Figure 3b presents similar results for the PC. Figure 3c shows that in 100% of the cases the distance between atlas predictions and the gold standard for MC is submillimetric, while it is only true in about 70% of the cases for the clinical selections. This figure also illustrates that manual selection can lead to relatively large errors in the selection of the MC, which is commonly used as the center of the coordinate system in stereotactic surgeries.
Fig. 3.
Cumulative distributions of the euclidian distances between STAPLE-based predictions using multiple atlases and gold standards (solid line), between the gold standards and the points chosen clinically (dotted line) for AC, PC and MC on 20 patients.
Discussion and Conclusion
Selection of the AC and PC points is done routinely for DBS procedures. However, in a study [2] involving 43 neurosurgeons from different institutions, we have shown substantial intersurgeon variability in the selection of these points on 2 MRI volumes. We found that the surgeon's experience was a contributing factor to the selection accuracy of these points. We have shown that, while the MC point is commonly used as the origin of the stereotactic reference system, the accuracy of AC and PC selection affects the target localization accuracy. We found the mean intersurgeon variability in indirect targeting of subthalamic nucleus, Vim and GPi due to variability in AC and PC selection to be up to 2.64, 2.75 and 3.31 mm, respectively, for the 3 targets. Therefore, accurate AC and PC selection is critical in indirect targeting. Our work demonstrates that by carefully creating the atlases and by combining predictions from different atlases, a system can be developed that is not only fully automatic but also produces results that are more accurate and reproducible than those obtained by experienced physicians in clinical practice. The error distribution produced by our system is probably as good as what is achievable with the resolution of clinically acquired images. Our statistical analysis shows a slight gain in performance when using more than 1 atlas. With current computer speed and multicore processors, multiple-atlas approaches are thus recommended. When the registrations were reasonable, the STAPLE-based approach we have used to weigh more the atlases which registered well did not produce statistically better predictions than the average of the predictions. However, it was able to eliminate the contribution of atlases that registered poorly with a patient. Further work is necessary to develop a reliable and robust method to identify the atlas(es), which register(s) best to a particular patient.
The system we have presented is a component of a larger system, which is currently being developed at our institution to facilitate the planning and intraoperative guidance of DBS procedures. Following the retrospective validation study presented herein, a prospective analysis has been initiated to test the hypothesis that our system can be used routinely in the clinical setting, thus reducing the time required for planning and eliminating 1 source of variability in the communication of target point coordinates.
Acknowledgement
This research has been supported by NIH grant R01-EB006136.
References
- 1.D'Haese P-F, Cetinkaya E, Konrad PE, Kao C, Dawant BM. Computer-Aided Placement of Deep Brain Stimulators: From Planning to Intraoperative Guidance, IEEE Trans Med Imaging. 2005;11:1469–1478. doi: 10.1109/TMI.2005.856752. [DOI] [PubMed] [Google Scholar]
- 2.Pallavaram S, Yu H, Spooner J, D'Haese P-F, Bodenheimer B, Konrad PE, Dawant BM. Inter-surgeon variability in the selection of anterior and posterior commissures and its potential effects on target localization. Stereotact Funct Neurosurg. 2008;2:113–119. doi: 10.1159/000116215. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Schaltenbrand G, Wahren W. Atlas for Stereotaxy of the Human Brain. Stuttgart: Thieme; 1977. [Google Scholar]
- 4.Pallavaram S, Yu H, Spooner J, D'Haese P-F, Koyama T, Bodenheimer B, Konrad PE, Dawant BM. Automated selection of anterior and posterior commissures based on a deformable atlas and its evaluation based on manual selections by neurosurgeons. SPIE Med Imaging. 2007;28:65091C.1. [Google Scholar]
- 5.Anbazhagan P, Carass A, Bazin P-L, Prince JL: Automatic estimation of midsagittal plane and AC-PC alignment based on nonrigid registration. IEEE Int Symp on Biomed Imaging, Arlington, 2006, pp 828–831.
- 6.Rhode GK, Aldroubi A, Dawant BM. The adaptive bases algorithm for intensity-based nonrigid image registration. IEEE Trans Med Imaging. 2003;11:1470–1479. doi: 10.1109/TMI.2003.819299. [DOI] [PubMed] [Google Scholar]
- 7.Maes F, Collignon A, Suetens P. Multimodality image registration by maximization of mutual information. IEEE Trans Med Imaging. 1997;2:187–198. doi: 10.1109/42.563664. [DOI] [PubMed] [Google Scholar]
- 8.Wells WM, Viola P, Atsumi H, Nakajima S, Kikinis R. Multi-modal volume registration by maximization of mutual information. Med Image Analysis. 1996;1:35–51. doi: 10.1016/s1361-8415(01)80004-9. [DOI] [PubMed] [Google Scholar]
- 9.Rohlfing T, Russakoff DB, Maurer CR. Performance-based classifier combination in atlas-based image segmentation using Expectation-Maximization parameter estimation. IEEE Trans Med Imaging. 2004;8:983–994. doi: 10.1109/TMI.2004.830803. [DOI] [PubMed] [Google Scholar]
- 10.Warfield SK, Zou KH, Wells WM. Simultaneous Truth and Performance Level Estimation (STAPLE): an algorithm for the validation of image segmentation. IEEE Trans Med Imaging. 2004;7:903–921. doi: 10.1109/TMI.2004.828354. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Guimond A, Meunier J, Thirion JP. Average brain models: a convergence study, Comput Vis Image Underst. 2000;9:192–210. [Google Scholar]
- 12.D'Haese P-F, Pallavaram S, Kao C, Konrad PE, Dawant BM. Automatic selection of DBS target points using multiple electrophysiological atlases. Med Image Comput Comput Assist Interv Int Conf Med Image Comput Comput Assist Interv. 2005;8:427–434. doi: 10.1007/11566489_53. [DOI] [PubMed] [Google Scholar]
- 13.R Development Core Team . A Language and Environment for Statistical Computing. Vienna: R Foundation for Statistical Computing; 2008. R. [Google Scholar]