Gradient Moment Compensated Magnetic Resonance Spectroscopic Imaging

Abstract

Spectroscopic imaging applications outside of the brain can suffer from artifacts due to inherent long scan times and susceptibility to motion. A fast spectroscopic imaging sequence has been devised with reduced sensitivity to motion. The sequence uses oscillating readout gradients and acquires k-space data in a spiral out–in fashion, which allows fast k-space coverage. We show that a spiral out–in readout acquisition is characterized by small gradient moments, reducing sensitivity to motion-induced artifacts. Data are acquired comparing the sequence to normal phase encoded spectroscopic imaging and conventional spiral spectroscopic imaging protocols. In addition, in vivo data are acquired from the liver, demonstrating potential usage as a multivoxel fat/water spectroscopic imaging tool. Results indicate that in the presence of motion, ghosting effects are reduced while metabolite signal increases of approximately 10% can be achieved.

Although the majority of clinical applications for proton magnetic resonance spectroscopic imaging (MRSI) concerns diseases in the brain, magnetic resonance spectroscopy (MRS) of other organs are of increasing interest. However, several technical issues complicate the successful implementation of MRSI in tissues outside of the brain, including limited spatial coverage due to the long scan time and artifacts related to motion.

All inner organs are susceptible to cardiac and respiratory motion. For single-voxel MRS, motion causes phase variations in the multiple acquisitions, leading to decreased signal intensity upon averaging. Frequency shifts during the readout due to motion can lead to line-broadening of the spectra (1-5). For phase-encoded MRSI, ghosting artifacts, commonly noticed in magnetic resonance (MR) imaging, can also be observed in addition to the above-mentioned loss of signal-to-noise ratio (SNR) and spectral resolution (6-8).

One method of reducing motion artifacts commonly used in MR imaging is to compensate phase buildup during the readout period by using moment compensated gradients (9,10). This technique, also referred to as gradient moment nulling, involves modifying the readout gradient waveforms so as to make the sequence more immune to artifacts coming from both periodic and nonperiodic motion. When combined with phase-encoding gradients, displacements artifacts also can be eliminated (11). Although many MR imaging applications have benefited from this approach, an extension of this procedure to MRSI has yet to be demonstrated. Fast MRSI sequences, which are characterized by long readout times in the presence of oscillatory gradients, significantly benefit by reducing phase buildup during this time interval.

In this manuscript, we describe a fast MRSI sequence characterized by readout gradient waveforms with small gradient moments. The technique is devised by using a spiral readout k-space trajectory (12). In particular, the readout gradient is in the form of a spiral-out spiral-in waveform, which we show to have reduced moment buildup (13). Simulations and phantom experiments are presented, comparing this approach with other MRSI methods. Finally, in vivo data from the human liver are collected to illustrate a potential application of the method.

THEORY

A pictorial description of gradient moment nulling (flow compensation) is shown in Figure 1. Each gradient lobe is depicted by an impulse (arrow) positioned in time at the center of the lobe and with length equal to the lobe area (G-ms/cm). Flow or motion-compensated gradients should have a null net gradient area at the echo time and, additionally, be symmetric in time. The readout gradient waveform in Figure 1a is not flow compensated, whereas the waveform in Figure 1b is flow compensated (symmetric in time) (14,15).

FIG. 1.

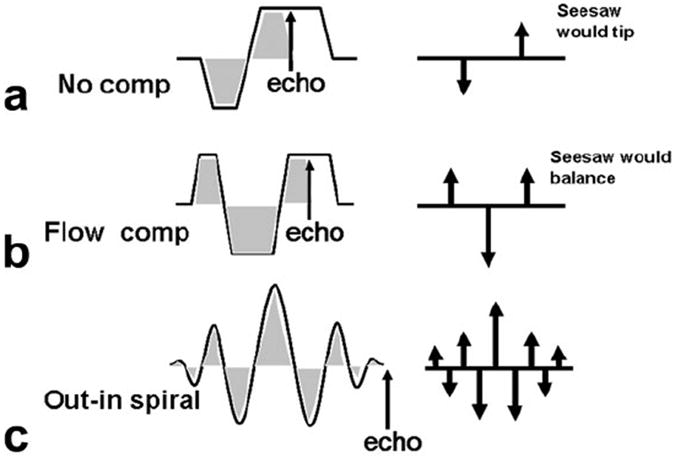
Gradient moment nulling scheme. a: During readout, gradient , weights are distributed (indicated by the arrows on the right). b: By the time the echo is formed, if these weights are symmetrically distributed, flow compensation is achieved. c: Spiral readouts for MRSI can be modified to achieve this symmetric weighting by using an out–in trajectory.

To achieve moment compensation for MRSI, we use a modified spiral k-space readout trajectory. In spiral MRSI, the spatial k-space data are acquired using spiral waveforms, which are repeated during the readout to obtain spectral information. These individual spirals are connected via rewinding gradients that bring the k-space trajectory back to the spatial k-space origin. In the presence of motion, however, unwanted phase can accrue due to nonzero gradient moments. As shown in Figure 1c, using an out–in spiral trajectory, which traverses out in k-space and then travels inward in a symmetric fashion time symmetric, we can achieve gradient moment nulling during the MRSI acquisition (16,17).

The basic gradient waveform for the out–in spiral trajectory is illustrated in Figure 2. The k-space trajectory as a function of time is shown on the left, while its projected traversal through spatial k-space is illustrated on the right. Shown on the top row is a conventional spiral trajectory accompanied with the rewinding lobes. Although the rewinding portion of the trajectory somewhat reduces the gradient moment, small amounts of phase can build up when the spiral lobes are repeated throughout the whole readout interval. However, the out–in spiral trajectory shown on the bottom row has reduced gradient moments due to the symmetric nature in terms of its k-space traversal path. The k-space trajectory can be divided into its k_x and k_y components. Although the gradients of each axis do not follow a perfectly symmetric path, the gradient moments of each axis are significantly smaller than the conventional spirals. It is worth noting that the effective field of view (FOV) of the out–in spiral is reduced in comparison to the conventional spirals by about a factor of 2 because the k-space sampling density is reduced for the same gradient duration and slew rate, but this can be compensated using spatial interleaving by additionally acquiring data with the spirals rotated by 180 degrees.

FIG. 2.

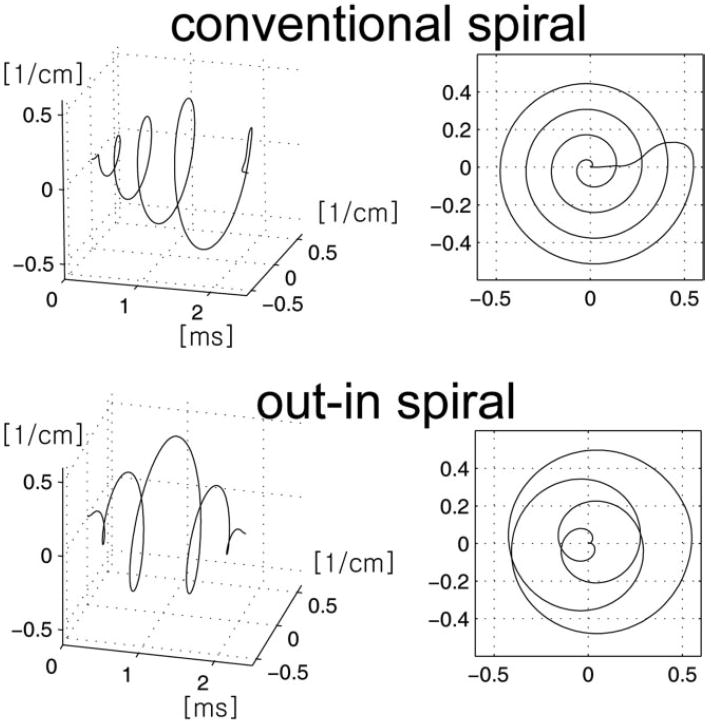
Illustrative example of the conventional spiral (top row) and out–in spiral (bottom row) used in MRSI. The left column shows spiral trajectory as a function of time, while the right column shows the projected trajectory on to the k_xy plane. In MRSI, spiral lobes are repeatedly played out during a readout; therefore, each spiral lobe ends at the k_x = k_y = 0 position. This is achieved using rewinders for the conventional spiral, while for the out–in spiral the symmetry of the gradients played out naturally returns the trajectory back to origin.

METHODS

Spiral out–in trajectories were designed and compared with conventional rewinder-based spiral MRSI and normal phase encoded MRSI. Both trajectories were designed using the analytic spiral design methods first described by Glover (18). Gradient moments (first and higher moments) were calculated and compared for spiral waveforms with matrix size parameters of 8 × 8, 16 × 16, and 32 × 32. To demonstrate the reduced ghosting artifacts, 16 × 16 voxel spiral out–in trajectory was compared with normal phase encoding readouts. Data were acquired with a PRESS excitation scheme on a moving brain MRS phantom(19). Therefore, the pulse sequence basically consisted of a 90°–90°–180° excitation scheme followed by the spiral readout. The echo time was 133 ms. Movement was induced by using a motion-generating feature available in our 1.5T scanner (GE Healthcare, Waukesha, WI, USA). The sinusoidal motion that was generated traveled 10 mm with peak velocity of 5 mm/s (frequency 0.25 Hz) similar to respiratory motion. The central 10 cm was prescribed by the PRESS box over a 20-cm FOV. The slice thickness was 1 cm. Data analysis was performed by examining the variation of the water spectra measured from both inside and outside the PRESS selected region.

For comparison with conventional rewinder-based MRSI, 32 × 32 matrix size spiral trajectories were used. First, simulations of the spectral point spread function were performed to estimate the amount of spectral ringing of a moving impulsive water component. By assuming that the impulse was located at δ² [x, y − x(t); y(t)] during data acquisition, where x(t) and y(t) correspond to the location of the impulse, raw data were simulated and reconstruction was performed on this data set. The impulsive water component was assumed to be centered at the origin moving periodically in the in-plane direction (Y direction) at 1 cm/s during readout. Data from a spectroscopy phantom were also collected with and without motion to evaluate the performance of both trajectories. Periodic motion similar to respiration was induced using the built-in table motion feature of our scanner. For both trajectories, the readout length was set to 0.5 s, with a total scan time of 2 min (echo time[TE]/pulse repetition time [TR] 133/ 1500 ms). The conventional spiral had approximately 350 lobes, and each lobe had length of 1.6 ms, whereas the out–in spiral had approximately 256 lobes and each lobe had length of 2 ms. Data analysis was performed by examining the average SNR of the N-acetyl aspartate (NAA) spectra measured from conventional and out–in spiral acquisitions.

Finally, to illustrate the potential for in vivo use, we applied our sequence to water/fat spectroscopic imaging of the body. In this example, we evaluated multivoxel spectroscopy of the human liver for imaging water and fat components, which can be a useful tool for liver fat assessment. Spiral-based MRSI data sets, both conventional and out–in spirals, were acquired using a phased array abdominal coil on healthy volunteers from an axial slice through the liver (TE/TR 133/1500 ms, 30 cm FOV with 10 cm PRESS box). For both cases, a 32 × 32 voxel over a 32-cm FOV acquisition was used to look at the distribution of water and fat components. The out–in trajectory requires twice the number of readouts compared to conventional spirals due to the factor of two decrease in the effective FOV (Fig. 2). For our experiment, the total imaging time was kept the same for both trajectories by acquiring multiple averages for the conventional spirals. The total scan time was therefore 1.5 min for each data set. No water suppression or spatial saturation pulses were used during the acquisition because the objective of the study was to evaluate the water and fat components explicitly. To the degree possible, volunteers were asked to take short breaths during the dead time of the sequence and to not breathe during pulse excitation and readout period.

All phantom and in vivo data sets were reconstructed with gridding, apodization, and inverse FFT in the k_x, k_y, and k_f directions. Prior to gridding, a phase correction scheme was used to further reduce any phase discrepancies (20). The Institutional Review Board (IRB) approved all in vivo studies.

RESULTS

In Figure 3, the first, second, and third moment for the conventional spiral (top row) and out–in spiral (bottom row) trajectories are indicated. The figure shows that compared to the conventional spiral trajectory, the moments of the out–in spirals ends near zero (as indicated by the asterisk “*” sign). This is true for not only the first moment, but also for higher moments as well. Out–in spiral trajectories with different matrix size gave similar results. During MRSI data acquisition, spiral lobes are repeatedly played out. Therefore, the moments of each spiral lobe will continue to accumulate during the readout interval. In the presence of motion, phase accrual due to nonzero moments leads to reduced SNR, increased line broadening, and enhanced ghosting artifacts.

FIG. 3.

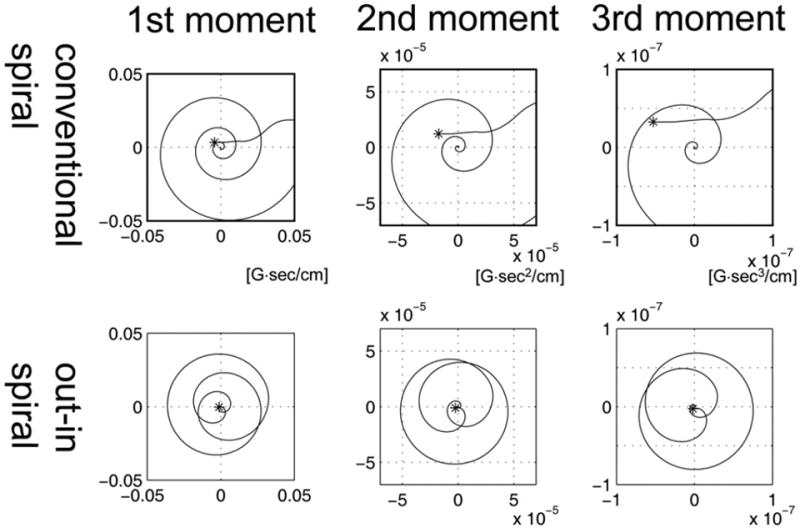
Gradient moments for the conventional spiral (top row) and out–in spiral (bottom row) during a single spiral lobe. Simulation results of the first (left column, linear motion model), second (middle column, acceleration model), and third (right column, jerk motion model) moments are shown. Out–in spirals have smaller nth moments (n = 1, 2, 3, …) compared to conventional spirals. Typical spiral readout in MRSI would have approximately 128 to 256 spiral lobes during a readout interval, which, in the presence of motion, will increase phase accrual leading to decreased signal and T₂* shortening.

Simulation of a moving impulsive object resulted in a spectral point-spread function indicating spectral ringing and line broadening to be more visible using the conventional spiral acquisition compared to the out–in spiral acquisition (spectrum not shown). A quantitative analysis showed that the relative SNR was 0.39 using the conventional spiral and 0.87 when using the out–in spiral assuming the relative motion-free SNR is 1.

Figure 4a shows the reconstructed water images from phantom experiments comparing normal phase encoded MRSI and out–in spiral MRSI along with the excited region of the PRESS box shown on the reconstructed water images. Phase-encoded MRSI gives ghost-like artifacts throughout the excited region while these are significantly reduced with the out–in spiral acquisition. Inside the excited region, the standard variation of water signal for phase-encoded MRSI was ±15.3% of the mean value while for out–in spiral MRSI, the standard variation of water signal reduced to ±10.2% of its mean value. Outside the PRESS excitation box, the average signal intensity level of water in this region for phase encoded MRSI was 47 ± 14% compared to the inside region, while this was reduced to 28.9 ± 14% for the out–in spiral acquisition indicating an ~18% reduction of the ghosting effect using out–in spiral MRSI.

FIG. 4.

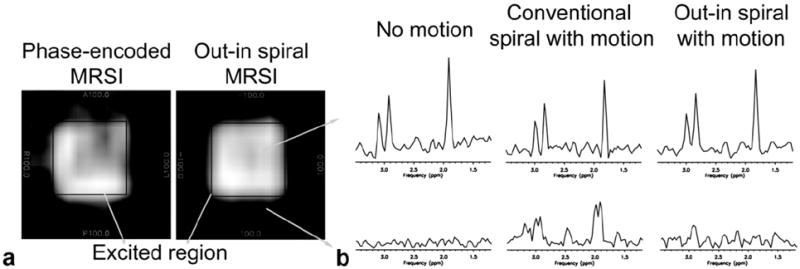
a: Reconstructed water phantom images from phase-encoded MRSI (left) and out–in spiral (right) acquisitions in the presence of motion similar to respiration. Due to motion, normal phase-encoded MRSI results in artifacts appearing outside the excited PRESS box. This is reduced with an out–in spiral acquisition. Motion was induced in the R–L direction. b: Representative metabolite spectra from a spectroscopy phantom experiment using conventional and out–in spiral. The top row illustrates spectra obtained from within the excited region. The reconstructed data using an out–in spiral has increased SNR and reduced artifacts compared to the conventional spiral readout.

Results using a spectroscopy phantom to illustrate the differences of the conventional and out–in spirals are given in Figure 4b. Reference spectra in the absence of motion are shown from voxels both inside and outside of the excited region. Similar to the results shown in Figure 4a, conventional spirals in the presence of motion leads to artifacts arising outside of the excited region while the SNR is decreased inside the PRESS box. The use of out–in spirals reduces these effects. Quantitative analysis of the NAA spectra showed that the SNR using the out–in spiral increased by approximately 10% compared to conventional spiral acquisition.

Results from a human volunteer are presented in Figure 5. Spectra comparing the conventional and out–in spiral acquisition are shown for regions both inside and outside of the body. It can be seen that conventional spirals have increased ghosting artifacts as demonstrated by the signal outside of the body. Studies on phantoms without any motion show no major differences among the spectra. Given this observation, we can speculate that spectra within the body are more accurately represented by the out–in spiral. This method can be useful for directly examining the fat and water content in vivo from multiple regions of the body.

FIG. 5.

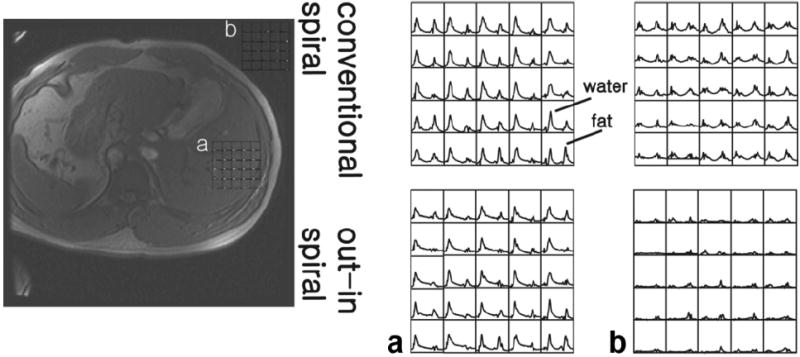
Water and fat spectra obtained from an in vivo study of a healthy adult volunteer. Selected spectra from 32 × 32 acquisition using conventional and out–in spirals are shown from within the liver (a) and regions outside of the body (b). Due to motion effects, data reconstruction with the conventional spiral resulted in spectral artifacts appearing outside of the body (b). This is reduced using an out–in spiral trajectory. Overall, out–in spirals reduce effects due to motion allowing spatial variations of water and fat content to be readily observed.

DISCUSSION

Based on the observation that a readout trajectory with symmetric weightings during gradient echo formation has moment compensating characteristics, we have incorporated an MRSI readout sequence with a symmetric out–in spiral trajectory. We have shown that the out–in spiral readout has small gradient moment buildup during the long readout period of typical MRSI acquisitions, and that this can be particularly useful when motion effects are problematic. Simulations and experimental studies comparing our method with phase-encoded MRSI and conventional spiral MRSI have been conducted, which show the potential usefulness of this approach. Because moment compensating gradients are played out in both k-space dimensions (k_x and k_y) during the readout, the technique is suited for reducing phase buildup due to motion occurring in the in-plane direction.

As mentioned, the symmetric nature of the k-space sampling scheme constrains the moments from diverging, leading to reduced-phase accumulation in the presence of motion. Due to the symmetry, however, the trajectory has a reduced effective FOV (as shown in Fig. 2) for a given resolution compared to conventional spirals. The penalty is an added spatial interleave acquisition with the spirals rotated by 180 degrees to achieve full FOV sampling.

The devised protocol can be potentially useful in several applications where motion can be of a problem including breast, prostate, liver, and whole-body water and fat imaging. In our study, we demonstrated a ¹H-MRSI acquisition for water and fat imaging of the liver. It has been shown that the presence or absence of fat in lesions can have important diagnostic implications (21). Previous spectroscopic attempts have been largely limited single-voxel studies. MR imaging attempts to resolve water and fat have shown good spatial resolution, but its quantitative accuracy is still under question. We believe that our approach, which addresses the issues of direct examination of fat and water content, increased spatial coverage compared to single-voxel methods, and the ability to compensate for motion-induced artifacts can have important diagnostic utility.

In reality, motion arises not only during the readout portion but also can come during the excitation portion of the sequence. The effects of motion during the excitation can be as problematic as motion during the readout phase. For example, motion during the crusher gradients surrounding the excitation or refocusing pulses can create an unwanted phase. Saturation pulses or other forms of suppression pulses accompanied with gradients can also give rise to motion-induced artifacts. Future work includes developing excitation and/or suppression pulses insensitive to motion effects. At the present time, however, we can use gating techniques to limit motion artifacts during the excitation, although the accuracy of this approach has yet to be fully quantified.

CONCLUSIONS

We have shown that spiral-out spiral-in trajectories, which are time symmetric, have the characteristic of moment compensation, which, when used during the readout interval of an MRSI study, reduce motion-induced phase artifacts. This approach is potentially useful for ¹H-MRSI of regions outside of the brain where motion artifacts can dominate image quality.