Abstract
The commonly used two-sample tests of equal area-under-the-curve (AUC), where AUC is based on the linear trapezoidal rule, may have poor properties when observations are missing, even if they are missing completely at random (MCAR). We propose two tests: one that has good properties when data are MCAR and another that has good properties when the data are missing at random (MAR), provided that the pattern of missingness is monotonic. In addition, we discuss other non-parametric tests of hypotheses that are similar, but not identical, to the hypothesis of equal AUCs, but that often have better statistical properties than do AUC tests and may be more scientifically appropriate for many settings.
1. Introduction
In many clinical trials subjects are evaluated for a continuous outcome (e.g. drug concentration, HIV-1 viral load, CD4 T-Cell count) at multiple fixed study timepoints, and the randomized groups are compared by testing whether there is a difference in the mean area-under-the-curve (AUC) of the outcome (or the outcome minus its baseline value) over time by group. Commonly, each subject’s AUC is estimated by the linear trapezoidal method (Yeh and Kwan, 1978) ignoring any missing observations, and a two-sample t-test (or Wilcoxon Rank Sum test) is employed to test the null hypothesis of equality of the mean AUCs (or stochastic identity of the AUC distributions). When the length of follow up varies by subject, this procedure is commonly modified by defining time-averaged AUC as the area under the curve from the first to the last observed evaluation, divided by the time from the first to the last observed evaluation, and then testing for equality of the mean time-averaged AUCs.
Although AUC analyses may be most commonly used in pharmacology, these analyses are increasingly used in other settings because they provide an obvious way to combine measurements across timepoints, even if data may be missing at certain timepoints. For example in the briefing document produced by Gilead for the NDA review of tenofovir, the mean AUC of HIV-1 RNA at 24 weeks adjusted for baseline was compared between patients receiving tenofovir and those receiving placebo within subgroups defined by baseline resistance mutations (FDA, 2001). The co-primary endpoint of the randomized placebo-controlled clinical trial of a Merck therapeutic vaccine for HIV, A5197, in the AIDS Clinical Trial Group, is the HIV-1 RNA AUC during a sixteen week analytical treatment interruption phase (AACTG, 2007). In a clinical trial of colloids versus crystalloids for fluid resuscitation in critically ill patients a secondary endpoint was the AUC of mean arterial pressure over 24 hours (NCT00318942, 2007). The secondary endpoints of the HEGPOL randomized placebo-controlled trial of glycine in the postoperative phase of liver transplantation included the AUCs of AST, ALT and bilirubin serum levels over the first eight days after transplantation (HEGPOL, 2005).
The analytic procedures described above have good properties as long as there are no missing data. But typically in clinical research, some evaluations are missing due either to a missed clinic visit, the inability of a laboratory to obtain an assay result from the subject’s specimen, or some other reason. A special case, considered in section 4, is when the missingness is monotonic (once missing, always missing subsequently.) In the Merck A5197 clinical trial, for example, if a subject resumes antiretroviral therapy before the end of the treatment interruption phase, then the HIV-1 RNA evaluations from that point on are missing since they are no longer off-therapy evaluations. Monotonic missingness is common in clinical trials due to patients dropping out early due to toxicity, loss of efficacy or some other reason.
In section 2 we demonstrate that these commonly used tests of equal mean AUCs (or time-averaged AUCs) may have poor properties (failure to protect the type I error, poor power and possibly bias in the test) in the presence of missing data, even when the data are missing completely at random (MCAR Rubin (1976)), i.e. when the probability of an observation being missing may depend on the group but is independent of any observed or unobserved outcomes in the study. Section 3 proposes a two-group test of equality of mean AUC, which is unbiased when data are MCAR. Section 4 proposes a test based on semi-parametric methods, which is unbiased when the data are missing at random (MAR), (i.e. possibly associated with the group and with observed outcomes but not with unobserved outcomes) and the pattern of missingness is monotonic. In AIDS clinical trials, for example, a common endpoint is based on HIV viral load during a period in which anti-retroviral treatment is interrupted; some subjects typically resume anti-retroviral treatment prematurely due to high levels of HIV viremia, resulting in MAR and monotonic missing data. Section 5 presents simulation results; and section 6 provides a comparison of the method described in section 4 to the trapezoidal method, in an analysis of data from ACTG 398, a recent study conducted by the AIDS Clinical Trials Group (AACTG, 2007). Section 7 discusses other possible null hypotheses that may be of greater scientific relevance in the repeated measures context, besides equality of AUC or time-averaged AUC.
The methods commonly used to test AUC hypotheses in the presence of missing data are often appropriate in the settings for which they were developed, but may not be appropriate in other types of settings, in which they are increasingly applied. For example, in analyses of results from pharmacology studies, there are widely accepted non-linear compartmental models of the type discussed by Davidian and Giltinan (1995), which may be fitted to longitudinal data with MAR missingness and then used to estimate and test AUC. In other settings, however, such as randomized clinical trials where the outcome is plasma HIV RNA, there typically is no widely accepted scientific model. Standard statistical methods that accommodate missing data, such as multiple imputation (MI) or weighted generalized estimating equation (GEE) modeling have disadvantages, which are overcome, at least in part, by the method proposed here. For example, in a randomized clinical trial the goal is not simply to estimate or model an outcome such as drug or viral exposure, but to find the best treatments for different groups of patients. Robustness to assumptions (provided by the use of non-parametric methods) is of great importance in this setting. The virtue of the semi-parametric methods we discuss in section 4 are their robustness to misspecification of the model for missingness; furthermore, when that model is correctly specified, such methods achieve the semi-parametric efficiency bound. These methods are particularly well-suited for analyses of results from clinical trials because they do not require confidence in a model for the entire longitudinal profile.
Estimating and testing AUCs under the MAR condition require fairly strong model assumptions, when mixed effects models, or GEE are used. In particular these approaches require obtaining estimates of the variance-covariance matrix parameters (of the longitudinal outcomes), which are well known to be difficult to achieve with good precision (Davidian and Giltinan, 1995, p. 330). In contrast, the semi-parametric method proposed in section 4 requires only the estimation of parameters giving the association between the probability of a subject missing data at a timepoint and observations on that subject at prior timepoints, which is easier to do with good precision.
In addition, mixed effects modeling and MI methods generally require distributional assumptions, which may compromise the credibility of conclusions. Therefore, these approaches may be less appealing for the analysis of results from randomized clinical trials than others that are more robust to distributional assumptions and provide semi-parametric efficiency.
2. Bias of the trapezoidal method
To demonstrate how a test based on the trapezoidal method of estimating the AUC may have poor properties in the presence of data missing completely at random, we consider the following two examples. In the first, a study has evaluations at times 0, 1, and 2; and in group A, the expected value of the outcome is 1 at each of these three timepoints. In group B, the expected values of the outcome at the three timepoints are 0, 2, and 0 respectively. In both groups the true mean AUC by the trapezoidal rule is 2, and the true mean time-averaged AUC is 1. If the observation at each timepoint is missing with a probability of .4 independently of everything else, a test based on the trapezoidal-method estimates of time-averaged AUC (ignoring any subjects with fewer than two observations) will have poor properties. As can be easily verified, the expected value of the estimated time-averaged AUC will be 1 in group A (and thus not biased) but in group B it will be approximately 0.78 (and thus biased.) In group A the estimated time-adjusted AUC would be 1 regardless of which observation is missing; but in group B, the corresponding estimate would be 1 if the first or the last timepoint were missing and zero if the middle timepoint were missing. Because the expected values of the estimator of time-averaged AUC are different in the two groups when the data are missing completely at random in this scenario, even though the true expected values of time-averaged AUC are the same in both groups, any test based on these biased estimates will have poor properties.
The direction and magnitude of the bias in a particular study depend upon the times of observation and the mean values of the outcomes in each group. The following example illustrates bias in the opposite direction from the first. Suppose the timepoints are 0, 1, 2, and 3 and the expected values in group A are 1 at every timepoint, and in group B, are 0, 1.2, 0, and 3.6 respectively. Then the expected AUC and time-averaged AUC are 3 and 1 respectively in both groups. If, as before, evaluations at a given time are missing with probability 4 independently of everything else and subjects with fewer than two observations are ignored, then the expected value of the trapezoidal- method estimate of time-averaged AUC in group A is 1, but in group B it is approximately 1.11.
3. A test (“Mean AUC”) of equal mean AUCs when data are MCAR
Let Xijk be the observation on the ith subject at the jth timepoint in arm k, for i in 1, . . . , Nk, j in 1, . . . , J and k in 1, 2, for randomly sampled and independent subjects (i.e. for each group, the vector of observations on each subject are iid). The trapezoidal-method estimate of the AUC for a given subject with observations Xi, j = 1, . . . , J, is where the weights, wj, are the average of (t(j+1) – tj) and (tj – t(j–1)) with t0 defined as equal to t1 and t(J+1) defined as equal to tJ. With MCAR data, an unbiased estimator of the expected AUC in the kth arm is where X̄jk is the mean of the observed values at time j on arm k. Because the expected value of the sample mean with data MCAR is equal to the expected value of the population sampled, it follows that if the observations for a given arm and timepoint are approximately normally distributed, or the sample size is large, and the null hypothesis of equal mean AUCs in both groups is true, then by large-sample theory the statistic , divided by an unbiased and asymptotically efficient estimator of its standard deviation will be a standard normal random variable, making possible a test of equal AUCs with good properties.
An unbiased and asymptotically efficient estimator of the standard deviation of is
| (1) |
where
| (2) |
| (3) |
where
| (4) |
where njj′k is the number of subjects in group k with observations at both timepoints j and j′; njk is the number of subjects in group k with observations at timepoint j; and
| (5) |
where Rijk = 1 if Xijk is observed, otherwise 0, and
| (6) |
This estimator is analogous to one based on the usual unbiased sample variance-covariance matrix, but uses only the observed data. Provided that the data are MCAR, it will also be unbiased and asymptotically efficient like its analog in the compete-data setting.
4. A test of equal mean AUCs when the data are MAR with monotonic missingness
4.1. When the only missingness mechanism is monotonic MAR
If only the group assignment (k) and observed values for the ith subject in group k are associated with the probability that Xijk is missing, then the data are missing at random (MAR). If whenever Xijk is missing, then Xij′k is also missing for all j′> j then the missingness is monotonic. When the missingness is both MAR and monotonic, then a valid semi-parametric test of equal AUCs based on the methods of Schisterman and Rotnitzky (2001) is asymptotically possible under the following condition: for every outcome vector, (Xi1k, . . . , XiJk)′, in the sample space with a positive probability of being realized, the probability of being completely observed is also non-zero. For finite sample sizes, one would need to assume that the sample size is large enough so that outcomes with a low probability of being completely observed are completely observed at least once in the sample.
The test statistic we consider is a U statistic
| (7) |
where Γ is the set of all pairs, (i, i′), such that the ith and i′th subjects in groups 1 and 2 respectively have complete data; is an unbiased estimate, based on some efficient parametric model fitted to all of the observed data, of the probability that the ith subject in group k has complete data, given k and Xijk, j = 1, . . . , (J − 1); and ϕ(·, ·) is a “kernel” function whose first and second arguments are vectors of observations from group 1 and 2 respectively, and which returns a scalar whose value is zero if the estimated AUC of each vector is the same and otherwise is a value larger or smaller than zero that indicates directional evidence against the null hypothesis of equality of the AUCs. For testing the null hypothesis of equal mean AUCs, ϕ(x, y) could be defined as the estimated AUC from y minus the estimated AUC from x (a t-test type kernel.) For testing the null hypothesis of stochastic equality of the distributions of AUC in the simulation study below, ϕ(x, y) is defined as −1, 0 or +1 according to whether the estimated AUC of y is less than, equal to or greater than the estimated AUC of x.
As we will show, under the null hypothesis of equal expected AUCs in both groups, T divided by a consistent estimate of its standard deviation is asymptotically a standard normal random variable, and provides the basis for a test of the null hypothesis.
T clearly has a mean of zero under the null hypothesis because the null hypothesis is that the kernel function, ϕ, has a mean of zero. The asymptotic normality and consistency of T stems from the fact that T is a special case of Schisterman and Rotnitzky’s ν̂(π) defined in their section 3 and modified as in their section 6, which they show to be an asymptotically normal and consistent estimator of ν under the assumption of regularity conditions.
A consistent estimator of the standard deviation of T may be obtained by using the method described by Wei and Johnson (1985) in section 2, with the following considerations: 1) in this AUC context we have only one “repeated measurement,” which is the estimated AUC of subjects with complete data, and so Wei and Johnson’s indices for the repeated measures, k and l, are always 1 in our case; 2) because Γ includes only subjects with complete data, their indicators of non-missingness, δ and ε, are always 1 in our case; 3) the kernel function must include division by the product of πi1 and πi′2; 4) two typographical errors in Biometrika should be noted: where it reads “j < j′” and “i < i′” it should read “j ≠ j′” and “i ≠ i′”; 5) the expected value of the kernel function under the null should be replaced with the sample mean of the kernel function value, as this has the same asymptotic properties but also may improve the test’s efficiency. In terms of this paper’s notation, Wei and Johnson’s estimator of the standard deviation of T is where
| (8) |
and where m and n are the number of subjects with complete data in groups 1 and 2, respectively, and N = m + n; and where
| (9) |
where , ; Γ1 is the set of all triples, (i, j, j′) such that the ith subject has complete data in group 1 and the jth and j′th subject have complete data in group 2 and j ≠ j′; also
| (10) |
where Γ2 is the set of all triples, (i, i′, j) such that the ith and i′th subject have complete data in group 1 and the jth subject has complete data in group 2 and i ≠ i′.
By Slutsky’s theorem, therefore, T divided by its consistently estimated standard deviation is a standard normal random variable under the null hypothesis that the expected value of the kernel function, ϕ, is zero.
The probabilities, πik, may be estimated as follows, taking advantage of the monotonic missingness pattern. Let be an estimator of Prob (Rijk = 1 | k; Ri(j–1)k = 1; Xij′k, j′ < j), j = 2, . . . , J based on fitting a logistic or other appropriate model, regressing Rijk on Xij′k, j′ < j, for all i such that the ith subject in group k has observed data through timepoint (j – 1). Then define to be the product of , j = 2, . . . , J.
At first glance it may seem as if this method uses only a subset of the data since the test statistic, T, has the form of a sum over only those subjects with complete data. All of the data, however, is incorporated into T because even those subjects without complete data contribute to the estimation of the probabilities, πik, that are used in the calculation of T.
4.2. When there are two missingness mechanisms: monotonic MAR, and MCAR
Frequently both types of missingness, montonic MAR as well as MCAR, occur in the same study. If one assumes that the two types of missingness mechanism are independent, and that the mechanism that caused each missing datum is known, then one way to handle this case is as follows: The method described above for monotonic MAR alone is used with the modification that the probabilities, πik (conditional probabilities of being completely observed despite both types of possible missingness) are estimated as the product of the conditional probabilities of having no monotonic MAR missingness and of having no MCAR missingness. The former probabilities are estimated by regression modeling as described above, but eliminating subjects from the regressions if they are missing any of the required observations, no matter the cause of the missingness. For each group, unbiased estimates of the latter probabilities are obtained as the product of the empirical estimates of the probability of missing due to the MCAR mechanism at each timepoint. These empirical estimates combine data from all timepoints that are presumed to have the same true MCAR law and are calculated for each group at each time point (or set of combined timepoints) as the number of non-missing observations divided by the number of intended observations that are observed or that are missing due to the MCAR mechanism (excluding those missing by the MAR mechanism). Preliminary simulations (not shown) imply that the type I error is preserved with this approach in this setting.
5. Simulation results
5.1. Generation of the data
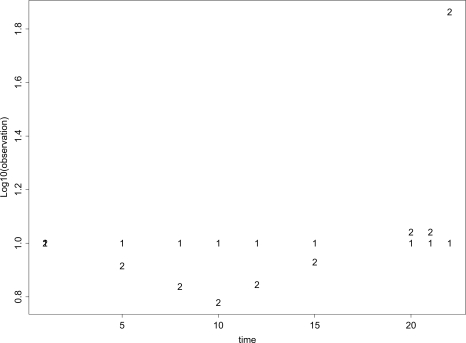
Data were simulated for two treatment arms, each with nine observations at the following times: 1,5,8,10,12,15,20,21, and 22. The outcomes for each subject in arm k were from distributions with mean vectors μk, k = 1, 2, where μ1 was [10,10,10,10,10,10,10,10,10] and μ2 under the null hypothesis was [10, , , 6, 7, 8.5, 11, 11, 73] (Figure 1). We chose these values to produce identical mean AUCs in a setting that accentuates the biasing effects of missingness that is completely at random for standard tests of AUCs. For alternative-hypothesis simulations, the data were generated the same way except that each element of μ2 was increased by 0.2. AUCs based on μ1 and the null version of μ2 are the same, but the shapes are very different and thus provide any test with a “challenging” version of the null hypothesis, in particular one very sensitive to random missingness. Each result below is based on 1000 simulated data sets.
Figure 1.
Arm 1 and 2 Mean Outcome versus Time under the Null of Equal AUC
For each method and data set, the null hypothesis of identically distributed AUCs in both arms was tested at the α = 0.05 level against the one-sided alternative of larger AUCs in arm 2, and against the two-sided alternative of different distributions. For Table 1, the outcomes for each subject in a given arm were from iid standard multivariate normal distributions, uncorrelated across timepoints. The sample size in each arm was 100. Each observation was made missing completely at random (MCAR), with an independent probability of .40. One thousand simulations were run for each set of conditions. The “trapezoidal” method had an observed Type I error for the two-sided test of 0.10, reflecting the bias of this estimator. The “mean AUC” method, in contrast, had an observed Type I error of 0.050 and 0.049 for the one- and two-sided tests, respectively.
Table 1.
Bias and Power for Normal Data MCAR
| Null | Alternative | |||
|---|---|---|---|---|
| Methods | Type I error (1 sided) (95% C.I.) |
Type I error (2 sided) (95% C.I.) |
Power (1 sided) (95% C.I.) |
Power (2 sided) (95% C.I.) |
| Trapezoidal | 0.021 (0.013, 0.032) | 0.100 (0.082, 0.120) | 0.130 (0.102, 0.163) | 0.076 (0.054, 0.103) |
| Mean AUC | 0.050 (0.037, 0.065) | 0.049 (0.036, 0.064) | 0.910 (0.881, 0.933) | 0.842 (0.807, 0.873) |
For Table 2, the data and missingness pattern were generated the same way as in Table 1 except that the data at the ith timepoint were generated from an exponential distribution (mean = 1) shifted to have the mean specified by the ith element of μk, k = 1, 2. The results are similar to those of Table 1 when the data come from an exponential rather than a normal distribution.
Table 2.
Bias and Power for Exponential Data MCAR
| Null | Alternative | |||
|---|---|---|---|---|
| Methods | Type I error (1 sided) (95% C.I.) |
Type I error (2 sided) (95% C.I.) |
Power (1 sided) (95% C.I.) |
Power (2 sided) (95% C.I.) |
| Trapezoidal | 0.035 (0.025, 0.048) | 0.096 (0.078, 0.116) | 0.172 (0.140, 0.208) | 0.118 (0.091, 0.150) |
| Mean AUC | 0.058 (0.044, 0.074) | 0.049 (0.036, 0.064) | 0.910 (0.881, 0.934) | 0.840 (0.805, 0.871) |
For Table 3, the data were generated from iid standard multivariate normal distributions as in Table 1 but with within-subject correlations in arm k=2 of .5, .4, .3, .2, .1, 0, 0, and 0 for timepoints that were separated by 1, 2, 3, 4, 5, 6, 7, and 8 time-points, respectively; and uncorrelated data in arm k = 1. These data were created with a dependency over time in arm 2 in order to illustrate the effect of the two arms having different correlations over time in this setting. A pattern of MAR monotonically missing data was created using three different probability laws, denoted in the table (“Missing” column) as “logistic,” “U-shape” and “Threshold.” The “logistic” law made logit(Pr[Xijk is missing |Xi(j–1)k]) = β0 + β1Xi(j–1)k. The “U-shape” law made Pr[Xijk is missing |Xi(j–1)k] = [exp(β1) (Xi(j–1)k – β0)2]/[1 + exp(β1) (Xi(j–1)k – β0)2]. Thus for the “U-shape” law observations following a very low- or a very high-valued observation are more likely to be missing than values following intermediate-valued observations. The “Threshold” law made Pr[Xijk is missing | Xi(j–1)k] = .5 if Xi(j–1)k > qth quantile of (X1jk,. . . , XNkjk)′ in the given arm, otherwise zero. In each case the arm-specific parameters in these three probability laws were selected to yield complete observations in approximately 80% of subjects in each arm. Table 3 (“Estimate” column) also indicates the model for the missingness probability law that was employed by the Inverse Complete Cases Probability Weighting (ICCPW) method to estimate the missingness probabilities. “Truth” means the correct model was employed, “Logit” means a logistic model with only an intercept and the previous observation in the model was employed. The sample size in each arm was 200, and 500 simulations were run for each set of conditions.
Table 3.
Bias and Power for Normal Data MAR
| Null | Alternative | |||||
|---|---|---|---|---|---|---|
| Methods | Estimate | Missing | Type I error (1 sided) (95% C.I.) |
Type I error (2 sided) (95% C.I.) |
Power (1 sided) (95% C.I.) |
Power (2 sided) (95% C.I.) |
| Trapezoidal | Logistic | 0.000 (0.000, 0.004) | 0.872 (0.850, 0.892) | |||
| ICCPW | Truth | Logistic | 0.048 (0.036, 0.063) | 0.053 (0.040, 0.069) | 0.917 (0.898, 0.933) | 0.865 (0.842, 0.886) |
| ICCPW | Truth | U-shape | 0.045 (0.033, 0.060) | 0.045 (0.033, 0.059) | 0.898 (0.878, 0.916) | 0.848 (0.824, 0.870) |
| ICCPW | Logistic | U-shape | 0.045 (0.033, 0.060) | 0.040 (0.029, 0.054) | 0.940 (0.923, 0.954) | 0.893 (0.872, 0.911) |
| ICCPW | Truth | Threshold | 0.025 (0.016, 0.037) | 0.037 (0.026, 0.050) | 0.762 (0.734, 0.788) | 0.620 (0.589, 0.650) |
| ICCPW | Logistic | Threshold | 0.006 (0.002, 0.013) | 0.009 (0.004, 0.017) | 0.320 (0.291, 0.350) | 0.169 (0.146, 0.194) |
Table 3 shows that the “trapezoidal” method rejection rate for the two-sided test under the null hypothesis is far greater than α. This table also shows that the ICCPW method has Type I error rates close to the nominal α when the model for the MAR missingness is correctly specified and when there are 80% complete cases, except when the missingness is generated by a threshold probability law. When the missingness model is incorrectly specified the null rejection rates are close to α in some cases and much lower in others. In simulation results (not shown) under the same conditions as Table 3 but with no within-subject correlation of outcomes, model mis-specification was less of a problem. Model mis-specification is more serious when the within-subject correlation is different in the two arms. If the correlation is the same in the two arms then model mis-specification would result in giving complete cases the wrong weight, but the same wrong weight in both arms and thus potentially introducing less bias in the test. When the correlation is different in the two arms then different wrong weights in the two arms result, introducing possibly more bias.
6. Application of the method of section 4 to data from ACTG 398
To illustrate the issues described above, we apply different AUC testing methods for comparing repeated measures of plasma HIV-1 RNA between two groups of patients defined by the number of antiretroviral drug resistance mutations measured at baseline in protocol 398 of the AIDS Clinical Trials Group (ACTG). ACTG 398 was a randomized clinical trial that compared time to virological failure (rebound) among patients receiving drug regimens containing either one or two drugs of the protease inhibitor class. While there was little difference in virological response to treatment among the randomized groups, the presence of certain antiretroviral drug mutations did have a major effect on this response. In particular, the mutation K103N, which confers resistance to the drug efavirenz, from the class of non-nucleoside reverse transcriptase inhibitors sharply reduced virological response. Our interest was in the comparison of two groups of patients defined by the presence or not of at least two mutations that confer resistance to the class of nucleoside reverse transcriptase inhibitor (NRTI) drugs. (In this illustration we do not investigate the possibility of unknown confounders of the association between group membership based on mutations and the AUC of HIV-1 RNA.)
The data we used consisted of measurements of plasma HIV-1 RNA that were made at weeks 0, 8, 16, and 24 weeks after randomization. Data on 430 subjects were included in the analysis, of which 243 had at least 2 NRTI mutations. Of the 187 patients with fewer than 2 mutations, 37%, 22% and 11% of patients were missing visits at 24, 16 and 8 weeks, whereas in 243 patients with ≥ 2 mutations, these percentages were lower: 22% 13% and 4%. Three different AUC tests (two-sided) were considered: 1) the method based on the trapezoidal rule, 2) the method based on a linear mixed effects model, and 3) the method based on the semi-parametric test. The first method yielded a two-sided p-value of 0.024, implying a significant effect of two or more NRTI mutations on decreasing the HIV-1 RNA response to treatment at the 0.05 level. The second method was based on a linear mixed effects model that had fixed effects for group (≥ 2 or < 2 mutations), for an intercept, for dummy variables for means at the three post-baseline timepoints, and for interactions between group and the timepoint dummy variables; random effects for intercept and each timepoint dummy variable; and an unstructured variance-covariance matrix for within-subject RNA levels. This model was used to test for a difference in AUC between the two groups by forming the appropriate linear combinations of the fixed effects and finding its standard error; this method yielded a p-value of p=0.10. The third method, based on our proposed semi-parametric test, used a logistic regression model to estimate the probability of missing a measurement as a function of all previous RNA measurements. The choice of this logistic model was based on inspection of plots of proportion of missing data at given timepoints versus RNA level (categorized into five intervals) at the previous timepoints; these plots were approximately sigmoid-shaped implying the appropriateness of a logistic model. Selection of the covariates for inclusion in the final model was based on a likelihood ratio test of nested models; all previous RNA measurements were included in the final model. The semi-parametric test yielded p= 0.20, which fails to provide evidence of a group effect on RNA AUC.
The difference between the semi-parametric and the trapezoidal methods appears to result from the fact that the patterns of missingness differ between these two groups. Patients with 2 or more NRTI resistance mutations were consistently less likely to have missed visits and therefore had fewer missing HIV RNA measurements throughout the study. This difference may reflect the fact that patients with higher rates of resistance to NRTI drugs may have had fewer treatment options outside of the study, and therefore were more likely to remain in the study. In addition, the dependence of missingness on the previous RNA measurement differed between the two arms across timepoints: for example, higher RNA values at baseline were associated with a greater probability of having an observed value at week 8 for the more resistant patients but a lower probability for the more sensitive patients. The semi-parametric method accounts for the difference between the two groups in the number of missed visits and the dependence of missingness on previous measurements, whereas the trapezoidal method does not.
While the method based on the linear mixed effects model does accommodate the missing data, and, like the semi-parametric method, finds the difference between groups to be non-significant, this result requires estimation of a covariance matrix. A fully flexible model would require estimation of many parameters and therefore a large dataset in order to provide reliable results. Using a highly structured covariance matrix permits obtaining results with a dataset of modest size, but at the cost of fairly strong parametric assumptions. This need for the linear mixed effects method to estimate a covariance matrix may make it less preferable than the semi-parametric approach in many settings. As Davidian and Giltinan (1995, p. 330) write, “Second moment behavior is inherently difficult to characterize, and this is especially true for correlation parameters.” Estimated within-group means at each timepoint (and hence the estimated AUC) based on the linear mixed effects method can be sensitive to the estimated covariance matrix, which in turn may be sensitive to the pattern of missingness. In contrast, the semi-parametric method trades a) the need to estimate a covariance matrix for the RNA outcome for b) the need to estimate, for subjects without missing data, the probability of their being fully observed conditional on their observed data. The latter estimates of probabilities across timepoints require no assumption about their joint distribution. Furthermore, in contrast to the difficulty of estimating a covariance matrix, there are many flexible and efficient methods (such as logistic regression) available for estimating a probability – methods that can be selected according to how well their different required assumptions about the distribution of the outcome (missingness in this case) fit the data. Additionally, the most commonly used methods for fitting linear mixed effects model rely on an assumption of normality, whereas no such assumption is required by the semi-parametric method. While more flexible methods for fitting such models exist, they nonetheless rely on estimation of a covariance matrix (Zhang and Davidian, 2001), as would approaches based on generalized estimating equations.
7. Non-parametric alternatives to testing the AUC
In some settings the AUC is of particular scientific interest. For example, in pharmacokinetics studies the AUC is conceptually the cumulative drug exposure and has intuitive value as a statistic. In other settings, however, the AUC may not necessarily be the most scientifically relevant summary statistic. For example, when repeated measures of HIV viral load are obtained, testing the null hypothesis of equal mean AUCs may not be as appropriate as testing the null hypothesis that mean HIV levels are the same at each timepoint against the alternative hypothesis that in one group the mean levels are greater than or equal to the corresponding levels in the other group with strict inequality applying to at least one timepoint. This latter null hypothesis may be tested when the data are MCAR by using the fully non-parametric method described by Wei and Johnson (1985). In this method one specifies a priori the alternative hypothesis, against which one wants greatest efficiency, by assigning weights to the timepoints reflecting the relative deviation from equality between groups at each timepoint. One could choose these weights to be the same as the weights (wj in section 3) for the linear combination of observations that yield the estimated AUC, in which case the test would weight each datum by an amount based on its timepoint’s contribution to the estimated AUC as well as on its correlation with the data from other timepoints. Alternatively, the U-statistic and its estimated variance-covariance matrix obtained from the Wei and Johnson method may be used to perform a test without first specifying an alternative hypothesis, in the manner described by Xu, Tian and Wei (Xu et al., 2003).
8. Discussion
Area under the curve is a widely used method for comparing two groups in which there are repeated measurements on each experimental unit. Sometimes AUC is appropriate because of prior theoretical considerations. Drug concentration area under the curve, for example, is the theoretical measure of an organism’s cumulative exposure to a drug. But in other cases, for example repeated measurements of HIV-1 viral level in a clinical trial, there may be no clear rationale for using area under the curve as an endpoint, and in cases like this it is sometimes used for convenience or for lack of immediate access to a more appropriate method.
We have shown that analyses based on the trapezoidal method for estimating AUC may have very poor properties in the presence of missing data, even when the data are missing completely at random (MCAR), i.e. the likelihood of an event being unobserved is independent of either observed or unobserved events. This potential problem is a frequently overlooked shortcoming in analyses of AUC, and distinguishes them from many standard analysis methods that have good properties when data are MCAR.
We propose two strategies for analyzing AUC when data are MCAR: 1) In the absence of compelling theoretical reasons to use the AUC metric, use unbiased approaches for 2-group comparisons, e.g. the Wei and Johnson method. Like methods based on AUC, it also makes use of all of the measurements to test a null hypothesis of group equality, but with a null hypothesis regarding equality that is defined differently from hypotheses regarding mean AUC; 2) Use the AUC metric, but avoid methods that require estimating the AUC of an individual experimental unit with missing data and thereby introduce potential bias. For the latter strategy we propose both a test of equal mean AUCs when the data are MCAR and another test when the data are not MCAR but rather missing at random (MAR) monotonically, i.e. after the first unobserved event all subsequent events in that experimental unit are also unobserved, and the likelihood of an event being unobserved depends only upon group membership and observed events.
Further work is required to handle the setting where the data are MAR but not monotonically missing. This would occur, for example, in a clinical trial if the outcome of interest at a given time were associated with previously observed values and also associated with a subject’s ability or willingness to come to the clinic on a scheduled visit to have the outcome observed. This might be the case with any number of clinical outcomes experienced subjectively by the subject. In some situations, however, the only non-monotonic missingness is due to an MCAR mechanism operating in addition to, and independently of, a monotonic MAR mechanism, and it is known which missingness mechanism is responsible for each missing observation. This would be the case, for example, in an HIV clinical trial with an analytical treatment interruption (ATI) readout period during which subjects remain off of antiretroviral medications to see how well they control the virus without them, and interest focuses on the AUC of viral level during the ATI. In this context, some ATI viral measurements may be missing MCAR (not monotonic), for example due to a difficulty in attending the clinic for a scheduled visit, but other viral measurements may be missing MAR monotonically because of recommendations for patients to resume antiretroviral medications if their virus level exceeds some threshold value during the ATI. For this situation we have proposed a simple modification of the method for the case of data monotonic MAR. Preliminary simulations of this approach look promising, but further work is required to establish its properties in a variety of scenarios.
In some cases a test comparing the partial AUC is appropriate, based on the area under only some part of the outcome curve, for example only the part corresponding to the analytical treatment interruption period of a clinical trial as discussed above. In this case, the methods we propose can be used by applying them only to the outcomes from the time-interval of interest, while, in the case of MAR monotonic missingness, still allowing all outcomes before a given timepoint to be used when modeling the probability of missingness at that timepoint.
Footnotes
The authors would like to acknowledge a helpful conversation with Andrea Rotnitzky. This research is supported by NIH/NIAID grants R01AI51164 and 5U01 AI38855.
References
- Yeh KC, Kwan KC. “A comparison of numerical integrating algorithms by trapezoidal, Lagrange, and spline approximation,”. Journal of Pharmacokinetics and Biopharmaceutics. 1978;6(1):79–98. doi: 10.1007/BF01066064. [DOI] [PubMed] [Google Scholar]
- FDA http://www.fda.gov/ohrms/dockets/ac/01/briefing/3792b_10_1gilead.pdf
- AACTG http://www.aactg.org/
- NCT00318942 http://www.clinicaltrials.gov/ct/gui/show/NCT00318942;jsessionid=01BDA74439B69E35430AE0D61F04391A?order=5
- HEGBOL http://www.pubmedcentral.nih.gov/articlerender.fcgi?artid=1208918
- Rubin DB. “Inference and missing data,”. Biometrika. 1976;63:581–592. doi: 10.1093/biomet/63.3.581. [DOI] [Google Scholar]
- Schisterman E, Rotnitzky A. “Estimation of the mean of a K-sample U-statistic with missing outcomes and auxiliaries,”. Biometrika. 2001;88(3):713–725. doi: 10.1093/biomet/88.3.713. [DOI] [Google Scholar]
- Wei LJ, Johnson WE. “Combining dependent tests with incomplete repeated measurements,”. Biometrika. 1985;72(2):359–364. doi: 10.1093/biomet/72.2.359. [DOI] [Google Scholar]
- Xu X, Tian I, Wei LJ. “Combining dependent tests for linkage or association across multiple phenotypic traits,”. Biostatistics. 2003;4(2):223–229. doi: 10.1093/biostatistics/4.2.223. [DOI] [PubMed] [Google Scholar]
- Davidian M, Giltinan D. Nonlinear Models for Repeated Measurement Data. Chapman and Hall; London: 1995. [Google Scholar]
- Zhang D, Davidian M. Linear Mixed Models with Flexible Distributions of Random Effects for Longitundinal Data. 2001. unpublished manuscript. [DOI] [PubMed]