Extended Instrumental Variables Estimation for Overall Effects

Abstract

We consider a method for extending instrumental variables methods in order to estimate the overall effect of a treatment or exposure. The approach is designed for settings in which the instrument influences both the treatment of interest and a secondary treatment also influenced by the primary treatment. We demonstrate that, while instrumental variables methods may be used to estimate the joint effects of the primary and secondary treatments, they cannot by themselves be used to estimate the overall effect of the primary treatment. However, instrumental variables methods may be used in conjunction with approaches for estimating the effect of the primary on the secondary treatment to estimate the overall effect of the primary treatment. We consider extending the proposed methods to deal with confounding of the effect of the instrument, mediation of the effect of the instrument by other variables, failure-time outcomes, and time-varying secondary treatments. We motivate our discussion by considering estimation of the overall effect of the type of vascular access among hemodialysis patients.

1 Introduction

Instrumental variables (IV) methods have been used successfully to control for confounding in a number of settings in which conventional methods fail (Davey Smith and Ebrahim, 2003; Mark and Robins, 1993; McClellan and Newhouse, 1997). IV methods may be used in estimating the component and joint effects of multiple treatments or exposures (Stock, 2001). However, when one of the treatments under study affects another, IV methods will not by themselves provide valid estimates of the overall effect of the former. We consider extension of IV methods that allow estimation of the overall effects of the initial treatment.

For motivation, we consider estimating the overall effects of type of vascular access (VA) among hemodialysis (HD) patients on clinical outcomes (e.g., mortality). VA can affect the dose of dialysis received (Sehgal et al., 1998; Dhingra, Young, Hulbert-Shearon, Leavey and Port, 2001). The clinical center at which dialysis is provided may be a good instrument for the joint effects of VA and dose, but, as we will argue, it is not an instrument for the overall effect of VA. We will thus need to use extended IV methods.

This manuscript is organized as follows. First, we consider the VA problem in more detail. Then, using both graphical and counterfactual approaches to causality, we show how, under our assumptions, IV methods are appropriate for estimating the component and joint effects of VA and dose (the earlier and later treatments), but not the overall effect of VA (the earlier treatment). We then show how to estimate the overall effect, and consider extensions to situations with confounders or additional mediators of the effect of the instrument, to failure-time outcomes, and to time-varying auxiliary treatments.

2 Vascular access in hemodialysis

Hemodialysis (HD) is one of the principal modalities of renal replacement therapy in end-stage renal disease (ESRD), a condition in which a person’s kidneys no longer function adequately. In HD, blood is removed from the body, filtered, and then returned to the vascular system. This process requires access to the vascular system. This access can take the form of a catheter, implantation of synthetic material between an artery and vein (graft), or a native arteriovenous fistula.

The type of VA can impact the dose of dialysis that can be delivered, and thus can influence the dose of dialysis actually received. VA may influence clinical outcomes, including mortality (Dhingra et al. 2001; Wolfe, Dhingra, Hulbert-Shearon, Leavey and Port, 2000). A good part of the effect of VA may be mediated by delivered dialysis dose. Type of VA may affect clinical outcomes by other pathways as well.

In ESRD, many of the treatments used to treat various aspects of ESRD or its consequences are subject to confounding by indication (Feldman et al., 2004; Reddan et al., 2002), i.e., subjects with an indication for a particular treatment often have more severe disease than other subjects. There are a number of reasons that patients who receive dialysis catheters may be sicker than those who are treated via fistula or graft. Fistula/graft creation requires vascular surgery, and patients with more comorbid disease often are not surgical candidates. In addition, fistulas and grafts require suitably healthy vascular systems, which may not be present in older, frailer patients or those with extensive cardiovascular disease. Finally, grafts and, particularly, fistulas require time to mature after they are placed and before they are ready for use, whereas catheters are ready instantaneously upon placement. Patients with less access to health care, and who therefore are less likely to receive care for other diseases, are less likely to present in time to receive fistulas or grafts, and more likely to receive catheters.

Confounding by indication is often difficult to control analytically using standard methods, e.g., regression. IV analysis provides an alternative approach to controlling confounding. For this method to work, the instrumental variable should be related to the outcome only through its effect on the treatment(s) of interest. The center at which dialysis is provided is a plausible candidate for an instrument. The choice of center for dialysis patients might be expected to be driven primarily by factors not intimately related to prognosis, such as geographical proximity of the patient to the center. Inasmuch as center is not strongly associated with prognosis, center may fulfill the criterion for an instrumental variable that it only be related to the outcome through its effect on the treatment(s) of interest; this criterion has implicitly been used to provide causal interpretation to associations between average levels of compliance within centers to guidelines about dialysis dose and hematocrit with center-specific mortality (Wolfe, Hulbert-Shearon, Ashby, Mahadevan and Port, 2004). For similar reasons, we propose using center as an instrument for estimating the effect of VA type on outcome.

3 The effect of vascular access

To define our problem, it is useful to consider the various pathways by which the primary treatment (VA) might affect clinical outcomes, and other ways associations between the primary treatment and outcome might be generated. Causal diagrams (Pearl, 1995; Pearl, 2000) are useful for this purpose. We will consider these diagrams together with formal definitions of effects based on the potential outcomes model (Rubin, 1974; Rubin, 1978; Neyman, 1990).

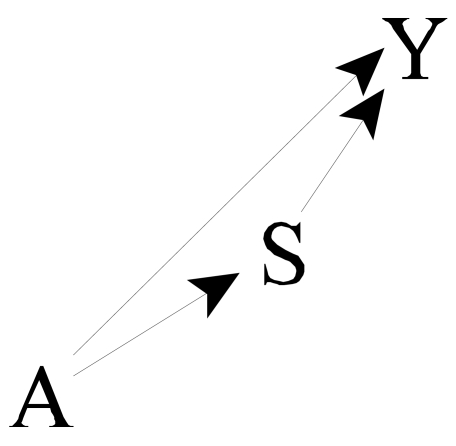
We begin with a simple diagram showing relations between the main variables of interest (Figure 2). Let A denote the primary treatment (type of VA), S denote the auxiliary treatment (dose of dialysis), and Y the clinical outcome of interest (e.g., mortality). We presume that A affects S, thus we draw an arrow from A to S (A→S). The auxiliary treatment (dialysis dose) may affect clinical outcomes (S→Y). Further, the primary treatment may affect clinical outcomes directly (i.e., through pathways not containing S), thus, we also draw an arrow A→Y. The overall impact of the primary treatment (VA) on clinical outcomes is represented by considering both paths from A to Y (i.e., A→Y and A→S→Y). The direct effect of the primary treatment (VA), controlling for the auxiliary treatment (dialysis dose), is represented by the path A→Y; the indirect effect is represented by the path A→S→Y. In our example, because VA can determine the dose of dialysis, the indirect path A→S→Y cannot be ignored in assessing the impact of VA on outcome.

Figure 2.

Augmented causal diagram showing relations between instrument, confounders, key treatments, and outcomes.

We supplement the causal diagrams with a potential outcomes approach to more formally define overall, direct, and indirect effects (Pearl, 2001; Robins and Greenland, 1992). Let Y^as denote the outcome that would be seen in a subject were that person to receive level a of the primary treatment and level s of the auxiliary treatment. S^a denotes the value that S would assume were treatment level a provided, without S being manipulated by the investigator. Y^a is the outcome that would be seen were the investigator to provide primary treatment a but leave the choice of S subject to the same possibly unknown factors governing it during the study; thus, under a consistency assumption (Robins and Rotnitzky, 2004), Y^a=Y^aSa. Overall effects of A are contrasts of Y^a and Y^a′, a ≠ a′.. The direct effect of A is a contrast of Y^as and Y^a′s, i.e, a contrast of outcomes holding s physically constant but varying a. There are several direct effects, depending on the choice of s. Prescriptive direct effects require prespecification of s; for natural direct effects, s is the value it would assume under a reference level a^* of the primary treatment A, i.e., s=S^a*. Natural indirect effects are contrasts of Y^a*Sa and Y^a*Sa′,i.e., allow S to vary as it would by varying A, but fix A to some common value. There is no nonparametric definition of prescriptive indirect effects, although there are several definitions based on parametric models (MacKinnon, Lockwood, West and Sheets, 2002).

In our example, because the type of access determines to a degree the possible dose of dialysis, in ascertaining the impact of VA, we cannot simply control or adjust for dose. Thus, we will concentrate on estimating the overall impact of VA. However, the direct and indirect effects will be of interest, not only for mechanistic understanding and explanation, but also for deriving estimates of the overall effect.

4 Identification and estimation

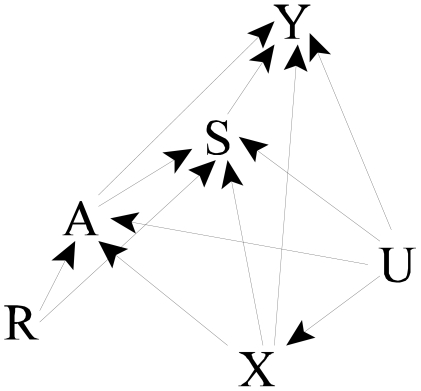
To understand appropriate approaches for estimation, we supplement the causal diagram (Figure 2) with other variables. In particular, we add both measured (X) and unmeasured (U) confounders of the effect of A and S; X and U influence A, S, and Y. The presence of unmeasured confounders makes standard adjustments for confounders X inadequate for estimating the effects of A and S. We also add a node for an instrumental variable (IV) R, whose association with outcome is presumed to be solely due to its effect on A and S. As with other IVs, R influences treatment (A and S), but has no direct effect on Y (no R → Y arc, i.e., an exclusion restriction (Angrist, Imbens and Rubin, 1996) holds), and there are no unmeasured common causes of R and Y. Figure 2 represents these relationships.

In this setup, R is an instrument for the joint effects of A and S but not for the overall effect of A. To see this, note that R is d-separated from Y in the graph removing the effects of A and S (i.e., the arrows out of A and S), and A and S are affected by R; R then satisfies graphical criteria (Pearl 2000) but not necessarily standard econometric criteria for an instrument. Suppose we assume a linear, no interaction model for the effect of A and S on Y:

$$Y=Y^{AS}=Y^{00}+A{\mathrm{\Psi }}_A+S{\mathrm{\Psi }}_S.$$ (1)

We call this a structural model, as it models the relations between the structural variables Y^AS and Y⁰⁰; as expressed in (1), this is a rank-preserving structural nested (distribution) model (Robins, Blevins, Ritter and Wulfsohn, 1992; Robins, Rotnitzky and Scharfstein, 2000; Ten Have et al., 2007). Using standard theory (Joffe and Greene, 2007), we have that, if R is unassociated with the potential outcome Y⁰⁰ (as it would be if there are no unmeasured common causes of R and Y),

$$\begin{array}{l}E(Y\mid R,V)=E(Y^{00}\mid R,V)+E(A\mid R,V){\mathrm{\Psi }}_A+E(S\mid R,V){\mathrm{\Psi }}_S\\ =E(Y^{00}\mid V)+E(A\mid R,V){\mathrm{\Psi }}_A+E(S\mid R,V){\mathrm{\Psi }}_S,\end{array}$$ (2)

where V is a selected subset of the elements in X. Under linear model assumptions, we substitute Vβ for E(Y⁰⁰|V).E(A|R,V) and E(S|R,V) are unknown but may be estimated. The design matrix made up of V, Ê(A|R,V), and Ê(S|R,V) must be of full rank to estimate this model using standard methods (e.g., least squares). If R is binary, we need some covariates in V (and, if linear models are used for E(A|R,V) and E(S|R,V), an interaction R*V in at least one of those models) to achieve this. If R has more than 2 levels, a full rank design matrix may be achievable even if V is the empty set; here, R may be operationalized as a series of dummy variables. Two-stage least squares (2SLS) may be used for the estimation (Albert, 2007).

Semiparametric estimation of Ψ ≡{Ψ_A,Ψ_S} using G-estimation is also possible (Robins and Greenland, 1994; Joffe, Small and Hsu, 2007; Ten Have, Elliott, Joffe, Zanutto and Datto, 2004; Ten Have et al. 2007). Heuristically, G-estimation is based on the fact that, under our assumptions, the potential outcome Y⁰⁰ is independent of the instrument R. Under (1), we can compute a value for Y⁰⁰ under an assumed causal theory Ψ by removing the effects of A and S as Y⁰⁰(Ψ) ≡ Y − AΨ_A − SΨ_S. Point and interval estimation are based on tests of the independence of Y⁰⁰(Ψ) and R. Unlike 2SLS, consistency of G-estimation does not depend on correct specification of the model for E(Y⁰⁰|V).

5 Estimation of overall effects

In contrast to the component effects of A and S, the overall effect of A cannot be estimated using standard IV methods alone. To see this, we consider graphical criteria (Pearl 1995; Pearl 2000). The path R → S → Y is not blocked by A; therefore, A does not d-separate R and Y (in the graph in which the effects of A is blocked; i.e., the arrows out of A are removed) and so R is not an instrument. Loosely speaking, part of the effect of R on Y is not mediated by A.

To estimate the overall effect of A on Y, we can combine our estimates of the joint effects of A and S on Y with estimates, which we now consider, of the effect of A on S. Under our assumptions, the effect of A on S is confounded by R, X, and U; therefore, even controlling for the measured variables R and X will not be sufficient to obtain valid estimates. Instead, we consider a two-stage least squares estimating procedure, in which we will also estimate the direct effect or influence of R on S controlling for A. Let S^ra denote the level of S that would be observed were we to set R to r and A to a; S^a, discussed earlier, may be taken to equal S^Ra. Suppose first that we can use a linear structural model for the effect of R and A on S:

$$S^{RA}=S^{00}+R{\mathrm{\Phi }}_R+A{\mathrm{\Phi }}_A.$$ (3)

Then, write

$$\begin{array}{l}E(S\mid R,W)=E(S^{RA}\mid R,W)=E(S^{00}\mid R,W)+R{\mathrm{\Phi }}_R+E(A\mid R,W){\mathrm{\Phi }}_A\\ =E(S^{00}\mid W)+R{\mathrm{\Phi }}_R+E(A\mid R,W){\mathrm{\Phi }}_A,\end{array}$$ (4)

where W, like V, includes a subset of the variables in X. As before (section 4), Φ is estimable if the design matrix in the regression of S on R, W, and Ê(A|R,W) has full rank. If E(S⁰⁰|R,W) follows a linear no-interaction model (Joffe and Greene 2007) and R is ignorable (i.e., R⊥S⁰⁰) (Rosenbaum and Rubin, 1983), we have

$$E(S^{00}\mid W)=W{\beta }_W,$$ (5)

and then the model for E(A|R,W) must include an R by W interaction if a linear model is used (Albert 2007; Ten Have et al. 2007).

Under our linear no-interaction models ((1),(3)), all the direct effects of A are the same as each other, i.e., natural effects do not depend on the reference level of A, prescriptive effects do not depend on the reference level of S, and natural and prescriptive effects are the same. In this setting, the overall effect of treatment ρ_A may be calculated as

$${\rho }_A={\mathrm{\Psi }}_A+{\mathrm{\Phi }}_A{\mathrm{\Psi }}_S.$$ (6)

We estimate ρ_A by plugging into (5) estimates of Ψ_A and Ψ_S from the 2SLS approach in Section 4 and Φ_A from the 2SLS approach in this section, and call this the extended 2SLS estimate. Standard errors for the extended 2SLS estimates of ρ_A may be calculated analytically, or using a nonparametric bootstrap. Appendix 1 provides analytic formulas for the standard errors from the extended 2SLS approach, and compares these to a three-stage least squares (3SLS) approach, which can be more efficient under certain conditions.

6 Simulation study

We performed a small simulation study to examine the properties of the various estimators. Consider a setting where W consists of two variables that are generated as independent standard normals, there are 500 subjects and the parameters are the following (see Appendix 1 for definitions of γ and Σ): γ_R = 1, ${\gamma }_W=\left(\begin{array}{c}1\\ 0.5\end{array}\right)$, ${\gamma }_{RW}=\left(\begin{array}{c}0.8\\ 0.6\end{array}\right)$, β_R = 1, ${\beta }_W=\left(\begin{array}{c}1\\ 0.5\end{array}\right)$, Φ_A, = 0.5, ${\theta }_W=\left(\begin{array}{c}1\\ 0.5\end{array}\right)$, Ψ_A = 0.5, Ψ_S =0.5, $\mathrm{\Sigma }=\left(\begin{array}{ccc}1& 0.5& 0.5\\ 0.5& 1& 0.5\\ 0.5& 0.5& 1\end{array}\right)$. The total effect of A is ρ_A = Ψ_A + Φ_AΨ_S=0.5 +(0.5)*(0.5)=0.75.

Table 1 shows the bias and root mean square error of the path analysis estimate of the effect of A (which assumes no unmeasured confounding), the estimate of the total effect of A based on 2SLS, and the estimate of the total effect of A based on 3SLS in 2000 simulations. The 2SLS and 3SLS estimates performed virtually identically. The coverage of the 95% confidence intervals based on Vâr(ρ̂_A) from the simulation study was 0.9500 for the 2SLS approach and 0.9485 for the 3SLS approach.

Table 1.

Bias and root mean square error (RMSE) of various estimators of ρ_A in two different scenarios.

Estimator	Bias	RMSE
Scenario 1: (βW=(1,0.5)T)
Path Analysis	0.872	0.872
2SLS	−0.001	0.122
3SLS	0.002	0.122
Scenario 2: (βW=(1,0)T)
Path Analysis	0.970	0.970
2SLS	0.000	0.051
3SLS	0.001	0.039

The 3SLS estimates can provide efficiency gains in other situations in which different instruments are used for S compared to Y (this is analogous to the fact that seemingly unrelated regression (SUR) provides efficiency gains when the different equations have some different covariates, whereas SUR provides no efficiency gains if all the equations have exactly the same covariates). If we use the same simulation setting as above but assume that the second component of W is an instrument for S but not Y and let β_W=(1,0)^T, then the estimation results are shown in the second scenario in Table 1. The root mean squared error of the 3SLS estimate is 24% less than that of the 2SLS estimate for this scenario.

7 Extensions

We consider four extensions to this framework:

1. the presence of confounders of the effect of R on Y;

2. the presence of additional measured mediators of the “effect” of R on Y;

3. the use of failure-time outcomes instead of outcomes measured at a fixed time; and

4. settings in which the intermediate S is not fixed but rather time-varying.

7.1 Confounders of the instrument

Until now, we have supposed that associations between the instrument and outcome can be explained fully in terms of the associations of the instrument with the specified treatments A and S and the effects of those treatments on the outcome. In this and the following subsection, we weaken this requirement by allowing the instrument R to be associated with some other variable associated with the outcome. In some cases, this variable will be a confounder of the effect of R; in others, an intermediate treatment on a path from R to Y not involving A or S.

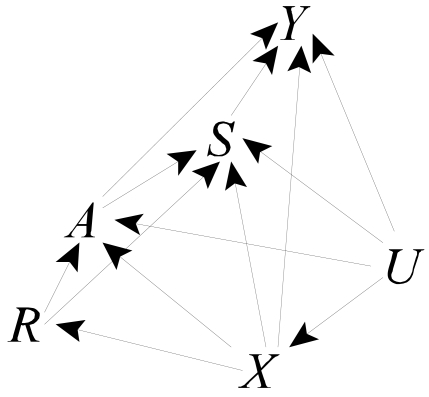
Suppose first that there are individual characteristics X that are associated with the instrument and the outcome (Figure 3). For example, it is possible that patients initiating dialysis at some centers are sicker, have higher income or education, or are older than patients initiating dialysis at other centers. These associations may lead to associations between the putative instrument R and outcome Y even in the absence of any effects of the treatments A and S on Y.

Figure 3.

Causal diagram 2, augmented to allow confounding of effect of instrument by measured variables.

For estimation, the same extended 2SLS approach taken previously is appropriate here, so long as appropriate confounders of the associations of the instrument R with Y and S are considered in the appropriate models. In particular, the effects of A and S on Y are estimable using (2) so long as E(Y⁰⁰|V,R)=E(Y⁰⁰|V) ; that is, if R is an instrument for the effects of A and S conditional on V. Thus, any common causes of R and Y⁰⁰ must be included in V. Similarly, the effect of A on S is estimable using (4) and (5) if those models are correctly specified and there are no unmeasured common causes of R and S⁰⁰; here, all measured common causes of R and S must be included in W.

7.2 Additional mediators of the effect of the instrument

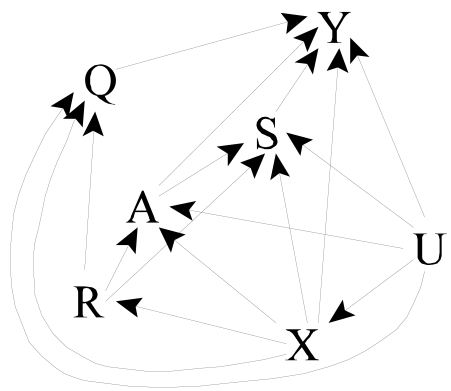
In our motivating example, center (R) is associated with a variation in a wide range of treatment patterns. For example, practice may affect dosing of erythropoetin and intravenous iron, both of which are used for treating the anemia prevalent among HD patients and which may affect other clinical outcomes, including mortality. Q denotes these additional mediating variables. We augment our causal graph to show these additional paths from R to Y, as well as paths from U and X to R (Figure 4). The approach sketched below will also be appropriate if Q affects A and S (i.e., additional arcs Q→A and Q→S are added to Figure 4).

Figure 4.

Causal diagram 3, augmented to allow additional mediators of the effect of the instrument.

For estimation, we augment our causal model (1) with a term for the effect of Q:

$$Y=Y^{\mathit{ASQ}}=Y^{000}+A{\mathrm{\Psi }}_A+S{\mathrm{\Psi }}_S+Q{\mathrm{\Psi }}_Q.$$ (7)

This again implies that

$$E(Y\mid R,V)=E(Y^{000}\mid V)+E(A\mid R,V){\mathrm{\Psi }}_A+E(S\mid R,V){\mathrm{\Psi }}_S+E(Q\mid R,V){\mathrm{\Psi }}_Q.$$ (8)

Estimation can again proceed using 2SLS; we now require that the design matrix comprised of V, E(A|R,V), E(S|R,V), and E(Q|R,V) have full rank. Estimating the effect of A on S can proceed as previously, as can combining inferences for the overall effect from the models for S and Y. The approach above allows Q=R as a special case. In this setting, the assumption of no direct effect of the instrument (i.e., no effect not explained by the measured variables (here A and S)) is equivalent to Ψ_Q=0 in (8) and so may be tested by testing Ψ_Q=0. This estimation and testing may be problematic where R consists of many unordered categories and so the dimension of Ψ_Q is high, as in our example.

7.3 Failure-time outcomes

In our motivating example, death is common, and time to death is arguably the most important outcome. Our system of linear models will not work for the popular but nonlinear Cox proportional hazards model (Cox, 1972), but the approach can apply to the accelerated failure-time model (AFTM), which is a linear model for the natural logarithm of the failure-time (Cox and Oakes, 1984). Henceforth, we use Y to denote the log of the failure-time.

In almost any study with failure-time outcomes, the failure-time will sometimes be censored. This complicates application of the methods discussed above, as expectations E(Y|·) cannot be calculated using least squares. This leaves two alternatives for estimation: 1) assume a parametric form or distribution for the error in f(Y|R,X) , or use a semiparametric G-estimation approach. Both approaches require appropriate ways to deal with censoring. We consider here two types of censoring: fixed (modified type I censoring) and “random” censoring. The first refers to planned censoring, where a potential censoring time is known for all subjects, regardless of whether a censoring event is actually observed. Random censoring refers to loss to follow-up or other reasons for unplanned or unpredictable censoring. For fixed censoring, one must use artificial censoring (Joffe and Brensinger, 2001; Robins, 1992; Robins et al. 1992) in the analysis. Artificial censoring results in difficulties in estimating the structural parameters Ψ due in part to the fact that the function to be optimized is no longer continuous. This complicates obtaining both point and interval estimates. Random censoring can be dealt with using inverse probability of censoring weighting methods (Robins et al. 1992); these methods rely on the censoring process being ignorable given the measured past.

7.4 Time-varying auxiliary treatments

In many cases, both main and auxiliary treatments may vary over time. In our example, both VA and dialysis dose may vary within an individual. Nonetheless, the type of VA may vary less frequently (as some surgical procedure is required to establish VA), and so we make the working assumption that VA is constant over an extended period, while dialysis dose may vary over time. In this setting, it is appealing to consider modeling the effect of the auxiliary intervention received at each point in time, then incorporating these effects into estimates of the overall effect of the main intervention. We consider briefly how to extend our approach to this setting.

Let S_t denote the level of S that applies at each discrete time t, and let S̄ denote the entire history of S. Consider first a model for the joint effects of A and S on Y; a fairly general linear model is

$$Y^{0,\overline{0}}=Y-A{\mathrm{\Psi }}_A-\sum _t{S}_t{\mathrm{\Psi }}_{S_t}.$$ (9)

The 2SLS approach (2) then becomes

$$E(Y\mid R,V)=E(Y^{00}\mid V)+E(A\mid R,V){\mathrm{\Psi }}_A+\sum _{t}E(S_t\mid R,V){\mathrm{\Psi }}_{S_t};$$ (10)

to estimate distinct parameters, we will need the design matrix formed from each of the individual elements in regression (10) to be full rank. Collinearity may be a severe problem if, as expected, the effect of R on the various S_ts is similar. Dimension reduction may be helpful here; suppose that Ψ_St is a low-dimension function of Ψ. The simplest such function is Ψ_St = Ψ_S, a common value for all t.

Estimating the effect of A on S requires less modification; (3) generalizes to

$$S_t^{RA}=S_t^{00}+R{\mathrm{\Phi }}_{Rt}+A{\mathrm{\Phi }}_{At},$$ (11)

and (4) becomes

$$E(S_t\mid R,W)=E(S_t^{00}\mid W)+R{\mathrm{\Phi }}_{Rt}+E(A\mid R,W){\mathrm{\Phi }}_{At}.$$ (12)

One can fit a separate model for each S_t, or one can model various S_ts jointly with a common parameter Φ, where the time-specific parameters Φ_t = {Φ_Rt, Φ_At} are functions of Φ. In the latter case, one will need to account for the nonindependence of the various S_ts in an individual in the variance calculation.

It is easy to show that, generalizing (6), the overall effect ρ_A may be calculated as

$${\rho }_A={\mathrm{\Psi }}_A+\sum _t{\mathrm{\Phi }}_{At}{\mathrm{\Psi }}_{St}.$$ (13)

Variance calculations can be based on generalizations of the 2SLS or 3SLS estimators considered in the appendix. One can also use semiparametric G-estimators for Ψ and Φ.

Estimation for failure-time outcomes with multiple measurements of the auxiliary treatment S is more complicated. Estimating the separate component effects of A and S is straightforward, using G-estimation. However, estimation of the overall effect of A under IV-like assumptions is problematic.

To estimate the component effects of A and S, we use a structural nested failure-time model (SNFTM). Let S(t) denote the level of S that applies at time t measured in continuous time; we presume that S(t) is constant on the interval between discrete measurement times t. The simplest SNFTM for this setting is an AFTM with time-varying covariates:

$$Y^{00}=\underset{0}{\overset{Y}{\int }}exp\{A{\mathrm{\Psi }}_A+S(t){\mathrm{\Psi }}_S\}dt.$$ (14)

Model (14) assumes no interaction between A and S(t). For a time-invariant S(t), this reduces to the standard AFTM. Estimation can use G-estimation, which is based on testing the independence of $Y^{00}(\mathrm{\Psi })\equiv \underset{0}{\overset{Y}{\int }}exp\{A{\mathrm{\Psi }}_A+S(t){\mathrm{\Psi }}_S\}dt$ and R; for model (14), this will require a 2 degree of freedom test.

Estimation of the effect of A on S can also use a generalization of the method sketched above. For now, we assume that, even though S may vary over time, the effect of A on S is constant on average, i.e., in (11), Φ_At = Φ_A, a constant. We can use 2SLS or G-estimation methods to estimate Φ. As before, the overall effect can be estimated as Ψ_A + Φ_A Ψ_S.

Inference under less restrictive assumptions is more complicated. Consider model (11) without the restriction of constant effects. We no longer have available a simple formula for obtaining overall effects. Let overlines denote the history of a variable over time, thus, S̄^a denotes the history of S(t). To obtain overall effects, one could in principle compute Y^aS̄a(Φ)(Ψ) from the data and models Ψ for the effect of A and S on Y and Φ for the effect of A on S. One could then compare Y^aS̄a(Φ)(Ψ) with Y^0S̄0(Φ) (Ψ) at an individual level, or average over a population, as a measure of overall effects. Let s*(t) ≡ {S̄^a(t), 0} denote the history of S that would be seen by following the observed history through t, then setting S(t) = 0 thereafter. One could in principle make this comparison by “blipping-up,” i.e., recursively computing Y^as*^(t) from Y^as*^(t−1), S^a(t), and Ψ_S using a rank-preserving structural nested model. Unfortunately, for a given individual, S⁰(t) will only be computable if S(t) is observed; if a subject fails before t and S(t) is no longer observable, as would be true if Y refers, even in part, to mortality, S(t) will not be observable for t>exp(Y). If the treatment A is beneficial overall at each point in time, so that Y^a>Y⁰, there will be some times t for which we cannot compute S^a(t) for some subjects. If the treatment is consistently harmful or failure never precludes observation of S subsequently, this approach can be used together with the restrictive assumption of rank-preservation. Appropriate coding of a so that large a is beneficial can finesse this issue.

8 Discussion

We have sketched an approach for estimating the overall effect of an exposure or treatment in settings in which conventional analysis fails because of unmeasured confounders. Here, IV-type assumptions may be valid for estimating the joint effects of the main and auxiliary treatments, but are not by themselves sufficient to identify the overall effect of the main treatment. So long as we can estimate the effect of the main treatment on the auxiliary one, we will be able to estimate the overall effect.

While the relaxation of the no-unmeasured confounders assumption is valuable, we have needed to substitute other assumptions. These are comprised of structural assumptions and modeling assumptions. The structural assumptions include: 1) the assumption that there are no effects of the IV on the main outcome except those mediated by measured variables (although this assumption is relaxed in 7.2), and 2) the assumption that the effect of the study treatment is deterministic (i.e., given one counterfactual and the true model, we could recover any other without error). Neither assumption is fully testable (Robins et al. 1992; Robins, 1994).

The assumption of deterministic treatment effects, roughly equivalent to rank-preservation, is often a heuristic for deriving and explaining estimation procedures, but may impose no restrictions on the joint distribution of the observables when compared with the less restrictive structural distribution models (Robins et al. 1992). In these settings, analyses that heuristically assume rank preservation can be useful (Robins et al. 1992; Ten Have et al. 2007). While this is true in the simpler settings in which both treatments are scalar, it is not true in general when the outcome is a failure-time precluding observation of future auxiliary treatments S(t). Rank-preservation will typically not be plausible; the reasonableness of analyses based on the assumption remains to be determined. Deterministic models are also not compatible with binary or count outcomes. Structural nested mean models and associated G-estimation in principle may be used for these types of models and outcomes. For the usual logit link used with binary outcomes, both semiparametric G-estimation and standard 2SLS approaches are problematic (Robins et al. 2000). Extension of the methods presented here to these types of outcomes will require further consideration.

We have also made some modeling assumptions, e.g., that the effects of the main variables are correctly modeled in (1) and (3) using a linear model and do not depend on each other or other measured variables. These assumptions are partially testable in some circumstances. When there are more instruments than are needed for identification (e.g., the dimension of W, V are 2 or greater in the setting of Appendix 1), the overidentifying restrictions test can be used to test these assumptions. This test basically uses the fact that if all the instruments are valid, then estimates based on different subsets of instruments should agree up to sampling error (Anderson and Rubin, 1949; Newey, 1985; Small, 2007).

The no-interactions assumptions can also be tested by elaborating the models to allow interactions, then testing the interaction terms. The power of such tests may be limited (Ten Have et al. 2007). In the presence of such interactions, our approach to estimating overall effects using (6) will fail. For interactions between baseline covariates X and the study treatments A and/or S, a relation like (6) may hold within strata of X; therefore, overall effects within these strata may be estimated. One can then average these overall effects over the target population of interest to estimate average overall effects for the population.

In our formulation, structural models (e.g., (1) and (3)) represent comparisons of the observed outcome with a baseline potential outcome (e.g., of Y=Y^AS with Y⁰⁰). Estimation of the marginal distribution of Y^as using our approach depends on additional assumptions of no current treatment interaction, i.e., that the effect of A (or S) is the same for subjects who receive A (S) and who do not receive it (Robins 1994; Robins et al. 2000). The same is true for estimation of overall effects (i.e., comparisons of Y^a).

We expect that our analyses will be less efficient than standard adjustments for confounding based on assumptions of ignorability of treatment assignment or no-unmeasured confounders, just as IV analysis is generally less efficient than regression adjustment for confounding. This inefficiency can be heightened when estimating multiple parameters in a single regression based on ignorability or randomization of R (Ten Have et al. 2007), as we do here. Thus, sample size requirements for studies using our analysis can be substantially greater than conventional regression analyses.

Figure 1.

Causal diagram showing relations between key treatments and outcomes.

Appendix 1. Details of variance estimation and three-stage least squares estimation

In this appendix, we calculate analytically the standard errors for the two-stage least squares estimator of the parameters of interest and describe how efficiency can be improved by a three-stage least squares procedure. We consider a setting corresponding to the hemodialysis example in which A could be an ordinal or continuous variable, S is a continuous variable and Y is a continuous variable. More specifically, we consider the following setting: 1) we have an i.i.d. sample of the random vector (V,W,A,S,Y); 2) V = W (V and W are the subsets of X in equations (2) and (4)); 3) an interaction between R and W affects A but not S⁰⁰ and Y⁰⁰; and 4) the following models hold:

$$\begin{array}{l}{E}^{*}(A\mid R,W,RW)=R{\gamma }_R+W^T{\gamma }_W+R{W}^T{\gamma }_{Rw}\\ E(S^{00}\mid R,W)=R{\beta }_R+W^T{\beta }_W\\ E(Y^{00}\mid R,W)W^T{\theta }_W,\end{array}$$

where E^* denotes the linear projection.

We can then represent the observed data as:

$$\begin{array}{l}A=R{\gamma }_R+W^T{\gamma }_W+R{W}^T{\gamma }_{RW}+{\varepsilon }_1\\ S=R{\beta }_R+W^T{\beta }_W+A{\mathrm{\Phi }}_A+{\varepsilon }_2\\ Y=W^T{\theta }_W+A{\mathrm{\Psi }}_A+S{\mathrm{\Psi }}_S+{\varepsilon }_3,\end{array}$$

where (ε₁, ε₂, ε₃) are mean zero “structural errors” with covariance matrix Σ. The observed data forms a simultaneous equation system. Note that the observed data can be represented as

$$\left(\begin{array}{c}A\\ S\\ Y\end{array}\right)=Z\mathrm{\Delta }+\left(\begin{array}{c}{\varepsilon }_1\\ {\varepsilon }_2\\ {\varepsilon }_3\end{array}\right),\text{where\hspace{0.28em}}\mathrm{\Delta }=\left(\begin{array}{c}{\gamma }_R\\ {\gamma }_W\\ {\gamma }_{RW}\\ {\beta }_R\\ {\beta }_W\\ {\mathrm{\Phi }}_A\\ {\theta }_W\\ {\mathrm{\Psi }}_A\\ {\mathrm{\Psi }}_S\end{array}\right),Z=\left(\begin{array}{ccccccccc}R& W^T& R*W^T& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& R& W^T& A& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& W^T& A& S\end{array}\right).$$

Let Â=Ê^*(A|R,W) be the predicted value of A from the least squares regression of A on R,W,R*W. Let Ŝ=Ê(S|R,W) be the predicted value of S from the least squares regression of S on R,W. Let $\widehat{Z}=\left(\begin{array}{ccccccccc}R& W^T& R*W^T& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& R& W^T& \widehat{A}& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& W^T& \widehat{A}& \widehat{S}\end{array}\right)$. Let $\mathit{T}=\left(\begin{array}{c}{A}_1\\ S_1\\ Y_1\\ ⋮\\ A_N\\ S_N\\ Y_N\end{array}\right)$ and $\widehat{\mathit{Z}}=\left(\begin{array}{c}{\widehat{Z}}_1\\ ⋮\\ {\widehat{Z}}_N\end{array}\right)$.

The 2SLS estimate of Δ is Δ̂_2SLS=(Ẑ^TẐ)⁻¹Ẑ^TT. The two stage least squares estimate Δ̂_2SLS is a consistent estimator of Δ; a consistent estimator of NVar(Δ̂_2SLS−Δ) is N(Ẑ^TẐ)⁻¹Ẑ^TΩ̂Ẑ(Ẑ^TẐ)⁻¹, where $\widehat{\mathrm{\Omega }}=\left(\begin{array}{ccc}\widehat{\mathrm{\Sigma }}& 0& 0\\ 0& \ddots & 0\\ 0& 0& \widehat{\mathrm{\Sigma }}\end{array}\right)$ and Σ̂ is the estimate of Σ that equals the sample covariance matrix of T − ZΔ̂_2SLS (Amemiya, 1985; Ch. 7).

A more efficient estimate of Δ can be obtained by the 3SLS procedure (Amemiya 1985). 3SLS is a generalized least squares type version of 2SLS that takes account of the covariance between (ε₁, ε₂, ε₃). The 3SLS estimate of Δ is Δ̂_3SLS = (Ẑ^TΩ̂⁻¹Ẑ)⁻¹ Ẑ^TΩ̂⁻¹T. A consistent estimate of NVar(Δ̂_3SLS−Δ)is N(Ẑ^TΩ̂⁻¹Ẑ)⁻¹. Note that N(Ẑ^TẐ)⁻¹Ẑ^TΩ̂Ẑ(Ẑ^TẐ)⁻¹ − N(Ẑ^TΩ̂⁻¹Ẑ)⁻¹ is positive semi-definite (Harris and Mátyás, 1999) so that Δ̂_3SLS is asymptotically efficient relative to Δ̂_2SLS.

Regardless of how we estimate Ψ_A, Ψ_S, and Φ_A, we estimate the total effect of the treatment A by ρ̂_A = Ψ̂_A + Φ̂_A Ψ̂_S and we can estimate the variance of ρ̂_A using the Delta Method:

$$\begin{array}{l}\widehat{\mathit{Var}}({\widehat{\rho }}_A)=\widehat{\mathit{Var}}({\widehat{\mathrm{\Psi }}}_A)+\widehat{\mathit{Var}}({\widehat{\mathrm{\Phi }}}_A){({\widehat{\mathrm{\Psi }}}_S)}^2+\widehat{\mathit{Var}}({\widehat{\mathrm{\Psi }}}_S){({\widehat{\mathrm{\Phi }}}_A)}^2\\ +2\widehat{\mathit{Cov}}({\widehat{\mathrm{\Psi }}}_A,{\widehat{\mathrm{\Phi }}}_A){\widehat{\mathrm{\Psi }}}_S+2\widehat{\mathit{Cov}}({\widehat{\mathrm{\Psi }}}_A,{\widehat{\mathrm{\Psi }}}_S){\widehat{\mathrm{\Phi }}}_A+2\widehat{\mathit{Cov}}({\widehat{\mathrm{\Phi }}}_A,{\widehat{\mathrm{\Psi }}}_S){\widehat{\mathrm{\Phi }}}_A{\widehat{\mathrm{\Psi }}}_S.\end{array}$$