The Classic: On the Inner Architecture of Bones and its Importance for Bone Growth

Abstract

This Classic article is a translation and abridgment by M.O. Heller, W.R. Taylor, N. Aslanidis, and Georg N. Duda of the original work by Julius Wolff, Ueber die Innere Architectur der Knochen und ihre Bedeutung für die Frage vom Knochenwachstum (supplemental materials are available with the online version of CORR). An accompanying biographical sketch on Julius Wolff is available at DOI 10.1007/s11999-010-1258-z. A second Classic article is available at DOI 10.1007/s11999-010-1240-9. An accompanying Editorial is available at DOI 10.1007/s11999-010-1238-3. The Classic Article is ©1870 and is reprinted from Wolff J. Ueber die innere Architectur der Knochen und ihre Bedeutung für die Frage vom Knochenwachsthum. Virchows Arch Pathol Anat Physiol. 1870;50:389–450.

Electronic supplementary material

The online version of this article (doi:10.1007/s11999-010-1239-2) contains supplementary material, which is available to authorized users.

In late 1867, Reichert and Du Bois-Reymond’sArchive published the short work by Hermann Meyer of Zurich on “The Architecture of Spongiosa,” in which it could be proven that the plates of the cancellous (spongiosa) segments in the bone appear in a specific, regular, and distinct configuration in every part of the body. To my knowledge this work has hitherto not been given any sort of consideration. And yet it seems to be, I believe, one of the most extraordinary discoveries of physiology, one of the most meaningful, actually, to which the examination of bones has led until today. Therefore it seems to be my duty as well as the right time to raise awareness of Meyer’s discovery and to follow its development.

The reason why this theory has not yet become well known is partly that Meyer himself has, until now, hardly engaged himself with the matter of how much his observations could have changed earlier explanations for understanding bone structure. In addition, he himself had illustrated his work merely with schematic drawings and no actual depictions of specimens, and for many readers, as well as myself, this fact gave reason to doubt the truth of the observations. While Meyer attempted to show in a most remarkable way a connection between the architecture of cancellous bone and the mechanical nature of bone, the most important thing and at the same time almost the only thing that seemed relevant to me in this work, ie the great discovery made by the mathematician Culmann that the architectural configuration in some bones resembles the theoretic lines of graphic statics, was mentioned only briefly, without further remark. Neither did he give explanations for tensile or compressive lines, shear forces, or other similar terms from the science of mechanics (“graphic statics”). However, the meaning of these terms, the understanding of which is quite necessary for the present topic, was certainly familiar to only a few of his readers, and certainly not for the general surgeons who have always been more interested in studies of the nature of bones than the physiologists.

While in Zurich last October I had the opportunity to ask professor Meyer to show me his specimens concerning the architecture of the cancellous bone, something he was very happy to do. Thanks to this fortunate circumstance I am now convinced that the cancellous bone structure is not a confused and disorganized meshwork of trabeculae and cavities, as it used to be believed until now, but that it is characterized instead by a “well motivated architecture”, which grants every one of its trabeculae a mechanical meaning and, so to speak, a certain role as a building block related to its usage in the grand structure that is the bone.

I have since concerned myself extensively with the architectural nature of the bones. Initially I did this due to the extraordinarily high interest of the topic as well as the necessity to fill the gaps in Meyer’s work, which very soon presented itself to me. But another more important reason led me to detailed consideration of this topic. The more I thought about the inner architecture of the bone and the more I turned my attention towards the comparison of the same in different stages of life down to the foetal stage, the more I became convinced Meyer’s discovery has extraordinary importance in the matter of bone growth, given the comparison of the mathematical certainty of the architecture of bone with the necessity of interstitial bone growth, and that for this reason the results of my experimental studies concerning this matter find full and irrevocable confirmation.

In my following elaborations about the mechanical (“statische”) importance of the inner architecture of bones I shall preferably keep to one specific example, ie, I will almost exclusively occupy myself with the description of the proximal end of the human femur (“Oberschenkel”). My reasons for choosing this part of the body are the following. For one, the mechanical conditions at the upper end of the proximal femur are extremely simple, for possibilities of movement in the hip joint are all rather restricted, while the chief mechanical function of the proximal femur is to carry the weight of the torso, which is transferred to it via the acetabulum. In addition, when the weight of the body lies on the upper end of the proximal femur, it is not only burdened with compression, but at the same time, as can easily be seen, with bending, due to the angle between the head and the stem. This fact, though, makes necessary a structure of trabeculae, which makes it possible to prove strictly mathematically the mechanical importance and the necessity of this structure, and this proof is my chief aim in this text. Lastly, I believe this same body region to be the most suitable one to allow me to explain my findings both for the growth in length and in thickness of hollow bones.

[Portions of Pages 392–393]

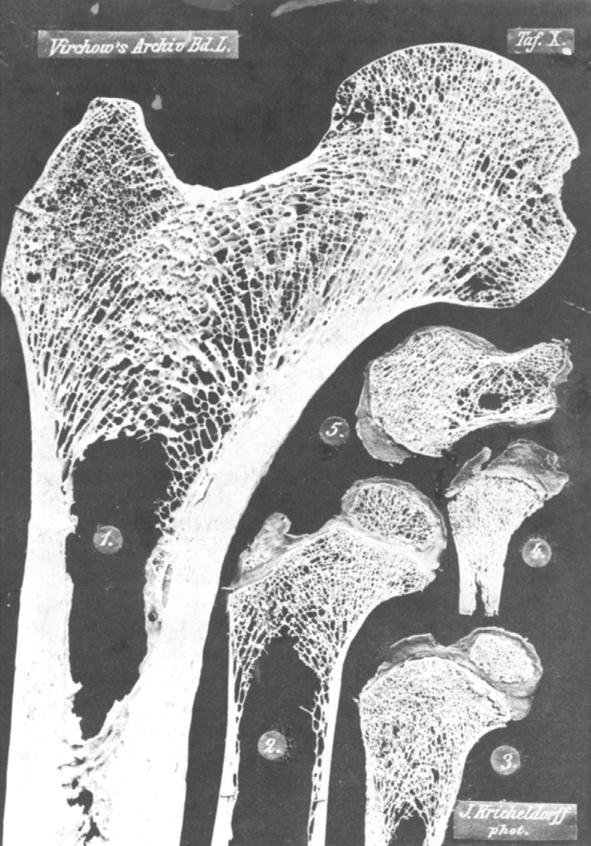
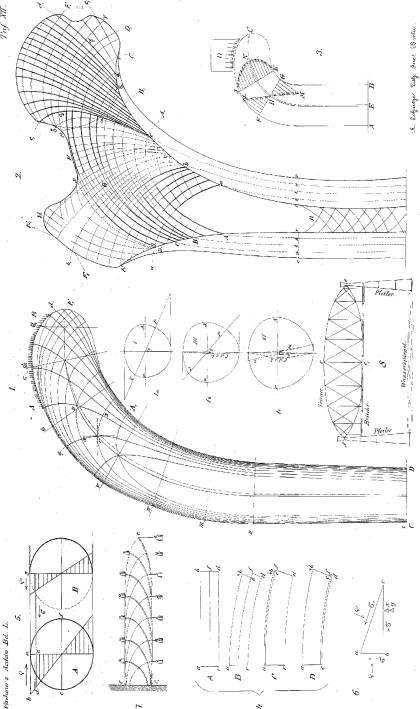
Figure 1, Plate (“Tafel”) X shows the photograph of a thin section taken from the upper end of an adult femur at actual size. As can be seen, the cut goes frontally straight through the head, the neck, the greater trochanter, and the middle portion of the bone. Figure 2, Table XII has been drawn after this specimen and, to simplify my explanation, has been kept somewhat schematic, but other than that, as can be seen, corresponds completely to the original.

Table X.

The images in this table have been photographed in natural size. The specimens depicted in Figures 1, 2 and 5 have been cut on the ivory cutting machine, those in Figures 3 and 4 have been cut freehand. Figure 1. Frontal longitudinal thin section, somewhat eccentric, closer to the dorsal surface, from the upper end of the right proximal femur of a 31-year-old man. Figure 2. A similar, but more centrally set longitudinal section from the proximal femur of a 3-year-old girl. Figure 3. The same from a 1¼-year-old boy. Figure 4. The same from a newborn boy. Figure 5. Sagittal longitudinal section through the middle of the Calcaneus of a 5-year-old girl.

Table XII.

Figure 1. Depiction of the forces and trajectories in effect inside a bone. Based on the original drawn by the students of professor Culmann and under his supervision in double the original size of a human proximal femur. This original drawing was first photographically reduced back to the natural size and later lithographed. Figures 1a, b and c depict the force distribution for the exemplary chosen cross sections I, III and VI. Figure 2. Schematic reproduction of the specimen photographed in Figure 1, Table X. Figures 3–7 are part of the explanations on graphical statics on pp. 402–407. Figure 8. Schematic depiction of a bridge built according to Pauly’s system.

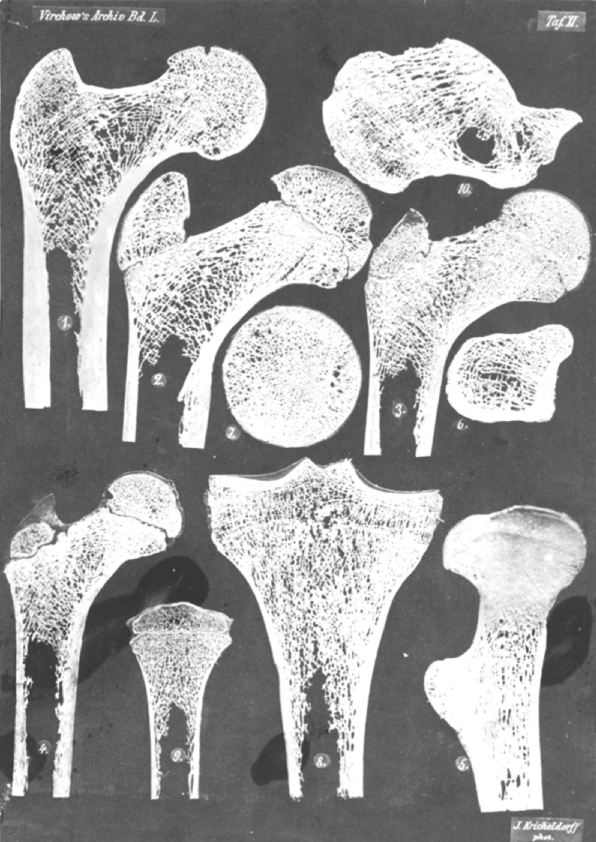
Figure 1, Table XI shows a similar cross section from an adult, photographed at half the original size.

Table XI.

All images in this table have been photographed in exactly half their natural size. It is advantageous to regard this table through a magnifying glass, for everything that might have been lost through the reduced depiction is completely recreated by this method of observation. The specimens depicted in Figures 1–4 and 8–10 have been cut on the ivory cutting machine, that in Figure 5 on the mechanical fret saw and those in Figures 6 and 7 by freehand. Figure 1. Frontal central longitudinal section from the femur of a 25-year-old woman. Figure 2. The same from the femur of a 20-year-old man. Figure 3. The same from a 13-year-old boy. Figure 4. The same from a 7-year-old girl. Figure 5. Sagittal longitudinal section, following the bent axis of the bone and thus depicting its neutral fiber layer, from the left proximal femur of a 29 year old man, seen from the concave (the medial, compression or adductor) side. The side of the specimen which intersects the dorsal surface of the proximal femur with the trochanter minor lies to the left. Figure 6. Cross-section (at a right angle to the axis) of the right proximal femur of the same man, at the height of the trochanter minor, seen from above. The side of the specimen which corresponds to the frontal surface of the proximal femur lies towards the lower side of the page, that of the dorsal surface (with the trochanter minor) towards the top, the tensile side respectively on the left, the compression side on the right. Figure 7. Cross-section of the same proximal femur, out of the femoral head, roughly in the region between its middle and lower third, seen from below. Here the side corresponding to the frontal surface of the proximal femur is again at the bottom, the side corresponding to the dorsal surface at the top, the tensile side at the left and the compressive side at the right. Figure 8. Frontal longitudinal section through the upper end of the lower leg of a 28-year-old woman. Figure 9. The same from a 5-year-old girl. Figure 10. Sagittal longitudinal section through the middle of the calcaneus of a 35-year-old man.

[Portions of Page 394]

The so-called compact substance (cortical bone), thickest in the middle of the bone, becomes increasingly thin on both sides towards the top until it completely disappears. This disappearance happens on the lateral side at the greater trochanter in the lower outer angle of the trochanter and on the medial side at the side of insertion of the adductors where the roundish bulge of the joint head begins, a little lower than the epiphysis boundary (α β in Figure 2, Table XII), which remains visible until a very high age as a scar.

[Portions of Page 394]

Closely below the lesser trochanter, the cancellous bone begins and fills out the whole space up to the upper end of the bone. It consists of roughly 50 trabeculae originating from the compact tissue on the adductor side and the same number from the trochanter side.

Regarding firstly the trabeculae on the adductor side, the lowest of them (originating between a and b on Figure 2, Table XII) curve in a very strong arch towards the trochanter side and end in the upper part of the femoral shaft and the lower part of the greater trochanter, almost exactly parallel to each other, ending in a₁ b₁. The next group of trabeculae, originating between b and c, fan out even more and reach the upper part of the trochanter, the femoral neck, and the extreme part of the femoral head, ending between b₁ and c₁ in our illustration. The middle group of these trabeculae, the ones originating in the apex of the round, obtuse angle between the head and the stem of the femur and grow upwards towards the saddle of the femoral neck, diverge especially strongly and even give off side branches in between. These are followed between c and d by another layer of more parallel trabeculae growing diagonally upwards and towards the inner side into the femoral head, which pass the epiphysis boundary at c₂ and d₂. The last, weaker group of trabeculae, starting at d e spread out in the innermost or lowest part of the femoral head.

The trabeculae originating from the trochanter side between A and D, however, all extend over in a similarly high and especially long arc to the adductor side, where they find their end near the epiphyseal boundary, on the lower side close to A₁ and on the upper side close to D₁. Here, as well, the middle trabeculae originating between B and C fan out more than the others, again often with side branches. The trabeculae higher up and those lower down, on the other hand, are more parallel to each other. The last trabeculae, which begin between D and E on the trochanter side, end in the greater trochanter.

These two trabeculae systems are completed by a small system of trabeculae, which becomes more dense in the saddle shaped impression of the femoral neck in a small region close to F, and fans out from here in two directions, outwards in the direction of F₂ into the greater trochanter and inwards in the direction of F₁ into the femoral head.

Furthermore, at the tip of the greater trochanter at the insertion point of the M, gluteus medius, at the point H, a small system of downwards trabeculae can be discerned.

Finally, eccentrically cut sections, as in Figure 1, Table X, will reveal networks of trabeculae at the lower end of the specimen (at the point R), which connect the compact systems on the medial and the lateral side with each other, and which can be regarded as the rest of those trabeculae which were created in the fetal stage in the region of the marrow cavity. These trabeculae fan out downwards, ie, in the opposite direction from those described before.

Observing more closely it is possible to see the trabeculae on the adductor side each one crossing one from the trochanter side roughly in the middle line of the bone. Furthermore it is possible to see how all of the uncountable crossings of trabeculae happen in 90° angles, and that this means that all of the hollow areas between the trabeculae are squares or rectangles. Although, in some points, these angles may be rounded, it is easy to see that the sides of these rounded angles still are in a right angle to each other. Furthermore, the ends of the trabeculae are also in a right angle towards the bone surface.

[Portions of Pages 397–400]

If we attempt to create a full picture of the architecture of the upper end of the femur from the findings from the longitudinal and transverse cross sections, we will firstly have to remark that the things that look like trabeculae on the thin sections are actually usually parts or sections of corresponding small plates, admittedly often perforated like a sieve by quadrangular holes.

Our photographs firstly show that one row of such plates runs from front to back on the medial side and another one just like it on the lateral side, and that these plates, converging towards the top, must essentially be roof-shaped.

[Portion of page 400]

After this anatomical presentation the question arises, what the meaning of this specific and always constant configuration of trabeculae or plates in the proximal femur is.

[Portion of page 401]

While regarding those specimens Culmann immediately realized that the cancellous trabeculae in many regions in the human body are constructed in exactly the same lines as those that mathematicians would develop in graphic statics on bodies which have similar shapes as the bones concerned and which are subject to similar forces as they are. He drew a crane, ie, a bent beam, meant to lift or bear loads, in the shape of the upper end of the human proximal femur, to which he assigned a load equivalent to the conditions in the human. He then had his students draw so-called tensile and compressive lines into this crane under his supervision. The result was astonishing! It came to be that the lines are the same ones that nature actually applied at the upper end of the proximal femur in the directions of the bone trabeculae.

Our illustration in Figure 2, Table XII, drawn from nature, when compared to Figure 1 next to it, which depicts Culmann’s crane, will astonish with its similarity at the first glance. At this point in my work I do not yet wish to refer to this similarity in more detail. I merely meant to have mentioned it, in order to justify the fact that I shall utilize the definition of a few laws of graphic statics, the understanding of which is essential in this matter.

[Portions of pages 402–404]

However, tension and compression are not the only effects of the exterior force D, which is applied to the beam. The (hypothetical) particles of any cross section in a material (“Körper”) attempting to withstand bending tend to shift their position in respect to the particles of the neighboring cross section, and the particles of any longitudinal section tend to shift their position in respect to the particles of the neighboring longitudinal section. The force by which this happens is called shearing force and it results in a shear stress in every section, which withstands the movement of two neighboring sections against each other.

[Portions of Pages 404–406]

Furthermore…(Culmann’s) pictures 104 and 106 depict the fact that in the sections, in which compression and tension become maximal, the shearing forces are = 0, which means that in the directions of maximal tension and maximal compression there are no shear forces.

If, however there is no shear force in a certain direction, then fibres at that location may be cut in that direction, without compromising the stability of the beam. This direction, of course, is a different one in every location on the beam. If, however, the beam was to be cut at any location, then two groups of lines or fibers would ensue, one group from the direction of maximal compression, the other from that of maximal tension, between which there is no shear force. Thus these two groups of lines, consisting of rods or pillars and bands or tie rods, can replace the solid, complete beam, as is shown in our picture 7, the reproduction of Culmann’s picture 107, p. 236. And the lines connecting these directions, originally called stress trajectories by Culmann, but soon after renamed as curves of pressure and tension, are what this text is about, and following these lines, as we are about to demonstrate, the upper end of the human upper leg is constructed.

[Portions of Page 407]

It is now apparent that it is possible to deduct from the compression and tension curves the magnitude and the character of the loading in each element of the material. Due to the fact that, as we were able to see, the stresses, which result from the external force, are kept in equilibrium by the internal resistance for as long as the bending strength of the material is not surmounted by the outer force, we are able to read out of these systems of lines in which directions the greatest resistance to the compression and tension in the beam caused by the load exists, and in which locations of these directions the maximum or the minimum of greatest resistance exists.

This last characteristic of tension and compression curves, in connection with a second, already known one, leads us to the practical relevance of these curves. We have seen that no shear forces are present in the directions of the latter. This means that the elements of the burdened body on both sides of those planes, the intersection lines or traces of which are the tension or compression curves in the longitudinal section, do not tend to slide along one another.

[Portions of Page 408]

The calculations discussed above are more than mere theories, but have already been applied in practice. I should not fail to remark here that Pauly’s bridge truss, which has recently been playing a very important role in bridge building, and which has, amongst other places, been used in the railroad bridge over the Rhine at Mainz, is based on the theory of tension and compression lines.

[Portions of Pages 409–411]

It is immensely important that Culmann’s cross sections were originally taken as solid, ie, that the trajectories were not originally drawn for a hollow crane like the bone, but for a solid one, and that despite this assumption the tension and compression lines were at the outer edge and provided a cross section with a hollow middle, as is the case in the actual bone.

[Portions of Pages 411–415]

We now understand the meaning of the trabeculae or plates in the cancellous bone. Those coming from the adductor side are compression trabeculae or plates, in which shear forces are eliminated, and which, at the same time, create the greatest possible resistance to the pressure effect of the body weight. The upper end of the proximal femur is compressed solely in the directions of these trabeculae, and if there had not been any or not sufficiently strong trabeculae, then the pressure would probably crush the bone. The trabeculae on the trochanter side are pressure trabeculae, in which there are no interfering shearing forces as well, and which, at the same time, are best suited to withstand the tension on the trochanter side caused by the body weight and prevent a fracture of the bone.

We now understand why long bones have to have the thickest compact structure in their middle portion. We have seen how compression and tension lines become more parallel and run closer together towards the surface, where they represent the stress maximum, the further away they are from the point of loading. In very much the same way trabeculae become a denser compact structure towards the middle portion of the bone, which has to be densest and thickest in the middle portion of the bone, far away from the point of loading, where tension and compression reach their maximum level, and where the bone has to resist more than anywhere else and to withstand the greatest tendency to be crushed.

[Portion of Page 416]

We also understand why bone has its large marrow cavity in the middle. It has always been apparent that the marrow cavity, much like the sponge like structure at the bone ends, would exist for material economy reasons, while at the same time creating a large circumference, which the bone needs to let its rich musculature attach to it. But only after having learned from mathematicians where the material is necessary and where it is unimportant, as we saw from Culmann in a cross section from the diaphysis taken to be completely solid the calculated trajectories all end up being close to the surface, we can that material has not been left out at any arbitrary place, but in places where it would have been unnecessary, where it would not have been put to use.

[Portions of Pages 416–420]

What remains for research is a wide and certainly very rich field. These conditions will certainly not be as easy to explain in any part of the body other than in the proximal femur. At least in most of the other long bones the application is a much more complicated one and thus we will have to encounter a much more complicated and much less easily analyzable crossover of different trabeculae systems in such bones.

[Portions of Pages 420–422]

I now come to the second part of the present examination, the deductions, which result from the inner architecture of the bone in the matter of bone growth.

Until the time of Du Hamel the matter of how bone would grow was not widely discussed. It was regarded to be obvious, something that now would need such a great deal of proof, that bone grows in the same way that all other vascularized tissues do, by expansion and with a living portion of all of its distinct parts. Since Du Hamel published his experimental research on bones, 130 years ago, a new, very artificial view on bone growth has been established, although possibly only partly due to the work of the scientist himself, which had not been supported in its total extent until John Hunter and Flourens, according to which a constant growth of layers at the ends and at the surfaces and a constant resorption on the inside of the bone was supposed to be taking place.

[Portions of Pages 422–426]

Figure 2, Table XI is a photograph in half linear size of a thin section which has been sawed frontally out of the middle of a femur of a 20-year-old man. All the conditions here are exactly as in the two specimens of adults, which have been shown earlier; there is, however, no bone connection at the epiphysis boundary in the joint head as well as at the trochanter, which means that the trochanter and the upper end of the joint head in specimens like this, will still detach if boiled in water. Figure 3, Table XI shows a similar thin section from the femur of a 13-year-old boy, Figure 4 one from a 7-year-old girl. In both specimens the ossification can be seen up to the end of the greater trochanter and to the line-shaped gap between the main portion of the bone and its two upper end pieces. The width of this gap is hardly more important than in the 20-year-old, apparently completely grown up, individual.

Figure 2, Table X finally is a frontal thin section from the femur of a 3-year-old girl in its natural size. In the trochanter there is only a small bone core, while the gap between diaphysis and epiphysis at the femoral head has still a certain width and appears as one continuous line with the trochanter gap.

It is immediately apparent that the inner architecture of the bone presents exactly the same Figure in all of these four specimens as the specimens of adult individuals depicted in Figure 1, Table X and Figure 1, Table XI. Without any doubt compressive and tensile trabeculae and their rectangular intersections can be recognized in every one of the specimens. In exactly the same places as in the adult the stronger or weaker development of the tensile and the compressive trabeculae can be seen. Everywhere the obvious intersection which corresponds to the point α in Figure 2, Table XII can be found everywhere also the triply different Figure of layer of cancellous bone closely below the epiphysis boundary of the femoral head. In other words, the description we have given above for Figure 1, Table X and for Figure 1, Table XI could, without any change, work for any one of the Figures 2–4, Table XI and Figure 2, Table X. Even in Figures 3 and 4, Table X, which show frontal longitudinal femur sections of a 1¼-year-old child and a newborn, and about which I will say more later, the same configuration can be recognized wherever ossification has been completed.

[Portions of Pages 427–428]

It is therefore clear that, if a photograph of a younger individual were to be enlarged exactly to the size of a specimen taken from an older individual, both Figures would, under certain circumstances, be indistinguishably similar. More simply put, all the things stated above result in the fact that the inner architecture of the bones presents a geometrically similar Figure for all ages.

[Portions of Pages 428–429]

The geometric similarity of bone architecture in different age levels, however, ensues in the following: the enlargement with conservation of geometric similarity of a structure as complicated as the architectural structure of the bones, can only happen if every single bit of material of the whole takes part in the enlargement in exactly proportional form. On the other hand the geometric similarity would have to be disturbed, if the enlargement would take place through addition of new material at the surfaces under partly or complete inactivity of already present particles, if the superficial material is part of a later growth period than the lower ones.

[Portions of Pages 429–433]

After having seen that any assumption of resorption at the marrow cavity surface in long bones will lead to absurd consequences, we reach the matter of apposition of new bone layers coming from the periosteum. I have earlier deduced, partly due to the fact that nothing is resorbed at the inside, partly due to other experiments, namely those with madder feeding and also with metal plates pushed under the periosteum, that a bedding of the periosteum can, if at all in normal growth, be quantitatively only extremely small and hardly significant. Regarding this point as well, I am now able to show that it must be as my experiments have shown.

[Portions of Page 434]

We have often been told that the thorough periosteal ossification in callus creation and the high osteogenetic power of transplanted periosteum, which has been shown in Ollier’s and my own experiments, would render the inactivity of the periosteum in normal bone growth rather improbable. I reply here that such a conclusion drawn from pathological ossification to normal bone growth conditions is not acceptable. This may best be shown in specimens about callus growth, which I own and which I would like to mention shortly. I have been able to demonstrate a sharp distinction of the periosteum callus from the marrow callus in fractures of the radius in animals, whose bones were dyed red by madder feeding before application of the fracture. This has shown that the marrow callus can be quantitatively more important than the periosteum callus. In the same way that we should not draw the conclusion that the marrow would create bone while growing, something that would lead to an obliteration in the marrow cavity, we may not try and draw conclusions from the behavior of the periosteum in an irritated or transplanted state to its behavior in growth. The same conclusions were drawn from the new experiments of Goujon and Baikow, who observed ossification of transplanted marrow substance.

[Portions of Pages 435–436]

Regarding longitudinal growth as well, I am now again, due to my experiments on the inner architecture of the bone, able to present the fact that any experiment conducted on this matter could or would give a result different from the one just mentioned, ie, no apposition could or should take place at the end of the diaphysis. Let us return to our Figure 2, Table XII, which again depicts a still growing femur. As long as people believed that the cancellous bone is an arbitrary wild meshwork of irregular and mechanically completely equal trabeculae, nothing would preclude the assumption that those trabeculae which today lie closely below the epiphysis boundary in the femoral head, should in a later growth move further down into the neck, then into the beginning portion of the diaphysis and eventually towards the boundary between cancellous bone and marrow cavity, where they would be resorbed.

[Portions of Pages 436–437]

If now someone would try to claim that the layer of cancellous bone of an adolescent individual closely below the epiphysis boundary in the femoral head, which, as we can see in Figure 2, Table XII, presents that triply different Figure closely described above, would move downwards in growth, then we shall be able to show in specimens of somewhat older or grown-up individuals, that this is not the case, and that furthermore this always, due to its triple differences, easily discernible layer, remains closely below the epiphysis boundary in every life age. We would be able to prove to him with a certainty that would satisfy all mathematical requirements that this remaining portion of the mentioned layer at the same spot could not allow for even a minimum of apposition at the epiphysis boundary. We could finally show him that there would not even be enough room in the femoral neck for possible bone layers pressing downwards from the top. For the neck itself has also achieved its own, unalienable architecture, never changing in all life stages, which cannot be pushed down.

The small, loose, irregular quadrangle e, d, d, d₂, γ at the adductor side is especially well-suited to support what has been said. We find it in every specimen from any age level, always in the same position and shape, always right below the epiphysis boundary, so that the lowest part of the latter d₂ γ stands for one part of the quadrangle, always in a size directly proportional to the size of the whole specimen, this means that they are just as geometrically similar in all specimens as the specimens themselves. If we would assume bone to be added at the epiphysis boundary, then we would either, in the case where the bone substance added directly above the quadrangle would present a different sort of structure than in the quadrangle itself, find the quadrangle again later in the neck or in the beginning portion of the stem; or, if the addition would happen alike to the structure in this quadrangle, then the quadrangle would have to slowly, at a constant or hardly changing height, grow thicker and thus completely change its shape. In reality, though, neither the one nor the other is the case.

In the same way it is possible to show for the long compressive trabeculae originating from cd, which continue past the epiphysis boundary, as if it wouldn’t exist at all, into the femoral head towards the acetabulum, that these would have to grow disproportionally long, if bone tissue were to be added in the part c₂d₂ of the epiphysis boundary, whereas the same reason for growth would not apply to the compressive trabeculae bc going into the neck and not intersecting the epiphysis boundary. Due to the fact, though, that the compressive trabeculae bc always retain a proportional length to the compressive trabeculae cd, an intermediate layering in the line c₂d₂ is completely impossible.

The most convincing, though, is the proof for the point α in our Figure, which represents the point of the triangle αcG. This point, characterized by an especially sharp intersection between the compressive trabeculae originating at c and the tensile trabeculae from C, is found, as we have seen, always at the point where the line δε, which emerges by imagining the femoral head as a full circle, intersects the neutral fiber layer. Due to the fact that it lies in the periphery of said imagined circle, its distance from the joint surface rises proportionally to the radius of the joint head, whereas it should reach a relatively longer distance from the joint head if an apposition should take place at βγ.

[Portions of Pages 438–443]

We have become acquainted with the bone as a structure, which consists of many distinct elements, tightly pressed together in the middle and fanned out at the ends, which appear as beams or columns in thin sections, but actually are plates, at the ends often interrupted, roof or cone shaped, in the middle more continuous and cylindrical. Every one of those plates is, as we have seen, unalienable and, if no pathological disruptions should take place, persistent throughout the entire lifespan. According to this the mathematical architectural image can only be retained if every single column or plate becomes proportionally wider, thicker and longer over the years, ie, if the growth would happen in every single column or plate, and would be tied to every single one.

[Portion of Page 443]

The idea that growth happens at every single architectural plate gives also an explanation for the slower longitudinal growth of long bones in the middle piece of their diaphysis in the most interesting way. This slower growth, which has strangely led to the widespread and significant assumption, finally disproved by my own experiments, that instead of slow growth, no growth would take place, and this over the whole bone, has been experimentally shown by me for the middle portion of the diaphysis as well. Regarding the lines in Culmann’s crane, you will find that according to this the slowest growth will take place where the lines are least complicated, where they run simply parallel to each other, ie, at the only place where neither the elongation nor the shrinking of the lines would significantly change the architectural image to which they belong. This interesting fact seems suitable to me to solidify the general mathematical assumption on bone tissue, which we have gained, even more, and to confirm anew that the so-called compact substance is actually pressurized cancellous bone, and to show that all aspects of the bone, probably the pathological ones as well, will have to withstand the test of our mathematical examination.

[Portions of Pages 444–445]

Finally, a third and immensely important matter primarily for pathological conditions, remains to be discussed, namely the matter of the influence of the mechanical conditions the bone is subject to on the development of its architecture including its normal maintenance and (pathological) disturbances. The relevant research I have conducted initially shows that the first development of the architectural structure of the bone is not a consequence of the mechanical conditions, but that the architecture for every single part of the body, as far as ossification has progressed, is predefined in fetal state already, at a point where the later mechanical conditions are not yet applied. Figure 3, Table X is a frontal thin section of the proximal femur of a 1¼-year-old, Figure 4 such a one of a newborn boy. As far as ossification has progressed, we can already recognize the respective tensile and compressive trabeculae relating to the ossified portion. Only the uppermost tensile trabeculae, originating from close to the trochanter basis (corresponding to the trabeculae CE in Figure 2, Table XII) and the upper ends of the compressive trabeculae of the caput and the femoral neck are not present yet, because the parts corresponding to these are still in cartilaginous form.

Thus it can be seen that the proximal femur does not only develop its tensile and compressive trabeculae when the child starts to stand and walk, but that they are handed down from the parent organism to the fetus and are present in complete functionality we have shown to exist at the time of the first attempts to stand or walk. As soon as any part of the body ossifies, it immediately receives the architecture necessary for later use.

[Portion of Page 446]

This observation leads us to the important and hitherto completely unknown law about the ossification of cartilaginous rudiment suggesting the ossification happens in a completely different way in each location, typical for that place.

[Portion of Page 447]

The matter of how far the maintenance of normal architecture for the duration of the complete lifespan depends on a normal behavior of mechanical conditions, and how far their disruptions influence the changes therein, must be the subject of further research.

I reserve the right to examine in the future whether a bone regenerating after subperiosteal resection under generally normal mechanical conditions will rebuild its normal architecture and whether a bone, bent as a result of rickets, but functional again, will change its architecture in relation to its changed shape and usage. From the start I believe that both is the case, and that it will thus be possible to confirm the mechanical conditions to be the direct cause of the architecture under pathological conditions. Because it seems almost certain that bone trabeculae will disappear in places where they are no longer in use due to the bone having been bent, and that in those directions where, in bone regeneration as well in bent bones, material is to be utilized anew, new bone trabeculae will have to grow.

[Portions of Pages 447–448]

I know the conclusions I have reached here regarding bone growth are in contrast to the opinions of the earlier assumptions of the most exquisite men, namely microscopists. This fact alone was reason enough for me to consider whether I could take the stand I have presented here. But the more often and the more carefully I have taken the reasons for my conclusions into account, the more certain I am being lead to the one conclusion that bone growth could never happen differently than exclusively interstitially. And for this reason I hope that my willing readers, who regard my reasons, will fare not differently from myself. I believe that the difference of my views with those of the relevant microscopists can be explained through the fact that the latter have only regarded fetal or chiefly cartilaginous bones for the matter of growth. The undisputed apposition of bones from the initial cartilage rudiments are in no way reason enough to draw the conclusion that a continuous recreation of cartilage at the epiphysis boundary through continuous apposition would have to continue to take place throughout the whole time of growth.

Soon after the publication of my preliminary publications on the present matter (Centralblatt, 6 December 1869), in which I first disputed the existence of any type of growth other than the interstitial one, I received great joy out of a confirmation of my views. Richard Volkmann, who had already earned great merits for his works on the matter of bone growth by disproving the passivity of bone tissue has taken (Centralblatt, 20 February 1870) a point of view, which is hardly different from mine. He now accepts out of completely reasonable and indisputable reasons of clinical observation the macroscopic success of interstitial growth and lets “the longitudinal growth of the long bones happen to such a great extent through interstitial growth processes, that in contrast to that the insertions at the epiphysis boundary hardly come into consideration.”

And so I show confidence that many more similar voices shall have to arise and that soon no one will talk of apposition growth as “hardly probable,” but rather that they will throw every last remainder of the juxtaposition theory overboard as clear and as unadorned as I have dared to in the present work.