Abstract
The inefficiency of nanoparticle penetration in tissues limits the therapeutic efficacy of such formulations for cancer applications. Recent work has indicated that modulation of tissue architecture with enzymes such as collagenase significantly increases macromolecule delivery. In this study we developed a mathematical model of nanoparticle penetration into multicellular spheroids that accounts for radially dependent changes in tumor architecture, as represented by the volume fraction of tissue accessible to nanoparticle diffusion. Parameters such as nanoparticle binding, internalization rate constants, and accessible volume fraction were determined experimentally. Unknown parameters of nanoparticle binding sites per cell in the spheroid and pore shape factor were determined by fitting to experimental data. The model was correlated with experimental studies of the penetration of 40 nm nanoparticles in SiHa multicellular spheroids with and without collagenase treatment and was able to accurately predict concentration profiles of nanoparticles within spheroids. The model was also used to investigate the effects of nanoparticle size. This model contributes toward the understanding of the role of tumor architecture on nanoparticle delivery efficiency.
Keywords: spheroids, modeling, nanoparticle, penetration, cancer, tumor
Introduction
Efficient transport of delivery vehicles into tumor tissue remains a critical issue in the application of nanoparticle carriers for cancer treatment. Systemically delivered agents reach target tumor sites by extravasation from tumor vessels, aided by the enhanced permeability and retention (EPR) effect. Accumulation of long-circulating material in tumors by the EPR effect results from leaky tumor vasculature and a lack of adequate lymphatic drainage within solid tumors (Iyer et al., 2006). However, the distribution of these delivery vehicles in the tissue is heterogeneous and confined mainly to areas immediately surrounding tumor vasculature (Dreher et al., 2006). This can reduce the potential efficacy of macromolecule therapeutics, as intervascular distances can be relatively large with significant avascular regions. The poor penetration of therapeutic agents has been attributed mainly to two factors: a high interstitial pressure compared to surrounding tissue that minimizes convective transport, and hindered diffusion due to extracellular matrix components, particle binding, and tightly packed cells (Davies et al., 2001; Grantab et al., 2006; Jain 2001; Kuppen et al., 2001; Netti et al., 2000). Although the adverse pressure gradient may play an initial role in hindering the movement of material into tumor tissue, previous research has shown that even with elimination of the pressure gradient, the penetration of macromolecules is severely hindered (Flessner et al., 2005). Diffusion within solid tumors has been shown to be improved by ECM-degrading enzymes such as hyaluronidase and collagenase (Kohno et al., 1994; Kuriyama et al., 2001), suggesting that the extracellular matrix is a primary barrier to particle diffusion within tumor tissue.
In vitro 3D cultures such as multicellular spheroids (MCS) provide a useful platform for studying particle penetration in avascular regions of tumor tissue because they mimic in vivo tumor properties such as the presence of ECM components and gradients of nutrients and wastes. As a result, spheroids also contain heterogeneous regions of tumor cell growth, including a proliferating region, a quiescent region, and a necrotic core (Fracasso and Colombatti, 2000). With proper growth conditions spheroids can be produced with highly reproducible morphology, and the simple spherical architecture lends itself well to monitoring particle penetration depth as well as allowing for reasonably straightforward mathematical modeling.
Modeling of particle penetration in the tumor tissue provides insight into the factors that affect the distribution of particles in avascular regions of tumors and provides information toward the design of improved therapeutic agents. Mathematical models for antibody and drug penetration into tumors have the potential to provide valuable information in predicting therapeutic efficacy. Notable literature precedence for modeling macromolecule delivery to tumors includes work by Banerjee et al. (2001) who used a finite element tumor model to predict antibody delivery to tumors and Graff and Wittrup (2003) who obtained numerical solutions to model antibody delivery to tumor spheroids. Although most spheroid models assume structural uniformity (Graff and Wittrup, 2003; Kwok et al., 1995), Wenning and Murphy (1999) also have considered the heterogeneous distribution of binding sites. The previous models have focused mainly on the penetration of macromolecules such as dextrans and antibodies and found significant diffusional barriers to these macromolecules, but few studies have modeled the penetration of larger nanoparticles, which would encounter even greater diffusional restrictions.
In this study, the physical parameters of tumor tissue that influence nanoparticle penetration were investigated by the development of a comprehensive mathematical model of nanoparticle penetration into multicellular spheroids. Our model extends previous spheroid models by accounting for structural non-uniformity of regions accessible to nanoparticles through a radially dependent porosity factor “ε.” In addition, kinetics of particle internalization were determined by experimental measurements from the cell line used to grow spheroids. The incorporation of the radially dependent ε parameter also allows for the prediction and evaluation of ECM modulation and its effect on nanoparticle delivery. Thus, the model presented here can be used to analyze the key parameters to consider in the design of nanoparticle drug carriers for increased tissue penetration. In this work, the developed mathematical model was also validated experimentally using SiHa multicellular spheroids as a tumor model and polystyrene nanoparticles as a model therapeutic delivery vector. Enzymatic degradation of the ECM collagen of spheroids was investigated and modeled, with good agreement between theoretical and experimental results.
Materials and Methods
Theoretical Model
Particle diffusion into spheroids, including particle binding and dissociation at the cell surfaces was modeled similar to previous studies (Graff and Wittrup, 2003), assuming spherical symmetry. The model used here was further developed by accounting for structural non-uniformity of the spheroid in the radial direction and internalization of particles:
| (1) |
where r is the radial coordinate (r = 0 is the center of the spheroid and r = R is its outer rim), t is the time variable, ε is the volumetric porosity of spheroids (fraction of the spheroid volume accessible to particles), C is the molar concentration of free particles in the spheroid volume (C/ε is the concentration of unbound particles in the accessible intercellular volume), Cb is the concentration of bound particles, Cbs is the concentration of available binding sites on cell surfaces, Ci is the concentration of internalized particles, D is the effective diffusion coefficient, ka is the association (binding) rate coefficient, kd is the dissociation rate coefficient, and ki is the internalization rate coefficient.
The initial and boundary conditions for the diffusion problem are:
| (2) |
where C0 is the concentration of particles outside spheroids, defined by experimental conditions. Due to the mixing in the stirred vessel, this concentration is assumed to be static and equal to the average particle concentration in the vessel. The effective diffusion coefficient, volumetric porosity, and initial concentration of binding sites are functions of the radial coordinate.
Using a simple parallel-pore model for porous media, the initial molar concentration of the binding sites inside the spheroid can be related to the spheroid structure and quantity of binding sites on the cell surfaces,
| (3) |
where α is the particle radius, rp is the effective pore radius, NA is Avogadro’s number, and β is the non-dimensional coefficient characterizing the density of available binding sites on the cell surface area (effective fraction of the cell surface area available for binding particles). Coefficient kβ accounts for the difference in the binding site density on surfaces of cells in monolayer cultures compared to cells in spheroids. The latter cells have a significant number of inaccessible binding sites due to cell-to-cell interactions and ECM components.
The diffusion coefficient can be modeled in one of the forms suggested for intercellular, porous spaces in biomaterials (Fournier, 1998; Saltzman, 2001). One of the models for the diffusion coefficient is defined as follows:
| (4) |
where D0 is the diffusion coefficient in unbounded liquid medium (the same solution as in the spheroid pores), kB is the Boltzmann’s constant, T is the absolute temperature, μ is the viscosity of the liquid, L(λ) is the factor responsible for hydrodynamic and steric reduction of the diffusion coefficient in the pore, τ(ε) is the tortuosity due to increased diffusional path length in the spheroid, and F > 1 is the shape factor that accounts for the hindrance in spheroid pores. The value for F or analogous coefficients in the diffusion coefficient can be either calculated for well-defined geometries (Satterfield, 1970), or, in biomedical research, it is often selected from the best fit to experimental data (Ramanujan et al., 2002). The effects of external convection, due to mixing, on fluid flow inside spheroids can be neglected due to the smallness of the pore radii and the short duration of the pressure fluctuations relative to observed times of particle penetration.
Parameters necessary for modeling particle diffusion (Eqs. 1–4) were obtained as follows. Particle concentration outside spheroids C0, spheroid radius R, particle radius a, temperature T, and exposure times tf, are well-defined experimental conditions. Geometrical properties of the spheroid structure, porosity ε, and pore radius rp were estimated from images of spheroid sections. Rate coefficients ka, kd, ki, and non-dimensional density of binding sites β were determined from experimental data. Endocytosis is not supported by dead cells, so ki approaches zero in the spheroid center. Parameters kβ and F were determined from approximate correspondence of model results to test data.
For given coefficients in Equations (1)–(4) and boundary and initial conditions, the system (1) was discretized and solved numerically in the space-time domain by standard methods (Ferziger and Peric, 1999). The total number of particles Ct retained in the spheroid at time t, which can be compared with experimental data, is defined as follows:
| (5) |
where the piecewise-linear window function w(r) is introduced to account for removal of particles near the spheroid outer rim (r1 ≈ 0.95R) during processing steps before image analysis.
In order to determine rate coefficients and the number of binding sites from experiments with the cell line used for spheroid cultures, an approximate model for a single cell that binds and internalizes particles was applied (Wilhelm et al., 2002):
| (6) |
where Nb(t) is the number of particles bound at the cell surface, Nbs(t) and B are the current and initial numbers of available binding sites, respectively, Ni(t) is the number of internalized particles, and the other parameters are the same as in Equation (1). Equation (6) invokes several assumptions: the concentration of particles in the vicinity of the cell equals to the average concentration of particles in the vessel, the cell surface area is not obstructed by other cells in the vessel, the binding sites are regenerated upon particle internalization (i.e., B = const), and any exocytosis is approximately accounted for by a reduced value of ki. The predominant mechanism of uptake for latex nanoparticles <200 nm in size is clathrin-mediated endocytosis (Rejman et al., 2004). The cell regenerates potential binding sites due to continuous turnover of the cell membrane; therefore binding sites are assumed to be constant. The effective fraction of the cell surface area available for binding (Eq. 3) relates to the initial number of the cell binding sites,
| (7) |
where Rc is the radius of an individual cell.
Solution of Equation (6) gives the evolution of the number of bound particles,
| (8) |
The total number of adhered particles (both bound and internalized) equals to
| (9) |
The rate coefficients and the binding site number can be determined by solving Equation (9) using experimental data from studies of particle binding behavior with cells (described in subsequent sections). A summary of nomenclature used in the mathematical model is included in Table I.
Table I.
Nomenclature.
| a | Particle radius |
| B | Initial number of binding sites per cell |
| β | Non-dimensional coefficient characterizing the density of available binding sites on the cell surface area |
| C | Molar concentration of free particles |
| D0 | Diffusion coefficient in unbounded liquid medium |
| ε | Volumetric porosity of spheroids |
| Cb | Concentration of bound particles |
| Cbs | Concentration of available binding sites on cell surfaces |
| Ci | Concentration of internalized particles |
| C0 | Initial concentration of particles outside spheroids |
| Ct | Total number of particles retained in spheroid at time t |
| D | Effective diffusion coefficient |
| F | Correctional shape factor to account for hindrance, such as from ECM components, in spheroid pores |
| ka | Association (binding) rate coefficient |
| kB | Boltzmann’s constant |
| kβ | Correction factor for differences in binding site number between monolayer to spheroid cells |
| kd | Dissociation rate coefficient |
| ki | Internalization rate coefficient |
| L(λ) | Factor responsible for hydrodynamic and steric reduction of the diffusion coefficient in spheroid pores |
| μ | Viscosity |
| Na | Avogadro’s number |
| Nb(t) | Number of particles bound to cell surface |
| Nbs(t) | Number of available binding sites at time t |
| Ni(t) | Number of internalized particles |
| Nt | Total number of adhered particles (bound and internalized) |
| R | Spheroid radius |
| Rc | Radius of an individual cell |
| r | Radial coordinate (r = 0 at center of spheroid and r = R at outer rim) |
| rp | Effective pore size |
| T | Absolute temperature |
| t | Time variable |
| τ(ε) | Tortuosity due to increased path length in the spheroid |
| w(r) | Piecewise linear window function to account for removal of particles near the spheroid outer rim (r1 ~ 0.95R) |
Cell Culture and Multicellular Spheroid Formation
Media, serum, and antibiotic-antimycotic (ABAM) solutions were purchased from Mediatech (Herdon, VA). Before formation of spheroids, SiHa cells (a kind gift from P. Olive, BC Cancer Research Centre, Vancouver, BC, Canada) were maintained in monolayer culture with complete MEM media (MEM supplemented with 10% fetal bovine serum (FBS) and ABAM solution) at 37°C in a humidified incubator with 5% CO2. To form spheroids, monolayer cells were trypsinized and added to spinner flasks (Belco, Vineland, NJ) at a concentration of 107 cells in 200 mL media. Cells were stirred in the spinner flask at 150 rpm in a 37°C incubator and fed with MEM with 5% FBS plus ABAM after 3 days, then daily until ready for use. At each feeding, spheroids were allowed to settle, and then 150 mL of media was removed and replaced with fresh media.
Determination of B, ka, kd, ki
The number of nanoparticle binding sites per cell as well as the rate constants for nanoparticle association, dissociation and internalization were determined using similar methods to those previously employed with cell monolayers (Wilhelm et al., 2002). For binding site number determination, SiHa cells were plated onto 24-well tissue culture plates (Corning Life Sciences, Lowell, MA) at a density of 440,000 cells per well and grown in complete MEM media for at least 24 h until they reached full confluence. Cells were then washed in phosphate buffered saline (PBS, pH 7.4) and media was replaced with OptiMEM (Invitrogen, Carlsbad, CA). In order to inhibit endocytosis, cells were incubated for 30 min at 4°C prior to the addition of nanoparticle solutions (Schroeder and Kinden, 1983). Red-fluorescent, carboxylate-modified, 40 nm diameter FluoSpheres® (Invitrogen) in pre-chilled solutions of OptiMEM, were then added to each well at different concentrations with each concentration treatment conducted in triplicate wells. Cells were exposed to these solutions of microspheres for 1 h at 4°C before they were washed three times with PBS and lysed. Cell lysis buffer containing known microsphere concentrations was used to produce standard curves of nanoparticle concentration, and unknown lysates were measured in triplicate. With confluent monolayers it was assumed that the exposed surface area of cell membrane was equal to the area of the well, allowing calculation of the number of nanoparticles bound per unit cell membrane area. The average diameter of trypsinized SiHa cells was measured using phase contrast microscopy to calculate the average surface area per cell, and used to convert the number of nanoparticles bound per unit cell surface area to the number of nanoparticles bound per cell. Equation (9) was fit to the data of nanoparticles bound as a function of concentration to derive an estimate for the parameter B. For this solution the internalization constant, ki, was assumed to be zero since endocytosis was inhibited at 4°C, and t was assumed to be infinite since binding had reached saturation. Writing the remaining variables of Equation (9) in terms of an equilibrium constant, K = ka/kd, allowed for a nonlinear least squares fit to the data.
Association and dissociation rate constants were determined by exposing SiHa monolayers to a 1.26 nM solution of microspheres at 4°C, and measuring the number of microspheres bound per cell as a function of time. In fitting data points to the analytical solution of Equation (9), ki was still assumed to be zero, and the number of binding sites per cell determined in the previous section was used to obtain values for ka and kd. These values were obtained using nonlinear least squares fitting. To determine the rate of internalization a similar procedure was followed as that used to determine association and dissociation rate constants with the exception that experiments were conducted at 37°C to allow endocytosis. Binding constants from previous experiments were then used in Equation (9) to estimate ki in a similar manner as above. The studies were also conducted with suspension cell cultures with mixing to minimize the effect of particle diffusion to the cell surface. The calculated constants using this approach were of the same order of magnitude as those obtained with monolayer cells, but with increased variability due to the necessity to centrifuge during washing steps.
Pore Size and Cell Radius Determination
In order to estimate the nanoparticle-accessible volume of SiHa spheroids, 20 spheroids, with an average diameter of ~500 µm, were hand-picked and placed in 1.5 mL eppendorf tubes. Complete growth media was replaced with OptiMEM and collagenase from Clostridium histolyticum (Sigma, St. Louis, MO) was added to a final concentration of 0.076 mg/mL (0.98 U/mg) for collagenase treated samples. Samples were then incubated at 37°C with rotation at ~1.5 rpm in siliconized eppendorf tubes for 1–3 h. After incubation, spheroids were fixed in half strength Karnovsky’s fixative (2% paraformaldehyde, 2.5% gluteraldehyde, 0.1 M cacodylate buffer, 3 mM CaCl2, pH 7.3) followed by secondary fixation in 1% osmium tetroxide. Samples were then stained with 2% uranyl acetate followed by dehydration with a graded series of alcohols and propylene oxide. Tissue samples were embedded in Eponate resin (Ted Pella, Redding, CA), and cut into 1 µm slices using a Reichert Ultracut E microtome. Tissue slices were then stained with 0.2% toluidine blue and mounted on microscope slides.
Phase contrast images were obtained using a Nikon inverted microscope with a 100× objective (N.A. 1.30). Pore diameters in the spheroid, defined as visibly accessible spaces between cells, from which pore radii were calculated, were measured manually with the caliper feature of MetaMorph after applying appropriate distance calibrations to images. The porosity was determined by applying a threshold of pixel intensity to images of sliced spheroids such that only empty space was included within the threshold. Areas of the spheroid (e.g., necrotic core) were then manually outlined and the ratio of thresholded area (representing pores) to total area was calculated using MetaMorph.
Experimental Measurement of Nanoparticle Penetration in Spheroids
The distribution of nanoparticles within multicellular spheroids after exposure was determined by fluorescence microscopy and image analysis. Twenty spheroids with diameters between 400 and 500 µm were handpicked and placed in 1.5 mL eppendorf tubes. Complete MEM media was replaced with OptiMEM, and green-fluorescent, carboxylate-modified, 40 nm diameter FluoSpheres® (Invitrogen), were added at various concentrations. Collagenase was also added to appropriate samples at a concentration of 0.076 mg/mL (0.98 Units/mg) to assess the effects of collagen degradation on particle penetration, and samples were moved to a 37°C incubator and rotated at approximately 1.5 rpm to maintain mixing. After incubation, spheroids were washed once with PBS, and snap-frozen in optimal cutting temperature compound (O.C.T.; Tissue-Tek, Torrance, CA) using liquid nitrogen. Cryosections were obtained using a CM1900 cryostat (Leica, Wetzlar, Germany) set to slice in 10 µm intervals. Sliced spheroids were then imaged using a Nikon TE2000 inverted epifluorescent microscope with a 10× objective. Line scans measuring pixel intensity as a function of radial position were obtained using MetaMorph software by manually drawing 10 lines through a spheroid image that intersected at the center of the spheroid. Line scans were taken from four independent spheroids for each sample and averaged following baseline subtraction, of background signal from spheroids without nanoparticles, using MatLab. Signal intensity was then normalized to the maximum intensity in the inner region of the spheroid (0 < r < 0.85R). Sections with a minimum diameter of 350 µm were used to ensure that the slice was near the center of the spheroid. Images of cryosections were also used to determine the size of necrotic cores within the spheroid sections. Least squares fitting using MatLab was used to determine values for the shape factor F and the binding site correction factor kβ that resulted in the best fit for the time course study of nanoparticle penetration in spheroids. The calculated values were then used for all subsequent model simulations.
Sensitivity Analysis
The following equations were applied for sensitivity analysis of theoretical parameters used to fit experimental data:
| (10) |
where dx is the number of particles in the interior region of the spheroid, defined as r ≤ 0.85R.
Results
Determination of B, ka, kd, ki
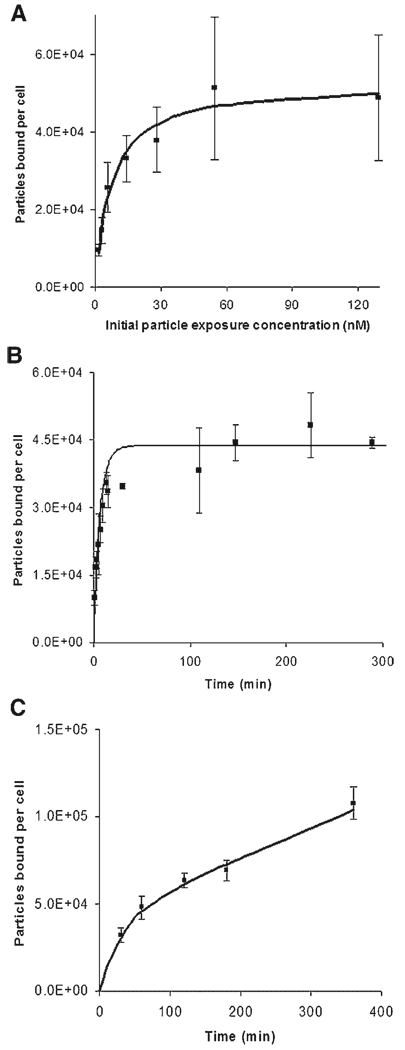
To determine the total number of binding sites per SiHa cell for 40 nm nanoparticles, SiHa cells grown in confluent monolayers were exposed to nanoparticles of various concentrations. Experiments were carried out at 4°C to minimize internalization. The average cell surface area, used to determine the number of particles bound per cell, was calculated using an average radius of 7.07 µm (±0.92 µm) per cell based on measurements of trypsinized cells. Results of binding studies are shown in Figure 1A, where particles bound per cell is shown as a function of the initial concentration of nanoparticles. A nonlinear least squares fit of the data to Equation (9) showed that binding reaches a maximum of 5.3 × 104 nanoparticles/cell. The association and dissociation rate constants of nanoparticle binding to SiHa cells were determined by measuring the number of cell-bound particles as a function of time. The rate constants were calculated for a nanoparticle concentration of 1.26 nM (Fig. 1B). Assuming no endocytosis (ki = 0; data collected at 4°C), data from the time course study was fit to Equation (9), to estimate the association constant, ka (1.71 × 106 m3/mol s) and the dissociation constant, kd (4.55 × 10−4/s).
Figure 1.
Experimental data (shown as squares with standard deviations of each data point) and fitted curves for determination of the number of binding sites B (shown in A), the association and dissociation rate constants ka and kd, respectively (shown in B), and the internalization constant ki (shown in C) for 40 nm nanoparticles with SiHa cells. Fitted curves for determination of final values were obtained using Equation (9). The incubation time for (A) was 1 h, and the initial exposure concentration for time course studies (B and C) was 1.26 nM. Experiments for (B) were done at 4°C to inhibit endocytosis while the studies for (C) were carried out at 37°C.
In order to determine the rate of internalization, binding studies were conducted at 37°C. At this temperature, endocytosis is active and the rate of internalization is reflected in increases in the number of cell-associated particles after saturation in binding has occurred. Nanoparticle binding and uptake as a function of time is shown in Figure 1C. The curve fit to the data points in the figure represents a best fit to Equation (9) using ka and kd values obtained previously. Using this method, the internalization rate, ki, was determined to be 0.69 × 10−4/s.
Estimation of Parameters Representing Spheroid Architecture
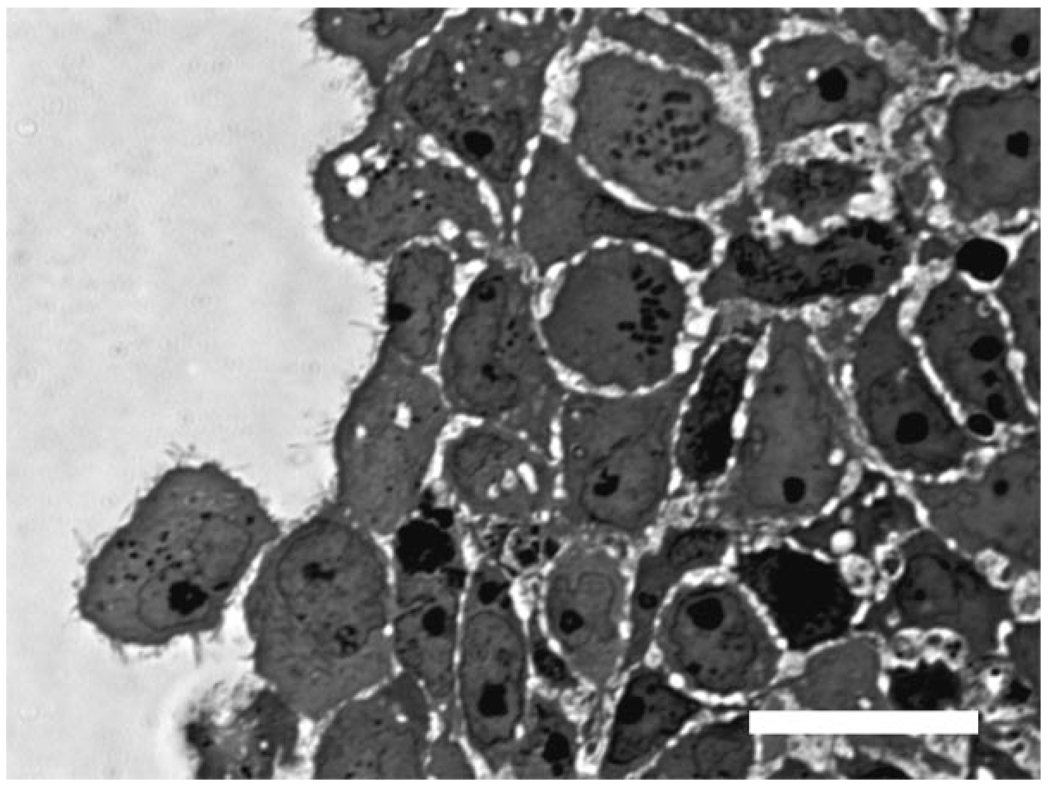
A representative image of a spheroid edge is shown in Figure 2. “Pore” areas were defined as the visible intercellular regions. Pore sizes in the spheroid differed significantly only in the necrotic core of the spheroids when compared with other regions within spheroids. Although significant differences in pore size were measured in necrotic and non-necrotic spheroid regions, the average pore diameter was not significantly different between spheroids treated with collagenase and untreated spheroids. Thus, pore sizes of 2.38 µm (±1.71 µm) and 1.23 µm (±1.09 µm) were used for the necrotic core region and non-necrotic regions, respectively, for both untreated and collagenase-treated spheroids.
Figure 2.
The edge of a fixed, stained section of a spheroid imaged at high magnification (100×) with brightfield microscopy. Pores between cells show up as unstained areas in the microscope image and were measured with MetaMorph software to obtain an estimate of pore size. Scale bar represents 20 µm.
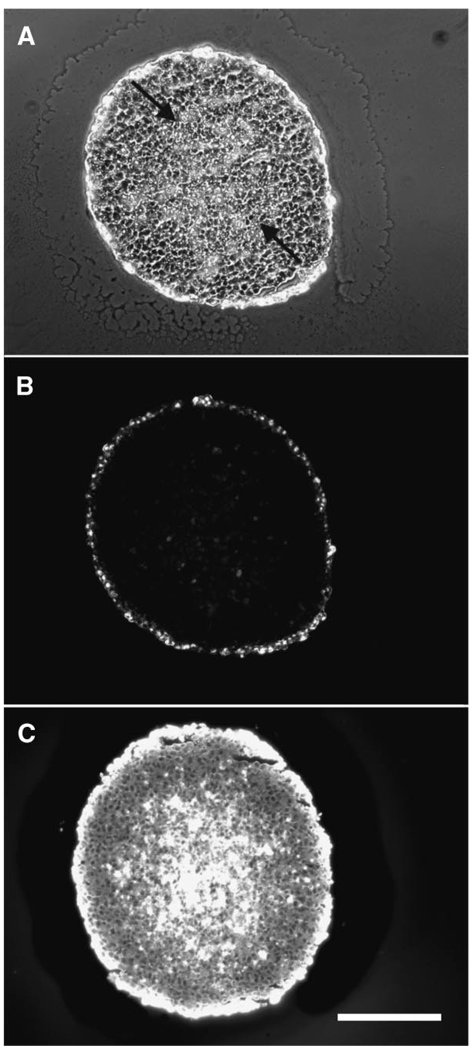
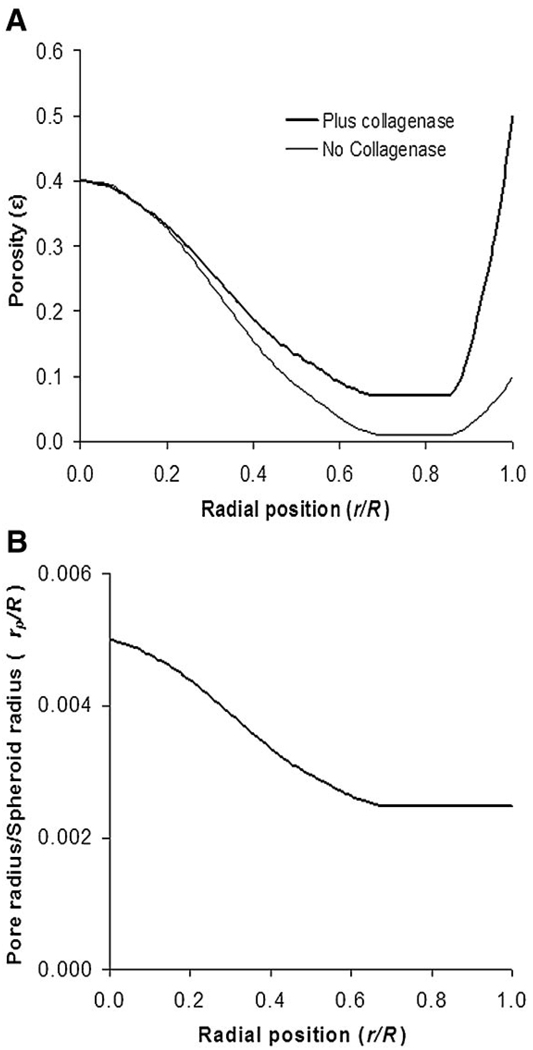
The effective volume fraction accessible for nanoparticle diffusion in spheroids, ε, was determined by image analysis of spheroid sections. The ε for the necrotic region, determined by dividing total non-cell areas by total spheroid areas in fixed spheroid sections, was found to be ~0.4 for both the untreated and collagenase-treated spheroids. Porosity measurements in the non-core region of spheroids were variable among different batches of spheroids, with values ranging from 0.01 up to 0.17. For modeling purposes, ε values of ~0.01 (non-collagenase treated) and ~0.08 (collagenase-treated) were selected for the area of the spheroid representing the middle quiescent region. Effects of collagenase treatment are most pronounced at the spheroid periphery resulting in cell loosening and even shedding (modeled by ε = 0.5). Untreated spheroids also have an edge of proliferating cells and experience some cell shedding due to experimental conditions (modeled by ε = 0.1). Based on these measurements, porosity profiles were defined to reflect three regions of the spheroid: the outer proliferating rim, the middle quiescent region, and the necrotic core regions. The necrotic core can be clearly seen in spheroid sections (Fig. 3A). The transition between these regions could be estimated by structurally defined regions in spheroid sections (Fig. 3A). Spheroids of an average radius of 248 µm (±24 µm) had an average necrotic core radius of 129 µm (±18 µm); thus the radial position (r/R) of transition from necrotic core to middle region for 500 µm spheroids was 0.52. The transition from middle region to edge was r/R = 0.85. Profiles for porosity, ε, and for pore size (expressed as the ratio of pore radius to spheroid radius, rp/R) used in the mathematical model are shown in Figure 4.
Figure 3.
Cryosections of spheroids exposed to 40 nm fluorescent nanoparticles. A spheroid exposed to fluorescent nanoparticles is shown as a phase contrast (A) and fluorescent image (B). The arrows indicate the approximate edge of the necrotic core. A fluorescent image of a cryosection from a spheroid that was co-incubated with 0.076 mg/mL collagenase and nanoparticles is shown in panel C. Scale bar is 200 µm.
Figure 4.
Porosity profile (ε), based on structural measurements of spheroid sections, in the presence and absence of collagenase treatment (A) as a function of radial position (where 0 is the center of the spheroid and 1 is the outer edge of the spheroid). Panel Bshows the ratio of pore size, rp, to spheroid radius, R, as a function of radial position within the spheroid. The values in (B) were used for collagenase treated and untreated samples in our model.
Determining Model Parameters From Experimental Data
Initial attempts to fit experimental data for particle penetration into spheroids with the mathematical model using experimentally determined values of binding site density from monolayer cells revealed no significant penetration into the spheroids even with collagenase treatment due to a binding site barrier. Because binding site density of cells grown in 3D spheroids is expected to be significantly less than that of cells grown in monolayer, it was necessary to introduce a factor, kβ, to account for these differences. A shape factor, F, is also present in the diffusion coefficient (Eq. 4) to adjust the Stokes–Einstein relationship for transport in hindered porous material. For this model, F represents factors such as ECM components. Thus, values for kβ and F were determined by model fitting to experimental data.
For experimental fitting, 40 nm fluorescently labeled nanoparticles were exposed to spheroids for specific times followed by cryopreservation. The spatial distribution of the labeled nanoparticles within the spheroid was assessed by fluorescence imaging of spheroid sections. The penetration of the particles was measured in the presence and absence of 0.076 mg/mL of collagenase treatment. As reported previously, the addition of collagenase leads to a dramatic increase in the penetration of the 40 nm nanoparticles (Fig. 3) (Goodman et al., 2007). Spheroids exposed to nanoparticles at a concentration of 2.36 nM were frozen at different time points, cryosectioned and imaged to obtain line scans of fluorescence intensity as a function of radial position within the spheroid. The normalized fluorescence profiles were used to fit for parameters kβ (0.01 for untreated spheroids and 0.015 for collagenase-treated spheroids) and F (7.5 for untreated spheroids and 1.0 for collagenase-treated spheroids).
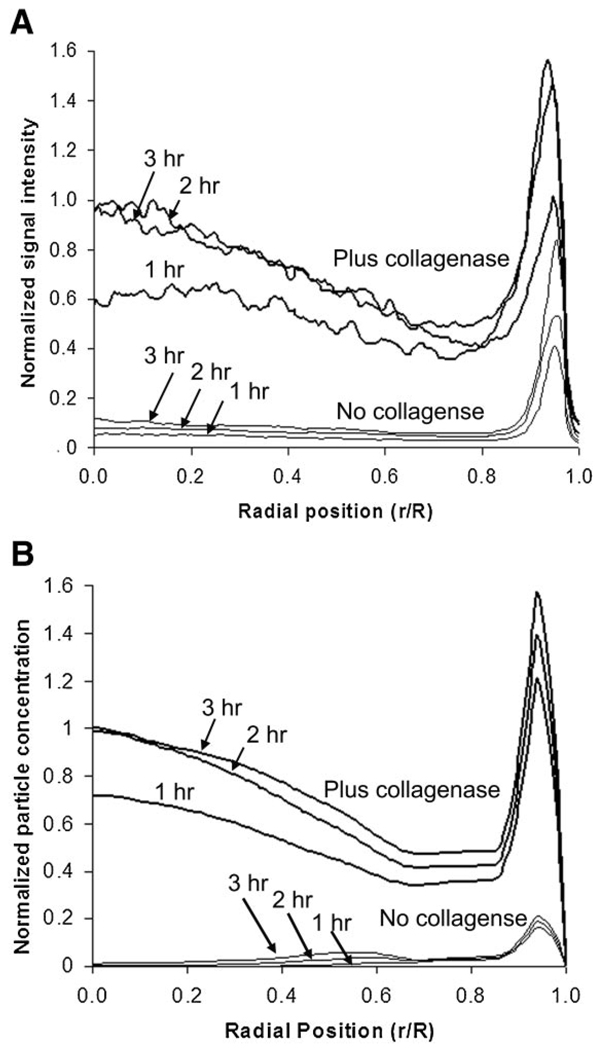
A comparison of predicted and experimental results with optimized model parameters is shown in Figure 5. Nanoparticle distributions in spheroids were measured after 1, 2, and 3 h of nanoparticle exposure. The model predicted well the nanoparticle concentrations in collagenase-treated spheroids excluding the proliferating edge (r ≤ 0.85R), but poorly predicted particle concentrations at the edge of the spheroid (r ≥ 0.85R). In the case of untreated spheroids, there was little penetration of the 40 nm particles so the signal-to-noise ratio for those measurements was low.
Figure 5.
Experimental (A) and model (B) concentration profiles for the penetration of 40 nm nanoparticles in the presence and absence of collagenase at various times. Concentrations from model results were normalized to the maximum concentration on the interior of the spheroid (r/R < 0.85), and experimental results were normalized to the maximum fluorescence intensity in the same region. The model results were fit to the experimental results by optimizing the values binding site number correction factor (kβ), and shape factor ( F). For this set of experiments C0 was 2.36 nM.
Model Validation
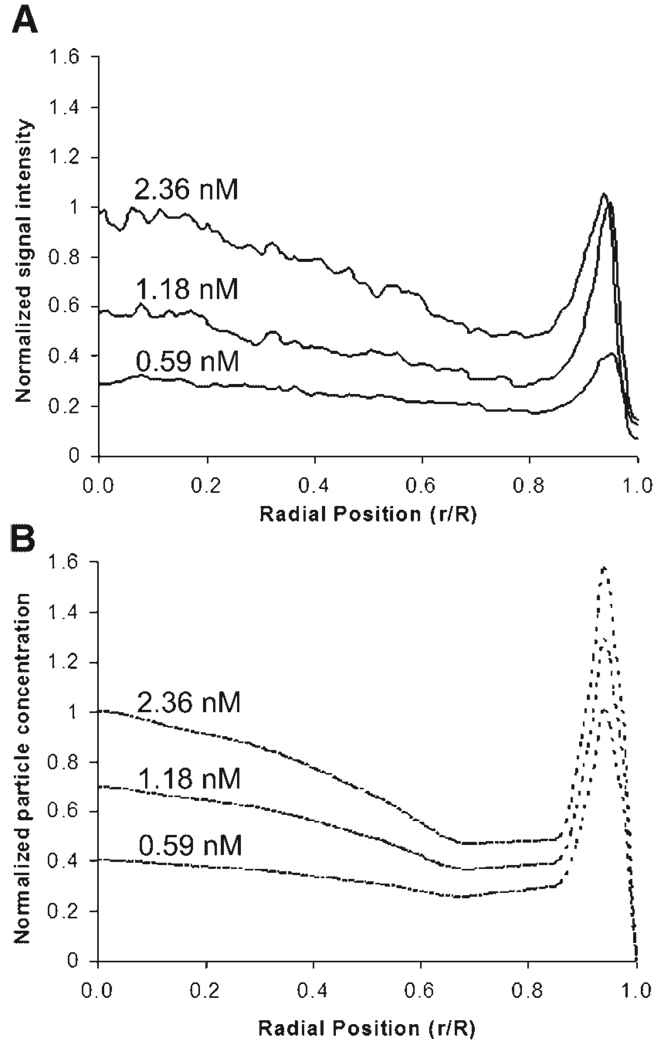
Experiments were conducted to test the mathematical model by comparing measured and predicted nanoparticle profiles in spheroids as a function of bulk nanoparticle concentrations added to the spheroids in solution (C0). Spheroids with an average diameter of ~500 µm were incubated in solutions of fluorescent 40 nm nanoparticles with nanoparticle concentrations of 0.59, 1.18, and 2.36 nM for 3 h under gentle rotation to maintain well-mixed solutions. Penetration studies were conducted in the presence of 0.076 mg/mL collagenase because the low signal-to-noise ratio of the untreated case prevents accurate measurements. Particle penetration was analyzed by fluorescence image analysis of spheroid sections to obtain profiles of fluorescence intensity as a function of radial position within the spheroid section. Experimental results compared to model predictions (Fig. 6) show a poor fit for the outer region of the spheroid (r ≥ 0.85R), but a good fit in the interior of the spheroid (r ≤ 0.85R).
Figure 6.
Experimental (A) and model (B) results for the penetration of 40 nm nanoparticles in the presence and absence of collagenase at various concentrations. Concentrations from model results were normalized to the maximum concentration on the interior spheroid (r/R < 0.85), and experimental results were normalized to the maximum fluorescence intensity in the same region. Values for initial concentrations that spheroids were exposed to (C0) are shown above the respective curves.
Predictions of the Effect of Nanoparticle Size on Penetration
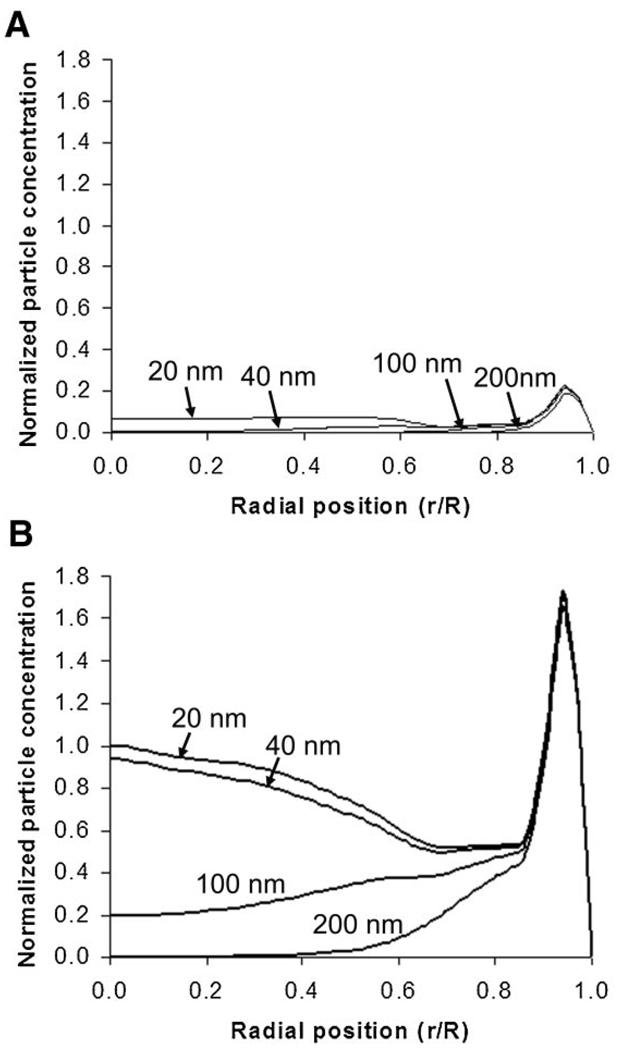
The effect of nanoparticle size on nanoparticle penetration was modeled, with results shown in Figure 7. The model predicts that nanoparticles of 20 and 40 nm diameter accumulate in the interior of the spheroid with dramatic increases upon treatment with collagenase, while 100 nm particles experience restricted penetration in untreated spheroids with minor increase in penetration with collagenase treatment. With larger particles of 200 nm, no penetration into the spheroid interior is expected even with collagenase treatment. Due to differences in fluorescence intensity between different sized nanoparticles it was not possible to directly compare line scans for spheroids exposed to different particle sizes, preventing quantitative comparison of experimental results from different sized nanoparticles using the methods employed in this study.
Figure 7.
Model predictions for the penetration of various sized nanoparticles using parameters from experimental results in the absence (A) and presence (B) of collagenase treatment. Concentrations from model results were normalized to the maximum concentration on the interior of the spheroid (r/R < 0.85) with collagenase treated spheroid. For this experiment C0 was 1.18 nM.
Discussion
In this work a mathematical model was developed to describe the delivery and penetration of nanoparticle drug carriers to multicellular spheroids taking into account structural changes in the spheroid in the radial direction. Model parameters included experimentally determined values of nanoparticle association, dissociation, and internalization rate constants, experimentally derived profiles of porosity and pore size, and fitted parameters of fraction of accessible binding sites within spheroids and shape factor. The model can be used to predict the penetration of nanoparticles into multicellular spheroids under various conditions. Specifically, this study focused on the effect of tissue modulation with collagenase treatment on nanoparticle delivery.
A sensitivity analysis was conducted on the parameters obtained by experimental fit. Particle concentration in the spheroid interior (0 ≤ r ≤ 0.85R) is highly sensitive to the fraction of accessible binding sites kβ (SN,kβ = 0.7) and less influenced by the shape factor F (SN,F = −0.07). The value of kβ determined by experimental fitting (kβ = 0.010 for untreated; kβ = 0.015 for collagenase treated spheroids) is reasonable from a structural perspective. The calculated value of B (total binding sites) was determined from experiments with 2D cultured cells where cell surfaces are fully available for nanoparticle binding. However, cells grown in spheroids are almost completely bounded at all surfaces to neighboring cells through cell–cell contacts or by ECM components (Fig. 2). In addition, the protein expression patterns in monolayer cells have been shown to be different from those in spheroid cultures (Oloumi et al., 2002), which could lead to different protein presentation on the cell surface, and thus a different number of sites available for binding. The kβ parameter adjusted for these factors; without the incorporation of kβ, predicted nanoparticle concentration profiles from the model revealed almost no particle penetration even in the presence of collagenase, illustrating an example of the “binding site barrier” (Fujimori et al., 1990). The value of kβ, indicating more available binding sites for collagenase-treated spheroids compared to untreated spheroids indicates that collagenase treatment results in increased available binding sites that would otherwise be masked by collagen. The less influential shape factor accounts for obstructions in pores and hindered diffusion that can occur from reversible non-specific binding to extracellular matrix components. The effect of reversible binding to a relatively rigid structure, like the ECM within the spheroids, leads to an effective reduction in the diffusion coefficient for nanoparticles that is accounted for by the shape factor, F. Parameter optimization resulted in a lower shape factor (F = 1.0) for collagenase treated spheroids compared to untreated spheroids (F = 7.5); the difference in these values may reflect the degradation of collagen in pores that reduces non-specific binding and hindrance to nanoparticle penetration. Significant collagen has been observed in untreated SiHa spheroids by antibody staining, and collagen concentration has been shown to decrease following collagenase treatment (Goodman et al., 2007). A similar effect has been shown previously in purified ECM gels (Kuhn et al., 2006).
The non-uniformity of spheroid architecture was represented by a radially dependent porosity factor, ε, that represents the accessible volume fraction in the spheroid for nanoparticles. Previous measurements of accessible volume measures in fibrosarcomas, using labeled albumin, have shown values ranging from 0.04 to 0.17 (Krol et al., 1999). The average porosity values used for the quiescent regions of our model are in a similar range. Collagenase treatment leads to estimated porosity values higher than those observed in the normal tumor tissue. The shape of the profile for porosity includes a center core region with high porosity, a middle region with decreased porosity, and an outer region characterized by high porosity. The spike in the outer region reflects the effects of collagenase loosening cells on the outer region of the spheroid which eventually leads to cell shedding. In the absence of collagenase there is still a small degree of cell shedding presumably due to mechanical stress in the tubes during stirring. The major structural difference in collagenase-treated samples is apparent in the quiescent, non-necrotic sections of the spheroid (0.52 < r/R < 0.85). The transition from the middle region to the center region in the model profile (r/R ~ 0.5) was estimated by the radial position of the necrotic core measured from spheroid sections (r/R ~ 0.52) (Fig. 3A). No significant difference in porosity was observed between collagenase-treated and untreated spheroids in the necrotic region. Cell death in that region results in reduced cell–cell junctions and cell attachments to ECM. Thus, additional enzymatic activity introduced by collagenase treatment may have a minimal effect in that region.
Although the addition of collagenase causes an increase in porosity by degrading collagen, it has also been shown that cell damage can increase the porosity of tumor tissue (Krol et al., 2003). Collagenase treatment under the stated conditions had a minimal effect on cell viability in spheroids as measured by colony forming assays and by propidium iodide exclusion assays (data not shown). The results from this study suggest that nanoparticle delivery to spheroids is limited by transport through non-necrotic spheroid regions and that the increased nanoparticle penetration observed with collagenase treatment is primarily due to structural changes that result in increased porosity in these regions.
The model was used to predict the effects of nanoparticle size on penetration into the interior of spheroids. Nanoparticles diameters of 20, 40, 100, and 200 nm were selected because sizes were smaller than pore diameters modeled for the spheroid and because of previous experiments using these particle sizes from our group (Goodman et al., 2007). Although quantitative comparison of experimental results with model predictions is precluded due to the difference in fluorescence intensity per particle for different sized particles, the model results are in good qualitative agreement with our previously published work (Goodman et al., 2007). Our pore size measurements along with our model results suggest that the main method of increased penetration to the core is through an increase in the number of pores available rather than a dramatic increase in the size of existing pores. No significant difference in pore size between collagenase treated and untreated spheroids was observed by imaging, although significant changes could occur in pores smaller than the optical detection limit. These results suggest that collagenase treatment will have a more limited effect on size cutoff for effective penetration, but a more dramatic effect in increasing particle concentrations with particles near the untreated spheroid size restriction. It is important to note that our model assumes immediate effects of collagenase. This is a reasonable assumption given that the enzyme diffusion should be much more rapid than nanoparticle diffusion.
Implications for the Design of Nanoparticle Drug Carriers
The results presented in this study highlight the importance of the architectural properties of the tumor in nanoparticle penetration into the tissue. Our experimental and model results suggest that porosity is a key component of this tumor architecture that affects nanoparticle delivery and can be increased with collagenase treatment. Experimental results show that particle penetration is poor in the absence of collagenase for 40 nm beads, and model predictions suggest that even with particle sizes as small as 20 nm there is still significantly hindered particle accumulation in the interior of spheroids. For effective nanoparticle treatment to tumor tissue, we suggest that a tumor modulating agent, such as collagenase, may significantly improve efficiency of nanoparticle delivery. Nanoparticle carriers can be designed for inclusion of such an adjuvant, as has already been demonstrated with collagenase (Kuhn et al., 2006). Even with this inclusion of an adjuvant it is still ideal to have a nanoparticle carrier that is smaller than 100 nm. The nanoparticle carrier should also be designed to exhibit binding properties that avoid the “binding site barrier” that our model shows can occur even with a relatively low binding constant at a sufficiently high binding sites number.
Limitations of the Model
Although this model introduces the important parameter of variable porosity and pore radius, these values were experimentally measured by methods that could lead to values considerably different than those actually present in live spheroids. Fixing procedures could lead to significant changes in the spheroid morphology, and pore size and porosity calculations could be further skewed by any unstained components that would affect particle penetration, but would not appear in microscope images. More refined methods to accurately determine these parameters would allow for a more global fit of model equations rather than finding one plausible fit for parameters. Development of refined methods for measuring binding interactions may also allow for separation of cell binding versus binding to the extracellular matrix components. This may allow further insight into the usefulness of digesting extracellular components.
The model is also limited in its ability to predict particle concentrations at the outer rim of the spheroids. This is due in large part to the absence of a factor accounting for cell shedding in the case of collagenase treated spheroids. A high degree of variability in the cell shedding was observed, preventing accurate modeling of the process. Additional studies that could accurately determine the rate of cell shedding with collagenase treatment would allow for incorporation of this process into the model for more accurate prediction of particle accumulation at the edge of spheroids.
Conclusions
In this study, we have developed a mathematical model that describes the diffusion of nanoparticles into multicellular spheroids in the presence of the extracellular matrix modulator, collagenase. Model parameters were fit to experimental data and then verified with a separate test case with good agreement between model and experimental results. The model was used to predict the effect of particle size on diffusion and provided good qualitative agreement with previously published results. The results from the model, in combination with experimental results, suggest that particle size, particle binding, and porosity of target tissue are key parameters to consider when designing nanoparticle drug carriers for tumor treatment. It is important to note that this model represents a description of expected nanoparticle distributions in avascular regions of tumor tissue. It does not account for regions where convective forces may dominate particle movement. Despite this, we feel the model can offer insight into particle penetration in deep regions of solid tumors where transport is facilitated primarily by diffusion. Particle penetration into these deep tissue regions is crucial for therapeutic methods, such as certain nucleic acid delivery applications, where the majority of the cell population of the tumor must be exposed to the therapeutic agent for maximum efficacy.
This model provides an improvement over previous models because it accounts for the structural non-uniformity of avascular regions within tumor tissue. The model could be extended to other spheroid cell lines provided that estimates of tumor architecture and particle binding information are known. The development of more accurate methods of determining tumor architecture would likely improve the models overall accuracy and predictive power.
Acknowledgments
TEM imaging of spheroid sections were completed with Steve MacFarlane and Stephanie Laura at the University of Washington Pathology Electron Microscopy Resource Center (Seattle, WA). Cryosections were obtained using a cryostat from Buddy Ratner and Cecilia Giachelli’s cell facility. We thank Prof. Paolo Vicini (UW) for helpful discussions and advice on statistical analysis for this work. This work is supported by NIH/NCI grant 1R21CA114141-01, the Alliance for Cancer Gene Therapy (SHP, Patricia Zoch Tate Young Investigator Award), and the National Science Foundation (TTG, Graduate Fellowship).
References
- Banerjee RK, van Osdol WW, Bungay PM, Sung C, Dedrick RL. Finite element model of antibody penetration in a prevascular tumor nodule embedded in normal tissue. J Control Release. 2001;74(1–3):193–202. doi: 10.1016/s0168-3659(01)00317-0. [DOI] [PubMed] [Google Scholar]
- Davies CD, Engesaeter BO, Haug I, Ormberg IW, Halgunset J, Brekken C. Uptake of IgG in osteosarcoma correlates inversely with interstitial fluid pressure, but not with interstitial constituents. Br J Cancer. 2001;85(12):1968–1977. doi: 10.1054/bjoc.2001.2180. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dreher MR, Liu WG, Michelich CR, Dewhirst MW, Yuan F, Chilkoti A. Tumor vascular permeability, accumulation, and penetration of macromolecular drug carriers. J Natl Cancer Inst. 2006;98(5):335–344. doi: 10.1093/jnci/djj070. [DOI] [PubMed] [Google Scholar]
- Ferziger JH, Peric M. Computational methods for fluid dynamics. New York, NY: Springer-Verlag; 1999. [Google Scholar]
- Flessner MF, Choi J, Credit K, Deverkadra R, Henderson K. Resistance of tumor interstitial pressure to the penetration of intraperitoneally delivered antibodies into metastatic ovarian tumors. Clin Cancer Res. 2005;11(8):3117–3125. doi: 10.1158/1078-0432.CCR-04-2332. [DOI] [PubMed] [Google Scholar]
- Fournier RL. Basic transport phenomena in biomedical engineering. Lillington, NC: Taylor & Francis; 1998. [Google Scholar]
- Fracasso G, Colombatti M. Effect of therapeutic macromolecules in spheroids. Crit Rev Oncol Hematol. 2000;36(2–3):159–178. doi: 10.1016/s1040-8428(00)00084-6. [DOI] [PubMed] [Google Scholar]
- Fujimori K, Covell DG, Fletcher JE, Weinstein JN. A modeling analysis of monoclonal-antibody percolation through tumors—a binding-site barrier. J Nucl Med. 1990;31(7):1191–1198. [PubMed] [Google Scholar]
- Goodman TT, Olive PL, Pun SH. Increased nanoparticle penetration in collagenase-treated multicellular spheroids. Int J Nanomed. 2007;2(2):265–274. [PMC free article] [PubMed] [Google Scholar]
- Graff CP, Wittrup KD. Theoretical analysis of antibody targeting of tumor spheroids: Importance of dosage for penetration, and affinity for retention. Cancer Res. 2003;63(6):1288–1296. [PubMed] [Google Scholar]
- Grantab R, Sivananthan S, Tannock IF. The penetration of anticancer drugs through tumor tissue as a function of cellular adhesion and packing density of tumor cells. Cancer Res. 2006;66(2):1033–1039. doi: 10.1158/0008-5472.CAN-05-3077. [DOI] [PubMed] [Google Scholar]
- Iyer AK, Khaled G, Fang J, Maeda H. Exploiting the enhanced permeability and retention effect for tumor targeting. Drug Discov Today. 2006;11(17–18):812–818. doi: 10.1016/j.drudis.2006.07.005. [DOI] [PubMed] [Google Scholar]
- Jain RK. Delivery of molecular and cellular medicine to solid tumors. Adv Drug Deliv Rev. 2001;46(1–3):149–168. doi: 10.1016/s0169-409x(00)00131-9. [DOI] [PubMed] [Google Scholar]
- Kohno N, Ohnuma T, Truog P. Effects of hyaluronidase on doxo-rubicin penetration into squamous carcinoma multicellular tumor spheroids and its cell lethality. J Cancer Res Clin Oncol. 1994;120(5):293–297. doi: 10.1007/BF01236386. [DOI] [PubMed] [Google Scholar]
- Krol A, Maresca J, Dewhirst MW, Yuan F. Available volume fraction of macromolecules in the extravascular space of a fibrosarcoma: Implications for drug delivery. Cancer Res. 1999;59(16):4136–4141. [PubMed] [Google Scholar]
- Krol A, Dewhirst MW, Yuan F. Effects of cell damage and glycosa-minoglycan degradation on available extravascular space of different dextrans in a rat fibrosarcoma. Int J Hyperthermia. 2003;19(2):154–164. doi: 10.1080/02656730210166519. [DOI] [PubMed] [Google Scholar]
- Kuhn SJ, Finch SK, Hallahan DE, Giorgio TD. Proteolytic surface functionalization enhances in vitro magnetic nanoparticle mobility through extracellular matrix. Nano Letters. 2006;6(2):306–312. doi: 10.1021/nl052241g. [DOI] [PubMed] [Google Scholar]
- Kuppen PJK, van der Eb MM, Jonges LE, Hagenaars M, Hokland ME, Nannmlark U, Goldfarb RH, Basse PH, Fleuren GJ, Hoeben RC, van de Veld CJ. Tumor structure and extracellular matrix as a possible barrier for therapeutic approaches using immune cells or adenoviruses in colorectal cancer. Histochem Cell Biol. 2001;115(1):67–72. doi: 10.1007/s004180000224. [DOI] [PubMed] [Google Scholar]
- Kuriyama N, Kuriyama H, Julin CM, Lamborn KR, Israel MA. Protease pretreatment increases the efficacy of adenovirus-mediated gene therapy for the treatment of an experimental glioblastoma model. Cancer Res. 2001;61(5):1805–1809. [PubMed] [Google Scholar]
- Kwok CS, Yu SK, Lee S. Mathematical-models of the uptake kinetics of antitumor antibodies in human-melanoma spheroids. Antibody Immunoconj Radiopharm. 1995;8(3):155–169. [Google Scholar]
- Netti PA, Berk DA, Swartz MA, Grodzinsky AJ, Jain RK. Role of extracellular matrix assembly in interstitial transport in solid tumors. Cancer Res. 2000;60(9):2497–2503. [PubMed] [Google Scholar]
- Oloumi A, Lam W, Banath JP, Olive PL. Identification of genes differentially expressed in V79 cells grown as multicell spheroids. Int J Radiat Biol. 2002;78(6):483–492. doi: 10.1080/09553000210122299. [DOI] [PubMed] [Google Scholar]
- Ramanujan S, Pluen A, McKee TD, Brown EB, Boucher Y, Jain RK. Diffusion and convection in collagen gels: Implications for transport in the tumor interstitium. Biophys J. 2002;83(3):1650–1660. doi: 10.1016/S0006-3495(02)73933-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rejman J, Oberle V, Zuhorn IS, Hoekstra D. Size-dependent internalization of particles via the pathways of clathrin- and caveolae-mediated endocytosis. Biochem J. 2004;1(377Pt 1):159–169. doi: 10.1042/BJ20031253. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saltzman WM. Drug delivery: Engineering principles for drug therapy. New York, NY: Oxford University Press; 2001. [Google Scholar]
- Satterfield CN. Mass transport in heterogeneous catalysis. Cambridge, MA: MIT Press; 1970. [Google Scholar]
- Schroeder F, Kinden DA. Measurement of phagocytosis using fluorescent latex beads. J Biochem Biophys Methods. 1983;8(1):15–27. doi: 10.1016/0165-022x(83)90017-9. [DOI] [PubMed] [Google Scholar]
- Wenning LA, Murphy RM. Coupled cellular trafficking and diffusional limitations in delivery of immunotoxins to multicell tumor spheroids. Biotechnol Bioeng. 1999;62(5):562–575. [PubMed] [Google Scholar]
- Wilhelm C, Gazeau F, Roger J, Pons JN, Bacri JC. Interaction of anionic superparamagnetic nanoparticles with cells: Kinetic analyses of membrane adsorption and subsequent internalization. Langmuir. 2002;18(21):8148–8155. [Google Scholar]