IQ Is Not Strongly Related to Response to Reading Instruction: A Meta-Analytic Interpretation

Abstract

A meta-analysis of 22 studies evaluating the relation of different assessments of IQ and intervention response did not support the hypothesis that IQ is an important predictor of response to instruction. We found an R² of .03 in models with IQ and the autoregressor as predictors and a unique lower estimated R² of .006 and a higher estimated R² of .013 in models with IQ, the autoregressor, and additional covariates as predictors. There was no evidence that these aggregated effect sizes were moderated by variables such as the type of IQ measure, outcome, age, or intervention. In simulations of the capacity of variables with effect sizes of .03 and .001 for predicting response to intervention, we found little evidence of practical significance.

The role of IQ test scores for the identification of children with learning disabilities (LD) continues to be controversial. This controversy was highlighted by the 2004 reauthorization of the Individuals With Disabilities Education Act (IDEA; U.S. Department of Education, 2006), which indicated that states could not require school districts to use IQ tests for identifying children with LDs. Although this regulatory change was controversial, it was preceded by more than 2 decades of research focusing on the validity of identifying children with LDs on the basis of a discrepancy between IQ and achievement as well as research examining how well IQ predicted different dimensions associated with LDs. Much of this research addressed children with LDs in reading, although there is also research on children with other forms of LDs as well as speech and language disorders (for a review, see chapter 3 in Fletcher, Lyon, Fuchs, & Barnes, 2007).

For the area of reading and LD, there is considerable accumulated evidence addressing this issue. Although some studies address the role of IQ in predicting prognosis and intervention response, most of this research has addressed the validity of differentiating groups of poor readers defined on the basis of discrepancies of IQ and achievement (IQ-discrepant poor readers) versus low achievement with no IQ-achievement discrepancies (low-achieving poor readers). In a meta-analysis of 46 studies comparing behavioral, academic, and cognitive skills in IQ-discrepant and low-achieving poor readers, Stuebing et al. (2002) found negligible effect size differences in behavior (−.05) and academic achievement (−.12) between the two groups. A small difference emerged for cognitive skills (.30) not used to define the two groups. However, this aggregated difference compared with an effect size difference in IQ of about 1 standard deviation favoring (as expected) the IQ-discrepant group. The variations across studies in effect sizes for cognitive skills could be accounted for by modeling variations in how the groups were formed. The researchers concluded that there was, at best, weak validity for differentiations of poor readers based on IQ scores.

In another meta-analysis of achievement and cognitive skills, Hoskyn and Swanson (2000) coded 19 studies comparing IQ-discrepant and low-achieving poor readers. This study reported negligible-to-small effect size differences that ranged from −.02 to .29 on measures of reading and phonological processing. However, larger differences were reported on measures of vocabulary (.55) and syntax (.87). Hoskyn and Swanson concluded, “our synthesis concurs with several individual studies indicating that the discrepancy … is not an important predictor of cognitive differences between low achieving children and children with RD [reading disability]” (p. 117).

In contrast, Fuchs, Fuchs, Mathes, and Lipsey (2000) completed a meta-analysis of 79 studies comparing children identified as LD with children who had poor academic achievement and no label of LD. Asking a different question than Stuebing et al. (2002) and Hoskyn and Swanson (2000), Fuchs et al. (2000) found that comparisons of the reading achievement of the two groups generated a moderate effect size difference (.61), concluding that the two groups could be validly differentiated.

A problem with both the latter two meta-analyses is that unlike Stuebing et al. (2002), Hoskyn and Swanson (2000) and Fuchs et al. (2000) did not differentiate variables used to define the groups (independent variables) from those used to evaluate the groups (dependent variables). Including reading scores, for example, that are used to define the groups leads to larger differences between IQ-discrepant and low achievers (Francis et al., 2005). This factor, along with the more inclusive sampling strategy of including children identified with LDs in any academic domain, is most likely why the effect size differences in reading are moderate for Fuchs et al., small for Hoskyn and Swanson, and negligible for Stuebing et al. To illustrate, in Fuchs et al., the effect size differences for measures of phonological awareness and rapid naming skills, both closely linked with reading, but not used to identify groups, were in the small range and comparable to estimates in the other two meta-analyses.

Prior to these empirical meta-analyses (Fuchs et al, 2000; Hoskyn & Swanson, 2000; Stuebing et al. 2002), there was significant controversy about the size of differences in academic and cognitive skills between IQ-discrepant and low achievers. For example, earlier quantitative assessments by two different research groups of essentially the same set of tests reached entirely different conclusions (Algozzine, Ysseldyke, & McGue, 1995; Kavale, 1995; Kavale, Fuchs, & Scruggs, 1994). Other qualitative reviewers of this literature concluded that cognitive differences were not important and questioned the validity of using IQ scores for identifying children with LDs in reading (Aaron, 1997; Fletcher et al., 1998; Siegel, 1992; Stanovich, 1991). However, the problem with these earlier studies and reviews is that they were based on single data sets or they were reviews of studies where the findings are mixed: Some studies show negligible differences and others find larger differences when comparing academic and cognitive skills in IQ-discrepant and low achievers. The value of a meta-analysis is that it empirically synthesizes results from multiple studies and allows the researcher to model the sources of differences across individual studies, avoiding the limitations of a “scorecard” approach to synthesis.

Another issue is that academic and cognitive skills are not the only dimensions in which IQ-discrepant and low-achieving groups may differ. For example, a higher IQ may be associated with a better prognosis, although studies based on the long-term development of reading skills from kindergarten to well into secondary school in the Connecticut longitudinal study (Francis, Shaywitz, Stuebing, Shaywitz, & Fletcher, 1996; Shaywitz et al., 1999) and the Dunedin study (Share, McGee, & Silva, 1989) did not find that IQ or IQ-discrepancy was associated with better reading outcomes. These findings were not consistent with an earlier report associating better outcomes with higher IQ scores (and IQ-discrepancy) by Rutter and Yule (1975). However, unlike the Connecticut and Dunedin studies, Rutter and Yule did not exclude children with brain injury and mental retardation.

Another relevant dimension is treatment response. A large study of children treated for reading difficulties beginning in kindergarten through Grade 2 found no differences in the intervention response of IQ-discrepant and low achievers (Vellutino, Scanlon, & Lyon, 2000). Through a score-card review of 10 studies addressing whether IQ scores predicted intervention response, Fletcher et al. (2007) concluded that “Most studies do not identify a relation, particularly an interaction that would demonstrate differential effects of the intervention across levels of IQ” (p. 37). In contrast, in another scorecard review of 13 studies partially overlapping with Fletcher et al., Fuchs and Young (2006) concluded that in 8 of 13 studies, IQ uniquely predicted response to reading instruction. They also argued that IQ was a stronger predictor in students who were older and when reading comprehension was targeted as a primary outcome relative to studies targeting phonological awareness and word recognition in younger students.

Although there is value to a systematic literature review and a scorecard approach to synthesizing a set of findings, when studies begin to accumulate, an empirical synthesis may more precisely address questions of the size of the relation of IQ for predicting intervention response and also for identifying factors that explain why various studies obtain different results. In this study, we used the two reviews by Fletcher et al. (2007) and Fuchs and Young (2006) as the basis for a meta-analysis of the relation of IQ and intervention response in which we systematically searched for studies addressing the relation of IQ and intervention response and then estimated aggregate effect sizes weighted for sample size and tested for homogeneity. Our expectation was that a meta-analytic approach would resolve the contrasting conclusions of the two scorecard reviews, permitting a more precise estimate of the relation of IQ and intervention response.

The central research question of this study is the extent to which intelligence scores predict intervention response in treatment studies of children with reading difficulties. Although Fuchs and Young’s (2006) synthesis indicates that intelligence does uniquely predict response to intervention and explains important variance in responsiveness, the review by Fletcher et al. (2007) came to different conclusions. Our hypothesis is that in a formal meta-analysis, the magnitude of the aggregated effect size estimate would be small after controlling for pretest levels of the reading outcome and small-to-negligible after controlling for pretest levels of the reading outcome and constructs closely related to reading (e.g., phonological awareness, rapid naming). In addition, we expected to identify whether the predictive power of IQ was uniform across different ages and reading outcomes, and to identify other pertinent study characteristics that accounted for variation in aggregated effect size estimates.

METHODS

Literature Search

A total of 1,070 articles were reviewed using several literature search strategies to identify both published and unpublished research. The first strategy involved a review of all articles cited in Fletcher et al. (2007) and Fuchs and Young (2006). The second strategy involved computer searches of (a) Educational Resources Information Center (ERIC) 1966 to 2002; (b) Psych Lit 1967 to 2002; (c) Exceptional Child Educational Resources 1969–2002; (d) PsycInfo 1967 to 2008; (e) Academic Search Premier 1975 to 2008; (f ) PubMed 1969–2008 electronic databases for documents cataloged before 1966; and (g) Dissertations and Theses Full Text 1975 to 2008. Varying combinations of the following terms were entered for all searches: intelligence and achievement, IQ-achievement discrepancy, and reading and intelligence. Next, several journals were hand searched to identify any articles that were relevant to this study: Journal of Educational Psychology, Exceptional Children, Journal of Experimental Child Psychology, Journal of Learning Disabilities, Journal of Special Education, Learning Disabilities Research and Practice, Reading Research Quarterly, Remedial and Special Education, and Scientific Studies of Reading. Seven researchers were also contacted directly to request data to tap research that would not otherwise be included because information necessary to calculate effect sizes were not included in their published articles. This request produced datasets from three studies (Allor, Fuchs, & Mathes, 2001; Nash & Snowling, 2006; Vellutino, Scanlon, Zhang, & Schatschneider, 2008).

A large number of sources are cited in a table on our Web site: www.texasldcenter.org/IQmetaanalysis. These sources included the reference sections of 79 articles and books related to intervention response and treatment of LD that were examined to determine if any cited works had titles and abstracts that might also be relevant. Seven meta-analyses were reviewed to identify any cited works that contained abstracts that might also apply. A total of 34 review articles with abstracts of all references were checked to determine if they could be included. Finally, the Society for the Scientific Studies of Reading’s membership directory was reviewed with all individuals entered into Psych Info to determine if any of their abstracts suggested that they were relevant to our study. The National Research Center on Learning Disabilities, the U.S. Department of Education, and the Center on Instruction Web sites were reviewed to determine if any cited works (e.g., presentations, articles, technical reports) suggested they be included in our review.

Criteria for Including Studies

For a study to be included in the research synthesis, several criteria had to be met. First, all studies had to include a clearly defined treatment component in which participants in the experimental condition had to receive some type of reading intervention. Second, because the capacity of IQ to predict response to instruction was of primary interest, all studies had to include a measure of IQ. If a study reported the effect of performance or nonverbal IQ, verbal IQ, full scale IQ, or a measure of vocabulary or another measure used as a proxy for IQ, the effect was recorded. Third, the study had to include a pretest–posttest or longitudinal design. Finally, the report had to include information necessary to calculate the effect of IQ in predicting response to instruction or the information had to be provided by the investigators.

Dependent Measures

The four key reading outcomes included in this analysis were (a) phonological awareness, when used as the target of intervention and an outcome; (b) word reading accuracy; (c) reading fluency; and (d) reading comprehension, all of which are common outcomes for a reading intervention study and which might be differentially related to IQ. Phonological awareness was defined as the ability to manipulate sounds in spoken words (National Reading Panel, 2000). Word reading accuracy was defined as the ability to decode words in text or isolation (Ehri, 1998). Reading fluency was defined as the ability to read lists of single words or connected text accurately and efficiently (Torgesen, Rashotte, & Alexander, 2001). Reading comprehension was defined as the ability to construct meaning from written text (National Reading Panel).

Data Coding

In order to explore the relation between preintervention ability as measured by IQ or its proxies and response to the intervention on a variety of achievement variables, we chose to code the correlation coefficient between the two constructs. Whereas Fuchs and Young (2006) coded R² to investigate the proportion of variance in response accounted for by ability, we chose to code the correlation for two reasons.

First, with correlations, we can take into account the directionality (positive, negative) of the relationship. The average size of effects reported in Fuchs and Young (2006) were small, and we expected that with correlations in the small range, the sampling distribution of effects would likely include some negative correlations. When we then aggregate over this distribution of effects, the combination of negative and positive effects results in a smaller average effect than if we averaged over R² and then took the square root to obtain an average estimated correlation. For example, if we had two effects, one of which was r = −.2 and the other was r = .3 and we average them, we get a mean r = .05 as our result. If we average the R²s associated with these two studies, we average .04 and .09, obtaining a mean variance accounted for of .065. When we take the square root to estimate the correlation, we get a mean r = .25. Obviously, this latter correlation is not a good estimate of the true correlation and is positively biased.

The second reason for choosing to base our meta-analysis on correlations is that there are well established formulae for converting available test statistics into correlations when the correlations themselves are not published (Arthur, Bennett, & Huffcutt, 2001). There are also well established techniques and protocols for carrying out the meta-analysis of correlation coefficients (Hunter & Schmidt, 1990).

After reviewing all of the articles, we categorized all of the correlation coefficients from the set of studies based on a hierarchical model. The three categories of effects we coded represent an ordered set of models where more predictors are added at each level to better explicate the relationship. The first category of correlations is based on the bivariate model where IQ prior to an intervention is related to achievement after the intervention. We called this the bivariate model. The second category includes models where the effect of IQ is examined in the presence of initial status on the achievement variable. We called this the autoregressor- only model. In the third set of correlations, additional predictors such as attention and rapid naming are added to the second model to estimate the unique contribution of IQ. Effects from the second and third categories are comparable to the effects coded by Fuchs and Young (2006).

An example of the bivariate correlation coefficient in this meta-analysis is the correlation between IQ as measured before the intervention correlated with achievement after the intervention. We include this category of effect sizes only for comparison purposes. The participant’s level and amount of growth on the achievement variable are confounded in this correlation, and, therefore, it is not a good indicator of response to instruction. We might, however, want to use this correlation as a point of reference for the other two categories of correlations. One study in which this effect was the only effect we could code was Case, Speece, and Molloy (2003). They divided subjects into three response groups based on whether they were in the lowest percentile group of the class based on both performance at the end of the intervention and amount of growth over the intervention. The groups were labeled NDD (Never Dually Discrepant), IDD (Infrequently Dually Discrepant), and FDD (Frequently Dually Discrepant). We expected the slopes to be steepest in the NDD group, moderate in the IDD group, and lowest in the FDD group. In this study, the correlation between group and IQ reflects the relation we are interested in studying. The correlation is inflated, however, because it also reflects the relation between the final level on the achievement test and IQ. As a result, we expect the bivariate correlations to be moderate and larger than the correlations obtained when controlling for initial status on the achievement variable.

In the second set of coded correlations, the initial status on achievement was controlled. In this autoregressor-only model, the IQ measure was used as a predictor in the presence of the autoregressor. Included in this set might be the effect of IQ on the achievement slopes in growth curve analyses or the semi-partial correlation of preintervention IQ with postintervention achievement while pretest achievement is controlled.

Two versions of the autoregressor-only model, a lower estimate and a higher estimate, are presented. In some cases, the investigator reported that this model was tested, but that the effect of the IQ predictor was not significant. In order to make use of the study, an estimate of the effect of the IQ predictor was obtained by determining the degrees of freedom available for the reported test and then calculating the largest possible effect size that could have been obtained without being significant for the given degrees of freedom. To the extent that this estimate is used and combined with the calculated estimates from the other studies, the average effect will be a higher estimate of the true effect. To gain a more balanced perspective, another approach was taken in which nonsignificant results were set at 0 when the effect of the IQ predictor was not given, but the investigators reported that the effect was not significant. The result is a lower estimate of the true effect. In all subsequent calculations of mean effects, we estimated the effects under both conditions to obtain a reasonable higher and lower estimate of the effect.

The third set of coded correlations was from analyses where the autoregressor and additional covariates were used to predict response to instruction. These models included predictors such as phonological awareness (when not used as the target of intervention or an outcome), attention, and rapid naming, in addition to the IQ predictor. We took the same approach to estimation in this class of models that we took with autoregressor- only models. When results were reported as nonsignificant, we estimated both the largest possible nonsignificant effect, and then also estimated the effect as 0. In this way we estimated the range of values we might expect for the effects within this model.

Estimation of Effect Sizes

Despite the encouragement given to researchers to report effect sizes in research studies, meta-analysts frequently find that the data needed for coding of effects is completely or partially missing. If omitting the data is related to the size of the effect, as is likely to occur when nonsignificant effects are not reported, the aggregate result of the meta-analysis will be biased in an upward direction. This problem has often been referred to as the “file drawer problem” (Rosenthal, 1979), referring to the number of relevant studies hidden away in file drawers and never submitted for publication because of small effect sizes or, more likely, nonsignificant results. A more common situation is that the data needed to code an effect even from published studies is not reported when the results are not significant. It is also common to find that the data required to code effects are partially missing from the published results.

The approach taken by most meta-analysts is to include only studies with complete and nonambiguously reported effect sizes. Although this is the easiest approach, it fails to make use of the partial information that exists in published reports, and results from this approach may not fairly represent the state of the field. We take the approach advocated by Lipsey and Wilson (2001), which is to estimate effect sizes with whatever data or qualitative information is available and to code effects for the degree of estimation required. This approach can yield average effects that are not only more representative of population effects, but it also results in better precision (i.e., narrower confidence intervals) in our estimates because we are aggregating over more studies and more participants. In contrast with Fletcher et al. (2007), who did not report any quantitative data as the basis for their conclusion that IQ was not related to response to intervention, and Fuchs and Young (2006), who reported quantitative data on 7 of the 13 studies they included in their review, we were able to code effects for all 13 studies (and an additional 9 studies) using varying levels of estimation. Lipsey and Wilson recommend a 5-point scale to code for the amount of estimation required to obtain each effect. This scale ranges from “No Estimation” to “Highly Estimated” and is summarized in Table 1. We treated the estimation code in the same way that we treated other potential moderators of effect size—we planned to test whether the degree of estimation was related to the magnitude of the effects. This would be done only if the distribution of effects showed significant heterogeneity.

TABLE 1.

Coding Scheme for Estimation of Effects

Code and Value Label	Examples of Estimation Effects
1: High estimation	Example 1 Results include the statement that the effect was nonsignificant but no quantitative data was given. Lower estimate was entered as 0 and higher estimate was entered as the largest possible r that would be nonsignificant given the degrees of freedom for the test.
	Example 2 Results reported that the effect was significant, but no quantitative data or test statistics were reported. The lower estimate was the smallest possible significant effect given the degrees of freedom for the test. The higher estimate was left missing, because there is no reasonable upper limit.
2: Moderate estimation	Example 1 Beta weights for predicting response to intervention from IQ or initial ability and from additional covariates such as phonological awareness and rapid naming are reported, but the correlations among the predictors is not included. R2 and r are computed by using correlations from large population studies as best guess for intercorrelations among predictors.
	Example 2 F statistic or change in R2 was reported, but the direction of the effect was unknown. We always coded a positive effect.
3: Some estimation	Example 1 In two studies the authors divided subjects into groups based on the amount of growth they showed in response to the intervention (Case, Speece, & Molloy, 2003; Vellutino, Scanlon, & Lyon, 2000). The authors also reported the IQ means, standard deviations, and sample sizes for each group. With this data it is possible to compute an eta2 for the linear relation between the ordered groups and the ability measure. We calculated sums of squares within, the sums of squares between, and the sums of squares due to the linear contrast only per Maxwell and Delaney (1990) and then formed the ratio of the sums of squares linear over the sums of squares total to arrive at an eta2 for the linear contrast.
4: Slight estimation	Example 1 The correlation matrix was given in the article, and we input the matrix into SAS (Arthur, Bennett, & Huffcutt, 2001) to compute the R2 change between models. To the extent that the reported correlations are not as precise as raw data, this approach might result in a small amount of misestimation.
5: No estimation	Example 1 Correlation coefficient was reported in the study.
	Example 2 Data was sent to our team by the authors of the study, and we analyzed it to obtain effect sizes.

Other Moderator Variables

The variables other than degree of estimation that we selected as potential moderators included participant age, type of IQ test, and type of reading outcome.

Age

Fuchs and Young (2006) hypothesized that IQ predicted response better at the early stages of reading acquisition (Grades K and 1) and had less predictive power in later grades when early reading achievement becomes a better predictor. This is consistent with other studies attempting to predict reading ability in the later grades, where direct assessments of print-related skills are typically more robust once the child has been exposed to reading instruction (Scarborough, 1998).

Type of IQ test

We thought it possible that the specific type of IQ predictor used might be a moderator of effect sizes, with the strongest effects coming from either vocabulary or verbal IQ measures and the weaker effects coming from performance IQ measures. In general, any assessment of language skills tends to be a stronger predictor than assessments of nonverbal skills or working memory (Scarborough, 1998). We thought that full-scale IQ would fall in between these domains because it is a composite of these skills.

Reading outcomes

A variety of different achievement variables were measured across the set of studies. Consistent with Fuchs and Young (2006), we hypothesized that IQ would be a better predictor of reading comprehension and a poorer predictor of reading accuracy or fluency. This prediction reflects the stronger association of reading comprehension with higher-level text processing skills (i.e., inference generation, comprehension monitoring, working memory capacity, and vocabulary; Cain, & Oakhill, 2006; Nation & Snowling, 2004) versus word reading accuracy and fluency skills, which are more strongly influenced by phonological awareness and rapid naming skills (Speece, Ritchey, Cooper, Roth, & Schatschneider, 2003; Wise, Sevcik, Morris, Lovett, & Wolf, 2007).

Covariates

In addition to IQ, many studies used additional cognitive measures to predict intervention response. The most common cognitive measures were assessments of phonological awareness and rapid naming skills. In addition, some studies used assessments of phonological and/or working memory, attention, and a variety of language measures. A few studies included sociodemographic variables, such as age, gender, and in one study, ethnicity (Foorman, Francis, Fletcher, Schatschneider, & Mehta, 1998). We coded effects from studies that included covariates to estimate the unique relation of IQ and reading outcome. We then aggregated these estimates across studies and tested for homogeneity. In some instances, the investigators reported models that yielded the unique effects of IQ. In others, we had a dataset that we analyzed to estimate the unique effect. Finally, some articles included the correlation matrix of IQ, covariates, and outcomes (including pre- and post-test assessments), and we derived the effect from these data. Because the covariates varied so widely across individual studies, we have not listed the specific measures in detail, especially because the selection of covariates was based on the study designed by the investigators, with a wide range of research questions for each study. The key question is whether the distribution of effects is homogeneous.

RESULTS

All data were entered into a database and analyses were run in SAS 9.1.3. Code from Arthur et al. (2001) was utilized to compute mean effects, confidence intervals, and to carry out chi square tests of homogeneity for each set of correlation coefficients. The code from Arthur et al. embodies the approach to the meta-analysis of correlation coefficients developed by Hunter and Schmidt (1990).

Features of Analyzed Studies

The literature search yielded 1,070 studies of which 22 met our criteria. Table 2 summarizes sample sizes, IQ measures, key moderator variables, and reading outcomes of the studies coded for the meta-analysis. As shown in Table 2, the studies are largely of elementary school-age children and vary widely in sample size. Most studies target beginning reading skills with fewer studies dedicated to reading comprehension abilities.

TABLE 2.

Studies Included in Meta-Analysis

Authors	Year	Design	Age	Grade	N	Ability Measure	Dependent Measure
Allor, Fuchs, & Mathes	2001	PPa		1	30	PPVT-R	WRMT-R Word Identification, Word Attack, Passage Comprehension
Berninger et al.	1999	GCb	7.5		48	WISC-III Verbal IQ	WRMT-R Word Identification, Word Attack; CBM Word Reading Accuracy
Berninger et al.	2002	PP		1	87	WISC-III Verbal IQ	WRMT-R Word Identification; WJ-R Word Attack
Case, Speece, & Molloy	2003	GC		1, 2, 3	36	WISC-R Full Scale IQ	Oral Reading Fluency CBM
Compton, Fuchs, Fuchs, & Bryant	2006	GC		1	206	WJ-R Oral Vocabulary	Word Identification Fluency CBM
Foorman, Flrancis, Fletcher, & Schatschneider	1998	GC		1–2	285	WISC-R Verbal IQ	Pre-CTOPP (synthesis and analysis tests); WJ-R Letter Word Identification
Hatcher & Hulme	1999	PP	7.5		93	WISC-R Verbal IQ	The BAS Word Reading Test A; Neale Analysis of Reading
Hecht & Close	2002	PP	5.5		42	Stanford-Binet Intelligence Test (4th ed.) Verbal IQ	WJ-R Letter Word Identification
Mathes et al.	2005	GC		1	161	WASI Verbal IQ	TOWRE Sight Word Efficiency, Phonemic Decoding Efficiency, TCARE; Foorman Word List
Nash, & Snowling	2006	PP	7.5		24	British Picture Vocabulary Scales–Revised	Neale Analysis of Reading Ability-R; Suffolk Reading Test
O’Connor, Jenkins, Leicester, & Slocum	1993	PP	4, 5, 6		36	McCarthy Scales of Children’s Abilities–Full Scale IQ	3 segmenting tasks not specified; 3 rhyming tasks not specified; 3 blending tasks not specified
O’Shaughnessy & Swanson	2000	GC		2	30	WISC-III Full Scale IQ	CBM Oral Reading Fluency; 90 Word Analogy Training (WAT) words, 90 Phonological Awareness Training in Reading (PAT) words; WRMT Word Identification; WRMT-R Word Attack, Passage Comprehension
Schneider, Ennemoser, Roth, & Kuspert	1999	PP		K	190	Culture Fair Intelligence Test– Performance IQ	Wurzburg Silent Reading Test
Stage, Abbott, Jenkins, & Berninger	2003	GC	6.73		128	WISC-III Verbal IQ	WRMT-R Word Identification, Word Attack
Torgesen, & Davis	1996	GC		K	60	Stanford-Binet Intelligence Test (4th ed.) Verbal IQ	Phoneme Blending (not specified); Phoneme Segmenting (not specified)
Torgesen et al.	1999	PP	5		106	Stanford-Binet Intelligence Test (4th ed.) Verbal IQ	WRMT-R Word Attack, Word Identification
Torgesen et al.	2001	PP	8, 9, 10		50	WISC-R Full Scale IQ	WRMT-R Word Identification, Word Attack, Passage Comprehension; GORT-III Rate
Uhry & Shepherd	1997	PP		1, 2	12	WPPSI-R or WISC-III Full Scale IQ	WRMT-R Word Identification, Word Attack
Vadasy, Jenkins, Antil, Wayne, & O’Connor	1997	PP		1	17	PPVT-R	WRAT-R Reading
Vellutino, Scanlon, & Lyon	2000	GC		K–2	74	WISC-R Verbal IQ, Performance IQ or Full Scale IQ	WRMT-R Basic Skills Cluster
Vellutino, Scanlon, Zhang, & Schatschneider	2008	GC		K–3	1373	WISC-III Verbal IQ, Performance IQ or Full Scale IQ	WRMT-R Word Identification, Word Attack
Wise, Ring, & Olson	1999	PP		2–5	104	WISC-R Full Scale IQ	PIAT Word Recognition untimed; WRAT Reading Subtest Level 1 (screener); PIAT Word Recognition time-limited; WRMT-R Word Attack; PIAT Reading Comprehension; Lindamood Auditory Conceptualization Test & revised Rosner Test of Auditory Analysis Skills

Note. WISC-III = Wechsler Intelligence Scale for Children-III; WISC-R = Wechsler Intelligence Scale for Children-Revised; WRMT-R = Word Reading Mastery Tests-Revised; WJ-III = Woodcock-Johnson-III; CBM = Curriculum-Based Measure; Pre-CTOPP = Pre Comprehensive Test of Phonological Processing; TOWRE = Test of Word Reading Efficiency; PIAT = Peabody Individual Achievement Test; PPVT-R = Peabody Picture Vocabulary Test-Revised; TCARE = Continuous Assessment for Reading Excellence; PAT = Phonological Awareness Training; GORT-III = Gray Oral Reading Test-III.

^aPP = pre–post design,

^bGC = growth curve design.

Reliability of Coding

Study Characteristics

All study characteristics (see Table 2) other than effect sizes were coded by the first author and independently verified by the second author. Because these characteristics were explicitly reported in all research studies (IQ measure, reading outcome measure, age, or grade), simple transcription was sufficient to code these characteristics and no judgments were required, thus minimizing the likelihood of coder bias or coder inference. When the entries for Table 2 were compared across the two coders, there was disagreement on only 1 data point that was resolved via discussion.

Effect Sizes

Two of the authors calculated the effect sizes for all studies and coded for the degree of estimation required to arrive at each effect. We coded for as many of the three categories of correlation coefficient as possible given the data reported in each study. The correlation between effects coded by the two coders was .94 and agreement between the coders for degree of estimation using the 5-point scale from Lipsey and Wilson (2001) was .88. All discrepancies were resolved via discussion.

Level of Estimation

Table 3 shows the distribution of effects across all studies with frequencies for each class of correlation by level of estimation required. A substantial number of the effects were classified in the “Moderate Estimation” category, that is, effects that were derived from R²s and from F tests. In this category the absolute magnitude of the effect can be quite precisely transcribed or estimated, but the direction of the effect is unknown. This is a minor issue in meta-analyses where the effect sizes are medium to large and the study sample sizes are large because even with sampling error, we would not expect a significant number of the effects to be negative. In this study, however, where the population effects may be close to zero, using the positive square root of the R² or taking the positive effect based on an F statistic can result in meaningful positive bias.

TABLE 3.

Distribution of Direction of Effects by Correlation Category and Distribution of Effects (5 levels) by Level of Estimation Required (5 levels)

	Direction of Effect			Level of Estimation
Category of r	Negative	Positive	Unknown	1- High Estimation	2- Moderate Estimation	3- Some Estimation	4- Slight Estimation	5- No Estimation
Bivariate	3	14	3	0	3	1	3	13
Autoregressor-only/lower estimate set	4	25	17	4	12	5	9	16
Autoregressor-only/upper estimate set	4	25	14	1	12	5	9	16
Autoregressor plus covariates/lower estimate set	4	16	25	6	19	0	12	7
Autoregressor plus covariates/upper estimate set	4	16	22	4	19	0	12	7

Note. In a small set of studies, both lower and upper estimates of effects were calculated to prevent bias that is due to choice of estimate. Lower and upper sets are reported separately.

Table 3 also shows the distribution of known negatives, known positives, and effects of unknown direction across our three categories of the correlation coefficient. Because we are able to code slightly different numbers of effects in the lower estimate and higher estimate conditions, we report both frequencies in Table 3. The number of effects with unknown direction is substantial. Because we always coded a positive effect when the direction was unknown, we should assume that the aggregated results from this set of studies will represent high estimates of the actual effect sizes.

Tests of Homogeneity

We computed the chi square within each set of the five sets of correlation coefficients to test for homogeneity of effects. A significant result would suggest that the effects should not be combined into one aggregate effect, but that a search for moderators was needed in order to explain the significant variance in effects.

In order to obtain a set of effects that met the assumption of independence of observations of the chi square test but still allowed for variability in the outcomes for different dependent measures, we aggregated effects within studies that were measures of the same dependent variable construct. For example, if a study looked at accuracy in decoding both real words and pseudowords and also looked at passage comprehension, we would combine the decoding effects at the study level before proceeding to the chi square test. That study would then contribute two effects to the meta-analysis. One effect would represent decoding, one would represent reading comprehension, and the difference between these effects could add variance to the total set of effects that was potentially explainable by the outcome category variable. We aggregated in this way within each of the levels of correlation coefficients. When there were multiple effects from a given study because they came from different groups of participants, we did not combine or average these effects.

As Table 4 shows, the chi squares for the effect sizes relevant to our research questions were nonsignificant, indicating that the variability in effect sizes within sets was consistent with the most parsimonious model, that is, sampling error or chance variation is the source of the observed variability. Thus, we did not do additional analyses to assess the predictive ability of our moderator variables to explain the variance in the effect sizes. Although the chi square for the bivariate correlations was significant, we did not do any additional analyses of these effects, because we computed their mean only as a reference point despite the fact that they are inflated because level of final achievement and amount of growth are confounded.

TABLE 4.

Table of Chi-squares for Each Set of Correlations (r), Mean Aggregated Effects, and Confidence Intervals

Category of r	χ2	df	p <	N	k	Lower 95% Confidence Interval	Mean Correlation Coefficient	Upper 95% Confidence Interval	R2
Bivariate	28.21	15	.02	476	11	.19	.27	.36	.07
Autoregressor-only/lower estimate set	38.77	32	.19	1223	19	.11	.17	.22	.03
Autoregressor-only/upper estimate set	36.51	30	.19	1271	18	.11	.17	.22	.03
Autoregressor plus covariates/lower estimate set	21.23	30	.88	1569	20	.03	.08	.13	.006
Autoregressor plus covariates/upper estimate set	19.92	30	.92	1569	20	.06	.11	.16	.01

Note. In a small set of studies, both lower and upper estimates of effects were calculated to prevent bias that is due to choice of estimate. Lower and upper sets are reported separately. Degrees of Freedom (df) represent the number of independent pieces of information available to estimate the chi square test. df is larger than k because after testing the set of effects for homogeneity, we aggregated within studies to come up with a set of independent effects. The number of effects (k) represents the total number of independent studies or samples of students utilized to calculate the mean correlation coefficient.

Mean Effects

Because the variability in effects was consistent with sampling error, we next aggregated across dependent variables within studies (e.g., pooling decoding and comprehension effects) and then computed mean effect sizes and confidence intervals within each of the three correlation categories, for both the higher and lower estimates where necessary. Table 4 shows that as expected, the highest mean effects were for the bivariate correlation coefficients, where the level of achievement is confounded with the amount of response or change in achievement. The smallest average r was associated with the average r between IQ and achievement when other covariates were controlled. The average r for the autoregressor-only model was in between the other two.

We completed a separate meta-analysis for both the lower estimate set of effects and the higher estimate set of effects within the autoregressor- only model and within the autoregressor plus covariates models. In the autoregressor-only models, the lower estimate and the higher estimate were virtually identical to two decimal places (r = .17), with the ability measure accounting for 3% of the variance in response to intervention. For the autoregressor plus covariates effects, the mean aggregated correlation coefficient for IQ and reading outcome ranged from a lower estimate of .077 to a higher estimate of .113. When we square these two effects to get the range of R² we find that the proportion of unique variance accounted for by IQ ranges from about .5% to 1%. We have accounted for virtually all of the variance in the outcome that is associated with the IQ predictor by including other predictors that usually are more theoretically linked to reading (e.g., phonological awareness). Note that these aggregate estimates, even those that are within the sets labeled lower estimates, still have a likely positive bias because of the high number of effects where only an R² or F test was available in the results and thus no direction was given.

Comparison with Previous Studies

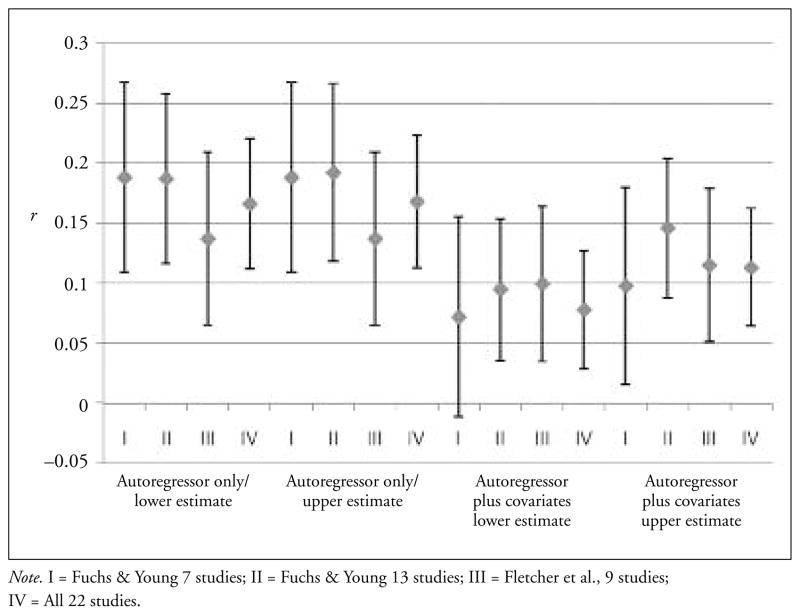
Our study differs from Fuchs and Young (2006) and Fletcher et al. (2007) by methodology (quantitative versus scorecard), by sample of studies, and by the fact that we estimated effects when possible. In order to evaluate these differences as reasons for the different results and conclusions we reached, we compared the results of this meta-analysis to the results that would have been obtained if we had used the set of 7 studies included in Fuchs and Young where they were able to code a quantitative result, to the results from all 13 of the studies from Fuchs and Young, and to the 9 codeable studies cited by Fletcher et al. As is apparent in Figure 1, the mean effects within the effect categories are remarkably similar across these four sets of studies. The primary difference is in the width of the confidence interval where the full set of studies gives us a confidence interval that is approximately two thirds the width of the smallest set of studies.

FIGURE 1. Comparison of Confidence Intervals Around the Meta-Analytic Mean Estimated Effects for Four Sets of Studies.

Note. I = Fuchs & Young 7 studies; II = Fuchs & Young 13 studies; III = Fletcher et al., 9 studies; IV = All 22 studies.

DISCUSSION

The present study supports the value of a quantitative synthesis of an accumulated set of studies as opposed to a scorecard or selective quantitative summary. Fletcher et al. (2007) flatly rejected the idea of a relation of IQ and intervention response based on an unsystematic selection and review of 10 articles, suggesting that in only 1 article was a significant relation demonstrated. They did not, however, consider the possibility that small effects were missed because significance tests were under-powered. In contrast, Fuchs and Young (2006) used a meta-analytic search strategy and reviewed more articles, attending to the possibility that variables like age, type of IQ test, and reading outcome would introduce heterogeneity to the estimation of effect size. Fuchs and Young concluded that

across the 13 studies, IQ became an increasingly important predictor of responsiveness to intervention as the reading measure became more complex … for reading comprehension, the average amount of unique variance explained by IQ was 15% for children in the more comprehensive interventions; 12% for those in PA (phonological awareness) training. For word identification: 6.77% for those in comprehensive interventions, 6.85% for those in PA training. For word attack, 4.96% for comprehensive interventions, 4.80% for PA training. Averaging across the PA training studies and more comprehensive studies, IQ explained 13.33%, 6.81%, and 4.88% of the variance in reading comprehension, word identification, and word attack measures, respectively. (p. 23)

Our meta-analysis, after a more systematic and updated search, correcting for missing data through estimation, and aggregating across all the reported effects from 22 studies, shows that the Fuchs and Young (2006) estimates are positively biased, reflecting in part the need to adjust effect size estimates for sample sizes, to estimate effects from all available studies, and to include studies with nonsignificant results in the estimates. Using a variety of estimation methods, we found that the highest value was a R² of .07 for the bivariate relation of IQ and intervention response, which is an overestimate because the level and amount of growth on the achievement variable are confounded. Fuchs and Young appropriately did not report this correlation, but it is noteworthy as the highest possible relation of IQ and intervention response, albeit confounded. Controlling for the initial level of achievement, both the higher and lower estimates concurred in estimating R² of .03. The most appropriate estimate, which is the unique contribution of IQ to intervention response, yielded a lower estimate of R² = .006 and a higher estimate of R² = .013. Thus, at most, IQ accounts for 1% to 3% of the variance in intervention response, a very small effect.

Restricting these estimates to the 7 studies for which quantitative data was reported in Fuchs and Young (2006), all 13 studies in Fuchs and Young, and the 9 codeable studies in Fletcher et al. (2007) yields estimates that are entirely consistent with those in Table 4. For example, our meta-analysis of the 7 studies from Fuchs and Young from which they coded quantitative data, yielded R² estimates for the unique relation of IQ and intervention response of .01 for the higher estimate and .005 for the lower estimate. In addition, we found no evidence that the effect sizes were heterogeneous, indicating that factors like type of IQ test, age, and reading outcome do not moderate the aggregated effect size estimates. Thus, our meta-analytic approach to the estimation of the relation of IQ and intervention response does not support the hypothesis that IQ is a strong predictor of response to intervention, a conclusion reached by many of the studies cited by Fletcher et al. and Fuchs and Young.

Implications for Practice

Even with our re-analysis, the aggregated effect size is significantly different from zero. An effect size of this magnitude may be relevant even though it is small. For example, Fuchs and Young (2006) cited Cohen (1988) in terms of thinking of the relation of R² and effect size, noting correctly that any interpretation of the magnitude depends on contextual factors associated with the study and the evidence base under examination (Rosenthal & DiMatteo, 2001). They argue in favor of interpretations of R²s < .001 as noteworthy, citing Rosenthal (1990) to suggest “that medical researchers view R² values as important when they are as low as .001” (p. 24).

Fuchs and Young’s (2006) emphasis on context should be seriously regarded when considering these results. Rosenthal (1990) reported on a study of physicians where a very inexpensive lifestyle modification (taking a daily aspirin) was associated with reduced odds of heart attack. The importance of the effect was a function of odds ratio of heart attacks in two groups (104 out of 11,037 in the aspirin group, and 189 out of 11,034 in the placebo group). This is a statistically significant effect, but more important, as a recent study (Stuebing, Barth, Cirino, Francis, & Fletcher, 2008) noted in interpreting small effects of reading interventions in the meta-analysis of the National Reading Panel (2000), it is practically significant because of the simplicity and low cost of the intervention, the seriousness and the high cost of the outcome, and the low base rate of the outcome.

The context for predicting response to intervention is different both in terms of the cost of the intervention, that is, assessing IQ, and the base rate of responsiveness, and has major implications for practice. Consider, for example, a situation in which an interdisciplinary team is attempting to predict a child’s response to intervention for a particular intervention protocol, represented here as a categorical decision like that in the aspirin study. If we assume that an effect size of .001 would be important in a RTI environment, let us consider 1,000 children who are struggling readers. Let us further assume that 50% of them will respond to a specialized reading intervention and that we would like to be able to predict which children will be the responders and the nonresponders. This estimate of 50% is based on observations that about 30% to 70% of students with a reading disability who receive a remedial intervention read in the average range at the end of the intervention (Fletcher et al., 2007). If we established a randomized trial and assigned children to either receive the intervention or not to receive the intervention, just by chance we would expect 250 children assigned to the reading intervention to respond adequately and 250 to respond inadequately. Likewise, we would expect 250 children assigned to the control condition to respond adequately and 250 to respond inadequately. Chance alone results in predictive accuracy of 50%. With a predictor that accounted for 0.1 of a percent of the variance in response (an R² of .001), we could improve slightly on chance assignment and increase the accuracy by a total of 16 children; 8 additional children could be identified as likely responders and could be assigned to the reading intervention. Likewise, 8 additional children would be predicted not to respond and would NOT be assigned to the reading intervention. If we take the 3% average effect that we identified for IQ with no additional predictors, this situation improves so that an additional 43 children would be expected to respond and an additional 43 would be expected not to respond. This improvement of 86 cases would require an average of 1.5 hr to administer a multi-factorial IQ test to each of 1,000 students in order to increase the predictive accuracy to 58.6, an increase of 8.6% over chance.

Now consider a more robust predictor. Based on data from Vellutino et al. (1996), Vellutino et al. (2000) found that the student’s initial level of word recognition skills at baseline yielded a unique eta² of .33. If performance on this test with this effect size was used to predict responder status, the accuracy increases to 28.6% above chance or 78.6% with an assessment that requires 5 to 10 min per child. Why would IQ be used instead of a shorter task with a much stronger relation with outcome? Indeed, we wonder whether variables other than the child’s baseline reading skills at the onset of intervention, which directly assess the outcomes of interest, could possibly contribute much unique variability even relative to the assessments of “phonological awareness, phonological encoding and discrimination, naming speed, attention to behavior, orthographic processing, and level of English proficiency” (Vellutino et al., 2000, p. 25) highlighted by Fuchs and Young (2006) as potentially important predictors of responder status. Little evidence presently supports this hypothesis or the existence of aptitude by treatment interactions (Vellutino, Scanlon, Small, & Fanuele, 2006).

Limitations of the Study

Although Fuchs and Young (2006) suggested that age and type of cognitive skill moderated the effect size estimate, and we also hypothesized that type of IQ predictor would moderate these effects, the heterogeneity tests did not achieve conventional levels of statistical significance (p > .05). Thus, we did not test formal hypotheses about these study moderators. In addition, the lack of evidence for heterogeneity indicates that the different procedures used to code missing data and estimate correlations did not introduce heterogeneity into the effect size estimates. As additional studies are completed and made available for future meta-analyses, results that are based on large samples where the obtained correlations are consistently and substantially larger than or smaller than zero could result in a body of results that is significantly heterogeneous. Until that time, parsimony suggests that the observed variability is due to sampling error.

Our results are based on 22 studies where the best estimated mean effect was based on the data from 1,569 students. One might argue that this is too small a sample of studies, including too few students, to draw confident conclusions. On the other hand, our search strategy was comprehensive, and it is not likely that we overlooked a substantial number of studies, so this sample may be representative of the current state of the science without obvious bias. There were, however, seven studies that met the eligibility criteria for inclusion into the meta-analysis but that did not include information necessary for coding effects. We obtained data from three studies (Allor et al., 2001; Nash & Snowling, 2006; Vellutino et al., 2008), and failed to obtain data for the other four studies (Berninger et al., 2000; Foorman et al., 1997; Hatcher et al., 2006; O’Connor, Notari-Syverson, & Vadasy, 1996). This set of four studies included 391 students. The effects from these studies would have to be uniformly different from our current set of effects for our results and conclusions both about mean effects and homogeneity of effects to change. None of these studies concluded that IQ was a robust predictor of reading outcome.

We chose to code the correlation coefficient to capture the relation between IQ and RTI. A limitation of this choice of effect is that it contains information only about the linear relation between two variables. If the relation is more complex, for example, is quadratic, the correlation coefficient is an underestimate of the relation. We explored this idea by examining the results in Vellutino et al. (2000). For that study, we estimated the correlation coefficient by taking the square root of the eta² for the linear contrast among group means. We also calculated the total between cell eta², which in this case would allow a quadratic and cubic relation in addition to the linear. The variance accounted for by the linear contrast was eta² = .025, and the variance accounted for by the linear, quadratic and cubic contrasts together was eta² = .027. In this case, at least, the failure to model a more elaborate relation was not necessary.

Because restriction of range on one or both variables will result in an observed correlation coefficient that is smaller than the population coefficient, we considered whether there was evidence that restriction of range was responsible for the weak correlations we found between IQ and RTI. Keep in mind that the key issues are either restriction because of selection on the basis of IQ or the amount of growth in reading; a cut point to define poor reading would only be relevant if it restricted growth in some way.

We looked at the evidence for restriction of range on IQ in a handful of studies where data were available and found some small evidence for restriction of range. Using the Vellutino et al. (2000) study as an example, poor readers in a Grade 1 intervention scored at least a 90 on an IQ measure. Their reading achievement was followed through spring of Grade 4. They were then divided into four equal groups by rank order on the basis of their growth over this period. The means and standard deviations of these four groups on verbal IQ were Very Low Growth (M = 100.89, SD = 14.47); Low Growth (M = 101.11, SD = 10.19); Good Growth (M = 104.11, SD = 10.46); and Very Good Growth (M = 105.42, SD = 12.01). These values are consistent with what we would expect to see given the use of IQ as a selection variable in that the means are close to the population mean and the standard deviations are smaller than 15. When we correct the obtained R² for this study for the observed amount of restriction of range, we go from accounting for 2.5% of the variance in growth to 3.8% of the variance. Although the amount of increase is notable, the absolute value of the final corrected R² is still small considering that no additional covariates are included in this model. Based on the available studies, we could not complete a more rigorous and comprehensive study of this issue, which is what is needed to determine the impact of IQ restriction of range on the overall effects.

Next, we considered whether it was likely that participants in these studies were selected in such a way that their potential for growth was limited. Because growth does not happen until well after selection, we can rule out explicit restriction of range. The question then is whether there is an indirect or implicit restriction of range on growth. For example, there could be a ceiling effect on the test used that might restrict the measured growth of these individuals. To address this issue, we turned to the plots of the average growth curves for word recognition and word attack skills from Vellutino et al. (2000) and took the raw score gain from the beginning of the intervention or winter of Grade 1 until the last follow-up data point collected in spring of Grade 4. For word attack, the four tutored groups gained 17 to 31 raw score points over this period. The two groups of typical readers, who scored above the 40th percentile on word recognition and word attack and were divided into an average IQ group and an above average IQ group, each grew an average of about 20 points and finished with mean scores at least a few points higher than any of the tutored groups. Thus, the tutored groups whose scores contributed to our meta-analysis were not apparently restricted in their possible growth by ceiling effects of the test. A similar pattern held for word recognition; the tutored groups gained 50 to 60 raw score points and the typical groups gained 35 to 40 points, but ended higher than the tutored groups by a few points. Although there did not appear to be restriction of range in the growth variable within this study, further studies could be designed to address this question in a more rigorous way.

None of the studies in this meta-analysis were explicitly designed to answer the question, Does IQ predict RTI? In most cases, to code effects for our study, the results we assessed were from secondary analyses or were not even reported in the original study but were derived from datasets or came from analyses of the correlation matrices in the study. It is possible that a set of studies designed to answer this specific question might produce different results.

There are limitations to meta-analysis and the approach that we took to this study. Meta-analysis is a quantitative approach where the richness of detail and the potential for hypothesis generation that can come from a good qualitative review are typically not found. Fortunately, this richness of detail may be found in existing reviews (Fuchs & Young, 2006) so the two types of reviews are complementary. Additionally, we took an approach to coding effects that has not been frequently taken, despite the powerful reasoning behind it. We estimated effects based on whatever data was given in a study as often as possible. In this way we incorporated the results from studies where nonsignificant findings were reported, even though no quantitative data were reported and partially avoided the publication bias problem (Rosenthal, 1979). Many of the results we coded suffered from positive bias because we coded from reported R²s or F tests and, thus, did not know the direction of the effect. The limitation here is that even through our mean estimates of effects are very small, they still have a likely positive bias.

CONCLUSIONS

The underlying issue that plagues research and diagnosis of LDs, which was highlighted by Fuchs and Young (2006), is the role of aptitude assessments in LDs and issues related to the differential diagnosis of LDs and mental retardation. Fuchs and Young suggested that not using an IQ test equates LDs with low achievement and threatens to destroy the construct of LDs because of blurring with mild mental retardation. In fact, meta-analyses (Hoskyn & Swanson, 2000; Stuebing et al., 2002) do not support the differentiation of IQ-discrepant and low-achieving children when IQ is outside the range associated with mental retardation. Moreover, not routinely administering IQ tests to children with LDs does not potentially equate LDs to mild mental retardation or low achievement. Rather, there are many other factors that would indicate that an IQ test was not needed to assess the child for mental retardation, such as a discrepancy between reading and math, achievement test scores consistently in the low average range, or adaptive behavior assessments that are more critical for determining the presence of mental retardation. Few children with achievement difficulties need an IQ test to rule out mental retardation. Nonetheless, Fuchs and Young suggest that “those who argue against its [IQ] regular use do so because they believe that low achievement definitions of LD will be cost effective, psychometrically justifiable, egalitarian, and inclusive” (pp. 12–13). In fact, the routine application of IQ tests for the classification of LD should not be supported because of the lack of evidence showing that IQ is necessary to identify LD and that IQ robustly predicts intervention response, prognosis, and school success (Fletcher et al., 2007).

The idea that IQ presents an indicator of aptitude or learning potential is conceptually flawed and commonly referred to as “milk and jug” thinking (Share et al., 1989). Such thinking about IQ was epitomized by Burt (1937), who equated a child’s educational capacity with a score of an IQ test: “Capacity must obviously limit content. It is impossible for a pint jug to hold more than a pint of milk, and it is equally impossible for a child’s educational attainment to rise higher than his educable capacity” (p. 477). IQ has a moderate correlation with achievement, but this does not translate to a conceptual model in which IQ is a robust determinant or cause of achievement. Indeed, there is considerable evidence that the cognitive problems that reduce achievement (e.g., language) also reduce IQ. Children who don’t learn to read show declines in IQ over time. IQ tests measure skills that are taught in school, such as vocabulary and critical reasoning. If IQ tests measured skills like phonological awareness and rapid naming, many children with reading problems would obtain substantially lower scores.

More compelling than the conceptual argument is the empirical demonstration from this meta-analysis. IQ accounts for a small amount of unique variance in predicting intervention response. IQ-discrepancies are weakly related to achievement and cognitive differences relative to simple low achievement (Hoskyn & Swanson, 2000; Stuebing et al., 2002) and to prognosis (Francis et al., 1996; Share et al., 1989), and they also present significant psychometric problems (Francis et al., 2005).