Measurement of unidirectional P_i to ATP flux in human visual cortex at 7 T by using in vivo ³¹P magnetic resonance spectroscopy

Abstract

Taking advantage of the high NMR detection sensitivity and the large chemical shift dispersion offered by ultra-high field strength of 7 T, the effect of magnetization transfer on inorganic phosphate (P_i) resonance during saturation of γ-ATP resonance, mediated by the ATP synthesis reaction, was observed noninvasively in the human primary visual cortex by using in vivo ³¹P magnetic resonance spectroscopy. The unidirectional flux from P_i to ATP was measured by using progressive saturation transfer experiments. The cerebral ATP synthesis rate in the human primary visual cortex measured by ³¹P magnetic resonance spectroscopy in this study was 12.1 ± 2.8 μmol ATP/g per min, which agreed well with the value that was calculated indirectly from the cerebral metabolic rate of glucose consumption reported previously.

Energy requirements in tissues are met predominantly through hydrolysis of the high-energy molecule ATP. In the brain, this molecule is synthesized almost exclusively by mitochondrial oxidative phosphorylation, with only a small contribution coming from nonoxidative glycolysis (1). Despite the critical role of ATP in cellular functions, the kinetics of ATP synthesis and hydrolysis is often difficult to measure directly in intact cells and even more so in intact animals and humans. Cerebral ATP synthesis rate has been calculated indirectly from experimentally measured cerebral metabolic rates of glucose (CMR_glu) and oxygen (CMRO₂) (1, 2), and it has been estimated to be ≈14 μmol ATP/g per min (2) in the resting human brain.

The magnetization transfer (MT) technique based on magnetic resonance spectroscopy (MRS) has the capability of measuring the reaction kinetics of enzymes noninvasively in situ when the reaction rates involved are relatively fast (e.g., for review see refs. 3 and 4). Using this technique to study the kinetics of ATP synthesis in biological tissues with ³¹P MRS was first introduced in the late 1970s in suspensions of Escherichia coli cells (5). Since then, it has been applied to yeast (6), intact perfused hearts (4, 7-11), liver (12), kidney (13), canine myocardium in vivo (14), skeletal muscle (15), and rat brain (16). It was demonstrated that, under appropriate conditions, the MT technique is capable of measuring the net rate of oxidative ATP synthesis catalyzed by mitochondrial ATPase (7-10); because, by definition, this rate is proportional to the oxygen consumption rate by the P/O ratio, those experiments yielded for the first time the P/O ratio in an intact organ under functional conditions.

Because of the relatively low concentration of P_i in normal intact tissues and the low intrinsic detection sensitivity of in vivo ³¹P MRS, virtually all previous experiments using the MT methodology to study P_i-ATP exchange were performed in excised perfused organ models or in small animals, where the radio frequency coil geometry relative to the organ of interest can be optimized to yield significant gains in signal-to-noise ratio compared with what is possible in humans. In addition, all such experiments were performed at very high magnetic fields (>4 T) that provide enhanced sensitivity and spectral resolution; the latter permits the detection of P_i resonance without the confounding effects of overlapping resonances in the in vivo ³¹P spectrum. However, such high magnetic fields have not been available for human studies until recently. In a recent study, the feasibility of performing in vivo ³¹P MRS on human brain with high sensitivity was demonstrated at 7 T (17). In this study, we have extended this effort to demonstrate that the high sensitivity and the large chemical shift dispersion offered by this ultra-high field strength also permit the noninvasive measurement of the unidirectional conversion rate of P_i to ATP in the human primary visual cortex.

Theory

Neglecting multiple-site chemical exchanges (11), the chemical reaction between P_i and ATP can be written as

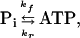[1]

where k_f and k_r are the pseudo first-order rate constants of the ATP synthesis and ATP hydrolysis reactions, respectively. P_i clearly participates in other reactions in the intact cell, and these reactions should in principle be considered when saturation transfer from the γ-ATP resonance is being examined. However, these other reactions can be neglected because they appear to be too slow compared with the spin-lattice relaxation rates of the exchanging compounds (9). Thus, their contribution, if any, will show up as a modification of the T₁ of P_i in the absence of exchange with ATP.

To measure k_f, the longitudinal magnetization of γ-ATP is saturated; one common approach is to saturate the γ-ATP resonance for different durations (i.e., the progressive saturation transfer experiment). Through the chemical reaction shown in Eq. 1, the saturated longitudinal magnetization of γ-ATP is transferred to P_i. If the lifetime of P_i molecule (i.e., 1/k_f) is in the same order of its spin-lattice relaxation time T₁, then, the longitudinal magnetization of P_i, as well as the P_i peak intensity in the MR spectrum changes during the saturation. The apparent rate constant k_f is then calculated from the decrease in P_i signal intensity caused by saturation transfer as a function of the saturation time (t_sat) of γ-ATP. Alternatively, the spin-lattice relaxation of P_i is determined while γ-ATP is continuously saturated, and from this apparent T₁ and the steady-state reduction in the intensity of P_i resonance during the saturation of the γ-ATP peak, the k_f value can be calculated. The constant k_f multiplied by the P_i content then yields the unidirectional rate for P_i + ADP to form ATP.

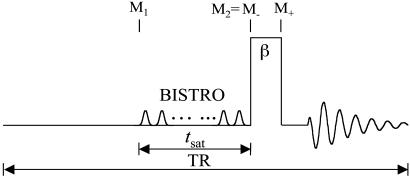
The saturation transfer experiments in this study were conducted by using the pulse sequence shown in Fig. 1. Because the total examination time is often limited for human subjects, a repetition time (TR) of 6.75 s was used, which is not sufficiently long for the ³¹P spins to reach the fully relaxed condition at 7 T (17). Under this circumstance, the recovery of longitudinal magnetization after each excitation pulse toward its thermal equilibrium value is incomplete, and partial saturation results. This effect is different from saturation transfer that originates from chemical exchange and complicates the calculation of k_f, as explained in detail in the following paragraphs.

Fig. 1.

Pulse sequence used for the saturation transfer experiments. Saturation pulse train with a duration of t_sat, constructed according to a B₁ insensitive selective train to obliterate signal (BISTRO) scheme, was used to saturate the γ-ATP resonance completely and was also applied downfield, symmetrically about the P_i resonance to serve as the control. TR was kept the same at 6.75 s regardless of t_sat. A hard excitation pulse (β)of200 μs was used. The symbols used in Eqs. 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 to represent the longitudinal magnetization of P_i (M) at different time points are also defined here.

When the P_i signal is averaged over repeated excitations and the fully relaxed condition is not satisfied, a steady state can be reached after a single or small number of transients depending on the flip angle (β) of the excitation pulse used. The amplitude of the steady-state longitudinal magnetization is determined by TR, β, and the longitudinal relaxation time of P_i. Because of its chemical exchange with γ-ATP, the longitudinal relaxation of P_i in the absence of saturation transfer is described by two exponentials with two different relaxation times, which, in principle, can be measured by conventional inversion-recovery experiments. However, in practice, the two exponentials are often difficult to resolve experimentally and, as a result, it is common that a single-exponential function is used to fit the actual double-exponential relaxation data to obtain an ”apparent” longitudinal relaxation time, which we will refer to as 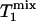. The longitudinal relaxation of P_i in the presence of complete saturation of γ-ATP is represented by a single-exponential function because the effect of chemical exchange has been eliminated through the saturation of γ-ATP; the longitudinal relaxation time under this condition is defined as 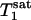and

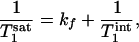[2]

where 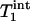is the intrinsic longitudinal relaxation time of P_i in the absence of chemical exchange. In theory, 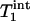> > 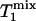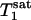because of the effect of chemical exchange and the fact that γ-ATP has a lower intrinsic longitudinal relaxation time than P_i.

By keeping TR the same and varying t_sat in the progressive saturation experiments (Fig. 1), the effect of short TR will also depend on the value of t_sat. Assuming that a steady state is reached and neglecting off-resonance effects, the evolution of the longitudinal magnetization (M) of P_i during the pulse sequence shown in Fig. 1 can be described by the following equations,

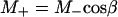[3]

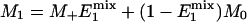[4]

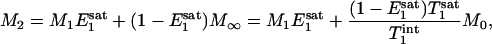[5]

where 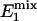= exp[-(TR - t_sat)/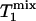] and 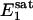= exp(-t_sat/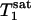); M_- and M₊ are M of P_i before and after the excitation pulse, respectively, and M_- is also the steady-state M of P_i; M₁ and M₂ are M of P_i at the time points right before and after the saturation pulse train, respectively (see Fig. 1); M₀ is the thermal equilibrium M of P_i; M_∞ is the steady-state M of P_i in the presence of complete saturation of γ-ATP; and

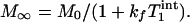[6]

Eqs. 4 and 5 describe the longitudinal relaxation of P_i in the absence and presence of complete saturation of γ-ATP, respectively, and M₂ equals M_- when the spin system reaches the steady state. Combining this relationship with Eqs. 3, 4, 5 and solving for M_-, one obtains

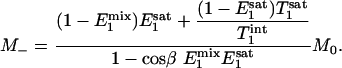[7]

Substituting t_sat = αTR with 0 ≤ α ≤ 1, Eq. 7 can be rewritten as

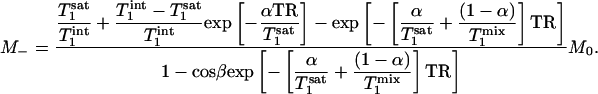[8]

Two special cases ought to be considered. First, when (1 - α)TR >> 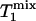, 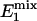approaches zero, and the fully relaxed condition is satisfied. Under this condition, Eq. 7 reduces to

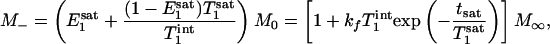[9]

which is the same as the expression that has been derived previously for the fully relaxed progressive saturation experiment (18). Second, in the control experiment in which α = 0, Eq. 8 reduces to the familiar form originally given by Ernst et al. (19)

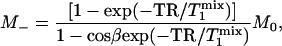[10]

which describes the partial saturation effect of repetitive pulsing when TR used is not long enough for full relaxation.

k_f can be derived by measuring the steady-state signal intensities of P_i in the saturation experiments (M_s) and that in the control experiments (M_c) at different t_sat with the same TR. Given TR, 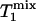and β as constants, the dependence of the ratio M_s/M_c on t_sat (or α) can be fitted to Eq. 11, which represents the result of combining Eqs. 8 and 10, using a least-square algorithm.

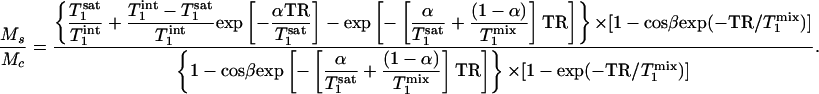[11]

Two parameters, 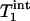and 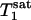, are obtained by fitting, which can then be used to calculate k_f by using the relationship described by Eq. 2.

Materials and Methods

Nine normal subjects (five men and four women, 19-28 years old) were recruited for this study. All procedures were approved by the Institutional Review Board at the University of Minnesota, and all subjects provided well-informed written consent. Studies were performed on a 90-cm bore 7T magnet (Magnex Scientific, Abingdon, U.K.) with a Varian INOVA console. A passively decoupled dual-coil configuration was used, with a linear butterfly proton surface coil for anatomical imaging and shimming, and a 5-cm-diameter single-loop surface coil, designed for covering the human primary visual cortex only, for ³¹P spectroscopy. In all experiments conducted at the phosphorus channel, specific absorption rate (SAR) was controlled by setting the SAR safety switch of the console, which controls the average radio frequency (RF) power allowed to be delivered to the RF coil, at a 1.0- to 1.3-W level (with 1.0 W being the minimal level). Anatomical images were obtained with an inversion-recovery-prepared TurboFLASH imaging sequence (inversion time: 1.6 s, TR/echo time: 8.0/3.6 ms; matrix size: 128 × 128; slice thickness: 3 mm). Localized shimming was performed on a 3 × 3 × 3-cm³ voxel placed in the primary visual cortex area by using a FASTMAP algorithm (20).

³¹P spectra were acquired with the pulse sequence shown in Fig. 1, using a hard excitation pulse of 200 μs length for maximal global signal intensity of phosphocreatine (PCr), a spectral width of 6,000 Hz, 1,500 data points, and 32 or 64 averages. No additional spatial localization was used except that achieved by the surface coil itself. Saturation pulse trains, constructed with multiple hyperbolic Sech pulses (duration of 50 ms; bandwidth of 150 Hz) of varying amplitudes according to a B₁ insensitive selective train to obliterate signal (BISTRO) scheme (21), were used to completely saturate the γ-ATP resonance in a B₁-insensitive fashion. The same saturation pulse train was also applied downfield of the P_i resonance (opposite side from the γ-ATP peak) with a frequency shift equal to the frequency difference between the P_i and γ-ATP resonances; this measurement served as the control for correcting any direct effects of the saturation pulses on the P_i peak itself. TR was kept constant at 6.75 s for all experiments. The P_i signal intensities in the saturation (M_s) and control (M_c) experiments were measured at five different t_sat values (0.62, 1.16, 1.71, 3.35, and 6.62 s), and the dependence of the ratio M_s/M_c on t_sat was used to derive k_f as described in Theory. k_f was calculated with different flip angles assumed for the excitation pulse, and 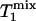was taken as a constant equal to 3.19 s (17).

Postacquisition spectral processing included zero-filling the free induction decays (FIDs) into 32-k data points, left-shifting the FIDs by four data points to remove the broad resonance components from immobile phosphates, and applying a 10-Hz exponential line-broadening. Each spectrum was phased individually and then corrected for dc offset and baseline. Peak height was used for quantification.

Results

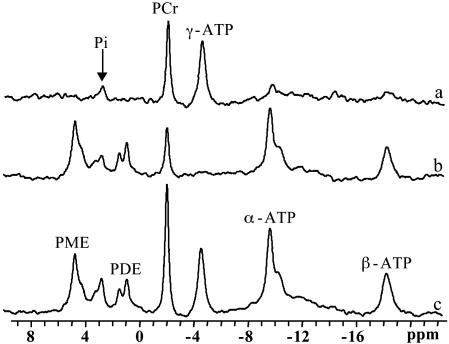
Fig. 2 shows ³¹P spectra acquired from a normal subject with (b) and without (c) complete saturation of the γ-ATP resonance (t_sat = 6.62 s) and the difference spectrum between the two (a). On irradiation of the γ-ATP resonance, the signal intensities of PCr, P_i, α-ATP, and β-ATP resonances all decreased, caused by either MT or direct (off-resonance) saturation. No observable signal intensity changes were found for the phosphodiester and phosphomonoester resonances surrounding and adjacent to the P_i resonance. In this particular subject, the PCr and P_i signal intensities decreased to 35% and 60% of their control levels, respectively.

Fig. 2.

³¹P spectra acquired from a normal subject with (b) and without (c) complete saturation of the γ-ATP resonance (t_sat = 6.62 s), and the difference spectrum between the two (a). PDE, phosphodiesters; PME, phosphomonoesters.

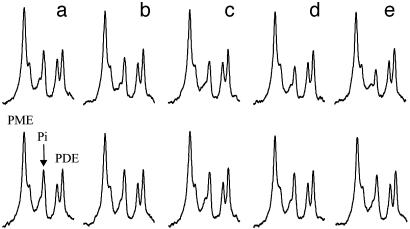
Fig. 3 shows the results of the progressive saturation transfer experiments. The ³¹P spectra were acquired with (Upper) and without (Lower) complete saturation of the γ-ATP peak at different saturation times. The spectra shown in Fig. 3 were averaged from four subjects. The signal intensity of the P_i resonance decreased progressively as t_sat increased from 0.62 to 6.62 s. No statistically significant signal intensity changes were found for the phosphodiester and phosphomonoester resonances between the saturation experiment and the control experiment at all t_sat and among different t_sat.

Fig. 3.

The P_i region of the ³¹P spectra acquired with (Upper) and without (Lower) complete saturation of the γ-ATP resonance at saturation times (t_sat)of 0.62 s (a), 1.17 s (b), 1.71 s (c), 3.35 s (d), and 6.62 s (e) with constant TR of 6.75 s. The spectra shown were averaged spectra over four subjects, and the spectra from each individual subject were averaged with normalized PCr signal intensities.

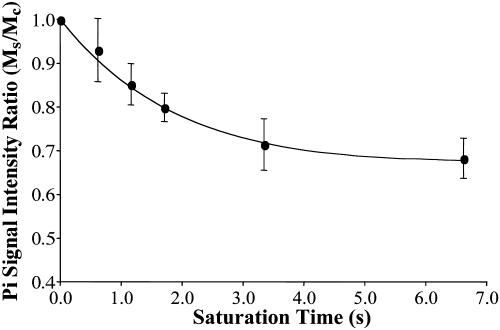
The dependence of the P_i signal intensity in the progressive saturation experiment (presented as averaged signal intensity ratio M_s/M_c over nine subjects) on t_sat is shown in Fig. 4. At t_sat = 6.62 s, the average M_s/M_c was 0.68 ± 0.05. The solid line in Fig. 4 represents a fit of the averaged experimental data (solid circles) to Eq. 11 by using the method described in Theory, and an assumed β of 90°. 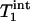and 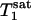obtained by fitting the average progressive saturation curve were 3.52 and 2.2 s, respectively, which gave a k_f value of 0.17 ± 0.04 s^-1. The 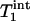value of P_i measured in this study is longer than both 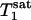and 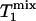, as predicted by theory. 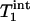and 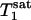of P_i in the rat brain measured at 4.3 T have been reported to be 3.0 s and 1.92 ± 0.11 s, respectively (16).

Fig. 4.

Dependence of the ratio M_s/M_c on t_sat. M_s and M_c are the P_i signal intensities obtained in the saturation experiment and the control experiment, respectively. The solid line represents a least-square fit of the experimental data (•) to Eq. 11 (assuming β = 90°).

Because the surface coil used in this study has an inhomogeneous B₁ field, there was a spatial distribution of flip angles across the sampling volume, which could potentially affect the results of the k_f measurement. The influence of the flip angle used for fitting on the results was therefore evaluated in each individual subject. 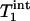, , 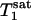and k_f tended to increase as the flip angle used for fitting increased from 45° to 100°, and the maximal variations in 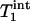, , 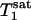and k_f in this flip angle range were 4%, 8%, and 6%, respectively. Single-factor ANOVA analysis revealed that such variations in the flip angle did not result in variations in the calculated k_f that can be distinguished from each other within the accuracy of the experimental data.

Discussion

Cerebral P_i → ATP Rate Measured by MT. The MT technique based on in vivo ³¹P MRS has previously been used to measure ATP synthesis and creatine kinase (CK) reaction rates in intact cells. The latter reaction is significantly easier to measure because of the large intracellular concentration of PCr in tissues such as muscle and brain that contain the CK enzyme. Consequently, ³¹P MT techniques have been used to measure the CK reaction in perfused organs (9, 22, 23), intact animals (14, 16, 24), and even in humans (17, 25, 26). The results presented here demonstrate that, at 7 T, effects of MT from γ-ATP to P_i caused by the ATP synthesis reaction is observable in the human primary visual cortex, and, furthermore, k_f can be measured reliably by using the progressive saturation transfer experiments noninvasively.

Upon saturating the γ-ATP resonance, decreases in signal intensity were observed for the resonances of PCr, P_i, α-ATP, and β-ATP (Fig. 2). The effects on PCr and P_i were the results of MT from the saturated γ-ATP resonance through the CK and the ATP synthesis reactions, respectively. The reduction in β-ATP signal intensity can also be attributed to saturation transfer, but from the β-ADP resonance through the adenylate kinase, the CK, and the ATP synthesis reactions. The β-ADP resonance overlaps with the γ-ATP resonance and thus is saturated simultaneously with γ-ATP. It has been suggested that the decrease in α-ATP peak intensity observed is not a result of saturation transfer, but rather caused by a negative ³¹P nuclear Overhauser enhancement (16) and possibly a small contribution from direct off-resonance saturation effects caused by the close proximity of this resonance to γ-ATP. The latter is expected to be negligible because the bandwidth of the saturation pulse was only 150 Hz.

In a previous study (17), localized full-relaxed ³¹P spectra were acquired by using 3D chemical shift imaging to measure the concentration of P_i in resting human visual cortex, which was derived from the peak area ratio of PCr and P_i (quantified by the AMARES method in the MRUI software package) and a PCr concentration of 5 mM (1). The average value (n = 3) obtained was 1.27 ± 0.38 mM, agreeing well with the reported value of 1.3-1.7 mM in the literature (1, 27). The rate constant k_f measured in the present study was 0.17 ± 0.04 s^-1. Using a P_i concentration of 1.3 mM and a brain tissue density of 1.1 g/ml, this yields a unidirectional flux from P_i to ATP of 12.1 ± 2.8 μmol/g per min. This flux is ≈5-fold smaller than the flux of the CK reaction of 65.5 μmol/g per min, which was calculated by using the concentration ratio of [PCr]/[P_i] = 3.85 and the rate constant of CK reaction = 0.24 s^-1 measured in the human visual cortex (17). The much faster flux of the CK reaction observed in the human brain should play an important role for stabilizing the cerebral ATP concentration during brain function with high-energy demand.

Oxidative ATP Synthesis and P_i → ATP Rate Measured by MT. CMR_glu in the human occipital pole was reported to be 0.42 μmol/g per min (28). Positron emission tomography (PET) studies have yielded CMRO₂/CMR_glu ratios of 4.1 ± 0.4 (28) to 4.9 ± 0.4 in the human cortical region (29). ATP synthesis rate caused by oxidative phosphorylation can then be calculated by multiplying CMR_glu with the P/O₂ and CMRO₂/CMR_glu ratios. Taking P/O₂ ratio as 6, the cerebral ATP synthesis rate predicted from the PET data will be 10.3-12.3 μmol/g per min in the occipital pole of the human brain. This estimated range is in excellent agreement with the cerebral ATP synthesis rate of 12.1 μmol/g per min measured directly in this study. Similarly, the P_i-to-ATP rate measured by the MT technique in the rat brain was found to be in good agreement with the net oxidative ATP synthesis rate calculated from the ratio of CMR_glu/ CMRO₂ (16).

Our results, therefore, suggest that in the brain, the P_i → ATP rate measured by MT reflects net oxidative ATP synthesis. Approximately 90-95% energy production and consumption in the brain is ascribed to neurons and occurs predominantly oxidatively (2, 30, 31). However, glucose uptake and conversion to lactate by glycolysis is thought to occur mainly in the glia (32-34), whereas the neurons (not glia) are responsible for most of the cerebral oxygen consumption (e.g., refs. 2 and 30 and references therein). Therefore, the P_i → ATP rate measured by MT in the brain appears to represent mainly neuronal ATP synthesis.

The MR measured P_i → ATP rate contains some contributions from both gray and white matter in the occipital pole. However, because the interhemispheric and calcarine fissures and the outer cortical surface of each hemisphere converge at the occipital pole, the gray matter volume is large compared with the white matter volume in this region. Thus, the ³¹P signal detected by MR will be more heavily weighted toward gray matter. Similar partial volume effects also exists for the PET data (28, 29) used for calculating the net rate of ATP synthesis for comparison with the present MR measurement. In the PET measurements, the nominal voxel size was ≈3 cm³, and the data were averaged over several voxels over the occipital pole. In this region of the brain, the PET data does not have the ability to accurately distinguish gray matter from the small amount of intertwined white matter. However, PET measurements in this region are often referred to as ”gray” matter values because the confluence of gray matter ribbons of the two fissures and the outer cortical surface does not leave much room for white matter. Separate measurements of white matter by the PET technique can be obtained only from the central regions of the brain where large and contiguous tracts of white matter can be found, for example in the centrum semiovale, where the CMRO₂/CMR_glu ratio of 5.8 ± 0.8 has been reported (29). Therefore, both the MR and PET data in the occipital pole will originate largely from gray matter but with some partial volume effects from white matter.

In addition to geometrical constraints, the MR measurement is weighted toward gray matter by the very nature of the method. The sensitivity of the surface coil probe will be largest along the outer surface of the brain adjacent to the coil and penetrate furthest into the brain approximately along the coil axis, which will be running largely through to the gray matter regions of interhemispheric and calcarine fissures. Furthermore, even when the MR signals originate from two compartments, the MT technique does not simply measure contributions from the two different compartments weighted by their respective volumes. Consider two compartments both containing P_i and ATP but in one compartment the P_i → ATP rate is zero or slow compared with spin-lattice relaxation and, in the other, it is fast enough to be measurable by MT. P_i → ATP rate in the latter compartment will be accurately determined in the MT experiment without getting confounded by the other compartment even though both compartments contribute to the detected P_i resonance. The CMRO₂ value in the white matter is expected to be ≈2-fold smaller (e.g., ref. 29); therefore, the MR measurement will be dominated by (if not exclusively originating from) the gray matter, more so than the PET measurements that would report a simple volume average of the two different rates of white and gray matter. Thus, the net ATP synthesis rate estimated by the PET data could be somewhat underestimated compared with the MT results even when the MT originates from only oxidative ATP synthesis alone.

Glycolytic Contributions to P_i → ATP Rate Measured by Saturation Transfer. The P_i → ATP rate measured experimentally by the saturation transfer technique contains, in principle, contributions from all reactions in the cell that can catalyze this conversion. Most such reactions are not sufficiently fast relative to the intrinsic T₁ of P_i to have a detectable contribution. However, the ATP synthesis reaction catalyzed by the coupled activities of glycolytic enzymes GAPDH and phosphoglycerate kinase (PGK) has been shown to be a major contributor to the P_i → ATP rate measured by saturation transfer in E. coli (35), yeast (36), liver (12), and the myocardium (9). In perfused hearts, it was demonstrated that when glucose is present as a carbon substrate, GAPDH and PGK enzyme couple mediates P_i-ATP exchange with fast unidirectional rates that significantly exceeded the net rate§ of ATP synthesis by the glycolysis pathway and hence these enzymes (9). It was also demonstrated that when glucose is present GAPDH/PGK-mediated exchange dominates the P_i → ATP rate measured by saturation transfer in the myocardium (9) and in E. coli, yeast, and liver (12, 35, 36). Under these circumstances, unequivocal detection of the P_i → ATP conversion caused by oxidative phosphorylation alone was feasible in the myocardium only after complete suppression of the GAPDH/PGK reactions in situ (9). If and only if the GAPDH/PGK effect was eliminated either directly by using exogenous inhibitor iodoacetate or indirectly by eliminating all exogenous and endogenous sources of glucose, the P_i → ATP rate measured in the myocardium by the saturation transfer method was found to be the same as the net rate of oxidative ATP synthesis calculated as the oxygen consumption rate multiplied with the P/O ratio. Contrary to these observations in the myocardium, and analogous observations in yeast, E. coli, and liver, the unidirectional P_i → ATP rate measured by MT in the brain is similar to the net oxidative ATP synthesis rate calculated from CMRO₂ and/or CMR_glu, and, therefore, ascribed to oxidative ATP synthesis, which occurs mainly in the neurons.

This large difference regarding GAPDH/PGK contribution to the unidirectional P_i → ATP rate between the brain and the other cells is unexpected, especially because glucose is the major carbon source for the brain. One possible explanation is that the GAPDH/ PGK couple simply operates far out of equilibrium in the brain, unlike other cell types. An alternative explanation, however, can be provided in the context of the glial/neuronal cellular compartmentation that exists in the brain; namely, the inability to detect GAPDH/PGK contribution to unidirectional P_i → ATP rate would be consistent with this cellular and metabolic compartmentation provided that P_i is low in glia and high in neurons (so that most of the P_i signal detected is of neuronal origin) and the GAPDH/PGK activity is low in neurons even though it is likely to be high in glia.

If the P_i concentration in glia is low compared with neurons, a large saturation transfer effect caused by GAPDH/PGK would not be detectable even if it mediates a fast P_i-ATP exchange. In cells, P_i concentration tends to be high when the ATP consumption rate is high, as would be expected. For example, in the heart, P_i levels increase with elevation of work performed (37) and are very low when contraction of the muscle is inhibited (38). In isolated mitochondrial preparations, P_i was found to stimulate mitochondrial NADH, and membrane potential generation and hence support higher oxygen consumption and ATP production (39). Therefore, because the majority of cerebral ATP consumption occurs because of neuronal signaling, neuronal P_i levels are expected to be higher than glial P_i content. This is supported by data in cell extracts where P_i/ATP and PCr/ATP ratios were reported to be significantly higher in extracts of neurons compared with astrocytes (40). It is thus likely that the P_i detected in the MR spectrum originates mainly from neurons. In this case, the saturation transfer effect on this P_i would represent mainly neuronal ATP synthesis. The metabolism of glucose to form lactate has been postulated to occur predominantly in the glia, and lactate (not glucose) is considered to be the dominant carbon source for the neurons (32-34). Consumption of lactate requires conversion of NAD to NADH and drives down cytoplasmic NAD levels and/or NAD/NADH ratio. Thus, even if neurons have a large amount of GAPDH/PGK enzymes present, low cytosolic NAD levels would lead to low P_i → ATP rate by the GAPDH/PGK because this reaction also requires NAD to NADH conversion.

If P_i is equally abundant in glia and neurons, then one must still conclude that GAPDH/PGK contribution to P_i → ATP conversion is negligible both in neurons and glia, because the ATP synthesis rates calculated from the MT data agree with those estimated from CMR_glu measurements by PET. In this case, still, the MT determined rate would be ascribed mainly to neuronal ATP synthesis. There is the possibility that the P_i level is low in neurons and high in glia and thus the MT measured rate reflects GAPDH/PGK activity only and originating predominantly from glia. In this case, the agreement on the ATP synthesis rates between the MT data and CMR_glu measurements by PET must be totally coincidental. This possibility is unlikely because of arguments given above about the correlation of P_i levels with oxidative ATP synthesis and ATP consumption in intact cells and isolated mitochondria, and the experimental data indicating the presence of higher P_i levels in neurons. In addition, when GAPDH activity was detected in other cell types where saturation transfer experiments were performed, it was several-fold higher than the net oxidative ATP synthesis rate. If indeed the detected MT effect on P_i arose exclusively from GAPDH/PGK contribution, a much higher number than the net oxidative ATP synthesis rate would be expected based on all previous data on other cell types where this measurement was performed.

Potential Sources of Error in MT Measurement. There were potentially three technical pitfalls in this study that have to be considered. First, k_f measurement is known to be susceptible to errors when a surface coil is used because of its inhomogeneous B₁ field that could result in nonuniform spin excitation and incomplete saturation of the γ-ATP resonance (26). This problem is eliminated in our study by the use of a B₁-insensitive pulse train for saturation. In addition, our results showed that k_f calculated was insensitive to the flip angle used for fitting. Second, an intermediate TR of 6.75 s was chosen as a compromise between the considerations of keeping the total acquisition time acceptable to the subjects and of having sufficient signal-to-noise ratio for the measurements. Under this circumstance, partial saturation of the longitudinal magnetization of P_i after repetitive pulsing can result, and this could complicate the calculation of k_f. A theory was therefore derived to solve this problem. Third, no additional spatial localization was used in the measurements except that achieved by the surface coil itself. It has previously been shown that, with the experimental configuration used in this study, most ³¹P signal detected comes from the primary visual cortex, and there is little contamination from extracranial skin and muscle (17). By any account, k_f measured in this study should represent an average value over all brain tissues contained within the sensitive volume of the surface coil.

There are other potential complications for the k_f measurements. It is known that the 2-phosphate of the 2,3-diphosphoglycerate, which resides primarily in the erythrocytes, has a chemical shift similartoP_i (41), and it has been suggested that it could contribute to the signals observed in this region. However, at 7 T, these resonances are expected to be resolved. In addition, this contribution is expected to be negligible in brain studies given the small brain blood volume (i.e., 2-5%) (42). It should also be noted that ATP is not the only form of NTP in the brain, and the γ-phosphate resonance of other forms of NTP (i.e., CTP, UTP, and GTP) overlaps with that of ATP. Therefore, strictly speaking, k_f measured by saturation transfer should describes the unidirectional exchange between P_i and the whole pool of NTP. However, the P_i-NTP exchange rate for nucleotides other than adenosine is thought to be slow because in all cells and tissues studied so far oxidative ATP synthesis and/or GAPDH/PGK-catalyzed P_i-ATP exchange accounted for all of the P_i-ATP exchange measured by MT.

Conclusion

In summary, MT due to the P_i to γ-ATP conversion rate caused by the ATP synthesis reaction is observable in the human primary visual cortex at 7 T, and the unidirectional P_i to ATP flux can be measured reliably and noninvasively by using the progressive saturation transfer approach. This technique could prove useful in studying the central role of the cerebral energy metabolism in the human brain under normal and pathological conditions, as well as brain function. Finally, the measurement time of the ATP synthesis rate using the ³¹P MT approach could be substantially reduced because only two ³¹P spectra (control one and steady-state saturated one) are required if the constant of 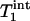or 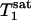measured in this study is applied.