Abstract
The motor symptoms of Parkinson's disease (PD) implicate the basal ganglia (BG) in some aspect of motor control, although the role the BG play in regulation of motor behavior is not completely understood. The modeling study presented here takes advantage of available cellular, systems, and clinical data on BG and PD to begin to build a biophysically based network model of pallidosubthalamic circuits of BG, to integrate this information and better understand the physiology of the normal BG and PD pathophysiology. The model reflects the experimentally supported hypothesis that the BG are involved in facilitation of the desired motor program and inhibition of competing motor programs that interfere with the desired movement. Our model network consists of subthalamic and pallidal (both external and internal segments) neural assemblies, with inputs from cortex and striatum. Functional subsets within each of the BG nuclei correspond to the desired motor program and the unwanted motor programs. A single compartment conductance-based model represents each subset. This network can discriminate between competing signals for motor program initiation, thus facilitating a single motor program. This ability depends on metabotropic γ-aminobutyric acid B projections from the external pallidum to subthalamic nucleus and rebound properties of subthalamic cells, as well as on the structure of projections between pallidum and subthalamus. The loss of this ability leads to hypokinesia, known PD motor deficits characterized by a slowness or inability to switch between motor programs.
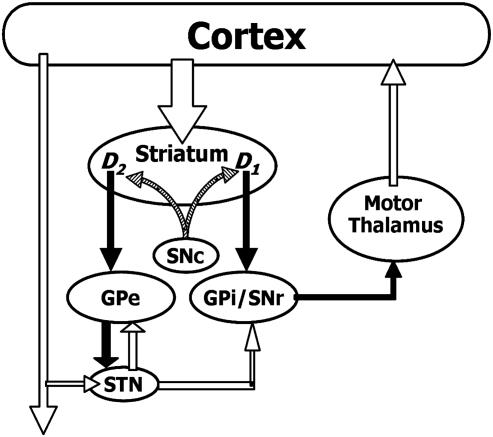
The basal ganglia (BG) play a significant role in motor control. Nevertheless, the physiological mechanisms responsible for this control and the pathophysiology responsible for Parkinson's disease (PD) motor symptoms remain unclear. The structures that make up the BG include the striatum, internal and external segments of the globus pallidus (GPi and GPe, respectively), substantia nigra pars compacta and pars reticulata (SNc and SNr), and subthalamic nucleus (STN). The standard models of BG function, such as that shown in Fig. 1, are based on the hypothesis that the BG consist of two processing streams: the direct and indirect pathways (1, 2). This model was originally formulated (1, 3) to provide a simple framework for understanding the hypo- and hyperkinetic extrapyramidal movement disorders (e.g., PD and Huntington's disease, respectively). However, the model fails to adequately explain control of motor programs, PD motor symptomatology, and the outcome of surgical interventions in BG (reviewed in refs. 4–6). The conceptual framework of the “box-and-arrow” standard model is that of a steady state model based only on anatomical connections and, thus, cannot adequately address either the dynamics associated with different ionic currents present in BG neurons or the spatiotemporal organization of activity within BG nuclei. The need for biophysically based modeling of BG motor control is widely acknowledged (see, e.g., refs. 7 and 8).
Fig. 1.
Standard model of primate BG. Filled arrows correspond to inhibitory connections, open arrows correspond to excitatory connections, and hatched arrows represent the dopaminergic innervation of the striatum. Cortical activation of the direct pathway (striatum–GPi–thalamus) facilitates movement by releasing the motor thalamus from inhibition from GPi and allowing excitation of corresponding cortical motor areas. Activation of the indirect pathway (striatum–GPe–STN–GPi–thalamus) has the opposite effects.
Development of computational models of the BG to date has primarily focused on reinforcement learning in striatum or learning of sequences (e.g., refs. 9–11) and on the development of simplified models (12–14), none of which incorporate dynamics of ionic channels. A recent beginning of biophysically based modeling (15) examined the dynamics of model networks of only GPe and STN neurons and found that the biophysical properties of the neurons in this simple model network can support a wide spectrum of spatiotemporal oscillatory activity patterns. This study is an important step toward understanding BG function, but it was not designed to model the control of motor behavior.
In studies of the relationships between behavior and neural activity in the BG, recordings have revealed many different patterns of activity, differently (and somewhat inconsistently) timed in relation to movement onset (see ref. 16 for review). Based on a series of experimental observations (17–19), Mink (4) suggested that the function of the BG is to control competing motor programs, inhibiting those that interfere with the voluntary movement being executed, and focusing disinhibition on this desired movement. This hypothesis was supported by evidence that movement-related activity in GPi occurs late compared with those of movement-related activity in motor regions of the cortex (16), and that ≈70% of GPi neurons with movement-related activity have an increased firing rate with movement while 30% have a decreased firing rate, consistent with the idea that GPi output inhibits more of its thalamic targets than it disinhibits (20–22).
Modeling of the BG's role in motor control requires a study of how BG networks respond to cortical input to influence thalamocortical circuits responsible for motor control. This article presents the development and analysis of a minimal biophysically based model of BG motor control circuitry. Our model is constructed within an experimentally motivated theory in which the BG are hypothesized to facilitate the motor programs to be executed and to inhibit motor programs that may interfere with the ongoing movement (4, 23–25). In this context, PD results in an inability to correctly inhibit unwanted motor programs and support wanted motor programs, leading to akinesia, bradykinesia, and rigidity. The modeling was developed to elucidate possible mechanisms for both normal motor control and the pathophysiology associated with PD.
Methods: Construction of the Model
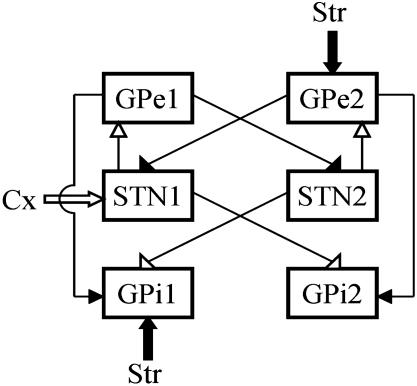
Network Architecture for Motor Control BG Circuits. To begin, we presume that groups of STN, GPe, and GPi neurons are transiently formed by input from cortex and striatum to participate in execution of a particular motor program. Other groups of pallidal and subthalamic neurons, at that moment, act to suppress motor programs that may interfere with the desired motion. This pattern of activation during movement is supported by experimental data recorded from non-human primates (e.g., 20). Subsequently, a new movement would require formation of new subsets of neurons within each nucleus. In our model circuit (Fig. 2), we have two subsets of GPe, STN, and GPi, each of which represents a transiently formed group of neurons. Input from the cortex and striatum determine which subset in their target structures are to be activated or suppressed. Obviously, the simple circuit considered here (Fig. 2) is limited to the control of only two motor programs, the goal being to represent the transient execution of only one motor program at a time (“wanted”) and the suppression of the other (“unwanted”). The connectivity of the circuit is based on the known anatomy of BG (reviewed in refs. 26 and 27). What we have added to this proposed circuit is the way in which pallidal and STN subsets are connected to one another. As will be discussed below, the cross-connections were chosen to provide a mechanism for discriminating between corticostriatal signals for the desired movement and inappropriate corticostriatal inputs.
Fig. 2.
Diagram of motor control model BG network (filled arrowheads correspond to inhibitory connections, and open arrowheads correspond to excitatory connections). The depicted pattern of corticostriatal input corresponds to the execution of motor program 1 (“wanted”) and the inhibition of motor program 2 (“unwanted”). The reversed, complementary structure of corticostriatal input (i.e., input to GPe1, STN2, and GPi2) will reverse wanted and unwanted motor programs: motor program 2 will be promoted, and motor program 1 will be inhibited.
In our minimal model, striatal and cortical inputs are represented as external signals to our model system with assigned timing targeted to specific subsets of the circuit. These input signals are not derived from biophysical modeling of corticostriatal networks. Instead, we use simple forms of spatial and temporal organization of input signals to GP–STN networks (in this study “spatial” is limited to only two subsets within each nucleus). This strategy simplifies the analysis of the model. Further support of this strategy is grounded in the fact that the GPi and STN are the effective sites for surgical procedures to alleviate the motor symptoms of PD. The striatum has been studied extensively (reviewed in refs. 26–30) and will provide the necessary experimental constraints on the timing and structure of corticostriatal input to pallidum and STN for more detailed modeling.
Modeling Pallidal/STN Subsets. The cellular physiology of STN and GPe has been studied extensively (STN in refs. 31–33, and GPe in refs. 34–36). Those studies gave rise to the formulation of conductance-based models of STN and GPe cells (15). We use these models for STN and pallidal subsets in our network. Experimental data available on GPi cell physiology is limited. Therefore, our GPi model has the same form as the GPe model, but its parameters are adjusted in such a way that the network behavior produces tonic GPi activity with a spiking rate similar to that observed in vivo. All these models include standard sodium, potassium, and leak currents and incorporate low threshold T-type Ca2+ current, high-threshold Ca2+ current, and Ca2+-activated voltage-independent afterhyperpolarization K+ current. The equation for membrane potential is
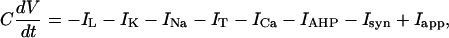 |
where leak current is IL = gL(V - VL), fast potassium and sodium currents are IK = gKn4(V - VK) and 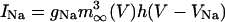 , calcium currents are
, calcium currents are  and
and 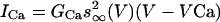 , the afterhyperpolarization current is IAHP = gAHP([Ca]/[Ca] + k1)(V - VK), where [Ca] is concentration of intracellular Ca2+ ions, and the equation of the calcium balance is d[Ca]/dt = ε(-ICa - IT - kCa[Ca]). n, h and r are slow gating variables described by first-order kinetic equations, and m, a and s are instantaneously activated gating variables and depend on voltage (see ref. 15 for details). The model parameters are from ref. 15, with the following differences: φh = 2.0,
, the afterhyperpolarization current is IAHP = gAHP([Ca]/[Ca] + k1)(V - VK), where [Ca] is concentration of intracellular Ca2+ ions, and the equation of the calcium balance is d[Ca]/dt = ε(-ICa - IT - kCa[Ca]). n, h and r are slow gating variables described by first-order kinetic equations, and m, a and s are instantaneously activated gating variables and depend on voltage (see ref. 15 for details). The model parameters are from ref. 15, with the following differences: φh = 2.0, 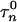 = 0.005,
= 0.005, 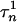 = 0.31, φh = 0.1, and φn = 0.005. The parameters for GPi model are the same as for GPe model with the exception of gT = 0.1, gCa = 0.03, gAHP = 10.0, and φn = 0.05, which makes the firing rate of GPi cells higher, as has been observed experimentally (see below).
= 0.31, φh = 0.1, and φn = 0.005. The parameters for GPi model are the same as for GPe model with the exception of gT = 0.1, gCa = 0.03, gAHP = 10.0, and φn = 0.05, which makes the firing rate of GPi cells higher, as has been observed experimentally (see below).
Modeling Synaptic Connections: Ionotropic and Metabotropic Synapses. All connections present in Fig. 2 represent ionotropic synapses [excitatory glutamatergic and inhibitory GABAergic (GABA, γ-aminobutyric acid)]. These synapses are modeled by first-order kinetic equations describing the fraction of activated receptors as in ref. 15:
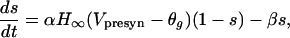 |
where sigmoidal function 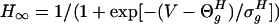 . The synaptic current from a single connection is given by
. The synaptic current from a single connection is given by
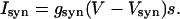 |
The values of parameters for ionotropic synapses are taken from ref. 15.
In our model, we include GPe–STN inhibitory metabotropic GABAB synapses (37, 38). The addition of these slow-acting synapses can inhibit STN for a sufficiently long time to induce a strong rebound after release from inhibition. The model of GABAB synapses consists of two kinetic equations, which include an equation describing the concentration of activated G protein (39):
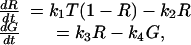 |
where R is the fraction of activated receptors and T = TmaxH∞. The synaptic current is given by
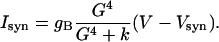 |
The values of parameters for GABAB synapses follow those considered in ref. 40 and are Tmax = 0.5, gB = 6.0, k1 = 0.5, k2 = 0.012, k3 = 0.18, k4 = 0.034, k = 100, and Vsyn= -80.0.
Modeling of Corticostriatal Input to BG Network. The input signal from cortex to STN and from striatum to GPe and GPi is modeled as a train of spikes in the form of f = (t/τ)exp(-t/τ) (for simplicity, when the new spike occurs f is set to zero). The current injected into BG model subsets is Iapp = gΣf, with g = gCx, gStr-e, and gStr-i for current injected to STN, GPe, and GPi, respectively. The parameters of the input currents are gCx = 80.0, gStr-e = 50.0, gStr-i = 50.0, τ = 1 ms, and the spiking rate is 100 spikes per second.
Experimental Constraints on Model Circuit Dynamics. Synaptic strength in the model network cannot be directly estimated from available experimental data. Therefore, to find values appropriate for the present modeling study, synaptic strength was adjusted in a series of simulations in such a way that the patterns of activity of the modeled neurons are physiologically reasonable. A recent paper (40) provides the results of simultaneous recordings from rodent STN and GP in several in vivo conditions. Firing patterns of BG structures in normal and Parkinsonian primates are reviewed in refs. 4 and 25. The values for synaptic strengths are gstn→gpe = 4.0, ggpe→stn = 1.0, gstn→gpi = 15.0, and ggpe→gpi = 0.5. The model network behavior is robust for these parameter values, although the chosen values are not a unique combination of parameters that yield the appropriate spiking rates in the model network.
Results: Behavior of BG Model Circuit in Movement Control
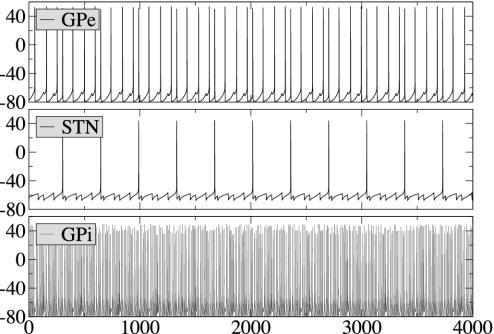
In the absence of any inputs, all subsets of the model network discharge tonically (Fig. 3). Note that GPi has a relatively high firing rate in the baseline regime, when no motor program is being executed (4) (in vivo GPi projects to thalamus and inhibits thalamocortical motor circuits to prevent movement execution).
Fig. 3.
Dynamics of isolated model circuit. Traces of membrane potential for GPe, STN, and GPi subsets are presented (in the absence of input, the dynamics of the network is symmetric: the activity in subsets 1 and 2 is the same). In all of the figures, horizontal axes are time in milliseconds, and vertical axes are membrane potential V in millivolts.
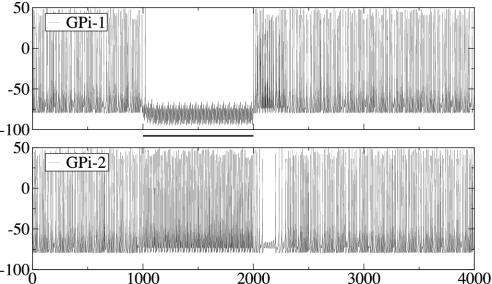
Model Circuit Under Corticostriatal Input: Execution of Single Movements and Switching Between Movements. A command to execute a single movement is modeled as a train of spikes arriving simultaneously in GPe2, STN1, and GPi1 (input 1), leading to the following restructuring of the network's behavior: STN1 firing frequency increases strongly because of the cortical input. In turn, STN firing leads to an increased frequency in GPe1, which inhibits GPi1 and STN2 (so STN2 does not excite GPi1). Striatal input to GPe2 releases STN1 and GPi2 from inhibition, and striatal input to GPi1 helps to suppress GPi1 firing. As a result, the following is observed in the output nucleus of BG network (Fig. 4): GPi1 ceases to fire spikes, and the GPi2 firing rate increases. After input signals vanish, firing rates return to the normal values after a period of transient dynamics (there is a short period of silence in GPi2, probably due to a rebound in GPe2, which inhibits GPi2; at the same time there is a period of increased firing in GPi1). So, during the movement, GPi1 is silent (releasing the corresponding parts of motor thalamus from inhibition, thus facilitating the desired movement) and GPi2 is overactive, thus inhibiting thalamocortical circuits responsible for “unwanted” motor programs.
Fig. 4.
Execution of a single movement. The traces of membrane potential represent the output of GPi subsets of our model circuit in Fig. 2 in response to corticostriatal signals lasting from t = 1–2 sec. In all of the figures, horizontal bars indicate the duration of input to the network (solid, input 1; dashed, input 2).
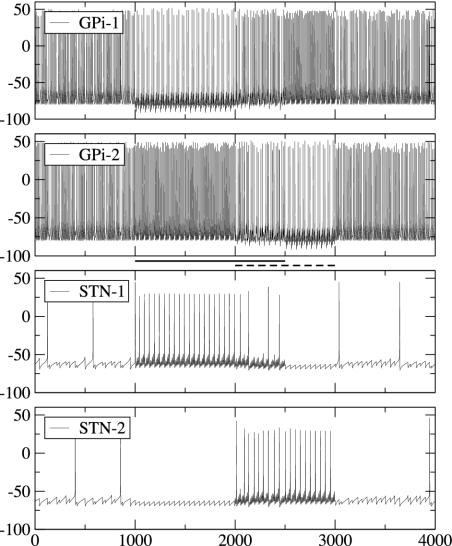
Because our goal was to develop a model relevant both to normal behavior and behavioral deficits in PD, we chose to simulate motor switching (e.g., simple opposing movements such as reaching and withdrawing or pronation/supination of the simple neurological examination), which is critically impaired in PD (41, 42). We simulated the dynamics of the model circuit by switching corticostriatal input from one set of network subsets to the complementary one. So, input 2 will drive GPe1, STN2, and GPi2. In this case (Fig. 5A), GPi1 ceases to fire for the time when input 1 is present and fires with a higher-than-baseline rate when input 2 is active, whereas GPi2 has the opposite behavior. As a result, motor program 1 is facilitated and motor program 2 is inhibited during activation of input 1, and when the input is switched to facilitate motor program 2 and to suppress the previously executed motor program 1, the pattern of GPi activity follows it.
Fig. 5.
Switching between different movements. (A) Corticostriatal input 1 is active from t = 1–2 sec, and input 2 (reversed, complementary signal) is active from t = 2–3 sec. (B and C) Overlapping corticostriatal inputs. Input 1 is active from t = 1–2.5 sec, and input 2 is active from t = 2–3 sec. Dynamics of GPi and STN are shown.
One can see that, even though the switching of the input signal to a complementary one is instantaneous, the switching in GPi output is not. GPi1 spiking appears 100 ms after input 1 vanishes and input 2 becomes active. So the temporal precision of motor program control by our model subthalamopallidal network is limited. In a series of simulations, we examined the effect of varying the duration Δ of input 2 (followed by a reversal back to input 1) on the behavior of the network. If Δ is 200 ms and smaller, then GPi2 continues to produce high-frequency spiking during that time and input 2 is not detected. For larger Δ, the short alternative signal is reflected in the GPi output and, so, the corresponding motor program is facilitated, whereas the competing motor program is inhibited. The value of the limit for temporal precision depends on the characteristics of rebound properties in STN (on the properties of GABAB synapses and IT current).
Model Circuit Under Conflicting Corticostriatal Inputs. We now consider the dynamics of subthalamopallidal networks under conflicting input signals, i.e., when two inputs, which correspond to conflicting motor programs 1 and 2, coexist for a certain amount of time. For numerical simulations of conflicting corticostriatal inputs, we consider input signals overlapped in time: input 2 starts some period before input 1 stops (the characteristics of input currents are the same for both inputs). A typical example is presented in the Fig. 5B. Here, input 1 ends 500 ms after input 2 is introduced. The spiking in GPi2 disappears, so new movement (movement 2) can start when input 2 starts, whereas the ongoing movement 1 should be suppressed because of intense GPi1 spiking. Thus, the output pattern changes to terminate ongoing movement and promote the new movement, even though the input signal for the old movement is still active. This is because high-frequency cortical input to STN2 at t = 2 sec depolarizes STN2, which leads to a strong rebound burst of spikes in STN2 (Fig. 5C). This rebound spiking in STN2 excites GPi1 and excites GPe2 (despite inhibitory input to GPe2, which is still present). This, in turn, helps to inhibit GPi2 and inhibit STN1 (which, otherwise, would excite GPi2), even though STN1 continues to receive cortical excitation. This is how spatial symmetry is broken in the network in response to temporal asymmetry: the network is symmetric (subsets 1 and 2 are identical in each nucleus) and the structure of inputs 1 and 2 is symmetric (have identical characteristics and target complementary subsets), but the timing of inputs is different, and this is reflected in the differences in the dynamics of the GPi subsets.
Slow GABAB Synapses Influence Model Circuit Behavior. The detection of the new signal in two overlapping signals relies on the slow metabotropic GABAB synaptic projection from GPe to STN. This synapse leads to hyperpolarization of STN as long as GPe produces intense spiking. When GPe stops intense spiking, STN is released from inhibition, resulting in a strong rebound burst due to the T-type transient calcium current in STN. Numerical simulations with a network with weak GABAB synapses or without GABAB synapses at all confirm this role of the slow GABAB synapse (Fig. 6). The network without these GABAB synapses is subject to the same overlapping corticostriatal inputs considered above. The dynamics of GPi are not as extreme as in the example in Fig. 5 (silence vs. high-frequency spiking) because the total amount of pallidal inhibition of STN has been changed, but the general pattern of GPi dynamics is easy to see. When there is only one input present at any moment of time, GPi activity facilitates motor program 1 and inhibits motor program 2. However, when the input signals overlap in time, both subsets of the BG output nuclei, GPi1 and GPi2, produce high-frequency spiking (Fig. 6 A and B). Therefore, both thalamocortical circuits, corresponding to two different motor programs, are inhibited and no movement is performed. This can be interpreted as an akinetic condition. In this case, there is no rebound burst, which was provided by GABAB synapses and transient calcium T current, in STN (Fig. 6C). As a consequence, spatial symmetry cannot be broken in response to the break in temporal symmetry, and the network loses the ability to discriminate between inputs.
Fig. 6.
Dynamics of BG model network with weak GABAB synapses (gB = 1) (A and C) and without GABAB synapses (gB = 0) (B). The configuration of the inputs is the same as in Fig. 5 B and C. In the network without GABAB synapses, the strength of synaptic connections was modified to compensate for the absence of GABAB inhibition of STN by GPe.
Nonreciprocal Structure of GPe–STN Connections Is Crucial for Model Circuit Function. The network architecture considered in this work involves nonreciprocal coupling between GPe and STN subsets. This hypothesized organization of the network helps to discriminate between competing corticostriatal inputs to the pallidosubthalamic network. We studied whether reciprocal links between GPe and STN (in addition to the nonreciprocal links in the network in Fig. 2) affect this ability. The addition of the reciprocal links with weak synaptic strengths (5% of nonreciprocal links' strengths) does not affect the performance of the network in response to the conflicting inputs, but the ability to discriminate between conflicting motor programs is gradually lost with the increase of the synaptic strengths of reciprocal links. As a result, the network behavior is similar to the one observed with weak GABAB synapses (Fig. 7): both GPi segments are activated, which leads to the inhibition of thalamus and prevention of the execution of both old and new motor programs, an akinesia-like condition. A plausible explanation for this effect is that reciprocal links provide a negative feedback to STN, when STN is being excited by cortex. Therefore, the STN firing rate becomes low, there is no rebound burst of activity at the time of initiation of the corticostriatal signal 2 (Fig. 7), and the ability to discriminate between corticostriatal inputs is lost. Note that even though in the present situation reciprocal connections do not affect the tonic behavior of model subsets, for other parameter values they can contribute to the occurrence of oscillatory activity in the baseline regime [oscillations in STN–GPe model networks with various types of coupling have been considered (15); the relation of these oscillations to PD tremor remains unclear].
Fig. 7.
Dynamics of BG model with additional reciprocal links between GPe and STN (the synaptic strength of these links is half the strength of nonreciprocal links). GPi and STN membrane potential traces are shown.
Discussion
Facilitation of Desired Motor Program and Inhibition of Competing Motor Programs. According to the present understanding of BG physiology, releasing thalamocortical circuits from pallidal inhibition allows movement execution. In our model network, there are two different subsets in GPi; activation of both subsets corresponds to the absence of movement, whereas deactivation of one or the other corresponds to the execution of one of two different motor programs. In the baseline dynamics of the model circuit (Fig. 3), both subsets of GPi discharge tonically at a high rate so that all thalamocortical circuits are under pallidal inhibition and no movement is possible. Incoming corticostriatal signals act to suppress the activity of one of the GPi subsets (depending on the spatial pattern of this signal, which subsets it targets). As simulations show, the network is able to perform such discrimination and facilitate only one motor program because of the action of slow GABAB synapses, rebound properties of STN neurons, and nonreciprocal architecture of connections between STN and GPe subsets.
Network models of action selection in BG have been suggested (12, 43). In these networks, the most “salient” input is selected by using lateral inhibition, and there is a hard-wired correspondence between specific neurons and specific motor programs. In particular, the study discussed in ref. 43 supposes that malfunction of lateral inhibition in striatum (acting by a winner-take-all mechanism) is directly responsible for failure of proper control of motor programs in PD. In contrast, the present model is not designed to detect the most “salient” action among many in striato-pallido-subthalamic pathways. Rather, it deals with the suppression of motor programs that interfere with the motor program being performed. A group of neurons within the pallidum or STN is dynamically formed in response to corticostriatal activity. The model subset representing this group can consist of different sets of real neurons from one moment to the next.
Hypokinetic Behavior of BG Model Network. PD motor symptoms include hypokinetic behavior: akinesia and bradykinesia. Akinesia-like behavior is exhibited in the model network when both subsets of GPi become active and significantly inhibit thalamocortical circuits, thus preventing facilitation of any motor program. This situation was observed during numerical simulation of the disrupted model network under the influence of competing corticostriatal inputs. If the GABAB GPe to STN projection is weak or absent, then both GPi subsets are active, a signature of hypokinetic behavior. The prediction about the effect of GABAB synapses on network function made in this modeling study calls for confirmation in in vivo or in vitro experiments. A related prediction from the model is that the Parkinsonian symptoms should be accompanied by a deficit in the function of metabotropic GABAergic projections from GPe to STN. Determining whether this happens in the Parkinsonian BG requires studies of changes in BG with Parkinsonian dopaminergic degeneration.
The introduction into the model network of reciprocal connections between BG nuclei subsets, in addition to nonreciprocal connections, also leads to akinetic dynamics. In PD, there is a loss of specificity of neuronal responses to passive movements in GPi (22, 44) and increased correlations between activity in distant neural territories (45). The action of reciprocal connections (which would be inhibited under normal conditions) may be a mechanism that contributes to the loss of specificity. This third prediction from the modeling could be tested by examining the changing structure of connectivity that might accompany the expansion of receptive fields. Further predictions about the role of the observed loss of specificity in hypokinetic behavior may result from modeling studies of larger versions of the network presented here.
Studies of PD patients' performance on specific motor tasks show that although the component movements of a motor sequence are performed more slowly than healthy subjects, the slowing is disproportionately greater if that sequence involves switching between muscle groups (41, 42). The observed change in the behavior of the network that accompanies deficits in switching between different motor programs is reminiscent of this slowness in motor switching. The function of the GABAB receptors and rebound properties of STN cells in vivo is unknown; it is possible that these phenomena in the model provide a mechanism to avoid hypokinetic behavior.
BG Model Networks for Control of Many Motor Programs. Our minimal model describes the control of only two different motor programs. We believe that this network is scalable to the large number of pallidal and STN subsets needed to investigate the mechanisms responsible for focused activation and rapid transition between the individual motor programs that accompany the fluid movements during ongoing behavior. In the larger network, the spatial pattern of connections could be implemented. The network would include “off-center” inhibitory projections from GPe to STN, allowing for inhibition of motor programs interfering with ongoing motion. However, full understanding of BG motor program control will also require more detailed modeling of the spatial and temporal patterns of input into the pallidal/STN networks from the cortex and striatum, which are necessary for the transient formation of the appropriate cell groups within the subthalamopallidal networks.
Acknowledgments
We thank Drs. J. W. Mink and C. J. Wilson for comments on a previous version of the manuscript. This work was supported by National Institutes of Health Grants NS39121 and MH47150.
Abbreviations: BG, basal ganglia; GABA, γ-aminobutyric acid; GPe, globus pallidus pars externa; GPi, globus pallidus pars interna; PD, Parkinson's disease; STN, subthalamic nucleus.
References
- 1.Albin, R. L., Young, A. B. & Penney, J. B. (1989) Trends Neurosci. 12, 366-375. [DOI] [PubMed] [Google Scholar]
- 2.Alexander, G. E., Crutcher, M. D. & DeLong, M. R. (1990) Prog. Brain Res. 85, 119-146. [PubMed] [Google Scholar]
- 3.DeLong, M. R. (1900) Trends Neurosci. 13, 281-285. [DOI] [PubMed] [Google Scholar]
- 4.Mink, J. W. (1996) Prog. Neurobiol. 50, 381-425. [DOI] [PubMed] [Google Scholar]
- 5.Wichmann, T. & DeLong, M. R. (1996) Curr. Opin. Neurobiol. 6, 751-758. [DOI] [PubMed] [Google Scholar]
- 6.Levy, R., Hazrati, L. N., Herrero, M. T., Vila, M., Hassani, O. K., Mouroux, M., Ruberg, M., Asensi, H., Agid, Y., Feger, J., et al. (1997) Neuroscience 76, 335-343. [DOI] [PubMed] [Google Scholar]
- 7.Bar-Gad, I. & Bergman, H. (2001) Curr. Opin. Neurobiol. 11, 689-695. [DOI] [PubMed] [Google Scholar]
- 8.Bergman, H. & Deuschl, G. (2002) Movement Disorders 17, Suppl., S28-S40. [DOI] [PubMed] [Google Scholar]
- 9.Houk, J., Adams, J. & Barto, A. (1995) in Models of Information Processing in the Basal Ganglia, eds. Houk, J. C., Davis, J. L. & Beiser, D. G. (MIT Press, Cambridge, MA), pp. 249-270.
- 10.Schultz, W., Dayan, P. & Montague, P. R. (1997) Science 275, 1593-1599. [DOI] [PubMed] [Google Scholar]
- 11.Berns, G. S. & Sejnowski, T. J. (1998) J. Cognit. Neurosci. 10, 108-121. [DOI] [PubMed] [Google Scholar]
- 12.Gurney, K., Prescott, T. J. & Redgrave, P. (2001) Biol. Cybern. 84, 411-423. [DOI] [PubMed] [Google Scholar]
- 13.Gillies, A. J. & Willshaw, D. J. (1998) Proc. R. Soc. London Ser. B 265, 2101-2109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Humphries, M. D. & Gurney, K. N. (2001) Neural Netw. 14, 845-863. [DOI] [PubMed] [Google Scholar]
- 15.Terman, D., Rubin, J. E., Yew, A. C. & Wilson, C. J. (2002) J. Neurosci. 22, 2963-2976. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Kimura, M. & Matsumoto, N. (1997) Adv. Neurol. 74, 111-118. [PubMed] [Google Scholar]
- 17.Georgopoulos, A. P., DeLong, M. R. & Crutcher, M. D. (1983) J. Neurosci. 3, 1586-1598. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Anderson, M. E. & Horak, F. B. (1985) J. Neurophysiol. 54, 433-448. [DOI] [PubMed] [Google Scholar]
- 19.Mink, J. W. & Thach, W. T. (1991) J. Neurophysiol. 65, 330-351. [DOI] [PubMed] [Google Scholar]
- 20.Turner, R. S. & Anderson, M. E. (1997) J. Neurophysiol. 77, 1051-1074. [DOI] [PubMed] [Google Scholar]
- 21.Wenger, K. K., Musch, K. L. & Mink, J. W. (1999) J. Neurophysiol. 82, 2049-2060. [DOI] [PubMed] [Google Scholar]
- 22.Boraud, T., Bezard, E., Bioulac, B. & Gross, C. E. (2000) J. Neurophysiol. 83, 1760-1763. [DOI] [PubMed] [Google Scholar]
- 23.Mink, J. W. & Thach, W. T. (1993) Curr. Opin. Neurobiol. 3, 950-957. [DOI] [PubMed] [Google Scholar]
- 24.Hikosaka, O., Takikawa, Y. & Kawagoe, R. (2000) Physiol. Rev. 80, 953-978. [DOI] [PubMed] [Google Scholar]
- 25.Boraud, T., Bezard, E., Bioulac, B. & Gross, C. E. (2002) Prog. Neurobiol. 66, 265-283. [DOI] [PubMed] [Google Scholar]
- 26.Wilson, C. J. (1998) in Synaptic Organization of the Brain, ed. Shepherd, G. M. (Oxford Univ. Press, New York), pp. 329-375.
- 27.Bolam, J. P., Hanley, J. J., Booth, P. A. & Bevan, M. D. (2000) J. Anat. 196, 527-542. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Gerfen, C. R. (1992) Annu. Rev. Neurosci. 15, 285-320. [DOI] [PubMed] [Google Scholar]
- 29.Flaherty, A. W. & Graybiel, A. M. (1994) in Movement Disorders 3, eds. Marsden, C. D. & Fahn, S. (Buterworth-Heinemann, Oxford), pp. 3-27.
- 30.Miller, R. & Wickens, J. R., eds. (2000) Brain Dynamics and Striatal Complex (Harwood Academic, Amsterdam).
- 31.Bevan, M. D. & Wilson, C. J. (1999) J. Neurosci. 19, 7617-7628. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Bevan, M. D., Wilson, C. J., Bolam, J. P. & Magill, P. J. (2000) J. Neurophysiol. 83, 3169-3172. [DOI] [PubMed] [Google Scholar]
- 33.Beurrier, C., Bioulac, B. & Hammond, C. (2000) J. Neurophysiol. 83, 1951-1957. [DOI] [PubMed] [Google Scholar]
- 34.Kita, H. & Kitai, S. T. (1991) Brain Res. 564, 296-305. [DOI] [PubMed] [Google Scholar]
- 35.Nambu, A. & Llinas, R. (1994) J. Neurophysiol. 72, 1127-1139. [DOI] [PubMed] [Google Scholar]
- 36.Cooper, A. J. & Stanford, I. M. (2000) J. Physiol. 527, 291-304. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Charara, A., Heilman, T. C., Levey, I. A. & Smith, Y. (2000) Neuroscience 95, 127-140. [DOI] [PubMed] [Google Scholar]
- 38.Smith, Y., Charara, A., Paquet, M., Kieval, J. Z., Pare, J. F., Hanson, J. E., Hubert, G. W., Kuwajima, M. & Levey A. I. (2002) J. Chem. Neuroanat. 22, 13-42. [DOI] [PubMed] [Google Scholar]
- 39.Destexhe, A., Mainen, Z. F. & Sejnowski, T. J. (1998) in Methods in Neuronal Modeling: From Ions to Channels, eds. Koch, C. & Segev, I. (MIT Press, Cambridge, MA), pp. 1-25.
- 40.Magill, P. J., Bolam, J. P. & Bevan, M. D. (2001) Neuroscience 106, 313-330. [DOI] [PubMed] [Google Scholar]
- 41.Benecke, R., Rothwell, J., Dick, J., Day, B. & Marsden, C. (1987) Brain 110, 361-379. [DOI] [PubMed] [Google Scholar]
- 42.Weiss, P., Stelmach, G. E. & Hefter, H. (1997) Brain 120, 91-102. [DOI] [PubMed] [Google Scholar]
- 43.Wickens, J. (1993) A Theory of the Striatum (Pergamon, Oxford).
- 44.Filion, M., Tremblay, L. & Bedard, P. J. (1988) Brain Res. 444, 165-176. [DOI] [PubMed] [Google Scholar]
- 45.Bergman, H., Feingold, A., Nini, A., Raz, A., Slovin, H., Abeles, M. & Vaadia, E. (1998) Trends Neurosci. 21, 32-38. [DOI] [PubMed] [Google Scholar]