Abstract
We have established a population average surface-based atlas of human cerebral cortex at term gestation and used it to compare infant and adult cortical shape characteristics. Accurate cortical surface reconstructions for each hemisphere of 12 healthy term gestation infants were generated from structural magnetic resonance imaging data using a novel segmentation algorithm. Each surface was inflated, flattened, mapped to a standard spherical configuration, and registered to a target atlas sphere that reflected shape characteristics of all 24 contributing hemispheres using landmark constrained surface registration. Population average maps of sulcal depth, depth variability, three-dimensional positional variability, and hemispheric depth asymmetry were generated and compared with previously established maps of adult cortex. We found that cortical structure in term infants is similar to the adult in many respects, including the pattern of individual variability and the presence of statistically significant structural asymmetries in lateral temporal cortex, including the planum temporale and superior temporal sulcus. These results indicate that several features of cortical shape are minimally influenced by the postnatal environment.
Introduction
The adult human cerebral cortex is highly convoluted, variable in shape across regions and across individuals, and asymmetric in both structure and function (Sperry, 1984; Ono et al., 1990; Gazzaniga, 2005; Van Essen, 2005). The formation of cortical convolutions is an important aspect of normal cerebral development (Welker, 1990). This is highlighted by the association of subtle folding abnormalities with a range of cognitive disorders, including schizophrenia (Wisco et al., 2007; Csernansky et al., 2008), bipolar disorder (Fornito et al., 2007), attention deficit hyperactivity disorder (Wolosin et al., 2009), Williams syndrome (Van Essen et al., 2006), and autism (Nordahl et al., 2007).
Cortical convolutions emerge in late gestation, with extensive folding occurring during the third trimester (Abe et al., 2003; Dubois et al., 2008a). At term birth, although the brain is only one-third of adult volume (Thompson et al., 2007; Lebel et al., 2008), the major sulci and gyri present in the adult are already established (Chi et al., 1977). Given the extensive cortical folding within the infant brain, it is of interest to determine whether the features of regional variability and/or asymmetry that characterize the adult cortex are already present at term. Understanding the relationship between cortical folding in infants and adults is important for establishing a baseline for normal cortical maturation and is clinically relevant to understanding what characteristics of cortical maturation may be selectively vulnerable to injury at different prenatal and postnatal ages.
Structural asymmetries are well documented in adults and children (Toga and Thompson, 2003), and several sulci appear earlier in the right hemisphere during gestation (Dubois et al., 2008a). Whether asymmetries are present at term remains unclear. Such information would aid in understanding the origins and developmental trajectory of hemispheric asymmetries, which may reflect asymmetries in gene expression during development (Sun et al., 2005) and/or postnatal environmental influences (Keenan et al., 2001).
In the present study, we generated the first surface-based atlas of human cortical structure at term gestation from a population of 12 healthy term-born human infants and used it to compare the term cortex with an existing atlas of adult human cortex (Van Essen, 2005). The term infant atlas was generated using the Population-Average, Landmark-and-Surface (PALS) approach to atlas construction (Van Essen, 2005) and is denoted the PALS-term12 atlas. A population-average atlas is desirable to capture the variety of cortical patterns and to ensure that any one individual does not bias subsequent analyses (Toga et al., 2006). Before the term infant atlas could be constructed, it was necessary to develop a novel semiautomated segmentation method. This is because currently available segmentation algorithms designed for adult brain magnetic resonance (MR) images fail on newborn MR images as a result of differences in shape, cortical thickness, and tissue contrast.
Using the PALS-term12 atlas dataset, we characterized several features of cortical folding at term, including the pattern of individual variability and the presence of structural asymmetries. This atlas dataset is freely available via the SumsDB database for visualization and cross-study comparisons.
Materials and Methods
Infant recruitment
Twelve term-born infants (six male, six female; mean gestational age, 39 weeks) from uncomplicated pregnancies were recruited from St. Louis Children's Hospital. Institutional review boards approved all procedures, and parents or legal guardians provided informed written consent for the study. All mothers resided in the greater St. Louis area, were at least 15 years old, and had no history of major medical or psychiatric illness, maternal medication treatment, or maternal substance abuse history during the pregnancy. Inclusion criteria for the infants included gestation >36 weeks, prenatal care (>5 visits), 5 min Apgar score >8, no admission to a neonatal or special care nursing unit, and no known risk for neurological abnormality (no cerebral abnormality on antenatal ultrasound, no concerns for any chromosomal abnormality or congenital or acquired infection, and no neonatal encephalopathy).
Magnetic resonance imaging scanning
Enrolled infants were transported and imaged within the first week of life by certified staff members. An infant-sized papoose bag (Contour Fabrications; CFI Medical Solutions) was used to support the infant. Sedation was not used. Images were collected using a turbo spin echo T2-weighted sequence (repetition time, 8500 ms; echo time, 160 ms; voxel size, 1 mm3; echo train length, 17) on a Siemens 3 T Trio located in St. Louis Children's Hospital. Images were automatically transferred to a clinical DICOM receiver and read by a certified pediatric neuroradiologist and neonatalogist (study investigator T.I.) at St. Louis Children's Hospital. Any image set with significant movement artifact or imaging abnormality was excluded from the analysis.
Preprocessing
DICOM files were converted into Analyze format image files using in-house software. Each brain was aligned to the anterior commissure–posterior commissure (AC–PC) orientation and origin by rigid body translation and rotation using Caret software (http://brainvis.wustl.edu) (Van Essen et al., 2001a). Brain dimensions were not scaled before segmentation because intersubject and regional intrasubject size variabilities are of interest. Each brain was cropped along the midline for separate processing of left and right hemispheres.
Segmentation
Segmentation was carried using a LIGASE method that included three main stages: (1) seed-growing, (2) neighbor refinement, and (3) dilation and manual patching (see below).
Stages 1 and 2, performed in MATLAB (MathWorks), relied on assigning each voxel initial “likelihood” values for three tissue types: white matter, gray matter, and CSF. Likelihood values were based on user estimates for the peak and width of the partially overlapping gray matter, white matter, and CSF profiles from a histogram of image voxel intensities. The likelihood value for each tissue type T was calculated according to Equation 1:
where L is the likelihood value, v is the voxel intensity, μ is the estimated profile peak for T, w is the estimated intensity at 10% of the peak for T on either the low (if v < μ) or high (if v ≥ μ) intensity side, and C = −2.2 was an empirically determined constant that gave reasonable results.
Seed-growing.
Starting from a user-specified seed voxel placed deep within white matter, an initial segmentation volume was generated by iteratively adding adjoining voxels estimated to be in the white matter and halting at the estimated gray–white boundary. Two “boundary” values were calculated for each tested voxel: a pairwise difference (intensity difference between the tested voxel and the previous voxel segmented) and a gradient value (magnitude of a vector whose components are the difference in intensity between adjacent face neighbors of the tested voxel along each axis). Tested voxels were included in the segmentation if they had high white matter likelihood and low boundary values. The user typically generated a small number of independent initial segmentation volumes by inputting two to four estimates for the width of the white matter profile and chose the most accurate segmentation by visual inspection.
Neighbor refinement.
The initial segmentation was refined by recursively adjusting the white matter likelihood value of each voxel based on the likelihood values of its 26 adjacent neighbors. In general, the white matter likelihood of a voxel was increased for each adjacent voxel having high white matter likelihood and decreased for each adjacent voxels having high gray matter or CSF likelihood. Voxels with final white matter likelihood exceeding a predetermined threshold were included in the segmentation.
Dilation and manual patching.
The segmentation volume was loaded into Caret and dilated by one voxel (1 mm) to achieve a boundary that approximated the cortical midthickness (cortical layer 4). Term infant cortex is ∼1–2 mm thick in most regions (Bayer and Altman, 2003); at a resolution of 1 × 1 × 1 mm, the term infant cortex typically included one clear gray matter voxel bounded by one voxel overlapping with white matter voxel and one voxel overlapping with CSF. The dilation placed the boundary of the segmentation at the outer edge of the clear gray matter voxel. Aiming for the cortical midthickness has the advantage that each square millimeter of surface area represents approximately the same cortical volume regardless of gyral or sulcal location (Van Essen, 2005).
In general, each hemisphere contained segmentation errors that required manual editing in Caret. This was especially common in medial temporal regions in which the transition to hippocampal cortex and amygdala is often difficult to determine with the automated algorithm. The fundus of the parahippocampal sulcus and the anterior extent of the hippocampus were delineated with the aid of a photographic atlas of human infant neuroanatomy (Bayer and Altman, 2003). A single trained individual with expertise in term infant neuroanatomy performed all segmentation and editing, thereby avoiding issues of inter-rater variability. Figure 1 illustrates the fidelity of this algorithm in capturing the shape of the cerebral cortex in two term-born individuals. Based on our experience, other existing semiautomated segmentation methods (Weisenfeld et al., 2006; Xue et al., 2007; Weisenfeld and Warfield, 2009) require a similar amount of manual editing to achieve the same accuracy on term infant volumes. (For additional details, see http://brainvis.wustl.edu/wiki/index.php/Caret:Download for the freely available LIGASE software and supplemental data, available at www.jneurosci.org as supplemental material.)
Figure 1.
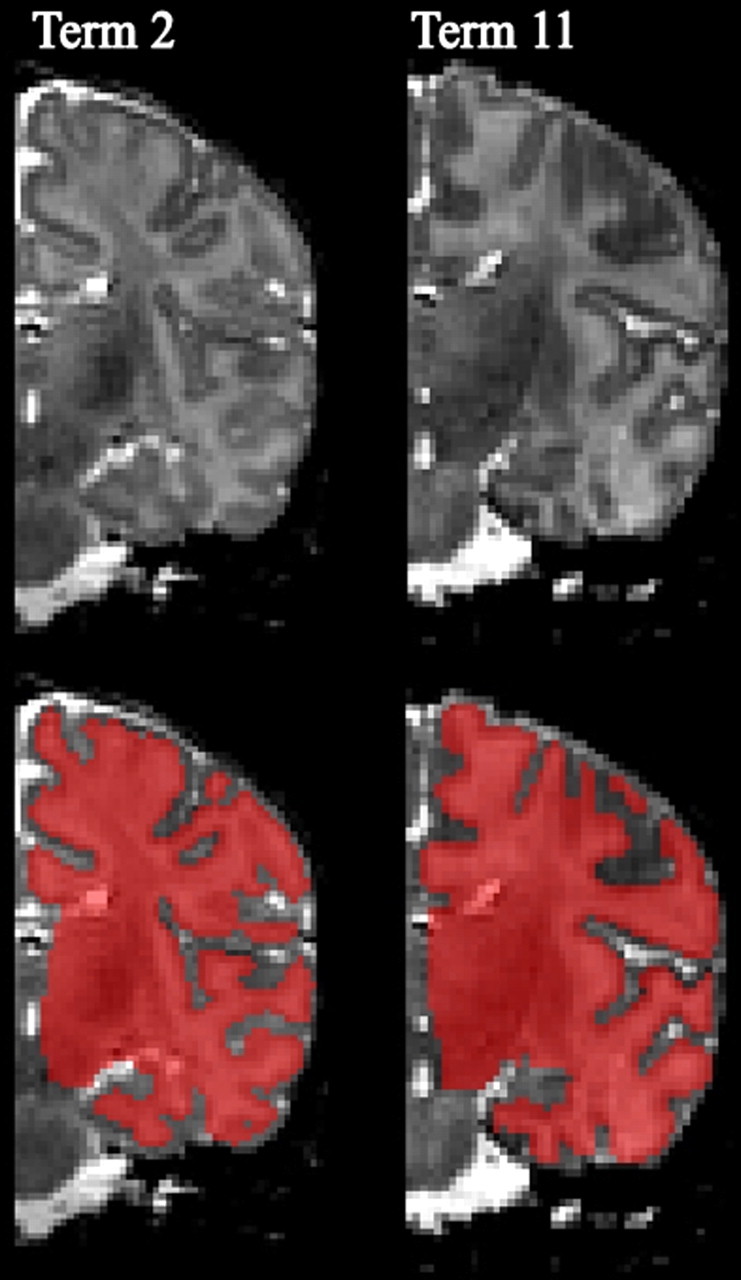
Example term infant segmentation volumes. The top row displays cropped T2-weighted MRI volumes for the right hemisphere viewed in the coronal plane for two term infants. The bottom row shows the final segmentation result created using the LIGASE method overlaid in red on the anatomic MRI. Note that the medial wall region (from the fundus of the parahippocampal sulcus inferiorly to callosal sulcus superiorly) was manually delineated and smoothed.
Surface reconstructions.
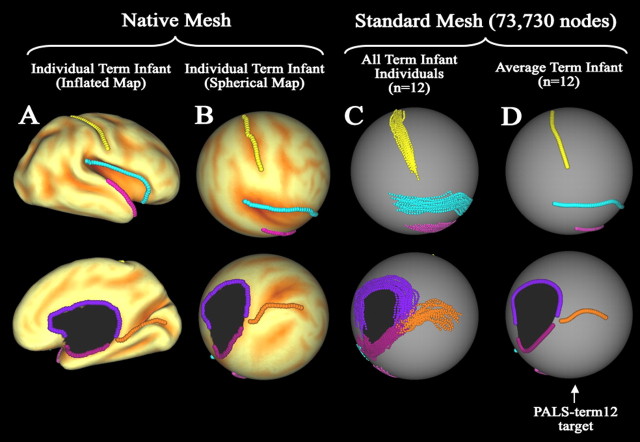
A “raw” surface was generated by a tessellation running along the boundary of the segmentation volume. The tessellation process gives each individual surface a distinct number of surface nodes, which we call the “native-mesh” representation for that individual. The raw surface was smoothed slightly to generate a “fiducial” surface that best represents the three-dimensional (3D) shape of the cortical midthickness (Fig. 2C). A closed contour along the boundary of the cortex with the corpus callosum, basal forebrain, and the fundus of the parahippocampal fissure was manually delineated in Caret. Surface nodes enclosed by this contour were designated as the noncortical “medial wall” and smoothed extensively so that its surface area was independent of irregularities in the original segmentation (see Fig. 4, bottom panel, left half). An inflated configuration was generated by applying 300 iterations of inflation to the fiducial surface (see Figs. 2E,F). A flat map, which assisted in landmark tracing, and a spherical surface used for registration (Fig. 3B) were also generated for each surface (Van Essen, 2005). The spherical surface was scaled so that its surface area was equal to that of the fiducial surface after medial wall smoothing. Multi-resolution morphing algorithms were used to reduce areal and angular distortions on spherical and flat maps (Drury et al., 1996). Spherical and flat maps were aligned to a standard orientation using the ventral tip of the central sulcus and the orientation of the central sulcus to define an axis (Van Essen, 2005).
Figure 2.
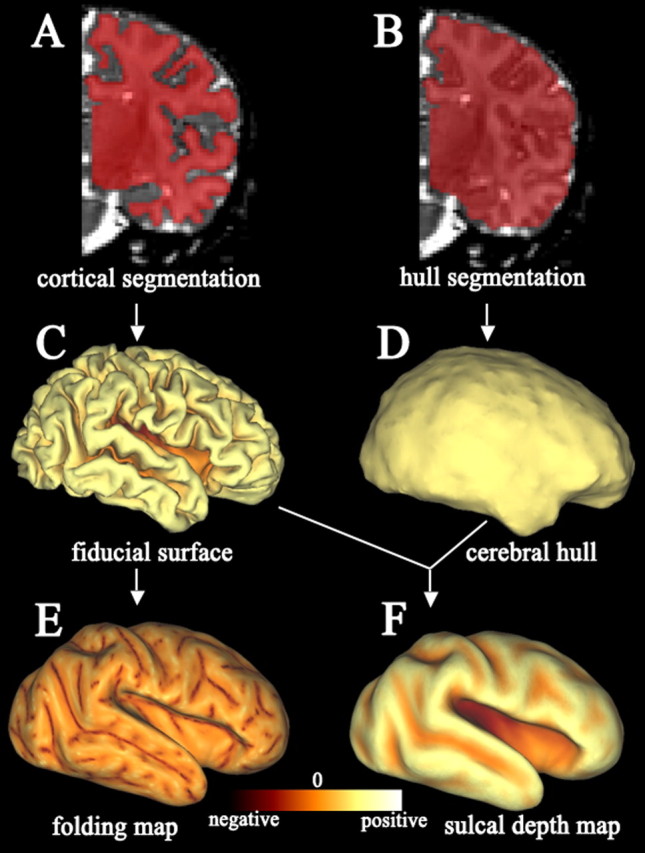
Key steps in term infant surface generation and regional shape analysis. A, Example right hemisphere cortical segmentation volume (red) overlaid on anatomic T2-weighted MRI volume. B, Cerebral hull segmentation volume used for calculating sulcal depth. C, Lateral view of a fiducial surface reconstruction generated by a tessellation running along the boundary of the cortical segmentation volume and slight smoothing. D, Lateral view of the cerebral hull surface generated by a tessellation that runs along the boundary of the cerebral hull segmentation volume. E, Lateral view of an inflated surface displaying a map of cortical folding. The inflated surface was generated by applying 300 iterations of inflation to the fiducial surface. F, Lateral view of an inflated surface displaying a map of sulcal depth.
Figure 4.
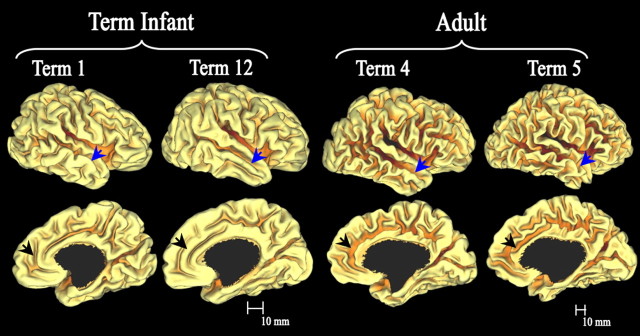
Standard-mesh fiducial surfaces for two term infants (left) and two adults (right), lateral views (top row) and the medial views (bottom row). Note the different scale bars. The particular individuals displayed have native-mesh surface areas closest to the age-specific population mean. Regions that hint at age differences in folding complexity include the anterior temporal region (blue arrow) and anterior cingulate region (black arrow).
Figure 3.
Registration landmarks and creation of PALS-term12 registration target. Individual, population, and population-average landmarks are shown on several surfaces. Lateral views are displayed in the top row and medial views in the bottom row. A, Native-mesh inflated surface configuration for one term infant overlaid with a map of sulcal depth. The six landmarks (Core 6) used for registration are displayed on the surface. On the lateral surface, these consisted of the fundus of the central sulcus (yellow), Sylvian fissure (blue), and anterior half of the superior temporal gyrus (pink). Medial landmarks are the calcarine sulcus (orange) and the cortical margin of the medial wall divided into dorsal (purple) and ventral (magenta) portions. B, Core 6 landmarks displayed on the native-mesh spherical surface map for the same individual overlaid with a map of sulcal depth. C, Core 6 landmarks from both hemispheres (right and mirror-flipped left) of all 12 term infants projected to the standard-mesh (73,730 node) PALS-term12 spherical map. D, Average trajectory of each landmark for the 12 term infants displayed on the standard-mesh sphere. These average landmarks served as the target for surface-based registration.
Local measures of cortical shape
Sulcal depth and cortical folding maps were generated for each surface by calculating these measures at each surface node (Van Essen, 2005) (Fig. 2E,F). Cortical folding (Fig. 2E) was computed as the mean of the two principal curvatures associated with each surface node (Van Essen and Drury, 1997). To calculate sulcal depth, a cerebral hull segmentation volume running along the margins of gyri without dipping into sulci was generated by applying to the midcortical segmentation six iterations of dilation, followed by six iterations of erosion (Van Essen, 2005) (Fig. 2B). A cerebral hull surface was generated by tessellating this cerebral hull segmentation volume (Fig. 2D). An affine transformation that normalized for overall brain dimensions in each population (see below) was applied to both the fiducial and cerebral hull surfaces. Sulcal depth (Fig. 2F) was defined as the distance from each node on the normalized fiducial surface to the nearest point in the normalized cerebral hull surface. The affine transformation had a small (<3%) effect on the estimation of sulcal depth at each node.
Atlas construction
Generation of the PALS-term12 atlas involved three main stages: (1) delineating landmarks on each individual hemisphere; (2) generating population-average landmarks to serve as the target for registration; and (3) registering each individual to the “standard-mesh” (73,730 node) atlas sphere and generating standard-mesh representations of each individual fiducial surface.
Delineating registration landmarks.
Six landmarks (“Core 6”) shown previously to be highly consistent in location and extent in adults (Van Essen, 2005) were confirmed by visual inspection to be comparably consistent in term infants. The left of Figure 3 illustrates these six landmarks on the inflated and spherical configurations of an individual term infant (native-mesh). Each landmark was delineated using criteria similar to those in adults (http://brainvis.wustl.edu/help/landmarks_core6/landmarks_core6.html). Most adult Core 6 landmarks terminate a specified distance relative to a nearby geographical feature. To accurately measure corresponding termination distances on the smaller term infant surfaces, these distances were scaled such that the distance relative to the total surface dimensions was the same as for the adults.
Population-average set of landmarks (atlas).
The population-average landmarks that served as the target for registration were generated in two stages. A target spherical surface was created using a standard-mesh 73,730 node sphere (Fig. 3C,D) whose surface area was scaled to the average surface area of all 12 term infant right hemisphere native-mesh spherical surface maps. Corresponding landmarks from each individual's native-mesh spherical surface were averaged together (after mirror-reflecting the left hemisphere landmarks) and projected to the standard-mesh target sphere. Figure 3C shows lateral (top) and medial (bottom) views of landmarks from right and mirror-flipped left hemispheres for all 12 term infants projected to the standard-mesh spherical surface. Individual variability in these landmarks is modest, and the choice of individuals should have only a small effect on the average contour of each landmark. Figure 3D shows average landmarks from all 12 term infant subjects that served as the PALS-term12 target for registration.
Registering individuals to the PALS-term12 atlas.
Each hemisphere was registered to the target atlas by the same spherical registration algorithm used for the PALS-B12 adult atlas (Van Essen, 2005). Briefly, the algorithm uses multiple cycles of landmark-constrained smoothing, coupled with shape-preserving morphing iterations that reduce local linear and angular distortions (Van Essen et al., 2001b; Van Essen, 2004). After registration, each individual hemisphere was resampled to the standard-mesh tessellation, thereby establishing node-to-node correspondences among all individuals. Resampling of term infant surfaces from native to standard mesh led to some spatial smoothing and a reduction of ∼5% in surface area.
Scale normalization
The adult anatomical magnetic resonance imaging (MRI) volumes for the PALS-B12 atlas had been registered to the 711–2C template of Washington University by affine transformation before segmentation (Buckner et al., 2004; Van Essen, 2005). Because estimates of native cortical surface area in the term infant population were of interest, the initial segmentation was performed on MRI volumes that were aligned to the AC–PC axis without volume-based scale normalization. Conversely, for many of the subsequent analyses, including comparison with adults, it was desirable to remove the effects of variability in overall brain dimensions. Accordingly, an affine transformation of each surface was computed by minimizing the mean square error between the transformed individual surface and an age-specific population average surface (Yu et al., 2007). This procedure entailed two stages of scale normalization. A first-pass average fiducial surface was generated separately for each hemisphere by taking the average 3D spatial coordinate of each standard-mesh surface node across all 12 term infants. An affine transform was computed between each individual and this initial population average and then applied to create first-pass normalized fiducial surfaces. The first-pass normalized fiducial surfaces were then averaged to create a second-pass average fiducial surface. A new affine transform, computed between original individual fiducial surfaces and the second-pass average fiducial surface, was used to generate second-pass individual fiducial surfaces. The same process was performed on all adult fiducial surfaces in the PALS-B12 atlas to obtain a set of surfaces as comparable as possible for between-group analyses. The second-pass affine transformed surfaces were used for all analyses, except when noted otherwise. As noted above, sulcal depth was computed after affine transformation.
Age-specific average surfaces and metrics
Age-specific surfaces and metrics were generated separately for the 12 term infants in PALS-term12 space and 12 adults in PALS-B12 space. Age-specific average fiducial and inflated surfaces were generated on the standard mesh by taking the average 3D spatial coordinate of each affine-transformed surface node from all 12 term infants and all 12 adults. The SD of the 3D coordinate position was calculated to create maps of 3D variability. Age-specific, population-average maps of sulcal depth and variability were created by calculating the mean and SD of sulcal depth at each node across the cortex. Age-specific depth difference maps were generated by subtracting the average sulcal depth map for the right hemisphere from that for the left hemisphere.
Hemispheric surface areas were calculated at two stages, before registration and after both registration and scale normalization, by summing the area of all tiles on the appropriate fiducial surface after excluding the noncortical medial wall.
Smoothing
Maps of sulcal depth variability and 3D positional variability were smoothed using an average neighbors algorithm similar to that described by Hagler et al. (2006) in which the value at a node is replaced by the average with its immediate neighbors. All smoothed maps were generated after 10 iterations of smoothing at a strength of 1.0, which corresponds to a 5–6 mm smoothing kernel.
Inter-atlas surface-based registration
To map population data from the PALS-B12 atlas (Van Essen, 2005) to the PALS-term12 atlas an inter-atlas registration was performed. A total of 22 registration landmarks were drawn on both the average “term12” right hemisphere fiducial surface in PALS-term12 space and the average right hemisphere “B12” fiducial surface in PALS-B12 space. The 22 landmarks chosen include the average Core 6 plus 16 other landmarks readily identifiable on each average surface (supplemental Fig. 4, available at www.jneurosci.org as supplemental material). The PALS-B12 landmarks were registered to the PALS-term12 landmarks to create a mapping between atlases. This mapping was used to register the extents of a significant depth asymmetry detected in adults (see Results) to the PALS-term12 atlas.
Hemispheric depth asymmetries
Sulcal depth asymmetries between the left and right hemispheres were tested by two independent methods: (1) a paired t test across the entire hemisphere and (2) a local region of interest (ROI) method applied to a selected sulcus.
Paired t test.
The strategy outlined by Nichols and Holmes (2002) was used, making the weak assumption that hemispheric depth differences were symmetric, as inspection of the depth difference histogram affirmed. Separately for each age group, (1) left and right hemispheres for each individual were paired, and a paired t statistic was calculated at each surface node with no spatial smoothing from the distribution of individual depth difference values. The t statistic was computed as the mean difference (left depth minus right depth) divided by the SEM difference. (2) The sign of subjects depth maps were randomly flipped 2500 times and corresponding paired t maps generated. (3) Each t map was smoothed four iterations at 0.5 strength using an average neighbors algorithm. (4) To determine statistical significance, a surface-based equivalent to the threshold-free cluster enhancement (TFCE) test described for volumetric data (Smith and Nichols, 2009) was implemented. This method removes the limitation of semi-arbitrarily choosing a cluster-forming threshold as the basis for determining which clusters are large enough to be considered statistically significant that is characteristic of suprathreshold cluster tests (Nichols and Holmes, 2002; Van Essen et al., 2006) but still incorporate information pertaining to both signal extent and intensity to determine significance. Each t map was transformed to a TFCE map by applying a TFCE transform to the t statistic at each surface node according to Equation 2:
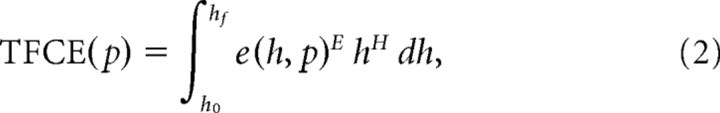 |
where h is the threshold applied to the t map, e(h,p) is the extent of the cluster (suprathreshold contiguous nodes of the same sign) at threshold h containing the node p, and E and H are parameters defining the weight given to signal extent and intensity, respectively. Although E = 0.5 and H = 2.0 are appropriate for volumetric analysis, we used E = 1.0 and H = 2.0, which are more appropriate for surface-based analysis (Thomas Nichols, personal communication). The bounds of the integral, h0 and hf, are typically chosen to be 0 and the maximum t value across all nodes, respectively. The integral could not be solved symbolically because cluster size can only be computed from the data and was approximated numerically. At a high level, our approach was to use many thresholds, computing the approximate integral for each “slice” with the trapezoidal rule, and summing across all thresholds at each node. A TFCE maximum value distribution was created from the maximum TFCE score for each randomized t map. The TFCE value corresponding to the 95th percentile of this TFCE maximum value distribution was set as the cutoff for statistical significance on the actual (nonrandomized) t map. (For a comparison of the results obtained using the TFCE test compared with the suprathreshold cluster test, see supplemental data, available at www.jneurosci.org as supplemental material).
Local ROI-based method.
The paired t test detected significant depth asymmetry along the middle portion of the superior temporal sulcus (STS) in adults but not term infants (see Results). To test whether the region of significance in adults was also significant in term infants, a local analysis focusing on the middle portion of the STS was performed in a manner that was not impacted by the variability in location of these sulci or by noise introduced via the registration algorithm. An STS ROI was constructed by first tracing the entire fundus of the STS manually on a flat map of each hemisphere of all subjects, using a map of mean curvature to assist in identifying the sulcal fundus. The significant STS depth asymmetry detected in adults (see Results) was mapped to the PALS-term12 atlas using the inter-atlas registration described above and used to limit the extent of the STS tracing in each term infant. The nodes at both the anterior and posterior endpoint of the adult cluster were used to define the end points of the STS ROI in each term infant. A narrow ROI was constructed around the fundus of the STS by selecting all nodes within 2 mm of the fundus between the endpoints. The mean sulcal depth within the each individual ROI was calculated, and the difference between paired left and right hemispheres was computed.
Data access and visualization.
All datasets illustrated in this study are accessible in the SumsDB database (http://sumsdb.wustl.edu/sums/directory.do?id=7052056) and can be viewed online (using WebCaret) or offline (using Caret software) as figure-specific “scenes” that recapitulate what is displayed in the individual figures.
Results
Mean surface areas
Table 1 shows total cortical surface area (excluding the noncortical medial wall) for both the term infant and adult populations. Columns 2 and 3 (native surface area) are the mean surface areas before registration and surface-based scale normalization. For the term infant population, these values represent our best estimates of actual cortical surface area and the population variability. No significant differences between left (mean ± SD, 300 ± 34 cm2) and right (mean ± SD, 305 ± 31 cm2) hemispheres or between male (mean ± SD, 308 ± 27 cm2) and female (mean ± SD, 297 ± 37 cm2) were detected.
Table 1.
Term infant and adult surface areas
| Subjects | Native surface area (10 cm2) |
Normalized surface area (10 cm2) |
Percentage reduction |
|||
|---|---|---|---|---|---|---|
| Right (Mean ± SD) | Left (Mean ± SD) | Right (Mean ± SD) | Left (Mean ± SD) | Right | Left | |
| All term infants (n = 12) | 305 ± 31 | 300 ± 34 | 273 ± 17 | 269 ± 18 | 10 | 10 |
| Male term infants (n = 6) | 309 ± 27 | 306 ± 30 | 273 ± 11 | 270 ± 15 | 12 | 12 |
| Female term infants (n = 6) | 301 ± 38 | 293 ± 39 | 273 ± 23 | 270 ± 22 | 9 | 8 |
| All adults (n = 12) | 938 ± 31 | 945 ± 32 | 805 ± 25 | 809 ± 21 | 14 | 13 |
| Male adults (n = 6) | 925 ± 37 | 932 ± 32 | 800 ± 30 | 807 ± 21 | 14 | 13 |
| Female adults (n = 6) | 950 ± 17 | 958 ± 28 | 810 ± 21 | 811 ± 22 | 15 | 15 |
Term infant and adult total cortical surface area estimates excluding the noncortical medial wall. For the term infant population, the leftmost two columns give surface area values in the native-mesh configurations after AC–PC alignment but before any scale normalization or registration. For adults, the leftmost two columns give values after volume-based normalization but before registration and surface-based scale normalization. The middle two columns give surface area values after registration to the appropriate age-specific atlas and surface-based scale normalization. The rightmost two columns give the percentage difference in surface area between native-mesh and normalized atlas mesh surfaces.
On average, hemispheric area was approximately threefold greater in adults than term infants (right hemisphere, 3.07; left hemisphere, 3.15). However, this is likely a modest (∼10%) overestimate because the surfaces used to estimate the hemispheric area in the adult population had undergone volume-based scale normalization to the 711–2C template of Washington University before surface reconstruction (Van Essen, 2005). This normalization resulted in modest increases in total intracranial volume on the order of 17% on average for young adults (Buckner et al., 2004), corresponding to an 11% increase in surface area.
For the remaining quantitative analyses, the infants were registered to the PALS-term12 atlas and normalized for scale using surface-based scale normalization (see Materials and Methods). The right half of Table 1 shows the effects of registration and surface-based scale normalization on estimates of cortical surface area. Combined, these processes decreased the estimated surface area by 10–15%, with approximately equal contributions from each procedure.
Individual cortical folding patterns
Figure 4 shows medial and lateral views of two representative (closest to the population average for native surface area) term infant and adult right hemispheres. Overall, the term cortex has many similarities to that of the adult. As expected, there is a large difference in overall size between age groups (note scale bars). All primary and secondary sulci are present at term as well as a large number of tertiary sulci, although many of them are notably shallow. These representations also suggest that several regions may be distinctly less convoluted in the infants, including the anterior cingulate (black arrow) and anterior temporal lobe (blue arrow).
Population average maps
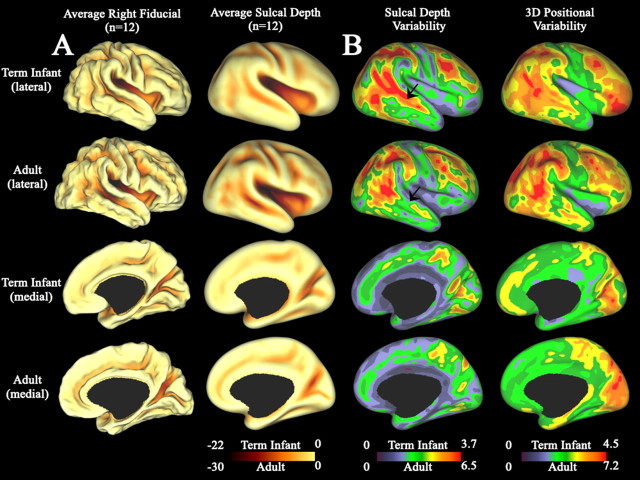
To characterize these patterns quantitatively within each age group, we created population average maps of cortical structure. Maps of average cortical shape and sulcal depth for each population are shown for lateral (Fig. 5A, top) and medial (Fig. 5A, bottom) surface views. For each point on the surface, the sulcal depth is defined as the distance from that point to the nearest point on a cerebral hull surface. Accordingly, this provides a quantitative measure of the depth of each sulcus. A quantitative regional comparison between age groups would require registration to a common hybrid atlas (our unpublished data). However, this side-by-side comparison demonstrates broad similarities between term infants (Fig. 5A, rows 1, 3) and adults (Fig. 5A, rows 2, 4). The average fiducial and average sulcal depth maps indicate that adult sulci are deeper by up to 10 mm, but the same overall shape (sulci and gyri in the average fiducial surfaces, dark and bright areas on the average sulcal depth map) is evident at both ages.
Figure 5.
Right hemisphere population-average maps for the term infant and adult populations. Rows 1 and 2 show lateral views for a population of 12 term infants and 12 adults, respectively. Rows 3 and 4 show corresponding medial views for term infants and adults, respectively. All maps were generated after surface-based scale normalization. A, Average fiducial and average sulcal depth maps. The average fiducial surface was created by calculating the average spatial coordinate from all 12 individuals after surface-based scale normalization. The average sulcal depth maps were created by calculating the average sulcal depth across individuals for each node. Note scale differences for each age group. B, Maps of sulcal depth and 3D positional variability. Sulcal depth variability maps display the SD in sulcal depth for all individuals. 3D positional variability maps display the SD in 3D fiducial coordinate position for all individuals. Note scale differences for each age group. Average sulcal depth variability and 3D positional variability maps for the term infants and adults are displayed on the PALS-term12 and PALS-B12 standard-mesh average inflated surfaces, respectively.
Because each individual has a unique cortical shape, we further investigated the regional population characteristics by assessing inter-individual variability in both sulcal depth (sulcal depth variability) and spatial position (3D coordinate variability) for each age group. These maps are shown for lateral (Fig. 5B, top) and medial (Fig. 5B, bottom) views for both infants (Fig. 5B, rows 1, 3) and adults (Fig. 5B, rows 2, 4). As these surfaces were normalized for overall cortical dimensions, the variability in each measure was minimally affected by differences in total brain dimensions. Similar results were obtained for surfaces before normalization. The pattern of variability is heterogeneous at each age, indicating that some regions of the cortex (blue/green) are more consistent in shape than others (orange/red). Importantly, the adult and term infant patterns of variability are quite similar overall, suggesting that this pattern is established by term birth and changes only modestly by adulthood. A possible exception is in the middle region of the superior temporal sulcus (Fig. 5B, arrow). Relative to the rest of the cortex, the term infant population shows a trend toward greater depth variability (red) in this region than the adult population (green). Such a region of proportionally higher variability in the term infant population might reflect either depth variability at the sulcal fundus or to sulcal trajectory variability that would cause the sulcal fundus of one individual to not align with the fundus of another. Quantitative regional comparisons between age groups will require registration to a common hybrid atlas. Similar maps for the left hemisphere are provided in supplemental Figure 5 (available at www.jneurosci.org as supplemental material).
Hemispheric asymmetries
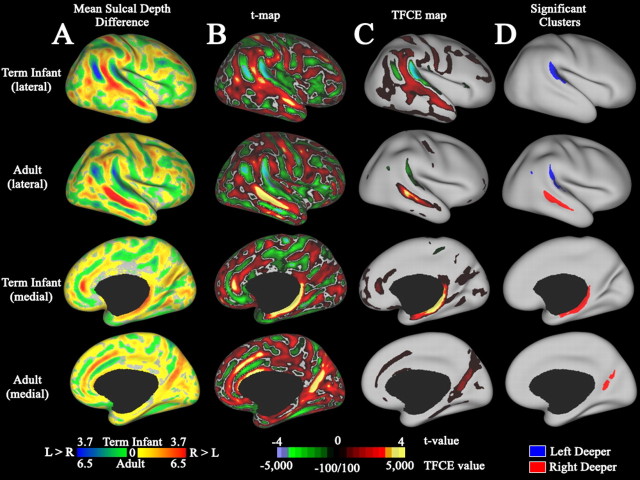
Figure 6 shows sulcal depth differences between left and right hemispheres for term infants (Fig. 6, rows 1, 3) and adults (Fig. 6, rows 2, 4) in lateral (Fig. 6, top) and medial (Fig. 6, bottom) views. A map of the difference between mean left and right sulcal depth maps (Fig. 6A) shows a complex pattern of left-deeper (green/blue) and right-deeper (yellow/red) that is qualitatively similar in term infants and adults despite the differences in absolute scale (note color scale bar). We used a paired t test to test for statistically significant (p < 0.05) depth asymmetries in each population. Intermediate stages in this statistical analysis include t statistic maps (Fig. 6B) and a transformation to the TFCE statistic values (Fig. 6C). The TFCE transform increases the t statistic values to the extent that each surface node is part of a large contiguous cluster (see Materials and Methods). Nodes that passed significance testing are shown in Figure 6D and colored according to laterality: deeper on the right (red) and deeper on the left (blue). In adults, four asymmetries were significant. On the lateral surface, this includes a left-deeper-than-right peri-Sylvian asymmetry centered on the planum temporale, a small left-deeper-than-right asymmetry in the posterior temporal lobe, and a right-deeper-than-left asymmetry along the middle extent of the STS (Fig. 6D, row 2). On the medial surface, a right-deeper-than-left asymmetry running along the wall of the parietal–occipital sulcus was significant (Fig. 6D, row 4). In term infants, there were two statistically significant asymmetries. On the lateral surface, this includes a significant peri-Sylvian asymmetry that was 3 mm deeper on average on the left and in the same location as the asymmetry seen in adults (Fig. 6D, row 1). On the medial surface, there was an apparent asymmetry running along the parahippocampal, and noncortical medial wall is in a region in which the limits of neocortex in the hippocampal fissure are difficult to delineate (Fig. 6D, row 4). Inspection of the MRI volumes in this region suggests that this is not a genuine biological asymmetry (see supplemental data, available at www.jneurosci.org as supplemental material).
Figure 6.
Analysis of hemispheric depth asymmetries. Rows 1 and 2 show lateral views for a population of 12 term infants and 12 adults, respectively. Rows 3 and 4 show corresponding medial views for term infants and adults, respectively. All maps are displayed on the age-specific standard-mesh average inflated surface. A, Maps of mean sulcal depth difference between hemispheres. Blue and green regions are deeper on the left; red and yellow regions are deeper on the right. B, Paired t statistic map for hemispheric depth difference. The paired t statistic was computed as the mean depth difference (left depth minus right depth) divided by the SEM. C, TFCE statistic map. This map was generated by applying the TFCE transform to the t statistic at each surface node. D, Location of significant depth difference clusters revealed by TFCE and permutation testing. Blue clusters are deeper on the left, and red clusters are deeper on the right.
A significant depth difference along the STS was not detected in term infants by TFCE analysis. However, the depth difference map in the term infant population indicates that the STS is deeper on the right over much of its extent (Fig. 6A, row 1, red). The sensitivity of the TFCE analysis is reduced by misalignment of the sulcal fundus, which is proportionally greater in infants as evidenced by the depth variability map (Fig. 5B, row 1, arrow). We therefore used a more sensitive method that is less affected by variability in sulcal trajectory and imperfections in the registration algorithm. We traced the sulcal fundus of each individual and tested for significant depth asymmetry within a narrow region along the middle portion of the STS in term infants, which corresponds to the region of significant asymmetry in adults. By this analysis, the central portion of the STS fundus was 1.7 mm deeper on average on the right than the left (t = 5.2, p < 0.01) (see supplemental data, available at www.jneurosci.org as supplemental material).
Discussion
We have characterized important aspects of cortical development by establishing the first population average surface atlas of human cortical structure at term gestation.
Surface-based approaches expand on volume-based approaches for studying the cerebral cortex because they facilitate visualization of the entire cortical sheet, including cortex buried in sulci, and provide quantitative measures of cortical folding and surface area (Drury et al., 1996; Van Essen and Drury, 1997; Van Essen et al., 1998; Fischl et al., 1999; Csernansky et al., 2008). Previous surface-based analyses of cortical development have studied preterm infants to qualitatively detail the timetable of cortical folding, quantitatively examine global changes in surface area and shape during development, and define the impact of cerebral lesions and intrauterine growth restriction on cortical structure (Dubois et al., 2008a,b). A significant methodological limitation to these studies was the lack of a common atlas space, which restricted regional quantitative comparisons across individuals to manually identified regions of consistent shape (Dubois et al., 2008a).
Our approach has capitalized on registration of term infants to the PALS-term12 atlas. This allows population-average measures of cortical shape and individual variability to be computed at every point across the cortex, regardless of individual folding patterns. The availability of this atlas as a registration target also facilitates subsequent regional comparisons of healthy term infants to other populations. The registration process (Van Essen, 2005) is associated with a small but unavoidable reduction in surface area measurements. Hence, the sulcal depth, depth variability, and 3D positional variability measures reported here might be slight underestimates of true biological values. Because the same procedure was applied to all individuals and the effects on each population were similar, this should not adversely affect comparisons between individuals or groups.
Cortical shape and variability
Human cerebral cortex contains a mosaic of perhaps 100–200 anatomically and functionally distinct cortical areas (O'Leary et al., 2007; Kaas, 2008) that are presumably connected by thousands of corticocortical pathways, as is the case for the macaque monkey (Felleman and Van Essen, 1991). In adult humans, cortical folding is regionally variable across individuals, with some regions much more consistent in shape than others (Thompson et al., 1996; Van Essen, 2005; Van Essen and Dierker, 2007). We found that the regional pattern of inter-individual variability in cortical convolutions is primarily established by term birth, changing only modestly thereafter.
Individual variability in cortical folding may be related to variability in the size of cortical areas or in the density of cortical connections between areas. In humans, cortical areas vary in size more than twofold across individuals (White et al., 1997; Dougherty et al., 2003). Studies in the cat report moderate individual variability (often approximately twofold) in the relative density of cortical connections between any given pair of areas (Hilgetag and Grant, 2000). The theory of tension-based cortical folding (Van Essen, 1997) predicts that cortical connectivity has a strong influence on the variability of cortical folds; consistent folding patterns occur in regions in which cortical connections are dominated by few pathways between large areas, whereas more variable folding is found in regions in which smaller areas are connected through more variable pathways. Because long-distance cortical connections are primarily established by term birth, the present observations support the hypothesis that cortical connectivity is a major factor influencing variability in cortical folding, whereas processes later in development, such as synaptic pruning, play less of a role.
Hemispheric asymmetries
Hemispheric asymmetries have fascinated neuroscientists since the pioneering work of Broca and Wernicke on language lateralization (Toga and Thompson, 2003) and studies involving split-brain patients (Sperry, 1984; Gazzaniga, 2005). The left hemisphere is dominant in language, logical reasoning, and mathematics, whereas the right hemisphere is dominant in visuospatial processing, emotional perception, and musical ability (Sperry, 1984; Borod, 1992; Gazzaniga, 2005). Modern imaging techniques have revealed several anatomic and functional asymmetries in adults. Among the most prominent anatomic asymmetries are the peri-Sylvian cortex and superior temporal sulcus (Blanton et al., 2001; Toga and Thompson, 2003; Van Essen, 2005; Sun and Walsh, 2006).
We found a left-deeper-than-right asymmetry centered on the planum temporale within the posterior Sylvian fissure in term infants that corresponds well to an adult asymmetry previously reported (Van Essen, 2005) and confirmed here. Structural asymmetries in this region have been reported by qualitative examination of postmortem human preterm infant brains. For example, at ∼32 weeks gestation, the left transverse temporal (Heschl's) gyrus first extends farther posterior, is shorter in height, and more obtusely angled (making more room for the planum temporale) than the right (Chi et al., 1977). Auditory evoked responses in human infants aged between 1 week and 10 months demonstrate a greater sensitivity to speech stimuli in the left temporal region than the right (Molfese et al., 1975). There are also significant asymmetries of gene expression in the peri-Sylvian region in humans at 12, 14, and 19 weeks gestation, including regions that later form the superior temporal gyrus and sulcus and the Sylvian fissure (Sun et al., 2005, 2006). Altogether, there is strong evidence for structural, functional, and molecular correspondence of asymmetries of peri-Sylvian cortex during normal prenatal cerebral development.
The STS is first visible at 23 weeks gestation and appears earlier on the right than the left (Chi et al., 1977; Dubois et al., 2008a). Consistent with this, we identified a right-deeper-than-left asymmetry along the posterior extent of the STS in term infants that is similar in location to that of adults. Bilateral activation in this region has been implicated in a host of functions, including speech processing, face processing, audiovisual integration, and biological motion processing (Hein and Knight, 2008). Greater functional activation is reported in the right posterior STS for biological motion processing and in monitoring intentions conveyed by biological motion cues from other individuals (Pelphrey and Carter, 2008; Wyk et al., 2009). Language-related functional and pathway asymmetries in the vicinity of the STS have been reported in both lesion and functional MRI studies (Glasser and Rilling, 2008). Therefore, structural and functional asymmetry is present and further supported by our findings.
Concluding remarks
Comparing the PALS-term12 atlas side by side with adult PALS-B12 atlas reveals that cortical structure in term infants is similar to the adult in many respects, including the pattern of individual variability and the presence of statistically significant structural asymmetries along the planum temporale and superior temporal sulcus. These results indicate that the postnatal environment minimally influences these structural features. This side-by-side comparison also suggests regional differences in the maturity of folding in term infants. These issues can be explored using quantitative comparisons that require registering infant and adult cortical surfaces to a common hybrid atlas space. The PALS-term12 atlas will be a valuable substrate for evaluating abnormal cortical development associated with conditions such as preterm birth and perinatal injury.
Footnotes
This project was supported by National Institutes of Health Grants R01HD057098 and R01-MH-60974 (funded by National Institute of Mental Health, National Institute of Biomedical Imaging and Bioengineering, and National Science Foundation) and the Doris Duke Foundation. We thank the National Institute of Child Health and Development, the National Institute of Mental Health, the National Institute for Biomedical Imaging and Bioengineering, the National Science Foundation, and the Doris Duke Foundation for their financial support of the project. We also acknowledge Jim Alexopolous, Karen Lukas, Joseph Ackerman Jr., Jennifer Walker, and Jayne Sicard-Su for subject recruitment, imaging, and data management, Erin Reid and Thomas Nichols for technical assistance, and Joshua Shimony and John Pruett for valuable discussions and manuscript feedback.
References
- Abe S, Takagi K, Yamamoto T, Okuhata Y, Kato T. Assessment of cortical gyrus and sulcus formation using MR images in normal fetuses. Prenat Diagn. 2003;23:225–231. doi: 10.1002/pd.561. [DOI] [PubMed] [Google Scholar]
- Bayer SA, Altman J. The human brain during the third trimester. Boca Raton, FL: CRC; 2003. [Google Scholar]
- Blanton RE, Levitt JG, Thompson PM, Narr KL, Capetillo-Cunliffe L, Nobel A, Singerman JD, McCracken JT, Toga AW. Mapping cortical asymmetry and complexity patterns in normal children. Psychiatry Res. 2001;107:29–43. doi: 10.1016/s0925-4927(01)00091-9. [DOI] [PubMed] [Google Scholar]
- Borod JC. Interhemispheric and intrahemispheric control of emotion: a focus on unilateral brain damage. J Consult Clin Psychol. 1992;60:339–348. doi: 10.1037//0022-006x.60.3.339. [DOI] [PubMed] [Google Scholar]
- Buckner RL, Head D, Parker J, Fotenos AF, Marcus D, Morris JC, Snyder AZ. A unified approach for morphometric and functional data analysis in young, old, and demented adults using automated atlas-based head size normalization: reliability and validation against manual measurement of total intracranial volume. Neuroimage. 2004;23:724–738. doi: 10.1016/j.neuroimage.2004.06.018. [DOI] [PubMed] [Google Scholar]
- Chi JG, Dooling EC, Gilles FH. Gyral development of the human brain. Ann Neurol. 1977;1:86–93. doi: 10.1002/ana.410010109. [DOI] [PubMed] [Google Scholar]
- Csernansky JG, Gillespie SK, Dierker DL, Anticevic A, Wang L, Barch DM, Van Essen DC. Symmetric abnormalities in sulcal patterning in schizophrenia. Neuroimage. 2008;43:440–446. doi: 10.1016/j.neuroimage.2008.07.034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dougherty RF, Koch VM, Brewer AA, Fischer B, Modersitzki J, Wandell BA. Visual field representations and locations of visual areas V1/2/3 in human visual cortex. J Vis. 2003;3:586–598. doi: 10.1167/3.10.1. [DOI] [PubMed] [Google Scholar]
- Drury HA, Van Essen DC, Anderson CH, Lee CW, Coogan TA, Lewis JW. Computerized mappings of the cerebral cortex: a multiresolution flattening method and a surface-based coordinate system. J Cogn Neurosci. 1996;8:1–28. doi: 10.1162/jocn.1996.8.1.1. [DOI] [PubMed] [Google Scholar]
- Dubois J, Benders M, Cachia A, Lazeyras F, Ha-Vinh Leuchter R, Sizonenko SV, Borradori-Tolsa C, Mangin JF, Hüppi PS. Mapping the early cortical folding process in the preterm newborn brain. Cereb Cortex. 2008a;18:1444–1454. doi: 10.1093/cercor/bhm180. [DOI] [PubMed] [Google Scholar]
- Dubois J, Benders M, Borradori-Tolsa C, Cachia A, Lazeyras F, Ha-Vinh Leuchter R, Sizonenko SV, Warfield SK, Mangin JF, Hüppi PS. Primary cortical folding in the human newborn: an early marker of later functional development. Brain. 2008b;131:2028–2041. doi: 10.1093/brain/awn137. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Felleman DJ, Van Essen DC. Distributed hierarchical processing in the primate cerebral cortex. Cereb Cortex. 1991;1:1–47. doi: 10.1093/cercor/1.1.1-a. [DOI] [PubMed] [Google Scholar]
- Fischl B, Sereno MI, Dale AM. Cortical surface-based analysis. II. Inflation, flattening, and a surface-based coordinate system. Neuroimage. 1999;9:195–207. doi: 10.1006/nimg.1998.0396. [DOI] [PubMed] [Google Scholar]
- Fornito A, Malhi GS, Lagopoulos J, Ivanovski B, Wood SJ, Velakoulis D, Saling MM, McGorry PD, Pantelis C, Yücel M. In vivo evidence for early neurodevelopmental anomaly of the anterior cingulate cortex in bipolar disorder. Acta Psychiatr Scand. 2007;116:467–472. doi: 10.1111/j.1600-0447.2007.01069.x. [DOI] [PubMed] [Google Scholar]
- Gazzaniga MS. Forty-five years of split-brain research and still going strong. Nat Rev Neurosci. 2005;6:653–659. doi: 10.1038/nrn1723. [DOI] [PubMed] [Google Scholar]
- Glasser MF, Rilling JK. DTI tractography of the human brain's language pathways. Cereb Cortex. 2008;18:2471–2482. doi: 10.1093/cercor/bhn011. [DOI] [PubMed] [Google Scholar]
- Hagler DJ, Jr, Saygin AP, Sereno MI. Smoothing and cluster thresholding for cortical surface-based group analysis of fMRI data. Neuroimage. 2006;33:1093–1103. doi: 10.1016/j.neuroimage.2006.07.036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hein G, Knight RT. Superior temporal sulcus—It's my area: or is it? J Cogn Neurosci. 2008;20:2125–2136. doi: 10.1162/jocn.2008.20148. [DOI] [PubMed] [Google Scholar]
- Hilgetag CC, Grant S. Uniformity, specificity and variability of corticocortical connectivity. Philos Trans R Soc Lond B Biol Sci. 2000;355:7–20. doi: 10.1098/rstb.2000.0546. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kaas JH. The evolution of the complex sensory and motor systems of the human brain. Brain Res Bull. 2008;75:384–390. doi: 10.1016/j.brainresbull.2007.10.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Keenan JP, Thangaraj V, Halpern AR, Schlaug G. Absolute pitch and planum temporale. Neuroimage. 2001;14:1402–1408. doi: 10.1006/nimg.2001.0925. [DOI] [PubMed] [Google Scholar]
- Lebel C, Walker L, Leemans A, Phillips L, Beaulieu C. Microstructural maturation of the human brain from childhood to adulthood. Neuroimage. 2008;40:1044–1055. doi: 10.1016/j.neuroimage.2007.12.053. [DOI] [PubMed] [Google Scholar]
- Molfese DL, Freeman RB, Jr, Palermo DS. The ontogeny of brain lateralization for speech and nonspeech stimuli. Brain Lang. 1975;2:356–368. doi: 10.1016/s0093-934x(75)80076-9. [DOI] [PubMed] [Google Scholar]
- Nichols TE, Holmes AP. Nonparametric permutation tests for functional neuroimaging: a primer with examples. Hum Brain Mapp. 2002;15:1–25. doi: 10.1002/hbm.1058. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nordahl CW, Dierker D, Mostafavi I, Schumann CM, Rivera SM, Amaral DG, Van Essen DC. Cortical folding abnormalities in autism revealed by surface-based morphometry. J Neurosci. 2007;27:11725–11735. doi: 10.1523/JNEUROSCI.0777-07.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- O'Leary DD, Chou SJ, Sahara S. Area patterning of the mammalian cortex. Neuron. 2007;56:252–269. doi: 10.1016/j.neuron.2007.10.010. [DOI] [PubMed] [Google Scholar]
- Ono M, Kubick S, Abernathey CD. Atlas of the cerebral sulci. New York: Thieme Medical; 1990. [Google Scholar]
- Pelphrey KA, Carter EJ. Brain mechanisms for social perception: lessons from autism and typical development. Ann N Y Acad Sci. 2008;1145:283–299. doi: 10.1196/annals.1416.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith SM, Nichols TE. Threshold-free cluster enhancement: addressing problems of smoothing, threshold dependence and localisation in cluster inference. Neuroimage. 2009;44:83–98. doi: 10.1016/j.neuroimage.2008.03.061. [DOI] [PubMed] [Google Scholar]
- Sperry R. Consciousness, personal identity and the divided brain. Neuropsychologia. 1984;22:661–673. doi: 10.1016/0028-3932(84)90093-9. [DOI] [PubMed] [Google Scholar]
- Sun T, Walsh CA. Molecular approaches to brain asymmetry and handedness. Nat Rev Neurosci. 2006;7:655–662. doi: 10.1038/nrn1930. [DOI] [PubMed] [Google Scholar]
- Sun T, Patoine C, Abu-Khalil A, Visvader J, Sum E, Cherry TJ, Orkin SH, Geschwind DH, Walsh CA. Early asymmetry of gene transcription in embryonic human left and right cerebral cortex. Science. 2005;308:1794–1798. doi: 10.1126/science.1110324. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sun T, Collura RV, Ruvolo M, Walsh CA. Genomic and evolutionary analyses of asymmetrically expressed genes in human fetal left and right cerebral cortex. Cereb Cortex. 2006;16(Suppl 1):i18–i25. doi: 10.1093/cercor/bhk026. [DOI] [PubMed] [Google Scholar]
- Thompson DK, Warfield SK, Carlin JB, Pavlovic M, Wang HX, Bear M, Kean MJ, Doyle LW, Egan GF, Inder TE. Perinatal risk factors altering regional brain structure in the preterm infant. Brain. 2007;130:667–677. doi: 10.1093/brain/awl277. [DOI] [PubMed] [Google Scholar]
- Thompson PM, Schwartz C, Lin RT, Khan AA, Toga AW. Three-dimensional statistical analysis of sulcal variability in the human brain. J Neurosci. 1996;16:4261–4274. doi: 10.1523/JNEUROSCI.16-13-04261.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Toga AW, Thompson PM. Mapping brain asymmetry. Nat Rev Neurosci. 2003;4:37–48. doi: 10.1038/nrn1009. [DOI] [PubMed] [Google Scholar]
- Toga AW, Thompson PM, Mori S, Amunts K, Zilles K. Towards multimodal atlases of the human brain. Nat Rev Neurosci. 2006;7:952–966. doi: 10.1038/nrn2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van Essen DC. A tension-based theory of morphogenesis and compact wiring in the central nervous system. Nature. 1997;385:313–318. doi: 10.1038/385313a0. [DOI] [PubMed] [Google Scholar]
- Van Essen DC. Surface-based approaches to spatial localization and registration in primate cerebral cortex. Neuroimage. 2004;23(Suppl 1):S97–S107. doi: 10.1016/j.neuroimage.2004.07.024. [DOI] [PubMed] [Google Scholar]
- Van Essen DC. A population-average, landmark- and surface-based (PALS) atlas of human cerebral cortex. Neuroimage. 2005;28:635–662. doi: 10.1016/j.neuroimage.2005.06.058. [DOI] [PubMed] [Google Scholar]
- Van Essen DC, Dierker DL. Surface-based and probabilistic atlases of primate cerebral cortex. Neuron. 2007;56:209–225. doi: 10.1016/j.neuron.2007.10.015. [DOI] [PubMed] [Google Scholar]
- Van Essen DC, Drury HA. Structural and functional analyses of human cerebral cortex using a surface-based atlas. J Neurosci. 1997;17:7079–7102. doi: 10.1523/JNEUROSCI.17-18-07079.1997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van Essen DC, Drury HA, Joshi S, Miller MI. Functional and structural mapping of human cerebral cortex: solutions are in the surfaces. Proc Natl Acad Sci U S A. 1998;95:788–795. doi: 10.1073/pnas.95.3.788. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van Essen DC, Drury HA, Dickson J, Harwell J, Hanlon D, Anderson CH. An integrated software suite for surface-based analyses of cerebral cortex. J Am Med Inform Assoc. 2001a;8:443–459. doi: 10.1136/jamia.2001.0080443. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van Essen DC, Lewis JW, Drury HA, Hadjikhani N, Tootell RB, Bakircioglu M, Miller MI. Mapping visual cortex in monkeys and humans using surface-based atlases. Vision Res. 2001b;41:1359–1378. doi: 10.1016/s0042-6989(01)00045-1. [DOI] [PubMed] [Google Scholar]
- Van Essen DC, Dierker D, Snyder AZ, Raichle ME, Reiss AL, Korenberg J. Symmetry of cortical folding abnormalities in Williams syndrome revealed by surface-based analyses. J Neurosci. 2006;26:5470–5483. doi: 10.1523/JNEUROSCI.4154-05.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weisenfeld NI, Warfield SK. Automatic segmentation of newborn brain MRI. Neuroimage. 2009;47:564–572. doi: 10.1016/j.neuroimage.2009.04.068. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weisenfeld NI, Mewes AU, Warfield SK. Highly accurate segmentation of brain tissue and subcortical gray matter from newborn MRI. Med Image Comput Comput Assist Interv. 2006;9:199–206. doi: 10.1007/11866565_25. [DOI] [PubMed] [Google Scholar]
- Welker WI. The significance of foliation and fissuration of cerebellar cortex. The cerebellar folium as a fundamental unit of sensorimotor integration. Arch Ital Biol. 1990;128:87–109. [PubMed] [Google Scholar]
- White LE, Andrews TJ, Hulette C, Richards A, Groelle M, Paydarfar J, Purves D. Structure of the human sensorimotor system. I. Morphology and cytoarchitecture of the central sulcus. Cereb Cortex. 1997;7:18–30. doi: 10.1093/cercor/7.1.18. [DOI] [PubMed] [Google Scholar]
- Wisco JJ, Kuperberg G, Manoach D, Quinn BT, Busa E, Fischl B, Heckers S, Sorensen AG. Abnormal cortical folding patterns within Broca's area in schizophrenia: evidence from structural MRI. Schizophr Res. 2007;94:317–327. doi: 10.1016/j.schres.2007.03.031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wolosin SM, Richardson ME, Hennessey JG, Denckla MB, Mostofsky SH. Abnormal cerebral cortex structure in children with ADHD. Hum Brain Mapp. 2009;30:175–184. doi: 10.1002/hbm.20496. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wyk BC, Hudac CM, Carter EJ, Sobel DM, Pelphrey KA. Action understanding in the superior temporal sulcus region. Psychol Sci. 2009;20:771–777. doi: 10.1111/j.1467-9280.2009.02359.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xue H, Srinivasan L, Jiang S, Rutherford M, Edwards AD, Rueckert D, Hajnal JV. Automatic cortical segmentation in the developing brain. Inf Process Med Imaging. 2007;20:257–269. doi: 10.1007/978-3-540-73273-0_22. [DOI] [PubMed] [Google Scholar]
- Yu P, Grant PE, Qi Y, Han X, Ségonne F, Pienaar R, Busa E, Pacheco J, Makris N, Buckner RL, Golland P, Fischl B. Cortical surface shape analysis based on spherical wavelets. IEEE Trans Med Imaging. 2007;26:582–597. doi: 10.1109/TMI.2007.892499. [DOI] [PMC free article] [PubMed] [Google Scholar]