A two-level structural equation model approach for analyzing multivariate longitudinal responses

SUMMARY

The analysis of longitudinal data to study changes in variables measured repeatedly over time has received considerable attention in many fields. This paper proposes a two-level structural equation model for analyzing multivariate longitudinal responses that are mixed continuous and ordered categorical variables. The first-level model is defined for measures taken at each time point nested within individuals for investigating their characteristics that are changed with time. The second level is defined for individuals to assess their characteristics that are invariant with time. The proposed model accommodates fixed covariates, nonlinear terms of the latent variables, and missing data. A maximum likelihood (ML) approach is developed for the estimation of parameters and model comparison. Results of a simulation study indicate that the performance of the ML estimation is satisfactory. The proposed methodology is applied to a longitudinal study concerning cocaine use.

1. INTRODUCTION

In public health and biomedical sciences, it is common to encounter latent variables or constructs that cannot be directly measured by a single observed variable, but instead assessed through a number of observed variables. Structural equation models (SEMs) [1] are a flexible class of models for complex modeling of multivariate correlated data to explain the interrelationships among observed and latent variables. In general, SEMs combine the ideas of factor analysis and regression. They are formulated by two major components. The first component is the measurement equation, which is basically a confirmatory factor analysis model for grouping correlated observed variables to `measure' their corresponding latent variables (factors) and for taking the measurement errors into account. The second component is a regression-type structural equation for assessing the effects of independent latent variables on dependent latent variables of interest. As the number of latent variables is much less than the number of original observed variables, the use of a structural equation with latent variables has its advantages over the application of the ordinary regression model with originally observed variables. Through the use of user-friendly software [2, 3], SEMs have been extensively applied to behavioral, educational, and social–psychological sciences in the past years and to biological and medical sciences in recent years. The basic theory and statistical properties of SEMs are mainly developed in the field of psychometrics for assessing latent constructs. Recently, advanced SEM methodologies have also appeared in mainstream statistical journals; see, for example, [4–10]. Moreover, Sanchez et al. [11] presented a review of the basic theory, including its connection to some latent variables models.

In this paper, we propose a novel, dynamic two-level SEM to analyze multivariate response variables measured at multiple time points. More specifically, let u_gt be a random vector for the gth (g=1,…,G) individual measured at time point t (t =1,…,T). A two-level model for u_gt will be defined by u_gt =y_g+v_gt, where y_g is the second-level random vector that is independent of t, and v_gt is the first-level random vector for accounting characteristics that change dynamically with t. A confirmatory factor analysis model with fixed covariates will be defined for y_g for accounting characteristics that are invariant with t. A nonlinear SEM with fixed covariates will be defined for v_gt, in which the latent variables at every time point are divided into independent and dependent latent variables, and their dynamic relationships over time are assessed by a flexible autoregressive nonlinear structural equation (see equation (5)). Here, latent variables are used to represent latent traits that are related to several observed variables (indicators). To cope with the complex nature of real-world data in substantive research, the proposed model also accommodates mixed continuous and ordered categorical variables, and missing data that are missing at random. A maximum likelihood (ML) approach will be developed for analyzing the proposed model. A Monte Carlo Expectation–Maximization (MCEM) algorithm [12] will be developed for obtaining the ML estimates, and the Louis formula [13] will be used to obtain the standard error estimates. The Bayesian information criterion (BIC) will be used for model comparison. Owing to the complexity of the model, the observed-data likelihood involved in the BIC includes intractable multiple integrals. A procedure based on path sampling [14] will be developed to evaluate the observed-data likelihood.

We illustrate our methodology through a longitudinal data set about cocaine use and related phenomena. Cocaine use is a major social and health problem in the United States. According to the 2002 National Survey on Drug Use and Health [15], an estimated 34 million Americans aged 12 years or older (14.4 per cent) reported cocaine use at least once in their lifetime; among them, an estimated 2 million persons reported cocaine use in the past month. Cocaine is consistently detected in the urine specimens from approximately one-third of arrestees tested across the nation each year [16]. Furthermore, cocaine is the illegal drug mentioned most often in emergency department records [17]. There are various latent traits that influence cocaine use. Specifically, many studies have shown substantial impact of psychiatric problems on cocaine-dependent patients [18–20] and that social support is another key latent trait [21–23].

Although treatment for cocaine use has received considerable attention in recent years [24, 25], the longitudinal phenomena of cocaine use in relation to psychiatric problems and social support have yet to be adequately explicated. To illustrate the application of the proposed methodologies, we analyze the UCLA longitudinal data set collected from cocaine-dependent patients at intake, 1 year, 2 years, and 12 years after treatment [26]. As this data set involves ordered categorical outcomes with missing entries, the proposed two-level SEM is required to assess the longitudinal effects of the latent traits (psychiatric problems and social support) to cocaine use.

Although some specific SEMs or latent variable models have been developed for analyzing longitudinal data, their objectives and/or formulations are quite different from the proposed dynamic two-level nonlinear SEMs. For instance, a standard growth curve model [27, 28] can be viewed as the following confirmatory factor analysis model: x_i =Λω_i +∊_i, where x_i is a vector of repeated measures of a univariate response variable, Λ is the factor loading matrix of sequential known values of the growth curve records, and ω_i is the latent growth factor containing the `initial status (intercept)' and `rate of change (slope),' and ∊_i is the vector of residuals. This is a single-level linear SEM, in which the latent variables in ω_i are used to assess the characteristic of change over time rather than latent traits such as `psychiatric problem' and `social support' in our example. Hence, the formulation of a growth curve model is less general, and the interpretation of the latent variables is very different. Dunson [29] recently analyzed multidimensional longitudinal data by developing dynamic latent variable models, which allow mixtures of count, and categorical and continuous response variables. In this model, to assess the changes between the latent variables at different time points, the latent variable ω_it at time t for individual i was regressed on the linear terms of the past latent vectors ω_i1,…,ω_i,t−1 through a regression equation with fixed covariates. Note that Dunson's [29] model is single-level and its latent variables are not divided into independent and dependent latent variables. Compared with Dunson's single-level model, our two-level model includes a second-level model for assessing the individuals' characteristics that are invariant with time. Moreover, latent variables at the first level of our model are divided into independent and dependent latent variables, and the dynamic nonlinear effects of the independent latent variables on the dependent latent variables are assessed through a rather general autoregressive nonlinear structural equation (see equation (5)). Similarly, the multilevel model [30] for the longitudinal profiling of health-care units does not involve an autoregressive nonlinear structural equation among covariates and latent variables. Other longitudinal models in the statistics literature, such as the linear mixed model [31] and the generalized linear mixed model [32], do not involve the latent traits and their associated structural equation. Clearly, the objectives and formulations of these models and our proposed model are very different. Finally, refer to the second remark given in Section 2.3 for the differences of the proposed model and the existing multilevel SEMs.

The contributions of this paper include (i) a novel dynamic two-level nonlinear SEM with fixed covariates for analyzing longitudinal data from mixed continuous and ordered categorical measures and missing data, (ii) a novel utilization of the computational tools, such as the MCEM algorithm [12] and path sampling [14] with the derivation of some new conditional distributions and derivatives for estimation and model comparison of the proposed model, and (iii) a novel application of the developed methodologies to the longitudinal study of cocaine use.

Section 2 presents the two-level SEM for analyzing multivariate random responses with mixed continuous and ordered categorical variables measured at multiple time points. An ML approach for estimation and model comparison in the proposed model framework is discussed in Section 3. A simulation study and a real example using the longitudinal data of cocaine use are presented in Sections 4 and 5, respectively. In Section 6, we discuss some limitations and outline several extensions for further research.

2. THE SEM FOR MULTIVARIATE LONGITUDINAL DATA

Consider a set of observations of a p×1 random vector u_gt for individual g 1, …, G, which was measured at multiple time points t =1, …, T. The collection U={u_gt :g=1, …, G, t =1, …, T} can be regarded as an observed sample of hierarchical observations that were measured at different time points (first level) and were nested in the individuals (second level). Hence, the following two-level SEM is proposed to model u_gt :

$${\mathbf{u}}_{gt}={\mathbf{y}}_g+{\mathbf{v}}_{gt}$$ (1)

where y_g and v_gt are the random vectors that, respectively, model the second-level effect of the individual g and the first-level effect with respect to the individual g at time t.

2.1. The second-level model

The second-level model for assessing characteristics of individuals that are invariant over time is defined by

$${\mathbf{y}}_g={\mathbf{A}}_0{\mathbf{c}}_{g0}+{\Lambda }_0{\omega }_{g0}+{\epsilon }_{g0}$$ (2)

where c_g0 is a vector of fixed covariates, ω_g0 is a vector of latent variables, ε_g0 is a vector of residual errors, and A₀ and Λ₀ are matrices of unknown coefficients. We assume that ω_g0 is identically and independently distributed (i.i.d.) as N[0,Φ₀] and that ε_g0 is independent of ω_g0, and i.i.d. as N[0,Ψ₀], where Ψ₀ is a diagonal matrix. This is a factor analysis model with covariates [33], which is defined for studying the relationships between the observed variables in u_gt and the latent variables in ω_g0 with respect to different individuals but common to all time points.

2.2. The first-level model

We define the following measurement model for the more important first-level random vector v_gt :

$${\mathbf{v}}_{gt}={\mathbf{A}}_t{\mathbf{c}}_{gt}+{\Lambda }_t{\omega }_{gt}+{\epsilon }_{gt},g=1,\dots ,G,t=1,\dots ,T$$ (3)

in which the definitions of A_t, c_gt, Λ_t, ω_gt, and ε_gt are similar to those given in equation (2); except here they are defined at time point t nested within the individual g, and the distribution of ε_gt is N[0,Ψ_t], where Ψ_t is assumed to be a diagonal matrix for brevity. Hence, we assume that the random vector u_gt conditional on y_g has the following structure:

$${\mathbf{u}}_{gt}={\mathbf{y}}_g+{\mathbf{A}}_t{\mathbf{c}}_{gt}+{\Lambda }_t{\omega }_{gt}+{\epsilon }_{gt},g=1,\dots ,G,t=1,\dots ,T$$ (4)

Conditional on y_g, equation (4) accounts for dependency among the observed variables measured for the individual g at a given time point t through the fixed covariates c_gt and the shared latent variables ω_gt. The relationships between the observed variables and the corresponding fixed covariates and latent variables that change dynamically over time can be assessed by estimating A_t and Λ_t.

According to the spirit of SEM, we consider a partition of ω_gt into $({\eta }_{gt}^{\prime },{\xi }_{gt}^{\prime })\prime$, where η_gt and ξ_gt are q₁-dimensional-dependent and q₂-dimensional-independent random latent vectors, respectively, q=q₁+q₂. Effects of the independent latent variables ξ_gt on the dependent latent variables η_gt are studied through the following autoregressive nonlinear structural equation: For g=1, …, G, t =1, …, T,

$${\eta }_{gt}={\mathbf{B}}_0{\mathbf{d}}_{g0}+{\mathbf{B}}_t{\mathbf{d}}_{gt}+{\Gamma }_t^{\ast }{\mathbf{F}}_t^{\ast }({\omega }_{g1},\dots ,{\omega }_{g,t-1},{\xi }_{gt})+{\delta }_{gt}$$ (5)

where B₀, B_t, and ${\Gamma }_t^{\ast }$ are matrices of unknown coefficients, d_g0 is a vector of fixed covariates, which is independent of t, d_gt is another vector of fixed covariates, δ_gt is a vector of residual errors, and ${\mathbf{F}}_t^{\ast }=(f_{t1},\dots ,f_{tr})$ is a vector-valued function in which f_tj is a differentiable function of the independent latent vector ξ_gt at the current time point and the latent vectors ω_g1, …, ω_g,t−1 at previous time points. The residual vector δ_gt is independent of ε_gt, ω_g1, …, ω_g,t−1, and ξ_gt. Moreover, these residual errors are i.i.d. N[0,Ψ_δt], where Ψ_δt is a diagonal matrix. Let ${\xi }_g=({\xi }_{g1}^{\prime },\dots ,{\xi }_{gT}^{\prime })\prime$; the distribution of ξ_g is assumed to be N[0,Φ], where Φ contains the variance-covariance matrix Φ_tt of ξ_gt, and the covariance matrix Φ_titj of ξ_gti and ξ_gtj at different time points t_i and t_j.

2.3. Remarks

1. The first and second terms of equation (5) allow for direct effects of observed predictors that are invariant over time (d_g0) and variant over time (d_gt) on the dependent latent variables. The term ${\Gamma }_t^{\ast }{\mathbf{F}}_t^{\ast }(\cdot )$ is very important for assessing the effects of independent latent variables on dependent latent variables to change dynamically over time. It allows various flexible autoregressive structures for recovering the dependency of the dependent latent variable η_gt at the current time point and across both dependent latent variables at previous time points and independent latent variables at previous and current time points. For example, typical special cases are

$$\left(\mathrm{a}\right){\eta }_{gt}={\beta }_{t-1}{\eta }_{g,t-1}+{\Gamma }_1{\xi }_{g1}+\cdots +{\Gamma }_{t-1}{\xi }_{g,t-1}+{\Gamma }_t{\mathbf{F}}_t\left({\xi }_{gt}\right)+{\delta }_{gt}$$

$$\left(\mathrm{b}\right){\eta }_{gt}={\beta }_1{\eta }_{g1}+\cdots +{\beta }_{t-1}{\eta }_{g,t-1}+{\Gamma }_t{\mathbf{F}}_t\left({\xi }_{gt}\right)+{\delta }_{gt}$$

where F_t is a vector of differentiable functions of ξ_gt. In the special case (a), η_gt is assessed by the effects of linear-independent latent vectors at all previous time points, the dependent-latent vector at t−1, and finally nonlinear terms of independent latent variables at the current time point. The autoregressive structure (b) allows the dependency of η_gt on the previous endogenous latent vector η_g1, …, η_g,t−1 and a general function F_t (ξ_gt) of the current exogenous latent vector ξ_gt. Note that the longitudinal models developed in Dunson [29] and Daniels and Normand [30] do not involve a structural equation in relation to covariates and latent variables.

2. Other multilevel SEMs have been developed to analyze hierarchical data collected from units that are nested within clusters [8, 34]. Owing to different objectives, the formulations of the first-level model for v_gt in those multilevel SEMs are quite different and do not accommodate certain important features of our dynamic model. For example, their matrices of coefficient parameters and covariance matrices of errors are variant with cluster g rather than t. Moreover, for t ≠r, their v_gt and v_gr are assumed to be independent; however, v_gt and v_gr could be correlated in our model.

2.4. Ordered categorical data and identification of the model

From its definition, u_gt is a vector of continuous observations. However, in most substantive research, the continuous measurements of some components of u_gt may not be available. Suppose that u_gt is composed of a subvector x_gt of observed measurements and a subvector w_gt of unobserved measurements whose information is given by ordered categorical observations. In the generic sense, the relationship between an ordered categorical variable z and its underlying continuous variable w is defined by z=k+1 if α_k≤w<α_k+1, for k=0, …, m−1, where {−∞=α₀<α₁<…<α_m=∞} is the set of threshold parameters that define the m categories. A special case with m=2 is the dichotomous or ordered binary variable. Missing data that are missing at random (MAR, [35]) are handled using the procedure given in [36]. Details are not included here for brevity.

The proposed model is not identified without imposing identification conditions. For example, the variance and thresholds associated with each ordered categorical variable are not identifiable; the first- and second-level covariance structures are not identified, and we cannot allow intercepts to simultaneously exist in equations (3) and (5). Existing methods suggested in the SEM literature can be adopted for identifying various components of the current model. For example, the identification problem associated with an ordered categorical variable can be solved by fixing the thresholds α₁ and/or α_m−1 at some appropriate preassigned values [6, 36], and the covariance structures in the first- and second-level models can be identified by the common practice in structural equation modeling by fixing appropriate elements in Λ₀ and Λ_t at preassigned values [8].

3. AN ML APPROACH

3.1. Estimation

Let α be the parameter vector of the unknown thresholds, and θ be the parameter vector that contains all the unknown distinct structural parameters that are involved in equations (2), (3), and (5). The likelihood function of the observed data involves high-dimensional intractable integrals that are induced by the ordered categorical variables and latent variables. One approach to handle this integral is using adaptive quadrature [34]. In this paper, we use the idea of data augmentation and the MCEM algorithm [12] in the ML estimation.

Let z_gt ={z_{gt j}; j =1, …, s} be a vector of ordered categorical observations, and let u_gt = {w_gt, x_gt}, where x_gt is a vector of continuous measurements and w_gt is the latent continuous measurement corresponding to z_gt, u_g ={u_gt; t =1, …, T}, Z={z_gt; g=1, …, G, t =1,…, T}, W={w_gt; g=1, …, G, t =1, …, T}, and X={x_gt; g=1, …, G, t =1, …, T}. Moreover, let ${\omega }_g=({\eta }_{g1}^{\prime },\dots ,{\eta }_{gT}^{\prime },{\xi }_{g1}^{\prime },\dots ,{\xi }_{gT}^{\prime })\prime$, Ω₁={ω_g; g=1,…, G}, Ω₀={ω_g0; g=1, …, G}, and Y={y_g;g=1,…, G} be matrices of latent vector at the first and second levels. Further, let ${\Pi }_t=\left({\mathbf{B}}_t^{\prime }{\Gamma }_t^{\ast \prime }\right)\prime$, and ${\mathbf{h}}_{gt}=({\mathbf{d}}_{gt}^{\prime },{\mathbf{F}}_t^{\ast }({\omega }_{g1},\dots ,{\omega }_{g,t-1},{\xi }_{gt})\prime )\prime$, then equation (5) can be rewritten as

$${\eta }_{gt}={\mathbf{B}}_0{\mathbf{d}}_{g0}+{\Pi }_t{\mathbf{h}}_{gt}+{\delta }_{gt}$$ (6)

The observed data set is (X,Z). The observed-data likelihood is very complicated due to the existence of latent quantities (Y,Ω₁,Ω₂,W). Utilizing the idea of data augmentation, we consider the complete data set, which is equal to {Y,Ω₀,Ω₁,W,X,Z}={Y,Ω₀,Ω₁,U,Z}. The complete data likelihood function is equal to

$$\begin{array}{cc}\hfill p& (\mathbf{Y},{\Omega }_0,{\Omega }_1,\mathbf{U},\mathbf{Z}\mid \alpha ,\theta )\hfill \\ \hfill & =p(\mathbf{Z}\mid \mathbf{Y},{\Omega }_0,{\Omega }_1,\mathbf{U},\alpha ,\theta )p(\mathbf{U}\mid \mathbf{Y},{\Omega }_1,\theta )p({\Omega }_1\mid \theta )p(\mathbf{Y}\mid {\Omega }_0,\theta )p({\Omega }_0\mid \theta )\hfill \\ \hfill & ={\left(2\pi \right)}^{-G{T}_p∕2}{\mid {\Psi }_t\mid }^{-GT∕2}\prod _{g=1}^G\prod _{t=1}^T\exp \{-\frac{1}{2}({\mathbf{u}}_{gt}-{\mathbf{y}}_g-{\mathbf{A}}_t{\mathbf{c}}_{gt}-{\Lambda }_t{\omega }_{gt})\prime {\Psi }_t^{-1}\phantom{\}}\hfill \\ \hfill & \times \phantom{\{}({\mathbf{u}}_{gt}-{\mathbf{y}}_g-{\mathbf{A}}_t{\mathbf{c}}_{gt}-{\Lambda }_t{\omega }_{gt})\}{\mathit{I}}_{{\mathbf{R}}_{gt}}\left({\mathbf{w}}_{gt}\right)\hfill \\ \hfill & \times {\left(2\pi \right)}^{-G{T}_{q_1}∕2}{\mid {\Psi }_{\delta t}\mid }^{-GT∕2}\prod _{g=1}^G\prod _{t=1}^T\exp \left\{-\frac{1}{2}({\eta }_{gt}-{\mathbf{B}}_0{\mathbf{d}}_{g0}-{\Pi }_t{\mathbf{h}}_{gt})\prime {\Psi }_{\delta t}^{-1}({\eta }_{gt}-{\mathbf{B}}_0{\mathbf{d}}_{g0}-{\Pi }_t{\mathbf{h}}_{gt})\right\}\hfill \\ \hfill & \times {\left(2\pi \right)}^{-G_{q_2}∕2}{\mid \Phi \mid }^{-G∕2}\prod _{g=1}^G\exp \left\{-\frac{1}{2}{\xi }_g^{\prime }{\Phi }^{-1}{\xi }_g\right\}\hfill \\ \hfill & \times {\left(2\pi \right)}^{-G_q∕2}{\mid {\Phi }_0\mid }^{-G∕2}\prod _{g=1}^G\exp \left\{-\frac{1}{2}{\omega }_{g0}^{\prime }{\Phi }_0^{-1}{\omega }_{g0}\right\}\hfill \\ \hfill & \times {\left(2\pi \right)}^{-G_p∕2}{\mid {\Psi }_0\mid }^{-G∕2}\prod _{g=1}^G\exp \left\{-\frac{1}{2}({\mathbf{y}}_g-{\mathbf{A}}_0{\mathbf{c}}_{g0}-{\Lambda }_0{\omega }_{g0})\prime {\Psi }_0^{-1}({\mathbf{y}}_g-{\mathbf{A}}_0{\mathbf{c}}_{g0}-{\Lambda }_0{\omega }_{g0})\right\}\hfill \end{array}$$ (7)

where I_Rgt (w_gt) is an indicator function that takes the value 1 if w_gt ∈ R_gt and zero otherwise, and R_gt =[α_1,zgt1,α_1,zgt1+1)×…×[α_s,zgts,α_s,zgts+1. Note that for every component w_gtj in w_gt, there exists one and only one [α_j,zgtj,α_j,zgtj+1) such that w_gtj is in [α_j,zgtj,α_j,zgtj+1). Hence, the indicator function and the corresponding value of the density function are nonzero. It can be shown from (7) that the complete-data log-likelihood function can be expressed as L_c(Y,Ω₀,Ω₁,U,Z;α,θ)=L₁+L₂, where

$$\begin{array}{cc}\hfill L_1=& -\frac{1}{2}\sum _{g=1}^G[q_2\log \left(2\pi \right)+\log \mid \Phi \mid +{\xi }_g^{\prime }{\Phi }^{-1}{\xi }_g+\sum _{t=1}^T\{(p+q_1)\log \left(2\pi \right)+\log \mid {\Psi }_t\mid \phantom{]}\hfill \\ \hfill & +\log \mid {\Psi }_{\delta t}\mid +({\mathbf{u}}_{gt}-{\mathbf{y}}_g-{\mathbf{A}}_t{\mathbf{c}}_{gt}-{\Lambda }_t{\omega }_{gt})\prime {\Psi }_t^{-1}({\mathbf{u}}_{gt}-{\mathbf{y}}_g-{\mathbf{A}}_t{\mathbf{c}}_{gt}-{\Lambda }_t{\omega }_{gt})\hfill \\ \hfill & \phantom{[}+({\eta }_{gt}-{\mathbf{B}}_0{\mathbf{d}}_{g0}-{\Pi }_t{\mathbf{h}}_{gt})\prime {\Psi }_{\delta t}^{-1}({\eta }_{gt}-{\mathbf{B}}_0{\mathbf{d}}_{g0}-{\Pi }_t{\mathbf{h}}_{gt})\}]\mathrm{for}{\mathbf{w}}_{gt}\in {\mathbf{R}}_{gt}\hfill \end{array}$$ (8)

$$\begin{array}{cc}\hfill L_2=& -\frac{1}{2}\sum _{g=1}^G\{(p+q)\log \left(2\pi \right)+\log \mid {\Psi }_0\mid +\log \mid {\Phi }_0\mid +{\omega }_{g0}^{\prime }{\Phi }_0^{-1}{\omega }_{g0},\phantom{\}}\hfill \\ \hfill & \phantom{\{}+({\mathbf{y}}_g-{\mathbf{A}}_0{\mathbf{c}}_{g0}-{\Lambda }_0{\omega }_{g0})\prime {\Psi }_0^{-1}({\mathbf{y}}_g-{\mathbf{A}}_0{\mathbf{c}}_{g0}-{\Lambda }_0{\omega }_{g0})\}\hfill \end{array}$$ (9)

Note that L_c decomposes into two separable functions, each with distinct sets of parameters. This property simplifies the estimation significantly, although due to the complex function h_gt, L₁ is still rather complicated. ML estimates of α and θ are obtained using the EM algorithm that consists of the following E-step and M-step at the lth iteration: E-step: Evaluate Q(α,θ|α^(l),θ^(l))=E{L_c(Y,Ω₀,Ω₁,U,Z;α,θ)|X,Z,α^(l),θ^(l)}, in which the expectation is taken with respect to the conditional distribution of (Y,Ω₀,Ω₁,W) given (X,Z) at (α^(l),θ^(l)). M-step: Determine (α^(l+1),θ^(l+1)) by maximizing Q(α,θ|α^(l),θ^(l)).

Evaluation of the E-step is rather complicated because the conditional expectations involve intractable multiple integrals. Inspired by the MCEM algorithm [12], we solve this problem by simulating a sufficiently large number of observations from the corresponding conditional distributions using a hybrid algorithm that combines the Gibbs sampler [37] and the Metropolis–Hastings (MH) algorithm [38, 39]. In this algorithm, observations are sampled interactively from the following conditional distributions: p(Y|Ω₀,Ω₁,U,Z,α,θ), p(Ω₀|Y,Ω₁,U,Z,α,θ), p(Ω₁|Y,Ω₀,U,Z,α,θ), and p(W|Y,Ω₀,Ω₁,X,Z,α,θ). Expressions for these conditional distributions are provided in Appendix A.

The M-step updates unknown parameters by maximizing the conditional expectations obtained in the E-step. Structural parameter θ can be updated by maximizing the conditional expectation of L₁ and L₂ with respect to θ by solving the following system of equations:

$$\frac{\partial Q(\alpha ,\theta \mid {\alpha }^{\left(l\right)},{\theta }^{\left(l\right)})}{\partial \theta }=E\left\{\frac{\partial }{\partial \theta }(L_1+L_2)\mid \mathbf{X},\mathbf{Z},{\alpha }^{\left(l\right)},{\theta }^{\left(l\right)}\right\}=0$$ (10)

Threshold parameters α can be updated according to the method described in Shi and Lee [6], and Lee and Song [8]. The M-step is completed by conditional maximization. Technical details on the derivatives of Q(α,θ|α^(l),θ^(l)) with respect to components of θ and the corresponding solutions are given in Appendix B. The convergence of the MCEM algorithm is monitored by the following method proposed in Shi and Copas [40]. After the m₀th MCEM iteration, ${\stackrel{‒}{\theta }}^{\left(l\right)}=({\theta }^{(l-m_0+1)}+\dots +{\theta }^{\left(l\right)})∕m_0$ is computed, and the convergence is monitored using the following stopping rule: For given small values ${\delta }_1^{\ast }$ and ${\delta }_2^{\ast }$ (e.g. 0.001), the procedure is stopped if $\Vert {\stackrel{‒}{\theta }}^{\left(l\right)}-{\stackrel{‒}{\theta }}^{(l-{\gamma }_o^{\ast })}\Vert ∕(\Vert {\stackrel{‒}{\theta }}^{(l-{\gamma }_0^{\ast })}\Vert +{\delta }_1^{\ast })$ is smaller than some predetermined small value ${\delta }_2^{\ast }$. To avoid the danger of stopping early, a value of ${\gamma }_0^{\ast }$ larger than 2 is suggested. Convergence is claimed after the stopping rule is satisfied for several consecutive iterations, and ${\stackrel{‒}{\theta }}^{\left(l\right)}$ is then taken to be the ML estimate. The sample observations of Ω₀ and Ω₁ simulated at the last iteration of the MCEM algorithm provide estimates of the latent variables. Shi and Copas [40] argued that for a sufficiently large m₀, the average of the associative Monte Carlo errors is negligible. To reduce the bias, an appropriate m₀ that can control the Monte Carlo errors within a bearable limit is taken. In the simulation study and the example given in Sections 4 and 5, we take m₀ =50. Finally, good starting values of some parameters (such as Λ_t and ∏_t) could be obtained from the estimates achieved through separate analysis of the individual model at each time point. As each individual model only involves a comparatively small number of parameters, little computing effort is required.

Standard error estimates of the structural parameters in θ are obtained by the following Louis formula [24] through the simulated observations and the ML estimates:

$$-\frac{{\partial }^{2}L(\mathbf{X},\mathbf{Z}\mid \alpha ,\theta )}{\partial \theta \partial {\theta }^{\mathrm{T}}}=E\left\{-\frac{{\partial }^{2}L(\mathbf{Y},{\Omega }_0,{\Omega }_1,\mathbf{U},\mathbf{Z}\mid \alpha ,\theta )}{\partial \theta \partial {\theta }^{\mathrm{T}}}\right\}-\mathrm{Var}\left\{\frac{\partial L(\mathbf{Y},{\Omega }_0,{\Omega }_1,\mathbf{U},\mathbf{Z}\mid \alpha ,\theta )}{\partial \theta }\right\}$$

where expectations are taken with respect to the conditional distribution of (Y,Ω₀,Ω₁,W) given (X,Z) and (α,θ), and the whole expression is evaluated at $(\widehat{\alpha },\widehat{\theta })$. These expectations are difficult to evaluate analytically due to existence of the latent quantities, but they can be approximated, respectively, by the sample mean and the sample covariance matrix of the random sample $\{({\mathbf{Y}}^{\left(j\right)},{\Omega }_0^{\left(j\right)},{\Omega }_1^{\left(j\right)},{\mathbf{W}}^{\left(j\right)});j=1,\dots ,J\}$, generated from $p(\mathbf{Y},{\Omega }_0,{\Omega }_1,\mathbf{W}\mid \mathbf{X},\mathbf{Z},\widehat{\alpha },\widehat{\theta })$ using the proposed hybrid algorithm. Details are not given to save space.

3.2. Model comparison

Model comparison is an important issue in SEM analysis. For the current two-level SEM, it is interesting to evaluate competing models that correspond to various hypotheses about the characteristics of the parameters with respect to time changes. In this article, competing models M₁ and M₂ are compared with the following BIC:

$${\mathrm{BIC}}_{12}=-2\{\log p(\mathbf{X},\mathbf{Z}\mid {\widehat{\alpha }}_1,{\widehat{\theta }}_1,M_1)-\log p(\mathbf{X},\mathbf{Z}\mid {\widehat{\alpha }}_2,{\widehat{\theta }}_2,M_2)\}+(d_1-d_2)\log \left(GT\right)$$ (11)

where $p(\mathbf{X},\mathbf{Z}\mid {\widehat{\alpha }}_k,{\widehat{\theta }}_k,M_k)$ is the observed-data likelihood evaluated at the ML estimates of α_k and θ_k under M_k, and d_k is the dimension of θ_k. The criterion given in Kass and Raftery [41] can be used for interpreting BIC₁₂.

In obtaining BIC₁₂, we must compute the observed-data log-likelihood $\log p(\mathbf{X},\mathbf{Z}\mid {\widehat{\alpha }}_h,{\widehat{\theta }}_h,M_h)$ which involves complicated multiple integrals. Inspired by its successful application in computing the observed-data likelihood for complex latent variable models [8, 42], we apply path sampling [14] to compute BIC₁₂. Path sampling is a generalization of bridge sampling [43] and gives more accurate results in computing complicated multiple integrals. It is conceptually simple, easy to implement, and applicable to a wide range of models [14].

4. A SIMULATION STUDY

We have conducted an extensive simulation study in different settings to empirically evaluate the performance of the MCEM algorithm. To save space, only the results obtained under the following settings are reported here. A special case of the two-level SEM defined in (2), (4), and (5) with p=9 and G=500 at three time points is considered. For the second-level model associated with individuals, c_g0 is a 2×1 vector of covariates, in which the first entry is taken to be 1 to represent the intercept, and the second entry is obtained from observations that are simulated from a standard normal distribution. The true population values of the parameters are given as follows:

$${\mathbf{A}}_0^{\prime }=\left[\begin{array}{ccccccccc}\hfill 0.0\hfill & \hfill 0.0\hfill & \hfill 0.0\hfill & \hfill 0.0\hfill & \hfill 0.0\hfill & \hfill 0.0\hfill & \hfill 0.0\hfill & \hfill 0.0\hfill & \hfill 0.0\hfill \\ \hfill 0.5\hfill & \hfill 0.5\hfill & \hfill 0.5\hfill & \hfill 0.5\hfill & \hfill 0.5\hfill & \hfill 0.5\hfill & \hfill 0.5\hfill & \hfill 0.5\hfill & \hfill 0.5\hfill \end{array}\right],{\Phi }_0=\left[\begin{array}{ccc}\hfill 1.0\hfill & \hfill 0.3\hfill & \hfill 0.3\hfill \\ \hfill 0.3\hfill & \hfill 1.0\hfill & \hfill 0.3\hfill \\ \hfill 0.3\hfill & \hfill 0.3\hfill & \hfill 1.0\hfill \end{array}\right]$$

$${\Lambda }_0^{\prime }=\left[\begin{array}{ccccccccc}\hfill 1.0\ast \hfill & \hfill 0.6\hfill & \hfill 0.6\hfill & \hfill 0.0\ast \hfill & \hfill 0.0\ast \hfill & \hfill 0.0\ast \hfill & \hfill 0.0\ast \hfill & \hfill 0.0\ast \hfill & \hfill 0.0\ast \hfill \\ \hfill 0.0\ast \hfill & \hfill 0.0\ast \hfill & \hfill 0.0\ast \hfill & \hfill 1.0\ast \hfill & \hfill 0.6\hfill & \hfill 0.6\hfill & \hfill 0.0\ast \hfill & \hfill 0.0\ast \hfill & \hfill 0.0\ast \hfill \\ \hfill 0.0\ast \hfill & \hfill 0.0\ast \hfill & \hfill 0.0\ast \hfill & \hfill 0.0\ast \hfill & \hfill 0.0\ast \hfill & \hfill 0.0\ast \hfill & \hfill 1.0\ast \hfill & \hfill 0.6\hfill & \hfill 0.6\hfill \end{array}\right],{\Psi }_0=\text{diag}(0.2,\dots ,0.2)$$

In this paper, parameters with an asterisk are fixed to identify the model. For the measurement equation of the first-level model associated with t =1,2,3 (see (3)), no fixed covariates are involved. The true values of parameters in Λ_t and Ψ_t are given by

$${\Lambda }_t^{\prime }=\left[\begin{array}{ccccccccc}\hfill 1.0\ast \hfill & \hfill 0.8\hfill & \hfill 0.8\hfill & \hfill 0.0\ast \hfill & \hfill 0.0\ast \hfill & \hfill 0.0\ast \hfill & \hfill 0.0\ast \hfill & \hfill 0.0\ast \hfill & \hfill 0.0\ast \hfill \\ \hfill 0.0\ast \hfill & \hfill 0.0\ast \hfill & \hfill 0.0\ast \hfill & \hfill 1.0\ast \hfill & \hfill 0.8\hfill & \hfill 0.8\hfill & \hfill 0.0\ast \hfill & \hfill 0.0\ast \hfill & \hfill 0.0\ast \hfill \\ \hfill 0.0\ast \hfill & \hfill 0.0\ast \hfill & \hfill 0.0\ast \hfill & \hfill 0.0\ast \hfill & \hfill 0.0\ast \hfill & \hfill 0.0\ast \hfill & \hfill 1.0\ast \hfill & \hfill 0.8\hfill & \hfill 0.8\hfill \end{array}\right],{\Psi }_t=\text{diag}(0.5,\dots ,0.5)$$

The latent variable in ω_gt=(η_gt,ξ_1gt,ξ_2gt)′ is modeled by the following structural equation:

$${\eta }_{gt}=b_{10}{d}_{1g0}+b_{20}{d}_{2g0}+b_t{d}_{gt}+{\beta }_{t-1}{\eta }_{g,t-1}+{\gamma }_{1t}{\xi }_{1gt}+{\gamma }_{2t}{\xi }_{2gt}+{\gamma }_{3t}{\xi }_{1gt}{\xi }_{2gt}+{\delta }_{gt}$$ (12)

where the two components in the fixed covariate vector d_g0=(d_1g0,d_2g0)′ are independently generated from the standard bivariate normal distribution, and the fixed covariate d_gt (t=1,2,3) are generated from Bernoulli distribution with probability of success 0.6. The true values of the parameters involved in (12) are: b₁₀=1.0,b₂₀=−1.0; and for all t =1,2,3, b_t =0.7,β_t−1=0.6, γ_1t =γ_2t =0.6, γ₃₁=−0.4,γ₃₂=−0.6,γ₃₃=−0.8, Ψ_δt=0.5, (ϕ_t11,ϕ_t12ϕ_t22) in Φ_tt equal to (1.0,0.3,1.0), and covariances of ξ_igtj and ξ_kgtl are all 0.3. Based on the above specifications of the model and the true parameter values, continuous observations of u_gt as defined by (4) can be obtained. To consider the model with ordered categorical outcomes, the 5th, 6th, and 9th entries in every u_gt were transformed to ordered categorical using the following thresholds (−1.2*,−0.6,0.6,1.2*). Moreover, missing data are considered by randomly deleting some entries in u_gt. About 80 per cent of the observations in the data set are fully observed. The total number of parameters in this two-level SEM is 142. In the MCEM algorithm for computing the ML estimates, we generate 100 observations to approximate the conditional expectations at the E-step of each MCEM iteration. Convergence can be monitored by the method of Shi and Copas [40] by using ${\gamma }_0=3,{\delta }_1^{\ast }={\delta }_2^{\ast }=0.001$. Convergence is claimed if the stopping rule is satisfied for three consecutive iterations. The algorithm stops at less than 100 MCEM iterations in all 100 replications.

Based on 100 replications, the bias (Bias) and the root mean squares (Rms) between the estimates and the true population values of the parameters were computed as follows:

$$\text{Bias of}\widehat{\theta }\left(h\right)={100}^{-1}\sum _{r=1}^{100}{\widehat{\theta }}_r\left(h\right)-{\theta }_0\left(h\right),\text{Rms of}\widehat{\theta }\left(h\right)={\left\{{100}^{-1}\sum _{r=1}^{100}{[{\widehat{\theta }}_r\left(h\right)-{\theta }_0\left(h\right)]}^2\right\}}^{\frac{1}{2}}$$

where θ₀(h) is the hth element of the true parameter vector, and ${\widehat{\theta }}_r\left(h\right)$ is its ML estimate. Standard error (SE) of the estimates were obtained by the arithmetic mean of SE computed through the Louis formula [13] in 100 replications. Simulation results obtained on the basis of 100 replications are presented in Tables I and II. We observe from these tables that the `Bias,' `Rms,' and `SE' are rather small. These results indicate that the empirical performance of the ML estimates obtained by the MCEM algorithm is satisfactory. To save space, results on the nuisance threshold parameters are not presented.

Table I.

Means, root mean squares, and standard errors of the parameter estimates in the first level.

First level
Measurement model				Structural equation
Par	Bias	Rms	SE	Par	Bias	Rms	SE	Par	Bias	Rms	SE
λ1,21	0.004	0.029	0.025	b10	−0.009	0.044	0.019	ϕ11	0.052	0.151	0.082
λ1,31	0.004	0.029	0.025	b20	0.017	0.047	0.020	ϕ12	0.003	0.075	0.071
λ1,52	−0.004	0.081	0.072	b1	0.001	0.096	0.079	ϕ13	0.043	0.091	0.068
λ1,62	−0.008	0.074	0.057	b2	0.001	0.079	0.064	ϕ14	0.013	0.086	0.061
λ1,83	−0.005	0.068	0.054	b3	−0.010	0.075	0.070	ϕ15	0.041	0.100	0.066
λ1,93	−0.020	0.074	0.063	β1	0.011	0.042	0.022	ϕ16	0.008	0.078	0.063
λ2,21	−0.000	0.018	0.016	β2	0.004	0.026	0.015	ϕ22	0.023	0.144	0.104
λ2,31	−0.001	0.019	0.016	γ11	0.004	0.091	0.053	ϕ23	0.008	0.090	0.059
λ2,52	0.001	0.072	0.064	γ21	−0.004	0.085	0.047	ϕ24	0.020	0.097	0.062
λ2,62	−0.016	0.068	0.058	γ31	0.034	0.081	0.031	ϕ25	0.010	0.079	0.064
λ2,83	0.005	0.066	0.044	γ12	−0.011	0.080	0.047	ϕ26	0.020	0.097	0.076
λ2,93	−0.001	0.064	0.065	γ22	−0.015	0.070	0.066	ϕ33	0.066	0.144	0.086
λ3,21	−0.001	0.015	0.011	γ32	0.045	0.096	0.047	ϕ34	0.023	0.090	0.061
λ3,31	−0.001	0.014	0.014	γ13	−0.022	0.090	0.063	ϕ35	0.049	0.101	0.064
λ3,52	−0.002	0.064	0.065	γ23	−0.020	0.078	0.052	ϕ36	0.013	0.085	0.067
λ3,62	−0.004	0.071	0.063	γ33	0.054	0.109	0.044	ϕ44	0.037	0.132	0.091
λ3,83	−0.007	0.063	0.041					ϕ45	0.017	0.088	0.066
λ3,93	0.001	0.071	0.070					ϕ46	0.029	0.105	0.062
								ϕ55	0.067	0.139	0.082
								ϕ56	0.014	0.077	0.060
								ϕ66	0.037	0.141	0.080

Table II.

Means, root mean squares, and standard errors of the parameter estimates in the second level.

Par	Bias	Rms	SE	Par	Bias	Rms	SE	Par	Bias	Rms	SE
a0,11	0.008	0.048	0.041	a0,21	−0.039	0.065	0.046	λ0,21	−0.043	0.065	0.042
a0,12	0.005	0.039	0.032	a0,22	−0.024	0.052	0.035	λ0,31	−0.037	0.061	0.041
a0,13	0.004	0.039	0.033	a0,23	−0.024	0.044	0.029	λ0,52	−0.041	0.067	0.049
a0,14	0.008	0.050	0.041	a0,24	−0.022	0.049	0.046	λ0,62	−0.029	0.055	0.049
a0,15	0.003	0.035	0.074	a0,25	−0.023	0.043	0.038	λ0,83	−0.034	0.060	0.042
a0,16	0.000	0.042	0.075	a0,26	−0.018	0.044	0.046	λ0,93	−0.033	0.063	0.047
a0,17	0.002	0.044	0.048	a0,27	−0.020	0.050	0.044	ϕ0,11	−0.040	0.173	0.099
a0,18	0.004	0.040	0.034	a0,28	−0.015	0.036	0.032	ϕ0,12	−0.024	0.103	0.073
a0,19	−0.001	0.041	0.062	a0,29	−0.013	0.043	0.040	ϕ0,13	−0.036	0.105	0.067
								ϕ0,22	0.008	0.122	0.097
								ϕ0,23	−0.009	0.077	0.062
								ϕ0,33	0.015	0.126	0.088

5. AN APPLICATION OF THE SEM APPROACH: THE LONGITUDINAL STUDY OF COCAINE USE

The data set in this example is obtained from a longitudinal study about cocaine use conducted at the UCLA Center for Advancing Longitudinal Drug Abuse Research. Various measures were collected from patients admitted to the West Los Angeles Veterans Affair Medical Center in 1988–1989 and who met the DSM III-R criteria for cocaine dependence [44]. These patients were assessed at baseline, one year after treatment, two years after treatment, and 12 years after treatment (t =t₁,t₂,t₃,t₄) in 2002–2003. Among these patients located at the 12-year follow-up, some were confirmed to be deceased, some declined to be interviewed, and some were either out of the country or too ill to be interviewed after one year, two years, or at the 12-year follow-up. Hence, there is a considerable amount of missing data. Seven observed variables at each t are involved in the current analysis: (i) cocaine use (CC), an ordered categorical variable with codings 1–5 to denote days of cocaine use per month that are fewer than 2 days, between 2 and 7 days, between 8 and 14 days, between 15 and 25 days, and more than 25 days, respectively; (ii) Beck inventory (BI), an ordered categorical variable with codings 1–5 to denote scores that are less than 3.0, between 3.0 and 8.0, between 9.0 and 20.0, between 21 and 30, and larger than 30; (iii) depression (DEP), an ordered categorical variable based on the Hopkin Symptom Checklist-58 scores, with codings 1–5 to denote scores that are less than 1.1, between 1.1 and 1.4, between 1.4 and 1.8, between 1.8 and 2.5, and larger than 2.50; (iv) number of friends (NF), an ordered categorical variable with codings 1–5 to denote no friend, 1 friend, 2–4 friends, 5–8 friends, more than 9 friends; (v) `have someone to talk to about problem (TP)'; (vi) `currently employed (EMP)'; and (vii) `alcohol dependence (AD) at baseline.' The last three variables are ordered binary variables with {0,1} for {No,Yes}. The sample size is 223, and the frequencies of all variables at different time points are given in Table III.

Table III.

Frequencies of the ordered categorical variables at different time points in the cocaine use example.

		Categories
Variables		1	2	3	4	5	No=0	Yes=1	Total
t = 1	CC	13	24	38	37	111			223
	BI	14	35	68	31	12			160
	DEP	15	29	29	57	26			156
	NF	27	30	64	27	8			150
	TP						30	170	200
	EMP						88	135	223
	AD						120	103	223
t = 2	CC	89	46	23	22	43			223
	BI	30	47	72	24	10			183
	DEP	37	46	40	48	18			189
	NF	25	27	90	21	18			181
	TP						15	178	193
	EMP						69	154	219
	AD						120	103	223
t = 3	CC	105	30	25	16	47			223
	BI	37	44	78	22	11			192
	DEP	47	40	47	40	13			187
	NF	22	22	94	29	23			190
	TP						9	202	211
	EMP						79	144	223
	AD						120	103	223
t = 4	CC	172	15	14	8	14			223
	BI	56	63	72	15	16			222
	DEP	63	51	43	46	20			223
	NF	21	37	113	26	23			220
	TP						22	198	220
	EMP						84	139	223
	AD						120	103	223

In this study, we consider observed variables (CC, BI, DEP, NF, TP) and two fixed covariates (EMP, AD) for each individual, which were measured at four time points. The proposed dynamic two-level SEM (see equations (1)–(3) and (5)) is applied to analyze this data set. The second-level model for assessing invariant effects over time is defined by the following two-factor confirmatory factor analysis model:

$${\mathbf{y}}_g={\mathbf{A}}_0{c}_{g0}+{\Lambda }_0{\omega }_{g0}+{\epsilon }_{g0},g=1,\dots ,223$$ (13)

where y_g corresponds to (CC, BI, DEP, NF, TP) of the gth individual, c_g0 is fixed at 1.0 so that A₀ is a vector of intercepts, ω_g0=(ω_g01,ω_g02)′, Ψ₀=diag(0.0*,ψ₀₂,ψ₀₃,ψ₀₄,ψ₀₅),

$${\Lambda }_0^{\prime }=\left[\begin{array}{ccccc}\hfill 1.0\ast \hfill & \hfill 0\ast \hfill & \hfill 0\ast \hfill & \hfill 0\ast \hfill & \hfill 0\ast \hfill \\ \hfill 0\ast \hfill & \hfill {\lambda }_{22,0}\hfill & \hfill {\lambda }_{32,0}\hfill & \hfill {\lambda }_{42,0}\hfill & \hfill {\lambda }_{52,0}\hfill \end{array}\right]\mathrm{and}{\Phi }_0=\left[\begin{array}{cc}\hfill 1.0\ast \hfill & \hfill \hfill \\ \hfill {\varphi }_{21,0}\hfill & \hfill 1.0\ast \hfill \end{array}\right]$$

In this example, parameters with an asterisk were fixed for specifying an identified model. Note that as y_g1 is fully defined by CC, λ_11,0 and ψ₀₁ are, respectively, fixed at 1.0 and 0.0 according to the usual practice of SEM [2]. In this formulation, ω_g01 can be interpreted as the invariant portion of cocaine use and ω_g02 can be interpreted as an invariant general latent factor that is not changed over time. The correlation of ω_g01 and ω_g02 is assessed by ϕ_21,0. The first-level model for assessing various dynamic effects that are changed over time is defined by the following nonlinear SEM. The measurement model is defined by

$${\mathbf{v}}_{gt}={\Lambda }_t{\omega }_{gt}+{\epsilon }_{gt},g=1,\dots ,223,t=t_1,t_2,t_3,t_4$$ (14)

where ω_gt =(η_gt,ξ_1gt,ξ_2gt)′, and

$${\Lambda }_t^{\prime }=\left[\begin{array}{ccccc}\hfill 1.0\ast \hfill & \hfill 0\ast \hfill & \hfill 0\ast \hfill & \hfill 0\ast \hfill & \hfill 0\ast \hfill \\ \hfill 0\ast \hfill & \hfill 1.0\ast \hfill & \hfill {\lambda }_{32,t}\hfill & \hfill 0\ast \hfill & \hfill 0\ast \hfill \\ \hfill 0\ast \hfill & \hfill 0\ast \hfill & \hfill 0\ast \hfill & \hfill 1.0\ast \hfill & \hfill {\lambda }_{53,t}\hfill \end{array}\right]$$

The nonoverlapping structure of Λ_t is used for achieving a clear interpretation of the latent variables. Based on the meaning of the observed variables and the nonoverlapping structure of Λ_t, latent variables η_gt,ξ_1gt,ξ_2gt can be clearly interpreted as `cocaine use (CC),' `psychiatric problems,' and `social support.' In the structural equations of the first-level model, cocaine use was treated as the dependent variable (η_gt), and it is regressed on various independent latent variables, together with fixed covariates EMP(d_gt) and AD(d_g0) that are variant and invariant over time, respectively. More specifically, the structural equations are defined by

$$\begin{array}{cc}\hfill \mathrm{for}t=t_1:& {\eta }_{g1}=b_0{d}_{g0}+b_1{d}_{g1}+{\gamma }_{11}{\xi }_{1g1}+{\gamma }_{21}{\xi }_{2g1}+{\delta }_{g1}\hfill \\ \hfill \mathrm{for}t=t_2,t_3,t_4:& {\eta }_{gt}=b_0{d}_{g0}+b_t{d}_{gt}+{\beta }_{t-1}{\eta }_{g,t-1}+{\gamma }_{1t}{\xi }_{1gt}+{\gamma }_{2t}{\xi }_{2gt}+{\delta }_{gt}\hfill \end{array}$$ (15)

Clearly, (15) is a special case of (5). So far, this dynamic two-level SEM involves 94 unknown parameters. As the sample size is relatively small (n=223), it is not worthwhile to treat the nuisance threshold parameters of the ordered categorical variables as unknown. Hence they are fixed at α_jh =Φ*⁻¹ (ρ_jh), where Φ* is the distribution function of N[0,1], and ρ_jh are the observed cumulative marginal proportions of the categories with z_j<h, see [6, 36].

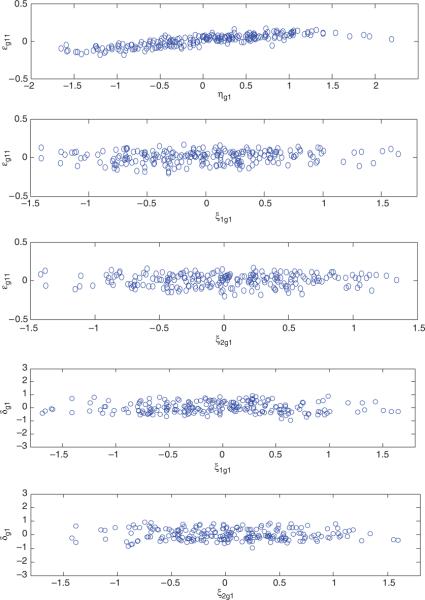
Let M₁ be the two-level model defined as above. To roughly illustrate model comparison with BIC, we compare it with M₂, which is a single-level model that is defined by equations (14) and (15) without the second level corresponding to y_g as given in (13). In the MCEM algorithm for computing the ML estimates under the competing models, we generate 30+5l observations to approximate the conditional expectations at the E-step of the lth iteration (see [8]). Based on the stopping rule given in Section 4, the algorithm stops at the 202nd MCEM iteration in M₁, and ${\stackrel{‒}{\theta }}^{\left(202\right)}$ is taken as the ML estimate in M₁. Fewer MCEM iterations are required to attain the convergence in the simpler model M₂. The BIC value for model comparison between M₁ and M₂ is BIC₁₂=−140.6. According to the interpretation of BIC [41], this result indicates that the two-level model M₁ is significantly better than the single-level model M₂. The ML estimates and their standard error estimates (which were computed using 5000 simulated observations) of parameters in the first and second level of the selected model M₁ are, respectively, presented in path diagrams displayed in Figures 1(a) and (b), while those corresponding to Φ are presented in Table IV. Inspired by the model checking technique in regression and the analysis in Lee and Song [8], we use the following estimated residuals to reveal the adequacy of the measurement models and the structural equation in proposed two-level SEM for fitting the data: ${\widehat{\epsilon }}_{gt}={\widehat{\mathbf{u}}}_{gt}-{\widehat{\mathbf{y}}}_g-{\widehat{\Lambda }}_t{\widehat{\omega }}_{gt}$, ${\widehat{\epsilon }}_{g0}={\widehat{\mathbf{y}}}_g-{\widehat{\mathbf{A}}}_0{\mathbf{c}}_{g0}-{\widehat{\Lambda }}_0{\widehat{\omega }}_{g0}$, ${\widehat{\delta }}_{g1}={\widehat{\eta }}_{g1}-{\widehat{b}}_0{d}_{g0}-{\widehat{b}}_1{d}_{g1}-{\widehat{\gamma }}_{11}{\widehat{\xi }}_{1g1}-{\widehat{\gamma }}_{21}{\widehat{\xi }}_{2g1}$, and ${\widehat{\delta }}_{gt}={\widehat{\eta }}_{gt}-{\widehat{b}}_0{d}_{g0}-{\widehat{b}}_t{d}_{gt}-{\widehat{\beta }}_{t-1}{\widehat{\eta }}_{g,t-1}-{\widehat{\gamma }}_{1t}{\widehat{\xi }}_{1gt}-{\widehat{\gamma }}_{2t}{\widehat{\xi }}_{2gt}$, for t =t₂, t₃, t₄. Plots of the estimated residual in the first level ${\widehat{\epsilon }}_{gt1}$ versus, ${\widehat{\eta }}_{gt}$, ${\widehat{\xi }}_{1gt}$, and ${\widehat{\xi }}_{2gt}$ and plots of ${\widehat{\delta }}_{gt}$ versus ${\widehat{\xi }}_{1gt}$ and ${\widehat{\xi }}_{2gt}$ at t =t₁ are presented in Figure 2. Other estimated residual plots have similar behaviors. These plots lie within two parallel horizontal lines that are centered at zero, and no linear or quadratic trends are detected. This roughly indicates that the proposed measurement models and the structural equation are adequate in fitting the data.

Figure 1.

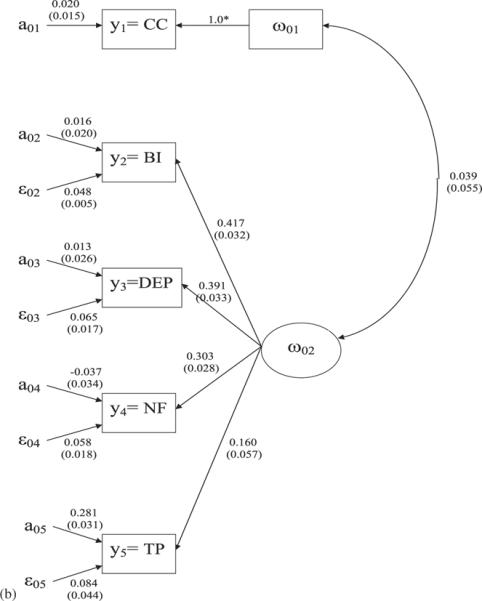
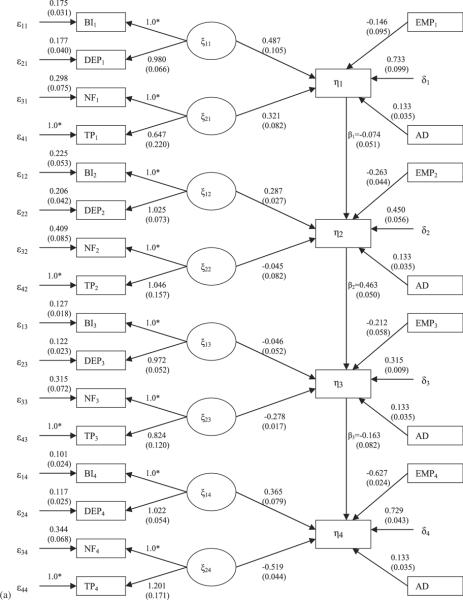
(a) Path diagram and estimates of some parameters of the first-level model in M₁, where observed variables are represented by rectangles, latent variables are represented by ellipse, and standard error estimates are in parenthesis. Here, η_t,ξ_1t, and ξ_2t, respectively, denote `cocaine use (CC),' `psychiatric problems,' and `social support' at t =1,2,3,4. (b) Path diagram and estimates of some parameters of the second-level model in M₁, where observed variables are represented by rectangles, latent variables are represented by ellipse, and standard error estimates are in parenthesis.

Table IV.

ML estimates and their standard error estimates (in parenthesis) of Φ [Φ_titj] in the cocaine use example.

t = 1	0.601 (0.054)
	−0.354 (0.049)	0.571 (0.056)
t = 2	0.317 (0.045)	−0.149 (0.029)	0.612 (0.065)				Symmetric part
	−0.283 (0.048)	0.272 (0.045)	−0.355 (0.040)	0.469 (0.051)
t = 3	0.304 (0.053)	−0.426 (0.031)	0.402 (0.061)	−0.324 (0.045)	0.689 (0.048)
	−0.166 (0.053)	0.374 (0.019)	−0.323 (0.051)	0.271 (0.006)	−0.435 (0.047)	0.544 (0.052)
t = 4	0.100 (0.047)	−0.155 (0.042)	0.093 (0.042)	−0.139 (0.039)	0.204 (0.054)	−0.120 (0.043)	0.605 (0.034)
	−0.007 (0.039)	0.137 (0.031)	−0.183 (0.056)	0.235 (0.040)	−0.228 (0.051)	0.149 (0.037)	−0.277 (0.040)	0.567 (0.066)

Figure 2.

Plots of ${\widehat{\epsilon }}_{g11}$ versus ${\widehat{\eta }}_{g1}$, ${\widehat{\xi }}_{1g1}$, and ${\widehat{\xi }}_{2g1}$, and plots of ${\widehat{\delta }}_{g1}$ versus ${\widehat{\xi }}_{1g1}$ and ${\widehat{\xi }}_{2g1}$.

We can conclude from the model comparison result given by BIC₁₂ (=−140.6) value that it is significantly better to include a second-level model y_g for incorporating characteristics that are invariant over time to analyze the longitudinal properties of u_gt, see equation (1). It follows from equation (13) and Figure 1(b) that the following findings can be achieved: (i) All the factor loading estimates are significant; this indicates substantial associations of the observed variables with the general latent factor. (ii) The correlation between the general latent factor and cocaine use is not significant. (iii) As expected, the intercept estimates corresponding to the ordered categorial variables are close to zero. The intercept estimate $\left({\widehat{a}}_{05}\right)$ corresponding to the dichotomous variable y₅ is 0.281. This indicates that y₅=0 if the underlying latent continuous variable is less than −0.281; otherwise y₅=1. Clearly, the above findings cannot be obtained by a single level model without the multilevel component.

The longitudinal patterns of the more important parameters in the first-level model are displayed in Figures 3(a) and (b). From Figures 1(a) and 3(a) and (b), the following phenomena are observed: (i) As λ₃₂ at all time points (t =t₁, t₂, t₃, t₄) are close to 1.0, BI and DEP give equal constant loadings over time to the latent variable `psychiatric problems, ξ<sub>1gt</sub>.' This indicates that the relationship between `psychiatric problems' and {BI,DEP} are very stable over time (they both measure depression symptoms). (ii) The fixed covariate AD has a positive effect on `cocaine use, CC.' (iii) The fixed covariate EMP has a negative effect on `cocaine use, CC' at all time points (see the line `b<sub>1</sub>'), which indicates that having a job reduces cocaine use. Also note that the effect of EMP is more substantial during the long-term follow-up period. (iv) The positive effect of the latent variable `social support' on cocaine use at baseline changed quickly to negative effects at two years after intake, as well as years after treatment (see the line γ₂). This indicates that social support had a substantial impact on reducing cocaine use during the post-treatment period. (v) Note also that the magnitude of ${\widehat{\gamma }}_1$ decreases from baseline to one or two years after intake, but rebounds during the long-term follow-up period. This indicates that the impact of `psychiatric problems' is still strong during a long period of time after treatment, although it may be reduced during treatment or shortly after. (vi) It is interesting to find that the variances ϕ₁₁,ϕ₂₂, and ϕ₁₂ are basically constant over time (see Figure 3(b)). (vii) For λ₅₃, γ₁, and γ₂, their changes are substantial from baseline to one or two years after intake, but less substantial in the subsequent years (see Figures 3(a) and (b)). (viii) The effects of cocaine use from t =t₁ to t =t₂, and from t =t₂ to t =t₃ are $-0.074(={\widehat{\beta }}_1)$, and $0.463(={\widehat{\beta }}_2)$, respectively. After a time difference of 10 years, the corresponding effect from t =t₃ to t =t₄ is reduced to $-0.163(={\widehat{\beta }}_3)$ (see Figure 1(a)). Most of these effects are significant. These findings are consistent with prior literature showing a strong stability of cocaine use over time. The present modeling results also demonstrate a positive association of psychiatric problems with cocaine use during two of the three follow-up points. The increasing negative association of social support with cocaine use is discernible at the later follow-up points, which suggests that social support becomes a stronger factor influencing cocaine use when the treatment effects dissipate at the longer follow-up point, and future studies are needed to further this investigation.

Figure 3.

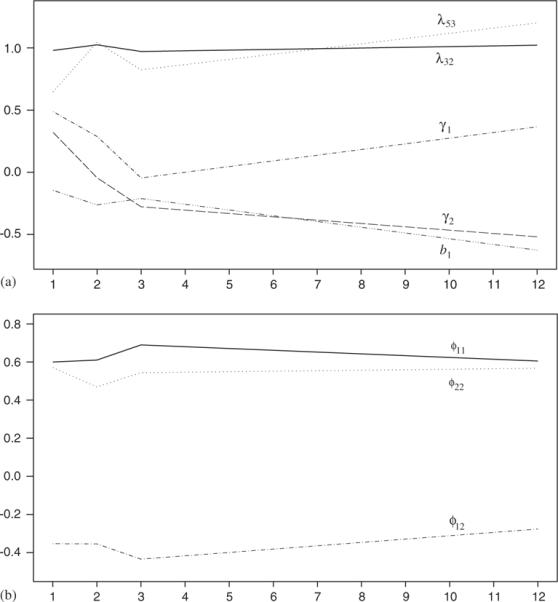
(a) Plots of ML estimates of λ₃₂,λ₅₃,b, γ₁, and γ₂ at t =t₁,t₂,t₃, and t₄ and (b) plots of ML estimates of ϕ₁₁,ϕ₁₂, and ϕ₂₂ at t =t₁,t₂,t₃, and t₄.

6. DISCUSSION

An appealing feature of SEMs is the ability to group the correlated observed variables into latent variables so that instead of dealing with a large number of observed variables, we can utilize the structural equation with a much smaller number of latent variables to assess inter-relationships among them. This feature is particularly advantageous in analyzing multivariate longitudinal data, because the comprehensive model that is simultaneously defined at every time point involves p×T observed variables, which may be too large for a regression model. Moreover, the interpretations based on latent variables are more clear and precise than those that are based on the original observed variables. The proposed two-level nonlinear SEM with covariates provides a rather general framework for assessing various characteristics of changes with respect to time.

There are a few limitations of the current approach that indicate areas needing future research. First, similar to many other statistical models, the proposed SEM depends on the assumption that the latent variables and the residual errors are normally distributed. As this assumption may be violated for many types of biomedical data, it is necessary to develop robust methods that are less reliant on this assumption [45]. Second, due to the complexities of the proposed two-level nonlinear SEM with ordered categorical variables, which involves observed data with a correlation structure and missing entries, and the fact that a saturated model does not exist in the context of nonlinear SEM, we do not have a classical likelihood ratio test statistic to assess the goodness-of-fit of the proposed model. In a Bayesian approach with the unknown parameters treated as random, goodness-of-fit of a hypothesized model can be assessed by using Bayesian predictive p-values (BPPs) [46], which required integration over the posterior distribution of the unknown parameters in the model. As it is simple to perform numerically using posterior simulation draws of the parameters within the iterations of a Markov chain Monte Carlo algorithm in the Bayesian estimation, the BPPs have been widely applied in Bayesian analyses of some latent variable models in biostatistics (see [47]) as well as many SEMs (see [48] and the references therein). However, there is a conceptual problem in applying BPPs in an ML analysis, because parameters are not considered as random and the posterior distribution of the unknown parameters is not related to the ML approach. Hence, we propose the BIC for model comparison, and residual plots for model checking (see Figure 2 in the example). Clearly, the development of a more formal statistic for goodness-of-fit of the model in the ML context is an interesting topic for future research. Alternatively, the Bayesian approach can be used. Third, the current ML method cannot handle unordered categorical data. As genotype variables are unordered categorical, it is important to develop methods to handle this kind of data for genetic analysis. Fourth, because the missing data considered here are missing at random, it is necessary to generalize the ML approach in analyzing missing data with a nonignorable missing mechanism.

APPENDIX A: CONDITIONAL DISTRIBUTIONS AND IMPLEMENTATION OF THE E-STEP

Based on the definition and properties of the current model, it can be shown that

$$p(\mathbf{Y}\mid {\Omega }_0,{\Omega }_1,\mathbf{U},\mathbf{Z},\alpha ,\theta )=\prod _{g=1}^{G}p({\mathbf{y}}_g\mid {\omega }_{g0},{\omega }_g,{\mathbf{u}}_g,\theta )$$

where

$$\begin{array}{cc}\hfill p& ({\mathbf{y}}_g\mid {\omega }_{g0},{\omega }_g,{\mathbf{u}}_g,\theta )\hfill \\ \hfill & \stackrel{D}{=}\mathrm{N}[{\Sigma }_v\{\sum _{t=1}^T{\Psi }_t^{-1}({\mathbf{u}}_{gt}-{\mathbf{A}}_t{\mathbf{c}}_{gt}-{\Lambda }_t{\omega }_{gt})\phantom{\}}\phantom{]}\hfill \\ \hfill & \phantom{[}\phantom{\{}+{\Psi }_0^{-1}({\mathbf{A}}_0{\mathbf{c}}_{g0}+{\Lambda }_0{\omega }_{g0})\},{\Sigma }_v]\mathrm{with}{\Sigma }_v={\left(\sum _{t=1}^T{\Psi }_t^{-1}+{\Psi }_0^{-1}\right)}^{-1}\hfill \end{array}$$ (A1)

$$p({\Omega }_0\mid \mathbf{Y},{\Omega }_1,\mathbf{U},\mathbf{Z},\alpha ,\theta )=\prod _{g=1}^{G}p({\omega }_{g0}\mid {\mathbf{y}}_g,\theta )$$

where

$$p({\omega }_{g0}\mid {\mathbf{y}}_g,\theta )\stackrel{D}{=}\mathrm{N}[{\mathbf{m}}_{g0},{\Sigma }_{g0}]$$ (A2)

in which

$$m_{g0}={\Sigma }_{g0}{\Lambda }_0^{\prime }{\Psi }_0^{-1}{\mathbf{y}}_g\mathrm{and}{\Sigma }_{g0}={({\Phi }_0^{-1}+{\Lambda }_0^{\prime }{\Psi }_0{\Lambda }_0)}^{-1}$$

$$p({\Omega }_1\mid \mathbf{Y},{\Omega }_0,\mathbf{U},{\mathbf{Z}}_{\mathrm{obs}},\alpha ,\theta )=\prod _{g=1}^{G}p({\omega }_g\mid {\mathbf{y}}_g,{\mathbf{u}}_g,\theta )$$

where

$$\begin{array}{cc}\hfill p({\omega }_g\mid {\mathbf{y}}_g,{\mathbf{u}}_g,\theta )\propto & \exp [-\frac{1}{2}\{{\xi }_g^{\prime }{\Phi }^{-1}{\xi }_g+\sum _{t=1}^T({\mathbf{u}}_{gt}-{\mathbf{y}}_g-{\mathbf{A}}_t{\mathbf{c}}_{gt}-{\Lambda }_t{\omega }_{gt})\prime \phantom{\}}\phantom{]}\hfill \\ \hfill & \times {\Psi }_t^{-1}({\mathbf{u}}_{gt}-{\mathbf{y}}_g-{\mathbf{A}}_t{\mathbf{c}}_{gt}-{\Lambda }_t{\omega }_{gt})\hfill \\ \hfill & \phantom{[}\phantom{\{}+({\eta }_{gt}-{\mathbf{B}}_0{\mathbf{d}}_{g0}-{\Pi }_t{\mathbf{h}}_{gt})\prime {\Psi }_{\delta t}^{-1}({\eta }_{gt}-{\mathbf{B}}_0{\mathbf{d}}_{g0}-{\Pi }_t{\mathbf{h}}_{gt})\}]\hfill \end{array}$$ (A3)

$$\begin{array}{cc}\hfill p(\mathbf{W}\mid \mathbf{Y},{\Omega }_0,{\Omega }_1,\mathbf{X},\mathbf{Z},\alpha ,\theta )& =p(\mathbf{W}\mid \mathbf{Y},{\Omega }_1,\mathbf{Z},\alpha ,\theta )\hfill \\ \hfill & =\prod _{g=1}^G\prod _{t=1}^T\prod _{j=1}^{s}p(w_{gtj}\mid y_{gj},{\omega }_{gt},z_{gtj},\alpha ,\theta )\hfill \end{array}$$

and

$$p(w_{gtj}\mid y_{gj},{\omega }_{gt},z_{gtj},\alpha ,\theta )\stackrel{D}{=}\mathrm{N}[y_{gj}+{\mathbf{A}}_{ij}^{\prime }{\mathbf{c}}_{gt}+{\Lambda }_{tj}^{\prime }{\omega }_{gt},{\psi }_{tj}]\mathit{I}(w_{gtj}\in ({\alpha }_{j,z_{gtj}},{\alpha }_{j,z_{gtj}}+1])$$ (A4)

where z_{gt j} is jth element of z_gt associated with ordered categorical variable w_{gt j}.

The conditional distributions given in (A1) and (A2) are standard normal distributions, drawing observations from them is straightforward. As (A3) is a nonstandard distribution, the MH algorithm is used to simulate observations from (A3). (A4) involves the univariate truncated normal distribution. Simulating observations from this distribution is done by the inverse distribution method proposed in Devroye [49].

To simulate observations from the target density p(ω_g|·) in (A3), let ${\eta }_g=({\eta }_1^{\prime },\dots ,{\eta }_T^{\prime })\prime$, Ψ=diag(Ψ₁, …, Ψ_T), Ψ_δ=diag(Ψ_δ1, …, Ψ_δT), λ_tm be the mth column of Λ_t,

$$\mathbf{A}=\left(\begin{array}{ccc}\hfill {\mathbf{A}}_1\hfill & \hfill \cdots \hfill & \hfill 0\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill \\ \hfill 0\hfill & \hfill \cdots \hfill & \hfill {\mathbf{A}}_T\hfill \end{array}\right),\Lambda =\left(\begin{array}{ccccccccccccc}\hfill {\lambda }_{11}\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 0\hfill & \hfill {\lambda }_{12}\hfill & \hfill \cdots \hfill & \hfill {\lambda }_{1q}\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill {\lambda }_{21}\hfill & \hfill \cdots \hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 0\hfill & \hfill {\lambda }_{22}\hfill & \hfill \cdots \hfill & \hfill {\lambda }_{2q}\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 0\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \cdots \hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \cdots \hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \cdots \hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \cdots \hfill & \hfill ⋮\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill {\lambda }_{T1}\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 0\hfill & \hfill {\lambda }_{T2}\hfill & \hfill \cdots \hfill & \hfill {\lambda }_{Tq}\hfill \end{array}\right)$$

$$\Pi =\left(\begin{array}{cccccccccccccc}\hfill {\mathbf{B}}_0\hfill & \hfill {\mathbf{B}}_1\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill {\Gamma }_1\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 0\hfill \\ \hfill {\mathbf{B}}_0\hfill & \hfill 0\hfill & \hfill {\mathbf{B}}_2\hfill & \hfill \cdots \hfill & \hfill 0\hfill & \hfill {\beta }_1\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill {\Gamma }_2\hfill & \hfill \cdots \hfill & \hfill 0\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \cdots \hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \cdots \hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \cdots \hfill & \hfill ⋮\hfill \\ \hfill {\mathbf{B}}_0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill {\mathbf{B}}_T\hfill & \hfill {\beta }_1\hfill & \hfill {\beta }_2\hfill & \hfill \cdots \hfill & \hfill {\beta }_{T-1}\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \hfill & \hfill {\Gamma }_T\hfill \end{array}\right)$$

and Π_*=I–Π, where I is an identity matrix with appropriate dimension. We choose N[·,σ²Σ_*] as the proposal distribution, where ${\sum }_{\ast }^{-1}={\sum }^{-1}+\Lambda \prime \Psi \Lambda$ and

$${\Sigma }^{-1}=\left[\begin{array}{cc}\hfill {\Pi }_{\ast }^{\prime }{\Psi }_{\delta }^{-1}{\Pi }_{\ast }\hfill & \hfill -{\Pi }_{\ast }^{\prime }{\Psi }_{\delta }^{-1}\Gamma \Delta \hfill \\ \hfill -{\Delta }^{\prime }{\Gamma }^{\prime }{\Psi }_{\delta }^{-1}{\Pi }_{\ast }\hfill & \hfill {\Phi }^{-1}+{\Delta }^{\prime }{\Gamma }^{\prime }{\Psi }_{\delta }^{-1}\Gamma \Delta \hfill \end{array}\right]$$

where $\Delta =\partial {\mathbf{F}}_1\left({\xi }_g\right)∕\partial {\xi }_g\mid {\xi }_g=0$. $\mathrm{Let}p(\cdot \mid {\mu }_g^{\ast },{\sigma }^2{\Sigma }_{\ast })$ be the density function corresponding to the proposal distribution $\mathrm{N}[{\mu }_g^{\ast },{\sigma }^2{\Sigma }_{\ast }]$; the MH algorithm is implemented as follows: At the lth iteration with a current value ${\omega }_g^{\left(l\right)}$, a new candidate ${\omega }_g^{\ast }$ is generated from $p(\cdot \mid {\omega }_g^{\left(l\right)},{\sigma }^2{\Sigma }_{\ast })$ and accepting this new candidate with probability min$\{1,p({\omega }_g^{\ast }\mid \cdot )∕p({\omega }_g^{\left(l\right)}\mid \cdot )\}$. The variance σ² can be chosen such that the average acceptance rate is approximately 0.25 or more, see [50].

APPENDIX B: DETAILS IN COMPLETING THE M-STEP

Let ${\mathbf{A}}_{tj}^{\prime }$, ${\mathbf{A}}_{0j}^{\prime }$, ${\Lambda }_{tj}^{\prime }$, ${\Lambda }_{0j}^{\prime }$, ${\Pi }_{tj}^{\prime }$, and B_0j be the jth rows of A_t, A₀, Λ_t, Λ₀, Π_t, and B₀. The derivatives involved in the system of equations given in ∂Q/∂θ=0 are

$$\frac{\partial L_1}{\partial {\mathbf{A}}_t}=\sum _{g=1}^G\sum _{t=1}^T{\Psi }_t^{-1}({\mathbf{u}}_{gt}-{\mathbf{y}}_g-{\mathbf{A}}_t{\mathbf{c}}_{gt}-{\Lambda }_t{\omega }_{gt}){\mathbf{c}}_{gt}^{\prime }$$

$$\frac{\partial L_1}{\partial {\Lambda }_{tj}}=\sum _{g=1}^G\sum _{t=1}^T{\psi }_{tj}^{-1}(u_{gtj}-y_{gj}-{\mathbf{A}}_{tj}{\mathbf{c}}_{gt}-{\Lambda }_{tj}{\omega }_{gt}){\omega }_{gt}^{\prime }$$

$$\begin{array}{cc}\hfill \frac{\partial L_1}{\partial \text{diag}\left({\Psi }_t\right)}=& \frac{1}{2}\text{diag}[\sum _{g=1}^G\sum _{t=1}^T{\Psi }_t^{-1}\{({\mathbf{u}}_{gt}-{\mathbf{y}}_g-{\mathbf{A}}_t{\mathbf{c}}_{gt}-{\Lambda }_t{\omega }_{gt})\phantom{]}\hfill \\ \hfill & \phantom{[}\times ({\mathbf{u}}_{gt}-{\mathbf{y}}_g-{\mathbf{A}}_t{\mathbf{c}}_{gt}-{\Lambda }_t{\omega }_{gt})\prime -{\Psi }_t\}{\Psi }_t^{-1}]\hfill \end{array}$$

$$\frac{\partial L_1}{\partial {\Pi }_{tj}}=\sum _{g=1}^G\sum _{t=1}^T{\psi }_{\delta tj}^{-1}({\eta }_{gtj}-{\mathbf{B}}_{0j}{\mathbf{d}}_{g0}-{\Pi }_{tj}{\mathbf{h}}_{gt}){\mathbf{h}}_{gt}^{\prime }$$

$$\frac{\partial L_1}{\partial {\mathbf{B}}_0}=\sum _{g=1}^G\sum _{t=1}^T{\Psi }_{\delta t}^{-1}({\eta }_{gt}-{\mathbf{B}}_0{\mathbf{d}}_{g0}-{\Pi }_t{\mathbf{h}}_{gt}){\mathbf{d}}_{g0}$$

$$\frac{\partial L_1}{\partial \Phi }=\frac{1}{2}{\Phi }^{-1}\sum _{g=1}^G({\xi }_g{\xi }_g^{\prime }-\Phi ){\Phi }^{-1}$$

$$\frac{\partial L_1}{\partial \text{diag}\left({\Psi }_{\delta t}\right)}=\frac{1}{2}\text{diag}\left[\sum _{g=1}^G\sum _{t=1}^T{\Psi }_{\delta t}^{-1}\{({\eta }_{gt}-{\mathbf{B}}_0{\mathbf{d}}_{g0}-{\Pi }_t{\mathbf{h}}_{gt})({\eta }_{gt}-{\mathbf{B}}_0{\mathbf{d}}_{g0}-{\Pi }_t{\mathbf{h}}_{gt})\prime -{\Psi }_{\delta t}\}{\Psi }_{\delta t}^{-1}\right]$$

$$\frac{\partial L_2}{\partial {\mathbf{A}}_0}={\Psi }_0^{-1}\sum _{g=1}^G({\mathbf{y}}_g-{\mathbf{A}}_0{\mathbf{c}}_{g0}-{\Lambda }_0{\omega }_{g0}){\mathbf{c}}_{g0}^{\prime }$$

$$\frac{\partial L_2}{\partial {\Lambda }_{0j}}={\psi }_{0j}^{-1}\sum _{g=1}^G(y_{gj}-{\mathbf{A}}_{0j}{\mathbf{c}}_{g0}-{\Lambda }_{0j}{\omega }_{g0}){\omega }_{g0}^{\prime }$$

$$\frac{\partial L_0}{\partial \mathrm{diag}\left({\Psi }_0\right)}=\frac{1}{2}\mathrm{diag}\left[{\Psi }_0^{-1}\sum _{g=1}^G\{({\mathbf{y}}_g-{\mathbf{A}}_0{\mathbf{c}}_{g0}-{\Lambda }_0{\omega }_{g0})({\mathbf{y}}_g-{\mathbf{A}}_0{\mathbf{c}}_{g0}-{\Lambda }_0{\omega }_{g0})\prime -{\Psi }_0\}{\Psi }_0^{-1}\right]$$

$$\frac{\partial L_2}{\partial {\Phi }_0}=\frac{1}{2}{\Phi }_0^{-1}\sum _{g=1}^G({\omega }_{g0}{\omega }_{g0}^{\prime }-{\Phi }_0){\Phi }_0^{-1}$$

Conditional on other parameters, the solution of each individual equation in ∂Q/∂θ=0 can be obtained as follows:

$${\mathbf{A}}_t={\left(\sum _{g=1}^G\sum _{t=1}^T{\mathbf{c}}_{gt}{\mathbf{c}}_{gt}^{\prime }\right)}^{-1}\sum _{g=1}^G\sum _{t=1}^{T}E[{\mathbf{u}}_{gt}-{\mathbf{y}}_g-{\Lambda }_t{\omega }_{gt}\mid \mathbf{X},\mathbf{Z},\alpha ,\theta ]$$

$${\Lambda }_{tj}^{\prime }={\left(\sum _{g=1}^G\sum _{t=1}^{T}E[{\omega }_{gt}{\omega }_{gt}^{\prime }\mid \mathbf{X},\mathbf{Z},\alpha ,\theta ]\right)}^{-1}\times \sum _{g=1}^G\sum _{t=1}^{T}E[{\omega }_{gt}(u_{gtj}-y_{gj}-{\mathbf{A}}_{tj}{\mathbf{c}}_{gt})\mid \mathbf{X},\mathbf{Z},\alpha ,\theta ]$$

$${\psi }_{tj}=\frac{1}{n}\sum _{g=1}^G\sum _{t=1}^{T}E[{(u_{gtj}-y_{gj}-{\mathbf{A}}_{tj}{\mathbf{c}}_{gt}-{\Lambda }_{tj}{\omega }_{gt})}^2\mid \mathbf{X},\mathbf{Z},\alpha ,\theta ]$$

$${\Pi }_{tj}^{\prime }={\left(\sum _{g=1}^G\sum _{t=1}^{T}E[{\mathbf{h}}_{gt}{\mathbf{h}}_{gt}^{\prime }\mid \mathbf{X},\mathbf{Z},\alpha ,\theta ]\right)}^{-1}\sum _{g=1}^G\sum _{t=1}^{T}E[{\mathbf{h}}_{gt}({\eta }_{gtj}-{\mathbf{B}}_{0j}{\mathbf{d}}_{g0})\mid \mathbf{X},\mathbf{Z},\alpha ,\theta ]$$

$${\mathbf{B}}_0={\left(\sum _{g=1}^G{\mathbf{d}}_{g0}{\mathbf{d}}_{g0}^{\prime }\right)}^{-1}\sum _{g=1}^G\sum _{t=1}^{T}E[{\eta }_{gt}-{\Pi }_t{\mathbf{h}}_{gt}\mid \mathbf{X},\mathbf{Z},\alpha ,\theta ]$$

$$\Phi =\frac{1}{n}\sum _{g=1}^{G}E[{\xi }_g{\xi }_g^{\prime }\mid \mathbf{X},\mathbf{Z},\alpha ,\theta ]$$

$${\psi }_{\delta tj}=\frac{1}{n}\sum _{g=1}^G\sum _{t=1}^{T}E[{({\eta }_{gtj}-{\mathbf{B}}_{0j}{\mathbf{d}}_{g0}-{\Pi }_{gtj}{\mathbf{h}}_{gt})}^2\mid \mathbf{X},\mathbf{Z},\alpha ,\theta ]$$

$${\mathbf{A}}_0={\left(\sum _{g=1}^G{\mathbf{c}}_{g0}{\mathbf{c}}_{g0}^{\prime }\right)}^{-1}\sum _{g=1}^{G}E[{\mathbf{y}}_g-{\Lambda }_0{\omega }_{g0}\mid \mathbf{X},\mathbf{Z},\alpha ,\theta ]$$

$${\Lambda }_{0j}^{\prime }={\left(\sum _{g=1}^{G}E[{\omega }_{g0}{\omega }_{g0}^{\prime }\mid \mathbf{X},\mathbf{Z},\alpha ,\theta ]\right)}^{-1}\sum _{g=1}^{G}E[{\omega }_{g0}(y_{gj}-{\mathbf{A}}_{0j}{\mathbf{c}}_{g0})\mid \mathbf{X},\mathbf{Z},\alpha ,\theta ]$$

$${\psi }_{0j}=\frac{1}{n}\sum _{g=1}^{G}E[{(y_{gj}-{\mathbf{A}}_{0j}{\mathbf{c}}_{g0}-{\Lambda }_0{\omega }_{g0})}^2\mid \mathbf{X},\mathbf{Z},\alpha ,\theta ]$$

$${\Phi }_0=\frac{1}{n}\sum _{g=1}^{G}E[{\omega }_{g0}{\omega }_{g0}^{\prime }\mid \mathbf{X},\mathbf{Z},\alpha ,\theta ]$$

Finally, to update the M-step, the conditional expectations involved in the above solutions are approximated by the corresponding observations simulated by the hybrid algorithm at the E-step.