Abstract
This paper presents a methodology to obtain candidate conformations of multidomain proteins for use in Molecular Replacement. For each separate domain, orientational relationship between the template and the target structure is obtained by using MR. Then, the orientational relationships of the domains are used to calculate the relative rotation between those domains in the target conformation by using pose estimation techniques from the field of Robotics and Computer Vision. With the angle of relative rotation between the domains as a cost function, iterative normal mode analysis is used to drive the template structure into the candidate conformation to match X-ray crystallography data obtained for the target conformation. As a validation, the proposed method is applied to three test proteins: Ribose-binding protein; Lactoferrin; and Calcium ATPase. In each test case, the orientation and translation of the final candidate conformation are generated correctly from the suggested procedure. The results show that the proposed method can yield applicable candidate conformations for MR and reveal the structural details of the target conformation and its position and orientation in the crystallographic unit cell.
1. Introduction
Molecular Replacement (MR) (Rossmann, 1972; Rossmann, 1990; Rossmann, 2001) for multidomain protein structures often fails because of the flexibility of the structures, where most of this flexibility is concentrated in the linking regions between domains. If large conformational changes occur in the protein, the phase information of the template protein cannot be adopted as that of the target protein. Such is often the case in ligand-bound proteins, even if the sequences of the template and the target are identical (Suhre & Sanejouand, 2004b). Thus, some methods are desirable to “morph” the template structure into candidate conformations which more closely match the X-ray data when MR cannot be applied directly for the multidomain proteins.
One can use the MR method with separate subunits to find the crystal structure of multidomain proteins (Cygler & Anderson, 1988a; Cygler & Anderson, 1988b; Bernstein & Hol, 1997). Because each domain remains more-or-less rigid during the conformational changes, one can sometimes obtain the position and orientation of each domain, and assemble them into the whole structure. Practically, however, the translation function often fails in finding the exact position of the each corresponding domain, even though the rotation function can frequently find the exact orientation of the domain (Rossmann, 1990; Giacovazzo et al., 1998). Brünger proposed Patterson correlation refinement, which can adjust the flexible parts between domains of a multidomain protein, and find a better conformation for use in computing the translation function (Brünger, 1990; Brünger, 1997). This method can also be used with the orientation of subunits, each of which is separately obtained by direct rotation function evaluation to improve the search (DeLano & Brünger, 1995). However, he also reported that this method is limited by the radius of convergence. In the present work, we propose a new method to substantially deform the template conformation into the target conformation, based on iterative normal mode analysis and the relative rotation between domains.
Many of largest conformational changes in multidomain proteins appear to be due to rigid-body motions between domains: some flexible parts between domains dominate conformational changes; and domain parts remain rigid. For instance, in the case of Lactoferrin which has an open form 1LFH and a closed form 1LFG, the root mean square deviation (RMSD) between these two conformations is 6.4Å when comparing their α-carbon traces. In contrast, the RMSD value in each corresponding domain is less than 0.6 Å (Norris et al., 1991). This also means that the collective motions of domains dominate the conformational changes, but the fluctuations of each residue do not.
Normal mode analysis (NMA) can be used to predict the conformational changes of multidomain proteins by calculating the collective motions. By using NMA, one can calculate harmonic motions of a given protein structure around an equilibrium conformation (Brooks et al., 1995; Hinsen, 1998; Moritsugu & Kidera, 2004), and calculate collective motions and dynamic fluctuations of given protein structures (Bahar et al., 1997; Atilgan et al., 2001; Li & Cui, 2002; Li & Cui, 2004; Kurkcuoglu et al., 2004; Schuyler & Chirikjian, 2004). The collective motions obtained by NMA can represent the dominant motion of any given structure, which is also related to conformational changes (Marques & Sanejouand, 1995; Tama & Sanejouand, 2001; Tama et al., 2004; Suhre & Sanejouand, 2004b; Schuyler & Chirikjian, 2005). Krebs et al. (Krebs et al., 2002) also reported that a few low frequency normal modes dominate the conformational change for about 50% of the protein structures which are registered in the Protein Data Base (Berman et al., 2000).
Recently, Suhre and Sanejouand proposed a novel method to obtain the candidate structures for MR by using NMA (Suhre & Sanejouand, 2004a; Suhre & Sanejouand, 2004b). After calculating normal modes shapes from elastic network model (Tirion, 1996; Bahar et al., 1997; Atilgan et al., 2001; Hinsen, 1998; Moritsugu & Kidera, 2004; Jeong et al., 2006), they apply arbitrary scale factors to the conformational deviations calculated from NMA. By adding these deviations into the original conformation, they could obtain the candidate conformations. Then, MR is performed for all of candidates in order to judge the exact conformation among candidates by NMA. Their method successfully revealed the crystal structures of several proteins: maltodextrin-binding protein; HIV-1 protease; and glutamine binding protein. When a large or complex conformational change is to be analyzed, however, linear amplification of modes may not be sufficient to deform the template into the target conformation. Since the normal modes guarantee only infinitesimal deviation of a given protein structure, excessive amplification can produce physically unrealistic candidate conformations for the target protein.
In order to make large conformational changes and to avoid nonphysical conformations at the same time, we use iterative normal mode analysis in this article (Tama et al., 2004; Hinsen et al., 2005). After obtaining an intermediate conformation by adding small motions from NMA, another NMA is applied to the newly obtained conformation until approaching the target conformation. At each iteration, one should determine the amplitude and directions of the participating normal modes in order to drive the template structure to the target, since one only can obtain the normal mode shapes without the amplitude and direction. Thus, a cost function for choosing the proper conformation is required to judge the closest conformation among the candidate conformations at each step. Tama et al. applied iterative normal mode method to morph the known protein structure into low-resolution electron density map from cryo-EM method (Tama et al., 2004). They iterated with a gradient search about the intermediate structure to match the target electron density. Here, we propose a different procedure of iterative NMA by using a result from the statistical mechanics of macromolecules (Kim, 2004).
In this work, the relative rotation between domains is used as a cost function to drive iterative NMA. After obtaining the rotation function of each domain by applying existing MR software to each separate domain, we convert the rotation function of each domain into the relative rotation between the domains in the target conformation by using pose estimation methods from the field of Robotics and Computer Vision (Chirikjian & Kyatkin, 2001). With the relative rotation between domains, we can drive iterative NMA and obtain good candidates which is similar to the target protein structure. Then, the candidate conformations can be used in MR to match the diffraction pattern of the target protein. That is, by molphing the template conformation into the target conformation using only rotation function, our method makes it easier to find the translation function of the whole proteins candidate conformation.
We explain our methodology in section 2. In this section we present the elastic network modeling, iterative normal mode methods, and a cost function for driving iNMA with relative rotation between domains. In section 3, we demonstrate the results produced by the proposed method for three protein structures: Ribose-binding protein, Lactoferrin, and Calcium ATPase which have open and closed form. We discuss the results and methods in section 4. Finally, we conclude this work in section 5.
2. Methods
2.1. Elastic network modeling
One can calculate normal modes of a given protein structure based on the elastic network model, which analyzes an equivalent mass-spring system in static equilibrium as a representative of the protein structure (Brooks et al., 1995). If only a few lowest normal modes are required, one can use the simplified α-carbon coarse-grained elastic network model, where only α-carbons are used to represent the corresponding residues (Tirion, 1996; Bahar et al., 1997; Kim et al., 2002a; Kim et al., 2002b). The simplified elastic network model is frequently used for many applications, because of its cost-effective feature in numerical calculation (Atilgan et al., 2001; Kim et al., 2003a; Kim et al., 2003b; Kim et al., 2005; Bahar & Jernigan, 1997; Kurkcuoglu et al., 2004). Hookean pairwise potential for the simplified elastic network model can be written such that
| (1) |
where xi and δi are the position and the deviation of the ith α-carbon. Here, Ri,j is the relative distance between the ith and the jth residues. One can get the normal modes by solving the eigenvalue problem of Eq. 1.
In this work, we use bond-cutoff connection rules in order to build an elastic network model (Jeong et al., 2006). This method can guarantee the stability of the elastic network model with any distance-cutoff value (Yan et al., 1988). Based on backbone modeling, we apply the distance-cutoff method to model interactions between α-carbons which are not located sequentially but within a distance-cutoff. Different Rc values are used for intra- and interdomain residues, respectively. A 10Å distance-cutoff value is used for intradomain residues, whereas, a 5Å distance cutoff value is used between interdomain residues. This strategy increases the rigidity of each domain of a test protein structure. Then, the non-rigid-body motion calculated from NMA mostly reflects the relative motion between domains with more connections inside domain.
2.2. Iterative procedure to simulate large conformational changes
When calculating the collective harmonic motions for a protein structure by using NMA, one can get only normal mode shapes without magnitude and with plus or minus directional ambiguity. Thus, these two properties of collective motion should be determined in order to drive the template conformation into the target. The magnitude of each normal mode is determined by using ideas from the statistical mechanics of protein structures. According to Kim (Kim, 2004), the root mean square fluctuation of each normal mode is inversely proportional to the frequency of the given mode. Thus, we multiply this inverse frequency to each corresponding normal mode to get the collective motions of protein structures. This procedure emphasizes the lowest non-rigid normal modes over the other normal modes.
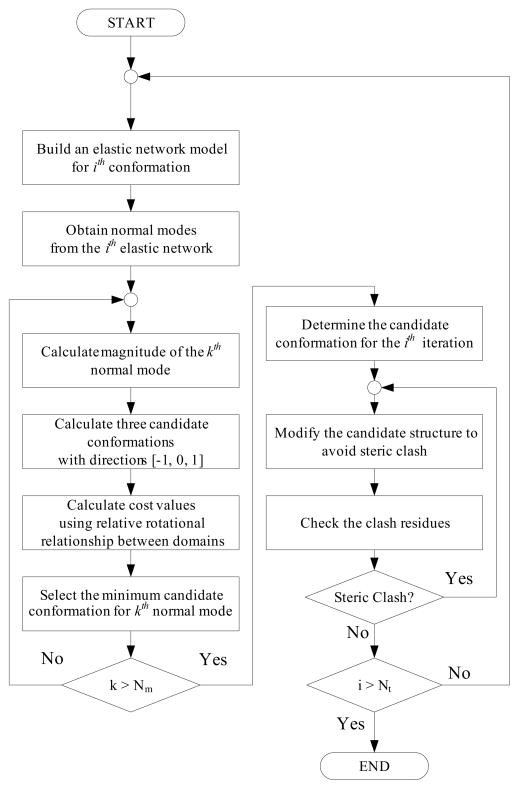
Next, one should decide the direction at each step from the template to the goal. Because we already set the amplitude, we only have to determine the direction of normal mode (plus or minus) for the intermediate conformation to approach the target. This procedure can be done by setting the cost function which represent the conformational changes and reducing its value to zero (See the following section about the cost function). We present the algorithm of the iterations as a flow chart in Fig. 1.
Fig. 1.
Flowchart of iterative normal mode analysis. By using normal mode shape and relative rotation between domains, one can morph the template conformation into near the target. Moreover, elastic network minimization algorithm is used to ensure the geometric constraints of protein structure during iteration.
When defining the ith intermediate conformation as Xi, its deviation Δi,k calculated by the kth normal mode can be given such that
| (2) |
where ωi,k is the natural frequency and vi,k is the mode shape of the kth normal mode after the ith iteration, respectively. The index i is the iteration number and takes values from 1 to the maximum number of iterations Nn. k is the index of non-rigid-body normal mode calculated from one to Nm.
Then, the direction of this deviation should be decided. We set the weight value ωj as −1, 0, or 1 to represent plus or minus direction, or to exclude the specific normal mode from the perturbation. This means that there are three candidate conformations for each normal mode. At the ith iteration, the frequency ωi−1 and mode vi−1 can be calculated by solving eigenvalue problem. Then, one can derive the candidate conformations Ci,j,k such that
| (3) |
where Xi−1 is the (i −1)th intermediate conformation. The parameter ε is a dimensionless scaling factor to adjust the magnitude of all the normal modes. After the candidate conformations are calculated at the ith iteration and the kth normal mode, one can get three candidate conformations with weight values.
One should evaluate the cost functions of these three conformations in order to select the closest candidate conformation to the target. After obtaining the direction which minimizes the cost function, one can determine the candidate conformation Ci,jmin,k for the kth normal mode. Then, we repeat the same procedure for the (k + 1)th normal mode. This procedure can be done for all normal modes under consideration. When the minimum cost function search for all the normal modes up to Nm is finished, the ith pathway conformation Xi can be obtained.
2.3. Keeping geometric constraints by using elastic network minimization
The geometric constraints of a protein structure should be kept during the iterative procedures of NMA. When driving the template structure into the target, at least several iterative steps of NMA are required. However, these multiple procedures may disturb the geometric constraints of an intermediate conformation such as preserving virtual bond lengths of the backbone trace, and avoiding steric clashes between domains. This comes from the deviation error from linearization of NMA, which can be accumulated during the iterations even if it is very small. In addition, the ‘sticking’ between domains is another problem. Along the intermediate pathways, two or more domains may pass each other very closely, for example, sliding motions between two domains. However, if two domains are too close and excessive virtual springs are established between these domains, then these will prevent domain motion perpendicular to these surfaces and NMA cannot produce the proper normal mode at the next iteration.
To overcome such a hurdle, we apply the elastic network minimization algorithm to keep geometric constraint during the iterations. In Eq. 1, we replace the current relative distance Ri,j between the ith and the jth residues with Li,j which is a predefined distance between the residues such that
| (4) |
where
is the relative distance of the template structure between the ith and jth residues. Then, the minimum deviation of all residue δ can be found by differentiating Eq. 4 (Kim et al., 2002a; Kim et al., 2002b). This procedure should be repeated for the candidates at each iteration of iterative NMA, until the abnormal relative distances between α-carbons do not exist any more.
2.4. Cost function using relative rotation between domains
2.4.1. Calculating interdomain rotational relationships of the target
To obtain the relative rotation between domains, firstly, one should calculate the rotation function of each separated domain by using Molecular Replacement. To do this, we use program packages or web services such as AMoRe (Navaza, 1994; Navaza, 2001) and MolRep program (Vagin & Teplyakov, 1997) in CaspR homepage (Claude et al., 2004) and CCP4 program suite (Collaborative computational project, 1994). We use the rotation functions for the test proteins after calculating rigid-body refinement algorithm (Castellano et al., 1992) in AMoRe and MolRep. That is, the candidate rotation functions are filtered by the rigid-body refinement algorithm of AMoRe and MolRep.
As the results of MR, one can obtain several of the highest peaks in the rotation function which are the most likely to reflect the true orientation of the corresponding domain in the target unit cell. Moreover, one should consider additional candidate rotations, since one cannot know which copy of the asymmetric unit in the unit cell corresponds to the peaks in the rotation function obtained from MR. Thus, one has to check all crystallographically symmetric copies of the rotation function peak to calculate the relative rotation between domains. We define the candidate orientation from the rotation function of ith domain between the template and the target such that
| (5) |
where is a rotation matrix of a peak calculated by MR, p is the index of crystallographic symmetry of the target unit cell, and Ψp is rotation matrix from crystallographic symmetry.
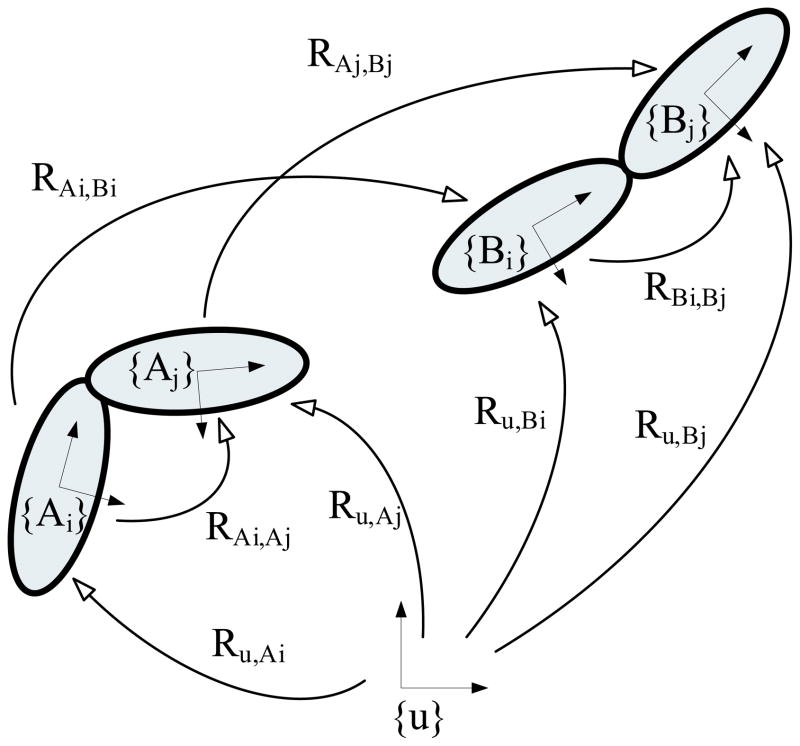
By using pose estimation methods (Chirikjian & Kyatkin, 2001), we can derive the relative orientations between domains in the ‘target’ unit cell. When assigning the template conformation as A and the target as B, our goal is to derive the relative rotation between the ith and jth domains in the target. One can derive the relative rotation between these two domains in the target such that
| (6) |
where u is the global coordinate, and RBi,Bj is the relative rotation between the ith and the jth domain of the target protein B. We present these relationships between rotations in Fig. 2.
Fig. 2.
The relationships between relative rotations. {u}is the global coordinate frame which is arbitrarily placed. {Ai} and {Bi} are the coordinate frames attached to the ith domain in the template and the target, respectively. Our goal is to calculate RBi,Bj the relative rotation between domains in the target, by using the rotations Ru,Ai, Ru,Aj, RAi,Bi, and RAj,Bj. One can obtain Ru,Ai and Ru,Aj from the structural details of the template conformation. One also can calculate RAi,Bi and RAj,Bj by converting the relative rotations HAi,Bi and HAj,Bj which are described in the global frame {u} into the relative rotations with respect to {Ai}local frame.
Then, one only has to calculate RAiBiand RAjBjfrom HAiBi and HAjBj which is calculated from MR. Heres HAiBi is a relative rotation of the ith domain from conformation A to B as viewed in the global coordinate frame {u}. Whereas, the relative rotation RAiBirepresents the same relative rotation as described in the {Ai}local frame. One can write the relationship between these two relative rotations by the adjoint mapping, such that
| (7) |
By using Eq. (7), one can convert Eq. (6) into
| (8) |
After putting Eq. (5) into Eq. (8), one can get the final equation such that
| (9) |
where because the crystallographic symmetry is a space group. As a result of Eq. 9, one can calculate several candidates of relative rotation, which are the same number of protein molecules in the target unit cell. Thus, the method to select the exact relative rotation is required.
2.4.2. Finding the corresponding pairs of rotation matrices
From the result of the previous section, one can get many candidates for relative rotations between each domain pair of the target. One can check these candidate conformations by trying all of relative orientation candidates to drive iterative NMA. Each candidate conformation is then submitted to an MR program such as AMoRe, which produces a structure solution and an R factor and correlated coefficient. The conformation with the lowest R is accepted.
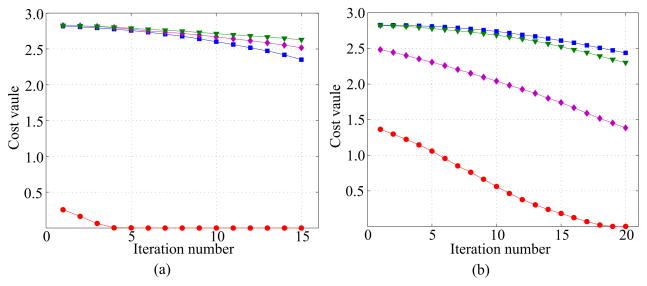
Another way to judge the proper relative rotation between domains is to drive iterative NMA with relative rotation candidates for each domain pair respectively. This method is based on the fact that the conformations of the given protein structure must have physically possible structures in 3D space. When driving the initial conformation into a candidate with an incorrect relative rotation relationship, iterative NMA cannot achieve the final conformation due to steric clash between domains, namely, one cannot minimize the cost function either. In Fig. 3, we present the cost values during iterations when trying to drive the initial conformation of Lactoferrin (1LFH) into possible candidates with each rotation relationship. This test is separately performed for each domain pair - i.e. four candidates for each inter-domain relative rotation in the target. In the figure, only one case converges to near-zero value after iterations. In contrast, the candidate conformations by iterative NMA could not converge in incorrectly matched cases, and retained over half of their initial cost value. From these results, one can observe that this provides a tool to weed out such rotations.
Fig. 3.
The change of cost value when each domain pair is tested separately with iterative NMA. The open form of Lactoferrin (1LFH) is tested as the template structure, and the closed form (1LFG) as the target. We test four cases of relative rotations for each target rotation. For each domain pair, only one case succeeds to converge. (a) Four relative rotations as target rotation between domain C1 to domain N1; (b) Four relative rotations as target rotation between domain C1 to domain N2.
One can consider another rule to judge the proper domain pair by statistical analysis of protein motions. Kreb and Gerstein reported that the maximum relative orientation by a hinge motion of conformational changes is 150 degree by surveying their ‘Molecular Movement Database’ (Krebs & Gerstein, 2000). This means that the possibility of hinge motion over than 150 degree will be rare statistically. In this work, we use this maximum angle as a criterion to judge the proper domain pairs. One can easily exclude the cases which difference angle exceeds 150 degree from the candidates of relative rotation between domain pair.
2.4.3. Rotational metric as a cost function
To drive iterative NMA, one needs to evaluate a cost value which represents the orientational difference between corresponding domain pairs in the current and target conformation. In this work, the following rotational metric to calculate the cost values Ci,j is calculated such that
| (10) |
where the function ‘trace(·)’ is the trace of a matrix. The symbol θi,j is the rotation angle between the two relative rotations RAiAj and RBiBj This represents the minimum rotational difference between two coordinate frames measured about the unique axis of rotation (Chirikjian & Kyatkin, 2001). Hence, the cost function reduces its value toward zero when an intermediate conformation approaches the target. In iterative NMA algorithm, we use the cost value from the proposed cost function in order to decide normal mode direction.
3. Results
To validate the proposed methodology, we test three proteins which have open and closed forms: Ribose-binding protein, Lactoferrin, and Calcium ATPase. The 15 lowest non-rigid-body normal modes, which are obtained from the elastic network model as described in the Methods section, are used as collective motions in order to morph the template protein structures. The bond-cutoff value (Bc) is set as three, Rintra as 10Å, and Rinter as 5Å to build the elastic network for all test proteins. We obtain the domain information for all test proteins from ‘3Dee’ and ‘SCOP’ (Dengler et al., 2001; Murzin et al., 1995). Four points inside domain, which tends to remain rigid with conformational changes, are selected for each domain to calculate the relative rotations between domains in the template structure. We present the PDB codes, the number of residue, the initial RMSD values between the template and target at Table 1.
Table 1.
The properties of test proteins: Ribose-binding protein, Lactoferrin, and Calcium ATPase. We also present the RMSD values as results of iterative NMA and the R factor and correlation coefficient after applying MR with the final conformations.
| Protein type | Ribose-binding protein | Lactoferrin | Calcium ATPase |
|---|---|---|---|
| Template PDB | 1URP | 1LFG | 1SU4 |
| Target PDB | 2DRI | 1LFH | 1T5S |
| Space group | P212121 | P212121 | C2 |
| Number of residues | 271 | 691 | 994 |
| Number of domains | 2 | 4 | 4 |
| Initial RMSD (Å) | 4.1 | 6.4 | 14.0 |
| Domain range | N (1~103, 236~264) | N1 (1~91, 251~339) | M (1~124, 240~343, 751~994) |
| C (104~235, 265~271) | N2 (92~250) | A (125~239) | |
| C1 (340~434, 595~691) | P (344~360, 600~750) | ||
| C2 (435~594) | N (361~599) | ||
| RMSD of the final candidate (Å) | 0.7 | 1.4 | 5.0 |
| R factor | 47.3 | 48.7 | 55.2 |
| Correlation Coefficient | 45.5 | 50.3 | 47.7 |
3.1. Lactoferrin
As the first test protein, we test Lactoferrin which has 691 residues and four domains labeled as C1, C2, N1, and N2. With hinge motion, it grabs and transports ligands such as Fe3+, Mg2+, Mn2+ ions. We set the open form (1LFH) as the target conformation, and the closed form (1LFG) as the template. The sequences of both structures are identical and the RMSD value between these two conformations is 6.4Å (Norris et al., 1991).
First, we execute MR with AMoRe program to find the rotation function of each domain in the target unit cell. We present the result of the MR in Table 2. In all MR procedures with each separated domain, one can easily determine the best candidate rotation of each domain, since the correlation factors of the highest peak are much higher than other candidates. Then, one can calculate the four candidate rotations for each domain by using the crystallographic symmetry of the target. With these first candidates of rotation matrix, one can try to drive the template conformation.
Table 2.
The results of rotation function when each separate domain of the open form of Lactoferrin 1LFH is applied to MR. Each separate domain of the closed form 1LFG is used as template conformation for MR. The AMoRe program is used to calculate the value of rotation function
| Domain | α | β | γ | a | b | c | CCF | RFF | CCI | |
|---|---|---|---|---|---|---|---|---|---|---|
| N1 | 1 | 107.73 | 88.93 | 248.20 | 0.4626 | 0.1298 | 0.1018 | 31.7 | 51.8 | 30.4 |
| 2 | 107.69 | 89.86 | 247.96 | 0.4625 | 0.1303 | 0.1015 | 31.7 | 51.8 | 30.5 | |
| 3 | 72.33 | 90.10 | 67.86 | 0.0374 | 0.1302 | 0.3985 | 31.6 | 51.8 | 30.5 | |
| 4 | 70.50 | 60.33 | 71.48 | 0.4255 | 0.1327 | 0.0076 | 26.9 | 53.2 | 26.9 | |
| N2 | 1 | 20.14 | 82.04 | 73.19 | 0.3916 | 0.4216 | 0.1502 | 31.8 | 52.1 | 32.4 |
| 2 | 19.79 | 83.30 | 73.52 | 0.3914 | 0.4215 | 0.1503 | 31.8 | 52.0 | 32.4 | |
| 3 | 9.98 | 6.83 | 9.85 | 0.2899 | 0.1956 | 0.3893 | 28.0 | 52.8 | 26.9 | |
| 4 | 69.61 | 79.63 | 71.07 | 0.3361 | 0.384 | 0.3209 | 28.0 | 52.9 | 27.7 | |
| C1 | 1 | 108.85 | 81.19 | 246.58 | 0.2194 | 0.2237 | 0.0211 | 41.4 | 49.0 | 41.1 |
| 2 | 71.15 | 92.05 | 67.55 | 0.2803 | 0.2236 | 0.4786 | 32.2 | 52.4 | 33.6 | |
| 3 | 110.48 | 48.34 | 26.99 | 0.2459 | 0.1645 | 0.4763 | 29.2 | 53.1 | 27.7 | |
| 4 | 89.47 | 32.67 | 97.60 | 0.2528 | 0.2905 | 0.1375 | 29.6 | 53.3 | 30.6 | |
| C2 | 1 | 109.58 | 82.15 | 246.88 | 0.2298 | 0.3925 | 0.339 | 37.0 | 49.2 | 34.5 |
| 2 | 64.29 | 61.84 | 83.03 | 0.2037 | 0.0357 | 0.1553 | 27.4 | 52.9 | 27.5 | |
| 3 | 70.81 | 91.42 | 66.33 | 0.2723 | 0.3788 | 0.1702 | 27.9 | 52.8 | 27.0 | |
| 4 | 1.01 | 23.53 | 201.21 | 0.2745 | 0.2325 | 0.4318 | 27.1 | 52.6 | 26.7 | |
Since the crystallographic symmetry of the target protein is P212121, there are four copies of protein structures in the unit cell. Moreover, at least three domain pairs should be considered for Lactoferrin because it has four domains. Hence, one has to check the proper relative rotation for each domain among the these four candidates. Thus, it should require 12 test-runs with each relative rotation when applying iterative NMA for one domain pair separately and checking the possibility of the domain orientation. The C1 domain is selected as the baseline from which the relative rotation to the other domains is considered in the cost function, because its highest peak has highest correlation factor.
Alternatively, one can select the proper relative rotations without driving iterative NMA, but by observing the initial relative rotation for two out of three domain pairs. That is, one can find the proper rotation if one of the initial difference angle is much smaller than the others. In Table 3, one of the initial difference angles is calculated as 1.3 degrees with which the iterative NMA should drive C2 based on C1 domains, whereas the angle difference of the other cases are around 180 degrees. This means that a candidate with the relative rotation 1.3 degrees between the C1 and C2 domains is already placed near its goal (i.e. near zero degree), but other candidates is not. Hence, if the conformational changes between the corresponding domains are very small in the target, one doesn’t have to drive iterative NMA. This procedure can be applied to the relative rotation between the C1 and N1 domains. The smallest relative rotation between the domains is 8.0 degrees, whereas, the initial angular differences of other candidates are near 180 degrees.
Table 3.
The initial angle differences between domain pairs of all test proteins. One can select the proper relative rotation pair by checking the initial values. In the case of Lactoferrin, one can select the domains pairs as one of the initial angle difference near zero. The domain pairs which relative rotation exceed 150 degree can be wiped out. (Unit: degree)
| p | 1 | 2 | 3 | 4 | |
|---|---|---|---|---|---|
| Lactoferrin (1LFG to 1LFH) | C1 to N1 | 8.0 | 172.1 | 179.1 | 179.0 |
| C1 to N2 | 173.1 | 129.6 | 53.9 | 163.4 | |
| C1 to C2 | 1.3 | 179.0 | 180.0 | 179.2 | |
| RBP (1URP to 2DRI) | N to C | 156.2 | 154.1 | 41.3 | 159.5 |
| Calcium ATPase (1SU4 to 1T5S) | M to A | 41.7 | 139.5 | ||
| M to P | 13.4 | 178.4 | |||
| M to N | 121.8 | 86.1 | |||
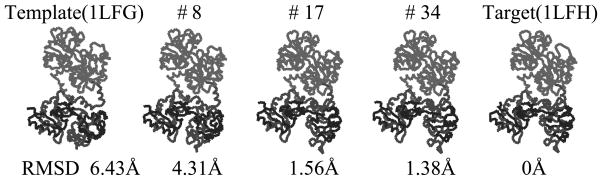
Thus, one only has to check the four relative rotations between C1 and N2 domains with two relative rotations determined above. One can exclude two out of four cases in this domain pair according to the maximum angle difference between the template to the target. That is, the initial relative rotation is over than 150 degrees when p is 1 or 2. We therefore need to check the final cost value for two candidates of relative rotations and when driving iterative NMA with the relative rotations of and together. Consequently, the cost value can converge only with . When we use with relative rotation and , the final cost value does not converge but retains its value of 2.45. In Fig. 4, conformational changes of the final candidate are presented when the proper relative rotation pair is chosen. One can observe the opening hinge motion of the second domain, and the final RMSD value for this case is 1.38Å.
Fig. 4.
The selected intermediate conformations in the case of Lactoferrin when applying iterative NMA from 1LFG to 1LFH. The RMSD value between each pathway and target conformation is given below each conformation. The final RMSD is 1.38Å.
With this final candidate, we try the MR procedure with diffraction pattern of 1LFH. Since we need to reconstruct a full atom model from a alpha-carbon trace from iterative NMA, we use the Maxsprout program (Holm & Sander, 1991) and the Deepview/Swiss PDBViewer (Guex & Peitsch, 1997) to relocate side chains of the candidate. As a result of MR, the final correlation coefficient (CCF) is 50.3 and the final R factor (RFF) is 48.7.
3.2. Ribose-binding protein
As the second case, we apply iterative NMA to the Ribose-binding protein (RBP). RBP consists of 271 residues grouped into two domains. We use 1URP as the open form, and 2DRI as the closed form (Bjorkman & Mowbray, 1998; Bjorkman et al., 1994), where two structures change their structures by hinge bending motion (Echols et al., 2003) and RMSD value between them is 4.1Å. We set the open form (1URP) as the template, and the closed form (2DRI) as the target.
First, we calculate the rotation function with the separated N and C domain by using AMoRe. As a result, one can get the some highest peaks which have higher correlation coefficient values CCF than the others. In the case of N domain, the highest four peaks with around 35.8 are revealed, but the others have less than 26.3. One can observe the similar results in the case of C domain too. The highest four peaks have 42.8, but the others have less than 26.3. We set the highest peaks for both domain as the rotation function to calculate the relative rotation.
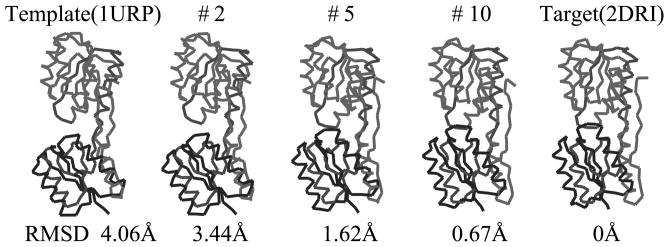
Since the crystallographic symmetry of the target is P212121, one should check four relative rotations between these two domains to select the proper target cost function. We present the initial angle differences of four candidate relative rotations between these two domains in Table 3. Just like Lactoferrin case, one can also obtain only one candidate relative rotation when p is 3. The other cases have over 150 degrees which is reported as a rare case for relative rotation (Krebs & Gerstein, 2000). When p is 3, the candidate conformation converges to the target structure after 10 iterations, and its final cost value goes down below 0.1 from the initial cost value 1.0. The RMSD value between the candidate and the target is 0.7Å.
We depict some intermediate conformations during the iterations from the template to the target in Fig. 5. One can observe the relative hinge motions of two domains. We reconstruct the side chains of the final candidate conformation by using Maxsprout and Deepview, and execute MR procedure with AMoRe. The final R factor is 47.3, and correlation coefficient is 45.5.
Fig. 5.
The selected intermediate conformations during iterations of Ribose-binding protein from the open form (1URP) to the closed form (2DRI). The relative rotation between N and C domains is used as the cost value of the iterative NMA. The final RMSD values is 0.67Å.
3.3. Calcium ATPase: from 1SU4 to 1T5S
As the final test protein, we select Calcium ATPase: 1SU4 and 1T5S, which are the largest protein structure in this work (Toyoshima et al., 2000; Sorensen et al., 2004). The protein consists of 994 residues and 4 domains labeled as M, A, P, and N domain. The open form 1SU4 is set as the template to obtain a candidate of the closed form 1T5S. To drive iterative NMA, we use six domain pairs: , and .
First, we try to calculate rotation function for each domain by using AMoRe. The each domain is separated and used for MR without flexible parts such as hinge residues. In the case of M domain, we only use the alpha helices from M4 to M10, which correspond to residues from 247 to 343 and from 751 to 994, in order to obtain the orientation of the domain (Toyoshima et al., 2000). However, we cannot get distinguished peaks in the cases of A and P domains, and the AMoRe program do not yield the rigid-body refinement solution for these two domains. Thus, we apply the MolRep program that can calculate real space rotation function with the separated domains. We present results of the rotation function when using AMoRe and MolRep in Table 4. From the results, we select the candidate rotation functions for domains as highest peak from MolRep.
Table 4.
The MR result of Calcium ATPase from 1SU4 to 1T5S by using MolRep and AMoRe respectively. One can distinguish peaks as result of rotational function calculated by MolRep, while the AMoRe cannot reveal the clear differences between peaks
| MolRep | AMoRe | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| α | β | γ | RotF | RotF/sigma | α | β | γ | CCF | RFF | CCI | |
| Domain M | |||||||||||
| 1 | 277.05 | 15.08 | 12.10 | 825.8 | 4.83 | 281.12 | 16.59 | 11.03 | 31.7 | 58.7 | 41.0 |
| 2 | 15.36 | 10.32 | 190.35 | 813.4 | 4.76 | 282.33 | 18.50 | 11.41 | 31.3 | 58.8 | 40.7 |
| 3 | 299.43 | 51.58 | 24.42 | 799.6 | 4.68 | 326.59 | 41.80 | 17.25 | 30.8 | 58.8 | 38.8 |
| 4 | 354.56 | 16.48 | 207.06 | 719.0 | 4.21 | 309.29 | 23.15 | 354.25 | 30.6 | 58.9 | 40.3 |
| 5 | 58.03 | 17.59 | 150.54 | 710.6 | 4.16 | 329.52 | 41.64 | 16.98 | 30.4 | 59.1 | 38.3 |
| Domain A | |||||||||||
| 1 | 208.61 | 39.70 | 96.04 | 3396 | 4.76 | 333.03 | 26.55 | 97.54 | 32.5 | 57.7 | 38.1 |
| 2 | 68.95 | 66.51 | 131.32 | 2820 | 3.95 | 209.51 | 41.95 | 94.83 | 32.5 | 57.7 | 37.4 |
| 3 | 12.89 | 20.32 | 73.06 | 2807 | 3.94 | 37.18 | 31.58 | 359.14 | 32.2 | 58.0 | 39.6 |
| 4 | 175.99 | 49.55 | 53.16 | 2794 | 3.92 | 23.74 | 35.29 | 336.23 | 32.2 | 57.9 | 39.1 |
| 5 | 335.36 | 29.50 | 195.34 | 2792 | 3.92 | 60.33 | 55.15 | 312.09 | 32.2 | 57.9 | 38.7 |
| Domain P | |||||||||||
| 1 | 268.02 | 27.86 | 18.00 | 2503 | 4.29 | 271.50 | 26.61 | 14.22 | 33.7 | 57.7 | 40.2 |
| 2 | 269.29 | 24.28 | 18.97 | 2487 | 4.26 | 268.75 | 29.46 | 14.81 | 33.6 | 57.8 | 40.6 |
| 3 | 83.70 | 74.86 | 325.09 | 2406 | 4.12 | 274.62 | 25.20 | 13.91 | 33.6 | 57.7 | 40.4 |
| 4 | 233.99 | 17.51 | 16.40 | 2224 | 3.81 | 276.50 | 25.65 | 13.50 | 33.5 | 57.7 | 40.6 |
| 5 | 15.60 | 56.84 | 108.75 | 2179 | 3.73 | 231.00 | 16.50 | 21.50 | 33.5 | 57.9 | 41.5 |
| Domain N | |||||||||||
| 1 | 312.20 | 84.36 | 238.16 | 2038 | 9.34 | 312.15 | 84.77 | 237.64 | 36.7 | 55.9 | 41.2 |
| 2 | 228.38 | 90.00 | 58.73 | 953.4 | 4.37 | 226.99 | 90.00 | 56.23 | 32.6 | 57.5 | 37.5 |
| 3 | 45.05 | 80.44 | 188.35 | 925.2 | 4.24 | 226.00 | 90.00 | 53.75 | 32.2 | 57.6 | 37.2 |
| 4 | 348.01 | 65.83 | 202.04 | 874.5 | 4.01 | 69.66 | 56.65 | 258.94 | 31.7 | 58.1 | 38.8 |
| 5 | 168.46 | 53.70 | 163.46 | 857.3 | 3.93 | 329.21 | 71.90 | 218.50 | 31.5 | 57.9 | 38.2 |
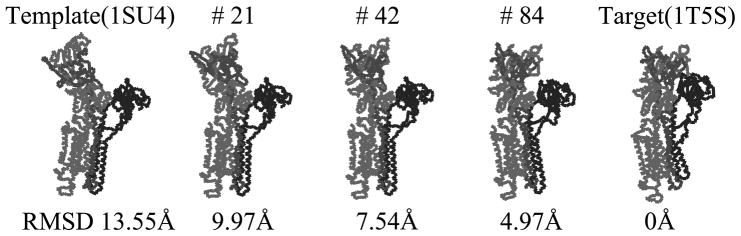
With selected rotation functions, one can obtain candidates of the relative rotations with respect to the crystallographic symmetry. Since the crystallographic symmetry of the target protein (1T5S) is C2, one only has to check two relative rotations per a domain pair. Then, one can select the possible relative rotation between domains of the target conformation, by observing the initial relative rotation between the corresponding domains. One can exclude the second case between M and P domains because it is near 180 degrees, whereas, the is about 13 degrees. This rule can also be applied to the relative rotation between RM,P. However, we have to check the relative rotation between M and N domain. Because corresponds 121.8 degree and 83.1 degree, we have to drive iterative NMA with both relative rotations. When we execute iterative NMA with , however, the cost function did not converge to zero. Finally, we can choose only one candidate, which converges to near zero: , and . The final RMSD value and the shape of the conformation are presented in Fig. 6. After 84 iterations, the conformation converges and the cost value does not reduce itself any more. The final RMSD value of the candidate conformation from the target conformation is 4.97Å.
Fig. 6.
The selected intermediate conformations during iterations of Calcium ATPase from the open form (1SU4) to the closed form (1T5S). The relative rotations between M, N, P and A domains are used as the cost function of the iterative NMA. The final RMSD values is 4.97Å.
With the final candidate for 1T5S conformation, we applied Maxsprout to rebuild the backbone chain from α-carbon traces. The final correlation coefficient and R factor from AMoRe was 47.7 and 55.2 respectively. The R factor of the final candidate conformation is realtively big, when comparing the results of Lactoferrin and Ribose-binding protein. We will discuss this problem in next section.
4. Discussion
When driving iterative NMA for the template structure into the target, we do not use translation function but only use relative rotation between domains. One has to know six degrees of freedom to describe position and orientation of a rigid body in 3D space. However, even though we only use the relative rotation between domains, the final candidate conformation of two tested globular proteins i.e. Lactoferrin and RBP are very close to their targets: RMSD values between the target and the final candidate conformation are only 1.38Å, 0.7Å in the cases of Lactoferrin and RBP. This result means that the conformational changes of multidomain protein structures can be described with less than six degrees of freedom. That is because each domain is connected with the others with short flexible residues, which act as the constraints of conformational changes.
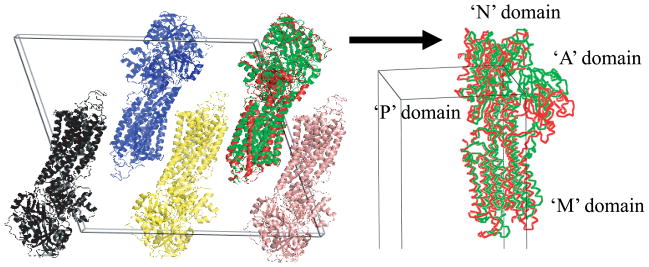
However, this is not the case of Calcium ATPase. The final candidate for the closed form of Calcium ATPase 1T5S has bigger RMSD value (4.97Å) and bigger R factor (55.2) than Lactoferrin and RBP have. The RMSD value and final R factor of Calcium ATPase is due to the relative translation of domain A as depicted in Fig. 7. Why can not the domain A of Calcium ATPase be placed into the proper position while the other domains in RBP, Lactoferrin, and even M, N, and P domain of Calcium ATPase can be done? One difference of domain A from the others is that it connects to M domain which is membrane domain and relatively more flexible than the globular one (Toyoshima et al., 2000; Sorensen et al., 2004). Moreover, it connects domain M with long flexible parts, which can give more than three degrees of freedom to domain A. Thus, even after assigning three angular constraints to domain A, the translation is still possible and the position of domain A can dwell on one position while it rotates. In contrast, the other domains, which connect each other with short hinge part and can move only rotational hinge motion, can give no more than three degrees of freedom to each domain connected. Thus, in the case of membrane proteins like the Calcium pump, translation should be considered to deal with the relative translation between domains.
Fig. 7.
The comparison between crystal packing of the target conformation (1T5S) and the position and orientation of the final candidate conformation morphed from 1SU4 after applying MR. Though the N, P, and M domains are determined properly, however, the domain A has positional error, while the orientation of the domain is placed near correct orientation. The target conformation is presented as green color, the final candidate conformation as red.
In most tests, the translation function of separate domain could not be obtained by AMoRe or MolRep. In the cases of finding the rotation function, the highest peaks are distinguished from the others and match the proper orientations of the corresponding domain. However, the translation function for each separate domain often place the domain at wrong position (Rossmann, 1990; DeLano & Brünger, 1995; Giacovazzo et al., 1998). In the case of Calcium ATPase, while we can calculate the rotation function for domain P and A of Calcium ATPase, we cannot obtain the correct translation function. In contrast, we could find the translation function for an entire molecule of Calcium ATPase after driving iterative NMA and finding the final candidate for MR. This result means that the proposed method can be used as a preconditioning procedure for multidomain proteins which can be followed by successful translation function computation.
When one calculates the rotation function by using program package such as AMoRe and MolRep, the orientational error might be included in each domain. In the case of Lactoferrin, the relative orientation of N2 domain, which is calculated from MR, is 53.9 degrees. This value is different from 56.1 degrees which is calculated by placing four points inside C1 and N2 domain and comparing their orientation between the template and the target conformation. Because the relative rotation is used as a cost function between domains, the orientational error can influence the final candidate conformation. To check the influence, we run the simulation about Lactoferrin and Ribose-binding protein (data is not shown). Even though there are about 2 degrees of angular difference between domains, however, the change of the final RMSD value is negligible: from 1.37Å to 1.38Å. The difference of Ribose-binding protein is also negligible. The angular differences between N and C domain are calculated 41.3 degrees and 43.3 degrees by MR and by calculating relative rotation with four points inside domain, respectively. However, the final RMSDs do not be changed much: 0.7Å and 0.8Å.
Next, we checked the geometric constraints of the candidate conformation, which should be kept after driving the template conformation into the final candidate conformation. Actually, the main reason for using an iterative procedure is to prevent physically unrealistic conformations during iterations. From the observation about the initial and the final conformations about test proteins, we obtain the maximum deviation of the relative distance between adjacent backbone: as the order of 0.01Å in the test case from 1SU4 to 1T5S; and as the order of 0.001Å in the cases of Lactoferrin and RBP. This results are due to elastic network minimization algorithm, which recovers the geometric constraints after the deviation from NMA is added to the current conformation. Thus, the each virtual bond length does not change itself much but retain its original value during the iterations. In addition, the algorithm also can guarantee a candidate conformation without steric clash between domains. Since the minimum distance between α-carbons in the different domains is set as 4.0Å and the conformation is updated until it has no steric clash, the iteration procedure can always keep this minimum distance during the iterations.
As the final issue, we discuss the possible methods if the search model or the template conformation is not enough to yield a distinguished peaks for the rotation function of the corresponding domain. First, just as we used in the case of Calcium ATPase, one can try to get the rotation function with various modern methodologies such as Real space rotation function, Direct rotation function, and Patterson refinement (Brünger, 1990; DeLano & Brünger, 1995; Brünger, 1997). Second, all peaks from the rotation function can be tried as a cost function for the iterative NMA. One can check the cost value for each possible conformation whether it reduces the cost value or not. If there were multiple candidate which satisfy the cost values preset, then, one can apply MR for these final candidates and check the R factor to find the exact conformation in the target crystal. In the second method, the number of possible candidates could be very large, since the crystallographic copies in the unit cell also should be considered. That is, large computational power will be needed. However, “the computer time is now virtually free in most cases” and it would not be a barrier any more because of the powerful computational ability of cheap PCs or workstations for MR (Jones, 2001).
5. Conclusion
In this work, we presented a method to find candidate conformations of multidomain proteins for use in Molecular Replacement. We suggested iterative normal mode analysis to generate candidate structures. We modeled the protein structure as an elastic network model, where all α-carbons (as representatives of each residue) are treated as point-masses with interactions between them modeled as springs. Using the elastic network model, we calculated the 15 lowest normal modes, and applied iterative procedures in order to obtain physically realistic conformations that approximate the final structure closely.
As a cost function to drive iterative NMA, we used the relative rotation between domains of the target protein structure and each candidate. The rotation function of each domain can be calculated by using MR programs such as AMoRe and MolRep. Then we converted the peaks in the rotation function of each domain into candidate relative orientations between domains in the target structure by using pose estimation techniques from the field of Robotics and Computer Vision.
As a validation of the proposed method, we tested three proteins which have open and closed forms: Ribose-binding protein, Lactoferrin, and Calcium ATPase. We showed that the template conformation could be morphed into near the target with the relative rotation cost function. In the cases of Ribose-binding protein and Lactoferrin we could obtain the proper candidate conformations with less than 1.5Å RMSD from their target structures. In the case of Calcium ATPase, we could derive the final candidate conformation with 4.97Å in RMSD. The proper orientation and position of M, N, and P domains of the final candidate conformation could be obtained by the iterative NMA. However, the domain A has positional error even though the relative rotation between domains could be matched correctly. The source of the error was discussed and denoted as additional degrees of freedom of domain A.
Consequently, the proposed method can extend the application of MR method of multidomain proteins, and can calculate the final candidate conformation without any radius of convergence, only if the rotation function for subunits of a multidomain protein can be revealed.
Acknowledgments
The authors appreciate all anonymous reviewers who have provided valuable comments to improve this work. JJ thanks Jinseob, Wooram, Kiju, Moonki, Adam, Yan, Aris, Georgios, Whitney, Yu Zhou and many collaborators who have worked with JJ for valuable discussion and with warm support. This work was financially supported by the Department of Energy of Unite States (DE-FG02-04ER25626), by the Korea Research Foundation Grant funded by Korea Government (MOEHRD) (KRF-2003-214-D00321), and under NIH grant R01GM075310 “Group-Theoretic Methods in Protein Structure Determination”.
References
- Atilgan AR, Durell SR, Jernigan RL, Demirel MC, Keskin O, Bahar I. Biophys J. 2001;80(1):505–515. doi: 10.1016/S0006-3495(01)76033-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bahar I, Atilgan AR, Erman B. Fold Des. 1997;2(3):173–181. doi: 10.1016/S1359-0278(97)00024-2. [DOI] [PubMed] [Google Scholar]
- Bahar I, Jernigan RL. J Mol Biol. 1997;266:195–214. doi: 10.1006/jmbi.1996.0758. [DOI] [PubMed] [Google Scholar]
- Berman HM, Westbrook J, Feng Z, Gilliland G, Bhat TN, Weissig H, Shindyalov IN, Bourne P. Trends Biochem Sci. 2000;28:235–242. doi: 10.1093/nar/28.1.235. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bernstein BE, Hol WJ. Acta Cryst. 1997;D53:756–764. doi: 10.1107/S0907444997010214. [DOI] [PubMed] [Google Scholar]
- Bjorkman AJ, Binnie RA, Zhang H, Cole LB, Hermodson MA, Mowbray SL. J Biol Chem. 1994;269:30206–30211. [PubMed] [Google Scholar]
- Bjorkman AJ, Mowbray SL. J Mol Biol. 1998;279:651–664. doi: 10.1006/jmbi.1998.1785. [DOI] [PubMed] [Google Scholar]
- Brooks BR, Janezic D, Karplus M. J Comput Chem. 1995;16(12):1522–1542. [Google Scholar]
- Brünger AT. Acta Cryst. 1990;A46:46–57. [Google Scholar]
- Brünger AT. Methods in Enzym. 1997;276:558–580. doi: 10.1016/S0076-6879(97)76078-6. [DOI] [PubMed] [Google Scholar]
- Castellano EE, Oliva G, Navaza J. J Appl Cryst. 1992;25:281–284. [Google Scholar]
- Chirikjian GS, Kyatkin A. Engineering Applications of Noncommutative harmonic analysis: with emphasis on rotation and motion groups. CRC press; 2001. [Google Scholar]
- Claude J, Suhre K, Notredame C, Claverie J, Abergel C. Nucleic Acids Res. 2004;32:W606–W609. doi: 10.1093/nar/gkh400. * http://igs-server.cnrs-mrs.fr/Caspr/ [DOI] [PMC free article] [PubMed]
- Cygler M, Anderson WF. Acta Cryst. 1988a;A44:38–45. doi: 10.1107/s0108767387008365. [DOI] [PubMed] [Google Scholar]
- Cygler M, Anderson WF. Acta Cryst. 1988b;A44:300–308. doi: 10.1107/s0108767387012236. [DOI] [PubMed] [Google Scholar]
- DeLano WL, Brünger AT. Acta Cryst. 1995;D51:740–748. doi: 10.1107/S0907444995001284. [DOI] [PubMed] [Google Scholar]
- Dengler U, Siddiqui AS, Barton GJ. Proteins. 2001;42:332–344. [PubMed] [Google Scholar]
- Echols N, Milburn D, Gerstein M. Nucleic Acids Res. 2003;31:478–482. doi: 10.1093/nar/gkg104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Giacovazzo C, Manna L, Siliqi D, Rizzi MB. Acta Cryst. 1998;A54:617–625. [Google Scholar]
- Guex N, Peitsch M. Electrophoresis. 1997;18:2714–2723. doi: 10.1002/elps.1150181505. [DOI] [PubMed] [Google Scholar]
- Hinsen K. Proteins. 1998;33(3):417–429. doi: 10.1002/(sici)1097-0134(19981115)33:3<417::aid-prot10>3.0.co;2-8. [DOI] [PubMed] [Google Scholar]
- Hinsen K, Reuter N, Navaza J, Stokes DL, Lacaperey J-J. Biophys J. 2005;88:818–827. doi: 10.1529/biophysj.104.050716. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Holm L, Sander C. J Mol Biol. 1991;218:183–194. doi: 10.1016/0022-2836(91)90883-8. [DOI] [PubMed] [Google Scholar]
- Jeong JI, Jang Y, Kim MK. J Mol Graph Model. 2006;24:296–306. doi: 10.1016/j.jmgm.2005.09.006. [DOI] [PubMed] [Google Scholar]
- Jones DT. Acta Cryst. 2001;D57:1428–1434. doi: 10.1107/s0907444901013403. [DOI] [PubMed] [Google Scholar]
- Kim MK. Ph.D. thesis. Johns hopkins university; Baltimore, Maryland: 2004. Elastic network models of biomolecular structure and dynamics. [Google Scholar]
- Kim MK, Chirikjian GS, Jernigan RL. J Mol Graph Model. 2002a;21(2):151–160. doi: 10.1016/s1093-3263(02)00143-2. [DOI] [PubMed] [Google Scholar]
- Kim MK, Jernigan RL, Chirikjian GS. Biophys J. 2002b;83(3):1620–1630. doi: 10.1016/S0006-3495(02)73931-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim MK, Jernigan RL, Chirikjian GS. J Struct Biol. 2003a;143(2):107–117. doi: 10.1016/s1047-8477(03)00126-6. [DOI] [PubMed] [Google Scholar]
- Kim MK, Jernigan RL, Chirikjian GS. Biophys J. 2005;89:43–55. doi: 10.1529/biophysj.104.044347. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim MK, Li W, Shapiro BA, Chirikjian GS. J Biomol Struct Dyn. 2003b;21(3):395–405. doi: 10.1080/07391102.2003.10506935. [DOI] [PubMed] [Google Scholar]
- Krebs WG, Alexandrov V, Wilson CA, Echols N, Yu HY, Gerstein M. Proteins. 2002;48(4):682–695. doi: 10.1002/prot.10168. [DOI] [PubMed] [Google Scholar]
- Krebs WG, Gerstein M. Nucleic Acids Res. 2000;28(8):1665–1675. doi: 10.1093/nar/28.8.1665. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kurkcuoglu O, Jernigan RL, Doruker P. Polymer. 2004;45:649–657. [Google Scholar]
- Li GH, Cui Q. Biophys J. 2002;83(5):2457–2474. doi: 10.1016/S0006-3495(02)75257-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li GH, Cui Q. Biophys J. 2004;86(2):743–763. doi: 10.1016/S0006-3495(04)74152-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marques O, Sanejouand YH. Proteins. 1995;23:557–560. doi: 10.1002/prot.340230410. [DOI] [PubMed] [Google Scholar]
- Moritsugu K, Kidera A. J Phy Chem B. 2004;108:3890–3898. [Google Scholar]
- Murzin AG, Brenner SE, Hubbard T, Chothia C. J Mol Biol. 1995;247:536–540. doi: 10.1006/jmbi.1995.0159. [DOI] [PubMed] [Google Scholar]
- Navaza J. Acta Cryst. 1994;A50:157–163. [Google Scholar]
- Navaza J. Acta Cryst. 2001;D57:1367–1372. doi: 10.1107/s0907444901012422. [DOI] [PubMed] [Google Scholar]
- Norris GE, Anderson BF, Baker EN. Acta Cryst. 1991;B47:998. doi: 10.1107/s0108768191008418. [DOI] [PubMed] [Google Scholar]
- Collaborative computational project, n. Acta Cryst. 1994;D50:760–763. [Google Scholar]
- Rossmann MG, editor. The molecular replacement method. New York: Gordon & Breach; 1972. [Google Scholar]
- Rossmann MG. Acta Cryst. 1990;A46:73–82. doi: 10.1107/s0108767389009815. [DOI] [PubMed] [Google Scholar]
- Rossmann MG. Acta Cryst. 2001;D57:1360–1366. doi: 10.1107/s0907444901009386. [DOI] [PubMed] [Google Scholar]
- Schuyler AD, Chirikjian GS. J Mol Graph Model. 2004;22:183–193. doi: 10.1016/S1093-3263(03)00158-X. [DOI] [PubMed] [Google Scholar]
- Schuyler AD, Chirikjian GS. J Mol Graph Model. 2005;24:46–58. doi: 10.1016/j.jmgm.2005.05.002. [DOI] [PubMed] [Google Scholar]
- Sorensen TL-M, Moller JV, Nissen P. Science. 2004;304(5677):1672–1675. doi: 10.1126/science.1099366. [DOI] [PubMed] [Google Scholar]
- Suhre K, Sanejouand Y. Nucleic Acids Res. 2004a;32:610–614. doi: 10.1093/nar/gkh368. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Suhre K, Sanejouand Y. Acta Cryst. 2004b;D60:796–799. doi: 10.1107/S0907444904001982. [DOI] [PubMed] [Google Scholar]
- Tama F, Miyashita O, Brooks CL., III J Mol Biol. 2004;337:985–999. doi: 10.1016/j.jmb.2004.01.048. [DOI] [PubMed] [Google Scholar]
- Tama F, Sanejouand Y. Protein Engineering. 2001;14:1–6. doi: 10.1093/protein/14.1.1. [DOI] [PubMed] [Google Scholar]
- Tirion MM. Phys Rev Lett. 1996;77(9):1905–1908. doi: 10.1103/PhysRevLett.77.1905. [DOI] [PubMed] [Google Scholar]
- Toyoshima C, Nakasako M, Nomura H, Ogawa H. Nature. 2000;405:647. doi: 10.1038/35015017. [DOI] [PubMed] [Google Scholar]
- Vagin A, Teplyakov A. J Appl Cryst. 1997;30:1022–1025. [Google Scholar]
- Yan H, Day AR, Thorpe MF. Physical review B. 1988;38(10):6876–6880. doi: 10.1103/physrevb.38.6876. [DOI] [PubMed] [Google Scholar]