An SEM Approach for the Evaluation of Intervention Effects Using Pre-Post-Post Designs

Abstract

This study analyzes latent change scores using latent curve models (LCMs) for evaluation research with pre-post-post designs. The paper extends a recent article by Willoughby, Vandergrift, Blair, and Granger (2007) on the use of LCMs for studies with pre-post-post designs, and demonstrates that intervention effects can be better tested using different parameterizations of LCMs. This study illustrates how to test the overall mean of a latent variable at the time of research interest, not just at baseline, as well as means of latent change variables between assessments, and introduces how individual differences in the referent outcome (i.e., level-2 random effects) and measurement-specific residuals (i.e., level-1 residuals) can be modeled and interpreted. Two intervention data examples are presented. This LCM approach to change is more advantageous than other methods for its handling of measurement errors and individual differences in response to treatment, avoiding unrealistic assumptions, and being more powerful and flexible.

Latent curve models (LCMs) are versatile research tools for studies with repeated measurements over time that have become increasingly popular among researchers in many disciplines (Bollen & Curran, 2006). However, despite their popularity, the utilization of LCMs has been rather limited to etiological research that aims to (1) find the aggregate level trajectory of a given behavior (unconditional LCMs), (2) find predictors of the growth parameters (conditional LCMs), or (3) examine outcomes of the growth parameters (LCM parameters as predictors). The primary goal of the current study is to demonstrate how LCMs can effectively be utilized to answer the question of program efficacy for evaluation studies utilizing a pre-post-post design.

Analysis of Intraindividual Change and Intervention Research

Curran and Muthén (1999) summarize three traditional approaches to examine change in intervention (longitudinal) research: (1) raw change score by subtraction, (2) residualized change score by including the earlier measurement in the model predicting the targeted outcome, and (3) repeated-measures multivariate analysis of variance (MANOVA) that examines linear or polynomial growth trends in a repeated measure series using singly (for a single repeated series) or doubly (for multiple repeated series) multivariate repeated-measures analysis of variance. After discussing limitations associated with these three approaches, Curran and Muthén then illustrate a new fourth approach, latent curve analysis, as a better analytic technique to examine whether an intervention alters the average normative developmental trajectory and the individual variability around the average growth parameters (e.g., acceleration or deceleration of the normative growth trajectory). Curran and Muthén suggest that this approach is advantageous, compared to the previously mentioned three traditional approaches for intervention studies. First, this analytic technique explicitly models individual differences in change over time, which reflects the fact that not all individuals respond to the intervention in the same way. Second, latent curve models tend to have more power to detect a treatment effect. Third, change may be best construed as a continuous growth process over time as opposed to time-specific discrete change, especially for behavior observed in childhood and adolescence.

The current study further develops an alternative, fifth approach to examine latent change (or difference) scores utilizing latent curve models (e.g., McArdle & Hamagami, 2001; McArdle & Nesselroade, 1994; Raykov, 1993, 1994). This approach of examining latent change scores using LCMs has rarely been utilized in evaluation research. The latent change scores approach should be more appealing for studies with a short time series as is the case in pre-post-post designs. Furthermore, the latent change scores approach may be helpful especially when modeling growth trends may not provide an adequate approximation to data, in which case modeling intervention/treatment effects will most likely not provide an adequate explanation for the data in terms of latent variable means, variances, and covariances. Therefore, if an intervention or treatment program is designed to bring a departure from each individual’s routine behavior (e.g., change in direction and/or magnitude), then change may be best construed as a discrete event over time, and thus, the latent change scores approach using latent curve models is a useful strategy in evaluating intraindividual change and interindividual differences in change brought on by an intervention.

The General LCMs and Modifications to the LCMs for Pre-Post-Post Designs

LCMs are extensively described in the literature (e.g., Bollen & Curran 2006; Skrondal & Rabe-Hesketh, 2004). Briefly, LCMs can be viewed as level-2 models in a design in which repeated measures are nested within the individual. Each repeated observation y for individual i at time t is modeled to be a weighted linear sum of a random intercept and random slope terms plus an individual- and time-specific residual. In matrix terms, the model-implied variance of the reduced form can be expressed as

$$\sum =\mathit{\Lambda }\mathit{\Psi }{\mathit{\Lambda }}^{\prime }+{\mathit{\Theta }}_{\mathit{\epsilon }}.$$

A simple linear trajectory model for a three-wave data set requires estimating four matrices: a 3 × 2 factor loading matrix,

$${\mathit{\Lambda }}_{\mathit{y}}=\left(\begin{array}{ll}\mathit{1}\hfill & \mathit{0}\hfill \\ \mathit{1}\hfill & \mathit{1}\hfill \\ \mathit{1}\hfill & \mathit{2}\hfill \end{array}\right)$$

with a 3 × 3 residual matrix,

$${\mathit{\Theta }}_{\mathit{\epsilon }}=\left(\begin{array}{ccc}\mathbf{var}({\mathit{\epsilon }}_{\mathit{1}})& \mathit{0}& \mathit{0}\\ \mathit{0}& \mathbf{var}({\mathit{\epsilon }}_{\mathit{2}})& \mathit{0}\\ \mathit{0}& \mathit{0}& \mathbf{var}({\mathit{\epsilon }}_{\mathit{3}})\end{array}\right)$$

and a 2 × 2 covariance matrix among latent variables,

$$\mathit{\Psi }=\left(\begin{array}{ll}{\mathit{\psi }}_{\mathit{\alpha }\mathit{\alpha }}\hfill & {\mathit{\psi }}_{\mathit{\beta }\mathit{\alpha }}\hfill \\ {\mathit{\psi }}_{\mathit{\alpha }\mathit{\beta }}\hfill & {\mathit{\psi }}_{\mathit{\beta }\mathit{\beta }}\hfill \end{array}\right)$$

and a 2 × 1 column vector of latent variable means,

$${\mathit{\mu }}_{\mathit{\eta }}=\left(\begin{array}{l}{\mathit{\mu }}_{\mathit{\alpha }}\hfill \\ {\mathit{\mu }}_{\mathit{\beta }}\hfill \end{array}\right).$$

This three-wave linear model estimates a total of eight parameters: three residual variances, two variances of latent variables, one covariance between two latent variables, and two latent variable means, thus leaving one degree of freedom.

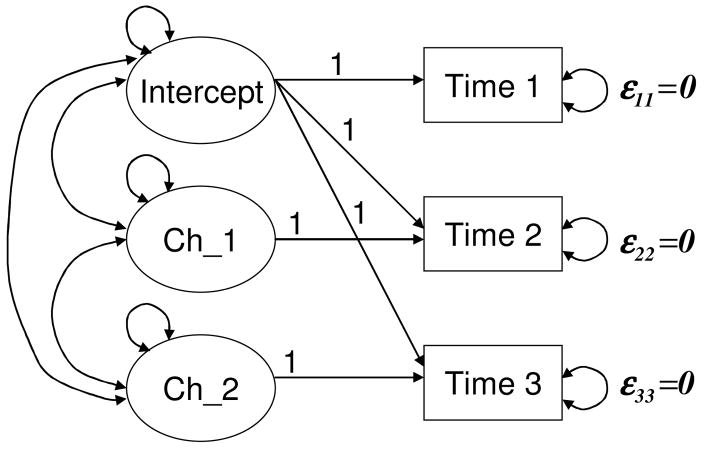
A recent study by Willoughby, Vandergrift, Blair, and Granger (2007) proposed adapting LCMs to accommodate the analysis of data from pre-post-post designs. Unconditional LCMs were proposed, and it was noted that, by setting up the measurement part of structural equation models (SEMs), LCMs can be made equivalent to a piecewise linear model or to a simple difference score model. Specifically, the unconditional model proposed by Willoughby et al. (2007) anchors the Time 1 assessment level as an intercept¹, so that subsequent changes can be tracked from the level shown at Time 1 (i.e., intercept) (see Figure 1). The proposed 3 × 3 factor loading matrix is

Figure 1.

The LCM model proposed by Willoughby et al. (2007) for pre-post-post designs

$$\mathit{\Lambda }=\left(\begin{array}{lll}\mathit{1}\hfill & \mathit{0}\hfill & \mathit{0}\hfill \\ \mathit{1}\hfill & \mathit{1}\hfill & \mathit{0}\hfill \\ \mathit{1}\hfill & \mathit{0}\hfill & \mathit{1}\hfill \end{array}\right).$$

The model proposed by Willoughby et al. estimates the mean intercept, the first mean change from Time 1 to Time 2, the second mean change from Time 1 to Time 3, and the variances and covariances of the intercept and two latent change variables while specifying the residual matrix as a zero matrix, leading to a total of nine parameters to be estimated for a total of nine available elements of the observed covariance matrix: six variances and covariances of the observed variables and three observed variable means.

However, three major issues render this model proposed by Willoughby et al. (2007) less desirable for a pre-post-post design. First, the proposed unconditional LCM by Willoughby et al. is a just-identified model that precludes the statistical evaluation of overall model fit or meaningful interpretation of change parameters. In addition, when one ultimately tries to examine intervention effects in the follow-up conditional LCM, it is not feasible to compare overall model fit statistics between the two LCMs. Second, in studies that utilize pre-post-post designs, participants are randomly assigned to treatment groups and there are typically no group differences at baseline. Therefore, specifying the baseline level (pre-treatment level) as the referent outcome does not represent an ideal use of available data.

Third, the unconditional LCM proposed by Willoughby et al. leads to setting the observed variance at baseline to be the variance of the latent variable corresponding to the intercept (i.e., referent measurement), resulting in the absorption of potential random variations around the intercept due to individual differences at baseline (i.e., level-2 residuals), as well as the time-specific variance associated with the referent assessment (i.e., level-1 residuals) into the 3 × 3 covariance matrix among latent variables. In essence, the model does not make any distinction between individual-specific random effects associated with the changes (i.e., individual differences in the referent outcome as well as in intraindividual change) and time-specific residual variances (e.g., measurement error). Thus, interpretation of the resulting covariance matrix among latent variables is far from straightforward since it includes not only the covariation among latent variables but also measurement-specific residual components. This is related to the observation that variance and covariance elements among latent variables are generally overestimated when latent variables are scaled to the observed measures (Bollen, 1989, pp. 151–154).

Identifiable Unconditional LCMs for Three-wave, Pre-Post-Post Data

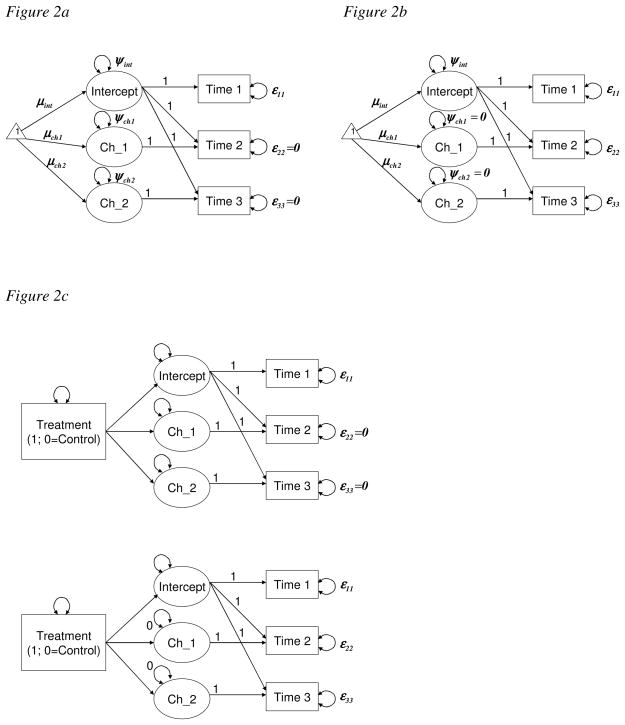
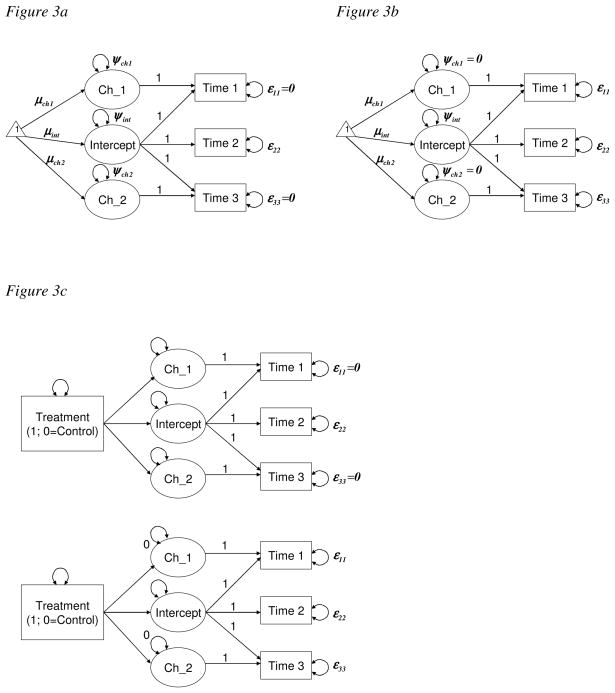
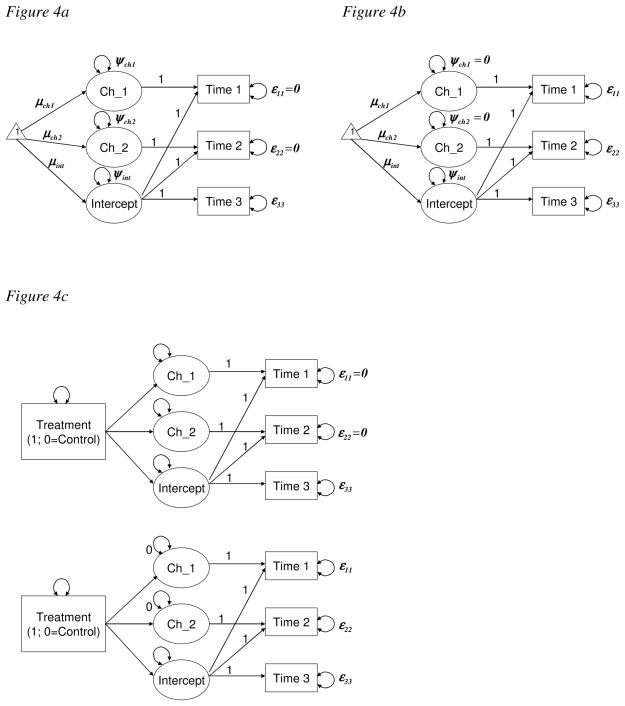
In the current article, we propose an over-identified model for the unconditional LCM (see Figures 2, 3, and 4) for pre-post-post designs that improves the model proposed by Willoughby et al. (2007). The proposed unconditional LCM is better suited for evaluation research for three-wave, pre-post-post data for three reasons. First, it is an over-identified model that allows the statistical evaluation of overall model fit. Second, this approach makes a better use of available data. Finally, this proposed LCM approach draws a distinction between individual-specific versus time-specific residuals and demonstrates how this distinction helps lead to a more parsimonious and better model that enables meaningful interpretation of parameters of change and intervention effects on change. We also illustrate how the proposed model is related to multilevel or hierarchical linear models (Raudenbush & Bryk, 2002). We present a pair of equivalent unconditional LCMs in Figures 2, 3, and 4.² The unconditional LCMs shown in Figures 2a, 3a, and 4a estimate three latent variable means, three latent variable variances, and one residual variance at the referent time (the time specified for the intercept level), thus leaving two degrees of freedom. Therefore, they are over-identified models that can test the overall model fit and, consequently, individual parameters. The unconditional LCMs shown in Figures 2b, 3b, and 4b estimate three latent variable means and one latent variable variance corresponding to latent intercept variable, and three residual variances. In both models, the parameterization of the latent variable means is the same. We highlight in the following section that the unconditional LCMs can yield more meaningful information for pre-post-post designs by selecting a referent measurement based on specific hypotheses.

Figure 2.

Proposed unconditional (2a, 2b) and conditional (2c) LCMs using Time 1 as the referent. The two models in Figures 2a and 2b are equivalent and so are the two models in Figure 2c.

Figure 3.

Proposed unconditional (3a, 3b) and conditional (3c) LCMs using Time 2 as the referent. The two models in Figures 3a and 3b are equivalent and so are the two models in Figure 3c.

Figure 4.

Proposed unconditional (4a, 4b) and conditional (4c) LCMs using Time 3 as the referent. The two models in Figures 4a and 4b are equivalent and so are the two models in Figure 4c.

Selection of the referent outcome and intraindividual change

An interesting approach to a pre-post-post design (baseline or pre-treatment, post-treatment or short-term follow-up, and long-term follow-up) involves defining the measurement at either Time 2 or Time 3 measurement as the intercept (an anchor point or a time referent). The unconditional LCMs in Figures 3a and 3b show that the latent intercept variable is created to match the observed mean level at Time 2. With a single measure of the latent variable (the intercept), λ₂₁ is a scaling constant (i.e., 1 in this study) that assigns the same metric to the latent variable as the observed outcome variable measured at Time 2, thus resulting in the mean outcome at Time 2 becoming the unbiased estimate of the mean latent variable outcome.³ The proposed 3 × 3 factor loading matrix for the models in Figure 3 is

$$\mathit{\Lambda }=\left(\begin{array}{lll}\mathit{1}\hfill & \mathit{1}\hfill & \mathit{0}\hfill \\ \mathit{1}\hfill & \mathit{0}\hfill & \mathit{0}\hfill \\ \mathit{1}\hfill & \mathit{0}\hfill & \mathit{1}\hfill \end{array}\right).$$

The unconditional LCMs in Figures 3a and 3b are over-identified, thus allowing one to test whether a significant change occurred between baseline (Time 1) and the first follow-up (Time 2), and between the first follow-up (Time 2) and the second follow-up (Time 3), which are indicated by estimated parameters for the first latent change variable (i.e., change 1) and the second latent change variable (i.e., change 2), respectively. More importantly, when the treatment effects are tested using the conditional models (see Figure 3c), one can test whether groups are different in their outcome levels at the first follow-up (Time 2) by comparing their latent intercept variable levels. Note that the conditional models in Figure 3c are also over-identified, which allows one to compare groups. In addition, researchers can test whether the groups’ changes from baseline to the first follow-up and from the first to the second follow-up differ depending on treatment conditions. This design can especially be useful for studies that utilize a wait-list control design where a treatment (indicated by “X” below; assessments noted by “O”) is offered to two groups but the control group gets the delayed treatment at the time of the first follow-up for the treatment group (see Kazdin, 1998 for more clinical evaluation designs). A wait-list control study using a pre-test can be illustrated as follows:

Group 1	O1	X	O2		O3
Group 2	O1		O2	X	O3

For a wait-list control design, whether the mean levels are different across groups at the second assessment (Time 2) is the most anticipated evaluation question (i.e., treatment effects), therefore, the latent intercept variable needs to be anchored at Time 2 (see Figure 3).

Alternatively, the models shown in Figure 4 propose the last follow-up as the point of interest. Often, long-term follow-up effects of treatments are of interest in evaluation research, and mean level differences between treatment and control groups can be tested by setting up the last measurement (Time 3) as the latent intercept. The proposed 3 × 3 factor loading matrix for the models in Figure 4 is

$$\mathit{\Lambda }=\left(\begin{array}{lll}\mathit{1}\hfill & \mathit{1}\hfill & \mathit{0}\hfill \\ \mathit{1}\hfill & \mathit{0}\hfill & \mathit{1}\hfill \\ \mathit{1}\hfill & \mathit{0}\hfill & \mathit{0}\hfill \end{array}\right).$$

The unconditional LCMs in Figures 4a and 4b reproduce the aggregated mean level of an outcome across treatment and control groups (the intercept level), the aggregated change (i.e., change 1) from baseline (Time 1) to the second follow-up (Time 3), and the aggregated change (i.e., change 2) from the first follow-up (Time 2) to the second follow-up (Time 3). The conditional model in Figure 4c tests whether treatment effects exist on the second follow-up level, and whether two change parameters are different across treatment and control groups.

Assumptions regarding individual-specific and measurement-specific residuals

For evaluation studies that utilize pre-post-post designs, two equivalent unconditional LCMs shown in Figures 3 and 4 are suitable. The first unconditional LCMs (Figures 2a, 3a, and 4a) estimate variance elements of all latent variables while specifying residual variances for the non-referent measurements to be zero. In contrast, the second equivalent unconditional LCMs (Figures 2b, 3b, and 4b) estimate all residual variances and the variance of the latent variable corresponding to the referent outcome while setting other variance elements of the latent change variables to be zero. In both of these LCM approaches, it is assumed that individuals are interchangeable and random.

Conceptually, the former LCMs hypothesize that measurement-specific residuals do not exist at non-referent assessments while specifying individual differences in the referent outcome and intraindividual change. On the one hand, this conceptualization may be useful when one’s primary aim is to model the proportion of variance explained by the fixed part of the model for both unconditional and conditional LCMs. The latter LCMs, on the other hand, can more easily be mapped into terms of the multilevel or hierarchical linear models (Raudenbush & Bryk, 2002; heterogeneous level-1 variance model, in particular, in this study).

In the proposed unconditional LCMs in the current study, time-specific residuals (θ_ε) are level-1 residuals (σ²) that are allowed to be different across measurements. Random effects due to individual differences are level-2 residuals (Ψ=T), of which only one random effect of the referent outcome is estimated in the unconditional LCMs in the current study. Table 1 illustrates how the two LCM parameterization approaches are equivalent, and how the unconditional LCMs can be interpreted from the perspective of multilevel linear models for the model in Figure 4b.⁴ Note that all three approaches produce the identical model-implied covariance matrix (fitted covariance matrix) and goodness of fit statistics, although conceptually they may be different.⁵ Note also that it is possible, if desirable, to estimate one more parameter (e.g., a random component/latent variable variance, or covariation among latent variables), resulting in one degree of freedom to test the overall model fit.

Table 1.

The Model-Implied Covariance Matrix and Mean Vector for the LCM Shown in Figures 4a and 4b

	Time 1	Time 2	Time 3
The Unconditional LCM: Figure 4a
Time 1	ψ̂11 +ψ̂22
Time 2	ψ̂11	ψ̂11 + ψ̂33
Time 3	ψ̂11	ψ̂11	ψ̂11 + θ̂ε33
Mean	α̂0 + α̂1	α̂0 + α̂2	α̂0
The Unconditional LCM: Figure 4b
Time 1	ψ̂11 + θ̂ε11
Time 2	ψ̂11	ψ̂11 + θ̂ε22
Time 3	ψ̂11	ψ̂11	ψ̂11+ θε33
Mean	α̂0 + α̂1	α̂0 + α̂2	α̂0
The Multilevel Linear Model: The Heterogeneous Level-1 Variance Model: Figure 4b
Time 1	${\widehat{\mathbf{\tau }}}_{\mathbf{00}}+{\widehat{\mathbf{\sigma }}}_{\mathbf{1}}^{\mathbf{2}}$
Time 2	τ̂00	${\widehat{\mathbf{\tau }}}_{\mathbf{00}}+{\widehat{\mathbf{\sigma }}}_{\mathbf{2}}^{\mathbf{2}}$
Time 3	τ̂00	τ̂00	${\widehat{\mathbf{\tau }}}_{\mathbf{00}}+{\widehat{\mathbf{\sigma }}}_{\mathbf{3}}^{\mathbf{2}}$
Mean	β̂0 + β̂1	β̂0 + β̂2	β̂0

Note. The observed variables were included in the model in chronological order while latent variables were included in the order of intercept (ψ̂₁₁), change 1 (ψ̂₂₂), and change 2 (ψ̂₃₃) in LCMs (see also Appendix). Of the ψ̂₂₂, ψ̂₃₃, θ̂_ε11, and θ̂_ε22 in the top covariance matrix, Figure 4a parameterizes θ̂_ε11 and θ̂_ε22 to be zero while Figure 4b parameterizes ψ̂₂₂ and ψ̂₃₃ to be zero.

Second, both unconditional LCM approaches assume that covariation among latent variables is either non-existent or non-substantial. The underlying assumption behind the ignorable covariation among latent variables is that a greater portion of the covariation between latent variables is taken into account when individual differences in the referent outcome are estimated as random effects. However, in situations where participants are heterogeneous at the outset of a study, it may be necessary to account for the heterogeneity in a sample by estimating, for example, the random effect at baseline, in addition to the estimation of their heterogeneous susceptibility to the treatment effect at the referent measurement. If the source for their heterogeneity can be identified, the variables attributed to observed individual differences at baseline may be used as covariates to control for their effects in subsequent conditional LCMs in which explanatory variables are included.⁶

Third, it is assumed that the random effect in the referent outcome is independent of the measurement-specific residual effect for the referent measure. This assumption is met if individuals are randomly assigned to treatment conditions, as it is typical for evaluation studies utilizing a pre-post-post design. Fourth, residuals for the observed variables are assumed to be uncorrelated (i.e., θ_ε21=θ_ε31=θ_ε32= 0). Finally, the proposed LCMs also assume that the intercept terms ν_y and/or ν_x in the y and x measurement equations y =ν_y + Λ_yη + ε and x = ν_x + Λ_xξ + δ are zero. The latter two are common assumptions for any LCMs.

Conditional LCMs and Treatment Effects for Three-wave, Pre-Post-Post Data

Using the dummy variable approach for treatment effects (1 = treatment group; 0 = control or comparison group), the unconditional LCMs become identifiable conditional LCMs in Figures 2c, 3c, and 4c by regressing LCM parameters on treatment, thus allowing direct tests of treatment effects on intraindividual change and the outcome. The model in Figure 2c tests treatment effects on the initial change between baseline (Time 1) and the first follow-up (Time 2), and between baseline (Time 1) and the second follow-up (Time 3). This model tests whether the changes recorded between two temporal phases are dependent on treatment conditions. This model also tests whether the mean levels at Time 1 (the intercept level) differ across treatment groups. However, this latter test of the intercept across groups is of little clinical significance because participants are routinely randomized in their group assignment and, therefore, generally no group differences are expected at baseline.

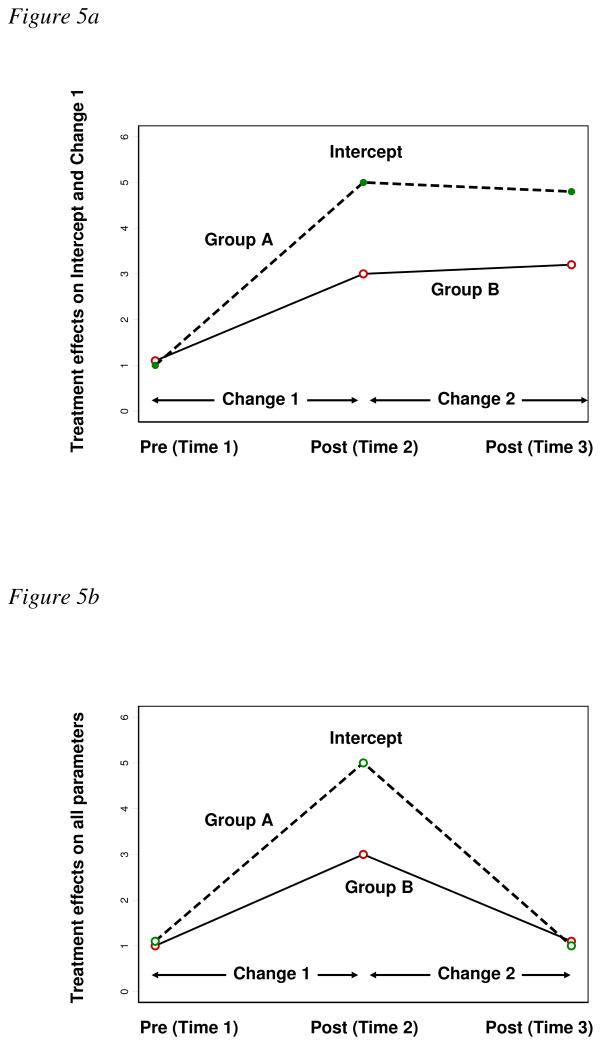
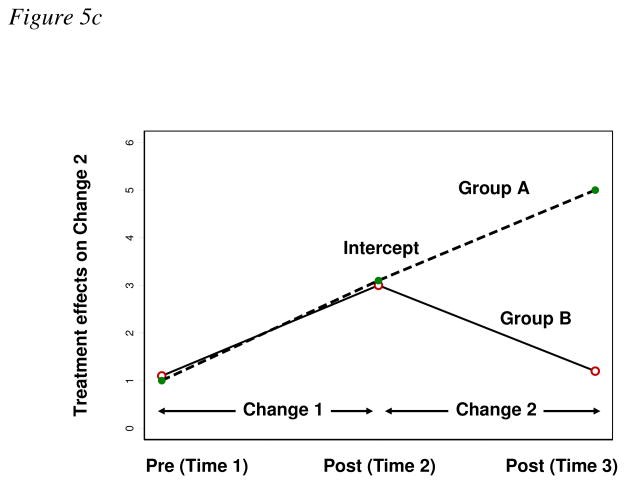
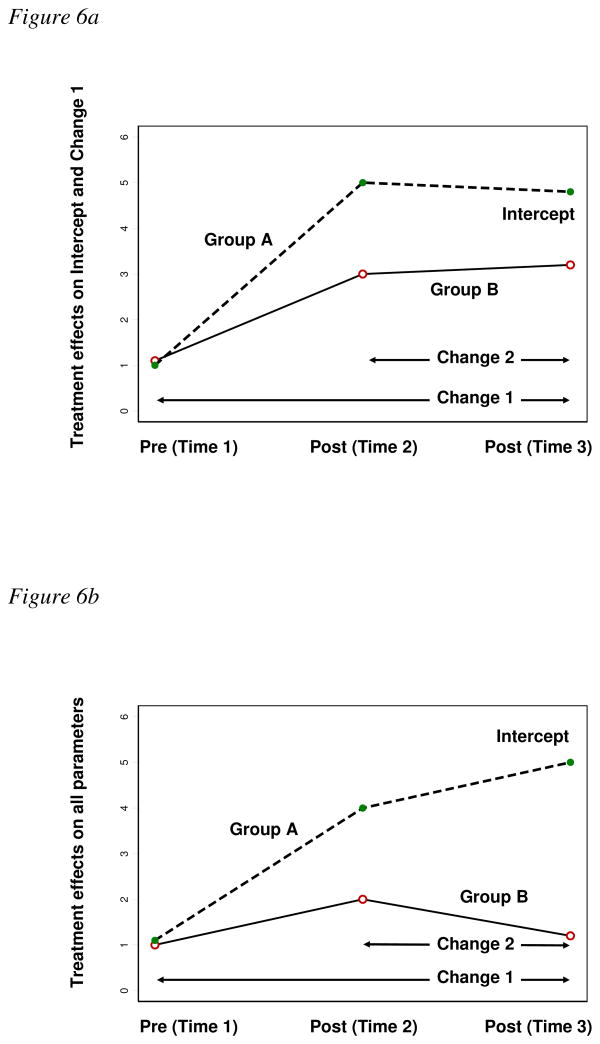
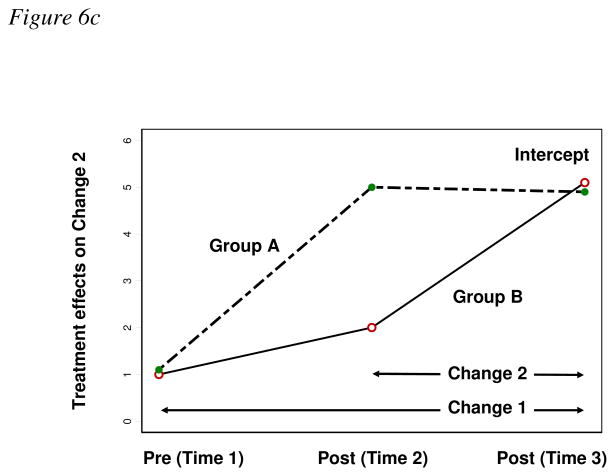
Figures 5 and 6 illustrate graphic examples of several likely treatment effects on the intercept level and on the change parameters using the models shown in Figures 3c and 4c, respectively, as templates. Figures 5a-c show the conditional LCMs where Time 2 is specified as the intercept. Figures 6a-c show the conditional LCMs where Time 3 is set up as the intercept. In both of models, the wide vertical gap between groups A and B at the intercept reflects treatment effects on the outcome level at the referent time. The unparallel lines indicating differential cross-time-change of groups A and B reflect treatment effects on the change parameters. Any parallel lines between time points indicate no treatment effects on the change parameters.

Figure 5.

Graphically illustrated possible treatment effects using the conditional LCMs in Figure 3c. The intercept is specified to match the level at Time 2 and the changes are measured against the level at Time 2. Figure 5a illustrates treatment effects on the intercept level and on the initial change from baseline (Time 1) to the first follow-up (Time 2). Figure 5b illustrates treatment effects on the intercept, the initial change, and the subsequent change. Figure 5c illustrates treatment effects on the change between Time 2 and Time 3.

Figure 6.

Graphically illustrated possible treatment effects using the conditional LCMs in Figure 4c. The intercept is specified to match the level at Time 3 and the changes are measured against the level at Time 3. Figure 6a illustrates treatment effects on the intercept and on the overall change from baseline (Time 1) to Time 3. Figure 6b illustrates treatment effects on the intercept and the long-term change from baseline to the last follow-up as well as the change from Time 2 to Time 3. Figure 6c illustrates treatment effects on the change from Time 2 and Time 3.

The following section of this article presents two empirical data examples that correspond to the LCMs shown in Figures 3 and 4. LISREL (Jöreskog & Sörbom, 2006) and Mplus (Muthén & Muthén, 1998–2006) source codes for the illustrated LCMs shown in Figure 4 are provided in Appendix. The source codes for Figure 3 can be adapted from those for Figure 4.

Application Examples

Participants

The first sample (Sample 1) in a wait-list control design consists of college students who were mandated to the Rutgers University Alcohol and Other Drug Assistance Program for Students (ADAPS) because of violation of university rules about alcohol and drug use in residence halls between September 2005 and February 2006. Because of the delayed treatment condition, the high-risk students were deemed clinically ineligible for the research project. Sample 1 consists of 230 (164 males, 71.3%) eligible students who agreed to participate in the research project. Most students were in the first two years of college (62.6% first, 27% second year). In the first session, all students referred to ADAPS completed a baseline assessment. Those deemed eligible were randomly assigned to either the immediate or the delayed personalized written feedback condition. Those students in the immediate condition (N = 111; 48.3%) were handed their personalized feedback profile while students in the delayed condition (N = 119; 51.7%) did not receive their profile at baseline. At the 2-month follow-up, students in both conditions again completed an assessment about their drinking and drug use during the past 2 months. Those in the immediate condition were given a personalized profile form based on the information from their second assessment. Students in the delayed condition were given both their baseline and 2-month personal profiles at the second session. Students then completed a third assessment 7 months after baseline. At baseline, students in the immediate and delayed intervention groups did not differ in terms of socio-demographic variables and baseline alcohol and drug use (see White, Mun, & Morgan, in press for more detail).

The second sample (Sample 2) for a pre-post-post design consists of students who were mandated to the Rutgers University ADAPS during the fall semester 2003, spring semester 2004, and fall semester 2004. Sample 2 consists of 348 (60.1% males) eligible students who agreed to participate in the research project. Most students were in their first (61.9%) or second (30.3%) year of college. About half (51.7%; n = 180) of the students were randomly assigned to receive a brief motivational interview including personalized written feedback (BMI), and the other half (48.3%; n = 168) received personalized written feedback only (WF). At baseline, the BMI and WF groups did not differ in terms of socio-demographic variables and baseline alcohol and drug use. Students in the BMI condition met individually with a counselor and discussed their written personalized profile, which they were given to take home. In addition, the counselor provided feedback in an empathic, non-confrontational, and nonjudgmental style based on the principles of motivational interviewing (Miller & Rollnick, 2002). Students in the WF condition were handed their written profile and left without discussing it with their counselor. Approximately 4 months and 15 months after the intervention, students completed follow-up assessments (see White, Mun, Pugh, & Morgan, 2007 for more detail).

Measures

Intervention condition

The immediate personalized feedback condition was coded 1 and the delayed feedback condition was coded 0 in Sample 1. BMI was coded 1 and WF was coded 0 in Sample 2.

Heavy episodic drinking

Students reported the number of occasions of heavy episodic drinking (five or more drinks for males and four or more for females during one drinking occasion) in the past month (Wechsler, Lee, Kuo, Seibring, Nelson, & Lee, 2002). The reported frequencies were log-transformed to normalize the over-dispersed distribution (see Table 2).

Table 2.

Descriptive Statistics of the Variables Measured and Correlations

	Mean	SD	Skew	Kurtosis	1	2	3
Sample 1 (N = 230)
1. Heavy episodic drinking at Time 1	.504	.613	.959	.082	1.000
2. Heavy episodic drinking at Time 2	.368	.519	1.182	.503	.437	1.000
3. Heavy episodic drinking at Time 3	.360	.621	1.790	2.896	.311	.518	1.000
4. Immediate (1; 0 = Delayed)	.483	.501	.070	−2.013	.004	−.061	.074
Sample 2 (N = 348)
1. Alcohol-related problems at Time 1	.878	.744	.192	−1.174	1.000
2. Alcohol-related problems at Time 2	.435	.614	1.265	.781	.284	1.000
3. Alcohol-related problems at Time 3	.692	.735	.696	−.653	.250	.412	1.000
4. BMI (1; 0 = WF)	.517	.500	−.069	−2.007	.093	−.073	−.149

Alcohol-related problems

Alcohol-related problems were measured using the shortened (18-item) version of Rutgers Alcohol Problem Index (RAPI, White & Labouvie, 1989, 2000). The total number of problems experienced in the last 3 months (range 0–18) (a = .66–.77 across the three assessments) was log-transformed (see Table 2).

Results

The Unconditional LCMs for Studies Using Pre-Post-Post Designs

Descriptive statistics for all measures in the current study are shown in Table 2. We analyzed first whether the specified unconditional LCMs adequately captured the two data examples (see Table 3). The overall model fit statistics were acceptable.⁷ The intercept for the first data (Sample 1) was devised to anchor at Time 2 and the estimated intercept coefficient of .37 matches the observed aggregated mean level at Time 2 in Table 2. The estimated coefficient for the first latent change variable (change 1) of .14 in Table 3 indicates that there has been an average decline in heavy drinking episodes by .14 at Time 2, compared to the baseline level. This parameterization results in the baseline heavy episodic drinking level of .50. The estimated coefficient for the second change variable (change 2) of −.01 was not significantly different from zero, and it indicates that students did not significantly change in their heavy episodic drinking behavior between Time 2 and Time 3. The observed difference of .01 between Time 2 and Time 3 from Table 2 is also reproduced by the parameterization of the unconditional LCMs shown in Figures 3a and 3b. In addition, significant individual differences (latent variable variance at the referent time = .15) existed at Time 2 measurement.

Table 3.

Estimated Parameters and Overall Fit Statistics Using the Unconditional LCMs Shown in Figures 3b and 4b

	Latent Variable Mean	Latent Variable Variance
Sample 1 (N = 230), Figure 3b
X2 (2) = 3.87, p = .14, RMSEA = .065, NFI = .97, CFI = .98
1. Intercept (Level at Time 2)	.37* (.03)	.15* (.02)
2. Change1 (Time 1 – Time 2)	.14* (.04)	.00
3. Change2 (Time 3 – Time 2)	−.01 (.04)	.00
Observed Residual Variances (Time 1, Time 2, and Time 3) = .25* (.03), .11* (.02), and .23* (.03), respectively.
Sample 2 (N = 348), Figure 4b,
X2 (2) = 4.15, p = .13, RMSEA = .057, NFI = .96, CFI = .98
1. Intercept (Level at Time 3)	.69* (.04)	.16* (.02)
2. Change1 (Time 1 – Time 3)	.19* (.05)	.00
3. Change2 (Time 2 – Time 3)	−.26* (.04)	.00
Observed Residual Variances (Time 1, Time 2, and Time 3) = .43* (.04), .22* (.02), and .37* (.03), respectively.

^*Note. p < .05

The second data set (Sample 2) used Time 3 as the referent (Time 3 = the intercept level). The estimated intercept level of .69 in Table 3 corresponds to the observed mean level of alcohol-related problems at Time 3 in Table 2. Furthermore, the changes between Time 1 and Time 3, and between Time 2 and Time 3 were estimated at .19 and −.26, respectively, which indicates that alcohol-related problems overall declined from baseline to 15 months post intervention (Time 3) by .19 but increased from Time 2 and Time 3 by .26 at the aggregate level. Based on these coefficients, we can estimate that alcohol-related problems at baseline and Time 2 would be .88 and .44, respectively, and these estimates match the observed aggregated mean levels shown in Table 2. Sample 2 also indicated significant individual differences in the referent outcome (latent variable variance at the referent time = .16).

The Conditional LCMs for Studies Using Pre-Post-Post Designs

We analyzed the proposed conditional LCMs to test treatment effects as illustrated in Figures 3c and 4c. The conditional LCMs for the two data examples showed very good model fit (see Table 4). Results for Sample 1 showed that college students in the delayed feedback condition who did not receive the personalized written feedback until 2 months after baseline assessment did not differ from those students who did receive the immediate feedback at Time 2. We can interpret this lack of treatment effects at Time 2 as suggesting that perhaps existing evaluation studies demonstrating efficaciousness of personalized feedback on mandated students’ drinking suffered from confounding effects of being caught and reprimanded. There were no significant treatment effects for the first phase between baseline and the first follow-up. However, we found treatment effects for the second temporal phase, coefficient = .16, SE = .08, t = 2.05, p < .05, indicating that the delayed written feedback had a positive effect beyond the reprimand. In addition, there existed individual-specific random effects, coefficient = .15, SE = .02, t = 7.55, p < .05, suggesting that treatment condition effects differed for different individuals. For example, some individuals in the immediate feedback condition curtailed their heavy drinking very little while many others in the same immediate feedback condition reduced their heavy drinking frequency much more. Similarly many individuals in the delayed feedback condition improved even without any provided treatment while others did not.

Table 4.

Estimated Parameters and Overall Fit Statistics Using the Conditional LCMs Shown in Figures 3c and 4c

	Coefficient
Sample 1 (N = 230), Figure 3c
X2 (2) = 4.18, p = .12, RMSEA = .069, NFI = .97, CFI = .98
1. Treatment effects on the intercept (Level at Time 2)	−.06 (.07)
2. Treatment effects on the change 1 (Time 1 – Time 2)	.07 (.08)
3. Treatment effects on the change 2 (Time 3 – Time 2)	.16* (.08)
Sample 2 (N = 348), Figure 4c
X2 (2) = 2.94, p = .23, RMSEA = .037, NFI = .98, CFI = .99
1. Treatment effects on the intercept (Level at Time 3)	−.22* (.08)
2. Treatment effects on the change 1 (Time 1 – Time 3)	.36* (.09)
3. Treatment effects on the change 2 (Time 2 – Time 3)	.13 (.08)

^*Note. p < .05.

Results for Sample 2 showed that the treatment group condition affected long-term outcomes for mandated college students. Treatment effects were significantly associated with the intercept and the change latent variable between baseline and the 15-month follow-up. At 15 months post intervention, the students in the BMI condition reported significantly lower levels of alcohol-related problems, compared to those in the written feedback only, coefficient = −.22, SE = .08, t = 2.86, p < .05. In addition, the students in the BMI condition reduced their alcohol-related problems more, compared to their counterparts in the WF condition from baseline to 15 months post intervention, coefficient = .36, SE = .09, t = 3.82, p < .05. Based on this finding, we can conclude that an in-person motivational interview intervention may be more efficacious in reducing alcohol-related problems among mandated college students, compared to written feedback only intervention, especially over a longer period of time. In addition to treatment effects, results indicated that treatment effects worked differently for different individuals, coefficient = .16, SE = .02, t = 7.63, p < .05.

Discussion

While the idea of using latent change (or difference) scores as an integral part of analytic models for studying correlates and predictors of change is not new (e.g., McArdle & Hamagami, 2001; Raykov, 1993, 1994, 1995, 1999), few empirical studies exist that have translated the idea into experimental or evaluation studies, which focus on the change due to an external intervention. The current study presents two typical data examples of evaluation studies utilizing a pre-post-post design and illustrates how to utilize LCMs. The time series for evaluation studies tend to be short with just two or three measurements including baseline measurement, and the main focus lies typically not on the outset of a study but on the follow-up. In this article, we propose ways to examine overall model fit and to utilize the latent intercept variable to match the observed outcome at follow-up assessment. In addition, we show how variance matrices among latent variables and among residuals of observed variables can be modeled and interpreted with the detailed discussion of necessary assumptions involved.

The LCMs shown in the current study are equivalent of the heterogeneous level-1 variance multilevel linear models. Although there are a few other ways to examine changes in pre-post-post designs using over-identified models, the proposed LCMs in the current study will most likely give the best and most parsimonious solution for data collected in pre-post-post designs. Using the dummy variable approach, the conditional LCMs can be tested for treatment effects on the overall level at the target assessment, and the changes between measurements. Note also that researchers can alternatively use a multi-group SEM approach to examine treatment effects for multiple groups⁸ (e.g., Curran & Muthén, 1999; McArdle, 1989). In studies where randomization occurs at the primary sampling unit (e.g., schools, classrooms, neighborhoods, etc.), the proposed LCMs can further be extended to include the hierarchically nested structure as part of the model or to adopt an alternative approach of adjusting standard errors for clustering in analyzing complex sample data in SEMs (see Stapleton, 2006, for an example).

The approach of examining latent change scores utilizing LCMs has a number of advantages compared to other methods (Curran & Muthén, 1999; Raykov, 1999). Five strengths seem most relevant in this study. First, this approach accounts for measurement error in the repeated measurements, as well as in the correlates and predictors of change. Second, this approach does not make the stringent and often unrealistic assumptions (e.g., assumptions of compound symmetry and sphericity) required for repeated-measures analysis of covariance or repeated-measures multivariate analysis of variance (see Hertzog & Rovine, 1985; McCall & Appelbaum, 1973 for detailed discussions), in addition to not requiring the assumptions required for analysis of variance (e.g., homogeneity of variance). Third, this approach explicitly takes into account that not all individuals respond to the intervention in the same way, and this assumption is an important part of the analyzed model, rather than being lumped to indistinctive residuals. Fourth, latent curve models tend to have greater statistical power to detect a given treatment effect than analysis of variance approaches (Curran & Muthén, 1999). Finally and importantly, this approach allows one to piggyback on the flexibility of SEM (see also Muthén & Curran, 1997; Raykov, 2007). For example, the LCM models suggested in the current study can be further extended to include outcomes of latent change variables, and to examine mediators of treatment effects. Multiple series of repeated measures can also be tested simultaneously as in parallel process models. In addition, researchers can try to find different treatment efficaciousness among a priori unknown subpopulations by utilizing factor mixture models (Lubke & Muthén, 2005) that make use of mixture distributions (Everitt & Hand, 1981; McLachlan & Peel, 2000).

APPENDIX

LISREL Source Code for the Unconditional LCM in Figure 4a

TI Unconditional Model – Sample 2: One Year Data

DA NO=348 NG=1 NI=3 MA=CM ME=ML

ME

0.878 0.435 0.692

SD

0.744 0.614 0.735

KM

1.000

0.284 1.000

0.250 0.412 1.000

LA

T1 T2 T3

MO NY=3 NE=3 TY=FI AL=FR TE=DI

LE

intercept change1 change2

FR TE(3,3)

FI TE(1,1) TE(2,2)

VA 1 LY(1,1) LY(2,1) LY(3,1)

VA 1 LY(1,2)

VA 1 LY(2,3)

PD

OU ND=3

LISREL Source Code for the Unconditional LCM in Figure 4b

TI Unconditional Model - Sample 2: One Year Data

DA NO=348 NG=1 NI=3 MA=CM ME=ML

ME

0.878 0.435 0.692

SD

0.744 0.614 0.735

KM

1.000

0.284 1.000

0.250 0.412 1.000

LA

T1 T2 T3

MO NY=3 NE=3 TY=FI PS=SY AL=FR TE=DI

LE

intercept change1 change2

FI PS(2,2) PS(3,3)

FR TE(1,1) TE(2,2) TE(3,3)

VA 1 LY(1,1) LY(2,1) LY(3,1)

VA 1 LY(1,2) LY(2,3)

PD

OU ND=3 AD=OFF

LISREL Source Code for the Conditional LCMs in Figure 4c

TI Conditional Model – Sample 2: One Year Data

DA NO=348 NG=1 NI=4 MA=CM ME=ML

ME

 0.878 0.435 0.692 0.517

SD

 0.744 0.614 0.735 0.500

KM

 1.000

 0.284  1.000

 0.250  0.412  1.000

 0.093 −0.073 −0.149  1.000

LA

T1 T2 T3 TRT

MO NX=1 NY=3 NE=3 BE=FI GA=FR TD=DI TE=DI

LE

intercept change1 change2

FI TD(1,1)

FI TE(1,1) TE(2,2)

FR TE(3,3)

VA 1 LY(1,1) LY(2,1) LY(3,1)

VA 1 LY(1,2) LY(2,3)

PD

OU ND=3

TI conditional Model - Sample 2: One Year Data

DA NO=348 NG=1 NI=4 MA=CM ME=ML

ME

 0.878 0.435 0.692 0.517

SD

 0.744 0.614 0.735 0.500

KM

 1.000

 0.284  1.000

 0.250  0.412  1.000

 0.093 −0.073 −0.149  1.000

LA

T1 T2 T3 TRT

MO NX=1 NY=3 NE=3 BE=FI PS=SY GA=FR TD=DI TE=DI

LE

intercept change1 change2

FI TD(1,1)

FR TE(1,1) TE(2,2) TE(3,3)

FI PS(2,2) PS(3,3)

VA 1 LY(1,1) LY(2,1) LY(3,1)

VA 1 LY(1,2) LY(2,3)

PD

OU ND=3 AD=OFF

Mplus Source Code for the Unconditional LCM in Figure 4a

TITLE: Unconditional Model – Sample 2: One Year Data;

  DATA:

    file = c:\eym\sem\mplus\oneyear.dat;

    format = 3f8.0, 3f8.2;

  VARIABLE:

    names = id bmi male rap1 rap2 rap3;

    usevariables = rap1-rap3;

  ANALYSIS:

    type = meanstructure;

  MODEL:

    intercpt by rap1-rap3@1;

    intercpt change1 | rap1@1 rap2@0 rap3@0;

    intercpt change2 | rap1@0 rap2@1 rap3@0;

    rap1@0;

    rap2@0;

    intercpt with change1@0;

    intercpt with change2@0;

    change1 with change2@0;

  OUTPUT:

    samp;

    tech1;

Mplus Source Code for the Unconditional LCM in Figure 4b

TITLE: Unconditional Model – Sample 2: One Year Data;

  DATA:

    file = c:\eym\sem\mplus\oneyear.dat;

    format = 3f8.0, 3f8.2;

  VARIABLE:

    names = id bmi male rap1 rap2 rap3;

    usevariables = rap1-rap3;

  ANALYSIS:

    type = meanstructure;

  MODEL:

    intercpt by rap1-rap3@1;

    intercpt change1 | rap1@1 rap2@0 rap3@0;

    intercpt change2 | rap1@0 rap2@1 rap3@0;

    !rap1@0;

    !rap2@0;

    change1@0;

    change2@0;

    intercpt with change1@0;

    intercpt with change2@0;

    change1 with change2@0;

  OUTPUT:

    samp;

    tech1;

Mplus Source Code for the Conditional LCM in Figure 4c

TITLE: Conditional Model – Sample 2: One Year Data;

  DATA:

    file = c:\eym\sem\mplus\oneyear.dat;

    format = 3f8.0, 3f8.2;

  VARIABLE:

    names = id bmi male rap1 rap2 rap3;

    usevariables = bmi rap1-rap3;

  ANALYSIS:

  MODEL:

    intercpt by rap1-rap3@1;

    intercpt change1 | rap1@1 rap2@0 rap3@0;

    intercpt change2 | rap1@0 rap2@1 rap3@0;

    rap1@0;

    rap2@0;

    bmi;

    intercpt with change1@0;

    intercpt with change2@0;

    change1 with change2@0;

    intercpt change1 change2 on bmi;

  OUTPUT:

    samp;

    tech1;

TITLE: Conditional Model – Sample 2: One Year Data;

  DATA:

    file = c:\eym\sem\mplus\oneyear.dat;

    format = 3f8.0, 3f8.2;

  VARIABLE:

    names = id bmi male rap1 rap2 rap3;

    usevariables = bmi rap1-rap3;

  ANALYSIS:

  MODEL:

    intercpt by rap1-rap3@1;

    intercpt change1 | rap1@1 rap2@0 rap3@0;

    intercpt change2 | rap1@0 rap2@1 rap3@0;

    !rap1@0;

    !rap2@0;

    bmi;

    change1@0;

    change2@0;

    intercpt with change1@0;

    intercpt with change2@0;

    change1 with change2@0;

    intercpt change1 change2 on bmi;

  OUTPUT:

    samp;

    tech1;