Block-Localized Density Functional Theory (BLDFT), Diabatic Coupling, and Their Use in Valence Bond Theory for Representing Reactive Potential Energy Surfaces

Abstract

A multistate density functional theory in the framework of the valence bond model is described. The method is based on a block-localized density functional theory (BLDFT) for the construction of valence-bond-like diabatic electronic states and is suitable for the study of electron transfer reactions and for the representation of reactive potential energy surfaces. The method is equivalent to a valence bond theory with the treatment of the localized configurations by using density functional theory (VBDFT). In VBDFT, the electron densities and energies of the valence bond states are determined by BLDFT. A functional estimate of the off-diagonal matrix elements of the VB Hamiltonian is proposed, making use of the overlap integral between Kohn–Sham determinants and the exchange-correlation functional for the ground state substituted with the transition (exchange) density. In addition, we describe an approximate approach, in which the off-diagonal matrix element is computed by wave function theory using block-localized Kohn–Sham orbitals. The key feature is that the electron density of the adiabatic ground state is not directly computed nor used to obtain the ground-state energy; the energy is determined by diagonalization of the multistate valence bond Hamiltonian. This represents a departure from the standard single-determinant Kohn–Sham density functional theory. The multistate VBDFT method is illustrated by the bond dissociation of ${\mathrm{H}}_2^{+}$ and a set of three nucleophilic substitution reactions in the DBH24 database. In the dissociation of ${\mathrm{H}}_2^{+}$, the VBDFT method yields the correct asymptotic behavior as the two protons stretch to infinity, whereas approximate functionals fail badly. For the S_N2 nucleophilic substitution reactions, the hybrid functional B3LYP severely underestimates the barrier heights, while the approximate two-state VBDFT method overcomes the self-interaction error, and overestimates the barrier heights. Inclusion of the ionic state in a three-state model, VBDFT(3), significantly improves the computed barrier heights, which are found to be in accord with accurate results. The BLDFT method is a versatile theory that can be used to analyze conventional DFT results to gain insight into chemical bonding properties, and it is illustrated by examining the intricate energy contributions to the ion–dipole complex stabilization.

1. Introduction

The construction of an effective two-state diabatic Hamiltonian provides an extremely useful tool for many chemical and biochemical applications.^1–5 Examples include the study of electron transfer (ET) using electronic structure methods and the representation of the potential energy surface (PES) of chemical reactions in condensed phases and in enzymes. Although these applications appear to be very different, the underlying principles to determine the PES are identical. In the Marcus–Hush electron transfer theory, the coupling matrix element between donor (H_D) and acceptor (H_A) potential energy surfaces, V_DA, is a crucial element in the calculation of the electron-transfer rate.⁶ At the crossing point where H_D = H_A, the coupling strength is the difference between the diabatic state energy and the adiabatic ground-state energy (ε₁):

$$V_{\text{DA}}=H_{\mathrm{A}}-{\epsilon }_1=\frac{|H_{\mathrm{A}}{S}_{\text{DA}}-H_{\text{DA}}|}{1+S_{\text{DA}}}$$ (1)

where H_DA = < Φ_D|H|Φ_A > and S_DA = < Φ_D|Φ_A > are, respectively, the exchange and overlap integrals of the donor and acceptor valence-bond electronic wave functions, Φ_D and Φ_A, and H is the electronic Hamiltonian of the system.

For chemical reactions, if Φ₁ and Φ₂ represent the valence bond electronic wave functions of the reactant and product states,⁷ the Born–Oppenheimer PES of the adiabatic ground state is given by the lower root, ε_g, of the 2 × 2 generalized secular equation:

$$\left|\begin{array}{cc}\hfill H_{11}-\epsilon \hfill & \hfill H_{12}-\epsilon S_{12}\hfill \\ \hfill H_{21}-\epsilon S_{21}\hfill & \hfill H_{22}-\epsilon \hfill \end{array}\right|=0$$ (2)

where the Hamiltonian matrix element is defined by H_ij = < Φ_i|H|Φ_j>, S_ij is the overlap integral, and H is the total effective Hamiltonian that includes both solute and solvent contributions. In this discussion, the electronic coupling may be defined as⁴

$$V_{12}=H_{12}-{\epsilon }_{\mathrm{g}}{S}_{12}$$ (3)

Then, the adiabatic ground-state potential energy has the simple form

$${\epsilon }_{\mathrm{g}}=\frac{1}{2}(H_{11}+H_{22})-\frac{1}{2}{[{(H_{11}-H_{22})}^2+4V_{12}^2]}^{1/2}$$ (4)

The electronic coupling matrix element V₁₂ may also be back-calculated from the diabatic and adiabatic ground-state potential energies:

$$V_{12}=\sqrt{(H_{11}-{\epsilon }_{\mathrm{g}})(H_{22}-{\epsilon }_{\mathrm{g}})}$$ (5)

The two expressions of V₁₂ in eqs 3 and 5 are equivalent, shown to emphasize an important point. The first shows the explicit dependence of the overlap integral, whereas this dependence is implicit in eq 5. In either case, there is no need to restrict the diabatic states to be orthogonal.

When the diabatic state energies and the adiabatic ground-state energy are determined at different levels of theory (or from experiments), one assumes that the difference in absolute energy is constant along the reaction path. As such, the adiabatic ground-state energy profile can be shifted by a constant Δ to yield an approximate V₁₂:

$$V_{12}=\sqrt{(H_{11}^{\text{LL}}-{\epsilon }_{\mathrm{g}}^{\text{HL}}+\mathrm{\Delta })(H_{22}^{\text{LL}}-{\epsilon }_{\mathrm{g}}^{\text{HL}}+\mathrm{\Delta })}$$ (6)

where LL and HL indicate energies are computed at lower-level and higher-level theories, and Δ can be chosen with the assumption that there is no diabatic coupling at the reactant state. Importantly, eq 6 provides a convenient connection between the diabatic and adiabatic PESs when they are obtained from different levels of theory, and hence, V₁₂ may be fitted globally or semiglobally to reproduce the all-dimensional adiabatic PES for a given two-state model.^8–12 In this case, the dependence on overlap is implicit. However, the effect of solvation on V₁₂ may not be adequately assessed using eq 6 if the diabatic PES (H₁₁ and H₂₂) and the adiabatic ground-state energy are not determined consistently with the same basis and theory or by optimizing both the orbital and configuration coefficients simultaneously.^3,13–16

The goal of this work is to develop a multistate density functional theory (MSDFT) in the framework of the valence bond model, in which the matrix elements are determined by Kohn–Sham (KS) density functional theory (DFT). In this way, dynamic electron correlation effects are treated by DFT for the diabatic (VB) states, whereas static electron correlation is partially described by the multiconfigurational valence bond Hamiltonian (keeping in mind the possibility of double-counting correlation effects using the current functionals). Since diabatic states are not uniquely defined, ^{3,4,7,17–20} the problem in these applications involves both the construction of the diabatic states and the accurate computation of the matrix elements.

Numerous methods have been developed.^{2,5,6,21–30} To this end, we have developed a mixed molecular orbital and valence bond (MOVB) theory,^3,13,14,16 based on a block-localized molecular orbital method.^31–38 In MOVB, diabatic states are defined as the valence bond configurations of the reactant and product structure, and the electronic wave functions are approximated by a single Slater determinant, in which the molecular orbitals (MOs) are strictly localized within the individual fragments of a molecular configuration. We note that the MOs within each fragment can be orthogonalized, but they are nonorthogonal between different fragments. Consequently, MOVB retains important characteristics of valence bond theory.^39–42 When the system contains just one fragment, MOVB reduces exactly to the conventional Hartree–Fock theory. On the other hand, when MOs are fully localized, MOVB becomes an ab initio valence bond self-consist field model,^41,43,44 which is equivalent to the complete active space (CASSCF) approach.

The single determinant, block-localized molecular orbitals can be used to compute the electron density in exactly the same way as that in the KS DFT approach.⁴⁵ Consequently, by construction, the total electron density of a molecular system is block-localized with the desired characteristics, and such a block-localized density functional theory (BLDFT) can be used to obtain the ground-state energy of the corresponding charge and spin-localized VB configuration. The block-localized MOs used in DFT calculations correspond to block-localized Kohn–Sham (BLKS) orbitals, which can be defined analogously as the MOVB definition of the reactant (donor) state and the product (acceptor) state for chemical (ET) reactions.^3,12,13,16 In this article, we describe two methods for computing the off-diagonal matrix elements using density functional theory. The MSDFT method can be adapted in VB calculations, so the method is also called the mixed VB and DFT (VBDFT) method. In this context, MSDFT and VBDFT can be interchangeably used, and we choose to use VBDFT throughout the rest of the paper. Clearly, an advantage of using BLDFT in VB calculations is the inclusion of electron correlation effects. Furthermore, because VBDFT is a multiconfigurational method, the self-interaction error in the existing functionals can, in principle, be eliminated in bond-making and -breaking processes.

For comparison, a related but distinct method is the constrained DFT (CDFT) formulated by Dederichs et al. in 1984,⁴⁶ in which a set of charge and spin constraints is introduced into KS-DFT calculations by the method of a Lagrange multiplier. The CDFT method has been used in a number of applications. Scheffler and co-workers studied the adsorption of triplet oxygen on the aluminum surface and reactions that are forbidden by the spin selection rule.^47,48 Van Voorhis described an approach to estimate the coupling matrix element in long-range ET reactions and used it in configuration interaction (CI) with CASSCF-inspired charge-and spin-constrained configurations.^29,30,49 Wesolowski developed a constrained DFT algorithm to describe intermolecular interactions.^50,51 In contrast, the VBDFT method follows a different strategy. We block-localize the KS orbitals, and hence the associated electron density is constrained by construction (e.g., the Mulliken population constraint is inherently imposed). The electron density for each diabatic state is derived from an antisymmetric wave function, consisting of both orthogonal and nonorthogonal BLKS orbitals, a feature distinct from the CDFT approach of Dederichs et al.⁴⁶ but characteristic of VB theory.⁷ Notably, the VBDFT method is applicable to both short-range (or strong-coupling) and long-range (or weak-coupling) ET reactions.

In the following, we first present the theoretical background of the VBDFT (or MSDFT) method and computational details. Then, we illustrate the VBDFT method by considering a set of applications involving S_N2 reactions. The paper is concluded with a summary of major findings and future perspectives.

2. Methods

Often, it is desirable to impose certain charge and spin constraints within a molecular system to describe the localized chemical bonding character to gain insight into properties such as resonance and charge transfer, concepts central to the understanding of the chemical bond. The MOVB method was developed to provide a computationally efficient procedure to study these effects as well as chemical reactions in solution and in enzymes.^3,13–16,52 In this section, we present an approach to use BLDFT to evaluate the matrix elements of VB Hamiltonians. Thus, this multireference density functional approach is also called the VBDFT method, which represents an extension of the MOVB model to include dynamic electron correlation effects in ab initio VB-like calculations.

Throughout this paper, we use the following convention. Subgroups of the molecular system are specified by Roman capital letters A, B, …; (block-localized) Kohn–Sham molecular orbitals are represented by |ψ>, labeled by the lower case letters, i, j, …; atomic orbital basis functions are denoted by |χ>, indexed by the lower case Greek letters, μ, v,… When A, B, … are used as superscripts over a matrix (distinguished by bold letters), they denote the dimension of the matrix in terms of the corresponding MOs in that subgroup, whereas when they are used as subscripts, the matrix is defined in terms of the basis functions. The elements of a column (row) in a matrix are always subscripted. VB configurations are specified by u, v, w, …

A. Block-Localized Density Functional Theory

In BLDFT, we first construct a set of BLKS orbitals corresponding to the desired charge and spin character.^31,32,45 For convenience of discussion, we consider a closed-shell system both for the entire system and for subgroups; generalization to open-shell and spin-constrained cases is straightforward and has been implemented. The full system consists of N electrons and M basis functions that are partitioned into K subgroups with n_A electrons and m_A basis functions in subgroup A. Then, the BLKS orbitals are expressed in terms of the atomic orbitals located on atoms in a particular subspace:

$$|{\psi }_i^A>={\chi }_A{\mathbf{C}}_i^A={\displaystyle \sum _{\mu =1}^{m_A}|{\chi }_{A\mu }>c_{\mu i}^A,A=1,\dots ,K}$$ (7)

where $c_{\mu i}^A$ is an element of the column coefficient vector $({\mathbf{C}}_i^A)$ of KS orbital $i(|{\psi }_i^A>),\text{and}\{|{\chi }_{A\mu }>{\}}_{\mu \stackrel{A}{=}1}^m$ are the basis functions in subgroup A, arranged as a row vector χ_A. Let ${\Omega }^A={\psi }_1^A\alpha {\psi }_1^A\beta \dots {\psi }_{n_A/2}^A\beta$ be a successive product of n_A occupied spin–orbitals in subgroup A, and α and β are spin functions. The Slater determinant function for the block-localized system is constructed as follows:

$${\mathrm{\Phi }}_u=N_u\widehat{A}\{{\mathrm{\Omega }}^1{\mathrm{\Omega }}^2\dots {\mathrm{\Omega }}^K\}$$ (8)

where  is an antisymmetrization operator, and N_u is the normalization constant.

The BLKS orbitals between different subgroups in eq 8 are not orthogonal. Orthogonalization of these orbitals can be done and is in fact part of the procedure to solve the self-consistent field equations; however, the orthorgonalized orbitals should not be used to interpret the properties of the strictly localized, individual blocks or separate molecules because they contain orthogonalization tails. Note that the KS orbitals within the same subgroup can be and are orthorgonalized, which does not affect the total energy by a unitary transformation. The overlap matrix of the MOs is given as follows

$$\mathbf{S}={\mathbf{C}}^{\mathbf{T}}\mathbf{\text{RC}}$$ (9)

where R = χ^Tχ is the overlap in terms of the basis functions and C is the transformation matrix:

$$\mathbf{C}=\left(\begin{array}{cccc}\hfill {\mathbf{C}}^1\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill {\mathbf{C}}^2\hfill & \hfill \cdots \hfill & \hfill 0\hfill \\ \hfill \cdots \hfill & \hfill \cdots \hfill & \hfill \cdots \hfill & \hfill \cdots \hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill {\mathbf{C}}^K\hfill \end{array}\right)$$ (10)

The one-particle density matrix from the occupied non-orthogonal BLKS orbitals is defined by

$$\mathbf{D}=\mathbf{C}({\mathbf{C}}^{\mathbf{T}}\mathbf{\text{RC}}{)}^{-1}{\mathbf{C}}^{\mathrm{T}}$$ (11)

which satisfies the symmetry (D^T = D), rank (Tr(DR) = N), and idempotency (DRD = D) conditions, and the electron density is given as follows

$$\rho (\mathbf{r})={\displaystyle \sum _{\mu v}^m|{\chi }_{\mu }(\mathbf{r})>D_{\mu v}<{\chi }_v(\mathbf{r})|=\chi (\mathbf{r})\mathbf{D}{\chi }^{\mathrm{T}}(\mathbf{r})}$$ (12)

Using the one-particle density matrix and electron density of eqs 11 and 12 computed from the nonorthogonal KS orbitals, we can express the BLDFT ground-state energy identically to that in the case of orthogonal KS orbitals:⁴⁵

$$E[\rho ]=\mathit{\text{Tr}}(\mathbf{\text{Dh}})+\frac{1}{2}\mathit{\text{Tr}}(\mathbf{\text{DJD}})+E_{\text{xc}}[\rho (\mathbf{r})]+E_{\text{nuc}}$$ (13)

where E_nuc is the coulomb energy of the nuclei, h and J are the usual Hamiltonian (one-electron) and Coulomb integral matrices, and E_xc[ρ(r)] is the exchange-correlation energy functional.

The corresponding block-localized Kohn–Sham equations for the nonorthogonal KS orbitals can be derived following the procedure described by Stoll et al.,⁵³ and later by a number of groups in various forms in molecular orbital theory,^{14,31–38,54} primarily for treating intermolecular interactions without basis set superposition errors and for energy decomposition analysis. Because the transformation matrix (eq 10) is block-diagonal, the conventional self-consistent field (SCF) procedure for the Kohn–Sham equations of the entire system can be cast into K separate KS equations, one set for each subgroup. First, we define the projection operator P̂_∉A in the space of occupied KS orbitals that exclude those in subgroup A, indicated by the subscripts ∉A:

$${\widehat{P}}_{\notin A}={\displaystyle \sum _{B,C\ne A}^K{\displaystyle \sum _{i,j}^{\text{occ}}|{\psi }_i^B>{[{\mathbf{S}}_{\notin A})}^{-1}{]}_{\mathit{\text{ij}}}<{\psi }_j^C|}}$$ (14)

where S_∉A is the overlap matrix without the occupied KS orbitals of subgroup A. Then, the KS equations for the orbitals of subgroup A are given as follows

$${\widehat{F}}^A|{\psi }_i^A>=(\widehat{1}-{\widehat{P}}_{\notin A})|{\psi }_i^A>{\epsilon }_i^A$$ (15)

where F̂^A is the projected KS operator

$${\widehat{F}}^A=(\widehat{1}-{\widehat{P}}_{\notin A})\widehat{F}(\widehat{1}-{\widehat{P}}_{\notin A})$$ (16)

with F̂ being the unprojected (conventional) KS operator,

$$\widehat{F}=-\frac{1}{2}{\nabla }^2+v_{\text{ext}}(r)+{\displaystyle \int }\frac{\rho (\mathbf{r}\prime )}{|\mathbf{r}-\mathbf{r}\prime |}\mathrm{d}\mathbf{r}\prime +v_{\text{xc}}[\rho (\mathbf{r})]$$ (17)

where v_xc[ρ(r)] is the exchange-correlation potential, and v_ext(r) is the nuclei–electron attraction, which may include the partial charges from the solvent in combined QM/MM calculations.

The KS orbitals in eq 15 can be optimized sequentially by Jacobi rotation,^13,31 which is straightforward to implement. Alternatively, in matrix form, in terms of the basis functions, the generalized secular equations can be written as follows:^14,37,54

$${\mathbf{F}}_{\mathit{\text{AA}}}^P{\mathbf{C}}_{\mathit{\text{AA}}}={\mathbf{R}}_{\mathit{\text{AA}}}^P{\mathbf{C}}_{\mathit{\text{AA}}}{\epsilon }_{\mathit{\text{AA}}}$$ (18)

where ε_AA is a diagonal matrix corresponding to orbital energies. Equation 18 was derived subject to the condition (which does not affect the energy):³⁴

$${({\mathbf{C}}_{\mathit{\text{AA}}})}^{\mathrm{T}}{\mathbf{R}}_{\mathit{\text{AA}}}^P{\mathbf{C}}_{\mathit{\text{AA}}}={\mathbf{1}}_{\mathit{\text{AA}}}$$ (19)

and the projected overlap $({\mathbf{R}}_{\mathit{\text{AA}}}^P)$ and KS-Fock $({\mathbf{F}}_{\mathit{\text{AA}}}^P)$ matrices are given as

$${\mathbf{R}}_{\mathit{\text{AA}}}^P=({\mathbf{R}}_{\mathit{\text{AA}}},{\mathbf{R}}_{\mathit{\text{AB}}}){\mathbf{P}}_{\notin A}$$ (20)

and

$${\mathbf{F}}_{\mathit{\text{AA}}}^P=({\mathbf{P}}_{\notin A}{)}^{\mathrm{T}}{\mathbf{\text{FP}}}_{\notin A}$$ (21)

The projection matrix is defined below. The computational procedure is conveniently described by considering an effective partition of two blocks, A and B, where the orbitals in A are being optimized and B includes all other subgroups of the molecular system. We arrange block A as the first block and B second; that is, we rearrange the basis in the following order, specified by a prime: χ′ = [χ_A, χ₁, …, χ_A−1, χ_A+1, …, χ_K] = [χ_A, χ_B], and thus the transformation matrix C′ = [C^A, C^B]. Then, the overlap, density, and projection matrices in terms of the basis functions and the overlap matrix in terms of KS orbitals in eqs 20 and 21 are given, respectively, as

$$\mathbf{R}\prime ={\chi \prime }^{\mathrm{T}}\chi \prime =\left(\begin{array}{cc}{\mathbf{R}}_{\mathit{\text{AA}}}\hfill & {\mathbf{R}}_{\mathit{\text{AB}}}\hfill \\ {\mathbf{R}}_{\mathit{\text{BA}}}\hfill & {\mathbf{R}}_{\mathit{\text{BB}}}\hfill \end{array}\right)$$ (22)

$${\mathbf{D}}_{\mathit{\text{BB}}}={\mathbf{C}}^B{({\mathbf{S}}^{\mathit{\text{BB}}})}^{-1}({\mathbf{C}}^B{)}^{\mathrm{T}}$$ (23)

$${\mathbf{P}}_{\notin A}=\left(\begin{array}{c}\hfill {\mathbf{1}}_{\mathit{\text{AA}}}\hfill \\ \hfill -{\mathbf{D}}_{\mathit{\text{BB}}}{\mathbf{R}}_{\mathit{\text{BA}}}\hfill \end{array}\right)$$ (24)

$$\mathbf{S}\prime =\left(\begin{array}{cc}{\mathbf{S}}^{\mathit{\text{AA}}}\hfill & {\mathbf{S}}^{\mathit{\text{AB}}}\hfill \\ {\mathbf{S}}^{\mathit{\text{BA}}}\hfill & {\mathbf{S}}^{\mathit{\text{BB}}}\hfill \end{array}\right)$$ (25)

Starting from an initial guess, typically generated from the extended Hückel method but preferably from calculations of individual subgroups, one iteratively optimizes the KS orbitals of each subgroup employing the densities generated previously for other subgroups until the total energy and density are converged. The key property of these orbitals is that they yield the exact electron density of the charge- and spin-constrained configuration through eq 12, which is then used to determine E_xc[ρ(r)] in eq 13.⁴⁵ Furthermore, as illustrated in Hartree–Fock theory by Nagata et al.,⁵⁴ it is straightforward to show that, if the electron density is partitioned in the sense of Mulliken population of the occupied, nonorthogonal BLKS orbitals, the electron densities of the individual subgroups are conserved without charge transfer between different ones. Thus, the total electron density is partitioned into subgroups as follows:

$$N=N^A+N^B=\mathit{\text{Tr}}({[\mathbf{\text{DR}}]}_{\mathit{\text{AA}}})+\mathit{\text{Tr}}({[\mathbf{\text{DR}}]}_{\mathit{\text{BB}}})$$ (26)

where [DR]_AA = D_AAR_AA + D_ABR_BA and [DR]_BB = D_BAR_AB + D_BBR_BB. The total electron density is similarly partitioned into the electron densities of the subgroups

$$\rho (\mathbf{r})={\rho }^A(\mathbf{r})+{\rho }^B(\mathbf{r})$$ (27)

which are given by

$${\rho }^A(\mathbf{r})={\chi }_A(\mathbf{r}){\mathbf{D}}_{\mathit{\text{AA}}}({\chi }_A{)}^{\mathrm{T}}(\mathbf{r})+{\chi }_A(\mathbf{r}){\mathbf{D}}_{\mathit{\text{AB}}}({\chi }_B{)}^{\mathrm{T}}(\mathbf{r})$$ (28)

$${\rho }^B(\mathbf{r})={\chi }_B(\mathbf{r}){\mathbf{D}}_{\mathit{\text{BB}}}({\chi }_B{)}^{\mathrm{T}}(\mathbf{r})+{\chi }_B(\mathbf{r}){\mathbf{D}}_{\mathit{\text{BA}}}({\chi }_A{)}^{\mathrm{T}}(\mathbf{r})$$ (29)

For subgroup A, the number of partitioned electrons is

$$N^A={\displaystyle \int }{\rho }^A(\mathbf{r})\mathrm{d}\mathbf{r}=\mathit{\text{Tr}}({\mathbf{D}}_{\mathit{\text{AA}}}{\mathbf{R}}_{\mathit{\text{AA}}}+{\mathbf{D}}_{\mathit{\text{AB}}}{\mathbf{R}}_{\mathit{\text{BA}}})=n_A$$ (30)

which is the number of constrained electrons in subgroup A. Therefore, the block-localized KS orbital partition defined by eq 8 is equivalent to imposing the constraint, δ(A), to the total electron density, such that

$${\displaystyle \int \delta (A)\rho (\mathbf{r})\mathrm{d}\mathbf{r}-n_A=}{\displaystyle \int {\rho }^A(\mathbf{r})\mathrm{d}\mathbf{r}-n_A=0}$$ (31)

Before we leave this section, it is of interest to make a comparison with constrained DFT (CDFT) introduced by Dederichs et al.,⁴⁶ in which the constrained KS equations are

$$[\widehat{F}+V_c{w}_c(\mathbf{r})]|{\varphi }_i^c>=|{\varphi }_i^c>{\epsilon }_i^c$$ (32)

where V_c is the Lagrangian multiplier for the constraint w_c(r) to yield a desired charge and spin property N_c, ∫ w_c(r) ρ(r) dr − N_c = 0. In CDFT, the constrained KS orbitals are expanded over the entire basis set, corresponding to a fully delocalized system with specific spatial restrictions (N_c) in practice.³⁰ In contrast, the present BLDFT builds charge and spin localization by construction, and the charge and spin densities are strictly constrained within each subgroup in the sense of Mulliken population partition without ambiguity or integration uncertainty (however, this should not be confused with the use of the Mulliken population constraint in CDFT calculations, in which case it is difficult to achieve charge localization because of the use of the intrinsically delocalized KS orbitals).³⁰ Note that the charge integration scheme in CDFT is rather arbitrarily defined and cannot yield the correct total charges for the constrained fragments in the dissociation of H₂⁺.

There are, of course, many other ways of representing constrained DFT calculations, including a useful method developed by Wesolowski et al. for studying intermolecular interactions.⁵¹ In this case, the molecular fragments are considered as separated systems under the influence of the mutual polarization of other densities, either frozen or optimized. An anonymous reviewer pointed out that, in principle, the method developed by Wesolowski can be used to construct the localized configurations as described here, provided if one knew the exact nonadditive part of the kinetic energy. “The problem is that the function isn’t known and the approximations currently used will fail when there is significant subgroup overlap.” Of course, subgroup overlap is significant in problems of interest to us. In this regard, the kinetic energy in the present BLDFT method is treated exactly as that in the KS-DFT scheme, and the resulting valence bond Hamiltonian corresponds to a multireference density functional theory, in which the densities for the VB-like diabatic (reference) states are uniquely defined.

B. Diabatic Coupling and Multireference Valence Bond Density Functional Theory

In this section, we formulate a two-state VB Hamiltonian, making use of BLDFT to determine the matrix elements. Clearly, the method is general and has been implemented for multiple states as illustrated in the following applications. For the S_N2 reaction between nucleophile Nu⁻ and substrate CH₃L, we define the reactant (Ψ_u: [Nu⁻][CH₃L]) and the product (Ψ_w: [NuCH₃][L⁻]) diabatic states on the basis of the VB structure of separate, but interacting, fragments:^3,13

$${\mathrm{\Psi }}_u(\mathbf{X})=N_u\widehat{A}\{{\Omega }^1[{\text{Nu}}^{-}]{\Omega }^2[{\text{CH}}_3\mathrm{L}]\}$$ (33)

$${\mathrm{\Psi }}_w(\mathbf{X})=N_w\widehat{A}\{{\Omega }^3[{\text{NuCH}}_3]{\Omega }^4[{\mathrm{L}}^{-}]\}$$ (34)

where N_u and N_w are normalization constants and X specifies the instantaneous atomic coordinates. Then, the VB wave function is written as a linear combination of the two VB configurations defined by 33 and 34, which is valid for the description of the entire adiabatic ground state and a coupling excited state:

$${\mathrm{\Phi }}^{\text{VB}}(\mathbf{X})=a_u{\mathrm{\Psi }}_u(\mathbf{X})+a_w{\mathrm{\Psi }}_w(\mathbf{X})$$ (35)

The adiabatic ground-state energy at a given molecular geometry, X, is the lower root of the generalized secular equation (eq 2), in which u = 1 and w = 2.

Note that the wave function of eq 35 is used purely for the purpose of deriving the secular equation (eq 2). Importantly, Φ^VB(X) is determined corresponding to a unique potential v^VB(X), which in turn defines the adiabatic ground state density and the adiabatic ground-state energy within the block-localized configurations defined by eqs 33 and 34. However, Φ^VB(X) is not used to compute the electron density to determine the DFT energy—a departure from previous approaches employing multiconfigurational wave function to construct the one-particle density. The KS determinants defined in eqs 33 and 34 are used to generate the BLKS orbitals, which yield the exact electron densities for the individual diabatic states and the corresponding matrix elements H_uu and H_ww (eq 13). Unfortunately, the exact wave functions associated with the block-localized densities for the reactant and product diabatic states are not available. Thus, the exact overlap integral in eq 2 between two diabatic states defined by BLDFT cannot be directly computed. An obvious choice to circumvent this difficulty is to use the KS determinants to evaluate the overlap, S_uw. This strategy has been used by Wu and others.⁴⁹ Then, the overlap integral between Ψ_u and Ψ_w can be decomposed into the product of overlaps for the α and β spin orbitals.¹⁴ As we are considering closed-shell cases and each BLKS orbital is occupied by two electrons, the overlaps for the α and β spin orbitals are the same and equal to q_uw. Thus,

$$S_{\mathit{\text{uw}}}=<{\mathrm{\Psi }}^u|{\mathrm{\Psi }}^w>=q_{\mathit{\text{uw}}}^2$$ (36)

where q_uw is the determinant of the overlap matrix between the BLKS orbitals from the two states:

$${\mathbf{S}}^{\mathit{\text{uw}}}=({\mathbf{C}}^u{)}^{\mathrm{T}}{\mathbf{\text{RC}}}^w$$ (37)

$$q_{\mathit{\text{uw}}}=\text{det}|{\mathbf{S}}^{\mathit{\text{uw}}}|$$ (38)

where C^u and C^w are the transformation matrices of states Ψ_u and Ψ_w which have the same total basis functions and occupied orbitals, but, of course, are block-localized differently.

The coupling matrix element represents the transition between two diabatic states Ψ_u and Ψ_w whose energies are uniquely defined by their electron densities. However, H_uw is not a natural functional of the electron density, but it is a functional of both the electron densities ρ_u(r) and ρ_w(r) of states Ψ_u and Ψ_w. To evaluate the coupling matrix element using DFT, we make a comparison with the matrix element H_uw from two nonorthogonal wave functions determined using the MOVB theory and in other calculations.^{3,13,14,21,55} First, we define the one-particle exchange (or transition) density matrix and the exchange (transition) electron density as follows

$${\mathbf{D}}_{\mathit{\text{uw}}}={\mathbf{C}}^w{({\mathbf{S}}^{\mathit{\text{uw}}})}^{-1}({\mathbf{C}}^u{)}^{\mathrm{T}}={\mathbf{C}}^w[({\mathbf{C}}^u{)}^{\mathrm{T}}{\mathbf{\text{RC}}}^w{]}^{-1}({\mathbf{C}}^u{)}^{\mathrm{T}}$$ (39)

$${\rho }_{\mathit{\text{uw}}}(\mathbf{r})={\displaystyle \sum _{\mu v}^m|{\chi }_{\mu }(\mathbf{r})>({\mathbf{D}}_{\mathit{\text{uw}}}{)}_{\mu v}<{\chi }_v(\mathbf{r})|=\chi (\mathbf{r}){\mathbf{D}}_{\mathit{\text{uw}}}{\chi }^{\mathrm{T}}(\mathbf{r})}$$ (40)

Clearly, the density matrix D_uw is of rank N (i.e., ∫ ρ_uw(r) dr = N; if S^uw is also of rank N), but it is not symmetric. Importantly, D_uw satisfies the general idempotency condition

$${\mathbf{D}}_{\mathit{\text{uw}}}{\mathbf{\text{RD}}}_{\mathit{\text{uw}}}={\mathbf{D}}_{\mathit{\text{uw}}}$$ (41)

Consequently, the coupling matrix element between the two determinant states Ψ_u and Ψ_w can be computed in exactly the same way as that of Hartree–Fock energy expression; one simply replaces the symmetric ground-state one-particle density matrix with the asymmetric one-particle exchange density:

$$\begin{array}{cc}{H}_{\mathit{\text{uw}}}^{\text{KS}}=\hfill & S_{\mathit{\text{uw}}}^{\text{KS}}\{\mathit{\text{Tr}}[({\mathbf{D}}_{\mathit{\text{uw}}}{)}^{\mathrm{T}}\mathbf{h}]+\frac{1}{2}\mathit{\text{Tr}}[({\mathbf{D}}_{\mathit{\text{uw}}}{)}^{\mathrm{T}}{\mathbf{\text{JD}}}_{\mathit{\text{uw}}}]\hfill \\ \hfill & -\frac{1}{4}\mathit{\text{Tr}}[({\mathbf{D}}_{\mathit{\text{uw}}}{)}^{\mathrm{T}}{\mathbf{\text{KD}}}_{\mathit{\text{uw}}}]+E_{\text{nuc}}\}\hfill \end{array}$$ (42)

Here, we have used the superscript KS to indicate that the exchange, or coupling matrix element, is computed using KS orbitals along with the pure Hartree–Fock exchange, K.

Comparison with the KS-DFT energy expression (eq 13) shows that the only difference is in the exchange term. If we replace, as in ground-state KS-DFT calculations, the Hartree–Fock exchange term with the DFT exchange-correlation energy functional using the exchange density defined in eq 41 we may compute the VBDFT coupling matrix element between states characterized by the block-localized densities of ρ_u(r) and ρ_w(r) by

$$\begin{array}{cc}{H}_{\mathit{\text{uw}}}^{\text{VBDFT}}\equiv \hfill & E[{\rho }_{\mathit{\text{uw}}}(\mathbf{r})]=S_{\mathit{\text{uw}}}^{\text{KS}}\{\mathit{\text{Tr}}[({\mathbf{D}}_{\mathit{\text{uw}}}{)}^{\mathrm{T}}\mathbf{h}]+\frac{1}{2}\mathit{\text{Tr}}[({\mathbf{D}}_{\mathit{\text{uw}}}{)}^{\mathrm{T}}{\mathbf{\text{JD}}}_{\mathit{\text{uw}}}]\}\hfill \\ \hfill & +S_{\mathit{\text{uw}}}^{\text{KS}}{E}_{\mathit{\text{xc}}}[{\rho }_{\mathit{\text{uw}}}(\mathbf{r})]+S_{\mathit{\text{uw}}}^{\text{KS}}{E}_{\text{nuc}}\hfill \end{array}$$ (43)

Here, we have assumed that the approximate energy functional for the ground state is also applicable to the coupling energy between two interacting states using the transition density defined in eq 41. We note that it is possible to define the one-particle exchange density differently if a different form of the projection operator (eq 14) is used,^37,53 which corresponds to a different definition of the diabatic states. The projection operator in eq 14 satisfies Hermiticity.³⁴

The adiabatic ground-state energy can be computed by a two-state, mixed valence bond and DFT model, that is, VBDFT, in which 1 specifies the reactant and 2 the product state, through the generalized secular equation:

$$\left|\begin{array}{cc}\hfill E_{\mathit{\text{uu}}}^{\text{BL-DFT}}[{\rho }_u(\mathbf{r})]-\epsilon (\mathbf{X})\hfill & \hfill E_{\mathit{\text{uw}}}^{\text{BL-DFT}}[{\rho }_{\mathit{\text{uw}}}(\mathbf{r})]-\epsilon (\mathbf{X})S_{\mathit{\text{uw}}}^{\text{KS}}\hfill \\ \hfill E_{\mathit{\text{wu}}}^{\text{BL-DFT}}[{\rho }_{\mathit{\text{wu}}}(\mathbf{r})]-\epsilon (\mathbf{X})S_{\mathit{\text{wu}}}^{\text{KS}}\hfill & \hfill E_{\mathit{\text{ww}}}^{\text{BL-DFT}}[{\rho }_w(\mathbf{r})]-\epsilon (\mathbf{X})\hfill \end{array}\right|=0$$ (44)

Here, we have used the superscripts to indicate the method by which the energy is computed. The numerical performance of eq 43 will be thoroughly addressed in a subsequent publication. In the present work, we describe an alternative, approximate method below, which will be applied to the test cases by using the off-diagonal matrix elements computed using the KS determinants.

In the second approach, the off-diagonal matrix element is approximated by one determined with the KS determinants of block-localized valence bond states. To make the electronic energy compatible with that computed using density functional theory, we assume that the relative energies computed at the DFT level and the Hartree–Fock level with KS determinants can be shifted by an amount corresponding to the absolute energy difference in the two diabatic states (a constant at a given geometry). Thus,

$$H_{\mathit{\text{uw}}}\approx H_{\mathit{\text{uw}}}^{\text{KS}}+\frac{1}{2}{S}_{\mathit{\text{uw}}}(E_u[{\rho }_u(\mathbf{r})]+E_w[{\rho }_w(\mathbf{r})]-E_u^{\text{KS}}-E_w^{\text{KS}})$$ (45)

where the BLDFT energies E_u[ρ_u(r)] and E_w[ρ_w(r)] for the states characterized by the densities ρu(r) and ρ_w(r) are determined by eq 13, and $E_u^{\text{KS}}(\mathbf{K})\text{and}{E}_w^{\text{KS}}(\mathbf{K})$ are the Hartree–Fock energies determined by using the BLKS orbitals. As we shall see below, the use of the approximate coupling-matrix element of eq 45 can overcome the self-interaction errors in approximate functionals, but it typically yields barrier heights greater than the corresponding accurate results if only two states are used. Inclusion of the ionic configuration in a three-state model for the S_N2 reactions is examined here; the computed energies of reaction are found to be in accord with accurate results (below). We note that Wu et al. proposed a different way of estimating the off-diagonal matrix element,^49,56 which also involves the overlap scaled sum of the energies of the two diabatic states, but it is corrected by the overlap scaled constraint integrals. Equation 45 implicitly assumes that the relative change of BLDFT and KS energies for the diabatic states is approximately similar.

Obviously, the method presented here is not restricted to two states, and it can easily be generalized to any number of states, defined by a given characteristic feature of charge and spin. In the present work, we also examined a three-state treatment of the S_N2 reactions. At this point, we note the difference of the two acronyms, BLDFT and VBDFT (or equivalently MSDFT). The multistate VBDFT Hamiltonian that we present here employs the BLDFT method to determine matrix elements; as noted in the beginning of this work, it can also be called a multistate density functional theory based on multiple Kohn–Sham reference densities of valence bond-like states. BLDFT is also a general theory within its own right, which can be used to investigate properties of the chemical bond,⁴⁵ such as resonance delocalization energy,^32,45 aromaticity,^57,58 polarization and charge transfer energy,^59–63 hyperconjugation and negative hyperconjugation,^32,64 and steric effects.^65,66 The VBDFT method is designed for the representation of the PES of chemical reactions, both in the gas phase and in solution and enzymes (simply by including the electrostatic potential in the term v_ext(r) in eq 17). The diabatic states defined in eqs 33 and 34 can be used to define the Marcus reaction coordinate,⁶⁷ and to represent the solvent reaction coordinate along with the use of the adiabatic potential surface from the same or a different level of theory in condensed phase reactions. Methods for carrying out this type of calculation have been described previously.^13–15

3. Computational Details

All calculations are carried out using the Xiamen Valence Bond⁴¹ program and a modified version of GAMESS.⁶⁸ Geometry optimizations were performed with Gaussian 03.⁶⁹ The 6-31G+(d) basis set was used throughout for all calculations, except that for the ${\mathrm{H}}_2^{+}$ system, which employs the aug-cc-pVTZ basis set. Geometries for the S_N2 reactions of [Cl⁻ + CH₃Cl], [F⁻ + CH₃Cl], and [HO⁻ + CH₃F] along the reaction coordinate defined below are optimized at the B3LYP/6-31+G(d) level. We used a version of the B3LYP implementation that employs the VWN5 functional in GAMESS, which differs from the standard B3LYP employing the VWN1 functional.^70–73 All results are obtained using the VBDFT method employing eq 45 in the present study.

To describe the change in energy and wave function of the two Lewis bond states for each reaction, we define the reaction coordinate as the difference between the bond length of the central carbon and the leaving group R(C–L), where L = Cl, Cl, and F, and that of the nucleophile and the central carbon R(Nu–C), where Nu = Cl, F, and O, respectively, for the three reactions:

$$\text{Rc}=R(\mathrm{C}-\mathrm{L})-R(\text{Nu}-\mathrm{C})$$ (46)

Of course, one can use other definitions to monitor the progress of the reaction, including the difference between the corresponding bond orders or energies of the two Lewis bond states. The geometrical variable, corresponding to the asymmetric bond stretch coordinate, is a good choice and chemically intuitive for the S_N2 reactions.

4. Results and Discussion

We first examine the simple but illustrative case of the dissociation of ${\mathrm{H}}_2^{+}$ to show that the BLDFT method can effectively localize charge configurations and the localized states can be used in VB-like configuration interaction calculations to yield a qualitatively correct energy profile. Then, we present the results for the nucleophilic substitution reactions of [Cl⁻ + CH₃Cl], [F⁻ + CH₃Cl], and [HO⁻ + CH₃F] that are included in the DBH24 database designed for testing the performance of new functionals.

A. Energy Profile of ${\mathrm{H}}_2^{+}$

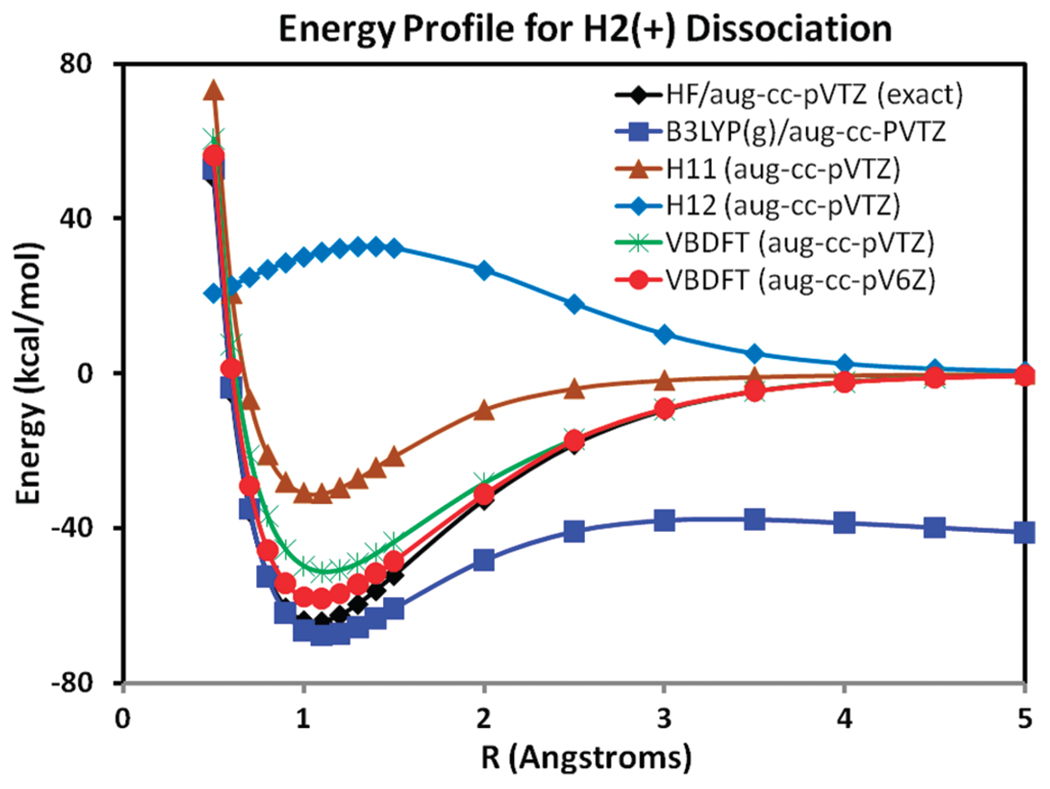
Recently, Yang and co-workers⁷⁴ vividly illustrated the well-known self-interaction error (charge delocalization error) in current approximate functionals by considering the simple one-electron system ${\mathrm{H}}_2^{+}$. In this case, the Hartree–Fock result is exact with a given basis set, and DFT describes the chemical bond very well. However, approximate functionals, as illustrated with B3LYP in Figure 1, fail badly as the distance between the two protons increases;⁷⁴ the potential energy profile first reaches a barrier of about 20 kcal/mol above the minimum and then falls off continuously because the electron is delocalized over two centers at infinite separation. This has been attributed to the self-interaction error.^74,75 This error can also be regarded as a need for multiconfigurational treatment of the dissociation process (also in the case of H₂ associated with spin delocalization). Cohen et al. pointed out that this charge delocalization error causes the computed barrier for a chemical reaction to be too low, a molecular polarizability that is too high, and unphysical charge transfer in molecular electronic devices using approximate functionals.⁷⁴

Figure 1.

Computed adiabatic ground-state energy profile for the diassociation of ${\mathrm{H}}_2^{+}$ using Hartree–Fock (HF) theory (black), density functional theory with the hybrid B3LYP functional (blue), and multireference valence bond-density functional theory (VBDFT) using the B3LYP functional with the aug-cc-pVTZ basis set (green) and with the aug-cc-pV6Z basis set (red). The diabatic energy profile for the degenerate block-localized electronic configuration Ψ([H⁺][H•]) computed using the BLDFT method is shown in brown, and the coupling energy V₁₂ is given in light blue, both using the aug-cc-pVTZ basis functions.

In VBDFT, we employ two degenerate block-localized configurations, corresponding to the electron localized on the “left” proton, Ψ₁([H•][H⁺]), and on the “right” proton, Ψ₂([H⁺][H•]), respectively. The energy profile of the block-localized VB state is shown in Figure 1 by the curve denoted as H₁₁, which gives the electrostatic and polarization interaction energy between a localized (but polarizable) hydrogen atom and a proton. The computed interaction energy at the minimum is −31 kcal/mol, slightly less than half of the total binding energy at the Hartree–Fock level. Using the wave-function-based estimate of the off-diagonal element in the VBDFT method, we obtain a bond-dissociation energy about 10 kcal/mol smaller than the exact result. Although both Hartree–Fock and B3LYP results are well converged with the aug-cc-pVTZ basis set, the use of a larger basis set in VBDFT calculations can further improve the estimated binding energy. For example, using the aug-cc-pV6Z basis, the calculated VBBLD result is −58.3 kcal/mol compared with the Hartree–Fock (exact) value of −63.5 kcal/mol. Thus, the block-localized density functional theory is more sensitive to the atomic orbital basis functions because of the extreme localization of Kohn–Sham orbitals. Importantly, the qualitative behavior of the dissociation curve at large interatomic distances is correctly reproduced. Wu and co-workers showed that their CDFT-CI approach can also effectively describe the correct dissociation energy.⁴⁹

Depicted in Figure 1 also is the coupling energy, defined by eq 3( $V_{12}=|H_{12}-{\epsilon }_{\mathrm{g}}{S}_{12}^{\text{KS}}|$). The largest coupling energy is in the bonding region and goes to zero as the interatomic separation becomes large. Figure 1 shows that the BLDFT method can effectively localize charge density for VB-like configurations. It is interesting to note that the CDFT method used by Wu and co-workers employs a spatial integration to constrain electron density, which cannot be exactly unity on the constrained atom unless the integration is over the entire space.⁴⁹ This limitation is not obvious for molecular systems with more than one electron, but its implication, due to the use of fully delocalized Kohn–Sham orbitals, is clearly illustrated in the one-electron case. In the BLDFT method, integration of the electron density defined by eq 12 yields exactly the number of electrons in the localized fragment (one for a hydrogen atom).

B. S_N2 Reactions

B.1. Diabatic Energies

We consider the diabatic potential energy profiles for the three model S_N2 reactions, [Cl⁻ + CH₃Cl], [F⁻ + CH₃Cl], and [HO⁻ + CH₃F], included in the DBH24 (24 diverse barrier heights) database.⁷⁶ In each case, the reactant state is defined by the VB configuration characterized by the substrate Lewis structure in the presence of the nucleophile as a “spectator ion” (eq 33) and the product state by the product Lewis structure in the presence of the leaving group ion (eq 34).³ In addition, we constructed a three-state model by including the ionic configuration:

$${\mathrm{\Psi }}_x(\mathbf{X})=N_x\widehat{A}\{{\Omega }^6[{\text{Nu}}^{-}]{\Omega }^7[{\text{CH}}_3^{+}]{\Omega }^8[{\mathrm{L}}^{-1}]\}$$ (47)

The VB configuration of eq 47 closely resembles the structure of the transition state. The reactant and product diabatic energy profiles for the three S_N2 reactions, computed using the BLDFT method and Hartree–Fock theory with BLKS orbitals, are shown in Figure 2, along with the VBDFT adiabatic ground-state potential energy. The relative energies are determined with respect to the infinitely separated nucleophile and substrate species (reactant state). Thus, the absolute electronic energies of the diabatic and adiabatic states can be obtained by adding the sum of the corresponding DFT energies of the separate molecules.

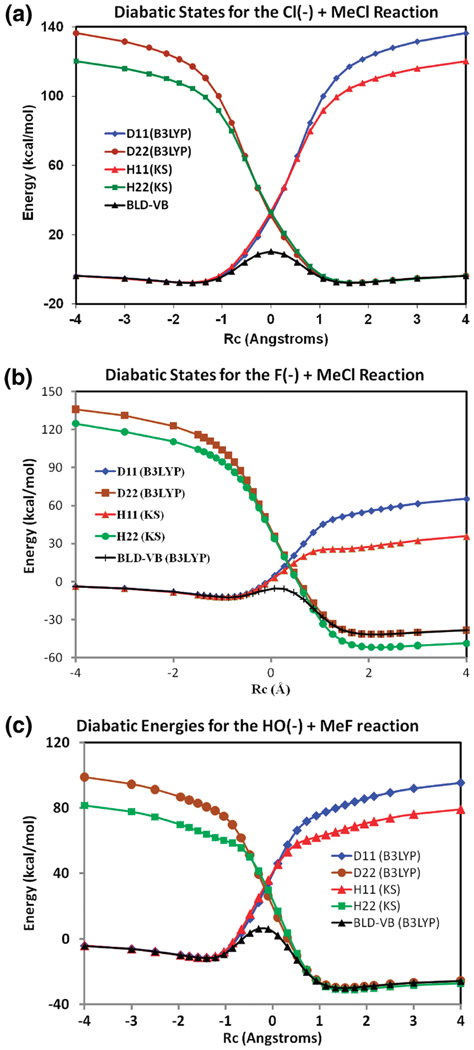
Figure 2.

Diabatic energy profiles of the reactant state computed using the BLDFT method (D11 in blue) and wave function theory with the block-localized Kohn–Sham orbitals (H11(KS) in red) and of the product state using the BLDFT method (D22 in brown) and wave function theory (H22(KS) in green) for (a) [Cl⁻ + CH₃Cl], (b) [F⁻ + CH₃Cl], and (c) [HO⁻ + CH₃F] reactions.

The three S_N2 reactions represent very different features in the electron-withdrawing power of the nucleophiles and the leaving groups. The chloride ion exchange reaction is thermal neutral, whereas as the reaction between F⁻ and CH₃Cl and that between HO⁻ and CH₃F are highly exothermic (Table 1). The diabatic energy differences between the reactant and product ion–dipole complexes are, respectively, 0.0, −29.5, and −18.4 kcal/mol for the three reactions from the BLDFT model, which are in good accord with the difference of the adiabatic ground state (Table 1). In the reactant and product state region up to the crossing point (transition state), the respective diabatic energies computed using the BLDFT method and block-localized MOs are in very good accord (Figure 2). However, beyond the crossing point, BLDFT results show a somewhat greater energy increase than that of the Hartree–Fock results (using BLKS orbitals, i.e., $H_{\mathit{\text{ii}}}^{\text{KS}}$) as the reaction coordinates further deviates from equilibrium geometries. Note that the latter is not used as the diabatic state energy in the VBDFT Hamiltonian, and it is shown to illustrate the trend of the energy change in comparison with the BLDFT results. Thus, the appearance that $H_{22}^{\text{KS}}$ is below the VBDFT adiabatic ground-state energy for the [F⁻ + CH₃Cl] reaction in Figure 2b is due to different energy scales between the absolute energies from DFT and Hartree–Fock methods (in VBDFT, the variational principle ensures that ${\epsilon }_{\mathrm{g}}\le H_{\mathit{\text{ii}}}^{\text{BL-DFT}}$).

Table 1.

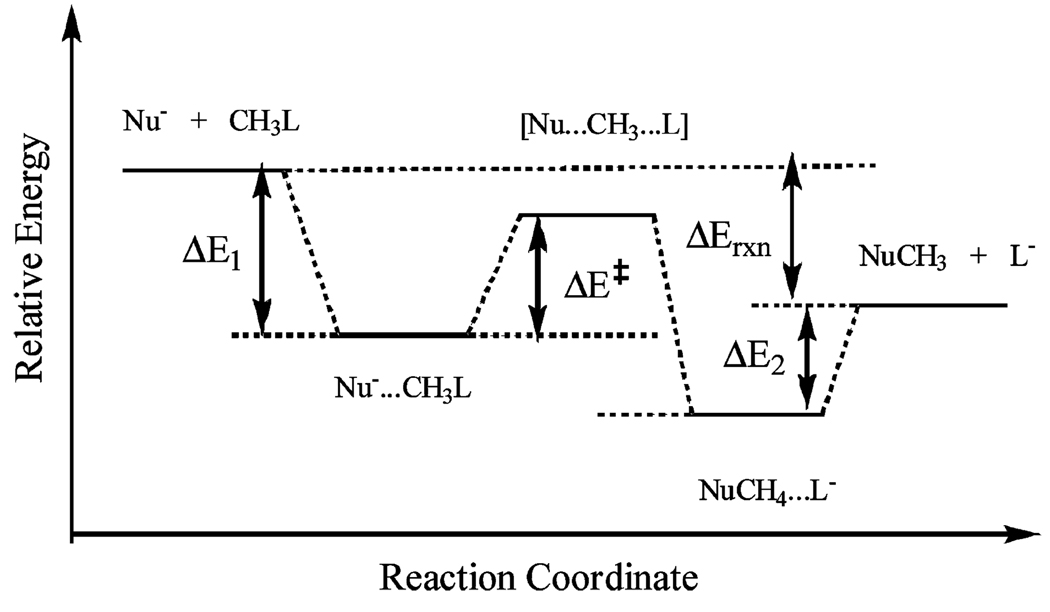
Computed Binding Energies (kcal/mol) for the Formation of the Ion-Dipole (ΔE₁) Complex, the Barrier Height Relative to the the IP Complex (ΔE^‡), the Relative Energy between the Reactant and Product Ion–Dipole Complexes (ΔE₂), and the Net Energy of Reaction (ΔE_rxn) between the Product and Reactant States for the S_N2 Reactions (see Scheme 1)

	DFT-VB(2)a	DFT-VB(3)a	B3LYPa	M06-2Xb	CCSD(T)b	NSBH6c
			[Cl− + CH3Cl]
ΔE1	−7.8	−9.0	−9.5	−11.3	−10.9	−10.5
ΔE‡	18.3	12.5	8.6	13.2	12.6	13.6
ΔE2	−7.8	−9.0	−9.5	−11.3	−10.9	−10.5
ΔErxn	0.0	0.0	0.0	0.0	0.0	0
			[F− + CH3Cl]
ΔE1	−12.3	−15.0	−16.0	−17.1	−16.1	−16.4
ΔE‡	7.1	2.5	0.3	3.6	2.9	2.9
ΔE2	−7.4	−8.0	−8.4	−10.0	−9.7	−10.5
ΔErxn	−34.3	−34.3	−34.3	−35.8	−32.2	−32.7
			[HO− + CH3F]
ΔE1	−11.6	−10.0	−13.7	−14.6	−13.8	−13.7
ΔE‡	17.9	10.7	6.1	12.3	10.8	11.0
ΔE2	−6.6	−7.5	−8.1	−9.6	−9.2
ΔErxn	−23.3	−23.3	−23.3	−20.7	−19.6	−20.1

^aThe VWN5 functional was used in the B3LYP implementation in GAMESS with the 6-31+G(d) basis set. Values in parentheses are computed using three VB configurations.

^bComputed using the aug-cc-pVTZ basis set at the QCISD/MG3 geometry.

^cRef ⁷⁶.

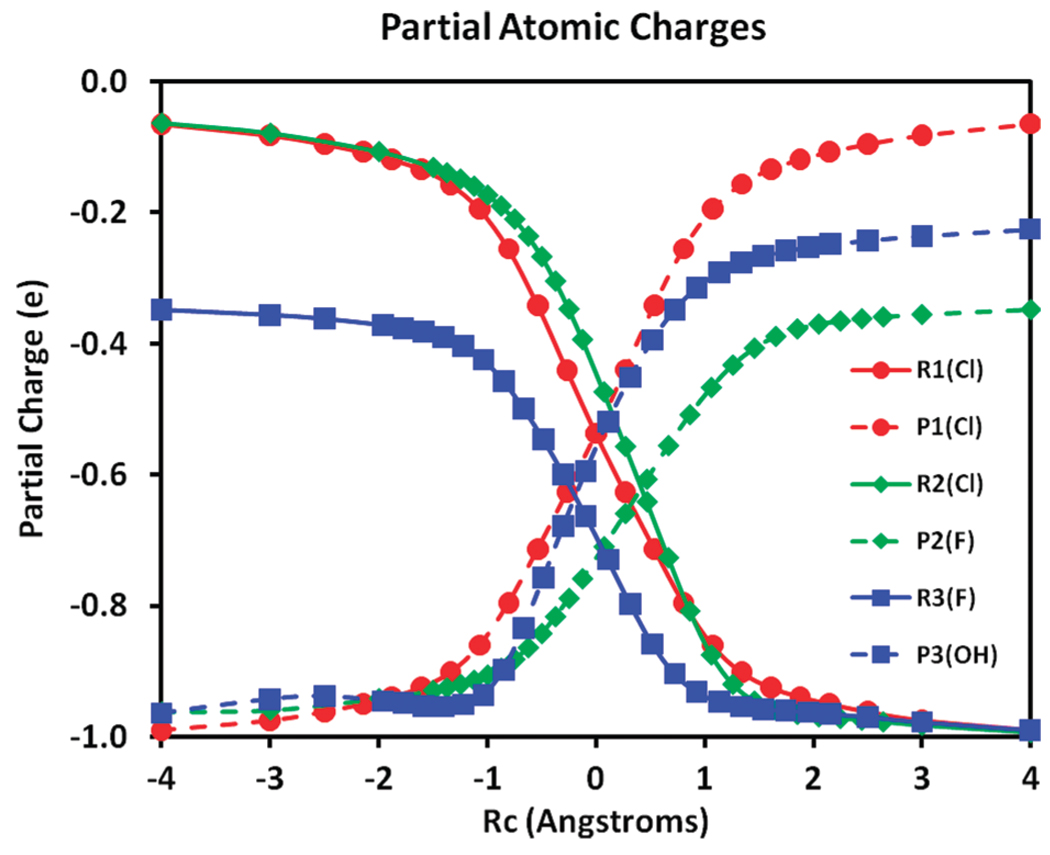
Figure 3 shows the partial atomic charges of the leaving group in the reactant state configuration, and those of the nucleophiles in the product configuration as a function of Rc for all three reactions. The two-state model, VBDFT(2), where the number in parentheses specifies the number of VB states, was used in these analyses. By definition, the total charge densities of the nucleophiles in the reactant states and those of the leaving group in the product states are unity (eqs 33 and 34), which are confirmed by the corresponding Mulliken populations (not shown). Figure 3 highlights the effects of polarization of the Lewis structures by the neighboring ions in the respective diabatic states. Consequently, although the total charge of the subgroups of the substrate species in the reactant state and of the product Lewis structure in the product state are constrained to be zero by virtue of block-localization of the total electron density, the electronic structures of these subgroups are significantly polarized by the “neighboring” ions. For example, in the reaction of [F⁻ + CH₃Cl], the subgroup representing the reactant Lewis structure [CH₃ − Cl] ([CH₃ − L] in eq 33) is essentially ionized by the F⁻ ion at the product state geometry. In all three reactions, there is significant ionic character developed in the neutral subgroups both in the reactant and product diabatic states at the crossing point (transition state), suggesting that it may be useful to include the ionic VB configuration (eq 47) in the VBDFT Hamiltonian. It is also interesting that the CH₃Cl subgroup in the reactions of [Cl⁻ + CH₃Cl] and [F⁻ + CH₃Cl] exhibits different charge polarizations by the nucleophiles, although the trends of the partial atomic charge on the chlorine atom are similar.

Figure 3.

Mulliken population charges for the leaving group in the reactant diabatic state in the [Cl⁻ + CH₃Cl] reaction (red), R1(Cl); in the [F⁻ + CH₃Cl] reaction (yellow), R2(Cl); and in the [HO⁻ + CH₃F] reaction (blue), R3(F). Mulliken population charges for the nucleophile in the product diabatic state configuration are shown as dashed lines of the same colors for the three reactions given above. Partial charges are given in atomic units.

B.2. Energy Profiles of the Adiabatic Ground State

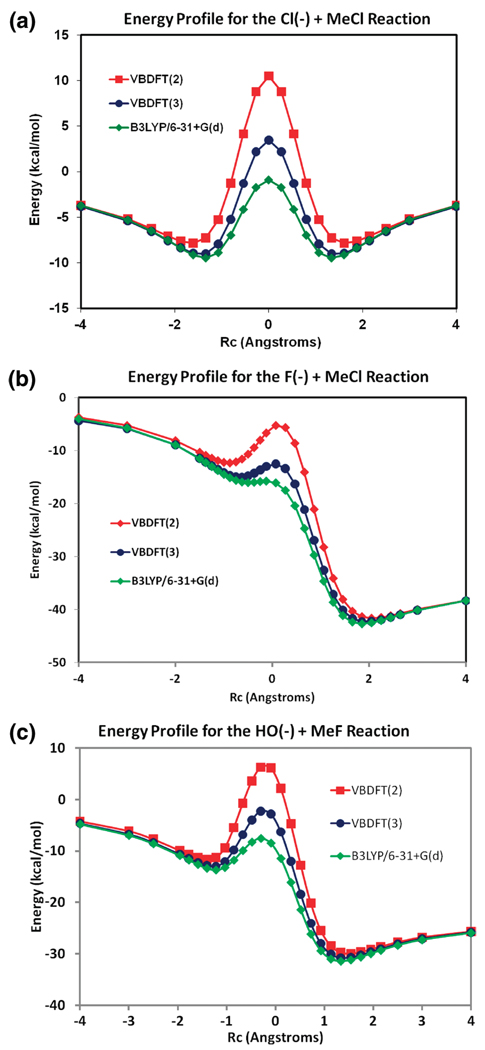
The adiabatic ground-state potential energy profiles for the three S_N2 reactions considered in this work are given in Figure 4 along the reaction coordinate defined by the asymmetric stretch coordinate (eq 46). These effective diabatic states are not unique,^{3,4,7,17–19} and in ab initio VB theory, this can be rationalized by an arbitrary (although quite reasonable) partition of the ionic structures (eq 47) into the two diabatic Lewis configurations.³ In BLDFT, they are treated by the block-localized electronic structure and are fully delocalized within each subgroup due to the use of a single determinant that produces the exact electron density with the Kohn–Sham approach. As noted previously, the reduction of VB configurations from a complete VB space to a two-state model leads to a loss of static correlation, in addition to reduced delocalization effects. There is no reason to expect a true ab initio two-state model to be able to reproduce the exact results (unless these two states are reconstructed from the full VB wave function as in the CDC-MOVB (consistent diabatic configuration) method described in ref 3 or transformed from the adiabatic ground state and its coupling excited state^3,4,28). This is clearly reflected by the results shown in Figure 4, in which the computed barrier heights from the two-state VBDFT(2) model are noticeably greater than the adiabatic B3LYP (the same level of theoretical model) results.

Figure 4.

Adiabatic ground-state potential energy profiles determined using the hybrid B3LYP density function theory (green), the VBDFT(2) method with two states (red), and VBDFT(3) with three states (blue) for (a) the [Cl⁻ + CH₃Cl], (b) the [F⁻ + CH₃Cl], and (c) the [HO⁻ + CH₃F] reactions.

For the three S_N2 reactions, the hybrid functional underestimates the barriers considerably, a well-known problem for these reactions, which may be attributed to the presence of two degenerate VB-like diabatic states at the transition state (Figure 2).³ The relatively high barriers from VBDFT(2) calculations in comparison with accurate results⁷⁶ are due to three main factors. First, the block-localized Kohn–Sham orbitals are more sensitive to the basis set used than the standard ground-state calculations, as shown in the one-electron case (Figure 1). Thus, larger basis functions may improve the accuracy of the computed energies of the diabatic states as well as the off-diagonal matrix element. For the [Cl⁻ + CH₃Cl] reaction, the barrier decreases by 0.2 kcal/mol on switching to the 6-311+G(d,p) basis set. In the case of the [HO⁻ + CH₃F], the barrier is reduced by 1.0 kcal/mol using aug-cc-pVDZ and 1.4 kcal/mol using aug-cc-pVTZ. Second, the off-diagonal matrix elements are computed with an approximate method. Third, other valence bond configurations also contribute significantly to the stabilization of the transition state (see below). Nevertheless, a key finding of Figure 4 is that the present multistate VBDFT method can help correct the self-interaction errors in standard approximate functionals for group-transfer reactions examined here.

To illustrate the effects of the ionic configuration on the computed reaction barrier, we include a third state,^3,13 eq 47, in the VBDFT(3) calculation for the three S_N2 reactions. Remarkably, the inclusion of the ionic configuration significantly improves the computed barrier heights, in comparison with the M06-2X and CCSD(T) results.⁷⁶ The reaction involving [HO⁻ + CH₃F] is a particularly challenging case in the DBH24 database because of the high electronegativity and small size of the nucleophile and leaving group ions.⁷⁶ As shown in Figure 3, the covalent bond for both the reactant and product diabatic states are significantly more polarized than the other two reactions.

Listed in Table 1 are the relative energies of all stationary points (depicted in Scheme 1) for the three S_N2 reactions along the reaction coordinate. The VBDFT(3) results are in good accord with currently the most accurate DFT (M06-2X/aug-cc-pVTZ) results,⁷⁶ as well as with high-level wave function theories (CCSD(T)/aug-cc-pVTZ),⁷⁶ suggesting that multistate VBDFT can provide an adequate description of the reaction PES. Finally, we note that the distances in the ion–dipole complex minima are slightly longer by about 0.1–0.2 Å from DFT-VB calculations than the B3LYP results.

Scheme 1.

Definition of Relative Energies

B.3. Polarization, Charge Transfer, and Coupling Energies

The BLDFT method used to construct the diabatic state in the multireference VBDFT approach is a versatile theoretical model that can be used to study chemical bonding properties and to decompose the component of intermolecular interaction energies.⁴⁵ It provides a useful tool to analyze DFT results to gain chemical insight into the system. In the Appendix, we illustrate the utility of the BLDFT method and shed light on the contributing components of the interaction energies for the ion–dipole complexes.

It is useful to consider the energy difference between the VBDFT ${\epsilon }_{\mathrm{g}}^{\text{VBDFT}}$ and the conventional DFT (E^DFT[ρ(Nu⁻ •CH₃L)]) method:

$$\mathrm{\Delta }{E}_{\text{rcr}}={\epsilon }_{\mathrm{g}}^{\text{VBDFT}}-E^{\text{DFT}}[\rho ({\text{Nu}}^{-}•{\text{CH}}_3\mathrm{L})]$$ (48)

where the superscript DFT in E^DFT[ρ(Nu⁻ •CH₃L)] is used to emphasize that the energy is determined by conventional KS-DFT. In VBDFT, each diabatic state is completely defined by its Hamiltonian, and the Hohenberg–Kohn theorem ensures that its ground-state energy is solely determined by the block-localized density.^78,79 Obviously, localization of the electron density loses electronic delocalization (resonance) energy between different fragments or blocks (thus, the steep rise of diabatic energy shown in Figure 2). In addition, dynamic correlation effects will also be different in the diabatic states from that of the adiabatic ground state. VB configuration interaction in the complete VB space recovers delocalization effects and introduces static correlation; however, resonance and dynamic correlation effects are not necessarily fully restored in the adiabatic ground state if a minimal number of VB configurations is used. ΔE_rcr is a measure of the residual correlation–resonance (rcr) effect in the multistate, multireference VBDFT method for stable molecules where one diabatic state dominates the VB wave function. If Hartree–Fock theory is used, the dominant effect in ΔE_rcr is the residual resonance energy, thereby providing an estimate of residual correlation effects.

At the transition state (diabatic crossing point), the reactant and product diabatic configurations are degenerate, which has the largest self-interaction error along the reaction path. The quantity ΔE_rcr now gives a reasonable indication of the relative magnitude of the self-interaction energy error, keeping in mind that ΔE_rcr also contains delocalization energy not fully recovered by the multistate VB model. Of course, in such a multiconfigurational treatment, there is also a concern of double counting of correlation effects,⁸⁰ which is an issue to be investigated in the future by comparison with experimental results.

Table 2 shows that, in the present VBDFT method, the ΔE_rcr term is found to be positive, indicating that the loss in charge delocalization and dynamic correlation in constructing the diabatic states is not fully compensated for by the multiconfigurational VB Hamiltonian. Not surprisingly, the absolute value of the ΔE_rcr energy is similar to that of the charge transfer component. This is consistent with the interpretation that the ΔE_rcr term is mainly due to reduction in the resonance delocalization and dynamic correlation effect in the ion–dipole complex state. It is interesting to notice that inclusion of the ionic configurations significantly reduces ΔE_rcr values, indicating the importance of the ionic configuration even at the stable, ion–dipole complex geometry.

Table 2.

Computed Energy Components and Coupling Effects for Ion–Dipole Complexes^a

complex	ΔEint	ΔER	ΔEstat	ΔEpol	ΔECT	ΔErcr(2)	ΔErcr(3)
Cl− • CH3Cl	−9.5	0.5	−5.0	−2.7	−2.3	2.2	0.5
Cl− • CH3F	−8.6	0.2	−5.7	−1.7	−1.5	1.4	0.4
F− • CH3Cl	−16.0	2.7	−4.7	−7.4	−6.7	5.4	1.3
F− • CH3OH	−8.0	0.6	−3.2	−3.7	−1.8	1.7	0.6
HO− • CH3F	−13.7	0.9	−8.0	−3.9	−2.7	2.4	0.7

^aAll energies are given in kilocalories per mole.

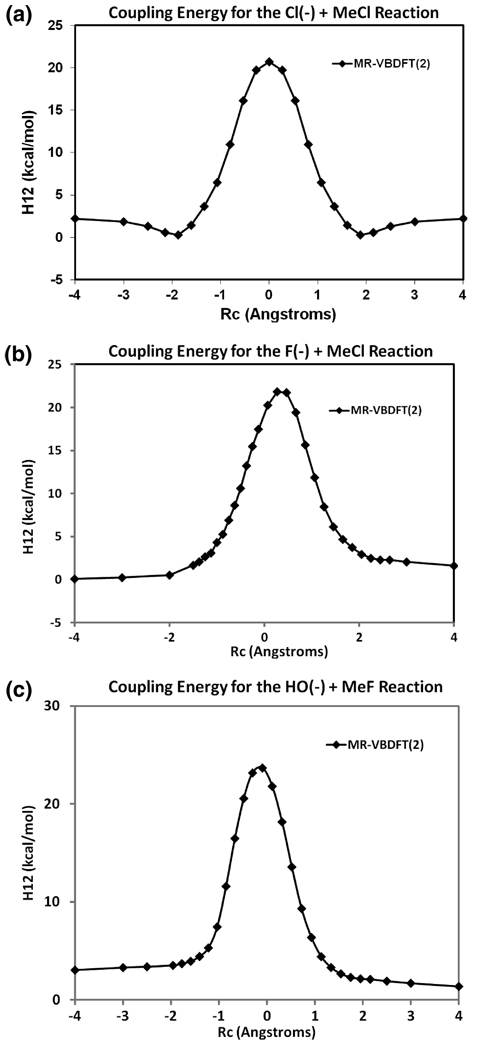
The computed coupling energies, V₁₂ = |H₁₂ − ε_gS₁₂|, using VBDFT(2) at the transition state are shown in Table 3, and the variation of V₁₂ along the reaction coordinate is shown in Figure 5. For all three reactions, V₁₂ has the largest values at the transition state and decays rapidly as the reaction coordinate moves away from the transition state. V₁₂ is essentially zero at the ion–dipole complex structure. For a comparison with ion–dipole complexes above, there is greater reduction in ΔE_rcr with the inclusion of the ionic configuration at the transition state (Table 3), indicating that the ionic configuration makes greater contributions than the stabilization of the reactant state energy. It is interesting to note that the change, Δ(ΔE_rcr) = ΔE_rcr(2) − ΔE_rcr(3), is nearly the amount of energy needed to increase V₁₂ in the two-state model to yield the correct barrier height.

Table 3.

Computed Coupling Energy V₁₂ and Residue Correlation-Resonance ΔE_rcr Energy (kcal/mol) at the Transition State for the Nucleophilic Substitution Reactions

	ΔErcr(2)a	ΔErcr(3)a	V12	Δ(ΔErcr)b
[Cl− + CH3Cl]	11.4	4.4	20.7	7.0
[F− + CH3Cl]	10.5	3.2	20.2	7.3
[HO− + CH3F]	13.8	5.3	23.2	8.5

^aThe number in parentheses indicates the number of configurations used in VBDFT calculations.

^bΔ(ΔE_rcr) = ΔE_rcr(2) − ΔE_rcr(3).

Figure 5.

Computed coupling energy, V₁₂, for (a) the [Cl⁻ + CH₃Cl], (b) the [F⁻ + CH₃Cl], and (c) the [HO⁻ + CH₃F] reactions.

5. Conclusions

In this article, we describe BLDFT for the construction of valence-bond-like diabatic electronic states, suitable for the study of electron transfer reactions and for the representation of the reactive potential energy surface. The BLDFT method has been used previously in intermolecular interaction energy decomposition analysis, which is an extension of the corresponding wave function theory approach. Here, we further examine some of the properties of the BLDFT method. Importantly, the BLDFT method is used to formulate a multistate density functional theory in the framework of the valence bond, making use of a reduced configuration representation and of a single determinant strategy for each VB configuration. Thus, the method is equivalent to a valence bond Hamiltonian using density functional theory, which can be called the VBDFT method. The most important result of this study is to propose a functional estimate of the off-diagonal matrix elements of the VB Hamiltonian, assuming that the overlap integral between KS determinants of nonorthogonal block-localized orbitals is a reasonable approximation to the overlap of the diabatic state defined by their ground-state electron density, and the exchange-correlation functional for the ground state can also be used to describe the exchange (transition) matrix elements.

We also described an approximate approach in which the off-diagonal matrix element is computed by using the determinant of nonorthogonal BLKS orbitals. The use of the approximate algorithm in VBDFT calculations was illustrated by applications to the bond dissociation of ${\mathrm{H}}_2^{+}$, a simple example to illustrate the self-interaction energy error in approximate functionals, and a set of three nucleophilic substitution reactions in the DBH24 database designed for validating computational accuracy. In the dissociation of ${\mathrm{H}}_2^{+}$, the DFT-VB method yields the correct asymptotic behavior as the two protons are stretched to infinity, whereas approximate density functionals fail badly. The computed bonding energy from the VBDFT method is more dependent on the size of basis set than that of the hybrid B3LYP functional due to the extreme localization of the Kohn–Sham orbitals. For the S_N2 nucleophilic substitution reactions, the hybrid functional B3LYP severely underestimates the barrier heights, while the two-state VBDFT model overestimates the barrier heights, in comparison with results from the M06-2X functional and CCSD(T) wave function model. With the inclusion of the ionic configuration, the VBDFT results are found to be in good accord with these high-level accurate results.

The BLDFT method is a versatile theory that can be used to analyze conventional DFT results to gain insight into chemical bonding properties, and it is illustrated by examining the intricate energy contributions in the ion–dipole complex stabilization in the Appendix. It is found that electrostatic interactions provide the largest contribution to the binding interaction in the ion–dipole complex, followed by polarization effects and charge transfer contributions. At the transition state, diabatic coupling is very strong, lowering the diabatic state energy by 26 to 32 kcal/mol to stabilize the transition state of the adiabatic ground-state potential surface. The overstabilization of the transition state energy using approximate density functionals because of the presence of degenerate diabatic states is corrected with the use of the multistate, multireference VBDFT Hamiltonian. It is of interest to use the BLDFT and VBDFT methods to study chemical and electron reactions in solution and in enzymes.

Appendix: Energy Decomposition Analysis of Intermolecular Interactions

The interaction energy of an ion–dipole complex is computed by

$$\mathrm{\Delta }{E}_{\text{int}}=\mathrm{\Delta }{E}_1=E[{\text{Nu}}^{-}•{\text{CH}}_3\mathrm{L}]-(E[{\text{Nu}}^{-}]+E[{\text{CH}}_3\mathrm{L}])$$ (A1)

where E[Nu⁻ •CH₃L], E[Nu⁻], and E[CH₃L] are, respectively, the energies of the complex, individual ion, and molecule. ΔE_int can be decomposed into the following energy terms, including geometry distortion ΔE_R, static electrostatic interaction energy ΔE_stat, electronic polarization ΔE_pol, and charge transfer energy ΔE_CT:³²,³³,³⁷,³⁸,⁴⁵,⁵⁹,⁶⁰,⁶²–⁶⁶,⁷⁷

$$\mathrm{\Delta }{E}_1=\mathrm{\Delta }{E}_R+\mathrm{\Delta }{E}_{\text{stat}}+\mathrm{\Delta }{E}_{\text{pol}}+\mathrm{\Delta }{E}_{\text{CT}}$$ (A2)

ΔE_R represents the energy penalty due to geometry distortion of the individual molecules in the complex, which is a small factor for the ion–dipole complex (Table 2).

The remaining terms are determined using the optimized ion–dipole complex geometry. ΔE_stat, which is the sum of Coulomb and exchange repulsion energies, is determined from the energy of the block-localized electronic configuration with the subgroup KS orbitals taken from the isolated fragments by

$$\begin{array}{c}\mathrm{\Delta }{E}_{\text{stat}}=E[{\rho }_o^{\text{BL-DFT}}({\text{Nu}}^{-}•{\text{CH}}_3\mathrm{L})]-E[{\rho }_o({\text{Nu}}^{-})]-\hfill \\ \hfill E[{\rho }_o({\text{CH}}_3\mathrm{L})]\end{array}$$ (A3)

where the subscript “o” indicates that the electron density is computed using the antisymmetric wave function constructed using the KS orbitals of the individual (isolated) molecules, in parentheses, optimized when they are infinitely separated. The energy $E[{\rho }_o^{\text{BL-DFT}}({\text{Nu}}^{-}•{\text{CH}}_3\mathrm{L})]$ is that of the first iteration in BLKS-SCF calculations when the optimized KS orbitals for Nu⁻ and CH₃L are read in as the initial guess.

Relaxation of the subgroup BLKS orbitals in the presence of the other subgroups yields electronic polarization energy in the complex:

$$\mathrm{\Delta }{E}_{\text{pol}}=E[{\rho }^{\text{BL-DFT}}({\text{Nu}}^{-}•{\text{CH}}_3\mathrm{L})]-E[{\rho }_o^{\text{BL-DFT}}({\text{Nu}}^{-}•{\text{CH}}_3\mathrm{L})]$$ (A4)

where ρ^BL-DFT(Nu⁻ •CH₃L) is the fully relaxed (optimized) block-localized density. The extension of the basis set expansion to the full molecular system, that is, conventional DFT calculations, results in the energy component due to charge transfer:

$$\mathrm{\Delta }{E}_{\text{CT}}=E[\rho ({\text{Nu}}^{-}•{\text{CH}}_3\mathrm{L})]-E[{\rho }^{\text{BL-DFT}}({\text{Nu}}^{-}•{\text{CH}}_3\mathrm{L})]$$ (A5)

Notice that, for the reactant diabatic state of the S_N2 reactions considered here, E[ρ^BL-DFT(Nu⁻ •CH₃L)] = H₁₁, whereas for the product complex, E[ρ^BL-DFT (Nu⁻ •CH₃L)] = H₂₂.

Table 2 lists the energy components for the five unique ion–dipole complexes in the three nucleophilic substitution reactions. We do not perform energy decomposition analysis for the transition state because the isolated subgroups lose meaning in such highly distorted geometries. In all cases, except the complex F⁻ •CH₃Cl, the formation of the complex results in relatively small geometrical distortion (ΔE_R). In the F⁻ •CH₃Cl structure, there are also relatively greater effects from polarization and charge transfer than for the other four complexes, suggesting significant covalent bond character has been formed. Overall, static–electrostatic interaction has the greatest contribution, followed by polarization and charge transfer, to the stabilization of ion–dipole complexes.