Projections Onto Super-Half-Spaces for Monotone Variational Inequality Problems in Finite-Dimensional Space

Abstract

The variational inequality problem (VIP) is considered here. We present a general algorithmic scheme which employs projections onto hyperplanes that separate balls from the feasible set of the VIP instead of projections onto the feasible set itself. Our algorithmic scheme includes the classical projection method and Fukushima’s subgradient projection method as special cases.

1 Introduction

We consider the variational inequality problem (VIP) in the Euclidean space Rⁿ. Given a nonempty closed convex set X ⊆ Rⁿ and a function f : Rⁿ → Rⁿ, the VIP is to find a point x ^* such that

$$x\text{*}\in X\text{and}\langle f\left(x^{*}\right),x-x^{*}\rangle \ge 0,\text{\hspace{1em} for all}x\in X.$$ (1)

This problem was well-studied in the last decades, see, e.g., the treatise of Facchinei and Pang [7] and the review papers by Noor [12] and by Xiu and Zhang [13]. In particular, algorithmic approaches were investigated, using projections of different types, in order to generate a sequence of iterates that converges to a solution. See, e.g., Yang [15], Yamada and Ogura [14], Auslender and Teboulle [3] or Censor, Iusem and Zenios [5], to name but (very) few out of the existing vast literature. The importance of VIPs stems from the fact that some fundamental problems can be cast in this form, see, e.g., [7, Volume I, Subsection 1.4].

Some algorithms for solving the VIP fit into the framework of the following general iterative scheme.

Algorithm 1

Initialization

Let ${\{{\tau }_k\}}_{k=0}^{\infty }$ be a user-chosen positive real sequence, select an arbitrary starting point x⁰ ∈ Rⁿ and set the iteration index k = 0.

Iterative step

Given the current iterate x^k, calculate the next iterate

$$x^{k+1}=P_X(x^k-{\tau }_k{G}^{-1}f(x^k)),$$

where G is a symmetric positive definite matrix, P_X is the projection operator onto X with respect to the G-norm ∥z∥_G = 〈z, Gz〉^1/2.

See, Auslender [2] and consult [7, Volume 2, Subsection 12.1] for more details. Such methods are particularly useful when the set X is simple enough to project on. However, in general, one has to solve at each iterative step the minimization problem

$$\text{min}\{\parallel x-(x^k-{\tau }_k{G}^{-1}f(x^k)){\parallel }_G|\text{for all}x\in X\}.$$

The efficiency of such a projection method may be seriously affected by the need to solve such optimization problems at each iterative step.

An orthogonal projection of a point z onto a set X can be viewed as an orthogonal projection of z onto the hyperplane H which separates z from X, and supports X at the closest point to z in X. But, of course, at the time of performing such an orthogonal projection, neither the closest point to z in X, nor the separating and supporting hyperplane H are available. In view of the simplicity of an orthogonal projection onto a hyperplane, it is natural to ask whether one could use other separating supporting hyperplanes instead of that particular hyperplane H through the closest point to z. Aside from theoretical interest, this may lead to algorithms useful in practice, provided that the computational effort of finding such other hyperplanes favorably competes with the work involved in performing orthogonal projections directly onto the given sets.

To circumvent the difficulties associated with the orthogonal projections onto the feasible set of (1) Fukushima [10] developed a method that utilizes outer approximations of X. His method replaces the orthogonal projection onto the set X by a projection onto a half-space containing X, which is easier to calculate. Letting X ≔ {x ∈ Rⁿ | g(x) ≤ 0} where g : Rⁿ → R is convex, Fukushima’s algorithm is as follows.

Algorithm 2

Initialization

Let ${\{{\rho }_k\}}_{k=0}^{\infty }$ be a user-chosen positive real sequence, select an arbitrary starting point x ⁰ ∈ Rⁿ and set the iteration index k = 0.

Iterative step

Given the current iterate x^k,

1. choose a subgradient ξ^k ∈ ∂g(x^k) of g at x^k and let

   $$T^k≔\{x\in R^n|g(x^k)+\langle {\xi }^k,x-x^k\rangle \le 0\}.$$
2. Calculate the “shifted point”

   $$z^k≔x^k-{\rho }_k{G}^{-1}f(x^k)/\parallel f(x^k){\parallel }_2,$$

   and then the next iterate x^k+1 is the projection of z^k onto the half-space T^k with respect to the G-norm, namely,

   $$x^{k+1}=P_{T^k}(z^k).$$

3. If x^k+1 = x^k then stop, otherwise, set k = k + 1 and return to (1).

Since the bounding hyperplanes of the subgradiental half-spaces T^k, used by Fukushima, separate the current point z from the set X, the question again arises whether or not any other separating hyperplanes can be used in the algorithm while retaining the overall convergence to the solution.

This question presents a theoretical challenge and we are able to offer here answers that hold under some not too restrictive conditions. Under these conditions, we are able to show that, as a matter of fact, the hyperplanes need to separate not just the point z from the feasible set of (1), but rather separate a “small” ball around z from X. This is inspired by our earlier work [1] on the convex feasibility problem. Whether or not our current restrictions can be relaxed or removed still remains to be seen.

Our goal is to present the structural algorithmic discovery that both Algorithm 1 and Algorithm 2 are realizations of a more general algorithmic principle. Once we achieve this we are less concerned at the moment about the minimal strength of the conditions under which our results hold. This and generalizations of the new algorithmic structure to algorithms which use two projections per iteration for the VIP are currently under investigation. Our work is admittedly a theoretical development and no numerical advantages are claimed at this point. The large “degree of freedom” of choosing the super-sets, onto which the projections of the algorithm are performed, from a wide family of half-spaces may include specific algorithms that have not yet been explored. In Section 2 we present the algorithmic scheme and in Section 3 we give our convergence analysis. Section 4 discusses special cases.

2 The Algorithmic Scheme

2.1 Assumptions

Let X ≔ {x ∈ Rⁿ | g(x) ≤ 0} where g : Rⁿ → R is convex. Let G be a symmetric positive definite matrix and denote the distance from a point x ∈ Rⁿ to the set X with respect to the norm ∥ · ∥_G by

$$\text{dist}(x,X)≔\text{min}\{\parallel x-z{\parallel }_G|z\in X\}.$$

For any ε > 0, we denote

$$X_{\epsilon }≔\{x\in R^n|g(x)<\epsilon \}.$$

Following [10], we assume that the following conditions are satisfied.

Condition 3

f is continuous on X _ε for some ε > 0.

Condition 4

f is strongly monotone with constant α on X _ε for some ε > 0, i.e.,

$$\langle f(x)-f(y),x-y\rangle \ge \alpha \parallel x-y{\parallel }_2^2,\mathit{\text{\hspace{1em} for all}}x,y\in X_{\epsilon }\mathit{\text{\hspace{1em} and some}}\alpha >0.$$ (2)

Condition 5

For some y ∈ X, there exist a β > 0 and a bounded set D ⊂ Rⁿ such that

$$\langle f(x),x-y\rangle \ge \beta \parallel f(x){\parallel }_2,\mathit{for\; all}x\notin D.$$

It is well-known that under Conditions 3 and 4, the problem (1) has a unique solution, see, e.g., Kinderlehrer and Stampacchia [11, Corollary 4.3, p. 14].

2.2 The algorithmic scheme

In order to present the algorithmic scheme a few definitions are needed.

Definition 6

Let G be a symmetric positive definite matrix. Given a 0 ≤ δ ≤ 1, a closed convex set X ⊆ Rⁿ and a point x ∈ Rⁿ,

1. B(x,X,δ) ≔ B(x, δ dist(x, X)) = {z ∈ Rⁿ | ∥ x − z∥_G ≤ δ dist(x, X)} is the G-ball centered at x with radius δ dist(x, X),

2. for any x ∉ int X, denote by ℋ (x,X,δ) the set of all hyperplanes which separate B(x,X,δ) from X,

3. for x,y ∈ Rⁿ, define the mapping

   $${𝒜}_{X,\delta }(x,y)≔\{\begin{array}{ll}\left\{x\right\},\hfill & \mathit{if}x\in \text{int}X,\hfill \\ \{P_{H^{-}}(y)|H\in \mathscr{H}(x,X,\delta )\},\hfill & \mathit{if}x\notin \text{int}X,\hfill \end{array}$$

   where P_H⁻ is the projection operator, with respect to the G-norm, onto the half-space whose bounding hyperplane is H and such that X ⊆ H⁻.

The mapping 𝒜 defined above maps a quadruple (x, y, X, δ) onto a set. A selection from 𝒜_X,δ(x,y) means that if x ∉ int X a specific hyperplane H ∈ ℋ(x,X,δ) is chosen and P_H⁻(y) is selected. If x ∈ int X then x is selected.

Let ${\{{\rho }_k\}}_{k=0}^{\infty }$ be a sequence of positive numbers satisfying

$$\underset{k\to \infty }{\text{lim}}{\rho }_k=0\text{and}{\displaystyle \sum _{k=0}^{\infty }{\rho }_k=+\infty .}$$ (3)

Our algorithmic scheme for the VIP is as follows.

Algorithm 7

Initialization

Let ${\{{\rho }_k\}}_{k=0}^{\infty }$ be a user-chosen positive real sequence that fulfills (3). Choose a constant δ such that 0 < δ ≤ 1, select an arbitrary starting point x ⁰ ∈ Rⁿ and set k = 0.

Iterative step

Given the current iterate x^k,

1. calculate the “shifted point”

   $$z^k≔\{\begin{array}{ll}{x}^k-{\rho }_k{G}^{-1}f(x^k)/\parallel f(x^k){\parallel }_2,\hfill & \mathit{if}f(x^k)\ne 0,\hfill \\ x^k,\hfill & \mathit{if}f(x^k)=0.\hfill \end{array}$$ (4)
2. Calculate the next iterate by

   $$x^{k+1}\mathit{is\; a\; selection\; from}{𝒜}_{X,\delta }(x^k,z^k).$$ (5)

3. If x ^k+1 = x^k, stop, otherwise, set k = k + 1 and return to (1).

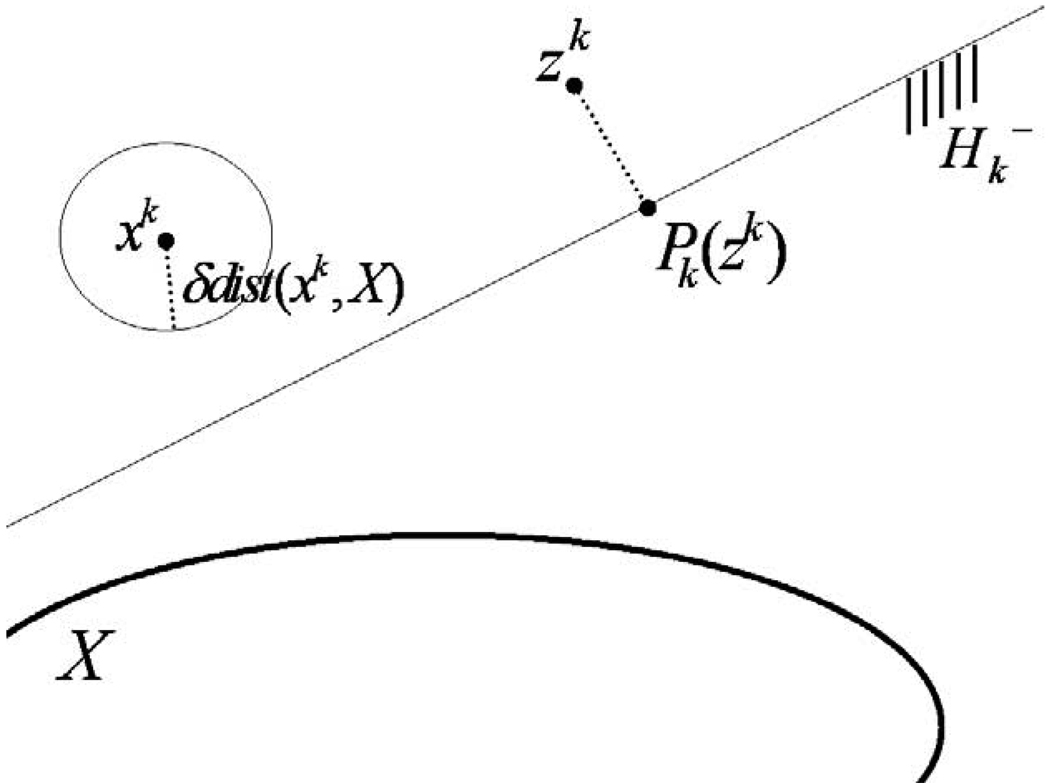
In what follows, we shall denote by P_k the projection operator onto $H_k^{-}$ where H_k is the selected hyperplane H_k ∈ ℋ (x^k, X, δ) Thus, in (5) we have

$$x^{k+1}=\{\begin{array}{ll}{x}^k,\hfill & \text{if}{x}^k\in \text{int}X,\hfill \\ P_k(z^k),\hfill & \text{if}{x}^k\notin \text{int}X.\hfill \end{array}$$ (6)

The iterative step of this algorithmic scheme is illustrated in Figure 1.

Figure 1.

Illustration of the algorithmic scheme in Algorithm 7.

Remark 8

Observe that there is no need to calculate in practice the radius δ dist(x^k, X) of the ball B(x^k, X, δ). If there would have been a need to calculate this then it would, obviously, amount to preforming a projection of x^k onto X, which is the very thing that we are trying to circumvent. All that is needed, when deriving from the algorithmic scheme a specific algorithm, is to show that the specific algorithm indeed “chooses” the hyperplanes in concert with the requirement of separating such B(x^k, X, δ) balls from the feasible set of (1). We demonstrate this in Section 4 below.

3 Convergence

First we show that if Algorithm 7 stops then it has reached the solution of the VIP.

Theorem 9

If x^k+1 = x^k occurs for some k ≥ 0 in Algorithm 7, then x^k is the solution of problem (1).

Proof

First assume that f(x^k) ≠ 0, then x^k+1 = x^k is possible only if the radius of B(x^k,X, δ) is zero which implies that x^k ∈ X since δ > 0. By definition, P_k(y¯) is the solution of the problem min $\{\parallel \overline{y}-w{\parallel }_G^2|w\in H_k^{-}\}$, where $H_k^{-}$ is the half-space determined by H_k and X ⊆ $H_k^{-}$. Applying [4, Theorem 2.4.2] with the Bregman function $h(\overline{y})=\frac{1}{2}{\parallel \overline{y}\parallel }_G^2$, whose zone is Rⁿ, for the set $H_k^{-}$, we get

$$\langle w-P_k(\overline{y}),\nabla h(\overline{y})-\nabla h(P_k(\overline{y}))\rangle \le 0,\text{\hspace{1em}for all}w\in H_k^{-},$$

where here ∇h(ȳ) = Gȳ, ∇h(P_k(ȳ)) = GP_k(ȳ). So, we have

$$\langle w-P_k(\overline{y}),G\overline{y}-G{P}_k(\overline{y})\rangle \le 0,\text{\hspace{1em} for all}w\in H_k^{-}.$$ (7)

Taking w = x̄, ȳ = z^k in (7) we get

$$\langle \overline{x}-P_k(z^k),G{z}^k-G{P}_k(z^k)\rangle \le 0,\text{\hspace{1em} for all}\overline{x}\in H_k^{-},$$ (8)

which, by (4), implies that for all $\overline{x}\in H_k^{-}$

$$\begin{array}{l}\langle \overline{x}-x^{k-1},G(x^k-{\rho }_k{G}^{-1}f(x^k)/\parallel f(x^k){\parallel }_2)-G{x}^{k+1}\rangle \\ =\langle \overline{x}-x^{k-1},G(x^k-x^{k+1})-{\rho }_{k}f(x^k)/\parallel f(x^k){\parallel }_2)\rangle \\ =\langle \overline{x}-x^{k-1},G(x^k-x^{k+1})\rangle -\langle \overline{x}-x^{k-1},{\rho }_{k}f(x^k)/\parallel f(x^k){\parallel }_2)\rangle \le 0.\end{array}$$

Since we assume that x ^k+1 = x^k

$$\langle \overline{x}-x^{k-1},G(x^k-x^{k+1})\rangle =0,$$

so we get

$$\langle \overline{x}-x^{k+1},{\rho }_{k}f(x^k)/\parallel f(x^k){\parallel }_2)\rangle \ge 0,\text{\hspace{1em} for all}\overline{x}\in H_k^{-},$$

and then ${\rho }_k/\parallel f(x^k){\parallel }_2>0,X\subseteq H_k^{-},$, and x ^k+1 = x^k lead to

$$\langle \overline{x}-x^k,f(x^k)\rangle \ge 0,\text{\hspace{1em} for all}\overline{x}\in X.$$

On the other hand, if f(x^k) = 0, then (8) holds with z^k = x^k, i.e.,

$$\langle \overline{x}-P_k(x^k),G{x}^k-G{P}_k(x^k)\rangle \le 0,\text{\hspace{1em} for all}\overline{x}\in H_k^{-},$$

or, by (6) and x ^k+1 = x^k,

$$\langle \overline{x}-x^k,0\rangle \le 0,\text{\hspace{1em} for all}\overline{x}\in H_k^{-},$$

which is true for all x̄ ∈ X since $X\subseteq H_k^{-}$ and the proof is complete.

In the remainder of this section we suppose that Algorithm 7 generates an infinite sequence ${\{x^k\}}_{k=0}^{\infty }$ and establish the next lemmas that will be useful in proving the convergence of our algorithmic scheme. The next lemma was proved in [8] for G = I and under the assumption that E is compact.

Lemma 10

Let A, E and F be nonempty closed convex sets in Rⁿ, such that A ⊂ E ⊂ F. For any point x ∈ F, let y be the point in E closest to x. Then we have

$${\parallel y-z\parallel }_G^2\le {\parallel x-z\parallel }_G^2-{\parallel y-x\parallel }_G^2,\mathit{\text{\hspace{1em} for all}}z\in A.$$ (9)

Furthermore,

$${(\text{dist}(y,A))}^2\le {(\text{dist}(x,A))}^2-{\parallel y-x\parallel }_G^2.$$ (10)

Proof

Since y is the optimal solution of the problem min $\{{\parallel e-x\parallel }_G^2|e\in E\}$, it must satisfy the inequality (see, e.g., [4, Theorem 2.4.2])

$$\langle e-y,Gx-Gy\rangle \le 0,\text{\hspace{1em} for all}e\in E.$$

Thus, for all e ∈ E,

$$\begin{array}{l}\begin{array}{ll}{\parallel x-e\parallel }_G^2-{\parallel y-x\parallel }_G^2-{\parallel y-e\parallel }_G^2\hfill & =2\langle y-e,Gx-Gy\rangle \hfill \\ \hfill & =-2\langle e-y,Gx-Gy\rangle \ge 0,\hfill \end{array}\\ \end{array}$$

and, since A ⊂ E, we get

$${\parallel x-z\parallel }_G^2-{\parallel y-x\parallel }_G^2-{\parallel y-z\parallel }_G^2\ge 0,\text{\hspace{1em} for all}z\in A,$$

which proves (9). In order to prove (10), let z̃ ∈ A be the closest point to x ∈ F. Then, using (9), we obtain

$$\begin{array}{l}\begin{array}{ll}{(\text{dist}(y,A))}^2\hfill & \le {\parallel y-\tilde{z}\parallel }_G^2\le {\parallel x-\tilde{z}\parallel }_G^2-{\parallel y-x\parallel }_G^2\hfill \\ \hfill & ={(\text{dist}(x,A))}^2-{\parallel y-x\parallel }_G^2,\hfill \end{array}\\ \\ \end{array}$$

which completes the proof.

Lemma 11

Let ȳ ∈ Rⁿ be an arbitrary point. Then, in Algorithm 7, for all k ≥ 0, we have the inequalities

$${\parallel P_k(\overline{y})-w\parallel }_G^2\le {\parallel \overline{y}-w\parallel }_G^2-{\parallel P_k(\overline{y})-\overline{y}\parallel }_G^2,\mathit{\text{\hspace{1em} for all}}w\in X.$$

Proof

This follows from Lemma 10 with A = X, E = $H_k^{-}$ and F = Rⁿ. The next lemma is quoted from [10, Lemma 2].

Lemma 12

Let ${\{a_k\}}_{k=0}^{\infty }$ and ${\{b_k\}}_{k=0}^{\infty }$ be sequences of nonnegative numbers, and let μ ∈ [0,1) be a constant. If the inequalities

$$a_{k+1}\le \mu a_k+b_k,k=0,1,\dots ,$$

hold and if $\underset{k\to \infty }{\text{lim}}{b}_k=0$, then $\underset{k\to \infty }{\text{lim}}{a}_k=0$.

Lemma 13

If Condition 5 is satisfied, then any sequence ${\{x^k\}}_{k=0}^{\infty }$, generated by Algorithm 7, is bounded.

Proof

The proof is structured along the lines of [10, Lemma 3]. First assume that f(x^k) ≠ 0. Let y ∈ X be a point for which Condition 5 holds and let M > 0 be such that ∥x − y∥_G < M, for all x ∈ D, where D is a bounded set given in Condition 5. Lemma 11 implies that, for each z^k ∈ Rⁿ,

$${\parallel P_k(z^k)-y\parallel }_G^2\le {\parallel z^k-y\parallel }_G^2.$$ (11)

Therefore,

$$\begin{array}{l}\begin{array}{ll}{\parallel x^{k+1}-y\parallel }_G^2\hfill & \le {\parallel x^k-{\rho }_k{G}^{-1}\frac{f(x^k)}{{\parallel f(x^k)\parallel }_2}-y\parallel }_G^2={\parallel x^k-y\parallel }_G^2\hfill \\ \hfill & -2\frac{{\rho }_k}{{\parallel f(x^k)\parallel }_2}\langle f(x^k),x^k-y\rangle +\frac{{\rho }_k^2}{{\parallel f(x^k)\parallel }_2^2}\langle f(x^k),G^{-1}f(x^k)\rangle .\hfill \end{array}\\ \end{array}$$ (12)

Thus, if ∥x^k − y∥_G ≥ M, then we have, by (12) and Condition 5,

$${\parallel x^{k+1}-y\parallel }_G^2\le {\parallel x^k-y\parallel }_G^2-2{\rho }_k\beta +\frac{{\rho }_k^2}{{\parallel f(x^k)\parallel }_2^2}\langle f(x^k),G^{-1}f(x^k)\rangle .$$ (13)

From Demmel [6, (5.2), page 199] we have

$$\langle f(x^k),G^{-1}f(x^k)\rangle \le \upsilon \langle f(x^k),f(x^k)\rangle ,$$

where υ is the largest eigenvalue of G ⁻¹, so that

$$\langle f(x^k),G^{-1}f(x^k)\rangle \le {\nu }^{-1}\langle f(x^k),f(x^k)\rangle ,$$ (14)

where ν is the smallest eigenvalue of G. By (13) and (14)

$${\parallel x^{k+1}-y\parallel }_G^2\le {\parallel x^k-y\parallel }_G^2-{\rho }_k(2\beta -{\rho }_k{\nu }^{-1}).$$

Since lim_k→∞ ρ_k = 0, the last inequality implies

$${\parallel x^{k+1}-y\parallel }_G<{\parallel x^k-y\parallel }_G,$$ (15)

provided that k is sufficiently large. On the other hand, since y ∈ X,

$$\begin{array}{ll}{\parallel x^{k+1}-y\parallel }_G\hfill & \le {\parallel z^k-y\parallel }_G={\parallel x^k-{\rho }_k{G}^{-1}\frac{f(x^k)}{{\parallel f(x^k)\parallel }_2}-y\parallel }_G\hfill \\ \hfill & ={\parallel (x^k-y)-{\rho }_k{G}^{-1}\frac{f(x^k)}{{\parallel f(x^k)\parallel }_2}\parallel }_G.\hfill \end{array}$$

Using the triangle inequality with G-norms and (14) we obtain

$${\parallel (x^k-y)-{\rho }_k{G}^{-1}\frac{f(x^k)}{{\parallel f(x^k)\parallel }_2}\parallel }_G\le {\parallel x^k-y\parallel }_G+{\rho }_k{\nu }^{-1/2},$$

so that

$${\parallel x^{k+1}-y\parallel }_G\le {\parallel x^k-y\parallel }_G+\epsilon ,$$ (16)

for all sufficiently large k, where ε > 0 is a small constant. Inequalities (15) and (16) imply that ${\{x^k\}}_{k=0}^{\infty }$ is bounded. If f(x^k) = 0 we have by (6) and (11)

$${\parallel x^{k+1}-y\parallel }_G^2\le {\parallel x^k-y\parallel }_G^2,$$

which implies (16) and the rest follows.

Lemma 14

Let X be a nonempty closed convex set X ⊆ Rⁿ and let 0 < δ ≤ 1. Let W ⊂ Rⁿ be a nonempty convex compact set, let W\X ≔ {x ∈ W | x ∉ X}. Denote by σ(x) a selection from 𝒜_X,δ(x,x), then there exists a constant μ ∈ [0,1) such that

$$\text{dist}(\sigma (x),X)\le \mu \text{dist}(x,X),\mathit{\text{\hspace{1em} for all}}x\in W\backslash X.$$

Proof

Since σ(x) is, by definition, the closest point to x in the convex set H ⁻, and X ⊆ H⁻, we get

$${(\text{dist}(\sigma (x),X))}^2\le {(\text{dist}(x,X))}^2-{\parallel \sigma (x)-x\parallel }_G^2.$$ (17)

This holds because

$${(\text{dist}(\sigma (x),X))}^2\le {\parallel \sigma (x)-P_X(x)\parallel }_G^2,$$ (18)

and, by Lemma 10, we get

$$\begin{array}{ll}{\parallel \sigma (x)-P_X(x)\parallel }_G^2\hfill & \le {\parallel x-P_X(x)\parallel }_G^2-{\parallel \sigma (x)-x\parallel }_G^2\hfill \\ \hfill & ={(\text{dist}(x,X))}^2-{\parallel \sigma (x)-x\parallel }_G^2.\hfill \end{array}$$ (19)

(18) and (19) imply (17). On the other hand, since σ(x) is a selection from 𝒜_X,δ(x,x) and x ∉ X, we have that σ(x) = P_H−(x) where H ∈ ℋ(x,X,δ), so

$$\text{dist}(x,X)·\delta \le {\parallel \sigma (x)-x\parallel }_G,\text{\hspace{1em} for all}x\in R^n,$$ (20)

(if x ∈ X then both sides of (20) are zero.) Since δ is a positive constant such that 0 < δ ≤ 1, we have

$$-{\delta }^2{(\text{dist}(x,X))}^2\ge -{\parallel \sigma (x)-x\parallel }_G^2,\text{\hspace{1em} for all}x\in W\backslash X,$$

so, by (17), for all x ∈ W\X

$$\begin{array}{ll}{(\text{dist}(\sigma (x),X))}^2\hfill & \le {(\text{dist}(x,X))}^2-{\delta }^2{(\text{dist}(x,X))}^2\hfill \\ \hfill & =(1-{\delta }^2){(\text{dist}(x,X))}^2.\hfill \end{array}$$

Since also 0 ≤ 1 − δ² < 1, taking $\mu =\sqrt{1-{\delta }^2}$ ∈ [0,1), we get

$$\text{dist}(\sigma (x),X)\le \mu \text{dist}(x,X),\text{\hspace{1em} for all}x\in W\backslash X,$$

which completes the proof.

Lemma 15

For any sequence ${\{x^k\}}_{k=0}^{\infty }$, generated by Algorithm 7, we have lim_k→∞ dist(x^k,X) = 0.

Proof

Assume that f(x^k) ≠ 0, by (10) of Lemma 10 we have

$${(\text{dist}(P_k(x^k),X))}^2\le {(\text{dist}(x^k,X))}^2-{\parallel P_k(x^k)-x^k\parallel }_G^2,\text{\hspace{1em} for all}k\ge 0,$$

and, by Lemma 14, there exists a constant μ ∈ [0,1) such that

$$\text{dist}(P_k(x^k),X)\le \mu \text{dist}(x^k,X),\text{\hspace{1em} for all}k\ge 0.$$ (21)

On the other hand, the nonexpansiveness of the projection operator and reuse of (14) implies

$$\begin{array}{ll}{\parallel x^{k-1}-P_k(x^k)\parallel }_G^2\hfill & ={\parallel P_k(z^k)-P_k(x^k)\parallel }_G^2\le {\parallel z^k-x^k\parallel }_G^2\hfill \\ \hfill & ={\parallel x^k-{\rho }_k{G}^{-1}\frac{f(x^k)}{{\parallel f(x^k)\parallel }_2}-x^k\parallel }_G^2\hfill \\ \hfill & ={\parallel {\rho }_k{G}^{-1}\frac{f(x^k)}{{\parallel f(x^k)\parallel }_2}\parallel }_G^2\le {\rho }_k^2{\nu }^{-1}.\hfill \end{array}$$

Therefore,

$${\parallel x^{k+1}-P_k(x^k)\parallel }_G\le \frac{{\rho }_k}{\sqrt{\nu }}.$$ (22)

Let s^k = P_X (P_k (x^k)), namely,

$${\parallel P_k(x^k)-s^k\parallel }_G=\text{dist}(P_k(x^k),X).$$

Then, by the triangle inequality, we get

$$\begin{array}{ll}{\parallel x^{k+1}-s^k)\parallel }_G\hfill & ={\parallel x^{k+1}-P_k(x^k)+P_k(x^k)-s^k\parallel }_G\hfill \\ \hfill & \le {\parallel x^{k+1}-P_k(x^k)\parallel }_G+{\parallel P_k(x^k)-s^k\parallel }_G.\hfill \end{array}$$

Now, since s^k ∈ X, we have

$$\text{dist}(x^{k+1},X)\le {\parallel x^{k+1}-s^k\parallel }_G.$$

From the last three inequalities we get

$$\text{dist}(x^{k+1},X)\le {\parallel x^{k+1}-P_k(x^k)\parallel }_G+\text{dist}(P_k(x^k),X),$$

and, using (21) and (22), we have

$$\text{dist}(x^{k+1},X)\le \frac{{\rho }_k}{\sqrt{\nu }}+\mu \text{dist}(x^k,X),\text{\hspace{1em} for all}k\ge 0.$$

So the result of this case is obtained by Lemma 12 and (3). In case f(x^k) = 0, (11) becomes

$$\text{dist}(x^{k+1},X)\le \mu \text{dist}(x^k,X),\text{\hspace{1em} for all}k\ge 0,$$

and, by Lemma 12 with ${\{a_k\}}_{k=0}^{\infty }={\{\text{dist}(x^k,X)\}}_{k=0}^{\infty }$ and b_k = 0, for all k ≥ 0, the desired result is obtained.

Lemma 16

For any iterative sequence ${\{x^k\}}_{k=0}^{\infty }$ , generated by Algorithm 7, ${\text{lim}}_{k\to \infty }{\parallel x^{k+1}-x^k\parallel }_G=0$.

Proof

Assume first that f(x^k) ≠ 0, using the triangle inequality with G-norms we have

$$\begin{array}{ll}{\parallel x^{k+1}-x^k\parallel }_G\hfill & ={\parallel x^{k+1}-P_k(x^k)+P_k(x^k)-x^k\parallel }_G\hfill \\ \hfill & \le {\parallel x^{k+1}-P_k(x^k)\parallel }_G+{\parallel P_k(x^k)-x^k\parallel }_G\hfill \\ \hfill & \le \frac{{\rho }_k}{\sqrt{\nu }}+(\text{dist}(x^k,H_k^{-})),\text{\hspace{1em} for all}k\ge 0,\hfill \end{array}$$ (23)

where the last inequality follows from (22) and the equality

$$\text{dist}(x^k,H_k^{-})={\parallel P_k(x^k)-x^k\parallel }_G.$$

Since $X\subseteq H_k^{-}$, we have

$$\text{dist}(x^k,H_k^{-})\le \text{dist}(x^k,X),$$

thus,

$${\parallel x^{k+1}-x^k\parallel }_G\le \frac{\rho k}{\sqrt{\nu }}+\text{dist}(x^k,X).$$

By Lemma 15 and (3) we now obtain the required result. In case f(x^k) = 0, (23) becomes

$$\begin{array}{ll}{\parallel x^{k+1}-x^k\parallel }_G\hfill & \le {\parallel x^{k+1}-P_k(x^k)\parallel }_G+{\parallel P_k(x^k)-x^k\parallel }_G={\parallel P_k(x^k)-x^k\parallel }_G\hfill \\ \hfill & =\text{dist}(x^k,H_k^{-})\le \text{dist}(x^k,X),\hfill \end{array}$$

where the last inequality follows from $X\subseteq H_k^{-}$. By Lemma 15 and taking limits as k → ∞, we get the required result.

Theorem 17

Consider the VIP(X, f) (1) and assume that Conditions 3-5 hold. Then any sequence ${\{x^k\}}_{k=0}^{\infty }$, generated by Algorithm 7, converges to the unique solution x^* of problem (1).

Proof

By Lemma 15, x^k ∈ X_ε, for all sufficiently large k, where X_ε is the set given in Conditions 3 and 4. (We assume without loss of generality that the value of ε is common in both conditions.) From Condition 4 we have

$$\langle f(x^k)-f(x^{*}),x^k-x^{*}\rangle \ge \alpha {\parallel x^k-x^{*}\parallel }_2^2,$$

and

$$\begin{array}{ll}\langle f(x^k)-f(x^{*}),x^k-x^{*}\rangle \hfill & =\langle f(x^k)-f(x^{*}),x^k-x^{k+1}+x^{k+1}-x^{*}\rangle \hfill \\ \hfill & \begin{array}{l}=\langle f(x^k),x^k-x^{k+1}\rangle +\langle f(x^k),x^{k+1}-x^{*}\rangle \\ \hspace{1em}-\langle f(x^{*}),x^k-x^{*}\rangle \end{array}\hfill \\ \hfill & \ge \alpha {\parallel x^k-x^{*}\parallel }_2^2.\hfill \end{array}$$

So, we obtain

$$\langle f(x^k),x^{k+1}-x^{*}\rangle \ge \alpha {\parallel x^k-x^{*}\parallel }_2^2+\langle f(x^{*}),x^k-x^{*}\rangle +\langle f(x^k),x^{k+1}-x^k\rangle .$$ (24)

Let λ be an arbitrary positive number. Since x ^* satisfies (1), it follows from Lemmas 13 and 15 that the following inequalities hold, for all sufficiently large k,

$$\langle f(x^{*}),x^k-x^{*}\rangle \ge -\lambda .$$ (25)

Using the Cauchy-Schwarz inequality

$$\langle f(x^k),x^{k+1}-x^k\rangle \ge -{\parallel f(x^k)\parallel }_2{\parallel x^{k+1}-x^k\parallel }_2.$$

By Lemma 13, ${\{x^k\}}_{k=0}^{\infty }$ is bounded, and with Condition 3 we get that ${\{f(x^k)\}}_{k=0}^{\infty }$ is also bounded. Lemma 16 guarantees

$$\langle f(x^k),x^{k+1}-x^k\rangle \ge -\lambda ,$$ (26)

for all sufficiently large k. Applying (25) and (26) to (24), we obtain

$$\langle f(x^k),x^{k+1}-x^{*}\rangle \ge \alpha {\parallel x^k-x^{*}\parallel }_2^2-2\lambda .$$ (27)

Let us divide the indices of ${\{x^k\}}_{k=0}^{\infty }$ as follows

$$\Gamma ≔\{k\ge 0|f(x^k)=0\}\text{and}\overline{\Gamma }≔\{k\ge 0|f(x^k)\ne 0\}.$$

Equation (27) implies, due to the arbitrariness of λ, that for f(x^k) = 0

$$\underset{k\to \infty ,k\in \Gamma }{\text{lim}}{x}^k=x^{*}.$$

Now consider the indices in Γ̄ and suppose that there exists a ζ > 0 such that

$${\parallel x^k-x^{*}\parallel }_2\ge \zeta ,\text{\hspace{1em} for all}k\in \overline{\Gamma }.$$ (28)

By Lemma 11

$$\begin{array}{ll}{\parallel x^{k+1}-x^{*}\parallel }_G^2\hfill & ={\parallel P_k(z^k)-x^{*}\parallel }_G^2\le {\parallel z^k-x^{*}\parallel }_G^2-{\parallel P_k(z^k)-z^k\parallel }_G^2\hfill \\ \hfill & ={\parallel \left(x^k-{\rho }_k{G}^{-1}\frac{f(x^k)}{\parallel f(x^k)\parallel }\right)-x^{*}\parallel }_G^2\hfill \\ \hfill & -{\parallel x^{k+1}-\left(x^k-{\rho }_k{G}^{-1}\frac{f(x^k)}{\parallel f(x^k)\parallel }\right)\parallel }_G^2\hfill \\ \hfill & ={\parallel x^k-x^{*}\parallel }_G^2-{\parallel x^{k+1}-x^k\parallel }_G^2-2\frac{{\rho }_k}{{\parallel f(x^k)\parallel }_2}\langle f(x^k),x^{k+1}-x^{*}\rangle \hfill \\ \hfill & \le {\parallel x^k-x^{*}\parallel }_G^2-2\frac{{\rho }_k}{{\parallel f(x^k)\parallel }_2}\langle f(x^k),x^{k+1}-x^{*}\rangle .\hfill \end{array}$$

So, we get

$${\parallel x^{k+1}-x^{*}\parallel }_G^2\le {\parallel x^k-x^{*}\parallel }_G^2-2\frac{{\rho }_k}{{\parallel f(x^k)\parallel }_2}\langle f(x^k),x^{k+1}-x^{*}\rangle .$$

Since λ in (27) is arbitrary, we choose λ = αζ²/4,

$$\langle f(x^k),x^{k+1}-x^{*}\rangle \ge \alpha {\parallel x^k-x^{*}\parallel }_2^2-\frac{\alpha {\zeta }^2}{2},$$

provided that k are sufficiently large. So,

$$\begin{array}{ll}-2\frac{{\rho }_k}{{\parallel f(x^k)\parallel }_2}\langle f(x^k),x^{k+1}-x^{*}\rangle \hfill & \le -2\frac{{\rho }_k}{{\parallel f(x^k)\parallel }_2}\left(\alpha {\parallel x^k-x^{*}\parallel }_2^2-\frac{\alpha {\zeta }^2}{2}\right)\hfill \\ \hfill & \le -\frac{\alpha {\zeta }^2{\rho }_k}{{\parallel f(x^k)\parallel }_2}.\hfill \end{array}$$

By Lemma 13, ${\{x^k\}}_{k=0}^{\infty }$ is bounded, thus Condition 3 implies that ${\{f(x^k)\}}_{k=0}^{\infty }$ is also bounded. So there exists a τ > 0 such that

$$-\frac{\alpha {\zeta }^2{\rho }_k}{{\parallel f(x^k)\parallel }_2}\le -\frac{\alpha {\zeta }^2{\rho }_k}{\tau },\text{\hspace{1em} for all}k\in \overline{\Gamma },$$

so that,

$${\parallel x^{k+1}-x^{*}\parallel }_G^2\le {\parallel x^k-x^{*}\parallel }_G^2-\frac{\alpha {\zeta }^2{\rho }_k}{\tau },$$

provided that k are sufficiently large. Then there exists an integer k̄ ∈ Γ̄ such that

$${\parallel x^{k+1}-x^{*}\parallel }_G^2\le {\parallel x^k-x^{*}\parallel }_G^2-\frac{\alpha {\zeta }^2{\rho }_k}{\tau },\text{\hspace{1em} for all}k\in \overline{\Gamma }\text{such that}k\ge \overline{k}.$$ (29)

By adding the inequalities (29) from k = k̄ to k̄ + ℓ, over indices k ∈ Γ̄, we have

$${\parallel x^{\overline{k}+\ell +1}-x^{*}\parallel }_G^2\le {\parallel x^{\overline{k}}-x^{*}\parallel }_G^2-\frac{\alpha {\zeta }^2}{\tau }{\displaystyle \sum _{k\in \overline{\Gamma },k=\overline{k}}^{\overline{k}+\ell }{\rho }_k,}$$

for any ℓ > 0. However, this is impossible due to (3), so there exists no ζ > 0 such that (28) is satisfied. Thus, {x^k}_k∈Γ̄ contains a subsequence {x^k}_k∈Γ̂, Γ̂ ⊆ Γ̄ converging to x ^*, and so there is a subsequence {x^k}_{k∈Γ∪Γ̂} of the whole sequence ${\{x^k\}}_{k=0}^{\infty }$ converging to x ^*. In order to prove that the entire sequence ${\{x^k\}}_{k=0}^{\infty }$ is convergent to x ^*, suppose to the contrary that there exists a subsequence of ${\{x^k\}}_{k=0}^{\infty }$ converging to x̂ ∈ X, x̂ ≠ x^*. Since, by Lemma 16, $\underset{k\to \infty }{\text{lim}}{\parallel x^{k+1}-x^k\parallel }_G=0$, there must exist a ζ > 0 and an arbitrarily large integer j ∈ Γ̄ such that

$${\parallel x^j-x^{*}\parallel }_G\ge \zeta \text{\hspace{1em} and \hspace{1em}}{\parallel x^{j+1}-x^{*}\parallel }_G\ge {\parallel x^j-x^{*}\parallel }_G.$$ (30)

However, if j is sufficiently large, we may apply an argument similar to that used to derive (29), and obtain the inequality

$${\parallel x^{j+1}-x^{*}\parallel }_G<{\parallel x^j-x^{*}\parallel }_G,$$

which contradicts (30). Therefore, the sequence ${\{x^k\}}_{k=0}^{\infty }$ must converge to the solution x ^*.

4 Special Cases of the Algorithmic Scheme

Our general algorithmic scheme (Algorithm 7) includes as a special case the classical projection method of Algorithm 1. This can be seen by using δ = 1 in Algorithm 7, which reduces the family of potential half-spaces to a singleton which includes only the half-space that supports X at the projection of z^k (of (4)) onto X.

Another important special case is obtained from Algorithm 7 if we choose the convex function g(x) ≔ dist(x, X). This is no restriction since any convex set X can be presented in this way and Fukushima’s method of Algorithm 2 is obtained as a special case of our algorithmic scheme.

4.1 An interior anchor point algorithm

To illustrate that additional algorithms can be derived from Algorithm 7 we present below an algorithm that uses other hyperplanes to project on. This particular realization requires that (the interior) int X is nonempty. The idea of using an interior point as an anchor to generate a separating hyperplane appeared previously in [1] for the convex feasibility problem, and in [9] for an outer approximation method.

Algorithm 18

Initialization

Let y ∈ int X be fixed and given. Select an arbitrary starting point x ⁰ ∈ Rⁿ and set k = 0.

Iterative step

Given the current iterate x^k,

1. if x^k ∈ X set x^k = x^k+1 and stop.

2. Otherwise, calculate the “shifted point”

   $$z^k≔\{\begin{array}{ll}{x}^k-{\rho }_k{G}^{-1}f(x^k)/{\parallel f(x^k)\parallel }_2,\hfill & \mathit{if}f(x^k)\ne 0,\hfill \\ x^k,\hfill & \mathit{if}f(x^k)=0.\hfill \end{array}$$ (31)

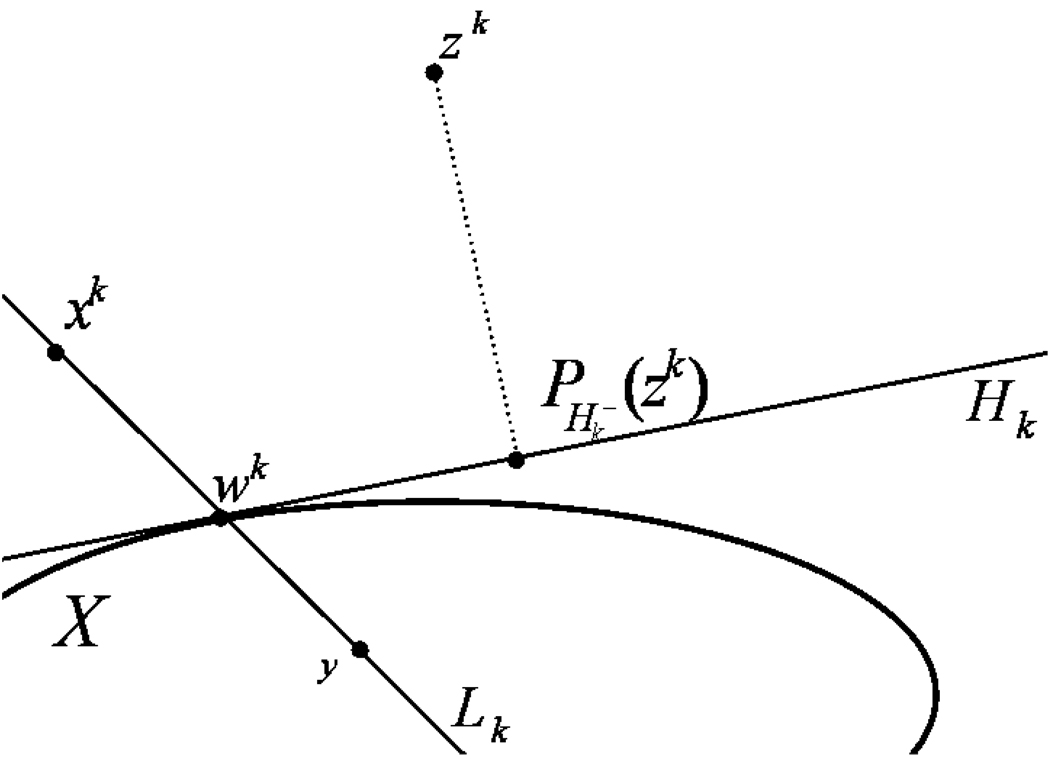
   and construct the line L_k through the points x^k and y.

3. Denote by w^k the point closet to x^k in the set L_k ∩ X.

4. Construct a hyperplane H_k separating x^k from X and supporting X at w^k.

5. Compute x ^k+1 = $P_{H_k^{-}}(z^k)$, where $H_k^{-}$ is the half-space whose bounding hyperplane is H_k and X ⊆ $H_k^{-}$, set k = k + 1 and return to (1).

The iterative step of this algorithm is illustrated in Figure 2. We show that Algorithm 18 generates sequences that converge to a solution of problem (1) by showing that it is a special case of Algorithm 7.

Figure 2.

Illustration of Algorithm 18: Interior anchor point

Theorem 19

Consider the VIP(X, f) (1) and assume that Conditions 3–5 hold and that int X ≠ ∅. Then any sequence ${\{x^k\}}_{k=0}^{\infty }$, generated by Algorithm 18, converges to the solution x^* of problem (1).

Proof

First assume that G = I, the unit matrix. Algorithm 18 is obviously a special case of Algorithm 7 where we choose at each step a separating hyperplane which also supports X at the point w^k. The stopping criterion is valid by Theorem 9. In order to invoke Theorem 17 we have to show that for such an algorithm δ > 0 always holds. By Lemma 13, ${\{x^k\}}_{k=0}^{\infty }$ is bounded and, since x^k ∉ X, we have

$${\parallel P_{H_k^{-}}(x^k)-x^k\parallel }_2=\frac{{\parallel x^k-w^k\parallel }_2{\parallel y-P_{H_k}(y)\parallel }_2}{{\parallel y-w^k\parallel }_2},$$ (32)

and we also have

$${\parallel x^k-w^k\parallel }_2\ge \text{dist}\left(x^k,X\right).$$

Defining d ≔ dist(y, bd X), since y ∈ int X,

$${\parallel y-P_{H_k}(y)\parallel }_2\ge d>0.$$

From the boundedness of ${\{x^k\}}_{k=0}^{\infty }$ we know that there exists a positive N such that ∥y − w^k∥₂ ≤ N, for all k ≥ 0. Combining these inequalities with (32) implies that

$${\parallel P_{H_k^{-}}(x^k)-x^k\parallel }_2\ge \frac{d}{N}\text{dist}(x^k,X),$$

which shows that the algorithm is of the same type of Algorithm 7 with δ ≔ d/N > 0.

To show convergence for a general symmetric positive definite matrix G we recall thatall norms are equivalent in Rⁿ so that there exists constants M ₁ and M ₂ such that, for all x ∈ Rⁿ,

$$M_1{\parallel x\parallel }_2\le {\parallel x\parallel }_G\le M_2{\parallel x\parallel }_2.$$

Actually,

$${\parallel x\parallel }_G\le \rho (G){\parallel x\parallel }_2,$$

where ρ(G) is the largest eigenvalue of G (see, e.g., [6, Equation (5.2), page 199]). So, we get

$${\parallel x^k-w^k\parallel }_2\ge \frac{1}{\rho (G)}{\parallel x^k-w^k\parallel }_G\ge \frac{1}{\rho (G)}\text{dist}(x^k,X),$$

thus,

$${\parallel y-P_{H_k}(y)\parallel }_2\ge \frac{1}{\rho (G)}{\parallel y-P_{H_k}(y)\parallel }_G\ge \frac{\widehat{d}}{\rho (G)},$$

where d̂ ≔ dist(y, bd X). Also,

$${\parallel y-w^k\parallel }_G\le M_2{\parallel y-w^k\parallel }_2\le M_{2}N.$$

So, by (32) and the last three inequalities, we get

$$\begin{array}{ll}{\parallel P_{H_k^{-}}(x^k)-x^k\parallel }_G\hfill & \ge M_1\cdot {\parallel P_{H_k^{-}}(x^k)-x^k\parallel }_2=M_1\cdot \frac{{\parallel x^k-w^k\parallel }_2{\parallel y-P_{H_k}(y)\parallel }_2}{{\parallel y-w^k\parallel }_2}\hfill \\ \hfill & \ge M_1\cdot \frac{\frac{1}{\rho (G)}\text{dist}(x^k,X)\cdot \frac{\widehat{d}}{\rho (G)}}{M_{2}N}=\widehat{M}\cdot \frac{\widehat{d}}{N}\text{dist}(x^k,X),\hfill \end{array}$$ (33)

where M̂ ≔ M ₁/(M ₂(ρ(G))²) and this completes the proof.