Kadison–Singer algebras: Hyperfinite case

Abstract

A new class of operator algebras, Kadison–Singer algebras (KS-algebras), is introduced. These highly noncommutative, non-self-adjoint algebras generalize triangular matrix algebras. They are determined by certain minimally generating lattices of projections in the von Neumann algebras corresponding to the commutant of the diagonals of the KS-algebras. A new invariant for the lattices is introduced to classify these algebras.

In ref. 1, Kadison and Singer initiate the study of non-self-adjoint algebras of bounded operators on Hilbert spaces. They introduce a class of algebras they call “triangular operator algebras.” An algebra is triangular (relative to a factor ) when is a maximal abelian (self-adjoint) algebra in the factor (see Definitions). When the factor is the algebra of all n × n complex matrices, this condition guarantees that there is a unitary matrix U such that the mapping A → UAU^∗ transforms onto a subalgebra of the upper triangular matrices.

Beginning with ref. 1, the theory of non-self-adjoint operator algebras has undergone a vigorous development parallel to, but not nearly as explosive as, that of the self-adjoint theory, the C*-algebra and von Neumann algebra theories. Of course, the self-adjoint theory began with the 1929–1930 von Neumann article (2), well before the 1960 (1) article appeared. Surprisingly, to the present authors, and apparently to Kadison and Singer as well (from private conversations), this parallel development has not produced the synergistic interactions we would have expected from subjects that are so closely and naturally related, and thus likely to benefit from cross-connections with one another.

Considerable effort has gone into the study of triangular-operator algebras (see refs. 3 and 4), and another class of non-self-adjoint operator algebras, the “reflexive algebras” (see refs. 5–8). Many definitive and interesting results are obtained during the course of these investigations. For the most part, these more detailed results rely on relations to compact, or even finite-rank, operators. This direction is taken in the seminal article (1), as well. In Section 3.2 of ref 1, a detailed and complete classification is given for an important class of (maximal) triangular algebras; but much depends on the analysis of those for which (the “diagonal”) is generated by one-dimensional projections. On the other hand, the emphasis of C*-algebra and von Neumann algebra theory is on those algebras where compact operators are (almost) absent.

One of our main goals in this article is to recapture the synergy that should exist between the powerful techniques that have developed in self-adjoint operator-algebra theory and those of the non-self-adjoint theory by conjoining the two theories. We do this by embodying those theories in a single class of algebras. For this, we mimic the defining relation for the triangular algebra, removing the commutativity assumption on the diagonal subalgebra of , and imposing suitable maximality and reflexivity conditions on (compare Definition 1). Our particular focus is the case where the diagonal algebra is a factor.

The non-self-adjoint operator algebras introduced in this article will combine triangularity, reflexivity, and von Neumann algebra properties in their structure. These algebras will be called algebras or “KS-algebras” for simplicity. They are reflexive and maximal triangular with respect to their “diagonal subalgebras.” Kadison–Singer factors (or KS-factors) are those with factors as their diagonal algebras. These are highly noncommutative and non-self-adjoint operator algebras. In standard form, where the diagonal and its commutant share a cyclic vector, such standard KS-algebras have a large self-adjoint part. Many self-adjoint features are preserved in them, and concepts can be borrowed directly from the theory of von Neumann algebras. In fact, a more direct connection of KS-algebras and von Neumann algebras is through the lattice of invariant projections of a KS-algebra. The lattice is reflexive and “minimally generating” in the sense that it generates the commutant of the diagonal as a von Neumann algebra. Most factors are generated by three projections (see ref. 9). One of our main results show that the reflexive algebra, which leaves three generating projections of a factor invariant, is often a KS-algebra, which agrees with the fact that three projections are minimally generating for a factor. Moreover, KS-algebras associated with three projections contain compact operators, and the reflexive lattice generated by the three projections is often homeomorphic to the two-dimensional sphere. We believe that the reflexive algebra given by four or more free projections is a KS-algebra and does not contain any nonzero compact operators. Indeed, we will show that the reflexive algebra associated with infinitely many free projections contains no nonzero compact operators. Through the study of minimal reflexive lattice generators of a von Neumann algebra, we may better understand the generator problem for von Neumann algebras and hence the isomorphism problem for free group factors. These are some of the deepest, most diffcult, and longest standing problems in von Neumann algebra theory. The techniques we use are closely related to those of the theory of self-adjoint operator algebras, especially some of the recently developed theories of free probability (10). For some of the important results and approaches in non self-adjoint theory, we refer to refs. 3 and 11–15, and many references in refs. 7and 16.

There are four sections in this paper, the first in a series. In the second section, Definitions, we give the definition of KS-algebras (as well as corresponding Kadison–Singer lattices) and a basic classification according to their diagonals. In the third section, Hypernite Kadison–Singer Factors, we construct KS-factors with hyperfinite factors as their diagonals. In the fourth section, Kadison–Singer Lattices, we describe the corresponding Kadison–Singer lattices in detail. A previously undescribed lattice invariant is introduced to distinguish these lattices.

We hope that our examples and constructions of non self-adjoint algebras will lead to new insights for some puzzling, old questions in operator theory (see refs. 7and 17).

Definitions

For basic theory on operator algebras, we refer to ref. 18. We recall the definitions of some well-known classes of non-self-adjoint operator algebras. For details on triangular algebras, we refer to ref. 1. For others, we refer to ref. 7.

Suppose is a separable Hilbert space and the algebra of all bounded linear operators on . Let be a von Neumann subalgebra of . A “triangular (operator) algebra” is a subalgebra of such that , a maximal abelian self-adjoint subalgebra (masa) of . One of the interesting cases is when .

Let be a set of (orthogonal) projections in . Define . Then is a weak-operator closed subalgebra of . Similarly, for a subset of , define a projection, TP = PTP, for all TϵS}. Then, is a strong-operator closed lattice of projections. A subalgebra of is called a “reflexive (operator) algebra” if . Similarly, a lattice of projections in is called a “reflexive lattice (of projections)” if . A “nest” is a totally ordered reflexive lattice. If is a nest, then is called a “nest algebra.” Nest algebras are generalizations of (hyperreducible) “maximal triangular” algebras introduced by Kadison and Singer in ref. 1. Kadison and Singer also show that nest algebras are the only maximal triangular reflexive algebras (with a commutative lattice of invariant projections). Motivated by this, we give the following definition.

Definition 1:

A subalgebra of is called a Kadison–Singer (operator) algebra (or KS-algebra) if is reflexive and maximal with respect to the diagonal subalgebra of , in the sense that if there is another reflexive subalgebra of such that and , then . When the diagonal of a KS-algebra is a factor, we call the KS-algebra a KS-factor or a Kadison–Singer factor. A lattice of projections in is called a Kadison–Singer lattice (or KS-lattice) if is a minimal reflexive lattice that generates the von Neumann algebra , or equivalently is reflexive and is a KS-algebra.

Clearly, nest algebras are KS-algebras. Since a nest generates an abelian von Neumann algebra, we may view nest algebras as “type I” KS-algebras and general KS-algebras as “quantized” nest algebras. The maximality condition for a KS-algebra requires that the associated lattice is “reflexive and minimal” in the sense that there is no smaller reflexive sublattice that generates the commutant of the diagonal algebra. We believe that the following statement is true:

Conjecture 1

If is a KS-algebra in and (≠ 0,I), then , i.e., a KS-algebra has no nontrivial reducing invariant subspaces.

The following lemma is an immediate consequence of the above definition.

Lemma 1

Suppose is a KS-algebra in and is the commutant of in . Then, and generates as a von Neumann algebra.

When is a KS-algebra and is a factor of type I, II, or III, then is called a KS-factor of the same type. In the same way, we can further classify KS-factors into type II₁,II_∞, etc., similar to usual factors. A KS-algebra is said to be in a “standard form”, or a “standard” KS-algebra, if the diagonal of is in a standard form, i.e., has a cyclic and separating vector in . In this case, the von Neumann algebra generated by (or the core, see ref. 1) is also in a standard form.

Theorem 2

If is a KS-algebra of type II or type III in , then is not self-adjoint.

In the present article, one of our main goals is to give some nontrivial examples of KS-algebras, in particular, KS-factors of type II and III. The following theorem shows that all type II and type III KS-algebras are truly non-self-adjoint algebras.

Proof:

Assume on the contrary that is self-adjoint. From our assumption we know that contains a 2 × 2 matrix subalgebra . Let E_ij, i,j = 1,2, be a matrix unit system for . Then one can construct a reflexive lattice generated by all projections in the relative commutant of in and two non commuting projections E₁₁ and in . It is easy to see that generates as a von Neumann algebra. One easily checks that is non-self-adjoint but reflexive. Moreover its diagonal is equal to the commutant of , which agrees with . This contradicts to the assumption that is a KS-algebra.

Similar argument shows that any nontrivial standard KS-algebra, even in the case of type I, is not self-adjoint. Standard KS-algebras can be viewed as “maximal” upper triangular algebras with a von Neumann algebra as its diagonal.

Definition 2

Two KS-algebras are said to be isomorphic if there is a norm preserving (algebraic) isomorphism between the two algebras. Two KS-algebras are called unitarily equivalent if there is a unitary operator between the underlying Hilbert spaces that induces an isomorphism between the KS-algebras.

It is easy to see that an isomorphism between two KS-algebras induces a * isomorphism between the diagonal subalgebras.

For lattices of projections on a Hilbert space, the definition of an isomorphism is subtle. We consider a simple example where a lattice contains two free projections of trace and 0,I in a type II₁ factor. As a lattice (with respect to union, intersection and ordering), it is isomorphic to the lattice generated by two rank-one projections on a two-dimensional euclidean space. We shall call such an isomorphism (which preserves only the lattice structure) an “algebraic (lattice) isomorphism”. An isomorphism between two lattices, in this paper, is an isomorphism that also induces a * isomorphism between the von Neumann algebras they generate. To avoid confusion, sometimes we call such isomorphisms “spatial isomorphisms” between two lattices of projections.

Hyperfinite KS-Factors

In this section, we shall construct some hyperfinite KS-factors. We begin with a UHF C*-algebra (see ref. 19) obtained by taking the completion (with respect to operator norm) of , denoted by (or equivalently, ). We denote by the kth copy of in (or ) and , i,j = 1,…,n, the standard matrix unit system for , for k = 1,2,…. Then we may write . Let (). Then . Now, we construct inductively a family of projections in .

When m = 1, define , for j = 1,…,n - 1, and 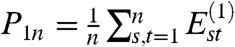. Suppose for k = m - 1, 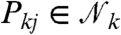are defined, for j = 1,…,n. Now we define

[1]

[2]

Denote by the lattice generated by {P_kj:1 ≤ k ≤ m,1 ≤ j ≤ n} and , the lattice generated by {P_kj:k≥1,1 ≤ j ≤ n}. We can easily show inductively that is generated by (as a finite-dimensional von Neumann algebra).

Let ρ_n be a faithful state on . We extend ρ_n to a state on , denoted by ρ, i.e., ρ = ρ_n⊗ρ_n⊗⋯. Let be the Hilbert space obtained by GNS construction on . It is well known (see ref. 20) that the weak-operator closure of in is a hyperfinite factor (when ρ is a trace, the factor is type II₁). Then and become lattices of projections in .

Theorem 3.

With the above notation, we have that is a Kadison–Singer factor containing the hyperfinite factor as its diagonal.

Our above defined hyperfinite KS-factor depends on n (≥2) appeared in the UHF algebra construction. We shall see in Section 4 that, when ρ is a trace, for different n, the KS-algebras constructed above are not unitarily equivalent.

To prove Theorem 3, we need some lemmas.

Lemma 2.

With defined above and , i,j = 1,…,n, the matrix units for , we have

Proof:

Let T be an element in . Since for j = 1,…,n - 1, we know that . From , we have

Multiplying the above equation by on left and on right, we have

The right-hand side is independent of l. By letting l = 1,…,n and applying when 1 ≤ j < i ≤ n, we have that . It is easy to check that when T satisfies those identities in the lemma, T must be an element in .

In terms of matrix representations of elements in with respect to matrix units in , we know from Lemma 2 that such an element T is upper triangular. Moreover, one can arbitrarily choose the strictly upper triangular part of T and use equations

to determine the diagonal entries of T so that

Lemma 3.

For any T in , there are T₁ in and T₂ in () such that T = T₁ + T₂. In particular, when , .

Proof:

Suppose and let

[3]

It is easy to check that when i ≠ j and, by Lemma 2, . Moreover, for all . This implies that ().

Clearly . Thus T₂P_1k = P_1kT₂P_1k, for k = 1,…,n. We need to show that T₂P_jk = P_jkT₂P_jk, for j≥2 and k = 1,…,n. By the definition of P_jk in ref. 1, we know that . for j≥2 Now, from , we have

This implies that 0 = (I - P_jk)T₂ = (I - P_jk)T₂P_jk. Thus we have .

Lemma 4.

If and (I - P_m,n-1)T = 0 for some m≥1, then .

When m = 1, the proof is given above. For a general m, the argument is similar. We omit its details here. From the construction of P_mk’s, we know that the differences between elements in and those in only occur within I - P_m,n-1 (). Thus we have the following lemma.

Lemma 5.

If , then if and only if, for j = 1,…,n, the projections (I - P_m,n-1)P_m+1,j(I - P_m,n-1) are invariant under (I - P_m,n-1)T(I - P_m,n-1).

Inductively, we can easily prove the following lemma which generalizes Lemma 3.

Lemma 6.

If , then there are T₁,…,T_m+1 in such that T = T₁ + ⋯+T_m+1, where , (I - P_i,n-1)T_i = 0 for i = 1,…,m (here we let ), and .

Lemma 7.

Suppose T is an element in and is the algebra generated by T and . If , then .

Proof:

Suppose is given. From the comments preceding Lemma 3 and by taking a difference from an element in , we may assume that, with respect to matrix units in , T is lower triangular, i.e., for i < j. Now we want to show that T is diagonal. If the strictly lower triangular entries of T are not all zero, then let i₀ be the largest integer such that for some j < i₀. Among all such j, let j₀ be the largest. Then we have that if i > j and i > i₀; or i = i₀ > j > j₀. It is easy to check (from Lemma 4) that . Then . Define . Then

Let , and

Then T₁ = T₂ + T₃. From Lemma 4 again, . This implies that .

Let be the polar decomposition (in ), where H is positive and V a partial isometry. From our assumption that , we have H ≠ 0, and . Then . Define

It is easy to check, from Lemma 3, that . Let

Clearly and . But T₆ is not upper triangular. Thus 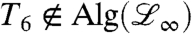. This implies that . This contradiction shows that T must be diagonal. Thus we have that . Now we show that for j = 1,…,n.

Assume that there is an i such that . Define

Then similar to the construction of T₁, we see that . Again write . One checks (by Lemma 3) that . Then

Set T₇ + T₈ = V^′H^′, the polar decomposition with V^′ a partial isometry. One easily checks that . Then . Since H^′ is self-adjoint, . But (with ). Thus (). This implies that . This contradiction shows that . Therefore .

Now we restate our Theorem 3 in a slightly stronger form.

Theorem 4.

Suppose is a subalgebra of such that and . Then .

Proof:

Without the loss of generality, we may assume that is generated by T and . From the above lemma, we have that . Suppose but . From Lemma 6, we write T = S + T^′ such that and . When we restrict all operators to the commutant of and working with matrix units , similar computation as in the proof of Lemma 7 will show that . This contradiction shows that .

In the above theorem, we did not assume the closedness of under any topology. Thus has an algebraic maximality property. Next section, we will show that is the strong-operator closure of .

KS-Lattices

It is hard to determine whether a given lattice is a KS-lattice. The only known class is the family of nests (1). Some finite distributive lattices (see refs. 5 and 21) are KS-lattices if they have a minimal generating property. In this section, we will show that the strong-operator closure of defined in Section 3 is a KS-lattice. For simplicity of description, we shall assume that the state ρ on is a trace, now denoted by τ. Let be the hyperfinite II₁ factor generated by (or ). The commutant of is the diagonal subalgebra of .

Theorem 5.

Let be the strong-operator closure of , the Hilbert space obtained by GNS construction on . Then we have that . For any r∈(0,1), if there are such that , then there are two distinct projections in with trace value r; otherwise there is only one projection in with trace r.

To understand the lattice structure of , we first analyze the lattice properties of . From the definition of P_1j, j = 1,…,n, the generators of , we know that consists of a nest {0,P₁₁,…,P_1,n-1,I} in () on the diagonal and a minimal projection P_1n. It is easy to see that P_1n∧P_1j = 0 for 1 ≤ j ≤ n - 1, and their unions give rise to another nest {0,P_1n,P_1n∨P₁₁,…,P_1n∨P_1,n-1 = I} in . The lattice is the union of these two nests. For any 1 ≤ k ≤ n - 1, there are two distinct projections in such that they have the same trace . This pattern of double nests appears in between any two trace values and , 0 ≤ k ≤ n - 1. To describe all these projections, we need more notation. For k = 1,2,…, define

Since and are tensorial relations for k ≠ k^′, we have and are projections in . Also when j ≤ n - i. We shall use τ to denote the unique trace on both and , , .

Lemma 8.

Suppose and P ≠ 0,I. Then , for some i∈{0,1,…,n - 1}, , and also . When P is given in this form, .

Proof:

First we show that if with Q described in the lemma, then .

For any , let T = T₁ + T₂, given by (3) in the proof of Lemma 3. Then it is easy to check that , (I - P_1,n-1)T₁ = 0 and . Because , we have , for j∈{1,2}. One can check directly that . Thus . Since Q commutes with , we have

The above equations hold when T is replaced by T₁ or T₂. From our assumptions that , and , we have

Next we show that , which implies that (I - P)T₁P = 0. Note that

By Lemma 3 and , we have . So . Thus (I - P)TP = 0 which implies that .

Now for any , let i₀, 1 ≤ i₀ ≤ n, be the smallest integer such that . Then for 1 ≤ i ≤ i₀ - 1 and , where P₁ is a projection and for i ≤ i₀ - 1. First we assume that i₀ ≤ n - 1. For any and i₁≥i₀ + 1, define . Then . Since , we have

From , the above equation implies that , for all i₁≥i₀. So, multiplying by (the adjoint of the above equation) on the right hand side, we have for all i₁,j≥i₀. This implies that , where Q is a projection in . If i₀ = n, then P₁ can be written as for . From , it is easy to see that .

Lemma 9.

Suppose . Then there exist and integers a_k such that

where 0 ≤ a_i ≤ n - 1 and which is a real number lies in the closed interval .

The above lemma follows easily from induction. The details are similar to the proof of Lemma 8.

Proof of Theorem 5.

To describe an arbitrary projection P in in more details, we need to know the trace value of P. First when , where 0 ≤ a_i ≤ n - 1 and a_k ≠ 0, then there are two cases, either

Note that the above two projections correspond to the case when Q = 0 for the decomposition , or respectively Q = I for in Lemma 9. So . Thus, for any for some integer l > 0 and any integer a such that 0 < a < n^l, there are exactly two projections in with trace r.

Secondly, when r∈(0,1) and for any positive integer l and any integer a with 0 < a < n^l, we shall show that there is a unique P in with trace r. For the given r, there is a unique expansion , where a_k is an integer with 0 ≤ a_k ≤ n - 1, there are infinitely many nonzero a_k’s and infinitely many a_k ≠ n - 1. (This is because repeating n - 1 as coefficients from certain place on will result r being , e.g., 0.09999⋯ = 0.1 when n = 10.) In fact, Lemma 9 gives the existence and uniqueness of such a projection:

It is not hard to see that P is the strong-operator limit of finite sums. The finite sums

Q₁ < Q₂ < ⋯ < Q_k < ⋯ < P and .

The following theorem gives us infinitely many non isomorphic KS-lattices.

Theorem 6.

For n ≠ k, and are not algebraically isomorphic as lattices.

Proof:

For any n≥2, first we observe from Lemma 9 that if is a minimal projection, then for m = 0,1,2,….

Suppose that is given as in Lemma 9,

where 0 ≤ a_i ≤ n - 1 and . We shall show that for some m≥0 if and only if a_m+1 = 0.

First if a_m+1 > 0, it is easy to check that the minimal projection . Conversely, if a_m+1 = 0, then

Let , and . We have . But

This shows that , here . Let . Then and

This shows that ξ = 0 and thus .

For any , we define

From the above, we know that, for any minimal projection ,

Now it is not hard to show that . The number of elements in this set is an invariant of .