Full distance-resolved folding energy landscape of one single protein molecule

Abstract

Kinetic bulk and single molecule folding experiments characterize barrier properties but the shape of folding landscapes between barrier top and native state is difficult to access. Here, we directly extract the full free energy landscape of a single molecule of the GCN4 leucine zipper using dual beam optical tweezers. To this end, we use deconvolution force spectroscopy to follow an individual molecule’s trajectory with high temporal and spatial resolution. We find a heterogeneous energy landscape of the GCN4 leucine zipper domain. The energy profile is divided into two stable C-terminal heptad repeats and two less stable repeats at the N-terminus. Energies and transition barrier positions were confirmed by single molecule kinetic analysis. We anticipate that deconvolution sampling is a powerful tool for the model-free investigation of protein energy landscapes.

The path of an unfolded protein toward its folded and functional conformation is entirely determined by its energy landscape (1). Experimental data often provide very limited view of these energy landscapes. Many proteins are classified as two-state folders, because barrier crossing is the rate limiting step and the subsequent motion toward the native state occurs extremely fast. Kinetic data hence lose almost all the information of the energy landscape on the native side of the transition state. A more detailed insight into the energy landscape of proteins consequently requires experimental data that go beyond classical kinetic assays (2). In recent years, single molecule mechanical methods have been successfully employed to study the energy landscape of biomolecules in increasing detail (3–7). Specifically for DNA, the analysis of equilibrium fluctuations upon application of mechanical load has provided sequence-resolved energy profiles of the full energy landscape (4). For proteins, such a detailed description has so far remained elusive.

The leucine zipper of the yeast transcriptional activator GCN4 is an ideal protein model system for studying real time folding/unfolding dynamics to obtain spatially resolved energy profiles. Because of its simple linear folding topology, the mechanically unzipped length can be directly linked to the amino acid position of the unzipping fork. The GCN4 zipper domain contains four heptad repeats forming a double-stranded α-helical coiled coil (8) and has been described as a two-state folder (9). Bulk folding studies have shown that folding of a cross-linked coiled coil is nucleated at the C-terminal end of the protein (10, 11). From there, zippering of the coiled coil proceeds toward the N-terminus. Activation energies and folding kinetics have been investigated extensively (9, 12, 13). Earlier single molecule mechanical experiments using atomic force microscopy have provided insight into the average unfolding forces of the zipper domain (14, 15). Limited force resolution in atomic force microscopy (AFM) experiments, however, has precluded the direct observation of folding/unfolding transitions in this system.

Here, we use single molecule force spectroscopy by optical tweezers (3) to directly measure the full free energy landscape of a GCN4 based leucine zipper. The experimental design is sketched in Fig. 1A. We used a fusion construct consisting of a sequence of three identical GCN4-p1q domains (construct LZ26, see Methods and SI Text) (11, 14). This triple zipper domain construct offers the possibility to study the GCN4-p1q energy landscape with nucleation (C-terminal domain shown in blue) and simultaneously nucleation free (N-terminal domains shown in green and red) (15). The protein is clamped between two beads using DNA handles attached to N-terminal Cysteins (see SI Text) (3). One bead is moveable with respect to the other to control the tension applied to the protein.

Fig. 1.

Experimental setup and characteristic sample traces. (A) Cartoon depicting the experimental setup. The LZ26 coiled coil containing three GCN4 leucine zipper domains is attached to two beads via dsDNA handles. Individual zipper domains are coloured red, green, and blue. The two α-helical strands are cross-linked by cysteines at the C-terminus to avoid dissociation upon complete unfolding (see SI Text). (B) Force vs. extension traces of the LZ26 coiled coil. Four sequential unzipping (Black) and rezipping (Blue) cycles at 500 nm/s are shown (offset in force for clarity) (Inset) Magnification of the cycle marked by the red square. Unfolding from the native state (N) to the unfolded state (U) occurs via two resolved intermediates (I₁ and I₂). Lines are fits of a serial worm-like-chain model to the data (see Table 1 and SI Text). The letters specify amino acid residues in A and D positions of the coiled coil. (C) Force vs. time record of the LZ26 coiled coil held at a pretension of 14.1 pN (Upper) at constant trap separation. The magnification (Lower) of the region marked by the red square allows observation of transitions between I₁ (Red Dashed Line), I₂ (Green Dashed Line), and U (Blue Dashed Line). The structure of these conformations is sketched on the right. The y axis represents bead deflection from the trap center, which is linearly connected to the force acting on the molecule.

Results and Discussion

In a first set of experiments we recorded force vs. extension traces at constant trap velocity. In Fig. 1B, four successive unzipping (Black) and rezipping (Blue) cycles pulled at 500 nm/s are shown. Unfolding of the LZ26 zipper results in a highly reproducible characteristic folding/unfolding pattern at forces between 8 and 15 pN (Fig. 1B, Inset). Upon force application, two intermediates (I₁ and I₂) can be observed. Starting from the fully folded state N, I₁ is populated in a smooth hump-like transition at equilibrium. Transition to I₂ occurs close to equilibrium; however, distinct flips of the molecule between the two intermediate states are resolved. If stretched further, a final transition occurs to the completely unfolded configuration U of the molecule. Upon reversal of the pulling process the molecule refolds, exhibiting a hysteresis at a pulling velocity of 500 nm/s. To relate the observed intermediate configurations to the sequence of the protein, we used a serial worm like chain model to fit the force vs. extension traces (see Table 1, SI Text, and Fig. S1). The positions of the intermediate states correspond well to the positions of asparagine residues in the sequence, which are known to destabilize the coiled coil (14, 16).

Table 1.

Energetic and kinetic parameters of the LZ26 coiled coil.

	Dwell time					Contour length	Probability distribution
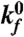Transition	(s-1)*	(s-1)*	ΔG0 (kBT)†	(nm)*	(nm)*	Δx (nm)‡	ΔG0 (kBT)‡
N, I1	--	--	--	--	--	9.3 ± 1.1	9.6 ± 1.1
I1, I2	(8.7 + 8.3 - 6.9) 10-4	(6.9 ± 4.1) 107	25.1 ± 2.0	8.7 ± 0.7	8.3 ± 0.1	19.9 ± 1.3	23.8 ± 0.4
I2, U	(2.5 ± 1.8) 10-5	(1.7 + 4.3 - 1.2) 1012§	38.8 ± 2.5	9.8 ± 0.4	24.9 ± 1.7§	33.2 ± 1.3	42.1 ± 0.4
	--	(5.0 ± 2.8) 103¶	--	--	7.9 ± 0.6¶
N, U	--	--	--	--	--	62.4 ± 1.0	75 ± 3∥

^*Errors are a combination of statistical and systematic errors due to trap stiffness uncertainty.

^†From the ratio of zero force rate constants.

^‡Errors are ± SD.

^§Fit to rate constants above 10.9 pN.

^¶Fit to rate constants below 10.9 pN.

^∥From Crooks’ fluctuation theorem.

The low instrumental drift of our setup allowed observation of thousands of transitions of one molecule between different protein conformations held at defined pretensions (the force acting on intermediate I₁) at constant trap separation. A typical force vs. time trace is shown in Fig. 1C (Upper). Because trap separation but not force is kept constant, every length change of the protein is associated with a change in tension. A zoom into the long data trace (Lower) allows observation of equilibrium transitions between the unfolding intermediates I₁ and I₂ as well as the completely unfolded protein U (shown as red, green, and blue dashed lines). The lines are determined as maxima of Gaussian fits to the data. The red and green lines appear slightly closer than expected from the contour length increases. This discrepancy indicates a deviation from a quadratic shape of the underlying folding energy landscape.

Increasing the separation between the two traps, and hence the pretension on the molecule, shifts the population probability from the folded to the unfolded state (Fig. 2A). These force vs. time traces contain a wealth of energetic and kinetic information about the folding process of the protein. Using the Boltzmann relation, differences in free energy between the stable states I₁, I₂, and U can be calculated from the population probability histograms (Fig. 2B, see Table 1 and Eq. S7). Further information about the equilibrium free energies can be obtained by exploiting the Crooks fluctuation theorem (17, 18) (Fig. 2C). The intersection (Red Circle) of folding (Blue) and unfolding (Black) work distributions obtained from nonequilibrium force vs. trap separation curves (Inset) defines the equilibrium free energy of folding of the complete LZ26 coiled coil of (75 ± 3) k_BT (see Table 1, Eq. S8, and Fig. S2).

Fig. 2.

Energetic and kinetic characterisation of the LZ26 coiled coil. (A) Force vs. time traces at different pretensions as indicated on the left. Dashed lines mark the conformations depicted in Fig. 1C. Total recorded times are (from bottom to top, in s): 12.1, 25.6, 117.2, 13.8, 114.5, 33.9. (B) Bead deflection histograms from the traces shown in A. Red, green, and blue lines are individual Gaussian components of a triple Gaussian fit to the histogram at 13.7 pN pretension. (Inset) Free energy differences between I₁ and I₂ (Open Symbols) and I₂ and U (Closed Symbols) at the indicated pretension (see Table 1). (C) Histogram of work associated with unfolding (Black Symbols, n = 65) and refolding (Blue Symbols, n = 65) of the complete LZ26 coiled coil (data from 10 molecules). The intercept of both work distributions (75 k_BT, Red Circle) corresponds to the total free energy of folding according to the Crooks fluctuation theorem (17, 18). Error bars represent SD. (Inset) Overlay of 37 folding (Blue) and unfolding (Black) cycles shown as force vs. trap separation. The light blue area corresponds to the work associated with folding of the molecule of one selected cycle, corrected for contributions of beads and DNA handles. (D) Force dependent rate constants for the transitions between I₁, I₂, and U. Lines are fits to the data according to a model accounting for elastic contributions from beads, handles, and unfolded protein chain (Eq. S9). The model yields curved lines that, however, appear straight in the displayed force range. The values are summarized in Table 1. Error bars represent SEM or an error estimated from missed events due to fast kinetics, if larger. (Inset) Integrated probability histograms of dwell times in I₁ preceding a transition to I₂ at varying pretensions (Dots). The distributions are well fit by a single exponential (Lines). (E) Check-points of the free energy surface. (Closed Symbols) Stable protein states with known position and energy. (Open Ellipses) Barrier positions whose energies depend on the preexponential factor (an interval between 10³ s^-1 and 10⁷ s^-1 is indicated).

The distributions of dwell time intervals τ (Fig. 2D, Inset) allow extraction of rate constants for transitions between I₁, I₂, and U. For extracting zero force rates it is important that movements of the transition state under load are modeled correctly. Such transition state movements were neglected in the simple Bell-type model (19), however several improved models have recently been proposed to extract transition state positions as well as zero force folding and unfolding rates from force dependent rate measurements (Fig. 2D) (20–23). We adapted a model initially proposed to describe folding under load (22) to model both folding and unfolding rate constants (SI Text). In brief, the unfolded conformation of the protein chain can be described by a worm-like chain (24) and corresponding transition barrier positions are very sensitive to force. For protein folding, we therefore use a model that accounts for the change in energy of the trapped beads, DNA linkers, and the unfolded protein chain associated with a length change of the protein upon folding (22) (Table 1 and Eq. S9). Because in our unzipping experiment force always acts at the unfolding fork, it is reasonable to assume that unfolding as well as folding occur turn by turn and each step directly translates into a length change of the unfolded peptide chain. Therefore, also for unfolding the change in energy of springs and linkers matters as the coiled coil gradually opens and the same model is suited to describe the unfolding rate constants (Table 1).

The free energy difference of 25 k_BT between I₁ and I₂ obtained from the ratio of zero force rate constants is in good agreement with the 24 k_BT derived from the position probability distributions. Likewise, the sum of the respective transition state positions for folding and unfolding of 17 nm corresponds to the extension of the protein obtained directly from the force extension measurements of 20 nm (see Table 1). The value of 5 × 10³ s^-1 for folding at zero force lies at the lower end of folding rates measured in ensemble studies (7.5 × 10³ - 2 × 10⁵ s^-1) (9, 10). A discrepancy between values obtained by bulk measurements and those from mechanical studies is to be expected. Chemical and mechanical methods generally perturb folding in distinct ways (25). However, Schlierf et al. (22) have shown that at moderate forces < 10 pN extrapolated folding rates are identical to those in the absence of load for an Ig domain from ddFilamin. Moreover, for coiled coils it is not a priori unreasonable that the folding pathway under load is related to the one occurring in solution. Meisner et al. (9) have reported that the solution pathway of the GCN4 zipper domain involves formation of a nucleus at the C-terminus with subsequent zippering toward the N-terminus. Interestingly, this is exactly the pathway that will be favored by the application of load to the N-terminus in our experiment.

Notably, the force-dependence of the rate constant for refolding (as shown by the open blue symbols in Fig. 2D) exhibits a bend. In principle, the strong force dependence of the unfolded protein state results in a curved rate versus force plot (26). This effect only accounts for a very slight curvature and is already included in the model used to calculate the force dependence of rates. Hence, the abrupt change in slope above 11 pN is an indication of a drastic change in transition barrier position (see Fig. S3, Dashed/Dotted Blue Lines). Such a change in barrier position could be either the consequence to two sequential barriers (27) or a broad transition barrier (28). At forces below 11 pN, we measure a value for Δx_UI2,1of 2 heptads for the initial nucleation of coiled-coil formation (Dashed Blue Line), consistent with previous findings (11, 15). A second fit of our model to the refolding rates above 11 pN (Dotted Blue Line) yields Δx_UI2,2 = 25 nm for the transition state distance to the second barrier. Together with the 10 nm for the reverse transition (Δx_I2U) this adds up to the full distance between states I₂ and U (see Table 1). Because evidence for this drastic change in transition state position hinges upon only a single data point, the extracted barrier distance might be subject to a considerable error. However, it is important to note that the single point at 11.2 pN in the UI₂ refolding rate is not the sole evidence for the existence and the quantification of this double barrier. Even if this point were disregarded, the overall conclusion would be unaffected. The transition state distance of Δx_UI2,1 = 8 nm as obtained from the dashed blue line together with the distance of the reverse transition is too short to account for the complete distance between I₂ and U (approximately 33 nm) and would hence indicate the existence of another hidden barrier. From this argument alone, a transition state position for the hidden barrier of ca. 23 nm could be deduced. This value coincides almost perfectly with our measured value of Δx_UI2,2 = 25 nm.

The energies and positions obtained so far define the important checkpoints along the folding landscape of the coiled coil that can be obtained in a combination of equilibrium and nonequilibrium experiments (Fig. 2E, Spheres). Deriving barrier heights from kinetic data, however, relies on the knowledge of the reconfiguration time of the protein chain, i.e. the preexponential factor k_ω in the Arrhenius equation. This preexponential factor could previously only be determined indirectly and has been estimated to 10³–10⁷ s^-1 (29). Therefore, the barrier heights in Fig. 2E are drawn with a large uncertainty (Open Ellipses).

Can we gain insight beyond the sketchy model of the folding free energy landscape of Fig. 2E? For DNA molecules, Woodside et al. (4) have recently provided proof of principle that equilibrium sampling can be used to extract the full energy landscape of biomolecules directly in a model-free way. When traversing between folded and unfolded states, the protein samples all possible conformations including the high energy states (transition state). Hence, the position distributions of Fig. 2B contain much more information than the coloured Gaussian fits suggest: specifically, the rare excursions to higher energy states along the folding pathway should give us much more detailed information about the underlying energy landscape. In principle, the full underlying energy distribution can be calculated from the position probability distribution P(x) using the Boltzmann relation ΔG(x) = k_BT ln(P(x)) + c (4, 30, 31).

In an optical trapping assay, the true protein fluctuations are masked by thermal fluctuations of the beads as well as the DNA handles (Fig. 3A, Black Line). The thermal noise contributions of beads and handles can be described by a point spread function (PSF(x)), which the fluctuations of the ends of the protein distribution are convolved with. To recover the true probability distribution of the protein ends (Fig. 3A, Red Line), we employed and modified a deconvolution procedure based on the work by Woodside et al. (4). In our approach, we use a nonconstant point spread function (PSF^a(x)) whose width depends on the bead deflection a, to account for the increase in width of the bead position distribution with decreasing force due to the nonlinear stiffness of the DNA handles (see SI Text for details). Introduction of the nonconstant PSF^a(x) was essential for convergence of the iterative deconvolution procedure. The resulting protein energy landscape is shown in Fig. 3B (Red Line). To increase the reliability of the recovered energy landscape, we averaged energy surfaces obtained from the same molecule at two different pretensions, after correcting them for these pretension differences (SI Text). After force correction, the difference between both energy surfaces has a standard deviation of ± 0.8 k_BT, which gives confidence into the accuracy of the energy surfaces obtained by our deconvolution method. Including drift, the spatial resolution is 2–3 nm. The averaged energy surface in Fig. 3C is now a direct measure of the distance-resolved energy landscape obtained from only one single molecule of the LZ26 leucine zipper held in an optical trapping potential at 14.1 pN pretension. The measured barrier heights ΔG^#(F) in combination with the transition rates k(F) allow an independent estimate of the preexponential factor k_ω for folding of the leucine zipper in our trap according to k_ω = k(F) × exp(ΔG^#(F)/k_BT). We chose to calibrate the preexponential factor using the barrier . It likely offers the best estimate of a barrier energy, because, due to the fast kinetics between I₁ and I₂, this barrier is crossed > 10,000 times. We derive a value of k_ω = 1.2(+1.6 - 0.6) × 10⁴ s^-1. This preexponential factor lies at the lower end of expected values (29). Tethering of the small protein to large beads may slow down the protein motion by coupling it to the motion under force of the much larger beads connected by the DNA linker (approximately 10⁴ s^-1) (32). In this scenario the measure of the barrier height would be unaffected. On the other hand, the diffusion time of the beads in the optical trap may preclude detection of faster internal protein motion and thus reduce the apparent preexponential factor. Therefore this value constitutes at least a lower bound for k_ω. This lower bound is slightly higher than lower boundaries for the preexponential factor ((2.7–5.5) × 10³ s^-1) calculated from measurements of the upper limit of the transition path time (33, 34).

Fig. 3.

Model-free reconstruction of the full energy landscape of the LZ26 coiled coil. (A) The protein probability distribution (Red Line) at 14.1 pN pretension is recovered from the bead deflection probability distribution (Continuous Black Line) by deconvolution with small residual error (Dotted Black Line) to remove thermal noise contributions of the series compliance of beads and elastic spacers. (B) Deconvolved free energy landscape (Red Line) of the protein at 14.1 pN pretension and blurred landscape including series compliance effects (Black Line). (C) Protein landscape (Colored Line) averaged from two landscapes at different pretensions, calculated to 14.1 pN pretension and check-points of the schematic energy landscape (closed and open symbols, Fig. 2E, Closed and Open symbols) with a preexponential factor of 1.2 × 10⁴ s^-1 derived from the measured barrier height. (D) Protein energy landscape and check-points of C in the absence of force. Colors indicate the three GCN4 leucine zipper domains of the LZ26 coiled coil. The GCN4 leucine zipper consists of two stable C-terminal heptads (Dark Colors) and two less stable N-terminal heptads (Light Colors).

The open and closed symbols in Fig. 3C correspond to the schematic energy landscape of Fig. 2E using our measured preexponential factor for the barrier height estimates. The directly measured landscape and the key check-points of the schematic landscape are in very good agreement. Notably, all barrier positions are reproduced surprisingly well in the deconvolved energy landscape.

It has been a long-standing debate whether broad barriers observed in protein folding experiments indicate a number of energetically equivalent conformations or rather two or more narrow sequential barriers that cannot be resolved due to resolution issues (35, 36). For the apparently broad major barrier between I₂ and U, located at 40–60 nm in Fig. 3C, the deconvolved energy landscape helps to distinguish between those two scenarios. The two maxima of this barrier with a depression at ca. 55 nm strongly argue for the sequential barrier model and justify our earlier analysis with a second transition barrier (two slopes for the open blue symbols in Fig. 2D). Furthermore, it is intriguing that the high energy minimum lies exactly at the position of the weak asparagine residue in the C-terminal zipper domain, in accordance with the positions of the intermediate states I₁ and I₂. However, it is important to point out that errors of the regions with high energy will be necessarily large due to limited thermal sampling of those regions. This error in part explains the smaller measured barrier heights of the last two barriers compared to the heights calculated from the kinetic parameters. Moreover, because barrier heights seem to be influenced by bead kinetics, the decreasing characteristic frequency of the trapped beads with decreasing force yields systematically decreasing barrier heights with increasing protein extension.

Between states N and I₁ the energy landscape appears linear. Because we do not observe distinct transition events for the N to I₁ transition, a barrier, if it exists, has to be lower than the barrier between I₁ and I₂. The linear shape suggests that I₁ does not represent a real intermediate at higher forces, because the thermodynamic state N represented by a local minimum in the energy landscape vanishes under load. An alternative interpretation would view I₁ as the new native state under load.

Back transformation of the folding free energy landscape to zero force conditions provides the energy landscape shown in Fig. 3D, exhibiting a remarkably detailed picture of the LZ26 leucine zipper stability and folding. The free energy of folding of the coiled coil extracted from this zero force energy landscape (approximately 75 k_BT) corresponds well to the energy derived from the fluctuation theorem of Crooks. The transformed landscape clearly shows a repetitive energy pattern reflecting the composition of LZ26 from three individual GCN4-p1q coiled coils.

Hydrogen exchange measurements have shown that folding of a C-terminally cross-linked GCN4 zipper domain is barrier-limited and thus exhibits two-state behavior (9). The C-terminal GCN4 zipper domain (Blue) of our LZ26 construct, which has a free energy of 21 k_BT, comparable to bulk measurements (9), is in accordance with this finding, albeit with a very low folding barrier. This domain contains the energy contributions of initial seed formation. In contrast to the C-terminal domain, we find the 2 N-terminal domains (Green and Red) do not exhibit a barrier. Apparently, folding of these domains proceeds in a downhill fashion. It is important to note that the intermediates I₁ and I₂ only exist and are populated in a force experiment where the elastic linkers under load shape the energy landscape in such a way that pronounced minima appear (Fig. 3C and D). It is this unique property of force experiments that allows us to look into the downhill part of a folding protein. We can only conclude about the downhill nature of the pathway populated under load, not necessarily about the solution pathway. However, as pointed out above, there are arguments why solution and mechanical folding pathways may be similar for a coiled coil. Comparison of the free energies of the downhill folding domains to the free energy of the domain including the seed now allows an estimate of the entropic costs of seed formation of approximately 6 k_BT. Moreover, the observation of barrierless folding of concatenated leucine zipper coiled coils shows that those domains can be fused seamlessly without energetic prices. This is in stark contrast to the neck coiled coil of kinesin, where a noncanonical N-terminal hydrophobic collar region prevents seamless elongation of the coiled coil (37).

In the energy landscape of Fig. 3D, both N-terminal zipper domains appear clearly separated into two differently stable regions, a stable C-terminal region comprising two heptad repeats and two significantly less stable N-terminal heptads (indicated with light and dark colors in Fig. 3D). The approximately linear energy increases within these regions indicate that neighboring core residues exhibit similar energy contributions. Even though the GCN4 system is one of the best investigated model systems for protein folding, direct evidence for such an energetic asymmetry has so far been missing. Interestingly, the point of division into the differently stable regions coincides with the location of the asparagine residue in the center of each GCN4-p1q domain. This asparagine residue has been found to be destabilizing for the total free energy of the leucine zipper (16). Whereas this colocalization may be coincidental, a noncanonical residue at the border between two regions of different stability is remarkable. Our results of an energetic asymmetry between the N- and C-terminal heptads can explain experiments that found that C-terminal heptads are more sensitive to mutations of core residues than the N-terminal heptads (38) on an energetic basis. The energetic asymmetry also offers an energetic explanation for the proposed C-terminal trigger sequences governing folding of many physiologically important coiled coil structures (39, 40).

Recently, Li and coworkers proposed a mechanism for protein folding against force in which the polypeptide chain folds via a cooperative collapse of the complete polypeptide chain (41). Using force-clamp AFM they observed slow (0.01–10 s) and continuous folding transients from the unfolded to the folded state. In contrast, even under mechanical loads, the transition times we measure occur extremely fast (approximately 10^-4 s). Such rapid transitions have also been observed recently in single molecule fluorescence experiments of folding proteins (34). The observation of a large transition barrier far from the native state at large protein extension precludes the formation of a collapsed state at the onset of GCN4 folding.

In this study we demonstrated that single molecule deconvolution equilibrium sampling can reproduce the full distance-resolved energy landscape of a protein and reveal energy modulations even on the native side of the folding barrier. We anticipate that this method will find numerous applications to measuring energy landscapes of proteins to yet unprecedented detail.

Methods

Experimental Procedures.

The coiled coil construct is derived from the GCN4-p1 leucine zipper domain (8, 11, 14): MASR MCQLEQK VEELLQK NYHLEQE VARLKQL VGELEQK VEELLQK NYHLEQE VARLKQL VGELEQK VEELLQK NYHLEQE VARLKQL VGECEGL (construct LZ26). The coiled coil was cross-linked via C-terminal cysteines. A second N-terminal cysteine pair at position B of the heptad repeat was used for handle attachment as introduced by Cecconi et al. (3) (see SI Text for details). Antidigoxigenin beads sparsely covered with protein DNA constructs and Neutravidin beads (both 1 μm, distinguished by fluorescence) were trapped and brought into close proximity to build a bead-DNA-protein dumbbell. Experiments were performed in PBS buffer in a custom build dual beam optical tweezers setup (see SI Text for more information).

Data Analysis.

Analysis was done on the difference signal of both beads to increase the signal to noise ratio (42). The force is not constant in our measurements. Every length change of the protein will be associated with a change in tension. A correction for the change in forces is therefore included in all calculations (see SI Text for more information).