Mathematical simulations of ligand-gated and cell-type specific effects on the action potential of human atrium

Abstract

In the mammalian heart, myocytes and fibroblasts can communicate via gap junction, or connexin-mediated current flow. Some of the effects of this electrotonic coupling on the action potential waveform of the human ventricular myocyte have been analyzed in detail. The present study employs a recently developed mathematical model of the human atrial myocyte to investigate the consequences of this heterogeneous cell–cell interaction on the action potential of the human atrium. Two independent physiological processes which alter the physiology of the human atrium have been studied. i) The effects of the autonomic transmitter acetylcholine on the atrial action potential have been investigated by inclusion of a time-independent, acetylcholine-activated K⁺ current in this mathematical model of the atrial myocyte. ii) A non-selective cation current which is activated by natriuretic peptides has been incorporated into a previously published mathematical model of the cardiac fibroblast. These results identify subtle effects of acetylcholine, which arise from the nonlinear interactions between ionic currents in the human atrial myocyte. They also illustrate marked alterations in the action potential waveform arising from fibroblast–myocyte source–sink principles when the natriuretic peptide-mediated cation conductance is activated. Additional calculations also illustrate the effects of simultaneous activation of both of these cell-type specific conductances within the atrial myocardium. This study provides a basis for beginning to assess the utility of mathematical modeling in understanding detailed cell–cell interactions within the complex paracrine environment of the human atrial myocardium.

1. Introduction

The mammalian myocardium is a functional syncytium: rapid and efficient cell–cell communication is essential for each heartbeat. This connexin-mediated electrotonic current flow between myocytes can modulate the excitability and the patterns of activation and subsequent contraction in both the atria and the ventricles. Often the complex and heterogeneous three-dimensional electrophysiological substrate in the mammalian heart is considered to be a homogeneous structure consisting mainly, or entirely, of cardiac myocytes. However, fibroblasts comprise 60–70% of the total cell number in the adult mammalian heart (Camelliti et al., 2005; Baudino et al., 2006). Recent immunohistochemical and electrophysiological findings have demonstrated that fibroblast/myofibroblast cell populations within the mammalian heart can communicate electrotonically with myocytes, as well as with one another (Kamkin et al., 1999; Gaudesius et al., 2003; Kohl et al., 2005; Camelliti et al., 2005; Miragoli et al., 2006; Chilton et al., 2007; Cabo et al., 2008). This cell–cell interaction occurs via gap junction-mediated electrotonic coupling with the connexin family of integral membrane proteins playing a key role (Rook et al., 1992). Such functional communication appears to be dynamic and can change significantly in pathophysiological contexts (Brown et al., 2005), including both ischemic heart disease and metabolic syndromes. Recently, the functional consequences of electrotonic coupling between heterogeneous cell types on the electrophysiology of the myocyte have been investigated using mathematical models in which variable numbers of fibroblasts/myofibroblasts are coupled to selected numbers of myocytes (MacCannell et al., 2007; Sachse et al., 2008; Jacquemet and Henriquez, 2007, 2008). Collectively, these experimental and theoretical studies have drawn attention to the significant effects of this electrotonic coupling on myocyte excitability and action potential waveform in both the adult atrium and ventricle as well as in the neonatal myocardium (for review see Baudino et al., 2006; Cabo, 2008; Burstein and Nattel, 2008). Many of these effects arise from the source–sink relationships between the fibroblasts and myocytes. However, marked changes in intercellular resistance could also be a significant variable following both acute myocardial challenges (e.g., reperfusion following ischaemia) or longer-term events including gap junction remodeling and changes in intercellular Ca²⁺ or pH.

In the present study, a recently developed model of the human atrial action potential (Nygren et al., 1998; Maleckar et al., submitted for publication), and a mathematical formulation which can simulate atrial myocyte and fibroblast interactions (Maleckar et al., submitted for publication-b) has been utilized to further investigate fibroblast–atrial myocyte interactions during selected conditions known to be important for autonomic regulation and for paracrine modulation of atrial electrophysiology. These computations are based on recent experimental findings (Shibukawa et al., 2005; Chilton et al., 2007; Rose and Giles, 2008; Cabo, 2008) and were motivated in part by the classical work of Spach and his colleagues. These papers (Spach et al., 1981; Spach and Boineau, 1997) were among the first to draw attention to significant effects of fibroblasts and fibrosis on atrial electrophysiology. The present model extends previous work in two significant ways: i) the human atrial model includes the actions of the autonomic neurotransmitter acetylcholine (ACh) on the human atrium (cf. Demir et al., 1999; Kneller et al., 2002) and ii) a recently described, quasi-linear conductance which is activated by natriuretic peptides, and is localized to the fibroblast (Rose et al., 2007; Rose and Giles, 2008), has been included. Specifically, a mathematical model which can account for ACh-induced activation of a ligand-gated, inwardly rectifying, ACh-sensitive K⁺ current, I_K(ACh) has been incorporated (Kneller et al., 2002) into our model of the human atrial myocyte (Maleckar et al., submitted for publication-a). In addition, a nonselective cation conductance, activated by nanomolar concentrations of natriuretic peptide (Rose et al., 2007), has been included in the mathematical formulation for the fibroblast (Shibukawa et al., 2005; MacCannell et al., 2007). The resulting simulations illustrate the marked changes in resting potential, atrialmyocyte excitability, and action potential waveform which are caused by the direct actions of acetylcholine via I_K(ACh). These computations also demonstrate the significant effects of natriuretic peptide-dependent activation of a ligand-gated conductance which is expressed only in the fibroblast.

Additional development of these types of integrative mathematical models will provide a useful complement to ongoing experimental work directed toward investigating the complex, but fundamental properties of the atrial syncytium, its autonomic innervation and its paracrine/autocrine environment. In this way mathematical modeling can, in principle, contribute to mechanistic investigations of atrial rhythm disturbances (Shiroshita-Takeshita et al., 2005; Van Wagoner and Nerbonne, 2000; Burstein and Nattel, 2008; Zlochiver et al., 2008).

2. Methods

Publications from our groups have included simulations based on reformulation and optimization of the K⁺ currents which are responsible for action potential repolarization in the human ventricle (Fink et al., 2006, 2008), and the human atrium (Maleckar et al., submitted for publication-a). These models have been used as a basis for exploring the consequences of electrotonic coupling between a selected number of fibroblasts or myofibroblasts and a fixed number of human ventricular myocytes (MacCannell et al., 2007) or human atrial myocytes (Maleckar et al., submitted for publication-b).

The present study extends this theoretical analysis and model development while focusing on human atrial electrophysiology. Additional model development allows some of the direct effects of cholinergic autonomic innervation of the atrium (c.f. Pappano and Mubagwa, 1991; Imai et al., 2001; Shibata et al., 2006), and one aspect of the electrophysiological changes produced by the local paracrine and autocrine environments to be addressed (Oliver et al., 1997; Horio et al., 2003; D’Souza et al., 2004; Kuhn, 2004).

2.1. Mathematical model of the human atrial myocyte

The updated mathematical model of the human atrial myocyte action potential which is used in this study (Maleckar et al., submitted for publication-a) includes many of the fundamental aspects which were first developed within the adult human atrial myocyte model of Nygren et al. (1998, 2001). As was the case in the parent (1998) model, the biophysical descriptors of the electrophysiological properties of the atrial cell (electrical equivalent circuit for the sarcolemma) include ionic currents based on Hodgkin– Huxley formalisms, as well as a fluid compartment model to account for changes in ionic concentrations. The cylindrical dimensions and capacitance of the human atrialmyocyte are 11 µm (diameter) × 130 µm (length) and 50 pF, respectively.

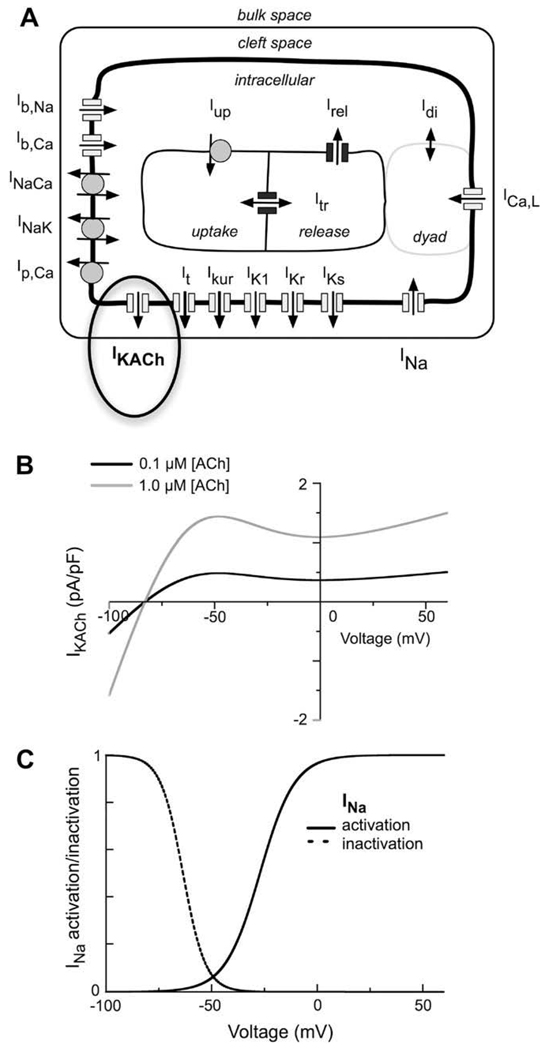
Fig. 1A is a schematic of the human atrial myocyte model. It includes the main time- and voltage-dependent ion currents which contribute to the generation of the human atrial action potential: I_Na, I_Ca,L, I_t, I_kur, I_K1, I_Kr, and I_Ks. This model also includes electrogenic pump and exchanger currents: the sarcolemmal Ca²⁺ pump current (I_Ca,P), the Na⁺–Ca²⁺ exchanger current (I_NaCa), and the Na⁺–K⁺ pump current (I_NaK). These transporters are responsible for the maintenance of intracellular ion concentrations, and are balanced by Na⁺ and Ca²⁺ time-independent or background currents, I_BNa and I_BCa.

Fig. 1.

Diagram of the equivalent circuit components of our mathematical model of the human atrial myocyte action potential. (A) A schematic of the time- and voltage-gated membrane currents, ion pumps and exchangers, as well as the ligand-gated K⁺ current, I_K(ACh), activated by muscarinic agonists. (B) I–V relationships of I_K(ACh) corresponding to two different concentrations of either acetylcholine (ACh). (C) Steady-state activation (solid line) and inactivation (dashed line) relationships for I_Na in this model of the human atrial myocyte.

The computations in the present paper utilize our recently developed model of the human atrial action potential (Maleckar et al., submitted for publication-a). A significant motivation for developing this model was to provide a more accurate reconstruction of the repolarization of the atrial action potential at a number of different steady-state frequencies of stimulation. Previous models had only limited success in this important application (Nygren et al., 1998; Courtemanche et al., 1998; Ramirez et al., 2000). Significant improvements in mathematical reconstruction of atrial action potential repolarization are now possible as a result of quite comprehensive experimental studies done on human atrial tissue and isolated myocytes from human atrium (c.f. Nattel and Opie, 2006). For example, in our recent model (Maleckar et al., submitted for publication-a) both the transient outward K⁺ current, I_t, and the ultra rapid delayed rectifier (sustained outward) K⁺ current, I_kur, were significantly reformulated based on additional experimental findings (Fedida et al., 1993, Amos et al., 1996; Dawodu et al., 1996; Feng et al., 1998; Dobrev et al., 2001; Wang et al., 2003; Gaborit et al., 2007).

In fact the original formulation of I_t (Shibata et al., 1989; Nygren et al., 1998) was based on rabbit atrial myocyte experimental data. It is now known that the voltage-gated K⁺ channel underlying I_t in the rabbit atrium is the Kv1.4 gene product. In contrast, in human atrium the α-subunit of this channel is encoded by Kv4.3 (Fermini et al., 1992; Wang et al., 2003, 2005). This change is very important since both the inactivation and the reactivation properties of Kv1.4 differ dramatically from those of Kv4.3 (for details see Maleckar et al., submitted for publication-a).

The equations describing another important repolarizing K⁺ current were also changed significantly. This so-called rapidly delayed rectifier, I_kur, is encoded by the voltage-gated K⁺ channel α-subunit Kv1.5 (Fedida et al.,1993). It activates very rapidly (<10 ms) (Amos et al., 1996) but inactivates very slowly (~3 s). In (Nygren et al., 1998) both the inactivation and recovery of this current had kinetics which were an order of magnitude more rapid than were observed in subsequent experiments. Accordingly, I_Kur was completely reformulated in our present model (Maleckar et al., submitted for publication-a).

The formulations of all remaining currents, ion fluxes, and Ca²⁺ homeostasis mechanisms were identical to those described previously (Nygren et al., 1998). In addition, the model of the human atrial myocyte employed in this study has eliminated the electro-neutral Na⁺ influx, Φ_en, of the model of Nygren et al. (Nygren et al., 1998) in order to achieve long-term stability in ionic concentrations over long periods of stimulation. A consequence of the incorporation of Φ_enwas a lack of charge conservation, as well as the absence of any true mathematical steady states (Jacquemet, 2007). The stimulus current delivered to the intracellular space is now attributed to the movement of K⁺ ions, as suggested by Hund et al. (2001) rather than balanced by the inclusion of Φ_en. As a result, charge is conserved within the system for any stimulation protocol.

2.2. Acetylcholine-activated K⁺ current I_K(ACh)

An acetylcholine-activated K⁺ current (I_K(ACh)) was incorporated into the present model of the human atrial myocyte, as has been done previously in a number of different mathematical models of the mammalian myocardium (cf. Demir et al., 1999) this addition is shown in bold and indicated by the ellipse in Fig. 1A. The mathematical formulation which we have utilized was the one in Kneller et al. (2002). Fig.1B consists of two steady-state current–voltage (I–V) relationships for I_K(ACh). These I–V curves illustrate the current density of I_K(ACh) within physiological voltage ranges for two representative concentrations of acetylcholine [ACh]. In the present study, [ACh] was varied systematically over two orders of magnitude in an attempt to simulate dose–response effects on the atrial myocyte action potential and resting potential. In any given simulation [ACh] was assumed to be at a fixed level of 0.03, 0.15, 0.3, 0.6, 1.5, or 3 µM. This range corresponds approximately to the experimental conditions in which carbamylcholine (CBC), a stable analogue of acetylcholine was applied at concentrations of 1, 5, 10, 20, 50, and 100 nM (Kneller et al., 2002).

2.3. Na⁺ current, I_Na

The peak magnitude of I_Na was increased in Maleckar et al. (submitted for publication-a) human atrial myocyte model by 12.5% to be consistent with experimental measurements of the maximum upstroke velocity of the human atrial action potential (Dawodu et al., 1996). The voltage dependence of the steady-state activation and inactivation of I_Na is presented in Fig. 1C. These biophysical descriptors are important for this paper because modulation of the myocyte resting membrane potential, following [ACh] treatment and/or coupling to fibroblasts, significantly alter myocyte excitability (see Fig. 3). In the human atrium, the resting potential, approximately −70 mV. As a result a significant fraction of the Na⁺ current is inactivated at this physiological membrane potential.

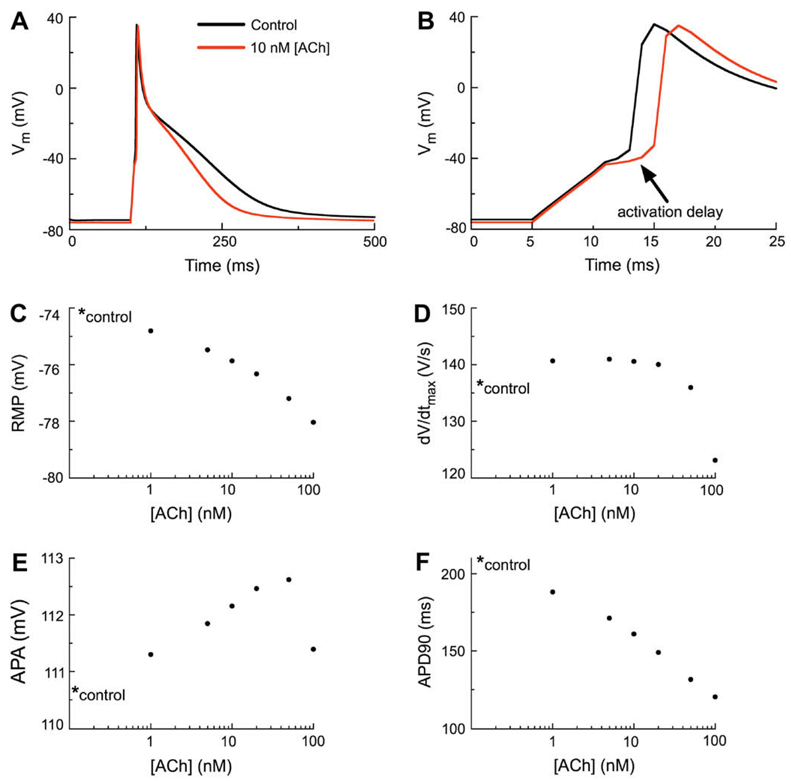
Fig. 3.

The effects of I_K(ACh) on the human atrial action potential waveform. (A) Simulated action potentials (APs) corresponding to the control (no I_K(ACh)) and to superfusion with 10 nM ACh (data shown in red). The stimulation protocol employed a 310 pA stimulus current lasting 6 ms at a basic cycle length of 1 s (1 Hz). As shown by the red trace, activation of I_K(ACh) hyperpolarizes the resting membrane potential (RMP) and abbreviates the action potential duration (APD). (B) Note that 10 nM ACh results in delayed activation of the human atrial myocyte AP (indicated by arrow). However, there is no decrease in the amplitude of the delayed AP. (C) Concentration–response relationship for [ACh] vs. RMP in the human atrial myocyte. In this and all subsequent panels the control value is marked with an asterisk. (D) Concentration–response relationship of [ACh] vs. dV/dt_max of the human atrial myocyte. (E) Concentration–response relationship of [ACh] vs. action potential amplitude (APA) of the human atrial myocyte. (F) Concentration–response relationship of [ACh] vs. action potential duration at 90% repolarization (APD90) of the human atrial myocyte.

2.4. Fibroblast–myocyte coupling

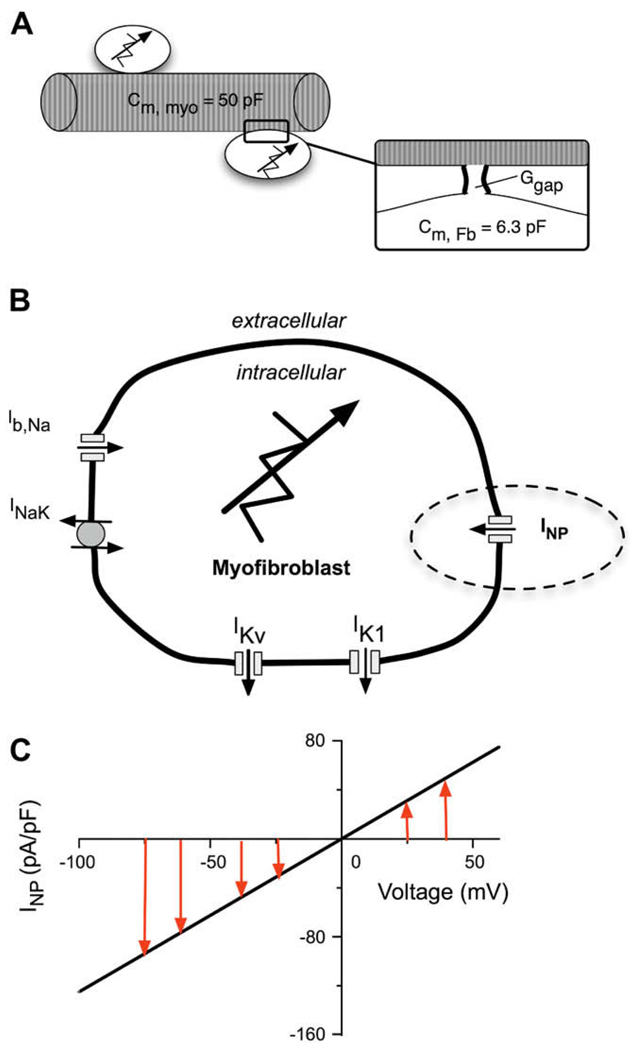
A schematic of fibroblast–myocyte electrotonic coupling is shown in Fig. 2A. All simulations which investigated the effects of electronic coupling were done assuming that a single fibroblast with a capacitance of 6.3 pF (Shibukawa et al., 2005)was coupled to one myocyte. A fixed gap junctional coupling conductance (G_gap) of 0.5 nS was assumed (Rook et al., 1992; c.f. Baudino et al., 2006; MacCannell et al., 2007). More details of the way in which we have formulated this cell–cell interaction model are presented in Maleckar et al. (submitted for publication-b).

Fig. 2.

Schematic diagram of the coupled human atrial myocyte/fibroblast paradigm which forms the basis of this study. (A) One human atrial myocyte was coupled to one fibroblast modeled according to (MacCannell et al., 2007), and assuming a gap junctional conductance, G_gap of 0.5 nS. The total capacitance of the human atrial myocyte is 50 pF and the capacitance of the fibroblast is 6.3 pF. (B) A schematic of the fibroblast which incorporates five active membrane conductances. The voltage-gated currents are a background Na⁺ current, I_b,Na; two K⁺ currents, I_K1, and I_Kv; the Na⁺–K⁺ pump current I_NaK. I_NP represents the novel ligand-gated transient receptor protein (TRP) channel current which is activated by natriuretic peptide. (C) The I–V curve for the natriuretic peptide-induced conductance in the fibroblast. Note, the linear relationship having a reversal potential near 0 mV.

In brief, the electrophysiological properties of the fibroblast membrane are represented by a model adapted very similarly to that developed by MacCannell et al. (2007). This model employs five time- and voltage-dependent active membrane conductances, as shown in Fig. 2B. For the purposes of this study, a ligand-gated non-selective cation current which is activated by natriuretic peptides (NP) in cardiac fibroblasts was simulated (see Rose et al., 2007). To explore the effects of this quasi-linear conductance the NP activated current (I_NP) was incorporated into the ionic model of the fibroblast, as indicated by the dashed ellipse in Fig. 2B. The I–V relationship of this time-independent current is essentially linear in the range of physiological potentials (Rose et al., 2007). I_NP was therefore modeled as:

$$I_{\text{NP}}=g_{\text{NP}}(V_{\text{Fb}}-E_{\text{NP}})$$

where g_NP is a constant conductance equal to 1.25 nS, V_Fb is the transmembrane potential of the fibroblast, and E_NP is the reversal potential of the channel, experimentally found to be approximately 0 mV. The I–V relationship of this time-independent, linear fibroblast conductance is shown in Fig. 2C.

2.5. Simulation protocol and data analysis

In a typical simulation one atrial myocyte was subjected to a selected [ACh] corresponding to 0 (control), 1, 5, 10, 20, 50, or 100 nM. Ten stimuli were applied at 1 Hz using a stimulus current of −6.2 pA/pF for 5 ms. Measurements of resting membrane potential (RMP), dV/dt_max, action potential amplitude (APA), and action potential duration at 90% repolarization (APD₉₀) were then performed. These parameters were used to construct the dose– response curves as shown in Results.

All simulations of electrotonic coupling assumed a one-to-one myocyte-to-fibroblast coupling ratio and a fixed intercellular conductance of 0.5 nS. Control conditions were defined and are illustrated based on coupling between a myocyte and a fibroblast in the absence of both ACh and NP. Simulations also investigated the effects of coupling between a single atrialmyocyte and fibroblast in the presence of natriuretic peptides (NP), or in the presence of both ACh and NP. The myocyte was again subjected to a selected concentrations of [ACh] and an identical train of 10 stimuli was applied. In these simulations a 1.5× threshold stimulus current (−5.6 pA/pF for 5 ms) was utilized. Measurements of resting membrane potential (RMP) were then performed and used to construct dose–response curves for [ACh].

3. Results

3.1. Effects of acetylcholine on human atrial action potential waveform

The six panels in Fig. 3 show output from action potential simulation (1.2 × threshold, at 1 Hz steady state) in which the effects of acetylcholine, (ACh) is applied. This autonomic transmitter results in instantaneous activation of a weakly inwardly rectifying K⁺ current, I_K(ACh), as shown in Fig. 1B. The main electrophysiological effect of ACh is the presence of an additional outward current at all membrane potentials positive to approximately −70 mV. This outward current would be expected to: i) hyperpolarize the resting potential, RMP, and ii) shorten the action potential duration, APD. Fig. 3 demonstrates that both of these effects are observed, and within limits, both of these effects scale progressively with increasing ACh concentrations. Concentration-dependent ACh-induced effects on the RMP, action potential duration at the point of 90% repolarization (APD₉₀), and action potential amplitude (APA) are shown/summarized in Fig. 3, Panels C, E and F, respectively.

Note that the ACh-induced effects on myocyte excitability (shown in Panels B and D) are somewhat unexpected. The two superimposed traces in Panel B demonstrate that ACh (10 nM) causes a delay in the initiation of the action potential in this isolated ‘in silico’ human atrial myocyte. This delay arises largely from the instantaneously activated outward current due to I_K(ACh). This effectively reduces the ability of the stimulus current to charge the myocyte to the threshold membrane potential. The ACh-induced small hyperpolarization of the RMP is also a contributing factor for the increased latency to action potential initiation.

Careful inspection reveals that the ACh-induced effects on atrial myocyte excitability and action potential waveform are complex. In part, this complexity arises from concentration dependent but diverse effects on key electrophysiological parameters. As illustrated in Fig. 3D the maximum rate of rise of the action potential increases as ACh concentration is raised in the range approximately 1–50 nM. This is because the ACh-induced hyperpolarization of the RMP removes steady-state inactivation of I_Na (see Fig. 1, Panel C). This ‘hyperexcitability’, however, is strongly concentration dependent. At ACh concentrations larger than approximately 50 nM, the outward current (I_K(ACh)) which is present in the range of membrane potentials close to the excitability threshold has a very strong influence. The net effect is an increased latency to firing and reduced excitability, sometimes including failure of this stimulus paradigm to produce an action potential, in spite of the hyperpolarization of the RMP.

3.2. Effects of acetylcholine on a minimal atrial functional syncytium: one myocyte coupled to one fibroblast

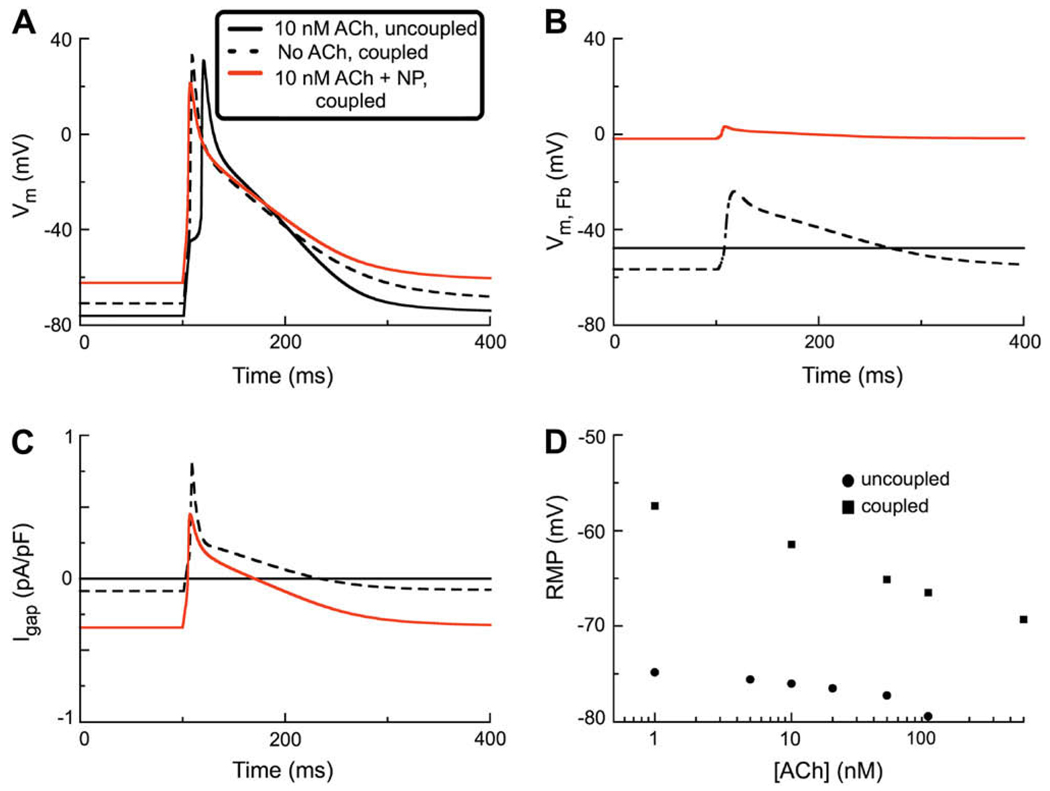
The next set of simulations was done to explore the changes in thehumanatrial action potential waveform in the presence of 10 nM ACh when one myocyte was coupled to one fibroblast through a coupling conductance at 0.5 nS. The 3 superimposed traces in Panel A of Fig. 4 illustrate these changes in action potential waveform. The solid black trace repeats data shown in Fig. 3, for reference. The dashed lines show the change in resting potential and action potential waveform when the fibroblast is coupled through a gap conductance of 0.5 nS. Note that there are 3 significant changes: (i) a depolarization of the myocyte resting potential, (ii) a decrease in the action potential duration (APD) during early repolarization and (iii) a lengthening of APD during late repolarization.

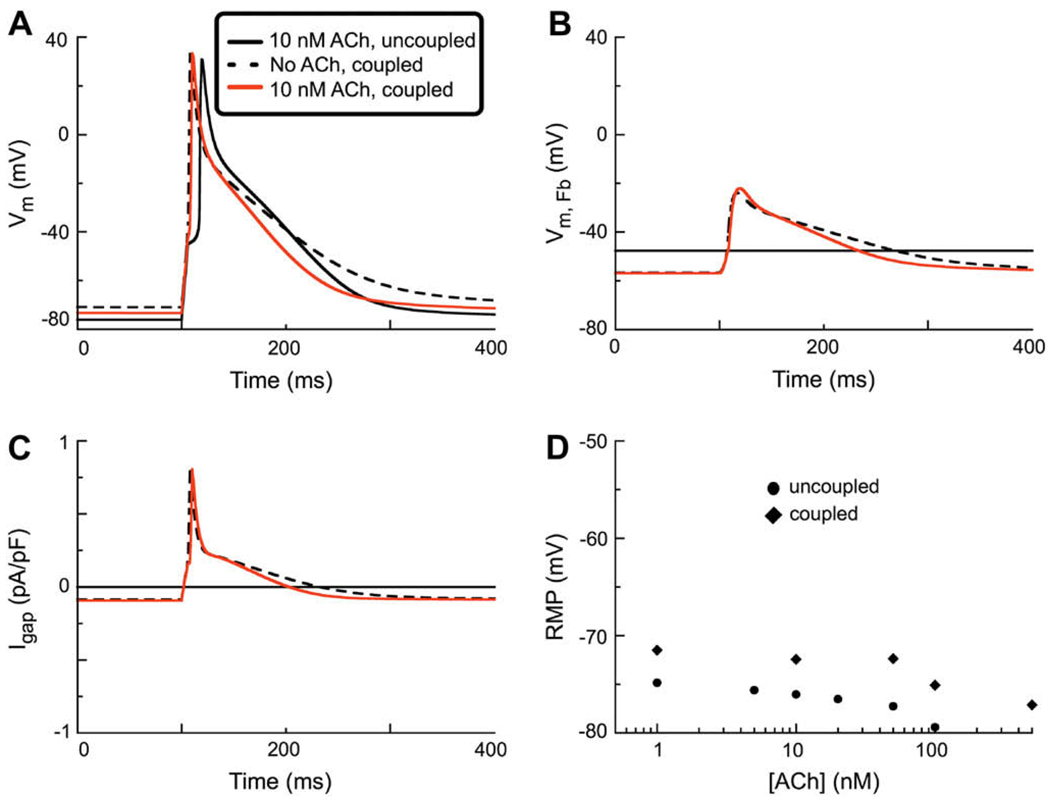
Fig. 4.

Action potential simulations made on the basis of a model system consisting of one human atrial myocyte (incorporating I_K(ACh) at 10 nM) coupled to a one fibroblast through a G_gap of 0.5 nS. (A) Comparison of AP waveforms during a stimulation protocol employing a 6 ms 280 pA stimulus current applied a basic cycle length of 1 s (1 Hz). Note that in the uncoupled myocyte when I_K(ACh) (black solid trace) is activated there is an activation delay. In contrast, since coupling the ACh-treated myocyte to a fibroblast depolarizes the RMP, application of ACh does not result in any activation delay in this situation (red line). Note that the coupled myocyte which is not treated with ACh has the most depolarized RMP, and a relative prolongation of APD (black dashed line). (B) Comparison of the electrotonic changes in the membrane potential of the fibroblast (V_Fb) as a result of coupling to one atrial myocyte. Solid black line represents the intrinsic or control RMP of the uncoupled fibroblast. Coupling to a myocyte (either with or without I_K(ACh)) results in a similar hyper-polarization of the fibroblast RMP. (C) Gap junctional current, Igap. Note that coupling one fibroblast to one myocyte either with or without I_K(ACh), results in a similar I_gap. (D) Concentration–response relationship for [ACh] vs. RMP in both the uncoupled (●) and coupled (◊) human atrial myocyte. The ligand-gated current, I_K(ACh), was active during each of these simulations in the myocyte model (black circles and diamonds, respectively).

The addition of ACh (10 nM), generates an outward current at all physiological membrane potentials. This has the expected effects: the resting membrane potential hyperpolarizes and the action potential in the coupled atrial myocyte shortens substantially. It is of interest to understand the changes in the electrophysiological status of the passive cell, the fibroblast in this syncytium. As shown in Fig. 4B the control resting potential in the uncoupled fibroblast is (approximately) −40 mV. This Figure also shows the substantial electrotonic depolarization of the membrane potential in the coupled fibroblast in response to each action potential in the myocyte. In this panel the dashed line depicts the electrotonic changes in membrane potential in the fibroblast under control conditions (no ACh), while the data depicted by the red line illustrates these changes in the presence of 10 nM ACh.

Fig. 4C shows the trans-gap current flow corresponding to the 3 sets of conditions in Panel 4A. The plot in Panel 4D focuses on the change in resting potential of the myocyte in the two conditions of interest. Note that under these conditions, the inward current generated by the relatively depolarized fibroblast tends to depolarize the restingmembrane potential of themyocyte. In summary the main effect of the coupled fibroblast is to reduce or remove the hyperpolarization in the myocyte which is caused by the activation of I_K(ACh) (c.f. Boyett et al., 1995; Christ et al., 2008).

3.3. Natriuretic peptide effects on the atrial fibroblast

The final set of simulations was done to begin to explore the interactions between autonomic tone (an effect of ACh) on the myocyte, and one aspect of the paracrine environment in the atrium – an electrophysiological effect of atrial natriuretic peptides. This effect is localized to the atrial fibroblast but, in principle, would be expected to alter myocyte electrophysiological properties as a result of connexin-mediated electrotonic current flow. In Fig. 5A, 2 of the 3 traces are analogous to those in Fig. 4A. Note, however, that the effect of the ligand-gated current, I_NP, which is activated only in the fibroblast tends to counteract the direct action of ACh in the myocyte. Under these conditions the net result is a marked depolarization of the myocyte resting membrane potential, and a pronounced action potential lengthening during the final repolarization phase. This is because the natriuretic peptide-induced current in the fibroblast is relatively large and net inward in the range of membrane potentials negative to its reversal potential which lies between −20 and 0 mV.

Fig. 5.

Simulations of the human atrial action potential in a coupled myocyte/fibroblast system with both I_K(ACh) and I_NP activated. The stimulus current (280 pA, 6 ms) was applied at 1 Hz and a fixed coupling resistance (0.5 nS) was assumed. A The action potential waveform denoted by the solid black trace illustrates the effect of activation of the I_K-ACh in this situation which assumed no intercellular coupling. Note the increased latency, or delay, in the firing of the AP. In this panel the superimposed red trace shows the changes produced by electrotonic coupling to one fibroblast in which I_NP is activated. Note: (i) depolarization of the RMP, and (ii) prolongation of the APD. The dashed line shows the AP waveform assuming no activation of I_K-ACh, in the presence of I_NP in one coupled fibroblast. B shows the corresponding changes in the fibroblast membrane potential V_Fb. Solid black line: control RMP in fibroblast (no coupling). Note that activation of I_NP causes a large depolarization (red trace). The dashed line is the V_FB with I_K(ACh) and I_NP activated. C shows the gap junction current under the three conditions chosen: black trace – resting, control fibroblast; red trace – I_NP activated; dashed trace – both I_K(ACh) and I_NP activated. D Two concentration–response relationships for RMP vs. [ACh]. The black circles (●) show the effect of activation of I_K-ACh on RMP in an uncoupled atrial myocyte (see also Fig. 3). The black squares (■) are analogous data from simulations assuming (i) myocyte–fibroblast coupling (0.5 nS); and (ii) activation of I_NP in the fibroblast.

Panel B of Fig. 5 shows the effect on the fibroblast of the ligand-gated current due to the natriuretic peptide. This is a marked depolarization of the fibroblast. The corresponding changes in gap junction currents are shown in Fig. 5C. The plot in Fig. 5D shows that under the conditions of these computations, the ligand-gated natriuretic peptide-induced current in the fibroblast, I_NP strongly reduces and then overcomes the hyperpolarizing effect of ACh at all ACh concentrations (1–100 nM) that were ‘tested’.

4. Discussion

This study has utilized our recently developed mathematical models of the human atrial myocyte and fibroblast (Maleckar et al., submitted for publication-a–b). In the present study cell–cell electrotonic interactions, as well as cell-specific effects of ligand-gated ion channels, are explored. As shown in Fig. 3– Fig. 5 concentration-dependent effects of the autonomic transmitter, acetylcholine, (ACh), on the human atrial action potential can be reproduced by our mathematical formulation. In this study and in previous work ACh activates an inwardly rectifying, time-independent K⁺ current, I_K(ACh) (cf. Demir et al.,1999; Boyett et al.,1995; Kneller et al., 2002). This outward current hyperpolarizes the resting membrane potential (RMP) and markedly shortens the action potential duration (APD) in the human atrium. In addition to this validation, our computations also replicate less well-known ACh effects. For example a delay in the initiation of the action potential upstroke is revealed and this is consistent with acetylcholine causing ‘hyper-excitability’ in selected tissues within the healthy mammalian myocardium (Kawara et al., 2001). This effect is mainly due to the reduction in the net inward stimulus current as a consequence of activation of the outward current, I_K(ACh). However, the hyperpolarization of the atrial RMP also contributes. Although this moves the resting membrane potential away from the action potential threshold; this hyperpolarization can cause a significant increase in excitability as a result of removal of inactivation of the Na⁺ current, INa in the human atrium.

A main goal of our study was to further investigate the electrotonic interactions between myocytes and fibroblasts within the normal or healthy adult human atrium (Maleckar et al., submitted for publication-b; Camelliti et al., 2005; Kamkin et al., 1999; Jacquemet and Henriquez, 2007). Our initial work has assumed a fixed 1:1 coupling ratio (myocyte/fibroblast) as well as a fixed intercellular conductance of 0.5 nS. These conditions were chosen in part, as a consequence of our experience with applying similar mathematical models of the human ventricular or atrial myocytes (c.f Nygren et al., 2001) coupled to selected numbers of fibroblasts (MacCannell et al., 2007; Maleckar et al., submitted for publication-b). As shown in Fig. 3 and Fig. 4 in the human atrium (as opposed to ventricle), electrotonic coupling to even one fibroblast was that the atrial myocyte resting potential depolarized significantly. In addition, the atrial myocyte action potential duration showed a marked shortening. The depolarization of the myocyte resting potential is driven by: i) the depolarized resting potential of the fibroblast (approximately −40mV), so that the myocyte–fibroblast difference in membrane potential acts as a current source. ii) The relatively high input resistance of the atrial myocyte, which results in even small currents causing substantial changes in resting membrane potential and action potential waveform (Joyner, 1982; Joyner and van Capelle, 1986; Joyner et al., 2000, 2007). The observed action potential shortening in themyocyte can be attributed in part to the current sink effect of the coupled fibroblast. Thus, during the action potential plateau in the myocyte, the fibroblast functions as a powerful current sink due to its time and voltage-dependent outward K⁺ conductances.

The inclusion of a natriuretic peptide-activated non-specific cation conductance, I_NP, in the fibroblast results in an enhanced capability of the coupled fibroblast to serve as a current source within the physiological range of membrane potentials. This conductance, which was modeled based on recent experimental data from our laboratory (Rose et al., 2007; Rose and Giles, 2008), is an essentially linear, non-selective cation current with a reversal potential near 0 mV. As a result, at membrane potentials negative to 0 mV, I_NP generates an inward current that can significantly depolarizes the resting membrane potential of the fibroblast and thence the myocyte. At strongly depolarized membrane potentials (>0 mV), however, I_NP is an outward current, and this promotes repolarization of the fibroblast, and enhances the ability of the fibroblast to serve as a current sink.

Our computations, although still very preliminary, serve as a basis for beginning to investigate, using mathematical modeling, the complex chemical (neurotransmitter, endogenous peptide) and electrophysiological interactions that take place in the heterogeneous atrial myocardium. Despite the fact that only the direct electrophysiological effects of ACh (activation of I_K(ACh)) in the myocyte and the fibroblast-specific effects of natriuretic peptides were considered, the effects on action potential waveform are complex, in part due to nonlinear interactions between I_K(ACh) and I_NP. These relationships can be explored further by more complete characterization of the concentration-dependent effects of I_K(ACh) and I_NP in the context of fibroblast–myocyte coupling.

4.1. Limitations of this model

We recognize that the present model has limitations which must be considered when using it even for integrative purposes. These arise from (i) initial assumptions used in model development, (ii) incomplete experimental data in some important areas, and (iii) the intrinsic (but incompletely characterized) heterogeneity of the adult mammalian atrium. We note that:

1. All of our simulations have been done assuming a 1:1 fibroblast to myocyte coupling ratio. There is no experimental data which can be used to justify this assumption. However, the relatively strong electrotonic effects of a single fibroblast seen in the results indicate that this ratio to be appropriate for use in this study. The classical experimental work of Spach et al. (1997) did draw attention to effects of ‘microfibrosis’ on atrial electrophysiology.

2. The choice of the one myocyte/one fibroblast coupling paradigm employed in this study, has the consequence that the known heterogeneities in the atrial action potential and cholinergic innervation of the atria have not been accounted for (Allessi et al., 1958; Ninomiya,1966; Li et al., 2001; Lomax et al., 2003; Gaborit et al., 2007). These differences are known to be mainly due to heterogeneous expression of K⁺ currents, including I_K(ACh), in the myocyte in different regions of the mammalian atria. These could be simulated by appropriate scaling of these currents in an additional study focusing on this atrial heterogeneity.

3. The cell-coupling paradigm of the present model is also limited by its failure to account for the electrophysiological effects of the extracellular matrix per sein the human atrium as well as the lack of inclusion of stretch-induced effects on either the fibroblast or the myocyte.

4. The present model does not incorporate any sophisticated formalisms for Ca²⁺ homeostasis in either the myocyte or the fibroblast. As a result changes in intracellular Ca²⁺ are not simulated accurately. Future studies of constitutive excitation–secretion coupling in the myocyte and coupled fibroblast will require further development of equations for Ca²⁺ transport, intracellular buffering and Ca²⁺-induced Ca²⁺ release. The electrogenic current due to Na+/Ca²⁺ exchange is known to modulate the contour of final repolarization in the mammalian atrial action potential.

These and other considerations will need to be taken into account before this model or others similar to it can be used for perhaps two of their most important applications: analysis of mechanisms of antiarrhythmic drugs which act selectively on the atrium (Rampe et al., 1993; Feng et al., 1997; Seti et al., 1999; Blaaw et al., 2007; Christ et al., 2008); or detailed analysis of the ways in which changes in or remodeling of expression levels of K⁺ currents can contribute to or account for atrial flutter or fibrillation (Schuessler et al., 1992; Brandt et al., 2000; Van Wagoner and Nerbonne, 2000; Burashnikov and Antzelevitch, 2006; Blaauw et al., 2007; Pijnappels et al., 2007; Burstein and Nattel, 2008).

List of symbols

APA

action potential amplitude

APD₉₀

action potential duration at 90% repolarization

B

background

Ca,P

sarcolemmal Ca²⁺ pump

CBC

carbamylcholine

dV/dt_max

maximum rate of change of voltage during action potential

E

reversal potential

Fb

fibroblast

G

conductance

gap

gap junctional

I

current

K(ACh)

acetylcholine-activated K⁺ channel

kur, K1, Kr, Ks

K⁺ current species

NaCa

Na⁺–Ca²⁺ exchanger

NaK

Na⁺–K⁺ pump

NP

natriuretic peptides

Φ_en

electroneutral Na⁺ influx

RMP

resting membrane potential

t

transient outward

V

membrane potential