Evaluation of a compartmental model for estimating tumor hypoxia via FMISO dynamic PET imaging

Abstract

This paper systematically evaluates a pharmacokinetic compartmental model for identifying tumor hypoxia using dynamic positron-emission-tomography (PET) imaging with 18F-fluoromisonidazole (FMISO). A generic irreversible one-plasma two-tissue compartmental model was used. A dynamic PET image dataset was simulated with 3 tumor regions -- normoxic, hypoxic and necrotic, embedded in a normal-tissue background, and with an image-based arterial input function. Each voxelized tissue’s time-activity-curve (TAC) was simulated with typical values of kinetic parameters, as deduced from FMISO-PET data from 9 head-and-neck cancer patients. The dynamic dataset was first produced without any statistical noise to ensure that correct kinetic parameters were reproducible. Next, to investigate the stability of kinetic parameter estimation in the presence of noise, 1000 noisy samples of the dynamic dataset were generated, from which 1000 noisy estimates of kinetic parameters were calculated and used to estimate the sample mean and covariance matrix. It is found that a more peaked input function gave less variation in various kinetic parameters, and the variation of kinetic parameters could also be reduced by two region-of-interest averaging techniques. To further investigate how bias in the arterial input function affected the kinetic parameter estimation, a shift error was introduced in the peak-amplitude and peak-location of the input TAC, and the bias of various kinetic parameters calculated. In summary, mathematical phantom studies have been used to determine the statistical accuracy and precision of model-based kinetic analysis, which helps to validate this analysis and provides guidance in planning clinical dynamic FMISO-PET studies.

1. Introduction

In normal tissues, there exists a homeostasis between oxygen supply from the capillary vasculature and oxygen consumption by tissue cells. In tumors, however, this homeostasis is frequently compromised, as uncontrolled cellular proliferation pushes cells further from blood vessels and into regions of progressively lower oxygen pressure (pO₂). As a consequence, the pO₂ within a tumor steadily decreases from physiologic levels at the capillary down to nearly zero at the boundary region of tumor necrosis. This phenomenon is called chronic hypoxia. The other form of hypoxia is acute hypoxia. It occurs from a temporary decrease or arrest of normal flow in a tumor blood vessel, and thus results in temporary depletion of oxygen in the cells surrounding the blood vessel. Tumor hypoxia, especially chronic hypoxia, i.e., the near-zero oxygen concentrations adjacent to regions of tumor necrosis, has important clinical and radiobiological consequences.

Tumor hypoxia has been known to impair the effectiveness of radiotherapy for over 50 years (Thomlinson and Gray 1955). The recent surge of interest in non-invasive measurement of tumor hypoxia has arisen due to the increasing number of reports associating poor treatment response and poor prognosis with increased fractional volume of tumor hypoxia as assessed by pO₂ Eppendorf probe histography and other means. Höckel et al 1993 demonstrated significantly shorter overall and recurrence-free survival for patients with hypoxic cervical tumors (median pO₂ < 10 mmHg). Similar results have been reported in head-and-neck cancer by Nordsmark et al 1996 and Brizel et al 1997, in sarcoma by Brizel et al 1996, in cervical cancer by Fyles et al 1998 and Knocke et al 1999, and in prostate cancer by Movsas et al 1999. In addition to direct pO₂ probe measurement, there is extensive immunohistochemical evidence showing that higher expression of endogenous markers of hypoxia, e.g., VEGF and HIF-1 alpha, identify those prostate cancer patients at higher risk of biochemical failure (Vergis et al 2008). These findings underscore the potential utility in developing a more practical technique for the quantitative assessment of tumor hypoxia, for identifying predictors of tumor aggressive and stratifying patients who may respond more poorly to treatment (Tatum et al 2006).

Positron-emission-tomography (PET) measurement of tumor hypoxia offers the advantages of being non-invasive, repeatable and potentially providing a quantitative three-dimensional image of the hypoxic region. In addition, it eliminates erroneous results (i.e., false negatives) resulting from the limited tissue sampling associated with probe-based measurements and tissue section-based methods such as immunohistochemistry. A number of PET radiotracers with which to specifically image viable hypoxic cells in solid tumors have been developed. These include most notably the 2-nitroimidazole family of compounds: ¹⁸F-labeled fluoro-misonidazole (¹⁸F-FMISO) (Rasey el al. 1996, Rajendran et al 2003, Lee et al 2008), ¹⁸F-fluoro-erythronitroimidazole (FETNIM) (Yang et al 1995, Lehtiö et al 2003 and 2004), 2-(2-nitro-1H-imidazol-1-yl)-N-(2,2,3,3,3-pentafluoropropyl)-acetamide (EF5) (Evans et al 2000, Ziemer et al 2003), ¹⁸F-fluoroazomycin-arabinosise (¹⁸F-FAZA) (Sorger et al 2003), and ¹²⁴I-labeled iodinated-azomycin-galactopyranoside (¹²⁴I-IAZGP) (Zanzonico et al 2004, Riedl et al 2008), as well as other tracers such as copper-diacetyl-bis(N⁴)-methylthiosemicarbazone (Cu-ATSM) (Lewis et al 2001, Dehdashti et al 2003).

The most widely used hypoxia tracer in clinical studies is ¹⁸F-FMISO. Its parent compound, misonidazole, a radiosensitizer similar to pimonidazole, is irreversibly bound in the cell under hypoxic conditions (Chapman et al 1989, Casciari et al 1995, Brown et al 1996). The drug is bioreductively activated by electron transport. The first-electron reaction produces the nitro radical anion, which is reversed in the presence of oxygen in the cell. In the absence of oxygen, however, a second electron reaction generates a bioreductive alkylation agent. This reduced FMISO bioreduction product then binds to macromolecules within the cell and is trapped over the time course of PET acquisition.

Clinical studies performed at the University of Washington have shown positive imaging of tumor hypoxia, but with low PET signal contrast. Analysis of the biodistribution of FMISO in patients imaged between 2 to 3 hours post-injection led to an operational definition of tumor hypoxia as corresponding to voxels having a tumor-to-blood activity concentration ratio of greater than 1.2–1.6 (Rasey et al 1996, Rajendran et al 2003, 2004 and 2006). One concern is the slow and potentially variable clearance of FMISO from normal (i.e., normoxic) tissues relative to the 110-minute half-life of ¹⁸F, which can lead to significant variability in PET images of hypoxia if segmented in the foregoing manner. Later PET imaging might lead to improved hypoxia-to-normoxia ratios, but incur the problem associated with poorer count statistics. An investigation of the variability in the hypoxia when applying segmentation to two baseline FMISO exams of the same set of 20 patients performed 3 days apart revealed considerable changes in the fraction of hypoxic voxels (Nehmeh et al 2008). The variability in tumor uptake of FMISO can be due to photon counting noise and/or acute tumor hypoxia.

In order to overcome the dependence on a single threshold criterion for discriminating hypoxic from non-hypoxic tumor sub-volumes, the current study investigates the feasibility of performing a pharmacokinetic compartmental analysis to model the transport and metabolism of the radiotracer uptake in tumors. The input required for such an analysis is dynamic PET imaging data for which region-of-interest (ROI) corresponding to tumor as well as arterial blood can be identified. The compartmental analysis tool used is based on a generic two-tissue model implemented in Philips Research’s Voxulus software package, which is also included in the research version of Pinnacle³™, Philips’ radiation treatment planning software, and in IMALYTICS, Philips’ preclinical research workspace. Voxulus is able to perform pharmacokinetic modeling for each image voxel as well as ROIs (i.e., contiguous groups of voxels). Prior investigations using this general approach have been published by Thorwarth et al 2005a and 2005b, who has already demonstrated the feasibility of compartmental analysis of dynamic FMISO data. The main purpose of this paper is to evaluate the feasibility of voxel-based compartmental analysis, tested using the one-plasma two-tissue irreversible compartmental model implemented within Voxulus.

2. Materials and Methods

2.1. Two-tissue compartmental model

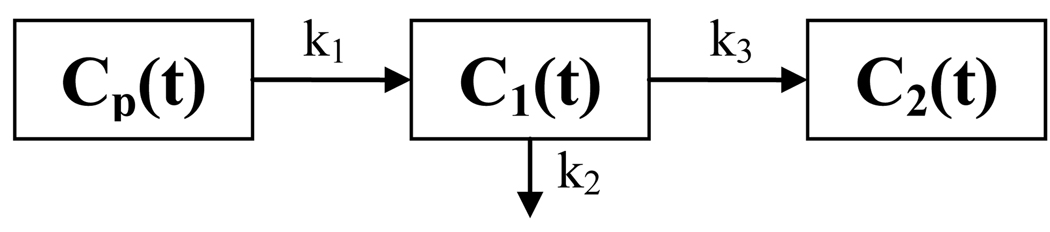
The irreversible one-plasma two-tissue compartmental model (Huang and Phelps 1986) is shown in figure 1, where C_p (t), C₁ (t) and C₂ (t) are activity concentration (unit in Bq/ml) as a function of time t (unit in min) post-administration in the plasma compartment, reversible tissue compartment and trapped tissue compartment, respectively; and k₁, k₂ and k₃ are kinetic reaction rate constants (unit in 1/min) between compartments.

Figure 1.

Generic irreversible one-plasma two-tissue compartmental model.

The rate of activity concentration in these two tissue compartments is then modeled as

$$\begin{array}{c}\frac{{\mathit{\text{dC}}}_1(t)}{\mathit{\text{dt}}}=k_1{C}_p(t)-(k_2+k_3)C_1(t)\hfill \\ \frac{{\mathit{\text{dC}}}_2(t)}{\mathit{\text{dt}}}=k_3{C}_1(t)\hfill \end{array}$$ (1)

By solving the above two differential equations, C₁ (t) and C₂ (t) can be expressed as

$$\begin{array}{c}{C}_1(t)=k_1{e}^{-(k_2+k_3)t}\otimes C_p(t)\hfill \\ C_2(t)=\frac{k_1{k}_3}{k_2+k_3}\left[1-e^{-(k_2+k_3)t}\right]\otimes C_p(t)\hfill \end{array}$$ (2)

where ⊗ denotes convolution. The activity concentration C_ROI (t) in a given ROI is a weighted sum of C_p (t), C₁ (t) and C₂ (t) :

$$C_{\mathit{\text{ROI}}}(t)=\beta C_p(t)+C_1(t)+C_2(t)$$ (3)

where β is the fraction of vascular space (a scalar between 0 and 1) in the ROI compared with the plasma input function. The ROI can be a single image voxel or a group of image voxels.

In Voxulus, the plasma input function is modeled as an analytical function

$$C_p(t)=A_{0}t{e}^{-C_{0}t}+{\displaystyle \sum _{i=1}^N{A}_i\left(e^{-C_{1i}t}-e^{-C_{2i}t}\right)},$$ (4)

where the unit of A₀ is Bq/(ml·min), of A_i Bq/ml, and of C₀, C_1i, C_2i 1/min. The input function parameters {A₀, C₀, A_i, C_1i, C_2i, i=1, …, N} can be estimated either from the arterial regions in the dynamic image dataset or from serial blood sampling.

Given the analytical ROI time-activity-curve (TAC) (3) with inserts (2) and (4), and a measured ROI TAC, a Levenberg-Marquardt least-square (LS) or weighted-least-square (WLS) optimization scheme is used in Voxulus to estimate the kinetic parameters {k₁, k₂. k₃,β}. The same optimization scheme is used for the input function parameters estimation. Note that for multiple-voxel ROI, Voxulus estimates each kinetic parameter on a voxel-by-voxel basis within the ROI, resulting in parametric images of each of the model parameters.

2.2. Physical interpretation of various tissue types

Inserting (2) into (3), the target tissue’s TAC is modeled as the summation of three components, as shown in (5): (a) the direct contribution from the input function due to the vascular space within the tissue, $C_{\mathit{\text{ROI}}}^{\mathit{\text{Vascular}}}(t)$ ; (b) the reversible (i.e., diffusion) contribution of the input function, $C_{\mathit{\text{ROI}}}^{\mathit{\text{Diffused}}}(t)$ , which is the convolution of an exponential function (with decay constant k₂+k₃) with the input function; (c) the irreversible or trapped contribution from the input function, $C_{\mathit{\text{ROI}}}^{\mathit{\text{Trapped}}}(t)$ , which is the convolution of a constant step function with the input function.

$$\begin{array}{c}{C}_{\mathit{\text{ROI}}}(t)=C_{\mathit{\text{ROI}}}^{\mathit{\text{Vascular}}}(t)+C_{\mathit{\text{ROI}}}^{\mathit{\text{Diffused}}}(t)+C_{\mathit{\text{ROI}}}^{\mathit{\text{Trapped}}}(t)\hfill \\ \begin{array}{cc}\hfill \text{where} C_{\mathit{\text{ROI}}}^{\mathit{\text{Vascular}}}(t)& =\beta C_p(t)\hfill \\ \hfill C_{\mathit{\text{ROI}}}^{\mathit{\text{Diffused}}}(t)& =\frac{k_1{k}_2}{k_2+k_3}{e}^{-(k_2+k_3)t}\otimes C_p(t)\hfill \\ \hfill C_{\mathit{\text{ROI}}}^{\mathit{\text{Trapped}}}(t)& =\frac{k_1{k}_3}{k_2+k_3}\otimes C_p(t)\hfill \end{array}\end{array}$$ (5)

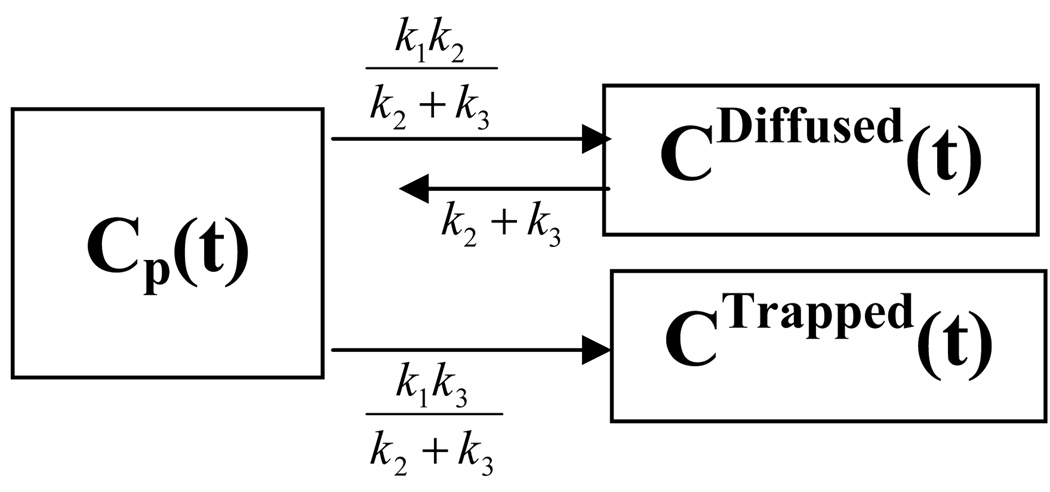
Note that the irreversible two-tissue compartmental model is equivalent to a system of two decoupled single-tissue compartmental models, as shown in figure 2 (Blomquist 1990). The influx rate constant $\frac{k_1{k}_3}{k_2+k_3}$ from the plasma compartment to the trapped compartment is denoted as K_i. These {k₁, k₂, k₃, β, K_i} are called kinetic parameters or kinetic rate constants.

Figure 2.

Two decoupled single-tissue compartmental models.

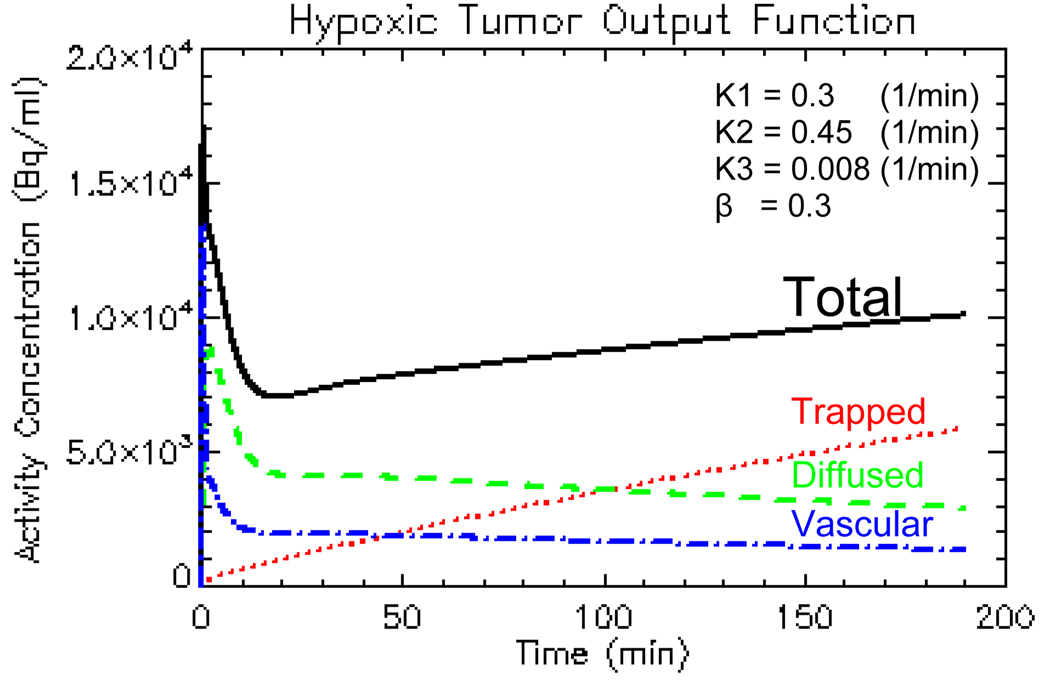
For a bolus-injection plasma input function, both the vascular and diffused components decrease with time while the trapped component increases with time. For hypoxic tumor, the trapped component dominates the other two components; while for normoxic tumor, the trapped component is small compared with the remaining two; and for necrotic tumor, the trapped component is a compromise of the previous two cases (Thorwarth et al 2005a). Figure 3 displays a TAC of hypoxic tumor as a decomposition of three components.

Figure 3.

The total time-activity-curve as a decomposition of vascular, diffused and trapped components.

2.3. Validation methods

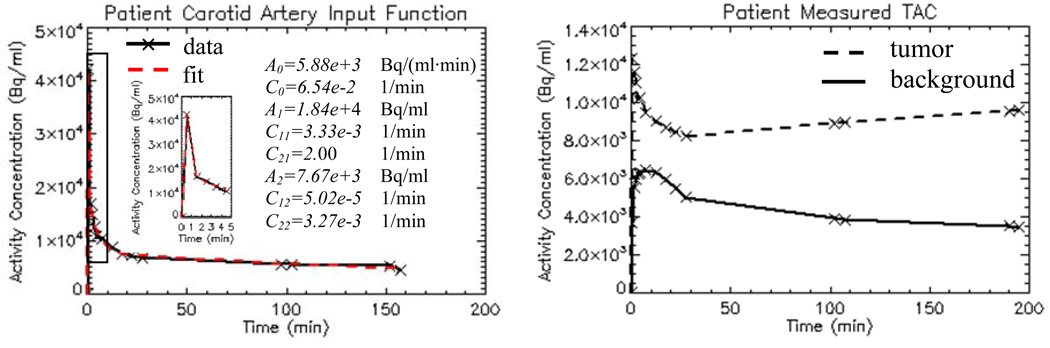
To help select values of the kinetic parameters that reflect actual clinical situation, nine head-and-neck cancer patients’ dynamic FMISO-PET data are analyzed with Voxulus and a representative set of kinetic parameters are estimated for the normoxic, hypoxic and necrotic tumor regions, and for the normal-tissue background region, respectively. A representative plasma input function is also derived from the dynamic image datasets from a region circumscribing the carotid artery. Figure 4(a) shows a patient’s measured and fitted image-based input function. Figure 4(b) shows a patient’s measured TACs of the tumor and background soft tissue regions, respectively. The actual time sampling points are shown as cross signs in these figures. The purpose of this paper is not to evaluate Voxulus using clinical data but to provide an analysis of the statistical reliability of voxel-based compartmental modeling using dynamic PET data.

Figure 4.

Head-and-neck cancer patient’s TAC of input function from carotid artery (a), and TACs of tumor and background soft tissue regions (b).

Using equations (2)–(4), a dynamic image dataset is generated with 4 distinct regions corresponding to: plasma, normoxic tumor, hypoxic tumor and necrotic tumor embedded in a normal-tissue background. An illustration of the mathematical dynamic image phantom simulated in this work is shown in figure 5. Note that the plasma region corresponds to a fixed set of input parameters, and each tumor region and background region corresponds to a particular set of kinetic parameters.

Figure 5.

Simulated noise-free images of multiple dynamic frames.

2.3.1. Noise-free and noisy samples

The dynamic image dataset is first simulated without any statistical noise to serve as a consistency check of the Voxulus software, that is, to verify that the correct kinetic parameter values are indeed estimated. Next, to investigate the stability of this voxel-wise analysis in the presence of noise, 1000 noisy samples of the dynamic image data are generated. The noise at each voxel n and at each dynamic frame i is simulated as a Gaussian, with standard deviation σ_n,i modeled as

$${\sigma }_{n,i}=c\sqrt{f_{n,i}{d}_i/t_i^{\mathit{\text{dur}}}}$$ (6)

where f_n,i is the activity concentration in the n^th image voxel and at the i^th dynamic frame after decay and frame-duration correction; d_i = exp(λt_i) is the isotope decay correction factor, with λ the decay constant and t_i acquisition time at the i^th frame; $t_i^{\mathit{\text{dur}}}$ is the duration time (in sec) at the i^th frame; thus $f_{n,i}{t}_i^{\mathit{\text{dur}}}/d_i$ represents the mean activity concentration before decay and duration correction; c is a constant which scales the Gaussian noise with standard deviation close to the clinical situation. In a reconstructed image with iterative reconstruction, the statistical noise obeys a multivariate log-normal distribution (Barrett et al 1994, Wilson et al 1994), which behaves more like a Gaussian than a Poisson distribution. In addition, there is slight correlation between nearby voxels. In this study, however, no such correlation is assumed.

2.3.2 %bias, %stddev and correlation coefficient

These 1000 samples of noisy data are first smoothed by a 3-point-boxcar-average filter in both the horizontal and vertical dimensions, run through Voxulus, and then 1000 noisy samples of the kinetic parameter images are estimated for each k₁, k₂, k₃ and β. For each tumor-tissue type, a central voxel is selected from the region and thus 1000 noisy samples for each kinetic parameter are obtained at that voxel. The percentage bias and percentage standard deviation are calculated with respect to the true value for each kinetic parameter and each tumor type, as shown below

$$\begin{array}{c}\%\mathit{\text{bias}}=\left({\mu }_{x_n}/x_n^{\mathit{\text{true}}}-1\right)\times 100\hfill \\ \%\mathit{\text{stddev}}=\left({\sigma }_{x_n}/x_n^{\mathit{\text{true}}}\right)\times 100\hfill \end{array}$$ (7)

where μ_xn, σ_xn, $x_n^{\mathit{\text{true}}}$ are the sample mean, sample standard deviation and true value of a kinetic parameter x at the n^th voxel. The linear Pearson correlation coefficient ρ(x_n, y_n) is computed for any two kinetic parameters x and y at the n^th voxel for each tumor type. The correlation coefficient is obtained by dividing the sample covariance of the two variables by the product of their sample standard deviations.

2.3.3. ROI-averaging

The kinetic parameters estimated from a single voxel inevitably have some statistical variation due to the noise in the dynamic data. To reduce noise, two ROI-average approaches are used. The first approach is called “estimate-and-average”. That is, the kinetic parameters are first estimated for each voxel, then a ROI is selected for voxels having similar kinetic parameters, and the average kinetic parameters are obtained over the ROI. The second approach is called “average-and-estimate”, where the TAC of the tumor region is first averaged over a pre-selected ROI, and then Voxulus is used to estimate the ROI TAC kinetic parameters. In clinical settings, the “estimate-and-average” approach would probably be preferred over the “average-and-estimate” approach, since averaging the ROI is easy to implement for the first approach when the kinetic parameters are already estimated. To investigate the stability of both ROI-average approaches, ROIs of different size are selected over the hypoxic tumor region, and the %bias and %stddev are then computed for each approach from these 1000 noisy samples. That is, the ROI %bias and %stddev are computed for each k₁, k₂, β, k₃ and K_i, as a function of ROI size for both approaches. Similarly, the %bias and %stddev are computed from the ROI TAC from the noisy dynamic dataset with respect to the true TAC. For the ROI TAC, the %bias and %stddev also depend on the dynamic frame. A late-time frame is used as the reference when reporting the statistics in the dynamic dataset and ROI TAC.

2.3.4. Impact of peak-to-tail ratio in input function

In clinical head-and-neck FMISO studies, the image-based input function method is used and the input region is selected from the carotid artery. The bolus injection speed affects the peak-to-tail ratio of the input function. The intensity threshold of voxels used in image-based input function also affects the peak-to-tail ratio of the input function. To investigate this effect, different peak-to-tail ratios of the input function are simulated, and the %stddev of various kinetic parameters is computed and compared with different sets of input function.

2.3.5. Impact of distortions in input function

To investigate how distortions in the input function affect the kinetic parameter estimation, a shift error is introduced in peak amplitude and peak location in time of the plasma input function, respectively, in the absence of noise. The %bias of various kinetic parameters is then computed.

3. Results

3.1. Mathematical phantom simulation

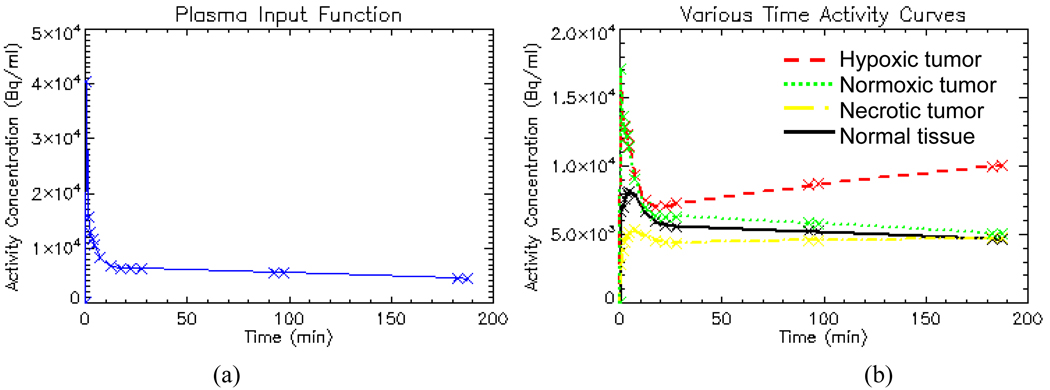
The simulated dynamic dataset consists of 14 frames with start acquisition time {0, 1, 2, 3, 4, 5, 10, 15, 20, 25, 90, 95, 180 and 185} minutes, respectively, where the first five frames have 1 minute duration time, and the rest frames have 5 minutes duration time. Figure 5 displays the dynamic images at multiple frames and their mid-frame acquisition time. The number of frames, acquisition time and duration time for each frame are selected from our FMISO head-and-neck cancer patient protocol. The plasma input function was simulated with {A₀=3.66e+5 Bq/(ml·min), C₀=3.42 1/min, N=2, A₁=2e+4 Bq/ml, C₁₁=0.21 1/min, C₂₁=1.2 1/min, A₂=7e+3 Bq/ml, C₁₂=2.4e-3 1/min, C₂₂=0.12 1/min}, with its TAC shown in figure 6(a). The kinetic parameters for three tumor regions and background normal tissue region are shown in table 1, with their respective TACs shown in figure 6(b).

Figure 6.

Simulated noise-free plasma input function (a) and noise-free time-activity-curves for various tissue regions (b).

Table 1.

True kinetic parameters for simulated image dataset.

	Hypoxic Tumor	Necrotic Tumor	Normoxic Tumor	Normal Tissue
k1 (1/min)	0.30	0.09	0.30	0.15
k2 (1/min)	0.45	0.15	0.45	0.20
k3 (1/min)	8e-3	3e-3	1e-3	1e-3
β	0.3	0.03	0.3	0.1
Ki (1/min)	5.24e-3	1.76e-3	6.65e-4	7.46e-4

3.2. Noiseless and noisy cases

Without noise, the estimated input function parameters and kinetic parameters match the true values exactly.

After adding Gaussian noise (c=150 in (6)), at a level equivalent to that observed in typical clinical FMISO PET data acquired on GE Discovery STE scanner with axial septa, the stddev of the activity concentration in each voxel in the hypoxic tumor region at late dynamic frame is approximately 15%. Table 2 shows the %bias and %stddev for a single voxel centered in each of three tumor regions and the background normal tissue region respectively with LS estimations. All kinetic parameters have less than 5 %bias, except that β has 28.2 %bias in the necrotic tumor region where it has very small true value of 0.03. In the hypoxic and necrotic tumor regions with high k₃ true value (0.008 and 0.003), the k₃ has comparable %stddev (13.5 and 15.9) with k₁ and k₂, but larger %stddev of 42.9 in normoxic tumor and 35.0 in normal tissue regions, where their true values are small (both are 0.001). In regions of hypoxic and normoxic tumors with high β true value of 0.3, its %stddev is 28; in the background normal tissue region with medium β true value of 0.1, its %stddev is 43.9; while in the necrotic tumor region with small β true value of 0.3, its %stddev is 81.8. Table 3 shows the correlation coefficient of various kinetic parameters for a single voxel centered in each of three tumor regions and the background normal tissue region respectively. We noticed that k₁ and k₂ are highly correlated; and both are negatively correlated with β; while k₃ has little correlation with k₁, k₂ or β.

Table 2.

% bias and % stddev at a single voxel in various tissue regions for 1000 noisy samples with LS estimation.

LS		% Bias	% Stddev
	k1 (1/min)	1.97	21.4
Hypoxic Tumor	k2 (1/min)	1.01	15.7
	k3 (1/min)	0.97	13.5
	β	−1.13	27.9
	Ki (1/min)	0.19	6.30
	k1 (1/min)	−2.92	11.5
Necrotic Tumor	k2 (1/min)	−2.05	10.7
	k3 (1/min)	0.66	15.9
	β	28.2	81.8
	Ki (1/min)	−0.80	13.3
	k1 (1/min)	1.74	20.1
Normoxic Tumor	k2 (1/min)	1.10	14.9
	k3 (1/min)	0.56	42.9
	β	−1.04	28.2
	Ki (1/min)	−0.45	40.6
	k1 (1/min)	−1.32	13.0
Normal Tissue	k2 (1/min)	−0.91	10.3
	k3 (1/min)	0.79	35.0
	β	4.97	43.9
	Ki (1/min)	−0.65	32.6

Table 3.

Correlation coefficient at a single voxel in various tissue regions for 1000 noisy samples with LS estimation.

LS	ρ(k1, k2)	ρ(k1,k3)	ρ(k2, k3)	ρ(k1, β)	ρ(k2, β)	ρ(k3, β)	ρ(Ki, β)
Hypoxic Tumor	0.85	−0.47	−0.01	−0.80	−0.43	0.69	−0.27
Necrotic Tumor	0.92	0.02	0.28	−0.77	−0.56	0.09	−0.14
Normoxic Tumor	0.81	0.14	0.41	−0.78	−0.32	0.01	−0.26
Normal Tissue	0.91	0.04	0.27	−0.80	−0.54	0.03	−0.13

We observed that the influx rate constant $K_i=\frac{k_1{k}_3}{k_2+k_3}$ is potentially a more stable and direct hypoxia index than k₃. From the objective function of the pharmacokinetic model, it can be shown that K_i estimate is a linear function of the ROI’s activity concentration, but not k₃. Thus, K_i is less sensitive to noise than k₃, e.g., the %stddev of K_i in hypoxia tumor region is 6.3 and of k₃ is 13.5. K_i also has less correlation with β than k₃, e.g., the correlation coefficient of K_i in hypoxia tumor region is −0.27 and of k₃ is 0.69. Note that the physical interpretation of K_i denotes the rate constant for activity entering the trapped compartment from the plasma compartment directly (i.e., without traversing the reversible compartment). Also, if the plasma input function approaches zero at late-time, the total activity concentration in a ROI approaches $K_i{\displaystyle \underset{0}{\overset{\infty }{\int }}{C}_p(\tau )d\tau }$ .

3.3. Kinetic parameters as a function of ROI size

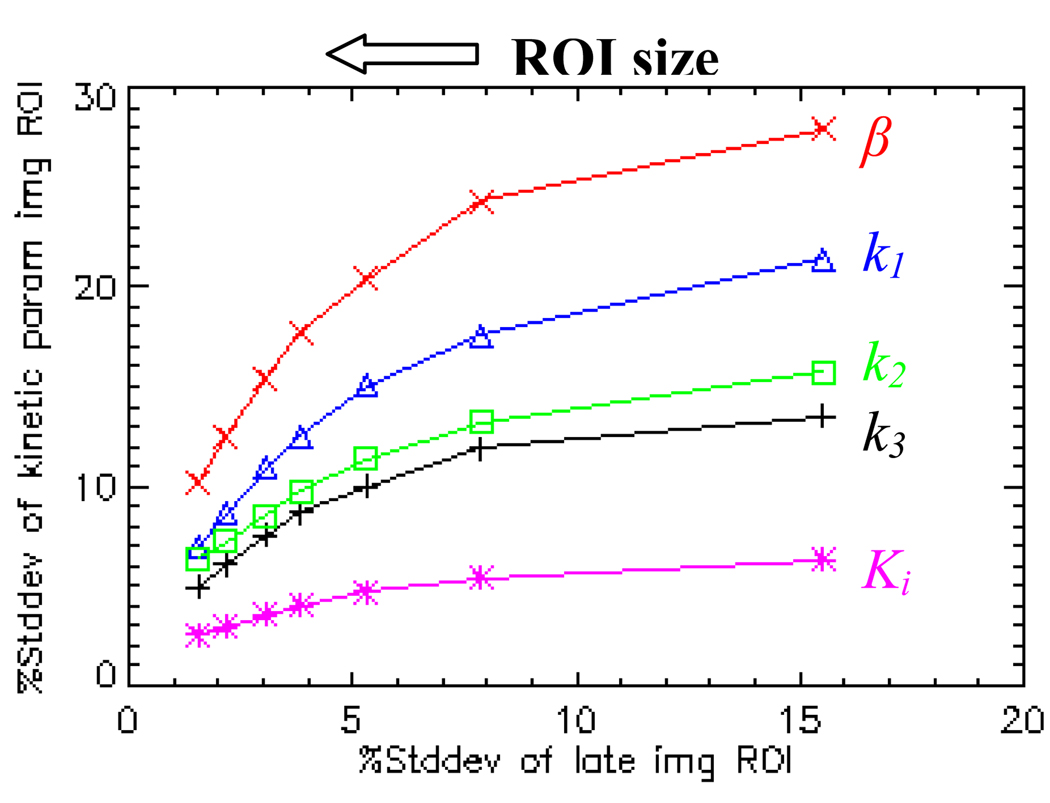
Seven sizes of ROI, 1, 4, 9, 16, 25, 50, and 100 voxels, were selected and centered on the hypoxic tumor region. Both “estimate-and-average” and “average-and-estimate” ROI %stddev were calculated for these 1000 noisy dynamic image samples and their corresponding kinetic parameter images. The ROI %bias for the late-time image and various kinetic parameters vary randomly within a small range (<2%) and are independent of the ROI size. Both the “estimate-and-average” and “average-and-estimate” give very similar result in ROI %stddev. Figure 7 displays the “estimate-and-average” ROI %stddev of various kinetic parameters (vertical axis) versus the ROI %stddev of the late-time image (horizontal axis) as a function of region size. The data points on each curve from right to left correspond to ROIs from small to large sizes. The ROI %stddevs of k₁, k₂, k₃, K_i and β decrease as the ROI size increases, but not as much as those of the late-time image. For example, increasing the size of the ROI from 1 voxel to 100 voxels, the ROI %stddev of the late-time image reduces by a factor of 10 (due to the approximate Poisson nature of the simulated image noise); while the ROI %stddev of various kinetic parameters reduces only by a factor of 2.5~3.0. Interestingly, the fact that both “estimate-and-average” and “average-and-estimate” give very similar ROI %stddev, suggests that at 15% low noise level, the pharmacokinetic model behaves like a linear operator. Thus it is acceptable to first estimate the voxelized kinetic parameter map, and then select ROI that contains similar kinetic parameter, and average the kinetic parameter over the ROI to reduce the statistical noise, i.e., using the “estimate-and-average” approach instead of the “average-and-estimate” approach.

Figure 7.

ROI %stddev of late-time image and various kinetic parameter images in hypoxic region as a function of ROI size for 1000 noisy samples with LS estimation. The curves from top to bottom are β (x), k₁ (Δ), k₂ (◻), k3 (+) and Ki (*), respectively.

3.4. Impact of peak-to-tail ratio in input function

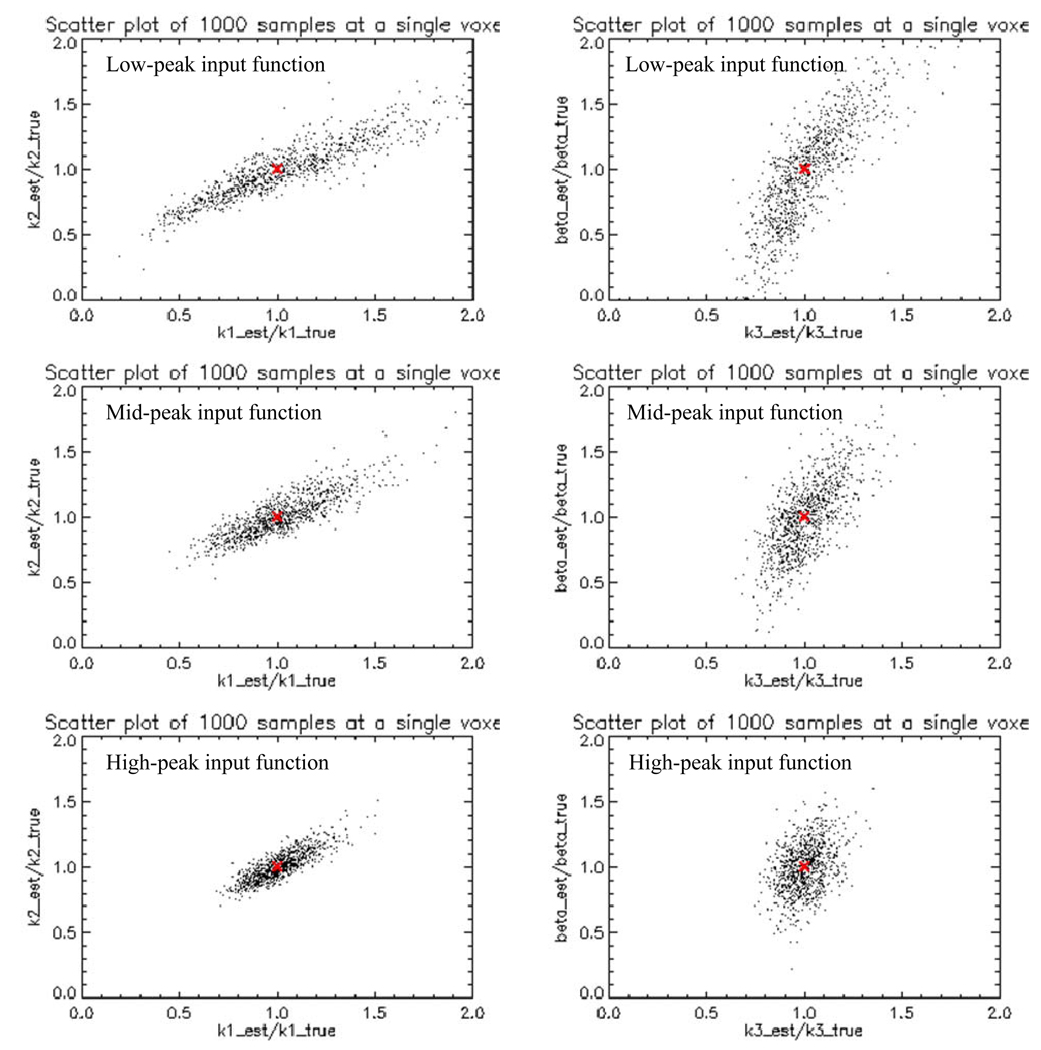
The peak-to-tail ratio of the input function listed in section 3.1 is 9:1, which corresponds to the median peak-to-tail ratio of the clinical input function. To simulate a low (4.5:1) and high (18:1) peak-to-tail ratio input function, A0=1.38e+5 Bq/(ml·min) and A0=8.04e+5 Bq/(ml·min) were used, respectively, where other input function parameters are the same as section 3.1. Similar dynamic images as figure 5 were simulated with the same kinetic parameter sets as shown in table 1. Figure 8 displays the noise-free TACs in the hypoxic tumor region for 3 different input functions. Despite their different height of peak at early-time, they have about the same tail height at late-time. Similar 1000 noisy samples of dynamic images were generated for both low and high peak input function at the same 15% noise level. Table 4 displays the %stddev of various kinetic parameters at a single voxel centered in the hypoxic tumor region from 1000 noisy samples with LS estimation for three input functions. The more peaked input function generates the more stable kinetic parameter estimation, e.g., the %stddev for k₃ are 20.4, 13.5 and 9.04 respectively for low, medium and high peak input function. Figure 9 shows the (k₁, k₂) (left column) and (k₃, β) (right column) scatter plots at a single voxel in the hypoxic tumor region from 1000 noisy samples for low, medium and high peak input functions (listed as the top, middle and bottom rows). Each point in the scatter plot corresponds to a noise realization. Thus there are 1000 points in each scatter plot. Each estimated kinetic parameter is displayed as a ratio of its true kinetic parameter. Thus point (1, 1) (indicated as the “+” sign) in each scatter plot corresponds to the true position of each pair of kinetic parameters. Despite the correlation between each parameter pair, the scatter plot spreads out more for the low peak input function, and becomes more clustered around the true position for the high peak input function. Therefore, it is preferable to use a fast bolus injection to create a high peak input function and set a high voxel intensity threshold to capture the high peak of the image-based input function.

Figure 8.

Hypoxic tumor noise-free time-activity-curves for low (dashed line), medium (solid line), and high (dotted line) peak-to-tail ratio input functions.

Table 4.

%stddev at a single voxel centered in the hypoxic tumor region for low, medium, and high peak input function from 1000 noisy samples with LS estimation.

%stddev	Low Peak-to-Tail (4.5:1)	Med Peak-to-Tail (9:1)	High Peak-to-Tail (18:1)
k1 (1/min)	36.6	21.4	12.6
k2 (1/min)	32.5	15.7	10.9
k3 (1/min)	20.4	13.5	9.04
β	40.9	27.9	18.5
Ki (1/min)	9.91	6.30	6.00

Figure 9.

Scatter plots of various estimated kinetic parameters centered at a single voxel in the hypoxic tumor region from 1000 noisy samples for different peak-height input function. Left column: k₁ versus k₂, right column: k₃ versus β. Top row: low-peak input function, middle row: medium-peak input function, bottom row: high-peak input function.

3.5. Impact of distortions in input function

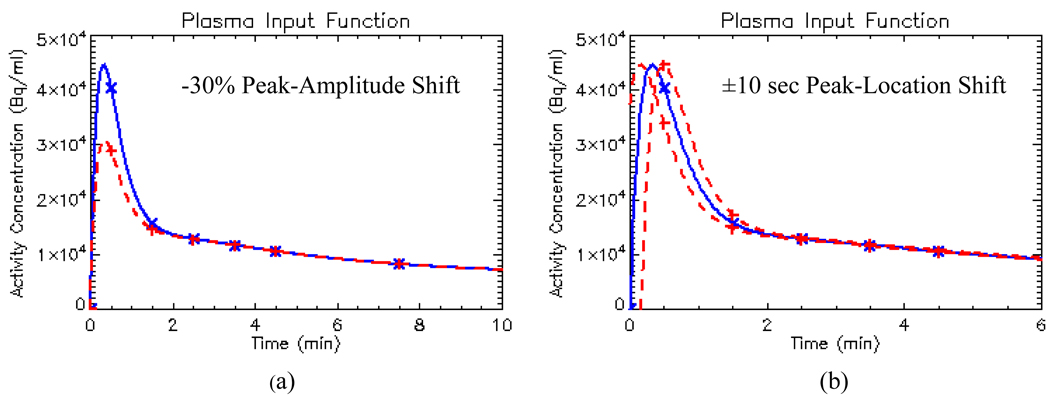
Various distortions in the plasma input function which were considered are shown in figure 10. Except the distorted input function, the same noise-free dynamic data set as section 3.1 were used, with the same true input function parameters and true kinetic parameters. Table 5 displays the %bias for various distortions at a single voxel centered in the hypoxic tumor region using LS estimation. Without noise, a 30% down-shift error in its peak-amplitude causes 18.8% bias on k₃ or 24.2% bias on K_i in the hypoxic tumor region. Note that in clinical PET imaging, a 30% contrast loss is quite common for high contrast fine structures, such as the carotid artery. However, due to the limited spatial resolution, over 100% contrast recovery is rarely seen in clinical PET imaging. Thus there was no up-shift error introduced in the peak-amplitude of the input function. In peak-location, a +10sec right shift overestimates the k₃ in the hypoxic region by 25.8% or underestimates the K_i by 17.1%; while the −10sec peak left shift only overestimates k₃ by 2.8% or underestimates K_i by 2.6%. This suggests that a “late” injection (i.e., starting the PET dynamic data acquisition earlier than bolus injection that delays the peak of the plasma input function) would over-estimate a hypoxic tumor more than an “early” injection. Fortunately, this situation is easy to correct in dynamic data analysis. We only need to shift the data to the right starting point. Therefore, capturing the correct peak-amplitude of the input function is more crucial in hypoxia imaging analysis than the peak-location.

Figure 10.

Illustration of various distortions in input function: (a) −30% peak amplitude shift; (b) ±10 sec peak location shift. The original input function is shown in solid line with “x’ sign, the shifted ones are shown with dashed line with “+” sign.

Table 5.

%bias at a single voxel centered in the hypoxic tumor region for −30% peak-amplitude shift and ±10sec peak-location shift in input function for LS estimation without any noise.

%Bias	−30% Peak Amplitude Shift	+10sec Peak Location Shift	−10sec Peak Location Shift
k1 (1/min)	15.7	−91.3	16.1
k2 (1/min)	42.4	−88.8	22.9
k3 (1/min)	18.8	25.8	2.8
β	53.0	105.3	21.4
Ki (1/min)	24.2	−17.1	−2.6

4. Conclusion and Discussion

Compartmental analysis of dynamic PET data is considerably more time-consuming than static imaging for the patient (requiring the patient to be scanned for up to 3-hours post-injection) and for the investigator performing the data processing. However, the advantage of utilizing the kinetic information at each voxel reduces the susceptibility to statistical variations and contrast changes for a tracer whose image contrast may be close to unity. The purpose of this paper is to determine the statistical accuracy and precision of the model-based kinetic analysis, which helps to validate this analysis and provides guidance in planning clinical dynamic FMISO-PET studies.

In this paper, we have conducted the validation and sensitivity analyses of the Philips Voxulus software’s implementation of an irreversible one-plasma two-tissue compartmental model for generating voxelized kinetic parametric maps of tumor hypoxia from dynamic FMISO PET studies. The analyses were performed by simulating a deterministic (i.e., with zero statistical noise) mathematical phantom with known plasma input function and various kinetic parametric tissue regions derived from actual clinical data. The noiseless kinetic parameter estimates matched their actual values exactly. We then tested its robustness for using a Gaussian-noise simulation comparable in dispersion to the actual clinical data. With 15% noise, the FMISO-trapping rate constant k₃ (whose value is presumably related to the presence of hypoxia) varied 13.5% in hypoxic region, at a level comparable to other kinetic parameters. Its magnitude of variation depends on the peak-to-tail ratio of the input function. A more peaked input function gave less variation in k₃. The plasma-to-diffusible tissue compartment and diffusible tissue compartment-to-plasma rate constants (k₁ and k₂, respectively) were highly correlated with each other, and both were negatively correlated with β (the ratio of tissue vasculature-to-input function); while k₃ exhibited little correlation with k₁, k₂ or β. We also observed that the influx rate constant $K_i=\frac{k_1{k}_3}{k_2+k_3}$ is potentially a more stable and direct hypoxia index than k₃.

In clinical PET imaging, photon counting noise is unavoidable. Values of kinetic parameters averaged over a multi-voxel ROI are thus preferable to single-voxel parameter values, however, important spatial information may be sacrificed. Two ROI averaging techniques were compared: “estimate-and-average” and “average-and-estimate”. We found that, at 15% low noise level, the Voxulus kinetic estimation can be approximated as a linear operator, since the statistics of the results of both approaches are equivalent to each other. Thus it is acceptable to use the more convenient “estimate-and-average” approach for easy selection of the averaging ROI. We also found that the variations of kinetic parameters reduce by increasing ROI size, but not as much as those of the late-time image, which implies that Voxulus kinetic estimation amplifies noise by a certain amount (about a factor of 3~4 at 15% noise level).

To further investigate how bias in the arterial input function affects the kinetic parameter estimation, a shift error was introduced in the peak-amplitude and peak-location of the input TAC. We found that capturing the correct peak-amplitude and the right injecting time of the input function are crucial in hypoxia imaging analysis.

All the kinetic parameter estimation algorithms used in this paper are LS. We found that LS is more stable than WLS in Voxulus. There are two LS/WLS fittings in Voxulus: one for the plasma input function and another for tissue/tumor TAC. The fitted plasma input function is then used as input for tissue/tumor TAC fitting. In WLS, the residual error at each time point is weighted by the reciprocal of the standard deviation of each measurement. For the plasma input function, the standard deviation of the peak measurement is higher than the tail. Thus, compared with LS, the WLS puts less weight in peak fitting than the tail fitting, which results in worse fitting at the peak of the plasma input function. For WLS estimation with data at 15% noise level, about 50 out of 1000 samples become outliners, i.e., the estimated input function does not match the measured one at all (under-fit at the peak and over-fit at the tail), and thus the estimated kinetic parameters for tumor TAC are way off from the true ones. Further, for those noisy samples with fitted input function matching the measured one, the WLS estimated C₂₁ parameter in the input function can be way off from the true one (under-fit at the peak, good-fit at the tail). Any error in fitting the plasma input function will propagate into the fitting of the kinetic parameters of the tumor TAC. Thus WLS was not used in this paper.

The phantom simulated in this work assumes a perfectly stationary tumor position, which may not be the case clinically. In corresponding clinical study, data were used from radiotherapy patients with head-and-neck cancers, in which the patients were rigidly immobilized for the PET scans in a custom face mask, so tumor motion was virtually eliminated. The plasma input function in this simulation work does not consider any partial volume effect, which in a clinical study, would be derived from an artery identified in the PET/CT image, since direct arterial sampling is generally avoided. It is preferable to collect data in the thorax or abdomen region, where a large volume of arterial blood pool (such as the left ventricle or abdominal aorta) can be found and partial volume effect can be reduced. The temporal sampling in this simulation work is coarse over the first 5-minute post-injection, which thereby under-samples the sharp peak of the input function in clinics. The availability of list-mode acquisition on PET scanners will allow optimum image frame times to be selected to satisfy adequate time sampling and adequate count statistics for future studies. Future work applying the Voxulus kinetic modeling tool to patient data is needed to demonstrate the feasibility of this approach. A test-re-test study of the same patient and bootstrap re-sampling of the list-mode dynamic data to derive multiple samples of the dynamic images is needed to confirm that the standard deviations of various kinetic parameters predicted from our analysis borne out in practice.