Dynamic, Nonlinear Feedback Regulation of Slow Pacemaking by A-Type Potassium Current in Ventral Tegmental Area Neurons

Abstract

We analyzed ionic currents that regulate pacemaking in dopaminergic neurons of the mouse ventral tegmental area by comparing voltage trajectories during spontaneous firing with ramp-evoked currents in voltage clamp. Most recordings were made in brain slice, with key experiments repeated using acutely dissociated neurons, which gave identical results. During spontaneous firing, net ionic current flowing between spikes was calculated from the time derivative of voltage multiplied by cell capacitance, signal-averaged over many firing cycles to enhance resolution. Net inward interspike current had a distinctive nonmonotonic shape, reaching a minimum (generally <1 pA) between −60 and −55 mV. Under voltage clamp, ramps over subthreshold voltages elicited a time- and voltage-dependent outward current that peaked near −55 mV. This current was undetectable with 5 mV/s ramps and increased steeply with depolarization rate over the range (10–50 mV/s) typical of natural pacemaking. Ramp-evoked subthreshold current was resistant to α-dendrotoxin, paxilline, apamin, and tetraethylammonium but sensitive to 4-aminopyridine and 0.5 mm Ba²⁺, consistent with A-type potassium current (I_A). Same-cell comparison of currents elicited by various ramp speeds with natural spontaneous depolarization showed how the steep dependence of I_A on depolarization rate results in small net inward currents during pacemaking. These results reveal a mechanism in which subthreshold I_A is near zero at steady state, but is engaged at depolarization rates >10 mV/s to act as a powerful, supralinear feedback element. This feedback mechanism explains how net ionic current can be constrained to <1–2 pA but reliably inward, thus enabling slow, regular firing.

Introduction

Many types of central neurons fire action potentials in a rhythmic manner in the absence of synaptic input. Such pacemaking activity occurs with a wide range of speeds in different types of neurons. Dopaminergic neurons of the ventral tegmental area (VTA) have intrinsic membrane properties that produce spontaneous firing at relatively low frequencies, typically 0.5–5 Hz (Johnson and North, 1992; Cameron et al., 1997; Neuhoff et al., 2002; Korotkova et al., 2003; Koyama et al., 2005; Margolis et al., 2006). The ionic mechanisms that enable stable firing at low frequencies in VTA and other pacemaking neurons in the mammalian brain are not well understood. In general, the ability to fire repetitively at low frequencies has been associated with the voltage-dependent potassium current known as A-type current (I_A), which activates and inactivates at subthreshold voltages (Connor and Stevens, 1971a,b; Rudy, 1988; Jerng et al., 2004). VTA neurons express prominent I_A (Koyama and Appel, 2006b), and in dopaminergic neurons of the substantia nigra, speed of pacemaking was found to be inversely correlated with I_A magnitude (Liss et al., 2001; Hahn et al., 2003, 2006). Thus, it is reasonable to suppose that I_A may play an important role in regulating firing of VTA neurons. However, the mechanism by which I_A influences firing rate (i.e., the time dependence and magnitude of I_A flowing between spikes) in VTA or other neurons is unclear and has been approached mainly by computer modeling (Connor and Stevens, 1971b; Gerber and Jakobsson, 1993; Rush and Rinzel, 1995; Xiao et al., 2004), with a lack of experimental data attempting to directly quantify flow of I_A during natural pacemaking.

In general, determining the role of individual conductances in controlling pacemaking is challenging, partly because of the small size of currents involved. Often the role of specific conductances in pacemaking is assessed by using pharmacological blockers in current-clamp recordings, but such results can be hard to interpret because changing one current generally causes indirect changes in other currents as a result of the altered voltage trajectory. Another approach is computer modeling, but this requires accurate kinetic models for multiple currents, which is especially difficult to accomplish for the small currents near threshold. We analyzed the conductances regulating pacemaking activity in dopaminergic neurons of the VTA using a different approach, taking advantage of the regularity of firing to signal-average interspike voltage trajectories, from which we could quantify the magnitude and voltage dependence of the net ionic current underlying pacemaking. Complementary experiments in voltage clamp, using voltage ramps at speeds similar to natural voltage trajectories, then distinguished individual components of subthreshold current based on time dependence, voltage dependence, and pharmacology. We found a dynamic component of outward current that activates at voltages as negative as −70 mV and has a complex time dependence and voltage dependence. This current, which could be identified as I_A, was unmeasurably small with very slow ramps (5 mV/s) but increased very steeply with ramp speed, making it a powerful, highly nonlinear negative feedback element to control pacemaking frequency.

Materials and Methods

Coronal brain slices containing the ventral tegmental area were prepared from postnatal day 14 (P14)–P30 transgenic mice in which enhanced green fluorescent protein (EGFP) is driven by the tyrosine hydroxylase (TH) promoter [the Tg(TH-EGFP)1Gsat Gene Expression Nervous System Atlas (GENSAT) line, obtained from the National Institutes of Health Mutant Mouse Regional Resource Center]. Animals were anesthetized with isoflurane and swiftly decapitated. Their brains were quickly removed and placed into an ice-cold sucrose slicing solution containing (in mm) 87 NaCl, 25 NaHCO₃, 1.25 NaH₂PO₄, 2.5 KCl, 7.5 MgCl₂, 75 sucrose, and 25 glucose, bubbled with 95/5% O₂/CO₂. Slices were cut using a vibratome (DSK model DTK-1000; Dosaka) and incubated for 1 h at 34°C, first for 30 min in slicing solution and then for 30 min in artificial CSF consisting of (in mm) 125 NaCl, 25 NaHCO₃, 1.25 NaH₂PO₄, 3.5 KCl, 1 MgCl₂, 2 CaCl₂, and 10 glucose, bubbled with 95/5% O₂/CO₂.

Slices were placed into a heated recording chamber (34 ± 1°C) and continuously perfused at a rate of 3 ml/min with a HEPES-buffered Tyrode's solution containing (in mm) 151 NaCl, 3.5 KCl, 2 CaCl₂, 1 MgCl₂, 10 glucose, and 10 HEPES, pH adjusted to 7.35 with NaOH. All recordings were made in the presence of blockers of fast synaptic transmission: 20 μm 6-cyano-7-nitroquinoxaline-2,3-dione (CNQX), 50 μm d,l-amino-5-phosphopentanoic acid (APV), and 100 μm picrotoxin. Dopaminergic neurons were identified as green fluorescent protein (GFP)-positive neurons using epifluorescence and a CCD camera (MTI) on a Nikon microscope (E600FN). Whole-cell current-clamp or voltage-clamp recordings were made with a Multiclamp 700B amplifier (Molecular Devices) using borosilicate patch electrodes (1–3 MΩ) wrapped with Parafilm to reduce pipette capacitance. Electrodes were filled with internal solution containing (in mm) 122 K-methanesulfonate, 9 NaCl, 1.8 MgCl₂, 4 Mg-ATP, 0.3 Na-GTP, 14 phosphocreatine, 0.45 EGTA, 0.1 CaCl₂, and 10 HEPES, pH adjusted to 7.35 with KOH.

Reported voltages are corrected for a liquid junction potential of −8 mV between the internal solution and the chamber solution, measured using a flowing 3 m KCl electrode as described by Neher (1992). Pipette series resistance (typically 4–8 MΩ) was compensated by 70–85% during voltage-clamp experiments and was checked frequently throughout the experiment; data were not used if series resistance changed by >15%. Current and voltage signals were filtered at 10 kHz and sampled at 20 μs using a Digidata 1322A data-acquisition interface (Molecular Devices) and pClamp 9 software (Molecular Devices).

After obtaining the seal and whole-cell configuration, the cells were perfused with HEPES-based extracellular solutions applied locally in the vicinity of the cell using a 700-μm-diameter quartz tube. Solutions were exchanged by switching between various solutions supplying this perfusion tube, which was heated by contact (∼9 cm) with a heated aluminum plate, controlled by a TC-344 (Warner Instruments) temperature controller. This system allowed relatively rapid solution changes with maintenance of a well-defined temperature. All experiments were done at a temperature of 34 ± 1°C.

During both current-clamp and voltage-clamp experiments, stable baseline values were obtained for 2–5 min before drug application. Experiments were aborted if significant drift was observed in baseline spike frequency or current amplitude. When solutions were prepared containing 4-aminopyridine (4-AP), pH was readjusted to 7.35 using HCl. In some experiments with 200 nm α-dendrotoxin, 1 mg/ml bovine serum albumin was added to reduce any binding of the toxin to the perfusion tube. Results with or without bovine serum albumin were indistinguishable.

Data analysis was done using pClamp9 and IgorPro version 4.06 (Wavemetrics), using DataAccess (Bruxton) to read pClamp files into Igor. In voltage-clamp experiments, capacitative transients were reduced by using electronic capacitance compensation in the amplifier circuit. For voltage protocols using step depolarizations, current records were corrected for small leak and remaining capacitative currents, using 5 or 10 mV hyperpolarizing or depolarizing steps (usually from −78 to −83 mV) to define linear capacitance and leak currents and then subtracting appropriately scaled currents for larger steps of voltage. For currents recorded using ramp voltage commands, current was plotted as a function of voltage and leak current was defined by a linear fit to current in the range from −78 to −70 mV, as shown in Figure 3B, and then subtracted as shown in Figure 3C. In cells in which nonlinear outward current began to activate at or below −70 mV, the fit for leak current was made over a slightly more negative range. In a few experiments, as noted in the Figure legends, 2 mm Cs⁺ was added to the external solution to block small currents from I_h that were sometimes present negative to −80 mV. This enabled more precise leak correction because background currents were more reliably linear over a wider voltage range. However, Cs⁺ was not used in most experiments because I_h was generally negligible positive to −80 mV. There was no apparent effect of Cs⁺ on the voltage dependence or magnitude of either step-evoked or ramp-evoked I_A, and statistics for current sizes used lumped values from experiments with or without 2 mm Cs⁺.

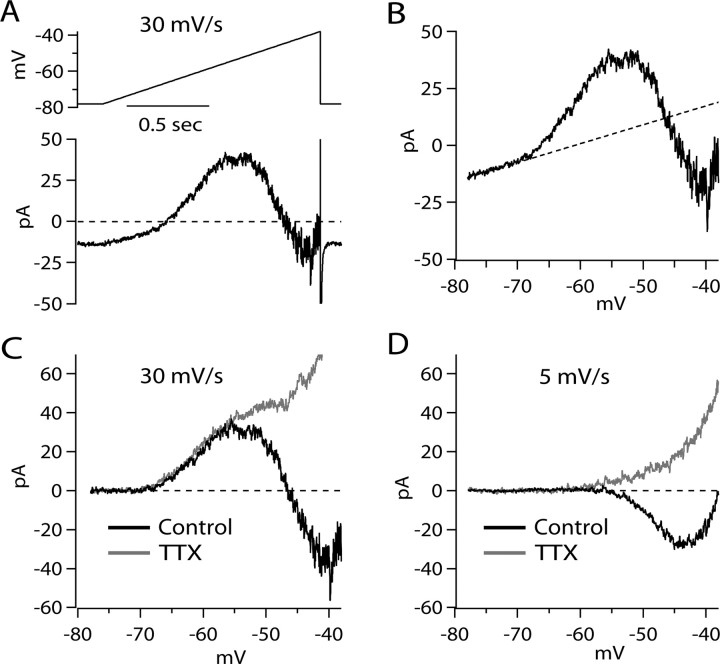
Figure 3.

Subthreshold currents evoked by slow voltage ramps. A, Raw current evoked by a 30 mV/s voltage ramp from −78 to −38 mV. B, Ramp-evoked current from A, plotted as a function of voltage. A fit-to-linear leak current between −78 and −70 mV is shown as a dotted line, extrapolated assuming ohmic behavior. C, Black trace, Ramp-evoked current corrected for linear leak current as determined in B. Gray trace, Same as the black trace, but after application of 300 nm TTX. D, Current–voltage relationship for current evoked by 5 mV/s ramp before and after application of 300 nm TTX (same cell as in A–C).

Interspike ionic current was calculated from −C × dV/dt, where C is the cell capacitance and dV/dt is the time derivative of the voltage during spontaneous firing. To increase resolution, voltage signals were signal-averaged over multiple cycles of firing (typically 40–100), aligning individual cycles at the spike peaks. The calculated ionic current was plotted as a function of voltage as in Figure 2C, and to further decrease noise, −C × dV/dt was averaged over bins corresponding to a 0.05 or 0.1 mV change in voltage.

Figure 2.

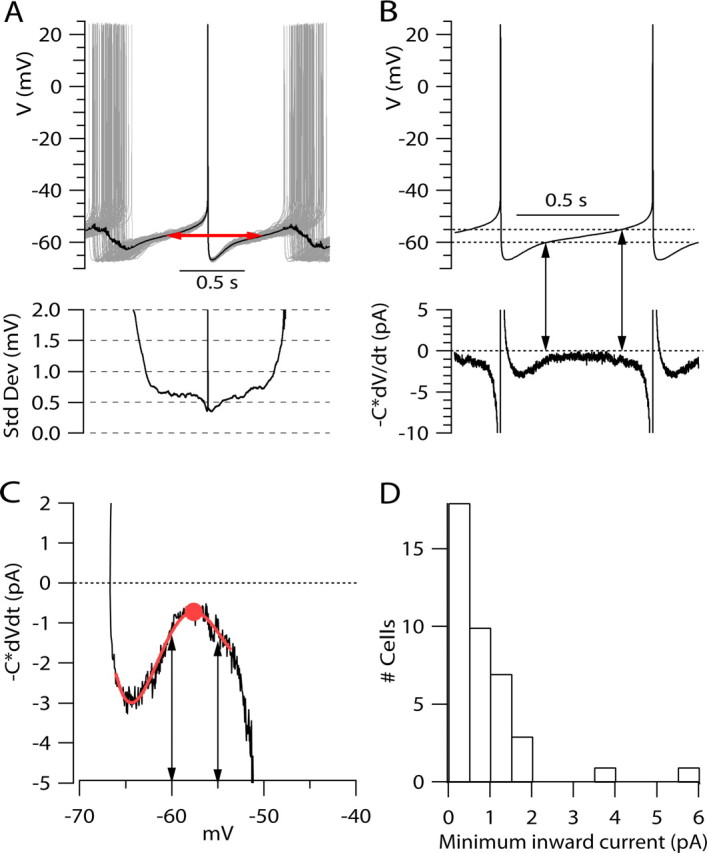
Analysis of net ionic current during the interspike interval from averaged voltage trajectories. A, One hundred successive spikes (gray traces) from a segment of spontaneous firing were aligned at their peaks and signal-averaged over a period (±950 ms from each peak) long enough to include preceding and succeeding spikes for each spike. Black trace shows the average. The red line with arrows indicates the segment of average voltage used for defining averaged voltage trajectory during the interspike interval. Bottom, SD of voltage calculated for each time point over the population of 100 traces aligned at spike peaks (same cell as Fig. 1). B, Top trace, Averaged voltage trajectory during the interspike interval defined from the signal-averaged trace in A. The unit cycle (defined by the red line in A) began and ended at the same voltage (−57.5 mV). The trace shown in B was formed by concatenation of the unit cycle, splicing together the beginning and ending points of the unit cycle; 1.6 cycles are shown. The dashed lines indicate −60 and −55 mV. Bottom trace, Net ionic current calculated from −C × dV/dt from the signal-averaged voltage trajectory. The trace was digitally filtered with a Gaussian function corresponding to a Bessel filter with corner frequency of 0.5 kHz. Cell capacitance was 61 pF. Vertical lines with arrows indicate times at which the interspike voltage crosses −60 mV and −55 mV levels. C, Net ionic current calculated from −C × dV/dt plotted as a function of voltage. Smooth red line, Fifth-order polynomial fit to the experimental record to allow better definition of the point at which minimum current is reached (solid red circle). Lines with arrows indicate −60 and −55 mV. D, Histogram of minimum inward current during the interspike interval (measured as in C) for 40 neurons.

Cell capacitance was measured by integrating capacitative transients from 5 or 10 mV steps given in the range between −78 and −68 mV. Capacitance values were obtained either by direct integration of uncompensated capacitative transients or from transients recorded with analog capacity compensation enabled on the amplifier, in which case the value of capacity used in the amplifier circuit to cancel the dominant fast component was summed with the integral of the remaining uncompensated slower components. The two procedures gave very similar results in cells in which both were compared.

For studies on acutely dissociated neurons, the ventral tegmental area was dissected from brain slices cut from P15–P18 Tg(TH-EGFP)1Gsat mice. Tissue was treated with 3 mg/ml protease XXIII (Sigma) for 10 min at 23°C in a solution consisting of (in mm) 82 Na₂SO₄, 30 K₂SO₄, 5 MgCl₂, 10 HEPES, and 10 glucose. After brief treatment with trypsin inhibitor (1 mg/ml), the tissue was stored in the same solution. Cells were isolated by gentle trituration, and dopaminergic VTA neurons were identified by EGFP fluorescence. Both current-clamp and voltage-clamp recordings were made at 34°C using the same internal and external solutions (except that synaptic blockers were omitted) and the same voltage protocols used for the slice recordings.

Statistics are given as mean ± SD, and statistical significance tests were done using nonparametric tests (Wilcoxon or Mann–Whitney).

Results

We recorded from dopaminergic neurons in the VTA in brain slices. To unambiguously identify dopaminergic neurons, all experiments were done using slices prepared from transgenic mice in which expression of EGFP is driven by the tyrosine hydroxylase promoter, generated as part of the GENSAT bacterial artificial chromosome project (Gong et al., 2003). We recorded from EGFP-expressing neurons located in the medial half of the VTA, away from the border of the VTA with the substantia nigra. Electrophysiological properties of the EGFP-expressing neurons were consistent with those reported previously for dopaminergic neurons in the VTA of wild-type mice (Ford et al., 2006), and we saw no differences in any properties or the health of cells from transgenic animals compared with our own recordings from presumptive dopaminergic neurons in the VTA of wild-type mice.

To focus on intrinsic membrane properties, all recordings were made in the presence of synaptic blockers (50 μm d-APV, 20 μm CNQX, and 100 μm picrotoxin). It has previously been described that there are subsets of principal dopaminergic neurons within the VTA with somewhat different electrophysiological properties (Wolfart et al., 2001; Neuhoff et al., 2002; Koyama et al., 2005; Ford et al., 2006; Lammel et al., 2008), which can be correlated to at least some extent with the brain regions to which they project (Ford et al., 2006; Lammel et al., 2008). Consistent with previous results using dissociated neurons (Koyama et al., 2005), we found that individual VTA neurons could show either regular or irregular spontaneous firing, even in the absence of fast synaptic input. Because our goal was to relate details of the voltage trajectory during pacemaking to currents in voltage clamp, we focused on neurons that showed regular firing, for which the voltage trajectory can be well defined by signal-averaging. These constituted the majority (∼75%) of all the neurons from which we recorded.

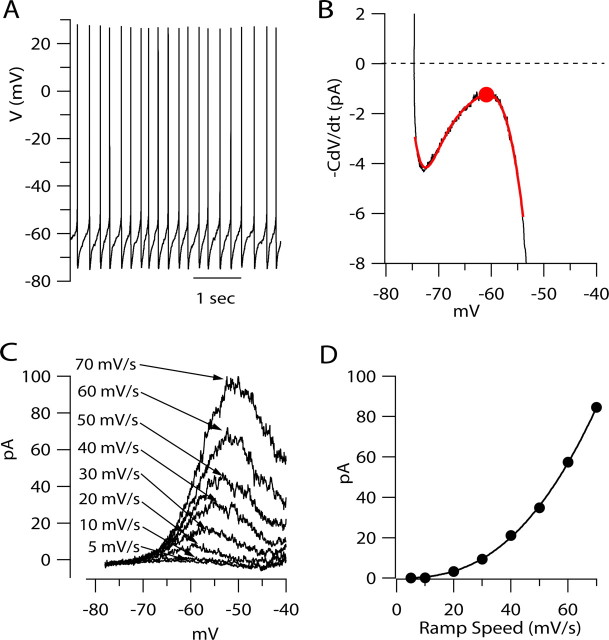
Figure 1A shows an example of spontaneous firing in a regular firing VTA neuron. The neuron fired at 1.3 Hz, and firing was highly rhythmic (Fig. 1A,B), with a coefficient of variation of 11% for the duration of interspike intervals. The firing rate of individual neurons varied from 0.5 to 6 Hz, with an average frequency of 2.1 ± 1.1 Hz (mean ± SD; n = 50) (Fig. 1C). The average coefficient of variation for interspike intervals was 13 ± 7% (mean ± SD; n = 50 cells). Action potentials had a width at half-maximum amplitude of 1.44 ± 0.31 ms (n = 50), in excellent agreement with previous recordings of principal dopaminergic neurons in the VTA at a similar temperature (Ford et al., 2006).

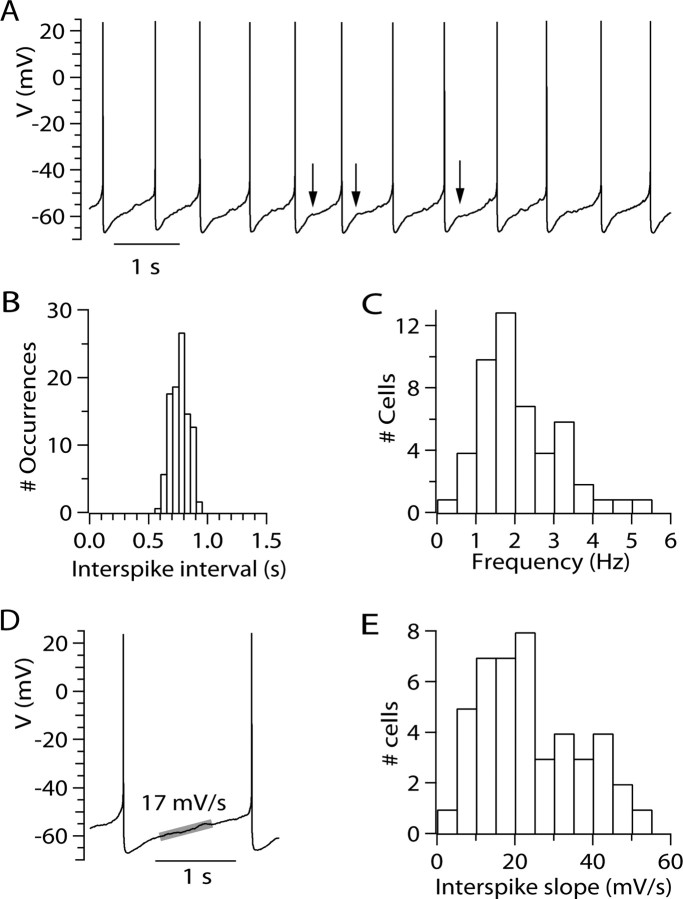
Figure 1.

Characteristics of pacemaking in VTA dopaminergic neurons. A, Spontaneous firing in a VTA dopaminergic neuron. Arrows indicate inflections in voltage trajectory consistent with voltage-dependent activation of outward current. B, Histogram of interspike intervals (over a 77 s period) for the cell whose firing is shown in A. C, Histogram of firing frequency for 50 VTA neurons. D, Trajectory of voltage during the interspike interval. Broad gray line shows fitted slope to the middle region of the interspike interval (fitted to the middle 40% of the interspike interval) for the first interspike interval in the record shown in A. E, Histogram of interspike slopes for 49 cells. The value for each cell was determined as the slope over the middle 40% of the interspike interval, for each cell averaged over 40–150 individual interspike intervals.

Figure 1D shows at higher resolution the voltage trajectory during the interspike interval of spontaneous firing in a typical VTA dopaminergic neuron. In this cell, which fired at 1.3 Hz, the most negative voltage reached after a spike was −67 mV, and the rate of spontaneous depolarization in the middle of the region between spikes was 17 mV/s. The rate of spontaneous depolarization during the interspike interval varied considerably from neuron to neuron, over a range from 5 to 100 mV/s, with an average rate of 29 ± 22 mV/s (measured in the middle 40% of the interspike interval; n = 49) (Fig. 1E).

In a neuron firing spontaneously without current injection, the spontaneous depolarization during the interspike interval results from flow of net inward ionic current, which depolarizes the voltage across the membrane capacitance. In the formalism introduced by Hodgkin et al. (1952), total membrane current can be divided into components of ionic current and capacitative current. In the absence of exogenously injected current, total membrane current is zero, so that net ionic current is equal and opposite to the capacitative current, C × dV/dt. Thus, by measuring the rate of interspike depolarization (dV/dt) and the membrane capacitance (C), it is possible to calculate the net ionic current flowing through the neuronal membrane during the spontaneous depolarization as −C × dV/dt. This simple calculation offers a powerful tool for quantifying the flow of ionic current during the interspike interval. During any individual interspike interval, the voltage trajectory is not completely smooth, and the calculated ionic current is very noisy at the picoampere scale. However, if the firing is sufficiently regular, it is possible to signal-average the voltage trajectory over many firing cycles to obtain better precision. Figure 2 illustrates the procedure for calculation of net ionic current during the interspike interval. From a record of spontaneous firing over 77 s (100 spikes), the average voltage trajectory between spikes was calculated by aligning individual spikes at their peaks and signal-averaging the voltage trajectories before and after the spike (Fig. 2A). Although there was some variability in each voltage trajectory, the SD of the voltage at each time relative to the spike (calculated over the population) was <1 mV for times less than half of the average interspike interval on either side of the spike. (This result was typical; in collected results for firing in 40 neurons, the SD of the voltage, measured at each end of a complete cycle of firing as in Fig. 2A, was on average 1.05 ± 0.36 mV.) The relatively small variability makes it seem reasonable to calculate an average voltage trajectory during a complete firing cycle, which we did by linking together signal-averaged hemicycles, one preceding and one succeeding the spike peak, each ending at the same voltage (limits are indicated in Fig. 2A, red line with arrows). Figure 2B shows the signal-averaged voltage trajectory for the complete cycle calculated in this way. From this, we calculated net ionic current at each time point from −C × dV/dt of the signal-averaged voltage (Fig. 2B, bottom trace). Although this calculation would be extremely noisy for any single cycle, the calculation from the signal-averaged voltage trajectory was smooth enough to give picoampere-level resolution. The calculation shows that the net inward current flowing during the interspike interval to drive pacemaking is remarkably small, amounting to <1.5 pA for most of the interspike interval. A large proportion of the total interspike interval is spent traversing the region of voltage from −60 to −55 mV, the part of the interspike interval where net inward current is smallest. Of the total interspike interval of 751 ms (spike peak to spike peak), 372 ms was spent depolarizing the membrane from −60 to −55 mV (Fig. 2B, arrows).

A useful view of ionic current flow during the interspike interval is provided by plotting ionic current (calculated from −C × dV/dt) as a function of voltage (Fig. 2C). In such plots, there was reliably a distinct concavity in the relationship between ionic current and membrane voltage, such that inward current reached a minimum between −60 and −55 mV. On average, the smallest inward current occurred at −58 ± 4 mV (n = 40) and varied from 0.1–6 pA in individual cells, with an average of 0.9 ± 1.0 pA (n = 40) (Fig. 2D).

To determine the types of ionic currents that contribute to net ionic current flow at subthreshold voltages, we recorded in voltage-clamp mode and elicited currents by voltage ramps delivered at rates similar to those typical of the spontaneous depolarization between spikes during pacemaking (Fig. 3). Figure 3A shows the total membrane current evoked by a depolarizing voltage ramp with a speed of 30 mV/s (chosen to be similar to a typical rate of spontaneous depolarization during the interspike interval). The ramp-evoked current was linear in the range from −78 to −70 mV, with a slope corresponding to an input resistance of 1.2 GΩ (on average, 0.95 ± 0.29 GΩ; n = 31). Positive to −70 mV, there were nonlinear components of the current–voltage relationship. These nonlinear components could be most clearly defined when the current–voltage relationship was corrected for the current corresponding to the linear background conductance (Fig. 3B). There were two components of nonlinear, voltage-dependent current evident (Fig. 3C): a low-threshold outward component of current that first activated between −70 and −65 mV and reached a peak near −55 mV, followed by an inward component that reached a peak near −40 mV. In collected results from 25 neurons, the low-threshold outward component of current evoked by ramps at 30 mV/s reached a maximum of 33 ± 15 pA at a voltage of −55 ± 2 mV. The voltage of peak outward current is very similar to the voltage of the minimum inward current value of the interspike −C × dV/dt concavity (Fig. 2C). The comparison suggests that the concavity results from active engagement of a voltage-dependent outward current.

Application of 300 nm TTX blocked the inward component of ramp-evoked current, suggesting that this component represents steady-state or persistent Na current. In the presence of TTX (Fig. 3C, gray trace), it was clear that the ramp-evoked outward current had two distinct phases: a low-threshold component that reached a plateau near −50 mV and a larger component that began to activate steeply near −45 mV.

To test whether the low-threshold component of outward current during 30 mV/s ramps is a true steady-state current, we tested very slow voltage ramps of 5 mV/s (Fig. 3D). We found that although the TTX-sensitive inward component was still present at slow ramp speeds, the low-threshold component of outward current was not. Instead, the total membrane current from −80 to approximately −55 mV was consistently either linear (most cells, as for that shown in Fig. 3) or, in a few cells, slightly inward. These results show that the low-threshold outward current is not a true steady-state current but rather an active current that is sensitive to the speed of depolarization. If there is any true steady-state nonlinear outward current at voltages negative to −55 mV, it is below the resolution possible in these experiments (limited by noise within traces, trace-to-trace variability and in some cells, a small voltage-dependent inward current). Based on the resolution in traces obtained with slow ramps of 5 mV/s in this and other cells, we can put an upper limit of ∼2 pA on any true steady-state voltage-dependent outward current in this voltage range.

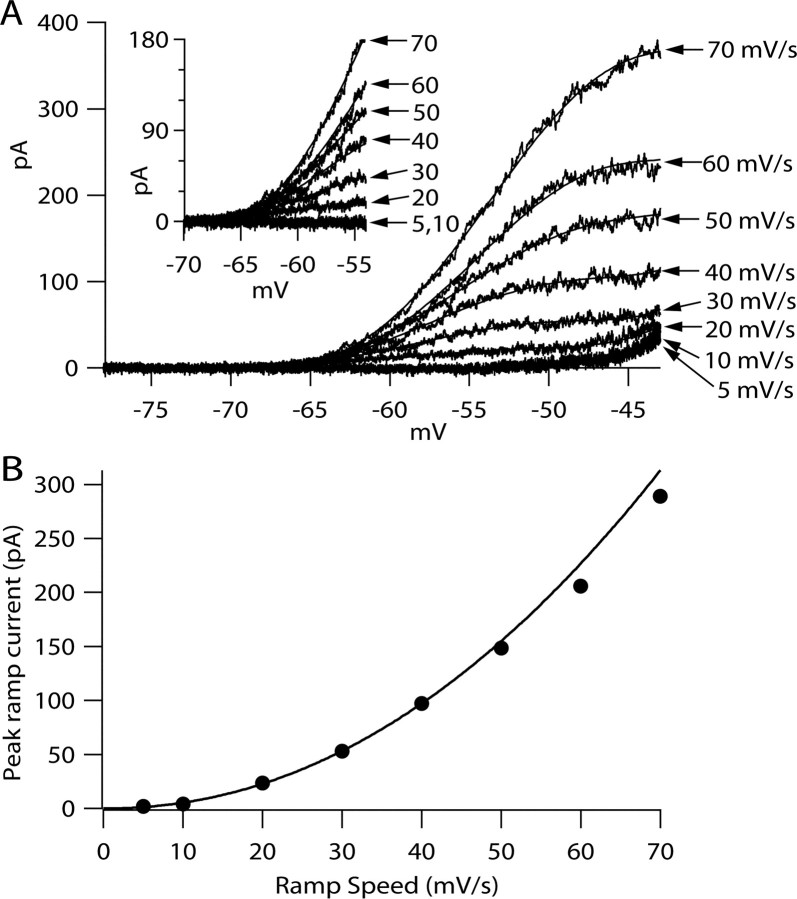
We next characterized the dependence of the low-threshold component of outward component on ramp speed over a range of speeds from 5 to 70 mV/s (Fig. 4). These experiments were done in the presence of 300 nm TTX to better isolate the component of nonlinear outward current. Ramps at 5 mV/s did not evoke clear nonlinear outward current below −55 mV. In most cells, the current evoked by ramps at 10 mV/s was barely detectably different from that evoked by 5 mV/s ramps, but 20 mV/s ramps always evoked clear nonlinear outward current. Low-threshold ramp-evoked current increased steeply with ramp speeds from 20 to 70 mV/s, amounting to an average of 13 ± 9 pA at 20 mV/s, 29 ± 20 pA at 30 mV/s, and 81 ± 46 pA at 60 mV/s (measured at −50 mV; n = 39). The highly nonlinear dependence of the low-threshold outward current on ramp speed was especially clear when the current was plotted as a function of ramp speed for each neuron. In the data from the cell shown in Figure 4, the relationship between 5 and 40 mV/s could be fit well with a power function with an exponent of 2.1 (Fig. 4B). In collected results from 31 neurons, the average exponent value was 2.6 ± 0.8. Thus, the low-threshold outward current in VTA dopaminergic neurons responds dynamically to changes in ramp speed by increasing in a highly supralinear manner.

Figure 4.

Nonlinear dependence of low-threshold outward current on ramp speed. A, Current–voltage relationship for current evoked by ramps delivered at speeds varying from 5 to 70 mV/s, measured in the presence of 300 nm TTX. Linear leak current was subtracted, using a linear fit to current between −78 and −70 mV to define leak. Traces are fit with seventh-order polynomial functions (solid lines). Inset, Current–voltage relationship for voltages from −70 to −54 mV shown at higher resolution. B, Ramp-evoked low-threshold outward current plotted against ramp speed. Peak low-threshold current was determined as maximum current between −70 and −50 mV. To reduce effect of noise, maximum was determined from the fitted seventh-order polynomial functions shown in A. Solid line, Fit to power function, f(x) = ax^b + c with a = 0.044, b = 2.10, and c = 0. The power function was fitted between 5 and 40 mV/s and extrapolated to higher values.

We next tested the pharmacology of the subthreshold outward current to determine what channel types contribute to it. Some voltage-activated potassium channels in the Kv1-family can activate at subthreshold voltages and strongly regulate firing. Such subthreshold Kv1-mediated current has been described in medium spiny striatal neurons (Shen et al., 2004), cerebellar Purkinje neurons (Khavandgar et al., 2005), hippocampal pyramidal neurons (Golding et al., 1999; Metz et al., 2007), and neocortical pyramidal neurons (Guan et al., 2007; Kole et al., 2007). In all of these cases, the current is blocked by α-dendrotoxin, which inhibits Kv1.1, Kv1.2, and Kv1.6-containing channels (Coetzee et al., 1999). We therefore tested 200 nm α-dendrotoxin on the ramp-evoked current. Dendrotoxin had little or no effect on the low-threshold component of ramp-evoked current (Fig. 5A). In collected results, current evoked by 60 mV/s ramps measured at −50 mV was reduced by 5 ± 13% by 200 nm α-dendrotoxin (n = 10). However, the effectiveness of the toxin was demonstrated by partial inhibition of the second phase of outward current flowing at voltages positive to −40 mV (Fig. 5A, inset) (outward current measured at −28 mV was reduced by 19 ± 9%; n = 5).

Figure 5.

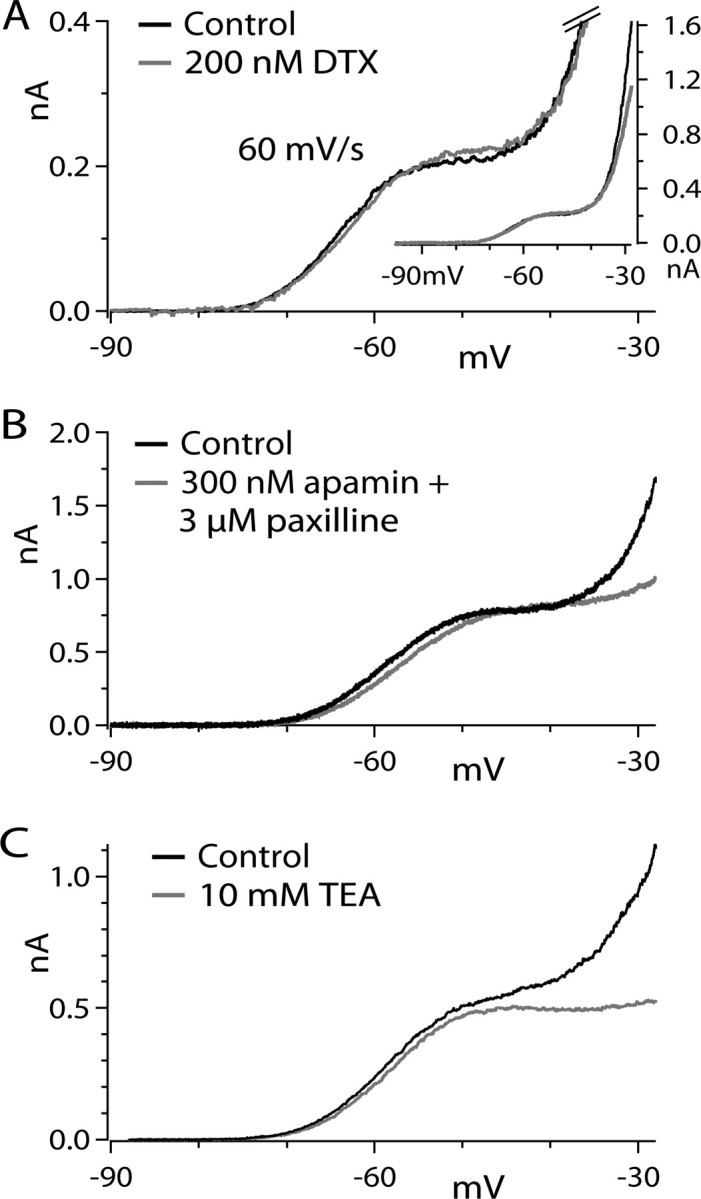
Pharmacology of ramp-evoked currents. A, Currents evoked by a 60 mV/s ramp from −98 to −28 mV before and after application of 200 nm α-dendrotoxin. Currents were recorded in 2 mm CsCl and 300 nm TTX. Currents are truncated at 400 pA to show low-threshold components more clearly. Inset, Currents shown at full scale to illustrate ∼25% inhibition of high-threshold component of the current. B, Currents evoked by a 60 mV/s ramp before and after application of 300 nm apamin plus 3 μm paxilline. Currents were recorded in 2 mm CsCl and 300 nm TTX. C, Currents evoked by a 60 mV/s ramp before and after application of 10 mm TEA. For all traces, linear leak current was subtracted, using a linear fit to current between −88 and −75 mV to define leak.

Another possibility is that the outward current represents calcium-activated potassium current. However, coapplying 300 nm apamin, a blocker of small conductance (SK) calcium-activated potassium currents, and 3 μm paxilline, a blocker of large conductance (BK) calcium-activated potassium currents, had very little effect on the subthreshold component of outward current (Fig. 5B), while substantially inhibiting higher-threshold current. In collected results, the combination of 300 nm apamin and 3 μm paxilline reduced ramp-evoked (60 mV/s) outward current measured at −50 mV by 7 ± 7% (n = 5) and reduced outward current measured at −28 mV by 40 ± 23% (n = 10). The results show that, although there is substantial calcium-activated potassium current present in the neurons, it contributes little or no current at subthreshold voltages during the voltage ramps.

We also tested the effect of 10 mm external tetraethylammonium (TEA), which inhibits a variety of potassium channels, including Kv1.1, Kv1.6, KCNQ, Kv3, and BK channels (Coetzee et al., 1999). TEA had little effect on the low-threshold component of ramp current (reduction by 9 ± 5% for current measured at −50 mV evoked by 60 mV/s ramp; n = 6) but dramatically reduced the higher-threshold component of outward current (reduction by 72 ± 19% of current measured at −28 mV; n = 8) (Fig. 5C).

The most obvious remaining possibility is that the low-threshold component of outward current represents A-type potassium current, which is prominent in VTA neurons (Koyama and Appel, 2006b) and can activate and inactivate over subthreshold voltages. Somatodendritic I_A in neurons is sensitive to 4-AP, with a typical half-blocking concentration of ∼1 mm (reviewed by Song, 2002; Jerng et al., 2004), and 4-AP is often used at millimolar concentrations to study functional roles of I_A in current-clamp experiments. We tested the effect of 10 mm 4-AP on step and ramp currents (Fig. 6). As expected from previous experiments testing 4-AP on I_A in VTA neurons (Koyama and Appel, 2006b), we found that 10 mm 4-AP effectively inhibited transient current elicited by step depolarizations (Fig. 6A). Peak current elicited by steps from −88 or −98 to −58 mV was inhibited by an average of 89 ± 4% (n = 4), consistent with a half-blocking concentration of 4-AP near 1 mm. In addition to inhibiting peak I_A, however, 4-AP appeared to slow its decay, so that current in 10 mm 4-AP was actually slightly larger than control after ∼300 ms. Similar “cross-over” of currents before and after 4-AP has been evident in previous experiments on cardiac and neuronal I_A (Thompson, 1982; Castle and Slawsky, 1993; Jackson and Bean, 2007), including in VTA neurons (Koyama and Appel, 2006b).

Figure 6.

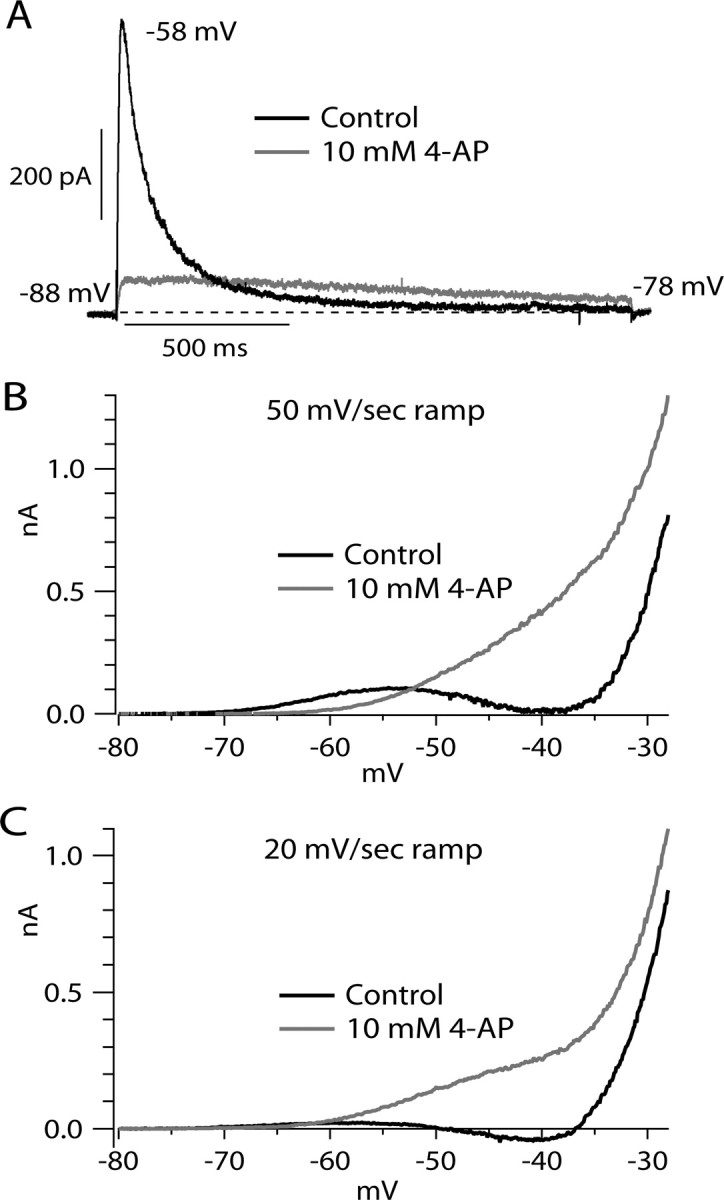
Effect of 4-AP on step- and ramp-evoked outward currents. A, Current evoked by voltage step from −88 to −58 mV before (black) and after (gray) application of 10 mm 4-AP. The dashed line indicates zero current. B, Current evoked by a 50 mV/s ramp before (black) and after (gray) application of 10 mm 4-AP. C, Same for currents evoked by 20 mV/s ramp (same cell). For traces in B and C, linear leak current was subtracted.

When studied with ramp-evoked currents, the most obvious effect of 4-AP was a dramatic enhancement of overall outward currents. Figure 6B shows an example of application of 10 mm 4-AP with a 50 mV/s ramp. In the presence of 10 mm 4-AP, the ramp-evoked current from −70 to −55 mV was inhibited, but there was a dramatic increase in the outward current evoked at voltages positive to −55 mV. Using ramps of 50 mV/s, there was on average a reduction of outward current at −58 mV by 81 ± 26% (n = 4) and an enhancement of outward current at −43 mV by 262 ± 284% (n = 6). With a ramp speed of 20 mV/s (Fig. 6C), there was less low-threshold outward current in control, and there was a less pronounced inhibitory effect of 4-AP on this current (although the inhibition was still present). However, there was a dramatic enhancement of the outward current positive to −60 mV, even more dramatic than with 50 mV/s ramps because the control current is so small with 20 mV/s ramps.

These effects of 4-AP are similar to those previously seen in acutely dissociated tuberomammillary nucleus neurons (Jackson and Bean, 2007), where they were interpreted as reflecting a state-dependent interaction of 4-AP with the channels underlying I_A, such that 4-AP binds tightly to closed channels but must unbind before channels can inactivate. According to this interpretation, the unbinding of toxin can produce a dramatic enhancement of current for some voltage protocols, especially slow depolarizations evoked by ramps.

The effectiveness of 4-AP in blocking the initial portion of the low-threshold ramp-evoked current is consistent with this current originating from I_A. However, the dramatic enhancement of the later portion of the low-threshold current obviously makes it impossible to isolate I_A by subtraction of traces before and after 4-AP. The mixed inhibition and enhancement also makes it virtually impossible to interpret the effects of 4-AP in current clamp. In fact, we found that 4-AP generally slows rather than speeds the spontaneous firing of VTA neurons (data not shown), suggesting that it produces a net enhancement of I_A during the interspike depolarization. Slowing of pacemaking by 4-AP was also seen previously in acutely dissociated histaminergic neurons of the tuberomammillary nucleus (Jackson and Bean, 2007). Thus, although 4-AP is generally considered to be an inhibitor of I_A, it may often have a net enhancing effect under physiological conditions, at least during pacemaking.

As a possible alternative to 4-AP as a blocker of I_A, we tested the effect of low concentrations of external Ba²⁺, which has been shown recently to block I_A in CA1 pyramidal neurons (Losonczy and Magee, 2006; Gasparini et al., 2007). Application of 0.5 mm Ba²⁺ reduced the peak of step-evoked transient I_A (Fig. 7A) by an average of 69 ± 11% (n = 10). Ba²⁺ inhibited the subthreshold ramp-evoked current with similar potency, reducing the low-threshold component of current elicited by a 60 mV/s ramp (Fig. 7B) by an average of 61 ± 10% (measured at −50 mV; n = 12). The nearly identical potency of Ba²⁺ on step-evoked and ramp-evoked current supports the idea that the ramp-evoked current is carried by the same I_A channels carrying the inactivating step-evoked current. Unlike 4-AP, Ba²⁺ reduced both step-evoked and ramp-evoked currents without changing their time dependence or voltage dependence. The lack of voltage dependence is consistent with Ba²⁺ inhibition of I_A in cardiac muscle cells (Shi et al., 2000).

Figure 7.

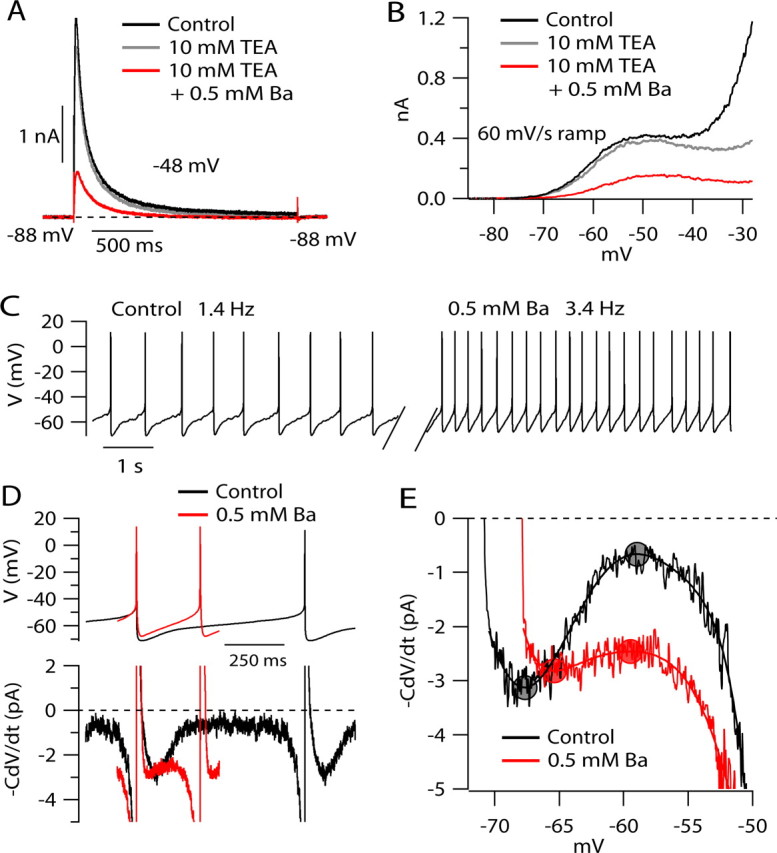
Effect of 0.5 mm Ba²⁺ on step- and ramp-evoked I_A and on net ionic current during the interspike voltage trajectory. A, Outward currents evoked by steps to −48 mV in control (black), after application of 10 mm TEA (gray), and in the presence of both TEA and 0.5 mm Ba²⁺ (red). Currents recorded in 300 nm TTX. B, Effect of TEA and Ba²⁺ on currents evoked by a 60 mV/s ramp. Currents were recorded in 300 nm TTX and were corrected for linear leak current. C, Effect of 0.5 mm Ba²⁺ on spontaneous firing. D, Effect of Ba²⁺ on net ionic current during the interspike interval, calculated from −C × dV/dt. Voltage trajectories were signal-averaged over 82 spikes in control and 102 spikes in the presence of 0.5 mm Ba. Net ionic current was calculated from −C × dV/dt and digitally filtered at 0.5 kHz. E, Net ionic current as a function of voltage in control and in the presence of 0.5 mm Ba. To measure maxima and minima for net ionic current in the interspike interval, the experimental record of −C × dV/dt in each condition was fit by a seventh-order polynomial, and the maxima and minima (filled circles) were determined from the fitted curve.

If the concavity in the plots of −CdV/dt versus voltage during the interspike interval results from activation of I_A, it should be reduced by application of 0.5 mm Ba²⁺. We therefore tested the effect of Ba²⁺ on the interspike current, as measured by −CdV/dt from a period of spontaneous firing. In the presence of 0.5 mm Ba²⁺, the rate of pacemaking increased dramatically (Fig. 7C), to an average of 355 ± 107% of control (1.02 ± 0.47 Hz in control, 3.33 ± 0.78 Hz in 0.5 mm Ba²⁺; n = 8). The increase in firing frequency produced by Ba²⁺ was accompanied by a striking change in the net ionic current calculated from −CdV/dt during the interspike interval (Fig. 7D,E). The inward current flowing immediately after a spike was similar in control and in the presence of Ba²⁺ (∼3 pA for the cell in Fig. 7C–E). However, in control the inward current then decreased to a minimum of 0.7 pA, corresponding to a long period for depolarization between −60 and −55 mV, whereas with Ba²⁺, the inward current decreased only a little during the interspike current, to a minimum of ∼2.5 pA, so that depolarization to threshold was much more rapid. These changes could be seen clearly when net ionic current was plotted as a function of voltage (Fig. 7E); the typical concavity was greatly reduced. In collected results, the minimum inward current during the interspike interval increased by an average of 742 ± 460%, from 0.66 ± 0.59 pA in control to 3.25 ± 2.68 pA in 0.5 mm Ba²⁺ (n = 8; p = 0.0078, nondirectional Wilcoxon test). To quantify the degree of concavity, we calculated the ratio of the minimum inward current to the maximal inward current reached shortly after the spike (Fig. 7E, filled circles). This ratio increased dramatically, from 0.16 ± 0.14 in control to 0.64 ± 0.19 after 0.5 mm Ba²⁺ (n = 8; p = 0.0078, nondirectional Wilcoxon test).

The effect of Ba²⁺ in greatly reducing the concavity of the net interspike ionic current is consistent with the hypothesis that this concavity results from activation of I_A. The loss of I_A during the interspike interval, and consequent increase in net inward current, will by itself speed the frequency of pacemaking by increasing dV/dt during the interspike interval. However, the speeding of firing by Ba²⁺ cannot necessarily be attributed to effects on I_A alone, because Ba²⁺ is also known to reduce other potassium currents, including resting potassium conductance mediated by two-pore domain weak inwardly rectifying K⁺ channel-related acid-sensitive K+ channel 1 (TASK) or TASK-like channels (Millar et al., 2000; De Jeu et al., 2002; Meuth et al., 2003). Consistent with this, we found that 0.5 mm Ba²⁺ increased the background or “leak” resistance of the cells. The input resistance of the neurons (measured in the range from −80 to −70 mV where the current–voltage relationship was ohmic) increased by an average of 26 ± 17% in the presence of 0.5 mm Ba²⁺ [from 1.2 ± 0.4 GΩ in control to 1.5 ± 0.5 GΩ (n = 6) in 0.5 mm Ba²⁺]. The effect on resting potassium conductance probably accounts, at least in part, for the effect of Ba²⁺ on the trough reached after a spike, which was shifted in the depolarizing direction by an average of 3.9 ± 1.4 mV (n = 8), from −71.8 ± 3.1 mV to −67.8 ± 3.5 mV. The effect on trough voltage might also reflect Ba²⁺ inhibition of potassium channels activated during the spike.

Although the overall effect of Ba²⁺ on firing frequency likely reflects actions on multiple types of potassium channels, reduction of I_A is likely to be a dominant element, based on the reduction of the concavity and dramatic increase of net inward ionic current during the interspike interval. For a different way of assessing the role of the subthreshold outward current mediated by I_A in regulating the rate of spontaneous firing, we took advantage of the cell-to-cell variability of firing rate to test whether there was a correlation between firing rate and the prominence of the dynamic outward current at subthreshold voltages. In these experiments, we first recorded spontaneous firing in current clamp and then did voltage-clamp experiments to explore the relationship between the voltage dependence of ramp-evoked current and the trajectory of the interspike voltage during spontaneous firing. The data in Figure 8, A and B, shows an example. In this neuron, which fired spontaneously at 1.3 Hz, the rate of interspike depolarization was 22 mV/s (measured in the central region of the interspike interval) (Fig. 8A). Figure 8B shows the subthreshold currents elicited by ramps delivered at speeds of 5, 10, 20, 30, or 40 mV/s in this neuron, recorded in the same physiological solutions used for current-clamp recordings, with no correction for leak conductance. As expected from the previous results, there were two components of nonlinear voltage-dependent current evident: an inward component corresponding to persistent sodium current, first evident positive to approximately −50 mV, and an outward component at more negative voltages, with the outward component showing a steep dependence on ramp speed. For ramp speeds of 5 or 10 mV/s, there was no obvious nonlinear outward component, and the net current was inward at all voltages. For the ramp at 20 mV/s, there was a small outward current, so that the total current was just below zero, approaching zero most closely near −60 mV. For the ramp at 30 mV/s, the outward current component was much larger, so that the net current was outward from −62 to −50 mV.

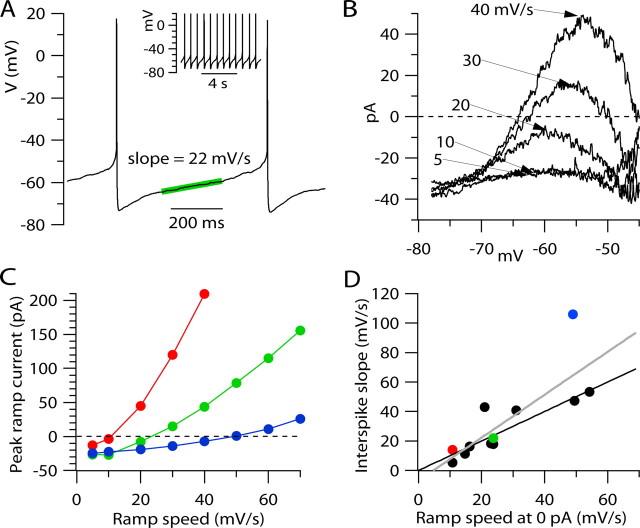
Figure 8.

Comparison between interspike depolarization during spontaneous firing and ramp-evoked currents in individual neurons. A, Interspike interval between two action potentials during spontaneous firing of VTA neuron. Green line, Linear fit to voltage trajectory during interspike interval in central region (30–70% of interval between spike peaks). Inset, Longer period of pacemaking in same neuron. B, Total membrane current evoked by ramps from −78 mV to −45 mV delivered at 5, 10, 20, 30, or 40 mV/s in same cell as in A, studied in voltage clamp. There was no correction for leak current. Current during the ramp is plotted as a function of ramp voltage (averaged in bins of 0.1 mV). C, Maximum (most positive) ramp current during ramps plotted against ramp speed. Each color indicates data from an individual cell (green corresponds to cell whose data are shown in A and B). D, Slope of interspike depolarization during current clamp (determined as in A) plotted against interpolated ramp speed at which current crosses 0 pA to become outward, determined from data as in C, for 12 individual neurons. Solid line, Slope of unity; gray line, linear fit (slope = 1.45; intercept = −6.73; linear correlation coefficient = 0.88; p = 0.003, Spearman rank correlation). Colored symbols correspond to cells shown in C.

This behavior in voltage-clamp seems well correlated with the speed of spontaneous depolarization during natural pacemaking in this neuron. Interpolating between the behavior during ramps delivered at 20 and 30 mV/s, it appears that the net ramp-evoked current would first cross zero to become outward with a ramp speed near ∼25 mV/s (Fig. 8C, green symbols), very close to the rate of natural spontaneous depolarization during the interspike interval. The different current–voltage relationships at different ramp speeds give a rationale for the natural interspike depolarization rate in this cell: it is the speed at which net ionic current barely remains net inward. Also, it is clear from the records that the differences in the current–voltage relationships for different ramp speeds is due almost entirely to the highly nonlinear behavior of the dynamic outward component of current from I_A, rather than changes in any other component of subthreshold current.

Figure 8C shows the maximum (i.e., most positive) current achieved as a function of ramp speed for three individual neurons. In each case, the net membrane current was below zero (inward) for ramp speeds of 5 and 10 mV/s, and increased steeply with more rapid ramp speeds. The steepness of the increase, and the magnitude of the outward currents, varied from cell to cell, so that the ramp speed at which net current crossed zero to become outward varied from ∼11 to ∼50 mVs among these three neurons. Figure 8D plots for 12 neurons the rate of interspike depolarization during spontaneous firing, measured in current clamp as in Figures 1D and 8A, as a function of the ramp speed at which net membrane current just became outward, determined from the zero-current intercept of voltage-clamp experiments as in Figure 8C. Although both values vary considerably from cell to cell, they showed a high degree of correlation. The most critical factor determining the ramp speed at which net current became outward was the steep dependence of the subthreshold outward component of current on ramp speed. Thus, this component of current appears to play an especially critical role in regulating the speed of interspike depolarization.

In our analysis, the calculation of ionic current from −C × dV/dt is precise in the case that the relevant areas of membrane are isopotential, so that changes in voltage (recorded at the cell body) reflect solely membrane ionic current rather than any axial current flow between adjacent compartments of the neuron. This may be a reasonable approximation for the slow changes in voltage during the interspike interval. In a study on dopaminergic neurons in the substantia nigra, Häusser et al. (1995) found that there is good isopotentiality over the dendritic tree for small voltage changes produced by current injection into the cell body, with <20% attenuation of the voltage change as far as 200 μm from the cell body, farther than the typical location of the initial segment of the axon (usually coming off a dendritic branch), where spike initiation occurs. Assuming that VTA neurons are not dramatically different, this suggests that the assumption of isopotentiality during the slow voltage changes of the interspike interval may be reasonable. Nevertheless, to more rigorously address this issue, we performed a series of experiments using acutely dissociated VTA neurons, in which isopotentiality is more certain.

We enzymatically dissociated neurons from the VTA region of P15–P18 mice and identified dopaminergic neurons by expression of EGFP. The isolated dopaminergic VTA neurons were almost always spontaneously active (Fig. 9A). The average firing rate was 4.9 ± 2.7 Hz (34°C; n = 9), faster than the average rate we measured in brain slice (2.1 ± 1.1 Hz). The faster firing of dissociated neurons might reflect loss of the dendritic tree if this acts as a net capacitative load. Average cell capacitance of dissociated neurons was 13 ± 6 pF (n = 14), compared with 54 ± 21 pF (n = 45) for cells in brain slice. Action potentials had a width at half-maximum amplitude of 1.4 ± 0.5 ms (n = 9), essentially identical to the brain slice recordings (1.4 ± 0.3 ms). As reported previously for VTA neurons isolated from rats (Koyama et al., 2005), the regularity of firing varied considerably from cell to cell, with an average coefficient of variation for interspike intervals of 26 ± 11% (mean ± SD; n = 9 cells).

Figure 9.

Nonmonotonic voltage dependence of net ionic current and subthreshold outward current in acutely dissociated VTA neurons. A, Spontaneous firing in a typical acutely dissociated VTA neuron (identified by EGFP fluorescence), recorded at 34°C. B, Net ionic current calculated from −C × dV/dt from the signal-averaged voltage trajectory during the interspike interval, plotted as a function of voltage (same cell as A). Smooth red line, Fifth-order polynomial fit to the experimental record, with point at which minimum current is reached (−61 mV) indicated by a solid red circle. Cell capacitance was 15 pF. C, Current–voltage relationship determined in voltage clamp (different cell than in A and B) for current evoked by ramps delivered at speeds varying from 5 to 70 mV/s, measured in the presence of 300 nm TTX and 10 mm TEA (34°C). No correction for leak current. D, Peak ramp-evoked low-threshold outward current plotted against ramp speed. Peak outward current between −70 and −50 mV was measured after correcting for linear leak as in Figure 3. Solid line, Fit to power function, f(x) = ax^b + c with a = 0.0016, b = 2.6, and c = 0. Power function was fitted between 5 and 40 mV/s and extrapolated to higher values.

The voltage range over which pacemaking occurred was very similar in dissociated neurons (average trough voltage, −68.2 ± 4.9 mV; average spike threshold, −37.9 ± 4.2 mV; n = 9) as in slice (average trough voltage, −67.7 ± 5.2 mV; average spike threshold, −41.1 ± 3.9 mV; n = 50). Figure 9B shows the net ionic current calculated from −C × dV/dt and plotted as a function of voltage for the cell whose spontaneous firing is shown in Figure 9A. The shape of net ionic current as a function of voltage during the interspike interval was essentially identical in isolated neurons as in slice recordings, with a distinct concavity such that inward current reached a minimum between −60 and −55 mV. On average, the smallest inward current occurred at −55 ± 5 mV (n = 9). The minimum in net inward current varied from 0.2 to 2.2 pA in individual cells, with an average of 1.0 ± 0.6 pA (n = 9). The degree of concavity, calculated as the ratio of the minimum inward current to the maximal inward current reached shortly after the spike, was 0.19 ± 0.17 (n = 9), very similar to the results from slice (0.16 ± 0.14; n = 8).

Voltage-clamp recordings of subthreshold I_A in dissociated neurons were also very similar to those in brain slice. Figure 9C shows ramp-evoked currents in a dissociated VTA neuron evoked by a series of ramps with speeds from 5 to 70 mV/s, recorded at 34°C (and in the presence of 300 nm TTX and 10 mm TEA to better define the component of subthreshold outward current). Ramps at 5 and 10 mV/s did not evoke clear nonlinear outward current, whereas ramps of 20 mV/s or faster evoked a substantial component of outward current in the range between −70 and −50 mV, with increasing amounts of current with faster ramps. The voltage dependence of low-threshold outward current was very similar as in slice recordings. For current evoked by ramps of 60 mV/s, current began to activate near −70 mV and (in the presence of TEA to block the higher-threshold current) reached a peak near −50 mV (Fig. 9C), essentially identical to the voltage dependence determined in slice recordings under the same conditions (Figs. 5C, 7B). When current was plotted as a function of ramp speed (Fig. 9D), the relationship for dissociated cells was highly nonlinear, with an average exponent of 2.5 ± 0.8 (n = 5), similar to slice recordings (2.6 ± 0.8). Thus, the behavior of the low-threshold outward current in dissociated VTA dopaminergic neurons was indistinguishable from that recorded in slice.

To our surprise, the magnitude of ramp-evoked subthreshold I_A was not dramatically less in dissociated cells than in intact cells in brain slice. The average magnitude of current evoked by a 60 mV/s ramp was 55 ± 35 pA (n = 5, measured at −50 mV in the presence of 300 nm TTX and 10 mm TEA) in dissociated neurons, compared with 64 ± 42 pA (n = 6) in brain slice recordings under the same conditions. When normalized to cell capacitance, the current density in dissociated cells was 5.6 ± 1.9 pA/pF (n = 5), substantially higher than in brain slice (2.2 ± 1.8 pA/pF; n = 6; p = 0.023, nondirectional Mann–Whitney test). The comparison suggests that I_A is expressed at higher density in the cell body than in the dendrites. This is consistent with the observations of Gentet and Williams (2007) in substantia nigra dopaminergic neurons, but opposite to CA1 hippocampal pyramidal neurons, where the density of I_A is higher in dendrites (Hoffman et al., 1997).

Discussion

Our results show that I_A flows at subthreshold voltages during voltage trajectories similar to normal pacemaking in VTA neurons and suggest that subthreshold I_A is an especially effective element for controlling pacemaking frequency because of its striking dependence on the rate of depolarization. I_A at subthreshold voltages is near zero in the steady state and, thus, does not interfere with depolarization to threshold for very slow rates of depolarization (e.g., 5 mV/s). However, the magnitude of subthreshold I_A increases very steeply with increasingly rapid rates of depolarization, especially in the range from 10 to 40 mV/s, rates typical of natural pacemaking. This steep increase provides a powerful negative feedback element to promote slow firing.

The analysis using current-clamp records shows that signal-averaging of voltage trajectories can be used to derive measurements of net ionic current at the sub-pA level. This technique should be generally useful for analyzing currents influencing pacemaking in a variety of neurons. By itself, the time and voltage dependence of net ionic current calculated from −C × dV/dt can only be suggestive of what current components are present. For example, the concavity of the current–voltage relationship in VTA neurons, with much smaller inward current between −60 and −55 mV than between −70 and −65 mV, could in principle result from voltage-dependent deactivation of an inward current such as I_h, rather than voltage-dependent activation of an outward current. However, complementary voltage-clamp experiments, which allow experimental variation of time and voltage dependence as well as pharmacological experiments more easily interpreted than in current clamp, can help identify components from specific channel types. In our experiments, the voltage-clamp results strongly suggest that the behavior of −C × dV/dt in current clamp represents dynamic activation of I_A, because the voltage-clamp experiments show that I_A is activated in exactly this voltage range, with no other active current components evident. It would be interesting to carry out a similar analysis in cells in which I_h plays a major role in pacemaking, such as thalamic relay neurons (McCormick and Pape, 1990) or a subset of dopaminergic neurons in the substantia nigra (Seutin et al., 2001; Neuhoff et al., 2002).

During natural firing, net inward ionic current typically reaches a local maximum of 3–5 pA near −65 mV, immediately after the spike. This is smaller than steady-state inward current near −65 mV, as determined by slow ramps, which is typically 10–30 pA (Figs. 3B, 8B,C, 9C). The difference likely reflects postspike potassium currents that are active during on-going spiking but not present during ramps (which start from a steady holding potential of −78 mV). Most likely, multiple voltage-dependent and calcium-activated potassium conductances are activated during spikes and then decay after the spike over tens of milliseconds. Some spike-activated conductances may decay slowly enough during the interspike interval to overlap with activation of I_A, and the decay of some (for example SK calcium-activated potassium current) might even be incomplete over the entire interspike interval. Such spike-evoked potassium currents will influence the net inward current during the interspike interval and thus influence pacemaking frequency. However, in all cases, their influence would be expected to decrease with time during the interspike interval, in contrast to the activation of I_A.

Other potassium currents able to be activated at subthreshold voltages, such as Kv1-mediated currents or M currents (known to be present in VTA neurons) (Koyama and Appel, 2006a), could be progressively activated during the interspike interval. These have relatively slow kinetics of activation and their activation would be minimal for fast rates of interspike depolarization and maximal for slow rates. This is opposite to the behavior of I_A and to the predominant component of subthreshold outward current in voltage clamp, and such currents would not have the feedback property of increasing with rate of depolarization. However, such currents might be activated and contribute to slowing interspike depolarization in cells in which depolarization is slowest, where interspike I_A is smallest. Blocking M current has inconsistent effects on pacemaking of VTA neurons, speeding firing in dissociated neurons but having no effect in brain slice (Koyama et al., 2007).

In previous recordings of I_A from neurons in the tuberomammillary nucleus, there was no detectable subthreshold outward current elicited by ramps at 20 mV/s (Jackson and Bean, 2007), but in VTA neurons this depolarization rate elicits a sizeable dynamic current attributable to I_A. Typical rates of interspike depolarization during natural pacemaking were faster in tuberomammillary neurons (65 ± 4 mV/s) (Jackson and Bean, 2007) compared with VTA neurons (29 ± 22 mV/s). Thus, it is plausible that the kinetic properties of I_A in different neurons are “tuned” to be appropriate for regulating different firing rates. Somatodendritic A-type channels are believed to be complexes of Kv4 pore-forming subunits with two types of accessory proteins, Kv-channel-interacting proteins and dipeptidyl-peptidase-like proteins (for review, see Jerng et al., 2004). The accessory subunits occur in multiple forms and can strongly influence gating kinetics, perhaps underlying such cell-specific tuning (An et al., 2000; Beck et al., 2002; Zagha et al., 2005; Barghaan et al., 2008). It would be interesting to relate the kinetic behavior of native currents in VTA neurons to specific channel subunits, as done recently for A-type channels in cerebellar granule neurons (Amarillo et al., 2008).

I_A is similar to voltage-dependent sodium current in that both are inactivating voltage-dependent currents that can produce small currents at subthreshold voltages as well as large transient currents for larger depolarizations. However, our results show that they differ in an important way, in that there is no measurable I_A at subthreshold voltages in the steady state. In contrast, subthreshold sodium current is present as a true steady-state current, regardless of how slowly ramps are presented (Fig. 2D) (Fleidervish and Gutnick, 1996; Raman and Bean, 1997). The steady-state current for sodium channels amounts to at least 0.5% of the peak transient current (Taddese and Bean, 2002) and is often much larger (Raman et al., 1997; Maurice et al., 2001; Ptak et al., 2005). If there were an equivalent amount of steady-state I_A, it would amount to 25–50 pA in a typical VTA neuron (with peak transient I_A of 10–20 nA for steps to −30 or −20 mV) (data not shown). Current of this magnitude was present when elicited by ramps of 20–70 mV/s but is clearly not present in the steady state (as defined by 5 mV/s ramps). We estimate an upper limit of ∼2 pA for any true steady-state I_A current below −55 mV, based on traces like those in Figures 3D, 4A, 8B, and 9C.

The lack of substantial steady-state I_A is also at odds with previous computer models of I_A that have been used to assess its role in slow repetitive firing. These models have used Hodgkin-Huxley-like equations based on independent activation and inactivation processes (Connor and Stevens, 1971b; Gerber and Jakobsson, 1993; Rush and Rinzel, 1995; Xiao et al., 2004) and have had overlapping steady-state activation and inactivation curves, thus predicting substantial steady-state I_A“window” current. For example, the model of Connor and Stevens (1971b) for I_A predicts steady-state I_A near −60 mV amounting to 4% of maximally activated current. Such a current in a VTA neuron would completely prevent spontaneous firing by producing a net steady-state outward current near −60 mV of greater than 200 pA when added to the background inward current of 10–30 pA at these voltages. Thus, the difference between the actual behavior of I_A in VTA neurons and that predicted by the models is highly significant functionally.

Recently, studies of gating kinetics of cloned Kv4 channels have led to Markov models with nonindependent activation and inactivation processes (Beck et al., 2002; Barghaan et al., 2008; Kaulin et al., 2008). These models resemble modern gating models of sodium channels, with inactivation allosterically coupled to activation. However, they differ from sodium channel models in having preferential closed-state inactivation, whereby inactivation is faster from pre-open closed states than from the open state (Bahring et al., 2001; Beck et al., 2002; Jackson and Bean, 2007; Barghaan et al., 2008; Kaulin et al., 2008). Preferential closed-state inactivation might result in minimal steady-state current if inactivation is sufficiently complete with subthreshold depolarizations. Our results suggest the importance of focusing on steady-state current in further modeling of I_A kinetics and in future experimental studies with particular combinations of cloned subunits.

A remarkable feature of pacemaking in VTA neurons is that the net inward current that drives spontaneous firing is on average only ∼1 pA in the middle of the interspike interval, less than the single-channel current for many types of channels. Our results help explain how it is that the sum of currents through all ion channels active at subthreshold voltages can be reliably regulated to be such a small inward net current, thus producing slow pacemaking. By acting as a dynamic element that adjusts its size in a highly nonlinear manner, the subthreshold current from I_A serves as a “governor” that can regulate net ionic current to be just barely inward, thus promoting slow but reliable pacemaking.