Abstract
The internal dynamics of proteins inside of cells may be affected by the crowded intracellular environments. Here, we test a novel approach to simulations of crowding, in which simulations in the absence of crowders are postprocessed to predict crowding effects, against the direct approach of simulations in the presence of crowders. The effects of crowding on the flap dynamics of HIV-1 protease predicted by the postprocessing approach are found to agree well with those calculated by the direct approach. The postprocessing approach presents distinct advantages over the direct approach in terms of accuracy and speed and is expected to have broad impact on atomistic simulations of macromolecular crowding.
Macromolecules occupy ∼30% of cytosolic volume, raising the possibility that dynamic properties of proteins inside of cells differ from those in dilute solutions.(1) Recent developments in NMR technology have allowed the probe of protein dynamics under crowded conditions(2) and inside of cells.3,4 The effects of crowding on internal dynamics(5) and on folding−unfolding transitions6,7 have also been studied by Brownian and molecular dynamics simulations. In these simulations, a protein molecule is placed inside of a box of crowders, and the motions of the protein and the crowders are followed simultaneously. Conformational sampling of the protein in the context of such large systems is particularly demanding. To lessen the demand, coarse-grained models are usually used in this “direct” approach to simulations of crowding.
Recently, we have proposed an alternative approach,(8) referred to here as “postprocessing”. In contrast to the direct approach, the motions of the protein and those of the crowders are followed in two separate simulations.(9) The effect of crowding is predicted by reweighting conformations sampled from the protein trajectory; the reweighting factor for each conformation is determined by the change in chemical potential if that conformation is fictitiously placed randomly inside of snapshots of the crowder trajectory. For the hard-core repulsions (e.g., as modeled by a r−12 type potential(5)) usually assumed between the protein and crowders, the change in chemical potential, Δμ, to a very good approximation is related to f, the fraction of successful placement via
where kB is Boltzmann’s constant and T is the absolute temperature. Then, the reweighting factor is just f. (Successful placement means that there is no volume overlap between the protein and any crowder.) An efficient algorithm for calculating f has been developed.(8) The postprocessing approach has been used to model effects of crowding on protein folding and binding stability, and its predictions are found to be supported by experimental results.8,10 However, it has not been tested against the direct approach.
Here, we report a test of the predictions of the postprocessing approach against simulation results of the direct approach for the effects of crowding on the flap open−closed transition of the HIV-1 protease homodimer (Figure 1). The flap dynamics is thought to be essential to enzyme function and has been subject to a large number of experimental and simulation studies.11−22 Results for the effect of crowding on the flap dynamics by the direct approach, using a Cα-only coarse-grained model, were published previously.(5) These direct simulations were extended in the present study in several ways. First, the simulation box side length was increased from 170 to 510 Å, allowing more crowders to be included in the simulation box. Second, more values, a total of eight, of the crowder volume fraction Φ, from 0.061 to just below the liquid−solid phase transition at Φ ≈ 0.496 (ref (23)) of the hard-sphere crowders, were studied (see Table 1). The simulations at each Φ were repeated six times with different random number seeds. In addition, we also carried out 42 independent simulations in the absence of crowders to allow for postprocessing. Each simulation was run for 21 μs, with the last 18 μs saved for analysis. For calculating the open fraction, the distance, r, between the flap tips, taken as the Gly51 residues of the two monomers, was saved every 200 ps. As before,(5) conformations with r < 10 Å were defined as closed and those with r ≥ 10 Å as open.
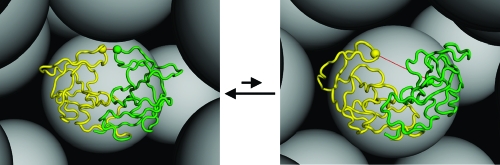
Figure 1.
Flap open−closed transitions of the HIV-1 protease dimer under crowded conditions. Open and closed conformations, displayed in the left and right panels, respectively, are monitored by the distance between the Gly51 residues (shown as balls) of the two monomers. The presence of the crowders (shown as gray spheres) shifts the open−closed equilibrium toward the latter.
Table 1. Input and Output Data of Direct and Postprocessing Approaches.
| direct
approach |
postprocessing
approach |
|||
|---|---|---|---|---|
| Φ | Na | po | Na | po |
| 0b | 0.19 ± 0.03 | 0.192 | ||
| 0.061 | 71 | 0.20 ± 0.02 | 535 | 0.190 |
| 0.122 | 143 | 0.21 ± 0.05 | 1078 | 0.187 |
| 0.183 | 215 | 0.24 ± 0.03 | 1621 | 0.183 |
| 0.245 | 287 | 0.19 ± 0.04 | 2164 | 0.178 |
| 0.306 | 359 | 0.22 ± 0.05 | 2707 | 0.171 |
| 0.367 | 431 | 0.17 ± 0.02 | 3249 | 0.162 |
| 0.429 | 503 | 0.13 ± 0.02 | 3792 | 0.148 |
| 0.490 | 575 | 0.15 ± 0.02 | 4334 | 0.131 |
Number of crowders. The radius of the crowders is 30 Å.
At Φ = 0, there is no difference between the direct and postprocessing approaches.
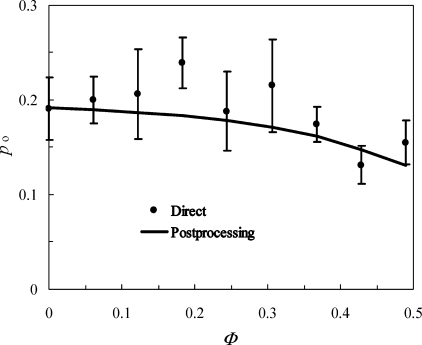
The open fraction, po, at each value of Φ is displayed in Figure 2 and listed in Table 1. The variation of po among the repeat simulations at each Φ is relatively large, but the average po clearly shows a decreasing trend with increasing Φ, changing from 0.20 ± 0.02 at Φ = 0.061 to 0.15 ± 0.02 at Φ = 0.490. Qualitatively, this trend is expected because the excluded volume of the crowders disproportionately penalizes the open conformations relative to the closed conformations. The open fractions reported here are somewhat different from those found previously.(5) Because a much larger simulation box was used here, the present results should be more reliable.
Figure 2.
Open fractions, po, calculated from the direct approach and predicted by the postprocessing approach. Φ is the crowder volume fraction.
From the simulations in the absence of crowders, protein conformations were saved every 100 ns for postprocessing. For each of these 42 × 180 conformations, say i, the fraction fi(Φ) of successful placements into a box of crowders at volume fraction Φ was obtained according to the previously developed algorithm.(8) The box used for postprocessing had a side length of 1000 Å, allowing for the number of crowders to be greater by a factor of (1000/510)3 = 7.5 than that in the direct simulations. In the direct simulations, the protein at each moment can only feel the presence of the small number of surrounding crowders. In contrast, in the postprocessing approach, the protein is randomly placed everywhere inside of the box of crowders. Averaging over the different locations inside of the crowder box leads to a significant gain in calculation statistics. The 7.5-fold increase in the number of crowders further accentuates the gain. As a result, only a small number of crowder configurations was sufficient for obtaining convergent results for fi;(8) 10 configurations were used here. Generation of these configurations followed our previous study.(8) The same radii of the crowders (30 Å) and the protein Cα atoms (7 Å) in the direct simulations were used for the postprocessing.
The postprocessing approach predicts the open fraction at the crowder volume fraction Φ as
where Ii(ri) = 1 when ri ≥ 10 Å and 0 otherwise. Note that the same simulations in the absence of crowders are used to predict the flap open fractions at different Φ values. For a given protein conformation, the state of the flap (open or closed) is fixed, but the reweighting factor fi(Φ) changes with Φ. In Figure 2, the open fractions predicted by the postprocessing approach are compared against the results from the direct simulations. It can be seen that they match over the whole range of crowder volume fractions studied.
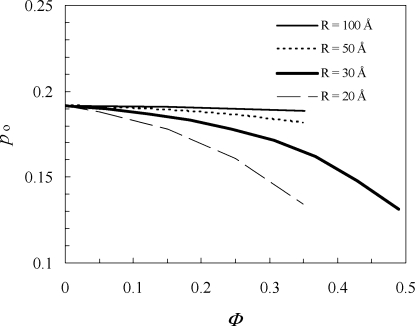
We also used the same simulations in the absence of crowders to predict the open fractions for other crowder sizes (Figure 3). At the same crowder volume fraction, the decrease in the open fraction by the presence of crowders becomes more significant as the crowder radius is reduced from 100 to 20 Å. This dependence on crowder size is in line with previous results for the effects of crowding on protein folding and binding stability.8,10 As noted previously, at the same volume fraction, the small voids left by small crowders are more discriminating (between the open and closed conformations in the present case) than the large voids left by large crowders. At a crowder radius of 100 Å, the open fraction is virtually unchanged up to a crowder volume fraction of 0.35. The last result provides an explanation for the recent experimental observation of Galiano et al.(18) that the presence of Ficoll400, a crowding agent with a Stokes radius of ∼100 Å, at a relatively low w/v percentage (6%) did not result in a discernible change in the distribution of the interflap distance.
Figure 3.
Open fractions in the presence of crowders with different radii (denoted by R).
On the other hand, our postprocessing approach predicts that the presence of a smaller crowder (e.g., with a 20 Å radius) at a high volume fraction would decrease the open fraction by several fold. Such an effect by crowding is of biological significance. In particular, a major effect of some drug-resistant mutations is to reduce the open fraction,11,19 also by several fold.(11) The implication is then that in vitro assessment(24) of potential drugs should account for macromolecular crowding in order to better predict their efficacies in the physiological setting.
The present study illustrates three distinct advantages of the postprocessing approach over the direct simulation approach. First, since the protein simulations are carried out in the absence of crowders, more exhaustive sampling and/or a more detailed representation, such as an all-atom model in explicit solvent, can be afforded for the protein. Without crowders, achieving convergent results for the flap dynamics by all-atom simulations in implicit solvent is already a challenge.(15) Adding crowders to the simulations would increase the challenge enormously. Second, the postprocessing approach uses the same simulations in the absence of crowders to predict the effects of crowding under different crowding conditions (e.g., with varying crowder sizes, shapes, concentrations, and mixing ratios). Third, in contrast to the direct approach, in which the protein at each moment can only feel the presence of the small number of crowders around it, the protein in the postprocessing approach is randomly placed everywhere inside of the box of crowders. Averaging over the different locations inside of the crowder box leads to a significant gain in calculation statistics. Consequently, only a relatively small number of crowder configurations are sufficient for obtaining convergent results.
While the present study is limited to a simple shape for the crowders and hard-core repulsions between the protein and crowders, the postprocessing approach can be generalized to atomistically represented crowders and more general types of protein−crowder interactions (Qin and Zhou, unpublished). These more realistic ingredients would present formidable computational challenges to direct simulations of protein−crowder mixtures. The postprocessing approach is expected to have broad impact on atomistic simulations of crowding, as it can be applied to the numerous molecular dynamics simulations already in the literature to predict crowding effects.
Acknowledgments
This work was supported by NIH, NSF, HHMI, CTBP, and NBCR.
Funding Statement
National Institutes of Health, United States
References
- Zhou H.-X.; Rivas G.; Minton A. P. Macromolecular Crowding and Confinement: Biochemical, Biophysical, and Potential Physiological Consequences. Annu. Rev. Biophys. 2008, 37, 375–397. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pielak G. J.; Li C.; Miklos A. C.; Schlesinger A. P.; Slade K. M.; Wang G. F.; Zigoneanu I. G. Protein Nuclear Magnetic Resonance under Physiological Conditions. Biochemistry 2009, 48, 226–234. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sakakibara D.; et al. Protein Structure Determination in Living Cells by In-Cell NMR Spectroscopy. Nature 2009, 458, 102–105. [DOI] [PubMed] [Google Scholar]
- Inomata K.; et al. High-Resolution Multi-Dimensional NMR Spectroscopy of Proteins in Human Cells. Nature 2009, 458, 106–109. [DOI] [PubMed] [Google Scholar]
- Minh D. D.; Chang C. E.; Trylska J.; Tozzini V.; McCammon J. A. The Influence of Macromolecular Crowding on HIV-1 Protease Internal Dynamics. J. Am. Chem. Soc. 2006, 128, 6006–6007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cheung M. S.; Klimov D.; Thirumalai D. Molecular Crowding Enhances Native State Stability and Refolding Rates of Globular Proteins. Proc. Natl. Acad. Sci. U.S.A. 2005, 102, 4753–4758. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stagg L.; Zhang S. Q.; Cheung M. S.; Wittung-Stafshede P. Molecular Crowding Enhances Native Structure and Stability of Alpha/Beta Protein Flavodoxin. Proc. Natl. Acad. Sci. U.S.A. 2007, 104, 18976–18981. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Qin S.; Zhou H.-X. Atomistic Modeling of Macromolecular Crowding Predicts Modest Increases in Protein Folding and Binding Stability. Biophys. J. 2009, 97, 12–19. [DOI] [PMC free article] [PubMed] [Google Scholar]
- It is noted that the postprocessing approach is similar in spirit to a model for accounting for the effects of osmolytes on protein folding stability, through simulations in the absence of osmolytes(O'Brien E. P.; Ziv G.; Haran G.; Brooks B. R.; Thirumalai D. Effects of Denaturants and Osmolytes on Proteins Are Accurately Predicted by the Molecular Transfer Model. Proc. Natl. Acad. Sci. U.S.A. 2008, 13403–13408). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Batra J.; Xu K.; Qin S.; Zhou H.-X. Effect of Macromolecular Crowding on Protein Binding Stability: Modest Stabilization and Significant Biological Consequences. Biophys. J. 2009, 97, 906–911. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chang C. E.; Shen T.; Trylska J.; Tozzini V.; McCammon J. A. Gated Binding of Ligands to HIV-1 Protease: Brownian Dynamics Simulations in a Coarse-Grained Model. Biophys. J. 2006, 90, 3880–3885. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hornak V.; Okur A.; Rizzo R. C.; Simmerling C. HIV-1 Protease Flaps Spontaneously Open and Reclose in Molecular Dynamics Simulations. Proc. Natl. Acad. Sci. U.S.A. 2006, 103, 915–920. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Trylska J.; Tozzini V.; Chang C. E.; McCammon J. A. HIV-1 Protease Substrate Binding and Product Release Pathways Explored with Coarse-Grained Molecular Dynamics. Biophys. J. 2007, 92, 4179–4187. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Galiano L.; Bonora M.; Fanucci G. E. Interflap Distances in HIV-1 Protease Determined by Pulsed EPR Measurements. J. Am. Chem. Soc. 2007, 129, 11004–11005. [DOI] [PubMed] [Google Scholar]
- Ding F.; Layten M.; Simmerling C. Solution Structure of HIV-1 Protease Flaps Probed by Comparison of Molecular Dynamics Simulation Ensembles and EPR Experiments. J. Am. Chem. Soc. 2008, 130, 7184–7185. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ishima R.; Louis J. M. A Diverse View of Protein Dynamics from NMR Studies of HIV-1 Protease Flaps. Proteins 2008, 70, 1408–1415. [DOI] [PubMed] [Google Scholar]
- Liu F.; Kovalevsky A. Y.; Tie Y.; Ghosh A. K.; Harrison R. W.; Weber I. T. Effect of Flap Mutations on Structure of HIV-1 Protease and Inhibition by Saquinavir and Darunavir. J. Mol. Biol. 2008, 381, 102–115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Galiano L.; Blackburn M. E.; Veloro A. M.; Bonora M.; Fanucci G. E. Solute Effects on Spin Labels at an Aqueous-Exposed Site in the Flap Region of HIV-1 Protease. J. Phys. Chem. B 2009, 113, 1673–1680. [DOI] [PubMed] [Google Scholar]
- Galiano L.; Ding F.; Veloro A. M.; Blackburn M. E.; Simmerling C.; Fanucci G. E. Drug Pressure Selected Mutations in HIV-1 Protease Alter Flap Conformations. J. Am. Chem. Soc. 2009, 131, 430–431. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blackburn M. E.; Veloro A. M.; Fanucci G. E.. Monitoring Inhibitor-Induced Conformational Population Shifts in HIV-1 Protease by Pulsed EPR Spectroscopy. Biochemistry 2009. [DOI] [PubMed] [Google Scholar]
- Lexa K. W.; Damm K. L.; Quintero J. J.; Gestwicki J. E.; Carlson H. A. Clarifying Allosteric Control of Flap Conformations in the 1TW7 Crystal Structure of HIV-1 Protease. Proteins 2009, 74, 872–880. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Torbeev V. Y.; Raghuraman H.; Mandal K.; Senapati S.; Perozo E.; Kent S. B. Dynamics Of “Flap” Structures in Three HIV-1 Protease/Inhibitor Complexes Probed by Total Chemical Synthesis and Pulse-EPR Spectroscopy. J. Am. Chem. Soc. 2009, 131, 884–885. [DOI] [PubMed] [Google Scholar]
- Hansen J. P.; McDonald I. R.. Theory of Simple Liquids, 2nd ed.; Academic Press: London, 1986. [Google Scholar]
- Altman M. D.; et al. HIV-1 Protease Inhibitors from Inverse Design in the Substrate Envelope Exhibit Subnanomolar Binding to Drug-Resistant Variants. J. Am. Chem. Soc. 2008, 130, 6099–6113. [DOI] [PMC free article] [PubMed] [Google Scholar]