Substrate Induced Population Shifts and Stochastic Gating in the PBCV-1 mRNA Capping Enzyme

Abstract

The 317 residue PBCV-1 mRNA capping enzyme catalyzes the second enzymatic reaction in the formation of an N-7-methyl-GMP cap on the 5′-end of the nascent mRNA. It is composed of two globular domains bound by a short flexible peptide linker, which have been shown to undergo opening and closing events. The small size and experimentally demonstrated domain mobility make the PBCV-1 capping enzyme an ideally suited model system to explore domain mobility in context of substrate binding. Here, we specifically address the following four questions: (1) How does substrate binding affect relative domain mobility: is the system better described by an induced fit or population shift mechanism? (2) What are the gross characteristics of a conformation capable of binding substrate? (3) Does “domain gating” of the active site affect the rate of substrate binding? (4) Does the magnitude of receptor conformational fluctuations confer substrate specificity by sterically occluding molecules of a particular size or geometry? We answer these questions using a combination of theory, Brownian dynamics, and molecular dynamics. Our results show that binding efficiency is a function of conformation but that isomerization between efficient and inefficient binding conformations does not impact the substrate association rate. Additionally, we show that conformational flexibility alone is insufficient to explain single stranded mRNA specificity. While our results are specific to the PBCV-1 mRNA capping enzyme, they provide a useful context within which the substrate binding behavior of similarly structured enzymes or proteins may be considered.

Introduction

An enzyme’s ability to change conformations in response to substrate binding is fundamentally important to efficient catalysis. For example, a number of enzymes (to name a few, adenylate kinase,(1) the PBCV-1 mRNA capping enzyme,(2) and DNA ligase(3)) have large accessory domains, which are covalently linked via short, flexible peptide hinges to their catalytic domains. When the enzyme binds substrate, these accessory domains close over the active site and provide a network of interactions that facilitate catalysis. The mRNA capping enzyme from the Paramecium bursaria Chlorella virus, PBCV-1, is a relatively small, 317 residue, GTP-dependent enzyme composed of two domains that are covalently linked via a flexible oligopeptide hinge. Crystal structures of the GTP-bound, or holo, form of the PBCV-1 mRNA capping enzyme show that the noncatalytic-accessory domain may undergo significant movement with respect to the catalytic domain during the catalytic cycle, moving from an “open” to a “closed” conformation (Figure 1).(2) The relatively small size of the capping enzyme and experimentally demonstrated mobility of the accessory domain make it an ideal model system to explore the functional importance of accessory domain mobility in the context of substrate binding. In this spirit, we explore the substrate binding behavior of the PBCV-1 mRNA capping enzyme using a combination of computational and theoretical approaches. While our results are specific to the capping enzyme, they provide a general context within which the substrate binding behavior of similarly structured enzymes and proteins may be considered.

Figure 1.

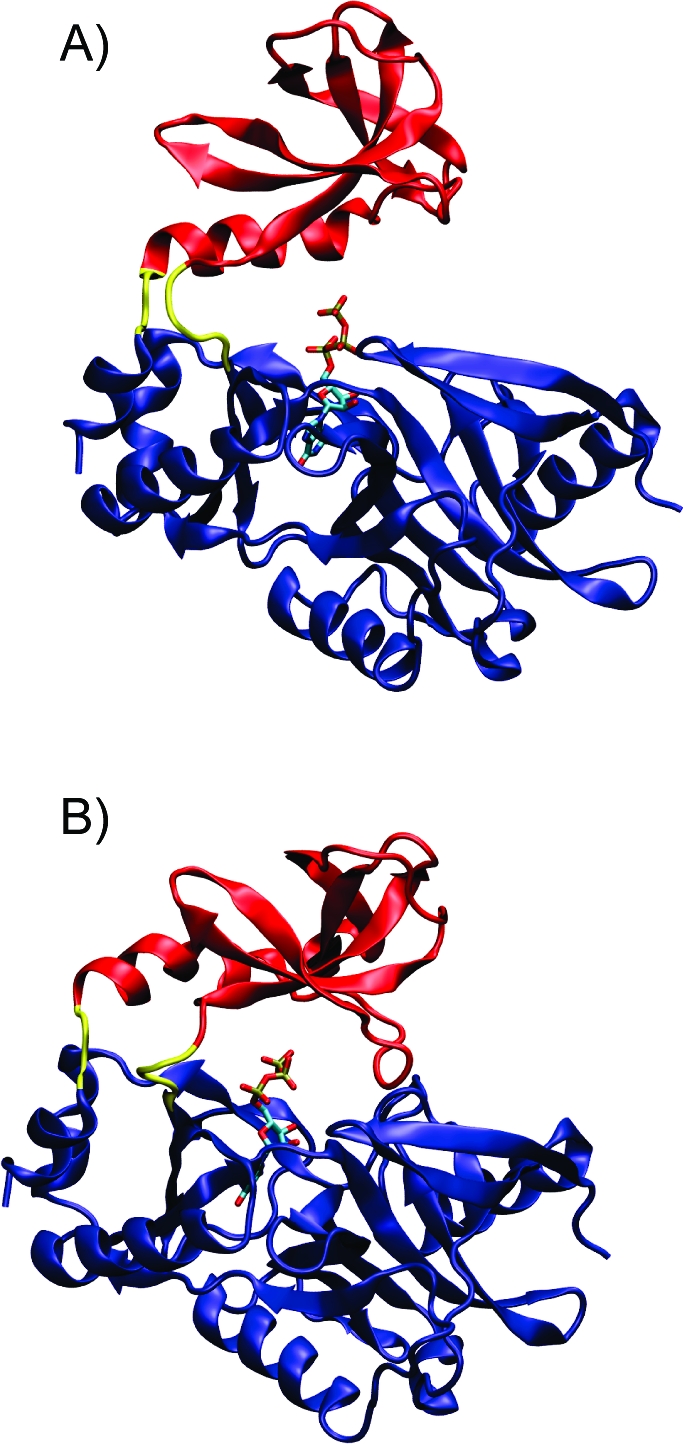
Quasirigid domain displacement: (A) Open crystal structure. The centers of mass of the OB domain (the noncatalytic-accessory domain), colored in red, and the nucleotidyltransferase domain (the catalytic domain), colored in blue, are separated by 30.3 Å. The hinge region is colored in yellow, and GTP is rendered in licorice and colored by atom type. (B) Closed crystal structure, coloring is as in (A). The centers of mass of the OB and nucleotidyltransferase domains are separated by 25.5 Å.

We begin by asking four questions regarding the varying functional roles that domain motion plays during substrate binding. We enumerate these four questions below, introducing them first in a general sense, which may be asked of any two domain, hinged protein, then in context of the PBCV-1 mRNA capping enzyme. We also introduce the methods that we have used to probe their answers.

(1) How does substrate binding lead to isomerization into a catalytically competent conformation? Two distinct models have been suggested to describe this phenomenon. In the first, proposed by Koshland in 1958 and called the induced fit model, the relationship between substrate binding and enzyme isomerization was explained by suggesting that a substrate-free, or apo, enzyme exists in a narrow range of conformations and that substrate binding compels enzyme reorganization into a conformation able to carry out catalysis.(4) The second proposed model makes use of contemporary notions of energy landscapes.^5,6 Called the pre-existing equilibrium, or population shift, model of substrate binding, this view suggests that the apo enzyme populates a range of conformations and that substrate binding stabilizes the lowest energy of these, thereby redistributing the pre-existing population.^7,8 In order to determine the model that better describes substrate binding by the PBCV-1 capping enzyme, we use molecular dynamics (MD) simulations to generate two conformational ensembles, one with GTP bound to the active site and one without GTP bound to the active site. By comparing the distribution of conformations in each state, the more suitable substrate binding model may be inferred.

(2) If the accessory domain populates a range of conformations and if the proximity of the accessory domain to the active site mediates the substrate’s access to the active site, what defines a binding competent conformation? Conceptually, this question is closely related to the concept of “domain gating”,⁹⁻¹¹ which draws an analogy between a hinged accessory domain and a gate. When the mobile-accessory domain prevents substrate binding, the gate is “closed”; the gate is “open” when substrate binding is allowed. Depending upon the specific protein−ligand, or enzyme−substrate system, different conformational requirements must be met before the gate can be considered open and the enzyme or protein can be considered in a “binding competent” conformation. In order to determine what defines a binding competent PBCV-1 mRNA capping enzyme conformation, we obtain and compare Brownian dynamics(12) association rates of GTP to two distinct apo conformations, which differ in the relative distance between the accessory and catalytic domains, that were generated during the MD simulations.

(3) If obtaining a binding competent conformation is a prerequisite of substrate binding, does the isomerization rate between binding competent and incompetent conformations affect the substrate association rate? This question was addressed by Szabo et al.,(9) who, extending the earlier work of Northrup and McCammon,(13) developed a general, quantitative method describing stochastically gated diffusional bimolecular association. This method predicts the effects of domain gating on the substrate binding rate in terms of two variables: the domain gating period, and the time required for the initial enzyme−substrate encounter complex to dissociate. Generally, the domain gating period will be tied to the underlying free energy surface along a reaction coordinate whose value describes the openness of the gate, while the time required for the enzyme−substrate encounter complex to dissociate is a function of the electrostatic interaction between the enzyme and the substrate and the translational diffusion coefficients of the enzyme and the substrate, which are roughly related to the average compactness of each molecule. Using a standard approximation of the time required for dissociation of the enzyme−substrate encounter complex and an analytic approximation of the domain gating period consistent with our MD results, we apply the Szabo model to evaluate the effects of gating on the GTP association rate.

(4) Do inherent conformational limitations confer substrate specificity by sterically occluding molecules of a certain size or shape from the active site? Fundamentally, this is a question of sterics and is closely related to the magnitude of receptor conformational fluctuations. For example, if the protein receptor does not sample conformations that accommodate a ligand of a particular size or geometry, binding will be prevented. On the basis of crystal structure data, such a mechanism was proposed to explain how the PBCV-1 mRNA capping enzyme selectively binds single-stranded mRNA while discriminating against double-stranded DNA.(2) Using our molecular dynamics results, along with homology to the PBCV-1 DNA ligase, we revisit this proposal and explore its validity.

In eukaryotes and their viruses, the process of mRNA capping is carried out cotranscriptionally by a set of three enzyme-catalyzed reactions that have been well described.(14) In the first enzymatic reaction, a triphosphatase cleaves the terminal phosphate from the 5′-terminal triphosphate of mRNA, forming a diphosphate end. The terminal diphosphate serves as the substrate for the mRNA capping enzyme, which transfers GMP from GTP to the 5′-end. In the final step, a methyltransferase transfers a methyl group to the N-7 nitrogen of GMP. In the mRNA capping enzyme, chemistry is initiated when a conserved, catalytic lysine attacks the α-phosphate of bound GTP, displacing pyrophosphate and forming a GMP−enzyme intermediate. In the second step, mRNA binds, and the GMP is transferred to the 5′-diphosphate end of the mRNA, completing the reaction. Formation of the 5′ cap is the first post-transcriptional modification of nascent mRNA and is essential in mRNA splicing, nuclear export, mRNA stability, and translation initiation.¹⁵⁻¹⁷

The mRNA capping enzyme belongs to the nucleotidyltransferase superfamily whose members also include ATP- and NAD⁺-dependent DNA ligases and ATP-dependent RNA ligases. Common chemistry and structural elements distinguish the superfamily.(18) Shared chemistry is characterized by the transfer of a nucleotide to the 5′-end of a polynucleotide via a nucleotide−enzyme intermediate. Shared structure is characterized by a catalytic N-terminal domain, or nucleotidyltransferase domain, and a noncatalytic-accessory-C-terminal domain that plays different roles depending on the superfamily member.(18) For example, in both the ATP-dependent DNA ligases and the mRNA capping enzymes, the C-terminal domain contains an oligonucleotide/oligosaccharide (OB) binding fold, which is thought to play a role in substrate positioning prior to and during catalysis.^2,18,19 The C- and N-terminal domains associate noncovalently in the ATP-dependent RNA ligases of kinetoplastids.(20) In all other superfamily members, the domains are covalently linked by a short, flexible oligopeptide.

The “open” and “closed” conformations of the holo state of the PBCV-1 mRNA capping enzyme show large quasirigid displacements of the C-terminal, or OB domain, relative to the nucleotidyltransferase domain (Figure 1).(2) In the open state, the centers of mass of the nucleotidyltransferase and OB domains are separated by 30.3 Å, and the GTP triphosphate is in an unreactive position, orthogonal to the nucleophile. In the closed state, the centers of mass of the domains are separated by 25.5 Å, and the triphosphate is in a reactive conformation, in line with the nucleophile. Subsequent opening and closing events are expected to mediate mRNA binding, GMP transfer, and product release.^2,18

Computational Methods and Theory

Molecular Dynamics Simulations

Carrying out several short simulations is a more effective method of covering phase space than carrying out a single long simulation.(21) In order to make use of this observation, six independent 20 ns simulations of the PBCV-1 mRNA capping enzyme in the apo state and six independent 20 ns simulations in the holo state were initiated from the open and closed conformations, respectively, of protein data bank (PDB) code 1CKM (Figure 1).(2) For the apo simulations, coordinates were taken from chain A after removing GTP. For the holo simulations, coordinates were taken from chain B of 1CKM. For both simulations, histidine protonation states were assigned using WHATIF.(22) All other hydrogen atoms and protein force field parameters were assigned using the AMBER99 force field(23) in the xleap program of Amber8.(24) GTP parameters were taken from the Meagher parameter set.(25) Following parametrization, the protein was immersed in a rectangular prism of pre-equilibrated TIP3P waters(26) that provided a 10 Å buffer between the protein and the next periodic image in each dimension. Three sodium ions were added in xleap to neutralize the system charge. Following parametrization, conjugate gradient minimization was carried out in four cycles. In the first 2000 step cycle, only hydrogen atoms were free to move while all other atoms were constrained. In the second 2000 step cycle, hydrogen, water, and ions were free to move while all other atoms were constrained. In the third 2000 step cycle, the protein backbone was constrained, and all other atoms were free to move. In the last 10 000 step cycle, all atoms were free to move. Once minimized, six MD simulations of the holo state and six MD simulations of the apo state were initiated in the NPT ensemble from different velocity seeds. The holo state was allowed to equilibrate for 50 ps. For the apo simulations, the protein was first constrained, allowing water to equilibrate to the proper density within the active site over 30 ps; this was to prevent spurious domain closure as a result of removing GTP. Following this 30 ps equilibration, the apo state was equilibrated constraint free for 50 ps. All MD simulations were carried out using a 1 fs time step, extracting configurations every 50 fs for analysis. The temperature was maintained at 300 K using Langevin dynamics, while the pressure was maintained at 1 atm using the hybrid Nose−Hoover−Langevin method(27) with period and decay times of 100 and 50 fs, respectively. Long-range electrostatics were calculated using the Particle Mesh Ewald method.(28) A multiple time-stepping algorithm was employed to improve integration efficiency. The long-range cutoff was set to 14 Å, and bonded interactions were calculated every time step. Short-range, nonbonded interactions were calculated every two time steps, and long-range electrostatics were calculated every four time steps. Simulations were carried out on NCSA’s Abe machine. Benchmarks running on 256 processors ranged from 0.11 days/ns to 0.16 days/ns. All molecular dynamics simulations were carried out using NAMD 2.6.(29)

Brownian Dynamics

Coordinates for the hyperopen and open states (defined in the Induced Fit versus Population Shift section) were taken from the apo MD simulations retaining all hydrogen atoms. GTP coordinates were taken from chain B of the PDB code 1CKM(2) and hydrogen atoms were assigned according to the Meagher parameter set.(25) The long-range electrostatics of the protein were modeled by solving the linearized Poisson−Boltzmann equation using a focusing calculation in the adaptive Poisson−Boltzmann solver (APBS).(30) Potential values were assigned to the nodes of a 129 × 129 × 129 node grid with 1 Å spacing between nodes. The long-range electrostatics of GTP were calculated by the same method, and potential values were assigned to the nodes of a 65 × 65 × 65 node grid with 1 Å spacing between nodes. For both the capping enzyme and GTP, the ionic strength was set to zero, the temperature to 298.15 K, the internal molecular dielectric constant to 2.0, and the solvent dielectric constant to 78.4.

The effective charge methodology(31) and desolvation energies,(32) as implemented in SDA,(12) were used during Brownian dynamics to model the long-range electrostatics and desolvation energies, respectively. In GTP, effective charges were positioned on the nonbridging β and γ oxygen atoms, as well as on the N2, N3, and O6 atoms. For the desolvation parameter, the α value was set to 4.

Short-range interactions were treated by an exclusion volume that prevents van der Waals overlap of the capping enzyme and GTP. The excluded volume of the capping enzyme is the region of space contained in a 1.4 Å probe accessible surface. If a BD step carries a surface exposed atom of GTP into the excluded volume of the capping enzyme, the step is repeated with a different random number until GTP no longer enters the excluded volume of the capping enzyme. The excluded volume is precalculated for the capping enzyme and stored on a grid with 0.5 Å spacing between nodes. A list of surface GTP atoms is also pregenerated and stored.

Brownian dynamics simulations were carried out using the SDA software,(12) which propagates dynamics by solving the Ermak−McCammon equations of motion.(33) For each capping enzyme conformation, 1.6 × 10⁶ trajectories were performed to ensure convergence of the calculated association rates. Each trajectory was run at 298.15 K with 0 ionic strength. The trajectories were initiated with the GTP and the capping enzyme separated by center to center distance b and were terminated when GTP and the capping enzyme were separated by a center to center distance c > b; c was set to 300 Å and b to 100 Å. Diffusion coefficients for GTP and the capping enzyme conformations were calculated using the program Hydropro(34) setting the temperature to 298.15 K, the viscosity to that of water at 298.15 K (0.890 cP), the bead radii of the protein to 3.2 Å, and the bead radii of GTP to 2.8 Å.

Rates were calculated using the formalism developed by Northrup et al.(35) The distance between the side chain nitrogen atom of the K82 nucleophile and the 03G nonbridging oxygen atom on the γ phosphate of GTP was used as the association criterion.

Gating Effects on GTP Association Kinetics

We begin by assuming domain gating is a two state process in which the domains may exist in either an open or a closed conformation, with opening and closing rates given by k_o and k_c, respectively. The two state assumption allows us to make use of the results of Szabo et al.,(9) who showed that the bimolecular association rate, in the presence of stochastic gating, can be written

where k_G is the bimolecular association rate in the presence of gating, k_UG is the steady-state-ungated bimolecular association rate to the enzyme fixed in its most open conformation, (k_o + k_c)⁻¹ is the domain gating period, and k̂(s)is the Laplace transform of s. Equation 1 reduces to two limiting cases depending on the relative values of the diffusional relaxation time of the system, τ_D, and the domain gating period,

where r_c is the collision distance of the system, approximated as the sum of the smallest radii of spheres that contain each molecule and D is the sum of the translational diffusion coefficients of the substrate and enzyme. Equations 2 and 3 represent substrate association in the presence of “slow” and “fast” gating, respectively; hence, domain motion only affects substrate binding kinetics in the slow gating limit.

Results and Discussion

Induced Fit versus Population Shift

The effect of substrate-mediated free energy reorganization on conformational variability has drawn increasing attention and is usefully described by either an induced fit(4) or a population shift model.^7,8 Examples of both models have been reported in the literature. For example, while approximately the same range of conformational space is sampled in both the apo and holo forms of the two domain glucose and ribose binding proteins, ligand binding biases the conformational populations toward a single conformation and is best described by a population shift model.^36,37 The same observations hold for adenylate kinase.(1) On the other hand, energy profiles in the presence and absence of acetylcholinesterase demonstrated that loop isomerization in the protein neurotoxin fasciculin-2 does not occur prior to acetylcholinesterase binding; it follows that the system is best described by an induced fit model.(38)

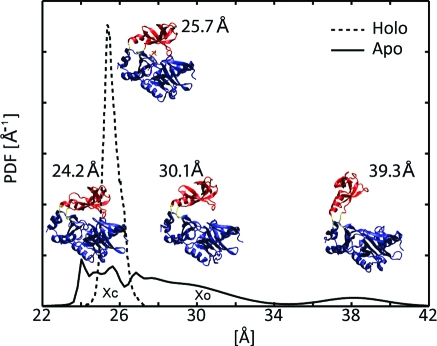
In order to determine whether GTP binding by the PBCV-1 capping enzyme is better described by the induced fit or the population shift model of substrate binding, we examine the distribution of conformations of the OB domain relative to the nucleotidyltransferase domain. As we are only interested in the relative motion of the OB domain, we neglect internal domain fluctuations and approximate the OB domain as a rigid body. This approximation is supported by earlier work in which OB-domain secondary structure was retained during isomerization from an open to a closed conformation.(19) By using the rigid body approximation, the position and orientation of the OB domain is described by three positional and three orientational degrees of freedom that are measured with respect to a coordinate system whose origin we center on the center of mass of the nucleotidyltransferase domain. Furthermore, relative to the large fluctuations between the centers of mass of the OB and nucleotidyltransferase domains observed during simulations of the apo state, fluctuations along the two orthogonal positional degrees of freedom, as well as fluctuations around the three orientational degrees of freedom, were modest. This observation is apparent in the three representative conformations from the apo state simulations shown in Figure 2. As fluctuations between the centers of mass of the OB and nucleotidyltransferase domains constitute the preponderance of relative domain motion, we approximate the distribution of conformations of the OB domain relative to the nucleotidyltransferase domain by the distribution of distances separating their centers of mass. The probability distribution functions (PDFs) of the distance separating the centers of mass of the domains in the apo and holo trajectories are reported in Figure 2. In the apo state, the two domains span a range of conformations and exhibit a bimodal distribution. Conversely, in the holo state, the distribution is localized around a single conformation that resembles the closed, holo crystal structure.

Figure 2.

Conformational distributions in the apo and holo states: Probability distribution functions (PDFs) of the distance separating the centers of mass of the OB and nucleotidyltransferase domains in the MD simulations. Xc and Xo indicate the locations of the closed and open crystal structures, respectively. The holo distribution is represented by a dashed line and the apo distribution by a solid line. Structures of selected conformations are labeled with the distance separating the centers of mass of their OB and nucleotidyltransferase domains. The three lower structures are representatives of the apo simulation while the single upper structure is a representative of the holo simulations. Coloring is the same as in Figure 1.

The induced fit model predicts that the apo state samples only small internal fluctuations, such as side-chain reorientations, in the vicinity of a narrow distribution of backbone conformations, which are clearly distinguishable from the predominant backbone conformations sampled in the holo state. Accordingly, the large distribution of distances separating the centers of mass of the OB and nucleotidyltransferase domains observed during simulations of the apo state rule out the induced fit model. Additionally, the narrow distribution of distances observed during simulations of the holo state, when considered in tandem with the distribution observed during simulations of the apo state, implies that the PBCV-1 capping enzyme follows a population shift model of substrate binding. While the possibility that the holo state significantly populates an open conformation at time scales longer than those accessed during the MD simulations cannot be ignored, this does not negate description by the population shift model (excluding the unlikely exception that the true apo and holo distributions are identical, in which case the population cannot be said to shift).

Population shift substrate-binding mechanisms have also been reported for both the glucose(36) and ribose(37) binding proteins, as well as adenylate kinase,(39) each of which is structurally similar to the PBCV-1 mRNA capping enzyme. While this correlation suggests that the population shift mechanism may be a commonly occurring substrate-binding mechanism among proteins formed by the fusion of two domains via a flexible linker, the data set is small, and exceptions are likely to be found.

In addition to specifying binding mechanism type, the distributions of distances shown in Figure 2 allow qualitative insight into binding thermodynamics. For example, the narrowing of the distributions that occurs upon substrate binding implies a reduction of entropy. By assuming spontaneous binding, the process must be driven by a decrease in enthalpy. This is consistent with an extensive network of hydrogen bonds between positively charged active site residues and the negatively charged nonbridging GTP oxygen atoms.^2,19

Interestingly, the apo simulations show a sparse distribution of states in which the centers of mass of the nucleotidyltransferase and OB domains are separated by 36−42 Å, which is 6−12 Å wider than the distance observed in the open crystal structure (Figure 1A). We designate these “hyperopen” states. As the substrate must bind prior to catalysis, the occurrence of hyperopen conformations may be functionally significant. For instance, if the OB domain is nearby the nucleotidyltransferase domain, GTP binding may be occluded or hindered, and the domains must open to allow facile binding.

Binding Competent Conformations

In order to clarify how extensively the domains must open prior to GTP binding, we carried out two Brownian dynamics simulations. The first simulation measured the association rate to a hyperopen conformation in which the centers of mass of the nucleotidyltransferase and OB domains were separated by 38.8 Å. The second simulation measured the association rate to an open conformation in which the centers of mass of the two domains were separated by 30.1 Å, which is a distance similar to that found in the open crystal structure. Table 1 reports the association rates at varying distances of encounter complex formation (the “encounter complex” is rigorously defined in the Computational Methods and Theory section). In the hyperopen conformation, encounter complex formation did not occur at distances shorter than 7.00 Å. In the open conformation, encounter complex formation was not observed at distances shorter than 15.00 Å. Figure 3 is a visual comparison of the surfaces that define the shortest encounter complexes formed in the hyperopen and open conformations and indicates that GTP is occluded from the active site while the enzyme is in the open state. These results imply that isomerization into a hyperopen conformation dramatically improves GTP binding efficiency.

Table 1. Brownian Dynamics GTP Association Rates as a Function of Encounter Complex Distance to Two PBCV-1 mRNA Capping Enzyme Conformations^a.

distance (Å)	hyperopen (M−1 s−1)	open (M−1 s−1)
7.00	4.2 × 104 ± (7 × 104)	-
9.00	4.8 × 104 ± (1 × 105)	-
11.00	4.1 × 106 ± (8 × 105)	-
13.00	1.9 × 107 ± (3 × 106)	-
15.00	1.1 × 109 ± (2 × 107)	1.7 × 105 ± (5 × 105)

^aStandard deviations over 1.6 × 10⁶ simulations are shown in parentheses. No encounter events are indicated by dashed entries.

Figure 3.

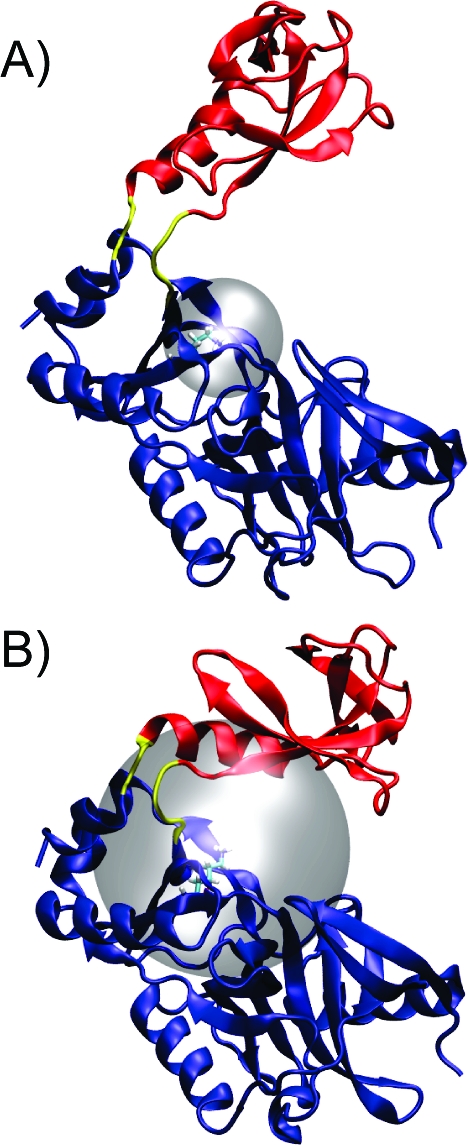
Shortest encounter complexes determined by Brownian dynamics simulations: Transparent spherical surfaces define the shortest observed encounter complexes. The volume contained within the spherical surface was inaccessible to GTP. (A) Representative hyperopen conformation. The centers of mass of the OB and nucleotidyltransferase domains are separated by 38.8 Å. (B) Representative open conformation resembling the open crystal structure. The centers of mass of the two domains are separated by 30.1 Å. Coloring is the same as in Figure 1.

The dramatic improvement in binding efficiency following isomerization into a hyperopen conformation is a specific instance of a more general behavior followed by proteins that behave according to the population shift mechanism of substrate binding. This follows from the observation that nonproductive substrate-binding conformations will be sampled in the apo state of proteins that follow a population shift type mechanism; consequently, isomerization into a conformation conducive to substrate binding enhances binding efficiency.

Neglecting conformational flexibility during BD simulations makes the calculated association rates sensitive to the reaction criteria defining the encounter complex;^12,32,40 as a result, our calculated rates cannot be expected to accurately predict the true association rate. However, the conclusion that isomerization into a hyperopen conformation is a prerequisite of GTP binding is based on relative association rates, to representative hyperopen and open conformations, and so is not affected by the inaccuracy of the reported absolute values.

Domain Gating and GTP Association Kinetics

If isomerization into a hyperopen conformation, or binding competent conformation, is a prerequisite of substrate binding, the isomerization rate may regulate the substrate-binding rate. Regulation occurs when an enzyme−substrate encounter complex forms while the enzyme is in a binding incompetent conformation and the enzyme−substrate encounter complex dissociates faster than isomerization into a binding competent conformation occurs. In this case, called the slow gating limit, binding can only occur if the enzyme−substrate encounter complex forms while the enzyme is in a binding competent conformation and the association rate is proportional to the fraction of enzymes in the hyperopen, or binding competent conformation (eq 2). Conversely, regulation does not occur if the enzyme−substrate encounter complex forms when the enzyme is in a binding incompetent conformation and isomerization into a binding competent conformation occurs faster than the enzyme−substrate encounter complex dissociates. In this case, called the fast gating limit, the enzyme isomerizes between binding competent and incompetent conformations many times before the enzyme−substrate encounter complex dissociates. By virtue of the large number of isomerization events that occur prior to dissociation of the enzyme−substrate complex, the likelihood that the substrate recollides with a binding competent conformation is high, and the substrate binding rate is unaffected (eq 3).

In order to determine whether the PBCV-1 capping enzyme follows a slow or fast gating scenario, we compare the time scales of diffusional dissociation of the encounter complex, approximated using the diffusional relaxation time of the system (eq 4), to an analytical approximation of the period of domain gating. We first let r be the distance separating the centers of mass of the nucleotidyltransferase and OB domains. We then define an “open” conformation as one of the binding incompetent conformations characterized by the set of conformations with 24 Å < r < 35 Å and a “hyperopen” conformation as one of the binding competent conformations characterized by the set of conformations with 35 Å < r. The rate of isomerization between the open and hyperopen conformations can be determined by solving the Smoluchowski equation with appropriate boundary conditions:^41,42

where p(r, t) is the probability of finding the domains separated by a distance r at a time t, W(r) is the potential of mean force (PMF) at r, and D(r) is a position dependent diffusion coefficient. While limited sampling prevents W(r) from being accurately determined, the conformational variability of the apo state observed during the six 20 ns simulations implies that the energetic barrier separating the open state from the hyperopen state is roughly comparable to the available thermal energy. To a first approximation then, we take ∂W(r)/∂r ≈ 0 for all r, which describes diffusive domain motion along a flat free-energy surface. If we further assume that the diffusion coefficient is constant along r, then eq 5 reduces to

After fixing the center of mass of the nucleotidyltransferase domain at the origin and taking D as the sum of the diffusion coefficients of the two domains along r, eq 6 approximately describes relative domain motion. We solve eq 6 within an infinite square well potential of length L set to the difference between the maximum and minimum values of r that occur during simulations of the apo state. When r = 0, the enzyme is closed, and when r = L, the enzyme is in the most extended hyperopen conformation. We set a absorbing boundary condition p(0, t) = 0, and a no flux condition (∂p/∂t)_{r > L} = 0. The initial distribution is chosen as a delta-function centered at r = L. With these conditions, the solution to eq 6 is well-known, and the average time required for the domains to close is given τ = L²/2D.^43,44 Taking L = 17.5 Å and approximating D as the sum of the translational diffusion coefficients of the two domains, determined using Hydropro, gives a value of τ whose inverse is the closing rate, k_c = 1.5 × 10⁸ s⁻¹. By symmetry, the opening and closing rates are equal, and the period of domain gating is (k_o + k_c)⁻¹ = 3.3 ns. The characteristic diffusional relaxation time of the system is τ_D = 130 ns. The ratio of the diffusional relaxation time of the system and the domain gating period is τ_D/(k_o + k_c)^{− 1} = 39 implying that, on average, the domains open and close approximately 39 times before the encounter complex dissociates, providing many opportunities for the substrate to recollide with, and subsequently bind, a conformation that allows substrate binding. A more detailed analysis of the gating affects on the rate of GTP binding is unlikely to alter the conclusion that the rate of association is of the same order of magnitude as would be expected for the enzyme fixed in its hyperopen state. While crossing of the modest energy barrier during isomerization of the enzyme could slow the gating process somewhat, this is likely to be offset by the longer residence times of GTP in the initial encounter complex due to electrostatic interactions with the enzyme.

Polynucleotide Specificity

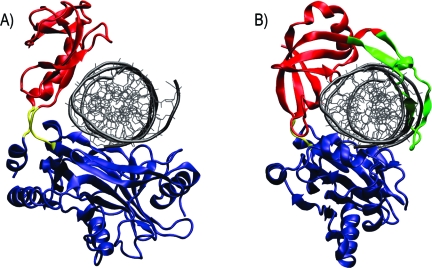
When the crystal structure of the PBCV-1 mRNA capping was reported, it was noted that the cleft between the OB and nucleotidyltransferase domains in the mRNA capping enzyme was narrower than the cleft in the DNA ligase homologue.(2) It was subsequently suggested that the narrower cleft of the mRNA capping enzyme serves a functional role, preventing double-stranded DNA (dsDNA) binding and conferring single-stranded mRNA specificity.(2) In contrast, the observation of hyperopen conformations sampled during the apo MD simulations suggest that this hypothesis is invalid. To clearly illustrate this, we aligned the PBCV-1 nucleotidyltransferase domain of a hyperopen conformation, with domain centers of mass opened 8.8 Å wider than the open crystal structure, to the nucleotidyltransferase domain of the PBCV-1 DNA ligase crystallized in complex with dsDNA.(3) The results are shown in Figure 4 and indicate that hyperopen conformations of the mRNA capping enzyme may accommodate dsDNA. Consequently, rather than arising from a narrow cleft that occludes dsDNA, mRNA specificity is likely conferred by an alternative mechanism.

Figure 4.

Hyperopen conformations may accommodate nicked dsDNA binding. (A) Hyperopen conformation of the PBCV-1 mRNA capping enzyme. The centers of mass of the OB and nucleotidyltransferase domains are separated by 38.8 Å. Coloring is the same as in Figure 1. dsDNA was superimposed on the active site by aligning the nucleotidyltransferase domains of the capping enzyme and PBCV-1 DNA ligase. (B) PBCV-1 DNA ligase crystallized in complex with dsDNA. A unique “latch” domain is colored in green. The nucleotidyltransferase domain is shown in blue, the OB domain in red, and the hinge region in yellow.

Comparison of the PBCV-1 DNA ligase and mRNA capping enzyme crystal structures offers a possible explanation of polynucleotide specificity. Figure 4B shows that the PBCV-1 DNA ligase contains a latch domain, shown in green, which extends from the OB domain and encircles the DNA substrate. In the DNA ligase, the latch domain is essential for the formation of a stable complex with nicked dsDNA.(3) Accordingly, the absence of a latch domain in the PBCV-1 mRNA capping enzyme implies that mRNA specificity may be imparted by the absence of the latch domain; that is, while conformational flexibility of the capping enzyme accommodates nicked dsDNA binding, the complex is likely unstable, rapidly dissociating before ligation can occur. On the other hand, single-stranded mRNA has a smaller diameter than dsDNA and may form a stable complex through interactions with only the nucleotidyltransferase and OB domains.

Conclusions

In this paper, we have analyzed several common functional themes related to substrate binding in enzymes and proteins whose tertiary structure is composed of two domains covalently bound by a short, flexible-linking peptide. While our results are specific to the PBCV-1 mRNA capping enzyme, the close relationship between biomolecular structure and function allows them to provide a useful context within which the substrate binding behavior of similarly structured proteins and enzymes may be explored.

By carrying out six independent 20 ns MD simulations of the apo state and six independent 20 ns MD simulations of the holo state of the GTP dependent PBCV-1 mRNA capping enzyme, we have shown that the apo enzyme samples a wide range of conformations and at the time scales accessed during our simulations is predisposed toward conformations that resemble the holo closed crystal structure. Rather than inducing a conformational change, substrate binding may further stabilize the more stable apo conformations and shift the equilibrium toward the predominant holo conformation. This is consistent with a population shift mechanism and is similar to results reported for both the ribose and glucose binding proteins,^36,37 as well as the adenylate kinase enzyme,(39) each of which shares a tertiary structure similar to that of the PBCV-1 mRNA capping enzyme. While the correlation suggests that the population shift mechanism may be a commonly occurring substrate-binding mechanism in proteins with two domains covalently bound via a short, flexible-linking peptide, the data set is limited and exceptions are likely to be found.

Additionally, the MD simulations revealed that the enzyme samples hyperopen conformations in which the centers of mass of the nucleotidyltransferase and OB domains open 6−12 Å wider than previously reported. As the relative proximity of the OB domain to the nucleotidyltransferase domain mediates the accessibility of the active site, the occurrence of the hyperopen conformations raises questions about their functional significance. To clarify their functionally role, BD simulations were used to show that isomerization into hyperopen conformations dramatically improves GTP binding efficiency by increasing active site accessibility.

The mobility of the OB domain and its role in mediating substrate accessibility leads to the question of whether or not the rate of isomerization into a hyperopen state impacts the substrate association rate. To answer this question, we made an analytic approximation of the domain gating period based on the results of our apo MD simulations. Comparing this result to the time required for the enzyme−substrate encounter complex to dissociate indicated that the substrate likely has many opportunities to recollide with a binding competent conformation prior to diffusing apart to a distance that precludes binding. This analysis indicates that the rate of OB domain isomerization is not likely a factor in determining the rate of substrate association. In other words, interactions provided by the OB domain that are essential for catalysis are gained without paying a penalty in the form of a decreased substrate association rate. It is possible that other similarly structured enzymes also behave in the same manner.

Finally, by modeling double-stranded DNA into the active site of a conformation in which the centers of mass of the OB and nucleotidyltransferase domains were separated by an additional 8.8 Å beyond the separation measured in the crystal structure, we showed that restricted conformational flexibility is insufficient to explain single-stranded mRNA specificity. These results serve as a reminder that, as valuable as crystal structure data is, some molecular phenomena must be explained by dynamic arguments.

Funding Statement

National Institutes of Health, United States