Effects of the anesthetic agent propofol on neural populations

Abstract

The neuronal mechanisms of general anesthesia are still poorly understood. Besides several characteristic features of anesthesia observed in experiments, a prominent effect is the bi-phasic change of power in the observed electroencephalogram (EEG), i.e. the initial increase and subsequent decrease of the EEG-power in several frequency bands while increasing the concentration of the anaesthetic agent. The present work aims to derive analytical conditions for this bi-phasic spectral behavior by the study of a neural population model. This model describes mathematically the effective membrane potential and involves excitatory and inhibitory synapses, excitatory and inhibitory cells, nonlocal spatial interactions and a finite axonal conduction speed. The work derives conditions for synaptic time constants based on experimental results and gives conditions on the resting state stability. Further the power spectrum of Local Field Potentials and EEG generated by the neural activity is derived analytically and allow for the detailed study of bi-spectral power changes. We find bi-phasic power changes both in monostable and bistable system regime, affirming the omnipresence of bi-spectral power changes in anesthesia. Further the work gives conditions for the strong increase of power in the δ-frequency band for large propofol concentrations as observed in experiments.

Introduction

General anesthesia (GA) is an indispensible tool in today’s medical surgery. In the optimal case, it leads to the patients immobility, amnesia and unconsciousness, i.e. lack of awareness towards external stimuli (Orser 2007; John and Prichep 2005). Although GA is omnipresent in recent medicine, its underlying mechanisms and the molecular action of anesthetic agents (AA) have been a long-standing mystery. One of the major obstacles towards its understanding is the occurrence of different effects. For instance, immobility is assumed to be generated in the spinal cord (Rampil and King 1996), and the dorsolateral prefrontal cortex and the thalamus are affected during amnesia (Veselis et al. 1997). Similarly the underlying mechanism of the loss of consciousness and its spatial location is unknown though some studies point out the importance of the thalamus (Carstens and Antognini 2005; Alkire et al. 2008; Stienen et al. 2008). The present work focusses on the loss of consciousness (LOC) and aims to model corresponding experimental findings.

To learn more about the effects of AAs, the pharmaco-kinetics of AA have attracted some attention in the last decades (Forrest et al. 1994; Dutta et al. 1997; Franks 2008), i.e. the binding of the agent molecule to the blood and the effective concentration at the neural site. It has been shown that the speed of the AAs experimental administration strongly affects the blood concentration and the effect-site concentration of the AAs. In other words the blood concentration of AA and its concentration at the effect site in the neural tissue may be different and may obey different temporal dynamics. These differences may yield hysteresis effects in the anesthetic action (Dutta et al. 1997). More recent studies examined the direct action of AA on single neurons (Antkowiak 1999; Franks and Lieb 1994) and synaptic and extrasynaptic receptors (Franks 2008; Hemmings Jr. et al. 2005; Orser 2007; Bai et al. 1999; Alkire et al. 2008). In this context one of the most important findings is the AAs weakening action on excitatory synaptic receptors and the enhancement of inhibitory synaptic activity. For instance, the AA ketamine inhibits synaptic NMDA-receptors, while the AA propofol enhances the action of inhibitory GABA_A synapses (Franks 2008).

In addition to these studies of microscopic actions, much research has been devoted to macroscopic effects of AA, such as the cardiovascular response of subjects to AAs (Mustola et al. 2003; Musizza et al. 2007) and the power spectrum of the subjects’ resting electroencephalogram (EEG) as a function of the blood concentration of AAs (Forrest et al. 1994; Dutta et al. 1997; Kuizenga et al. 2001; Fell et al. 2005; Han et al. 2005). The resting EEG power spectrum especially reflects the anesthetic action in a characteristic way and permits the classification of the depth of anesthesia by so-called monitors, see e.g. the review of Antkowiak (2002). These monitors are also used to pinpoint the LOC.

Considering the action of the AA propofol, increasing its blood concentration first increases and then decreases the spectral power in most frequencies up to the gamma-range (0−40 Hz). This bi-phasic behavior is characteristic for GA and has been observed both in rats (Dutta et al. 1997) and in human subjects (Kuizenga et al. 1998; Yang et al. 1995). Interestingly some studies reported LOC during the power increase in the EEG (Kuizenga et al. 1998, 2001), while most monitors use the decay-phase of the bi-phasic power changes as indicator for LOC. The present work aims to describe mathematically this bi-phasic behavior by a neuronal population model.

Our work focusses on the action of propofol, which is a widely-applied anesthetic agent (Marik 2004). It affects the cognitive abilities of subjects, such as the response to auditory stimuli (Kuizenga et al. 2001) or pain (Andrews et al. 1997). It acts mainly on GABA_A receptors and hence changes the response of inhibitory synapses, while NMDA- and non-NMDA excitatory receptors are insignificantly affected. Increasing the blood concentration of propofol increases the charge transfer in synaptic GABA_A-receptors and increases the decay time constant of their synaptic response function (Kitamura et al. 2002). We point out that the present work is not limited to the action of propofol and may be applied to the action of other anesthetic agents.

The question arises whether the resulting anesthetic effect originates from the action of a population of neurons in a single brain area or whether GA is a network effect, i.e. results from the interaction of several brain areas. In the following we discuss briefly this question. On one hand it is well-known that single brain areas play an important role, such as the thalamus (Carstens and Antognini 2005; Alkire et al. 2008) which generates spindle waves close to the point of LOC. Since the thalamus is the gateway for sensory information in the brain, GA appears as a network effect mainly triggered by the thalamic action. On the other hand GABA_A-receptors play an important role in the anesthetic action and are present in most cortical areas and some subcortical areas. Hence there is no unique action site of propofol; this may relate to the fact that the spatial location of the anesthetic action is still unknown, see e.g. studies on cortical neurons (McKernan et al. 1997) and thalamic relay neurons (Ying and Goldstein 2005). Consequently GA may represent an unspecific action on neural populations. This view is fostered by invitro experiments on cortical slices while applying anesthetic agents. Such experiments showed that the firing rates of neurons decreased during the administration of an increased concentration of the AA (Antkowiak 1999, 2002) similar to neural effects observed in invivo experiments. These findings indicate that anesthetic effects may occur in a single brain area and network interactions might not be necessary for their occurrence. Moreover the presence of a global heterogeneous network involving brain areas with specific actions may result in an EEG with spatially localized activity regions. However John and Prichep (2005) measured the EEG during the administration of propofol and found no spatial structure. Consequently these findings indicate that the anesthetic action is rather unspecific to brain areas and it is reasonable to treat a single brain area as a first approximation.

Besides the experimental studies, previous theoretical studies on GA assumed single neuron populations, i.e. single brain areas, and have reproduced successfully the characteristic EEG-power spectrum changes observed in experiments. These studies have explained the bi-phasic behavior in the EEG power spectrum by different mechanisms. Steyn-Ross et al. support the idea that the bi-phasic spectrum and the LOC result from a first-order phase transition in the population (Steyn-Ross and Steyn-Ross 1999; Steyn-Ross et al. 2001b, 2004). In this context the phase transition of first order reflects a sudden disappearance of the system’s resting state accompanied by a jump to another resting state. The associated pre-jump increase in state activity has been interpreted as the sudden loss of consciousness as observed in experiments. In contrast, Liley et al. (Bojak and Liley 2005; Liley and Bojak 2005) showed in an extensive numerical study of a slightly different model that such a phase transition is not necessary to reproduce bi-phasic power changes, but did not suggest a mechanism for the occurrence of LOC. Moreover Molaee-Ardekani et al. introduced the idea of slow adaptive firing rates which explains the bi-phasic spectrum and LOC without a phase transition (Molaee-Ardekani et al. 2007). The present work studies a neural population not embedded in a larger network and which is subjected to uncorrelated fluctuations. Consequently we aim to answer the question whether an isolated neural population is sufficient to model the biphasic behavior in the EEG-power spectrum. In contrast to the previous studies, we introduce a less complex neural population model which allows for a thorough analytical study.

The latter theoretical studies (Steyn-Ross and Steyn-Ross 1999; Bojak and Liley 2005; Molaee-Ardekani et al. 2007) are based on the model of Liley et al. (1999), whose basic elements we discuss briefly in the following. The model considers a continuous spatial mean-field of neurons in one or two spatial dimensions, synapses and axonal connections; the synapses and neurons (Bojak and Liley 2005) may be excitatory and inhibitory. This mean-field represents the spatial mean in a neural population description and thus averages the spiking activity of single neurons using a sigmoidal population firing rate. The firing activity is assumed to spread diffusively via a damped activity wave along the axonal trees and terminates at pre-synaptic terminals. The wave speed of this axonal wave is set to the mean axonal conduction speed. At the synaptic terminals the incoming pre-synaptic activity evokes the temporal synaptic response on the dendritic trees according to the dynamics of a single synapse, i.e. treating the membrane as an RC-circuit with a time-dependent conductance, see e.g. (Koch 1999). This model neglects the spatial extension of dendritic trees and assumes a volume conduction mechanisms for the spread along axonal fibers.

The model considered in the present work is similar to previous models (Foster et al. 2008) in several aspects such as the model of Liley et al. (1999) but differs in some important aspects. In contrast to the Liley-model our model considers a one-dimensional spatial domain and the population of synapses on dendritic trees [on average ∼7,800 synapses on each dendritic tree in rat cortex (Koch 1999)] and the passive activity spread on dendrites (Agmon-Sir and Segev 1993). Considering the propagation delay of evoked synaptic activity along dendritic branches, previous studies showed that the temporal synaptic response on the dendritic trees smears out temporally (Koch 1999; Smetters 1995; Agmon-Sir and Segev 1993). Consequently the synaptic response arriving at the soma differs from that at a single synapse. To cope with the various delay distributions caused by the spatial distribution of synapses on the dendritic branches, the present model considers an average synaptic population response which obeys an average synaptic response function, see (Freeman 1992; Gerstner and Kistler 2002) and section "Methods" in the present work. This model assumption contrasts to the Liley-model, that considers the dynamics of a single synapse to describe the population dynamics. In addition the present work models the activity transmission along axonal trees by taking into account the spatial probability density of axonal connections. This contrasts to the Liley-model, that considers a volume conduction mechanism for the activity spread along the axonal branch. It has been shown in previous theoretical studies that the choice of the axonal connection probability functions can significantly alter spatio-temporal dynamics of the neural population (Hutt 2008; Hutt and Atay 2005; Laing and Troy 2003; Bressloff 2001; Bressloff et al. 2002; Coombes 2005). This model of axonal activity spread has been shown to extend the damped activity wave considered in the model of Liley et al. (Coombes et al. 2007; Hutt 2007) to nonlocal interactions. Moreover, the model presented here is mathematically less complex than the Liley-model since it has less parameters. This aspect allows for an analytical treatment of the model and, consequently, the analytical derivation of conditions for physiological parameters.

To obtain dynamical criteria for the occurrence of anesthetic effects, and hence learn more about their importance and the underlying dynamics, the present work aims to extract some analytical relations between physiological parameters. To achieve this goal, the subsequent section introduces the model and discusses the chosen physiological parameters. Section “Results” extracts a condition on synaptic time scales from experimental data, and gives conditions on the number of resting states and their linear stability. In addition, that section derives the power spectrum of Local Field Potentials and EEG analytically and investigates the conditions for bi-phasic behavior in EEG. Finally the discussion section "Discussion" summarizes the results obtained and gives an outlook onto future work.

Methods

The model considers an ensemble of neurons on a mesoscopic spatial scale in the range of cortical hypercolumns, i.e. on a spatial scale of some millimeters. It considers two types of neurons, namely pyramidal cells and interneurons. The former cell type typically excites other cells by excitatory synapses, and thus the pyramidal cell is called an excitatory cell. In contrast, interneurons are known to inhibit other cells by inhibitory synapses and are called inhibitory cells. Consequently, taking into account excitatory and inhibitory cells involves the treatment of excitatory and inhibitory synapses. Moreover, both types of synapses may occur on dendritic branches of both cell types. In the following, we consider excitatory synapses (abbreviated by e) at excitatory (E) and inhibitory cells (I) in addition to inhibitory synapses (i) at both cell types.

By virtue of the large number of neurons in the ensemble, the activity of synapses and neurons are averages over the population in small spatial patches and short time windows (Hutt and Atay 2005; van Hemmen 2004; Eggert and van Hemmen 2001; Gerstner and Kistler 2002). Such spatial patches are assumed to represent fully-connected networks (cf. chap. 6.1 in Gerstner and Kistler 2002). In the following, mean values are the average values in the population of a patch in a short time window of about few milliseconds. Consequently the mean postsynaptic potentials (PSP) V_E,s(x,t) at excitatory cells in a spatial patch at spatial location x and at time t originate from excitatory (s = e) or inhibitory (s = i) synapses receiving activity from other pre-synaptic neurons. Similarly, the PSPs V_I,s(x,t) are evoked at inhibitory cells by pre-synaptic activity at excitatory (s = e) or inhibitory (s = i) synapses.

In a spatial patch, the PSPs may be modeled as the linear response V(t) − V^r to incoming firing activity where V(t) is the mean membrane potential evoked by incoming action potentials and V^r is the mean resting potential. The mean values result from the consideration of an ensemble of neurons, i.e. the spatial patch. Then the four PSPs may be modelled by [Sect. 6 in Gerstner and Kistler (2002)]

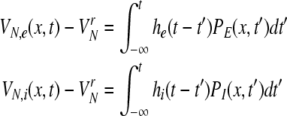with N = E for excitatory cells and N = I for inhibitory cells, V^r_N is the resting potential of neurons of type N and P_E and P_I denote the pre-synaptic mean pulse activity originating from excitatory and inhibitory cells, respectively. Here we assume that axonal connections from excitatory cells terminate at excitatory synapses, which holds true for over 80 percent of excitatory cells (Nunez 1995). Further h_e(t) and h_i(t) represent the mean synaptic impulse response functions of excitatory and inhibitory synapses. Here we choose the response functions known from experiments in single synapses (Koch 1999)

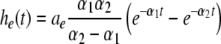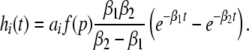with the temporal rates of the excitatory and inhibitory synapses α_1,2 and β_1,2, respectively. Specifically, 1/α₂ and 1/β₂ are the rise time of the response function for excitatory and inhibitory synapses, respectively, and 1/α₁ and 1/β₁ are the corresponding decay times. Moreover, the pre-factors in Eqs. 2 and 3 are chosen for convenience to normalize the response functions h_e and h_i (see the discussion below). The parameter p ≥ 1 denotes a weighting factor which reflects the propofol concentration and whose effect is studied in detail in subsequent sections. The function f(p) quantifies the action of the propofol concentration on the inhibitory synapses and will be specified in section "The weighting factor p". A similar model approach has been taken in previous studies to study the transitions in general anesthesia (Steyn-Ross et al. 2001a; Bojak and Liley 2005). Further a_e and a_i denote the synaptic gain or level excitation and inhibition, respectively. Equation 1 give the mean synaptic responses in the ensemble and thus represent averages over all microscopic details of the synapto-dendritic system in the ensemble. Hence, the model neglects microscopic properties of synapses, such as the reversal potentials of synapses considered in previous models (Liley et al. 1999; Steyn-Ross and Steyn-Ross 1999). This approach is reasonable on the mesoscopic spatial scale of a few millimeters, while the dendritic system of single neurons typically extends over some hundreds of micrometers and may behave differently.

Considering the synapses as Ohmic elements, the synaptic response functions h_e,i(t) represent electric currents. Hence the time integral ∫^∞₀h_e,i(t) dt is proportional to the charge transfer ρ_e,i through the synaptic cleft. Thus we find the following relations for excitatory and inhibitory charge transfer: ρ_e = a_e and ρ_i = a_if(p). In other words, increasing f(p), e.g. via propofol, increases the charge transfer of inhibitory synapses. The synaptic response in (1) is formulated as an integral equation of the form V_s(t) = ∫^t_−∞h_s(t − τ)P_s(τ)dτ. To formulate this equation as a differential equation, we find the differential operators (Hutt et al. 2003)

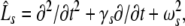for which 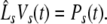After re-scaling of the time by 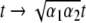we find the following differential formulation of (1):

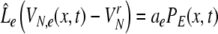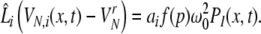with

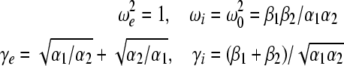To model the pre-synaptic mean pulse activity P_E(x,t), P_I(x,t) at spatial location x subject to the firing activity of other neurons at spatial location y, we assume spatial synaptic interactions via axonal branches with

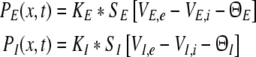with the notation

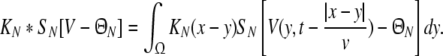We consider a one-dimensional spatial domain Ω that represents the spatial region of the neural population and assume periodic boundary conditions. Moreover v denotes the finite conduction speed of axonal connections. In other words, the delay term 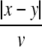in Eq. 8 takes into account the propagation delay of pulse activity to travel from x to y with speed v (Hutt et al. 2003; Hutt and Atay 2006). Further S_E[·], S_I[·] represent the somatic firing function of excitatory and inhibitory cells which have a sigmoidal shape (Hutt and Atay 2005; Gerstner and Kistler 2002; Freeman 1979). The firing rate functions S_E and S_I of the excitatory and inhibitory cells depend on the difference of the PSPs V_E,e − V_E,i and V_I,e − V_I,i, respectively, since the corresponding synaptically evoked post-synaptic currents sum up at the neuron somata [see (Freeman 1992), section 1.7 in Nunez and Srinivasan (2006) and the discussion below in section "The general power spectrum"]. Moreover Θ_E, Θ_I denote the corresponding firing threshold voltages. Since the present model considers populations of neurons, all variables under discussion are averages over small spatial patches and small time windows (Hutt and Atay 2005) and section 6 in Gerstner and Kistler (2002) for more details. The proposed model does not distinguish synapses at different cell types for simplicity, i.e. all excitatory synapses are identical in both cell types and the same holds for inhibitory synapses. In addition, the synapses respond to cells which are located at different spatial locations and the functions K_E, K_I account for the corresponding nonlocal connectivity. They represent the probability density of connections from excitatory and inhibitory cells to excitatory and inhibitory synapses, respectively. This definition requires the normalisation to unity, i.e. ∫_ΩK_E,I(x)dx = 1. This nonlocal approach generalizes previous diffusive models (Steyn-Ross et al. 2001a; Rennie et al. 2002; Bojak and Liley 2005) by considering higher spatial derivatives (Hutt and Atay 2005; Coombes et al. 2007).

Consequently, the PSPs at excitatory synapses for both cell types obey

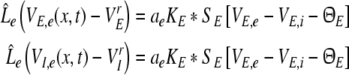and at inhibitory synapses

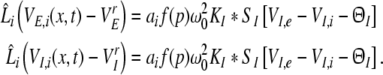From Eqs. 9 and 10, we find the relations V_E,e − V^r_E = V_I,e − V^r_I and V_E,i − V^r_E = V_I,i − V^r_I leading to V_E,e − V_E,i = V_I,e − V_I,i. Hence the effective membrane potentials in excitatory cells, i.e. V_E,e − V_E,i, and inhibitory cells, i.e. V_I,e − V_I,i, are identical. This is an important result derived from the model that originates from the independence of the synaptic actions on the post-synaptic neuron type as assumed in Eq. 1. Note however that the two cell types may differ in their firing rates due to their different sigmoidal firing functions S_E and S_I.

Moreover the extracted condition yields S_I[V_I,e − V_I,i − Θ_I] = S_I[V_E,e − V_E,i − Θ_I] and we obtain for excitatory cells

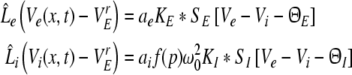and for inhibitory cells

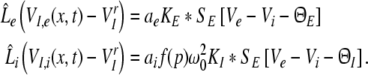with the excitatory and inhibitory PSPs now defined as V_e = V_E,e and V_i = V_E,i. The model (11) extends previous standard neural field models for a single neural population (Atay and Hutt 2005; Hutt et al. 2003; Amari 1977; Coombes et al. 2003) by an additional population. We observe that the right hand sides of Eqs. 11 and 12 depend only on V_e(x,t) and V_i(x,t), and that V_I,e(x,t), V_I,i(x,t) are driven by these variables. Consequently, the PSPs V_e(x,t) and V_i(x,t), and correspondingly Eq. 11, solely govern the systems dynamics.

Choice of physiological parameters

The proposed model considers several physiological parameters, such as mean efficacy of the synapses, their response time constants and the spatial range of axonal spread. These parameter values vary among brain areas and are not well known in neuronal ensembles. For example, the dendritic branches around pyramidal cells are very diverse in geometry and spatial spread and are not known in detail for each neuron (Braitenberg and Schütz 1998; Mell and Schiller 2004). This spatial diversion leads to a dispersion of propagation delays of activity in the dendritic branches (Koch 1999). Further the number and locations of excitatory and inhibitory synapses on the dendritic branches are not known and may only be estimated (Mell and Schiller 2004).

Specifically, the excitatory synapses occur mostly distant from the cell soma, while most inhibitory synapses are found close to the cell body. Since the amplitude of excitatory post-synaptic potentials decays during propagation along the dendritic tree, the somatic vicinity of the inhibitory synapses indicates stronger inhibition than excitation. However the relation of the number of excitatory and inhibitory synapses has been determined to 4:1 (Liu 2004) or 18:1 (Megias et al. 2001) in pyramidal hippocampal cells. In other words much more excitatory than inhibitory synapses populate the dendritic system, which may balance the stronger inhibition.

Further, the reported time scales and synaptic gains of single excitatory and inhibitory synapses might give the right order of magnitude, but deviations from the single synapse properties are reasonable in ensembles. For example, excitatory PSPs need a few milliseconds to propagate from their synaptic origin along the dendritic path to the trigger zone at the soma. Theoretical studies of the one-dimensional cable equation, which represents a simple model of the dendritic tree, have shown that synaptically evoked pulses propagate along the membrane while flattening their shape at both the front and back (Agmon-Sir and Segev 1993; Koch 1999). Since this activity spread may be viewed as increases of the rise and decay time of the activity, essentially the activity propagation increases the rise and decay time of the synaptic impulse response function h_e and thus decreases the rate constants α₁, α₂. To handle this parameter problem, previous neuron ensemble studies have either taken into account explicitly estimates of the physiological structure (Wright and Kydd 1992; Wright and Liley 2001, 1995) or have chosen suitable model parameters to fit optimally experimental encephalographic activity (Robinson et al. 2001, 2003, 2004; Bojak and Liley 2005). The present work takes a slightly different approach and aims to classify the ensemble dynamics as general as possible while ruling out totally unphysiological parameter regimes. This approach is shown explicitly for excitatory and inhibitory synapses in section Stability conditions in the absence of propofol in the context of a stability study.

However in some cases we will specify the time scales of excitatory and inhibitory synapses. Then the inhibitory synapses obey the dynamics of GABA_A-receptors with β₁ = 117 Hz, β₂ = 1,000 Hz, i.e. time scales 1/β₁ = 8.5 ms and 1/β₂ = 1 ms, which are reasonable parameters (cf. Koch 1999, p. 106). Since GABA_A synapses are located close to the cell body, no dendritic propagation delays occur and thus the chosen decay and rise rate hold in a good approximation. In addition, if not stated otherwise, excitatory synapses exhibit the decay time τ_decay = 4.5 ms and the rise time τ_rise = 0.5 ms, i.e. the rates α₁ = 1/τ_decay = 222 Hz and α₂ = 1/τ_rise = 5,000 Hz. This parameter choice reflects AMPA-receptors, but various own numerical simulations (not shown) indicate that the subsequent results may be found for NMDA-receptors as well, i.e. for longer rise and decay times (cf. Koch 1999, sect. 4.6) and thus smaller values of α₁ and α₂. In real neuronal populations, these parameters may vary due to the dendritic propagation delays.

Additional important parameters are a_e, a_i, which represent the synaptic gain or, equivalently, the mean charge transfer in synapses. As discussed above, synaptic weights may vary randomly due to the location on the dendritic tree and even to the pre-synaptic activity level. Consequently this parameter is not accurately known and a_e is fixed to a_e = 1 mV/s similar to the parameter ranges extracted and applied in the work of Robinson et al. (2003, 2004). The following sections vary the values of the inhibitory synaptic gain a_i if not given otherwise. In addition to the gains, the synaptic connections are defined by the kernel functions in (7), where their range represent the spatial spread of the axons. We choose

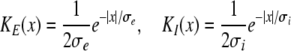with excitatory and inhibitory spatial ranges σ_e and σ_i and ∫K_E(x)dx = ∫K_I(x)dx = 1.

The present work focuses on a single brain area with intra-cortical connection. Since the spatial origin of anesthetic action is not known, the present work does not specify the brain area under study and thus the axonal connection structure is not known. We point out that the spatial interaction range of axonal connections are specific to the species, the brain area, the layer in the neural tissue and the number of connections. For instance, in layer 2 and 3 in rat visual cortex (Hellwig 2000), the average size of axonal branches is ∼18 mm and the probabiflity of axonal connections between a pyramidal neuron and a dendritic tree falls off to its half at a distance of about 200 μm. Moreover, in the monkey visual cortex area V4 (Yoshioka et al. 1992), layer 3 shows axonal extensions up to 1 mm. These examples show the diversity of axonal spatial ranges and it is clear that a spatial range in a model may take values of the same order. Since many excitatory neurons exhibit longer axonal connections than inhibitory neurons, e.g. interneurons (Nunez 1995), the spatial ranges are chosen to σ_e = 2 mm and σ_i = 0.5 mm (Nunez 1981).

The axonal connections exhibit a finite conduction speed which results in a delayed spatial interaction. The conduction speed depends on the spatial extension of the corresponding connection: the axonal fibers of long-range interactions are myelinated and exhibit larger propagation speeds than intra-cortical connections built of un-myelinated axons. Since the present work studies a single neuronal population, the assumption of un-myelinated axons is reasonable and we choose the low conduction speed to v = 1 m/s. This finite conduction speed causes a characteristic propagation delay of τ_e = σ_e/v = 2 ms and τ_i = σ_i/v = 0.5 m/s along excitatory and inhibitory connections, respectively.

Finally, the somatic firing functions S_E, S_I need to be specified. They reflect the integral of the statistical distribution of firing thresholds and exhibit a sigmoidal shape for unimodal threshold distributions (Hutt and Atay 2005; Amit 1989). A standard firing rate function is

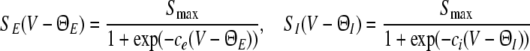for excitatory (E) and inhibitory (I) neurons with maximum firing rate S_m = 40 Hz and the mean firing thresholds Θ_E and Θ_I. The factor c_e,i is proportional to the inverse width of the underlying threshold distributions. In other words, the more similar the firing threshold in the neuron population is, the larger c_e,i (Hutt and Atay 2005). The following sections study the system’s properties with respect to Θ_E,I and c_e,i unless stated otherwise. Further, the firing threshold of inhibitory cells is chosen as Θ_I = −60 mV (see e.g. Otsuka and Kawaguchi 2009), while excitatory cells may exhibit the thresholds Θ_E = −50 mV or Θ_E = −60 mV if not stated otherwise.

Results

The weighting factor p

Our work aims to model the effect of varying the properties of inhibitory synapses on the spatio-temporal dynamics of the neural ensembles. Our approach is motivated by the experimental findings on anesthetic agents (Rundshagen et al. 2004; Kuizenga et al. 2001) with respect to their effect on excitatory and inhibitory synapses. For example, increasing the concentration of the agent propofol prolongs the temporal decay phase of inhibitory GABA_A synapses and increases the charge transfer in these synapse (Baker et al. 2002) while excitatory synapses remain more or less unaffected (Kitamura et al. 2002). In addition, to a good approximation the height of the synaptic response function is maintained for different propofol concentrations (Kitamura et al. 2002).

To implement a similar behavior in our model study, the factor p introduced in Eq. 3 reflects the target concentration of propofol in the neural population. We choose p = 1 for zero concentration. Since the function f(p) introduced in Eq. 3 affects the charge transfer in the inhibitory synapses by ρ_i = a_if(p), we choose the inhibitory charge transfer at vanishing propofol concentration as ρ_i = a_i, i.e. f(p = 1) = 1, and thus identify the mean charge transfers with the level of the synaptic excitation or inhibition. Moreover, our model assumes that increasing p reflects an increasing propofol concentration which decreases the inhibitory decay rate β₁ by β₁ = β⁰₁/p. Here β⁰₁ denotes the inhibitory decay rate in the absence of propofol. Consequently, by this definition p = (1/β₁)/(1/β⁰₁) represents the percentile increase of the inhibitory decay time constant. To mimic these experimental findings, we implement

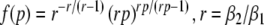which guarantees a constant height of the impulse response function h_i(t) and yields an increasing charge transfer of the synapse with increasing p, i.e. df/dp > 0, according to the experimental findings. We point out that Eq. 14 results directly from the condition of a constant maximum value of h_i(t) for all p assuming the specific response function (3). Further, typically the decay phase of the synaptic response curve is much longer than its rise phase, i.e. β₁ ≪ β₂, r ≫ 1 and thus f(p) ≈ p. In other words the charge transfer increases linearly with the factor p.

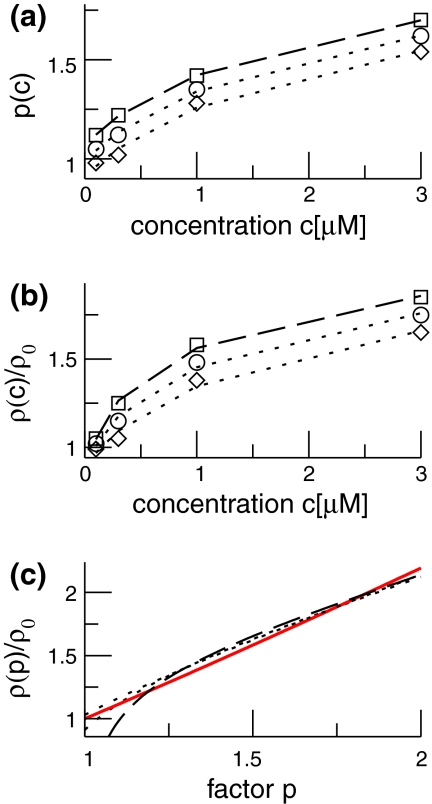
To investigate whether the latter model assumptions on the inhibitory synaptic response are valid, we consider experimental results on the synaptic response of GABA_A-synapses measured in vitro in cultured cortical neurons of rats (Kitamura et al. 2002). Figure 1a shows the mean values p obtained experimentally at GABA_A-synapses subject to the propofol concentration c, together with the extreme values of p at the borders of the error bars. We propose to model the relation of p to the concentration c by

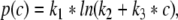which has been least mean square fitted to the experimental data with constants k₁, k₂, k₃. In addition Fig. 1b gives the corresponding mean and extreme values of the normalized charge transfer ρ(c)/ρ(0) obtained experimentally. To fit the function ρ(c)/ρ(0), we propose to fit the function

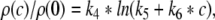where the constants k₄, k₅, k₆ are mean-least square fitted. Then the normalized charge transfer subjected to the factor p can be calculated from the latter fitted functions (15), (16) to

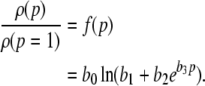with b₀ = k₄, b₁ = k₅ − k₂k₆/k₃, b₂ = k₆/k₃, b₃ = 1/k₁. Figure 1c presents this function, the corresponding functions obtained from the error borders and the model function (14) with r = 8.5. We observe that all curves show good agreement. Consequently the charge transfer model (14) is reasonable for β₂ ≈ 8.5β₁. Since the study on propofol effects in (Kitamura et al. 2002) are based on experiments on rats, it is interesting to link the results to humans. In human general anesthesia, the value EC₅₀ gives the concentration of the anesthetic agent for which 50 of 100 subjects are anesthesized, i.e. do not respond to external stimuli (Kuizenga et al. 1998) or surgical incision (de Jong and Eger 1975). For the administration of propofol, a typical concentration is 0.2 μM/ml (∼2 μg/ml) (Franks and Lieb 1994), which corresponds to p ≈ 1.2, cf. Fig. 1. For unit conversion of the propofol concentrations, the rule 1 μg ≈ 0.1 μM holds (Franks and Lieb 1994, Box 1).

Fig. 1.

Extraction of the charge transfer curve from experimental data (Fig. 6 in [Kitamura et al. 2002)] subjected to the factor p. a The experimentally measured mean (circles) percentile increase of the inhibitory decay time p = (1/β₁)/(1/β⁰₁), their maximum (squares) and minimum (diamonds) values at the error interval borders and the corresponding fitted functions (15) (dashed line for maximum values, dashed-dotted line for the mean value and dotted line for the minimum values). b The experimentally measured mean (circles) percentile increase of the charge transfer ρ(c)/ρ(0), their maximum (squares) and minimum (diamonds) values at the error interval borders and the corresponding functions (16). The line coding is the same as in a. c The calculated relation (17) for the mean values, the lower and upper value border and the model (14) (red solid line). The line coding is the same as in a

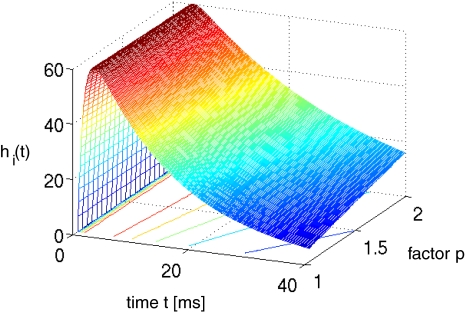
Summarizing, increasing the factor p prolongs the decay phase and increases the charge transfer in inhibitory synapses while maintaining the amplitude of the resulting IPSPs constant. Figure 2 shows the simulated temporal impulse response of an inhibitory GABA_A synapse h_i as a function of time and the factor p. We observe a constant amplitude and a prolonged decay phase for increasing p, as desired.

Fig. 2.

The temporal impulse response function h_i(t) of inhibitory GABA_A-synapses subject to various values of p taken from (3) and (14). Parameters are set to β⁰₁ = 75 Hz, β₂ = 1,000 Hz (Koch 1999)

The resting state

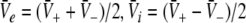To gain insight into the resting activity of the neural population, first let us investigate the stationary solutions of Eq. 11, which are assumed constant in space and time. For this purpose we introduce the new variables with and 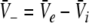is the stationary mean membrane potential. Then Eq. 11 decouple to

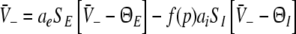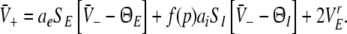Equations 18 and 19 reveal that it is sufficient to determine 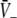from Eq. 18 to fi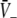nd and 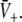Put differently, the number of solutions 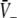gives the number of stationary solutions. As a first result, we find that a_e > f(p)a_i, Θ_E,Θ_I ≪ 0 and steep sigmoid functions S_E, S_I yield 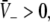and the corresponding firing rates take their maximum values 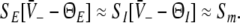In physiological terms, all neurons fire constantly and thus are highly excited.

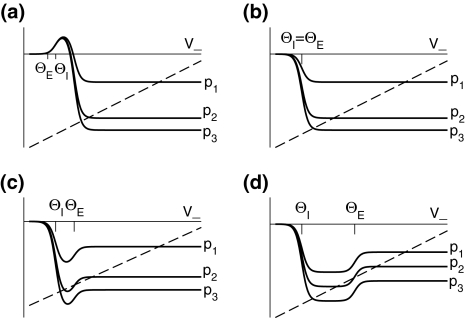
Figure 3 illustrates the conditions for different stationary solution types for identical steepness parameters c_e = c_i of the firing rate functions and different firing thresholds Θ_E, Θ_I. We observe that a single stationary solution 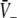occurs for all values of p if the firing threshold of excitatory neurons is equal to or lower than the threshold of inhibitory neurons, i.e. Θ_E ≤ Θ_I. In contrast, three stationary solutions may occur for some values of p if Θ_E > Θ_I. Moreover, three stationary solutions occur only for 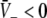and for stronger inhibition than excitation, i.e. a_e < f(p)a_i.

Fig. 3.

Construction of solutions of Eq. 18 for equal constants c_e = c_i and various firing thresholds Θ_e,Θ_i. The panels show the left hand side of (18), i.e. 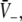encoded as the thin dashed diagonal, and the right hand side of (18), i.e.  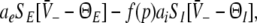decoded as thick solid lines. The plots are given for three parameters p₁ < p₂ < p₃. The vertical coordinates of the curve points are the values of the left and right hand side of (18) and the horizontal coordinate is 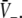By this graphical construction, the crossing points of the dashed line and the solid line give the stationary solutions 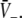In a the firing threshold of excitatory neurons Θ_E is lower than the threshold of inhibitory neurons Θ_I, b shows the case Θ_E = Θ_I, c Θ_E > Θ_I and d Θ_E ≫ Θ_I

In addition, Fig. 4 reveals that three stationary solutions may occur for different values of c_e, c_i and identical firing thresholds Θ_E = Θ_I, while a single stationary solution is present if c_e = c_i and Θ_E = Θ_I. A further detailed study also reveals three stationary solutions for c_e≠c_i and Θ_E≠Θ_I for some values of p (not shown). Summarizing these results,

• a single stationary solution occurs if Θ_E ≤ Θ_I and c_e = c_i. The resting state exhibits a membrane potential .

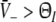• three stationary solutions occur otherwise for some values of p and .

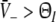Fig. 4.

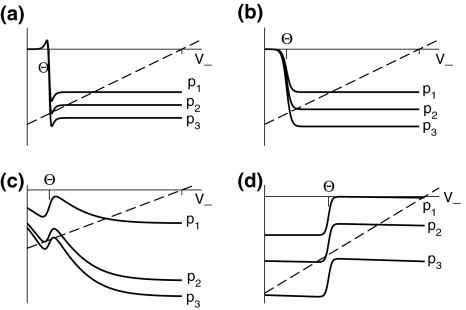
Construction of solutions of Eq. 18 for equal firing thresholds Θ_e = Θ_i = Θ and different constants c_e, c_i. The panels show the left hand side (thin dashed diagonal) and the right hand side (thick solid lines) of (18) for three parameters p₁ < p₂ < p₃. The crossing points of the dashed line and the solid line give the stationary solutions (a) illustrates the case c_e < c_i, (b) c_e = c_i, (c) c_e > c_i and (d) c_e ≫ c_i

In the context of propofol effects on neural populations, the three stationary solutions have been studied previously in some analytical details by Steyn-Ross et al. (2001a) and the single stationary solution has been considered numerically by Bojak and Liley (2005); Liley and Bojak (2005); Molaee-Ardekani et al. (2007). In the following, we refer to the case of the single stationary solution as the single solution case and to the case of three stationary solutions as the triple solution case.

An additional close look at Figs. 3 and 4 reveals that increasing p from p = 1 yields the monotonous decrease of the effective membrane potential 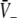and finally the saturation of 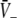to values close to the inhibitory firing threshold Θ_I for c_e − c_i not too large. This result is useful in later discussions of the EEG-power spectrum. Essentially to obtain the stationary solutions 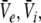one inserts the solutions 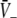into (19) to obtain 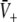and subsequently 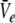and 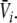Hence solving Eq. 18 suffices to obtain the stationary solutions 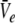and 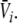In other words, the number of roots of Eq. 18 gives the number of stationary solutions for the two variables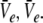

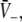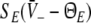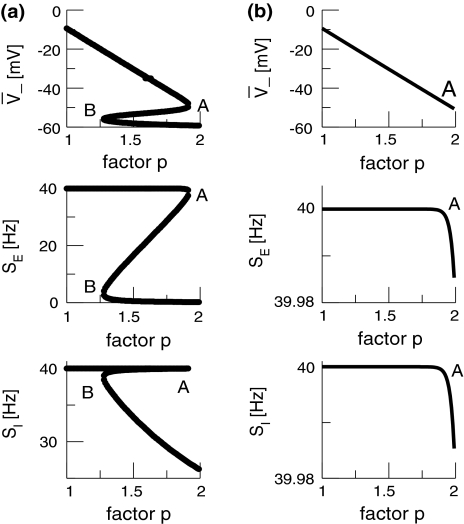
To gain further insights into the effect of increasing p, Fig. 5 shows the solutions and the resulting firing rates of excitatory and inhibitory neurons and 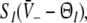resp., with respect to the weight factor p. In the triple solution case (Fig. 5a), the system starts at a high firing rate at p = 1 and shows an activity decrease up to point A. Then a further increase of p causes the stationary excitatory firing activity to discontinuously jump to smaller values. In addition we observe a top, center and bottom solution branch, similar to previous studies (Steyn-Ross et al. 2001a; Hutt and Schimansky-Geier 2008). Likewise, the single stationary solution (Fig. 5b) exhibits a decrease of the firing rate while increasing p. However, here the drop of activity is continuous and the firing rate changes less than in the triple solution case. Such a continuous decrease of the firing rate while increasing the propofol concentration has been reported experimentally in cultures of rat neocortical tissue (Antkowiak 1999).

Fig. 5.

The stationary solutions 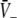of Eq. 18, the firing rates of excitatory and inhibitory neurons S_E = S_E(V₋ − Θ_E) and S_I = S_I(V₋ − Θ_I), respectively, for the triple (left) and the single (right) solution case. a Θ_E > Θ_I, c_e = c_i, b Θ_E = Θ_I,c_e = c_i. The specific parameters are a Θ_E = −53 mV, Θ_I = −60 mV, c_e = c_i = 0.84/mV, b Θ_E = Θ_I = −60 mV, c_e = c_i = 0.24/mV. Additional parameters are given in section "Methods"

In mathematical terms, the triple solution case exhibits a saddle-node bifurcation and the first discontinuous drop of activity at point A. This bifurcation occurs if the left and right hand side of Eq. 18 exhibit the same derivative with respect to 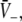i.e.

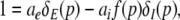cf. Figs. 3 and 4. Here δ_E(p) = ∂S_E[V(p) − Θ_E]/∂V, δ_I(p) = ∂S[V(p) − Θ_I]/∂V evaluated at 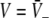represent the so-called non-linear gains of the system. Since δ_E(p), δ_I(p) are the slopes of the transfer functions S_E, S_I, they reflect the conversion of membrane potentials to the spike firing activity.

In contrast to the triple solution case, the single stationary solution does not show this activity drop and exhibits 1 > a_eδ_E(p) − a_if(p)δ_I(p) for all values of p, i.e. condition (20) never holds.

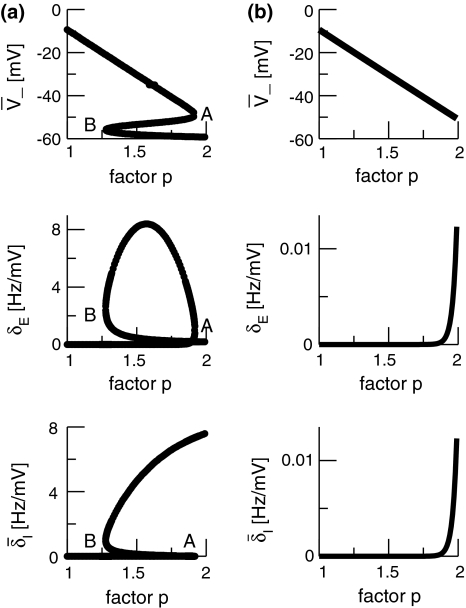
To learn more about the nonlinear gains and condition (20), Fig. 6 shows the nonlinear gain for excitatory neurons δ_E and the effective gain for inhibitory neurons 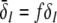with respect to p for both solution cases. Here 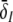represents the effective gain of the inhibitory neurons considering the propofol effect. We observe negligible excitatory and inhibitory gains for p ≈ 1, while larger p yields increased gains. In the triple solution case shown in Fig. 6a the upper and lower branch of 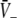exhibits low 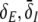and the center branch of 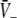between points A and B shows high gains since Eq. 20 holds at points A and B. Moreover, high values of p result again in low In addition, point A represents the saddle-node bifurcation point between the top and the center branch and denotes the right turning point in δ_E(p) but not the right turning point in 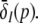This difference between δ_E(p) and 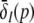results from the different firing thresholds Θ_E > Θ_I. Figure 6b gives the nonlinear gains for the single solution case and reveals a fast increase of the nonlinear gains at high values of p and the nonlinear gains do not return to low values. Summarizing,

• in the single solution case the nonlinear gains increase with increasing p, i.e. dδ_E(p)/dp, d(fδ_I)(p)/dp > 0, and 1 > a_eδ_E(p) − a_if(p)δ_I(p).

• in the triple solution case, the increase of p yields the increase (decrease) of nonlinear gains on the top (bottom) solution branch, while the center branch exhibits increasing and decreasing nonlinear gains. Moreover 1 > a_eδ_E(p) − a_if(p)δ_I(p) on the top and bottom branch, while 1 < a_eδ_E(p) − a_if(p)δ_I(p) on the center branch.

Fig. 6.

The nonlinear gains of excitatory and inhibitory neurons δ_E(p) and 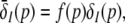respectively. a Θ_E > Θ_I, c_e = c_i, b Θ_E = Θ_I, c_e = c_i. In a the points A and B denote the saddle-node bifurcation points (top panel), represents the right (A) and left (B) turning points of δ_E where dδ_E/dp → ∞ (center panel). In addition in the bottom panel A and B mark the values of 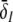corresponding to the top and center panel. The parameters are taken from Fig. 5

The next section shows the occurrence conditions and the number of homogeneous stationary states, which may be present in the neural population. Further Fig. 6 illustrates the properties of the nonlinear gains, which will turn out later to be important to understand the systems dynamics.

Linear stability

So far we have described the deterministic stationary states of the system. It is more biophysically realistic to include the effect of fluctuations, and investigate their effect on the existence of these states. Such fluctuations are omnipresent in real neural populations and may originate from internal random fluctuations of membrane and synaptic properties (Destexhe and Contreras 2006; Koch 1999) or external inputs from other populations. If the system’s activity remains close to the stationary state in the presence of small fluctuations, then the resting state is linearly stable and the system evolves close to the vicinity of the stationary state. If the stationary state is unstable, small fluctuations make the system leave the vicinity of the stationary state. The following paragraphs give the conditions on the stability of the resting state and hence the evolution in its vicinity.

For small deviations 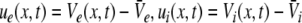from the stationary state, the evolution Eq. 11 reads

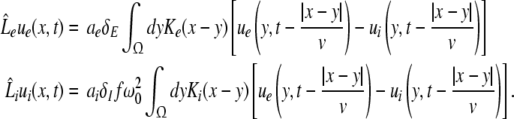Then applying the spatial Fourier transform we obtain

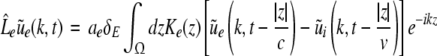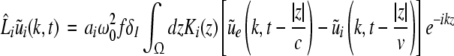with the Fourier transforms of the small deviations 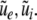The Eqs. 22 and 23 involve distributed delays and the spatial kernel functions K_e, K_i define the delay distribution functions (Hutt and Frank 2005). They define the temporal evolution of the Fourier transform of u_e(x,t), u_i(x,t) and give the dynamics of the spatial mode k with wavelength 2π/k. For example, the spatial mode k = 0 represents the spatially constant contribution to the spatio-temporal dynamics of the system.

The Laplace transform of Eqs. 22 and 23 in time yields conditions on the linear stability of the stationary state. The same conditions can be obtained by inserting the ansatz 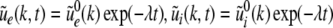into Eqs. 22 and 23. Then 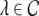is the Lyapunov exponent and yields

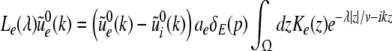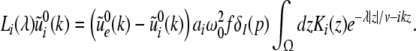Additionally let us assume the spatial kernels of the form K(x) = M(x/σ)/σ. This assumption does not limit the validity of the subsequent analysis steps, which also hold for general kernels (Atay and Hutt 2005), but simplifies the discussion of the propagation delay. Then the integrals in (24), (25) can be written as

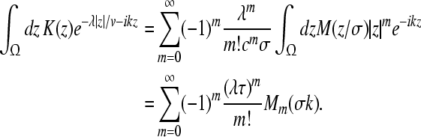with the characteristic propagation delay τ ≡ σ/v and the kernel Fourier moments (Atay and Hutt 2005)

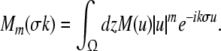If τλ ≪ 1, i.e. the propagation delay is much smaller than the smallest time scale in the system 1/λ, then

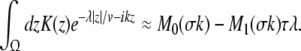Finally inserting the approximation (26) into Eqs. 24 and 25, the characteristic equation reads

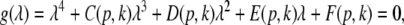with the prefactors 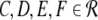defined in the Appendix section “Variables from section “Linear stability””. This result is valid for all spatial interaction kernels K_E(x), K_I(x) and second-order synaptic response functions h_e, h_i. The real part of the Lyapunov exponent λ defines the linear stability of the spatial mode k, i.e. Re(λ) < 0 reflects stability. The prefactors C, D, E, F depend on the nonlinear gains δ_E(p), δ_I(p) and hence the nonlinear gains affect the stability of spatial mode k, cf. Eq. 51 in the Appendix section “Variables from section “Linear stability””.

Now let us discuss the conditions of stability loss of the resting state while increasing p. In the following we distinguish the non-oscillatory instability with the specific cases k = 0 and k ≠ 0 as well as the oscillatory instability in time. In the case of Im(λ) = 0 the resting state becomes unstable by changing the sign of the Lyapunov exponent, i.e. λ crosses the imaginary axes at Re(λ) = 0 when p approaches the critical value p_c. In other words the unstable state does not oscillate at the stability threshold, i.e. it is non-oscillatory in time. From (27) we find the condition F(p,k) = 0 or more explicitly

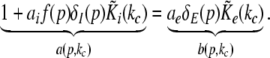This condition defines the critical wave number k_c and does not depend on the synaptic time scales and the conduction speed in accordance with previous studies on populations of a single neuron type (Hutt et al. 2003; Atay and Hutt 2005; Venkov et al. 2007).

Considering the loss of stability to the spatially homogeneous state (k = 0) the threshold condition reads 1 = δ_E(p)a_e − f(p)δ_I(p)a_i which coincides with the condition (20) for the points A and B, cf. Fig. 6. Since A and B exist in the triple solution case only and 1 > δ_E(p)a_e − f(p)δ_I(p)a_i for p = 1, we conclude that the center branch of the triple solution case (Fig. 5a) is unstable. Moreover, the stationary state in the single solution case does not show a non-oscillatory transition with k = 0 while increasing p from p = 1, since 1 = δ_E(p)a_e − f(p)δ_I(p)a_i never holds. In addition to the case k = 0, the resting state may lose its stability towards spatially periodic states with k ≠ 0; this is not further discussed here.

The oscillatory instability stipulates Im(λ) ≠ 0, and the separation of real and imaginary part of λ in (27) and 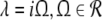yields the conditions

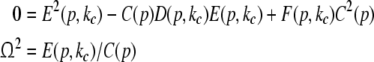with the critical frequency Ω and the corresponding wave number k_c. In contrast to the previous non-oscillatory transitions, Ω and k_c depend on the propagation speed and the synaptic time scales.

Stability conditions in the absence of propofol

For p = 1, the stationary state reflects the resting state at the absence of propofol. Assuming that this resting state is stable, the detailed analysis of Eqs. 28 and 29 for p = 1 yields the parameter regime for stable states and thus constrains the range of reasonable parameters. To begin with Fig. 6 shows that δ_E(1) ≈ 0, δ_I(1) ≈ 0. Consequently Eq. 28 does not hold and the resting state does not lose stability by a non-oscillatory instability. Further all polynomial pre-factors in Eq. 29 become positive and depend on the synaptic scales only, see Appendix section “Variables from section “Linear stability””. Then solving the polynomial (29) for E > 0, we find the condition

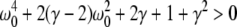with γ = γ_eγ_i and the stability is defined by the two dimensionless variables γ = (α₁ + α₂)(β₁ + β₂)/α₁α₂ and ω²₀ = β₁β₂/α₁α₂. Moreover we find that the resting state can not lose stability by an oscillatory instability either if γ ≥ 1/2 or

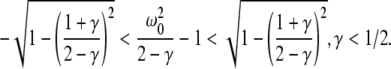Then considering the definition of ω₀ and γ, the result β₂ ≈ 8.5β₁ from section "The weighting factor p" stipulates

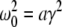with a = (8.5/9.5²)α₁α₂/(α₁ + α₂)² and the instability condition γ < 1/2 leads to

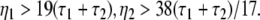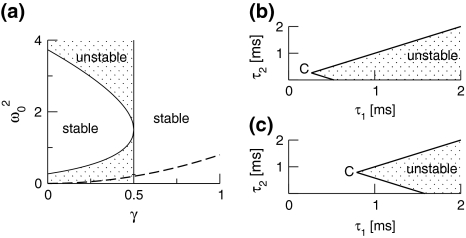
Here τ₂ = 1/α₂,τ₁ = 1/α₁ are the rise and decay times of excitatory synapses and η₂ = 1/β₂, η₁ = 1/β₁ the corresponding time constants of inhibitory synapses. Figure 7a illustrates the stability regime with respect to γ and ω²₀ based on Eq. 30. We observe that the resting state is unstable for γ < 1/2 only, whereas γ > 1/2 reflects a stable resting state. In addition, Fig. 7a reveals that the specific result β₂ ≈ 8.5β₁ yields unstable and stable solutions for γ < 1/2 and γ ≥ 1/2, respectively. The corresponding analytical study shows that this result holds true for all excitatory and inhibitory time scales (not shown).

Fig. 7.

Stability regimes of the resting state at p = 1, i.e. prior to the administration of propofol. a The stable regime is given by Eq. 30 for γ < 1/2, while γ ≥ 1/2 leads to stability for all ω²₀. The specific result β₂ ≈ 8.5β₁ yields the specific solutions (31) represented by the dashed line: for γ < 1/2 the solutions are unstable and for γ ≥ 1/2 they are stable. b, c show the stability regime with respect to the excitatory time scales τ₁, τ₂ for the specific case β₂ = 8.5β₁ according to Eq. 32. The border point C is located at τ₁ = τ₂ = η₁/38. b η₁ = 10ms, c η₁ = 30ms.

Moreover Fig. 7b, c show the instability regime for β₂ ≈ 8.5β₁ with respect to the excitatory synaptic time scales τ₁,τ₂ and the inhibitory decay time η₁. One observes that very small excitatory time scales destabilize the resting state. Further the increase of inhibitory time scales decreases the instability regime and shifts the critical excitatory time scales to higher values. Consequently large inhibitory decay times stabilize the resting state.

The general power spectrum

A prominent measure to determine the depth of general anesthesia are electrophysiological monitors, which are based on the power spectrum of the subject’s electroencephalogram (EEG), see e.g. (John and Prichep 2005). Most of these monitors are indices, i.e. numbers, which reflect the change of the EEG-power spectrum while changing the level of propofol concentration. The most prominent effect is the biphasic change of the power spectrum while increasing the propofol concentration, i.e. the increase and then decrease of spectral power in the δ-, θ-, α- and β-band. This biphasic behavior has been found both in rats (Dutta et al. 1997) and humans (Kuizenga et al. 2001; Fell et al. 2005; Han et al. 2005).

To model this change of the power spectrum with respect to the factor p reflecting the propofol concentration, the subsequent paragraphs derive the power spectrum of Local Field Potentials (LFP) and the EEG. The derivation of the power spectrum follows previous studies on the effect of finite axonal conduction speed on the activity of neural populations involving a single neuron type (Hutt and Atay 2007; Hutt and Frank 2005).

The power spectrum represents a statistical measure of the system’s linear response to a spatio-temporal external input. This input might originate from other neural populations or might represent direct external stimulation, as in (Hutt et al. 2008; Masuda et al. 2005; Chacron et al. 2005), and is assumed small compared to the resting states 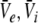defined by Eq. 19. Then Lyapunov’s stability theorem states that the stability of the driven system is determined by the undriven system. Consequently the stability criteria in section "Linear stability" still hold. Moreover the power spectrum is defined in the linear regime and the system remains about the resting state if it is linearly stable. Hence the subsequent analysis steps are valid only if the system is stable. However if the system approaches its instability point, critical fluctuations occur and the spectral power diverges (Hutt and Frank 2005). In the following, we assume the system to be stable, i.e. the roots of Eq. 27 have negative real parts, and the dynamics of the corresponding stable spatial modes define the spectral properties of the LFP and EEG.

Considering the excitatory external input Γ(x,t) and the identities 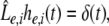Eq. 21 read

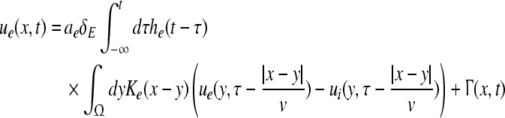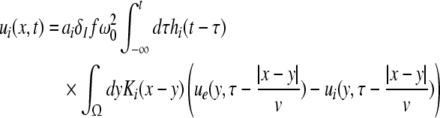The variables u_e and u_i denote the deviations of the PSPs V_e and V_i from the stationary state and are linearly dependent on the evoked currents in the membrane, that are present in the dendritic tree and its surrounding. Moreover, the evoked currents propagate along the dendritic branch towards and away from the trigger zone at the neuron soma. Since excitatory and inhibitory currents add up at the trigger zone and have different signs, the corresponding potentials also sum up at the trigger zone. This means the effective membrane potential u_e − i_i is proportional to the current that flows in the tissue close to the dendritic branch and along the dendritic branch. This physical effect is supposed to represent the origin of the EEG since the evoked current represents a current dipole that generates the electromagnetic activity on the scalp. We mention the important work of Paul Nunez on this topic, see e.g. (Nunez 1974, 2000, 1981) and (Nunez and Srinivasan 2006, section 1.7). Such currents are measured experimentally by electrodes in the neural tissue and the corresponding potentials are the LFPs. Consequently LFPs reflect the dendritic currents or correspondingly the membrane potentials on the dendrites (Nicholson and Freeman 1975; Freeman 1992). Since the EEG represents the spatial average of the dendritic activity (Nunez 2000), we consider the effective membrane potential u(x,t) = u_e(x,t) − u_i(x,t) which is proportional to the dendritic currents, see e.g. (Freeman 1992; Nunez 1974; Nunez and Srinivasan 2006) for the physical details. Moreover we point out that u_e − u_i represents the difference of PSP that is identical at excitatory and inhibitory neurons, as found while deriving Eq. 11 in section "Methods".

Moreover the system is assumed to be in a stationary state in the presence of the external stationary input. Then the ergodicity assumption holds and the power spectrum of u(x,t), i.e. the LFP, at the spatial location x is given by the relation

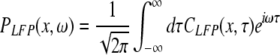with the autocorrelation function C_LFP(x,τ) = 〈u(x,t)u(x,t − τ)〉 and the ensemble average 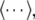i.e. the average over many realizations.

The external input to the network Γ(x,t) represents the excitatory synaptic responses to random fluctuations uncorrelated in space and time ξ(x,t) with 〈ξ(x,t)〉 = 0, 〈ξ(x,t)ξ(y,T)〉 = Qδ(x − y)δ(t − T) and the fluctuation strength Q. Then the input reads

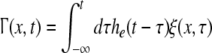with the synaptic response function h_e(t) taken from Eq. 2. To obtain the autocorrelation function, we apply standard linear response theory (see the Appendix section "The autocorrelation function").

The power spectrum of LFPs

The correlation function C_LFP(x,τ) reads

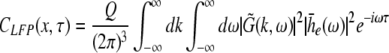and the power spectrum is given by

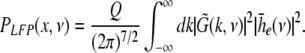with the frequency ν = ω/2π. Equations 37 and 38 reveal that the correlation function and the power spectrum are independent of the spatial location which reflects the spatial homogeneity of the population.

The power spectrum of the EEG

To obtain the power spectrum of the EEG, we take into account the large distance of the EEG-electrode from the neural sources and the spatial low-pass filtering of the scalp and bone (Srinivasan et al. 1998; Nunez and Srinivasan 2006). Then as a first good approximation the EEG activity represents the spatial summation of electric activity

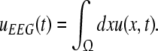Here we assume that the EEG-electrodes are far from the neural population compared to the spatial extension of the population. This is reasonable since EEG is measured on the scalp, which typically has a distance of a few centimeters from neural areas with a diameter of a few millimeters (Nunez 1995). Interestingly we find 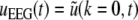with the Fourier transform in space 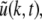i.e. the activity measured at the EEG-electrode just considers the spatially constant mode. This result also reflects the spatial low-pass filtering of the bone and scalp. In this context we mention previous studies which reveal effects of periodic spatial modes with k ≠ 0 (Nunez and Srinivasan 2006; Robinson et al. 2001). These studies show that modes with k > 0 contribute to the electric activity on the scalp and, for instance, affects the corresponding power spectrum but retain the power peaks (Robinson et al. 2001). Since the detailed study of the different mode contributions may exceed the major aim of the present study, the subsequent paragraphs consider k = 0 for the EEG power spectrum. Further assuming the external input as the excitatory synaptic response to uncorrelated random fluctuations, the similar application of the previous analysis steps yields

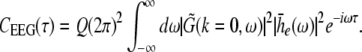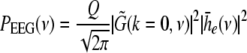with the fluctuation strength Q.

We observe that the EEG reflects the dynamics of the constant spatial mode with k = 0, i.e. the mean spatial activity, in contrast to the LFPs in Eqs. 37 and 38. Hence, the LFP considers all spatial modes whereas the EEG takes into account just the constant mode. This difference between EEG and LFP is expected to yield different power spectra of LFP and EEG. The effect of spatial modes on the power spectrum in neural populations has been investigated in great detail by Robinson’s group (Rennie et al. 2002; Robinson et al. 2001, 2004; Robinson 2003). Further we mention the study of Fell et al. (2005), who measured synchronously the EEG on the scalp and Local Field Potentials intracranially in humans as a function of the propofol concentration. They found, amongst other effects, that the power spectra of EEG and LFP had similar dependences on the propofol concentration. Consequently, this finding suggests that the major contribution to the propofol-induced changes in spectral power are due to the spatially constant mode. To this end, the subsequent section focusses on the EEG-power spectrum. Moreover it is important to note that the propofol-induced changes of the power spectrum have been found in invivo setups, in which neural populations are part of the brain network and thus the EEG-power changes may originate from the interactions of the population with other populations. From this point of view, the following paragraphs aim to answer the question whether a single neural population may generate the effects or a network of populations is necessary.

Biphasic EEG-power spectrum

A prominent experimental effect of propofol on neural populations is the biphasic power spectrum, i.e. the power increase and decrease at low and high frequencies while increasing the anesthetics concentration (Fell et al. 2005; Dutta et al. 1997; Forrest et al. 1994). In the following, we first study the increase and decrease of the power at low frequencies, and then reveal the biphasic power spectrum also at higher frequencies. Then an additional criterion for large frequencies allows an extended analysis.

The power increase at low frequencies is studied by choosing ν = 0 in Eq. 41 leading to

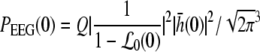with

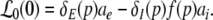Then dP_EEG(0)/dp > 0, i.e. the power increase at ν = 0 with increasing propofol concentration, yields

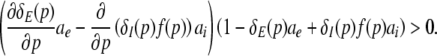Hence the condition

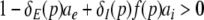requires a_e∂δ_E(p)/∂p − a_i∂(δ_I(p)f(p))/∂p > 0 or

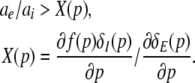The following paragraphs discuss the validity of the assumption (45).

Single solution case

This type of stationary solution occurs for 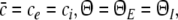i.e. δ = δ_E = δ_I and condition (45) reads 1 − δ(a_e − a_if) > 0 and holds for all p, cf. Eq. 28 for k_c = 0. Lengthy calculations yield

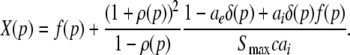with 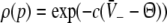and 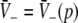. We find that X(p) increases with increasing p for all p, i.e. dX/dp > 0 (Appendix section "dX/dp > 0 in single stationary solutions"). Hence remembering that the minimal value of p is 1, it follows that:

• if a_e/a_i < X(1), then condition (46) never holds and the power at low frequencies decreases with increasing propofol concentration.

• if a_e/a_i ≥ X(1), then there is a threshold value of the propofol concentration p_c for which a_e/a_i = X(p_c) and the power at low frequencies increases for 1 ≤ p ≤ p_c and decreases for p > p_c.

Considering the definition of X(p) in (46), the condition a_e/a_i ≥ X(1) reads

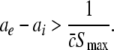This inequality relates the synaptic efficacy of both synapse types (left hand side) to the properties of the population firing rate function of the neurons (right hand side). Since 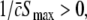Eq. 48 reveals a power enhancement in low frequencies if the population excitation is larger than its inhibition at the absence of propofol. Together with the previous constraint a_e < f(p)a_i, the single stationary solution exhibits power enhancement for 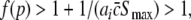i.e. for p > 1. Figure 8 shows the values of p with respect to 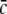for which the power enhancement occurs at low frequencies.

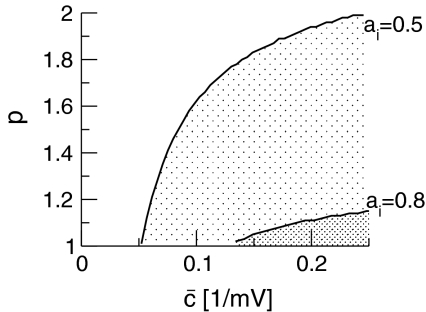
Fig. 8.

Parameter regime of power enhancement for single stationary solutions. The shaded areas give the parameter regime for p and 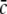where the power is enhanced in the δ-frequency band. Parameters are a_e = 1.0mVs, Θ_E = Θ_I = −60mV, with other parameters taken from section "Methods"

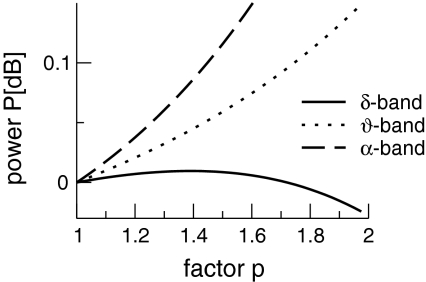
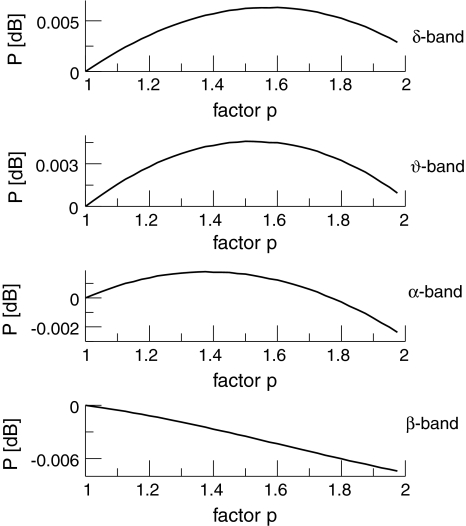
This enhancement is also visible in the spectral band power computed from (41) at low temporal frequencies (Fig. 9). We observe a power increase in the θ- and α-band and a sequential increase and decrease of power in the δ-band.

Fig. 9.

The spectral power in different frequency bands in the single solution case. p is the power enhancement and defined as p = 10log₁₀ (P_EEG(ν)/P_EEG(0)). The frequency bands are defined in the intervals [0.1 Hz;4 Hz] (δ-band), [4 Hz;8 Hz] (θ-band) and [8 Hz;12 Hz] (α-band). Here c_e = c_i = 0.06/mV and other parameters are taken from Fig. 8 and section "Methods"

Triple solution case

This type of resting state exists if 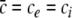and Θ_E > Θ_I as found in section "The resting state". The condition (45) holds for the top and bottom solution branch which may be stable for some values of p, while the solutions on the center branch are linearly unstable for all p (section "Linear stability") and do not satisfy (45). Since Eq. 41 gives the power spectrum for stable solutions, the subsequent paragraphs consider the top and bottom branch only.

The condition (46) reads

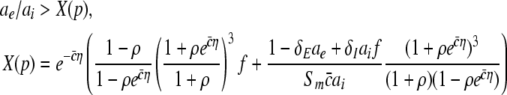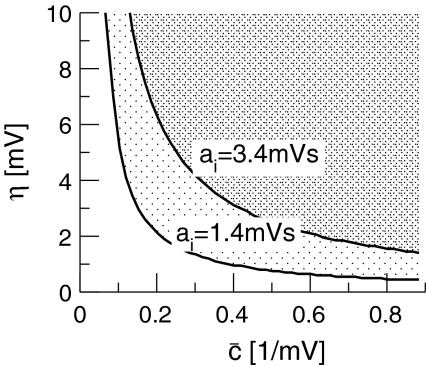
with 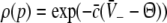and η = Θ_E − Θ_I > 0. In contrast to the previous single stationary solution, here dX/dp may take positive or negative values while increasing p. Figure 10 presents the parameter regime of (49) for which the power at low frequencies increases while increasing p, i.e. dP_EEG/dp > 0. Since η is the difference of the excitatory and inhibitory firing thresholds and 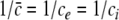reflects the slope of the corresponding firing rate functions and the width of the firing rate threshold distribution, the parameter regime of the power enhancement is large for shallow firing rate functions (corresponding to a large spread of firing thresholds).

Fig. 10.

The parameter regime of power enhancement at low frequencies for triple solutions according to Eq. 49. Here the upper branch of stationary solutions is considered. The corresponding regimes lie above the corresponding lines. The shaded areas give the parameter regime of η and where the power is enhanced in the δ-frequency band. Here a_e = 1.0 mVs and other parameters are taken from section "Methods"

The latter treatment assumes that the systems activity remains close to the stationary state, i.e. either on the top or on the bottom branch. Moreover it is well-known from stochastic dynamics that the system may also jump from one branch to the other due to the external noise as known e.g. in stochastic resonance (Gammaitoni et al. 1998). Since the analytical treatment of the corresponding power spectrum would exceed the aim of the present work, we neglect such jumps.

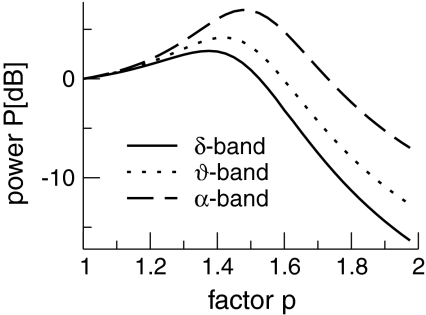
Essentially Fig. 11 shows the computed EEG-spectral power for the top branch according to Eq. 41 and reveals the sequential power increase and decrease in the δ-, θ- and the α band, i.e. biphasic behaviour. Since the condition (49) holds for the bottom solution branch as well, the power spectrum behavior with respect to p in Fig. 11 is expected to be also valid on the bottom solution branch. For further corresponding details, we refer to future work.

Fig. 11.

The spectral power enhancement on the top branch of the triple stationary solutions. The definition of p and the frequency bands are given in Fig. 9. Parameters are Θ_E = −50 mV, Θ_I = −60 mV, c_e = c_i = 0.114/mV, others are taken from Fig. 10

Comparison to general anesthesia

At a first glance the previous sequential increase and decrease of the EEG-power resembles the biphasic behavior found in propofol-induced general anesthesia. In addition, a closer look at Fig. 11 reveals a subtle difference to general anesthesia: the δ-power increases and decreases before the θ- and α-power follows, while the power spectra in general anesthesia reveal the power enhancement and attenuation at high frequencies first, followed by enhancement and attenuation at low frequencies. Consequently the theoretical results obtained are close to the experimental findings, but the sequence of enhancement and attenuation are the reverse of what is seen in experiments. The subsequent paragraphs investigates this reverse power spectrum behavior briefly.

We keep the condition dP_EEG(0)/dp > 0 and add the condition dP_EEG(ν)/dp < 0 at high frequencies ν. Similar to the previous paragraphs, the calculation of the Greens’ function 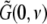leads to an expression of the power spectrum p_EEG(ν), see Appendix section "The power spectrum for large frequencies" for more details. The power spectrum is valid for both the single and triple solution case. Moreover, for a large but finite axonal conduction speed, we find the conditions

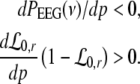In addition the condition for the power enhancement at low frequencies holds, i.e. a_e/a_i > X(p) with X(p) taken from (46). Consequently both conditions (50) and (46) define the parameter set for bi-phasic behavior. In the following we focus on the single solution case and apply a numerical parameter search in 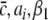which satisfies conditions (50) and (46) considering the previous result β₂ = 8.5β₁. Figure 12 presents the spectral power for a set of parameters obtained numerically. The power in the δ-,θ- and α-band exhibits a sequential increase and decrease of power in according to experiments. Moreover the maxima of the α- and δ-,θ-power occur at p ≈ 1.4 and p ≈ 1.6 and thus at concentrations 1 μM (∼0.5 μg) and 2 μM (∼1.1 μg), respectively. This result shows good accordance to the biphasic behavior observed experimentally in general anesthesia.

Fig. 12.

The spectral power of the single solution case with respect to p. The definition of P and the frequency bands are taken from Fig. 9. Parameters are Θ_E = Θ_I = −60 mV, c_e = c_i = 0.038/mV, a_e = 1.0 mVs, a_i = 0.2 mVs, β₂ = 5780 Hz, β₁ = 680 Hz, others are taken from Fig. 8

Hence the sequence order of enhancement and attenuation depends on specific parameters, at least on the single branch of solutions, and our model can thus be made compatible not only with the experimentally observed non-monotonic behavior of the power in the different bands, but also with the observed order in which the different spectral bands go through their maxima.

Considering the previous results, we learn that the bi-phasic power spectrum can be modelled both in the single and the triple solution case. Since the biphasic spectrum is an omnipresent feature in experimentally observed GA, we conclude that the present model can reproduce this experimental feature. This result also indicates that the assumption of a single neural population appears reasonable to explain the power spectrum of GA and no global network interaction is necessary.

Discussion

The present work aims to obtain some insight into the effect of propofol on neural populations. At first we derived a neural population model for anesthetic effects which, to our best knowledge, is the first to study the system's power spectrum in the presence of nonlocal interactions. The model extends previous standard neural field models of a single cell type (Atay and Hutt 2005) by an additional cell population and the action of propofol on the neural field. In addition, it extends a previous model involving two cell types (Hutt and Schimansky-Geier 2008) by the a realistic model for the inhibitory action of anesthetic agents. Moreover, the model is rather simple due to its two field variables and two evolution equations compared to other models such as the Steyn-Ross-model (Steyn-Ross et al. 2001a) with 12 field variables and 8 evolution equations. Further we have derived the relation of the inhibitory synaptic charge transfer and the scaling factor of the inhibitory synaptic decay time f(p) in section "The weighting factor p". In addition the subsequent modeling study of experimental results reveals the necessary condition β₂/β₁ = 8.5 that represents the condition between the rise and decay time of the inhibitory synaptic response. This relation guarantees the constancy of the amplitude of evoked inhibitory postsynaptic potentials with respect to the propofol concentration as found in experiments.

The subsequent sections investigate the resting state and its stability. We showed that the increase of the propofol concentration may render the resting state bistable (triple solution case) or monostable (single solution case). The former case has been investigated in detail in previous studies (Steyn-Ross et al. 2001a; Wilson et al. 2006), while the latter monostable case has been investigated by Molaee-Ardekani et al. (2007); Bojak and Liley (2005). Section "The resting state" reveals the existence of monostable states for excitatory firing thresholds lower than inhibitory thresholds at equal nonlinear gains, while the bistable resting state may occur for all other parameter sets. Hence the resting state may be bistable for some propofol concentrations for most sets of physiological parameters. We point out that the present work considers both cases.

Moreover section "The resting state" reveals a fast drop of the firing rate at larger propofol concentration, which reflects reduced resting state neural activity. This reduction of the firing rate has been found experimentally in cortical tissue slices (Antkowiak 1999). Further one may argue that the reduced resting activity indicates worse information transmission yielding LOC (Steyn-Ross et al. 2001a), which however is still an open question.

In healthy subjects, the resting state is expected to be stable in the absence of propofol. Section "Stability conditions in the absence of propofol" reveals the necessary conditions for the linear stability of the stationary state of the neuronal population. We find in particular that the relation of the sum of the excitatory synaptic time scales to the time scales of the inhibitory synapses plays an important role. This finding may be important for future modeling studies and even may be compared to experimental measurements

Further the derivation of the power spectrum in section "The general power spectrum" takes into account both the excitatory and inhibitory membrane potentials, whose difference represents the effective membrane potential (Freeman 1992) or, equivalently, the effective dendritic current generating experimental signals such as LFPs (Nicholson and Freeman 1975) and EEG (Nunez 2000). This approach is different to most previous studies of the power spectrum of neural populations (Steyn-Ross et al. 2001a; Wilson et al. 2006; Molaee-Ardekani et al. 2007; Bojak and Liley 2005; Liley and Bojak 2005; Rennie et al. 2002; Robinson 2003; Robinson et al. 2004), which consider the power spectrum of either the excitatory or inhibitory membrane potential only.

Moreover, the analytical study of the EEG-power spectrum in 3.6 reveals biphasic power spectra in both the single solution case and the triple solution case and reproduces the strong activity enhancement in the δ-frequency band observed in experiments. In this context it is interesting to note that Steyn-Ross et al. (Steyn-Ross et al. 2001a; Wilson et al. 2006) suppose the biphasic power spectrum observed in general anesthesia to originate from a first-order phase transition and thus assume the triple solution case. In contrast Liley and Bojak (Bojak and Liley 2005; Liley and Bojak 2005) and Molaee-Ardekani et al. (Molaee-Ardekani et al. 2007) treat a monostable resting state and also show biphasic power spectra indicating that first-order phase transitions are not compulsory to gain biphasic behavior. Hence our result supports both the findings of Liley, Bojak and Molaee-Ardekani et al., i.e. the bi-phasic power spectra may emerge in the presence of a single resting state, and the results of Steyn-Ross et al. who suppose an instability as the origin of the biphasic behavior. However in contrast to these studies, we performed a detailed analytical study and derived parameter conditions for both cases.

In addition, we point out that the LOC has been observed to be strongly related to the bi-phasic EEG-power spectrum which, our model predicts, may occur both in monostable and bistable systems. Consequently our results on the power spectrum concludes that the LOC may occur in both systems. It is interesting to note that the propofol concentration of LOC measured in experiments is larger than the propofol concentration of the return of consciousness (ROC), see e.g. (Wessen et al. 1993), i.e. a hysteresis effect is present. Previous studies indicate that this effect might not be fully explained by the pharmaco-kinetics of propofol (Kazama et al. 1998) and, in the context of our work, hence indicates the presence of a triple solution case. Since the present work studies in detail the bi-phasic power spectrum and not the origin of the LOC and ROC, the question of hysteresis is not attacked but may represent an exciting topic for future research.

Considering the results obtained, it is interesting to note that previous studies and the proposed model allow for the description of similar effects, e.g. the single and triple case of stationary solutions and the biphasic power spectrum although the models are different. The reason for the similarity of some of the results originates from the common major elements of neural populations in the models, namely the non-linear transfer function of membrane potentials to the population firing rate (typically a sigmoidal function), the involvement of two cell types (excitatory and inhibitory neurons) and the response function of both excitatory and inhibitory synapses. These elements may be viewed as the key elements in the neural population. Moreover, both the previous studies and the present work assume a single cell population, i.e. a single spatial domain, to reproduce the experimental biphasic power spectrum while neglecting any global network interaction. This result indicates that the generation of the bi-phasic power spectrum is rather unspecific to brain areas and does not depend on network interactions.

To verify the model assumptions and the corresponding theoretical results, various quantities may be verified by future experiments in cortical or subcortical areas. For instance the dependence of the experimentally obtained population firing rate on the propofol concentration as shown in Fig. 5 may give interesting insight into the basic assumption of a sigmoidal transfer function and the effect of propofol on the inhibitory synapses. Further the measurement of the rise and decay-time of inhibitory synapses subjected to the propofol concentration may verify the derived condition β₂/β₁ = 8.5 and thus indicate the validity of the derived function f(p). Finally the measurement of excitatory and inhibitory synaptic time scales may verify the stability conditions for the resting state in the absence of propofol.

The theoretical study of anesthetic agents and their effect on the neural processing remains challenging in many aspects due to its functional diversity such as synaptic receptor desensitization (Bai et al. 1999), off-synaptic action (Pittson et al. 2004; Franks 2008) or its action on the cerebral blood flow (Kaisti et al. 2002). In addition the importance of the interactions between brain structures is still under discussion, since anesthetic agents affect the neural activity in both invitro slices and invivo networks. Nevertheless theoretical studies of isolated neural populations may yield important insights, since they may answer the question on the major underlying neural mechanisms: which minimum assumptions and mechanisms are necessary to implement in a model to reproduce sufficiently the experimental findings? The answer may be found by reduced models such as the one presented here which consider basic mechanisms of neural populations such as synaptic response functions and nonlinear threshold dynamics of neurons. Future work may continue on the analytical treatment of the power spectrum in the presence of two stationary stable states to gain further analytical conditions on physiological parameters. Moreover the consideration of a neural population in two spatial dimensions and an additional neural population, e.g. the thalamus, may render the model more realistic and promises new insights into the effects of anesthetic agents.

Appendix

Variables from section "Linear stability"

This section gives the polynomial constants of the characteristic Eq. 27:

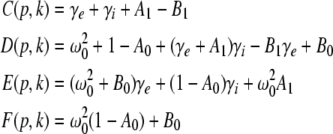with

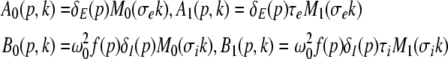and τ_e = σ_e/v,τ_i = σ_i/v. For p = 1, δ_E, δ_I ≈ 0 and A₀, B₀, A₁, B₁ ≈ 0. Hence the pre-factors of the polynom (27) read

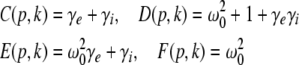The autocorrelation function

To obtain the effective membrane potential u(x,t) in section "The general power spectrum", we may write

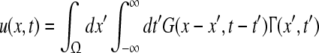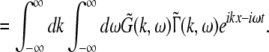Here G(x,t) is the Greens’ function of the system, 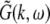denotes its Fourier transform and 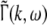is the Fourier transform of the external stimulus Γ(x,t). Considering (53), then the correlation function reads

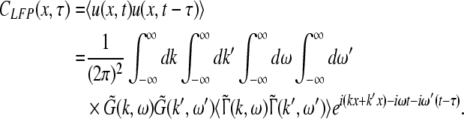Since the power spectrum p_LFP(x,ω) is defined by C_LFP(x,τ), we deduce from (54) that the power spectrum is determined by the Fourier transform of the Greens’ function 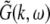and the input correlation function in Fourier space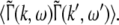

The Greens’ function

To compute the Greens function, we apply the Fourier transform in space to Eqs. 33 and 34, and obtain

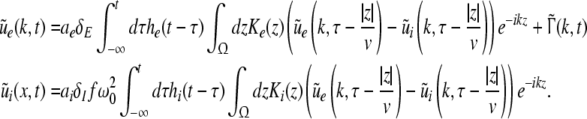Then it follows that

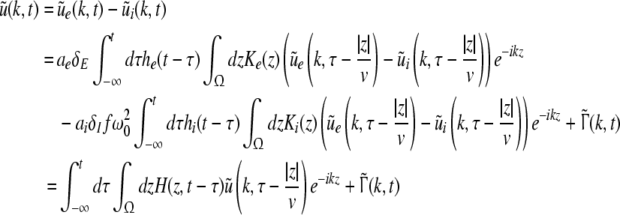with

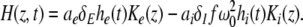In addition

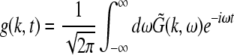is the spatial Fourier transform of G(x,t) and we write 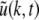using (52) as

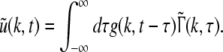Further we recall the identity (see e.g. Atay and Hutt 2006)

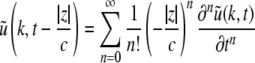and obtain from (55), (56), (57) and (58) after a Fourier transformation into frequency space

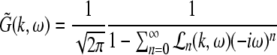with

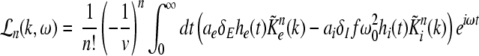and the kernel Fourier moments (Atay and Hutt 2005)

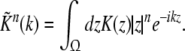The external input

Considering the input (36), then the Fourier transform in space and time yields

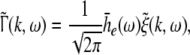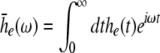with the Fourier transform of the external signal 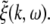Since the external fluctuations in Fourier space are uncorrelated,

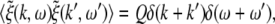we obtain finally

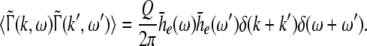dX/dp > 0 in single stationary solutions

Considering Eq. 47,

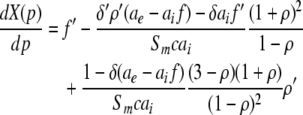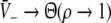with f′ = df/dp > 0, δ′ = ∂δ/∂ρ > and ρ′ = dρ/dp > 0. Further Fig. 3b illustrates the limits for p ≈ 1 and for p → ∞ and section "The resting state" shows that a_e − a_if < 0. Then (65) gives 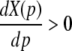for all p.

The power spectrum for large frequencies

To compute p_EEG(ν), we consider Eq. 41 and compute the Greens’ function (59) in the long wavelength limit as

with 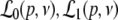defined as

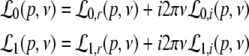with

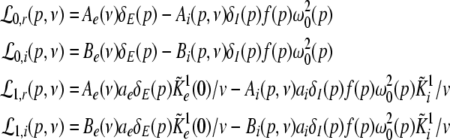and

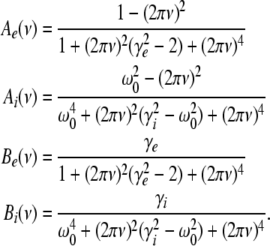Equation 66 assumes the approximation of a large but finite propagation speed v. Then inserting (66) into (41) yields the power spectrum

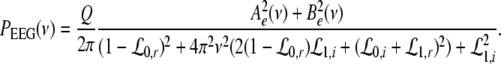The functions 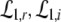depend on the propagation speed and are small compared to 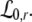Hence neglecting terms containing 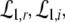we find the conditions (50).