Mapping of contextual modulation in the population response of primary visual cortex

Abstract

We review the evidence of long-range contextual modulation in V1. Populations of neurons in V1 are activated by a wide variety of stimuli outside of their classical receptive fields (RF), well beyond their surround region. These effects generally involve extra-RF features with an orientation component. The population mapping of orientation preferences to the upper layers of V1 is well understood, as far as the classical RF properties are concerned, and involves organization into pinwheel-like structures. We introduce a novel hypothesis regarding the organization of V1’s contextual response. We show that RF and extra-RF orientation preferences are mapped in related ways. Orientation pinwheels are the foci of both types of features. The mapping of contextual features onto the orientation pinwheel has a form that recapitulates the organization of the visual field: an iso-orientation patch within the pinwheel also responds to extra-RF stimuli of the same orientation. We hypothesize that the same form of mapping applies to other stimulus properties that are mapped out in V1, such as colour and contrast selectivity. A specific consequence is that fovea-like properties will be mapped in a systematic way to orientation pinwheels. We review the evidence that cytochrome oxidase blobs comprise the foci of this contextual remapping for colour and low contrasts. Neurodynamics and motion in the visual field are argued to play an important role in the shaping and maintenance of this type of mapping in V1.

Introduction

Population organization of receptive field properties

The function of neurons in V1 is described primarily in terms of their receptive fields (RFs). RFs are spatially localized in the visual field, and tuned for specific properties such as orientation, spatial frequency and temporal frequency (Schiller et al. 1976), and their inter-relationships as expressed by a concept like orientation spatio-temporal energy (Basole et al. 2003; Mante and Carandini 2005). Traditionally, most authors would agree that the tuning functions of RFs are largely context-independent (e.g. De Valois et al. 1979). Moreover, according to a large body of literature, the RF properties are organized spatially in distinctive patterns, running tangentially to the cortical surface of V1. The spatial organization of response properties has been described for ocular dominance (Levay et al. 1975; Obermayer and Blasdel 1993), orientation preference (Hubel and Wiesel 1974; Blasdel 1992) and spatial frequency preference (Tootell et al. 1981, 1988c; Edwards et al. 1995), contrast sensitivity (Tootell et al. 1988a; Edwards et al. 1995) and colour selectivity (Tootell et al. 1988b; Landisman and Ts’o 2002b).

More recent research has amended the notion of context-independence of RFs, demonstrating contextual influences from the region immediately surrounding the RF (Sceniak et al. 2001; Cavanaugh et al. 2002; Bair and Movshon 2004). The surround region can modify RF responses through inhibitory effects (Blakemore and Tobin 1972), spatial summation of low-contrast stimuli (Kapadia et al. 1999), and cross-orientation modulation (Sillito and Jones 1996; Cavanaugh et al. 2002; Kimura and Ohzawa 2009). These results have typically been obtained by using single-cell recordings, and so their consequence for population organization of orientation preference remains unclear.

Compared to surround effects, long-range contextual modulation has not yet received the same degree of attention. These are contextual effects in which the activity of a neuron is modulated by stimuli well beyond the classical RF and its immediate surround (Zipser et al. 1996; Lamme et al. 1998b; Lee et al. 1998). A number of long-range contextual effects have been observed, for instance in texture-defined boundaries (Lee et al. 1998). Other examples will be given in the next section. We will argue that long-range contextual modulation shows regularities at the level of the neuronal population. These regularities are closely tied to the well-documented regularities in the spatial layout of local RF properties.

RF properties change smoothly between neighbouring populations of neurons and many RF properties are periodic, so that patches of cortex with similar response functions recur at approximately 400 μm apart (in the macaque). The periodicities at which different response properties are mapped appear to have some degree of systematicity. This results in a tessellated pattern of spatially interlocking response properties, that is clearest in the macaque (Bartfeld and Grinvald 1992; Blasdel 1992); less so in cat (Hubener et al. 1997) and ferret (White et al. 2001). This functional regularity is reflected in the anatomical connections of V1; regions with similar response properties are connected by intrinsic patchy connections with a similar periodicity (Malach et al. 1993; Yoshioka et al. 1996).

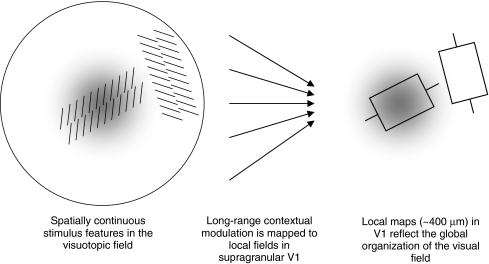
This paper will focus on the population organization of contextual modulation. This organization, as we shall argue, is related to the population organization of RF orientation preferences. Hubel and Wiesel (1977) have described the orientation preference maps as a tiling of hypercolumns; patches of cortex along which all orientation preferences for a single location in the visual field are systematically represented.1 Optical imaging techniques have since clarified the mapping of orientation preference in the supra-granular layers of V1 (Bonhoeffer and Grinvald 1991; Blasdel 1992), revealing the pervasiveness of orientation pinwheels. To reconcile this result with Hubel and Wiesel’s (1977) ice cube model, we have argued that orientation pinwheels are the building blocks in the organization of the orientation preference map (Alexander et al. 2004). In the section “The local-global map hypothesis”, we will further develop this idea, which assumes the presence of functional units of contextual modulation in V1 called local maps. These functional units tile V1 at the scale of the pinwheel and may have further significance for other response properties in V1 that have a similar periodicity.

In an orientation pinwheel, orientation preference changes smoothly with angle about the orientation singularity at the centre. In its simplest form, the orientation pinwheel can be described by the relation:

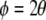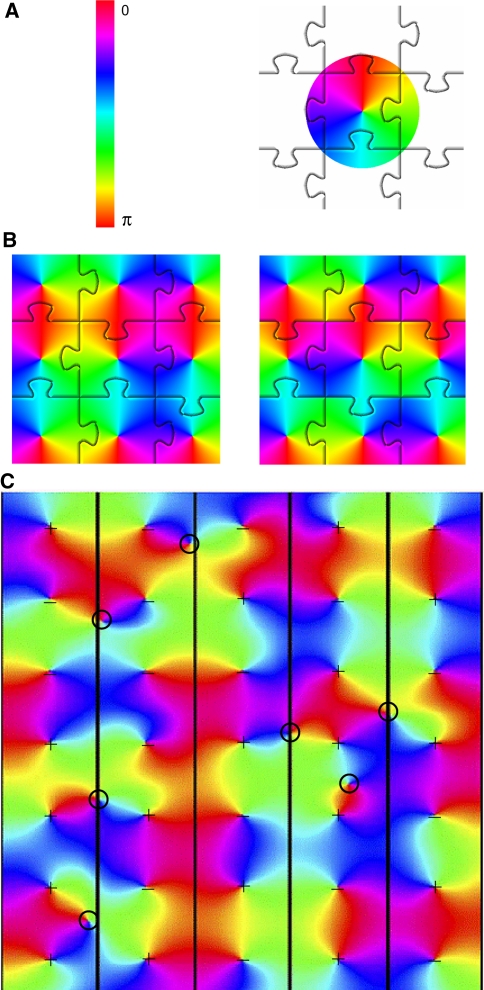
where ϕ is the polar angle of the pinwheel’s coordinates and θ is stimulus orientation as presented in the neuron’s receptive field. This is simply to say that stimulus orientation, which has a range 0 ≤ θ < π due to the rotational symmetry of oriented lines, maps to an approximately circular coordinate system i.e. a range 0 ≤ ϕ < 2π. Figure 1a illustrates the orientation pinwheel defined by Eq. 1.

Fig. 1.

Tiling of orientation pinwheels. a The variable orientation preference has a range between 0 and π, and is mapped by Eq. 1 onto a circle, with range 0–2π. The circle represents an orientation pinwheel. Orientation pinwheels can be regarded as the basic components of the orientation preference map, as is schematically represented here by their jigsaw puzzle tiling. b Results from a simple algorithm for generating orientation pinwheel tiling. Starting from the central pinwheel tile shown in (a), rows of tiles are added that are reflected about the vertical axis every other row; columns are added that are reflected about the horizontal axis every other column (only the centre nine tiles are shown). This tiling results in a saddle point pattern at each four-way junction of tiles (left). At a saddle point, the orientation preference increases with distance from the saddle point along one border direction (e.g. horizontal) and decreases with distance along the other border direction (e.g. vertical). The saddle-point pattern can be modified by shifting every second row of tiles to the left or right by one tile. This operation results in linear zones at tile borders (right). Here the orientation preference changes continuously along the vertical border. c Simulation of fluid tiling of orientation pinwheels (adapted from Wright et al. 2006). This simulation allows the polar angle of the pinwheel’s coordinate system to vary in phase from tile to tile. A regular spacing of pinwheels is imposed, resulting in a regular spacing of singularities (the pinwheel centres), seen most clearly here in the right-hand column. The fluid interactions at tile borders provide for a variety of further topological features, including saddle-points and ‘border’ singularities. This figure shows that a tessellation of orientation pinwheels need not result in a rigidly tiled orientation preference map. The sign of the singularity (direction of change of orientation preference about the singularity) in each tile is shown by a ‘+’ or ‘−’ sign. Analysis of the signs of singularities shows that saddle-points and linear zones generally arise at the borders of tiles containing two odd and two even singularities. ‘Border’ singularities are marked with circles. In each case it can be seen that these arise at tile borders where three or more tiles have singularities of the same sign. ‘Border’ singularities arise where local map borders cannot be resolved as a smooth transition in the orientation preference gradient

From this definition, other features of the orientation preference map naturally follow. Linear zones and saddle points (Blasdel 1992) arise as smooth transitions between orientation pinwheel borders (Alexander et al. 2004). In Fig. 1b, left, we show that these can be constructed; starting from the centre pinwheel tile of Fig. 1a, rows of tiles were added that are reflected about the vertical axis in every other row; columns of tiles were added that were reflected about the horizontal axis in every other column (only the centre nine tiles are shown). This tiling results in a saddle point pattern at each four-way junction of tiles. Starting with this saddle-point pattern, alternate rows of the pattern can be shifted horizontally by one tile; a vertical pattern of linear zones results (see Fig. 1b, right).

More realistic-looking orientation maps with the same border features can readily be obtained by assuming that pinwheels are placed on a regular grid, initially with random sign (clockwise or anti-clockwise) and a random angle offset to Eq. 1. This is followed by a relaxation procedure that optimizes border transition smoothness, by iteratively adjusting the angle offset of each pinwheel (Wright et al. 2006). Interestingly, in locations where the relaxation fails to resolve the tiling pattern as a smooth border transition, ‘border’ singularities can arise, typically halfway between the singularities at the centres of the pinwheels (see Fig. 1c).

Following Hubel and Wiesel’s (1977) ice-cube model, the examples shown in Fig. 1 increasingly relaxed the assumption that the basic ‘tiles’ of orientation preference maintain rigid, repeating spatial relationships. The many possible tessellation patterns that result allow a complex, fluid pattern in the overall map of orientation preference that more closely matches the qualitative features of maps seen using optical imaging measurements.

Equation 1 describes changes in orientation preference in the polar dimension of the pinwheel; however, the mapping of neuronal inputs also changes systematically in the radial dimension, i.e. depending upon distance from the singularity within the orientation pinwheel. The orientation tuning width of the sub-threshold response is broader in neurons located near the singularity compared to iso-orientation domains away from the singularity (Schummers et al. 2002; Marino et al. 2005). Consistent with this observation, optical imaging of the population response shows that orientation singularities have a weaker orientation response than iso-orientation domains (Blasdel 1992; Swindale et al. 2003; c.f. Schummers et al. 2008). While some studies have not found evidence for such an ordered spatial geometry in the orientation tuning width of spiking activity (Maldonado et al. 1997; Schummers et al. 2002; Marino et al. 2005), other studies have shown just such an effect (Ohki et al. 2006; Nauhaus et al. 2008). In the cat, neurons located near orientation singularities in area 18 are responsive to stimuli without any luminance edges, or uniform surfaces (Tani et al. 2003).

From focal injections of tracers, such as horseradish peroxidase (HRP), there is anatomical evidence that intrinsic connections to and from singularities are predominantly of short-range, whereas long-range intrinsic connections arise between iso-orientation domains (Yousef et al. 2001; Lund et al. 2003). This may explain the broader orientation tuning near pinwheel singularities, particularly evident in the sub-threshold response.

With large injections of HRP into monkey V1, large regions become stained with tracer. However, ‘lacunae’ appear; periodic patches of unstained tissue (Rockland and Lund 1983). Lund et al. (2003) suggested that lacunae result from the absence of long-range intrinsic connections. Thus, tracer lacunae provide a potential anatomical marker for the position of singularities.

In sum, there is functional and anatomical evidence for systematicity in the way orientation sensitivity changes, depending on the distance from the pinwheel singularities. An intriguing phenomenon that also belongs to this category is that singularities tend to be located at the centres of ocular dominance bands, so their population response also tends to be monocular (Bartfeld and Grinvald 1992; Blasdel 1992; Crair et al. 1997).

All the systematicities in the properties of singularities can be taken as cases in point for the proposed tiling based on pinwheels, provided that the radial dimension is taken into the equation. This can be realized by extending Eq. 1 to a more general form:

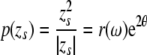where p(z_s) is a mapping of a complex variable z_s onto the complex coordinates of a pinwheel. The variable z_s parameterizes the properties of a stimulus s. In this mapping, p(z_s) = (0,0) is the location of the pinwheel centre, arg(p(z_s)) maps orientation preference and |p(z_s)| is the distance from the pinwheel centre. We can rewrite the complex variable z_s in polar coordinates by choosing θ = arg(z_s) and r(ω) = |z_s|. As in Eq. 1, θ on the right of Eq. 2 denotes stimulus orientation. The 2θ in the exponent has the same effect as in Eq. 1: mapping stimulus orientation, with a range of π, to the orientation pinwheel, with a range of 2π. The radial dimension r of the mapping is now explicitly included. In accordance with the observations that response properties of neurons vary with distance from the pinwheel centre, we may assume that r is a monotonically decreasing function of the orientation bandwidth, ω, of the stimulus. The orientation bandwidth represents the range of orientation components present in the stimulus. It is high in non-oriented dots, blobs and uniform surfaces but low in oriented lines, edges and gratings. This simply represents the weaker orientation-sensitivity closer to the pinwheel centre.

The systematicity in the functional organization of V1 is further revealed by staining with cytochrome oxidase (CO). The enzyme CO is an activity-dependent marker, indicating regions of chronic high activity (Wong-Riley 1979; Humphrey and Hendrickson 1983). Staining V1 with CO reveals a regular pattern of ‘blobs’ in the non-granular layers of the monkey. Consistent with their higher metabolic activity, CO blobs have 42% higher vascularization than interblob regions (Zheng et al. 1991). Staining of blobs is strongest in the supra-granular layers, weaker in the infra-granular layers, and absent in the granular layer (Layer 4) of V1 where the staining for CO is uniform. In the macaque, CO blobs generally have a ~400 μm spacing (Horton and Hubel 1981); notably the same approximate periodicity as iso-orientation patches.

The periodicity of CO blob regions is reflected in the mapping of population responses of stimulus features. The population responses to colour and low-contrast stimuli reveal a high degree of spatial overlap with CO blobs (Tootell et al. 1988a, b; Landisman and Ts’o 2002b). This is largely consistent with measurements taken at the single neuron level; neurons within CO blobs are more responsive to colour (Livingstone and Hubel 1984; Tso and Gilbert 1988; Landisman and Ts’o 2002a; c.f. Lennie et al. 1990; Leventhal et al. 1995) and low-contrast stimuli (Edwards et al. 1995) compared to interblob neurons.

So far we have mainly discussed the population mapping of RF properties such as orientation preference and selectivity for colour and low contrasts. In sections to follow we will show that there is a close relationship between the mapping of RF properties and the mapping of extra-RF properties. In the section “Population mapping of contextual modulation” we will show that extra-RF orientation features map to orientation pinwheels in a manner directly analogous to RF orientation. In the section “The local-global map hypothesis”, we will present a theory that will enable us to represent pinwheels in a more abstract form, the local map. This construct enables us to represent other contextual features as a function of orientation and position information. The theory has some surprising consequences, including the prediction that CO blobs are the foci of contextual remapping of foveal properties of colour and low-contrast sensitivity (Alexander et al. 1998).

Contextual modulation in V1

Whereas this paper is concerned with the population mapping of contextual modulation, most research has been at the single neuron level. The understanding of V1 cell responses has, for several decades, been infused by extra-RF influences, reminding us that the classical notion of RF is incomplete (for an early discussion, see Allman et al. 1985). Long-range contextual modulation effects have been found for a wide variety of stimulus configurations.

Figure 2 provides some examples of stimulus configurations from experiments in which long-range contextual influences have been observed in monkeys. In response to stimulation with high-contrast circular gratings (see Fig. 2a), some 30% of V1 neurons show the following behaviour: when presented with larger and larger gratings, their firing rate initially increases and reaches asymptote for the largest gratings. This response pattern differs markedly from the usual decrease in response to large gratings (Levitt and Lund 2002). The dominance of inhibitory influences in the population is usually interpreted as an effect of the retinotopic surround (Angelucci et al. 2002), but could equally well be explained from the more general principle of sparseness of neuronal coding. With natural stimulation, activity in neighbouring neurons becomes decorrelated and more specialized (Vinje and Gallant 2000; Yen et al. 2007). As stimulus complexity increases, therefore, a majority of neurons will receive net-inhibition, while a minority will receive net-excitation.

Fig. 2.

Examples of stimuli used to measure contextual modulation in the primary visual cortex: a A circular high-contrast grating displayed on a mean-luminance background used in surround inhibition experiments (e.g. Levitt and Lund 2002). b A wide-field grating (e.g. Vanduffel et al. 2002). c Artificial scotoma (Fiorani et al. 1992): long, drifting lines (black) can activate a V1 neuron even when the RF of that neuron is covered by a mask the size of which is many times that of the RF. dCurved lines used in a curve tracing experiment (Roelfsema et al. 1998; Khayat et al. 2004a); a monkey is trained to fixate to the end-point of a curve, which the animal then ‘traces’ with a series of saccades. Prior to the saccades, neurons with RF along the attended line show elevated levels of activity compared to a second, distracter curve. e Texture defined boundaries (e.g. Lee et al. 1998): neurons in V1 show an orientation specific response to second-order edges. These second-order edges can be defined by a variety of cues, including a change in orientation of first-order texture elements. f Distal colour patches (Wachtler et al. 2003): the RF response to a colour patch can be modified by colour patches placed in distal positions. The fixation point is shown with a cross, and the middle colour patch is placed in the RF of the measured neuron

Net-inhibitory modulation in most neurons is not inconsistent with a vigorous population response to large or otherwise complex stimuli. Across the measured population of neurons, a large high-contrast grating induces activation that is on average still 60% of the peak response obtained with smaller gratings (Levitt and Lund 2002). Additionally, measurements with population level techniques, such as optical imaging, metabolic tracer and fMRI, indicate that V1 is highly responsive to wide-field grating stimuli (Vanduffel et al. 2002; Basole et al. 2003; Sasaki et al. 2006; Harrison and Tong 2009). We also note that surround suppression is greatly diminished after a saccade (MacEvoy et al. 2008) or for centre and surround moving at different velocities (Cao and Schiller 2003).

Another stimulus type, shown in Fig. 2b, has been used to detect long-range contextual influences, by inducing ‘artificial scotomae’. These are masks used to cover the receptive field and extended surround of a given neuron. Some V1 neurons will respond with precise timing to a line ‘passing over’ their RFs even when the RF and surround are masked (Fiorani et al. 1992).

Also, attention can give rise to long-range modulation. Figure 2c shows a typical stimulus configuration used to induce attentional effects in V1. Eye-fixation on one end of a line (overt attention) can increase the activity in neurons driven by this line, compared to ones driven by a distracter line (Roelfsema et al. 1998; Khayat et al. 2004a).

Texture borders also show long-range effects. Figure 2d shows a texture-defined border, or second-order edge, that emerges where two different textures meet. Such boundaries can activate V1 neurons (Lee et al. 1998). By definition, second-order edges are extra-RF; they arise where properties defined by RFs change.

Finally, contextual effects occur with color stimuli. Figure 2e shows colour patches that, when placed well beyond the surround region of a neuron’s RF, induce contextual modulation (Wachtler et al. 2003). Distal patches can modulate the activity in the neuron’s receptive field; this modulation is net-excitatory for a substantial minority of neurons.

Given that individual V1 neurons differ in their preferred scales of contextual integration, what is the maximum range for which such a response could be found? Alexander and Wright (2006) reviewed the literature with the aim to estimate the maximum range of excitatory contextual modulation: they re-analyzed data from a number of experimental paradigms. It was found that excitatory contextual modulation can occur over wide ranges in the visual field. To control for the cortical magnification factor, distances at different eccentricities in the visual field were converted to cortical distance in V1. The resulting maximum scale of contextual integration spans almost the entire extent of V1 in monkeys, between 10 mm and 30 mm, depending on the experimental paradigm. Some experimental paradigms, such as curve tracing (Roelfsema et al. 1998; Khayat et al. 2004a), relative luminance of the surround (Kinoshita and Komatsu 2001), and texture defined boundaries (Lee et al. 1998) show unabated excitatory contextual modulation up to the largest sized stimuli tested.

Some neurons in V1, therefore, are tuned for inputs from a wide range in the visual field. This conclusion differs from ones obtained using high-contrast circular gratings (c.f. Levitt and Lund 2002; Angelucci et al. 2002). However, our conclusions are supported in a wide range of stimulus types. As we shall discuss in the section “Mechanisms of horizontal integration into V1”, long-range contextual modulation can occur through a number of known anatomical routes. The mechanisms of long-range modulation may differ from stimulus to stimulus, involving shifts in the dynamics of integration between feedforward inputs, V1 intrinsic connections and extra-striate feedback (Nauhaus et al. 2009).

The context-dependency tends to be most manifest in experiments introducing elements of naturalistic vision. In this paper we focus on the spatial organization of contextual modulation under wide-field stimulation. This means that we will only briefly touch on a number of other relevant phenomena, including the increased sparseness of the neuronal code in the presence of visual context beyond the RF (Vinje and Gallant 2000; Yen et al. 2007), the effect of visual working memory on the modulation of neural responses (Super et al. 2001; Harrison and Tong 2009), and the influence of contextual stimuli on response latency profiles (Kapadia et al. 1999; Li et al. 2000; Huang and Paradiso 2005). In the section “Mechanisms of horizontal integration into V1”, however, we will discuss in some detail the relevance of spatiotemporal dynamics of V1, as well as motion in the visual field induced by saccadic activity.

It should be noted that even in analyzing spatial organization of contextual modulation, timing is a critical issue. In general, contextual feedback is delayed with respect to feedforward input (Lamme et al. 1998a; Angelucci et al. 2002). This is consistent with constructive theory of how a perceptual representation develops over time, from context-independent to context-dependent (van Leeuwen 1995, 1998). A review of contextual modulation timing (Alexander and Wright 2006) shows that it extends from the initial impulse response at ~50 ms from stimulus onset (e.g. Sugita 1999), through components that are delayed a further 20–60 ms (e.g. Lee et al. 1998; Kapadia et al. 1999), to ones that persist for several hundred milliseconds (e.g. Juergens et al. 1999; Kinoshita and Komatsu 2001). Contextual modulation is therefore an ongoing process, continually supplying feedback to V1. For this reason, neuronal responses to contextual effects are typically measured over several seconds of stimulation (e.g. Ringach et al. 1997; Basole et al. 2003), rather than as the maximum firing rate at the impulse response. As we will discuss in the section “Mechanisms of horizontal integration into V1”, such methodological choices can have a strong impact on how we understand the function of V1.

Under naturalistic viewing conditions, features in the visual field have a high spatio-temporal predictability (Young 2000; Guo et al. 2007). In making use of this predictability, vision is a fundamentally anticipatory process. Even though some contextual components have a relatively long latency (Lamme et al. 1998a), the predictability of the visual scene allows context to play a critical role in the function of V1. MEG experiments, for example, have shown activity in V1 in the pre-cued hemi-field prior to stimulus onset (Plomp et al. 2009). This illustrates that feedback has an important role in the anticipation and prediction of visual input. While feedback from the higher visual areas to V1 has an obvious role to play in this process, feedback from V1 to the lateral geniculate nucleus (LGN) is important also; it allows processing in V1 to adapt in an ongoing manner to visual context, to adjust its own feedforward inputs (Marrocco et al. 1982; Briggs and Usrey 2007). The anticipatory role of feedback provides an overarching dynamical context that precedes strictly feedforward information.

Population mapping of contextual modulation

Orientation preference

We described a number of visual stimulus configurations for which long range excitatory contextual modulation has been observed. These, interestingly, each show 180° rotational symmetries; the relevant features were either straight (Fiorani et al. 1992; Lee et al. 1998; Levitt and Lund 2002) or approximately straight lines (Roelfsema et al. 1998; Khayat et al. 2004a), or were composed in a square configuration (Wachtler et al. 2003). Rotation of these stimulus features by 180° about the neuron’s RF leaves them approximately invariant. This contextual property may be the one V1 neurons most prefer (other examples: Zhou and Baker 1996; Toth et al. 1996; Ringach et al. 1997; Zhou et al. 2000; Rossi et al. 2001; Kinoshita and Komatsu 2001; Chisum et al. 2003). Since lines and edges share this property, the tuning is consistent with the classical RF preference for oriented lines. We might suspect that this is no coincidence, and that orientation preferences in the classical RF are intimately tied to the contextual response of V1. The question naturally arises as to whether the orientation-tuned, contextual response is mapped into the same orientation pinwheels as the classical RF response.

The standard methods for producing orientation preference maps do not unravel the contextual contribution to the mapping. These methods use optical imaging, complemented with measurements confirming map accuracy at the single cell level. Stimuli used to drive single cells, such as small oriented lines or small gratings, differ by an order of magnitude in spatial scale from the gratings used in optical imaging, which cover a wide region of the visual field (e.g. Das and Gilbert 1997). While optical imaging maps are understood to reflect the summation of the local receptive field activations, they may also contain a long-range component by virtue of the large stimuli used. We will argue that there is a genuine long-range component in these responses.

Of relevance here are the artificial scotoma studies by Fiorani et al. (1992). These authors have shown that some neurons in monkey V1 (chiefly in Layers 4 and 6) will fire in response to oriented lines even where the RF field and surround are covered by a large mask (see Fig. 2c). This interpolation response in single neurons maintains the exact orientation tuning and response latency of the unmasked stimulus. A similar effect has been found when a mask in the foreground obscures the neuron’s RF (Sugita 1999). In V1, neurons were shown to fire when a short line segment moved along its axis of orientation toward the RF, but disappears before reaching it (Guo et al. 2007). Whereas all these effects were obtained in monkey, in tree shrew V1 it is likewise possible to drive neurons with full-field gratings while the RF is obscured (Bosking and Fitzpatrick 1995; Fitzpatrick 1996). Each of these experiments demonstrates an orientation-tuned contextual response in the absence of direct RF stimulation.

At the population level, Toth et al. (1996) observed an orientation response to masked regions of a grating, using optical imaging in cat V1. The orientation map of the masked region matched the one derived from the unmasked grating. The masked region extended over approximately 3 mm in V1. Single cell measurements showed that, although the responses in the masked region consisted of largely sub-threshold activity, firing rate in neurons at the centre of the masked region was higher than when the whole screen was masked (Toth et al. 1996). Rossi et al. (2001) described a similar effect in single cells of monkey V1. Toth’s study demonstrates that the spatial organization of orientation preferences can be elicited in the absence of direct RF stimulation.

Responses of single neurons in V1 to a second order edge, such as a texture-defined boundary (see Fig. 2e), are extra-classical by definition (Schmid 2008). When a second-order edge is aligned with the orientation preference of a V1 neuron, this can produce a net-excitatory effect in the neuron. Unlike first-order edges, responses to second-order edges appear to be invariant with respect to their length (Lee et al. 1998); apparently there is no effect analogous to surround inhibition.

Orientation preference maps in V1 have been demonstrated for second-order edges in monkey (Ramsden et al. 2001) and cat (Sheth et al. 1996; Zhan and Baker 2006), and are consistent across a wide range of first-order cues from which they are composed. These maps are also consistent with ones produced using ordinary first-order gratings (Zhan and Baker 2008). This, provided the spatial frequency of the first-order gratings that make up the second order edges is above a critical threshold. Intriguingly, below this threshold, second-order orientation preference is offset by π.

Neither the data from masked regions nor second-order edges provide, in themselves, direct information about the extent of spatial integration in the mapping of contextual orientation responses. We expect the integration span to be at least as large as 10–30 mm in monkey V1, based on single cell recordings (Alexander and Wright 2006). In some animals, such as the ferret and the tree shrew, long-range spatial integration in V1 can be measured from the response to large first-order edges; either through the aperture effect or via the length summation property.

Through a small aperture, lines or gratings are always seen to move orthogonally to their orientation. Orientation preference measurement thus typically uses stimuli moving in a direction orthogonal to their orientation (e.g. drifting gratings). This turns out to be an important factor. When the stimulus is smaller than the aperture, orientation preference does depend on the exact direction of motion. Therefore any measurable effects on orientation preference of non-orthogonal motion can be used to gauge the range of spatial integration (Mante and Carandini 2005).

Basole et al. (2003) studied such effects in ferret V1, using texture fields composed of uniformly oriented line segments. They found that the non-orthogonal motion condition induced an offset in orientation preference. The orientation tuning of the neural population shifted by 30º as line segment length was increased from 2° to 10° of visual angle. The effects were confirmed in single cell measurements, using single line stimuli (Basole et al. 2003). These observations show that the orientation preference of a cell or population can be influenced by oriented stimuli spanning up to 10° angle in the visual field.

In the primary visual cortex of the tree shrew, many Layer 2/3 neurons exhibit length summation—increasing firing rates as line stimuli increase in length (Chisum et al. 2003). In contrast to monkey and cat, V1 neurons in tree shrew show length summation for stimuli up to 40° of visual angle (Bosking et al. 1997). Length summation over such a long-range is a manifestation of contextual integration, characteristic of the tree shrew. In tree shrew V1, and in contrast to monkey and cat, patchy intrinsic fibres can traverse the entire surface of V1 along an elongated axis (Bosking et al. 1997; Lyon et al. 1998; Chisum et al. 2003). Anterograde tracer techniques combined with optical imaging of orientation preference show that these patchy fibres connect neuronal populations of similar orientation preference. Moreover, the receptive fields of neurons connected by patchy fibres are all aligned with its elongated axis (Bosking et al. 1997). The result is a global connectivity pattern in which the elongated axis of the intrinsic fibres coincides with the retinotopic projection of an elongated stimulus.

Although these observations were made using anterograde tracer, intrinsic fibres connect like to like, and so the connections are reciprocal at the population scale. Axonal targets onto a neuron will therefore display the same elongated, orientation-specific pattern. As illustrated in Fig. 3, these observations are of significance for the population organization of orientation preference. As previously defined for local stimulus orientation θ in Eq. 1, a long-range stimulus with orientation Θ is mapped into an orientation pinwheel at orientation preference ϕ. This property is summarized by the equation:

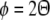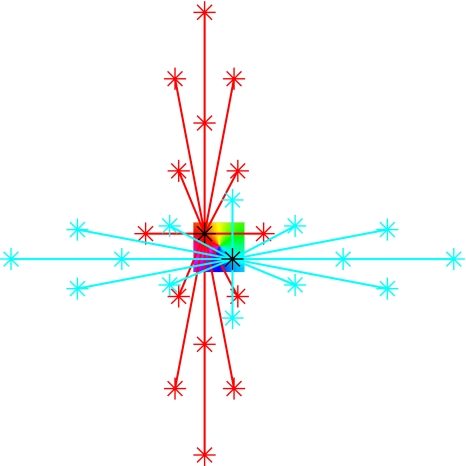
Fig. 3.

Schematic illustration of long-range connectivity patterns in the upper layers of the tree shrew. The square in the centre represents an orientation preference pinwheel; two black stars indicate injection sites of retrograde tracer. Neurons at the injection sites with orientation preference ϕ₁ (red zone) or ϕ₂ (blue zone) receive connections from neurons of similar orientation preference, indicated by the red and blue connectivity lines, respectively. In the tree shrew, these long range intrinsic connections can traverse the entire extent of V1. They form elongated patterns that match the orientation of elongated stimuli projected onto V1. The stimulus orientations Θ₁ or Θ₂ are consistent with the orientation preference at the site of injection. Thus the local field of orientation preference, ϕ, in the form of an orientation pinwheel, recapitulates the pattern of global input, Θ, which projects into the pinwheel

Notice that Eq. 3 applies, not only to long-range length summation, but also to the effects of non-orthogonal motion. Additionally, it applies to the contextual effects observed in the cat and monkey: the mapping of the orientation preference response to masked regions of an orientated grating (Toth et al. 1996) and second-order edges (Zhan and Baker 2008). This is simply to say that long-range influences on orientation preference are mapped to the same orientation pinwheels as RF orientation preferences.

Equation 3 describes the layout of contextual response properties in V1 that, in the case of the length summation in the tree shrew, is a straightforward and readily observable mapping of its intrinsic, monosynaptic input field. Equation 3 can therefore be taken as a description of the mapping of intrinsic inputs onto a pinwheel in the tree shrew; more specifically the mapping of the axis of elongation to orientation preference. In the monkey and the cat, by contrast, the contextual mapping is realized through a combination of multiple intrinsic and feedback routes, which is less easily observed. Equation 3 can therefore be regarded as a short-hand description of the mass action of the functional connectivity (Wright et al. 2006; Wennekers 2008; Wright and Bourke 2008) in these animals.

Contextual mapping of selectivity for low contrasts

Toth et al. (1996) have demonstrated that orientation preference is mapped to regions of V1 in the absence of direct RF inputs. Do corresponding contextual mappings also occur for other response properties, such as selectivity for low contrast? In order to address this question, we reanalysed data from Tootell et al. (1988a), Fig. 7. In this particular experiment, the central 5° of the visual field was stimulated binocularly with low-contrast (8%) gratings at multiple orientations and spatial frequencies. Deoxyglucose (DG) labeling was used to measure metabolic activity in V1 in combination with CO staining. Tootell et al. (1988a) report a high degree of overlap between areas of high DG uptake and CO blobs. This means that neurons within CO blobs have selectivity for low contrast.

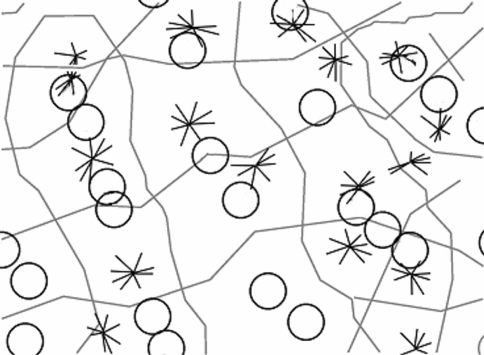
Fig. 7.

Tiling of response properties across the surface of V1 (adapted from Alexander et al. 1998; original imaging data from Bartfeld and Grinvald 1992). Circles indicate peaks in CO staining density, stars are pinwheel singularities. Grey lines either represent (a) ocular dominance borders or (b) run orthogonally to them, bisecting those points on the ocular dominance borders where orientation preference reverses direction. Each of the squares contains approximately one circle and one star and thus matches our definition of a local map. This demarcation of local maps is possible because a number of features have the same approximate periodicity

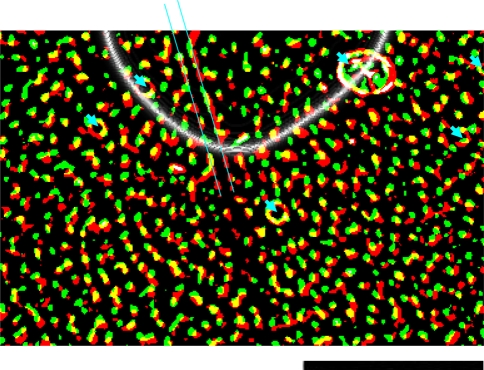
Not all of V1 had this pattern of DG uptake. This is a consequence of the restriction of spatial extent of the stimulus to within 5° of the visual field (Tootell et al. 1988a; Fig. 7b, upper right). The strong, punctate pattern of DG uptake in register with the CO blobs observed in the central region of V1 was considerably weaker outside the directly stimulated region. However, using image enhancement techniques, we were able to show that the same pattern exists in this region, nevertheless. We used difference of Gaussians followed by contrast thresholding Imagej software; http://rsbweb.nih.gov/ij/index.html), first to identify the boundaries between the two regions (bandpass 250–500 pixels), and second to bring out the pattern of CO blobs and DG uptake within these regions (bandpass 5–10 pixels). The results are shown in Fig. 4, using the same colour scheme as Tootell et al. (1988c). The figure shows that the pattern of overlap between CO blobs and regions of DG uptake remains invariant outside the directly driven region. Neurons in CO blobs are weakly but systematically activated by low-contrast gratings outside of their RF. This effect extends outward over cortical distances of up to at least 5 mm from the directly stimulated region. The effect is analogous to Toth’s et al. (1996) result for orientation preference. Fiorani’s et al. (1992) results are also consistent with this effect, because they used low-contrast lines in their measurement of the contextual response.

Fig. 4.

Relationship between CO blobs and DG uptake in Layer 3 of V1 (adapted from Tootell et al. 1988a). There is a large degree of overlap (yellow) between CO blobs (red) and DG uptake (green). Blood vessel artefacts are shown with blue arrows, and boundaries of a tear in the tissue are indicated by parallel blue lines. The animal was stimulated with low-contrast (8%) oriented lines of all orientations, out to 5° eccentricity. This created a crescent shaped region of cortex that was not exposed to the stimulus via direct, retinotopically organized inputs (above the boundary indicated by a white line). Within this region, the uptake of DG is faint. However, signal enhancement of the DG label uptake indicates the same overall pattern of overlap with CO blobs. Low-contrast gratings induce neuronal activity within CO blobs in regions of V1 not directly driven by stimulus activity. The scale bar at bottom right is 5 mm

In this section we have shown that the mapping of response properties using extra-RF stimuli often provides information that is complementary and not inconsistent with the mapping of RF properties. We discussed results for maps of orientation preference and maps of low contrast selectivity. Even in the absence of direct, feedforward inputs, contextual inputs can supply response properties to RFs appropriate for filling-in of the missing information. The organization of response properties under context-only stimulation conditions therefore has strong correspondences to those triggered by localized feedforward inputs and vice versa.

The local-global map hypothesis

Background

Let us now recede from the purely empirical to reflect on the systematicity of our observations. We described how contextual orientation preferences are mapped to local orientation pinwheels. We showed that another contextual property, selectivity for low contrast, is likewise mapped periodically in V1. Now we will proceed with the claim that contextual information in general is mapped in V1 with a similar periodicity. The mapping of contextual information, in other words, has a broad functional significance. We shall refer to the recipients of this contextual information as local maps, as distinct from the mapping of specific response properties, such as orientation preference or selectivity for low contrast. Whereas these are empirically derived, the local map is a theoretical construct. We will move our attention from the former to the latter.

We propose that local maps comprise the functional constituents of the population organization of contextual responses in V1, in the same way as the pinwheels are the building blocks of the orientation preference map. Because local maps are assumed to be of the same scale as the pinwheel, in the macaque they should have the dimensions of approximately 350 × 400 μm (Alexander et al. 1998). In the same fashion as demonstrated for orientation preference in Fig. 1, the fluid tiling of local maps results in a variegated pattern for each of contextual property. So even with the assumption of a unitary local map structure, the contextual properties of orientation preference, colour selectivity and contrast sensitivity will appear as overlapping domains with related spatial frequencies across the surface of V1 (c.f. Hubener et al. 1997; White et al. 2001).

The geometry of local maps is described by the local-global map (LGM) hypothesis of V1 (Alexander et al. 1998, 2004). The key concept of LGM hypothesis is that the mapping of contextual properties is visuotopic. Following Alexander et al. (2004), the term ‘visuotopic’ means ‘organized as a function of events arising in the visual field as they strike the retina’. ‘Visuotopic’ has a relational sense; for example, colour information is strongest for objects in the visual field that are both brightly coloured and foveated. Thus it is to be distinguished from retinotopic organization, which, somewhat paradoxically, refers to the organization of spatial locations in the visual field. The LGM hypothesis states that response properties such as orientation preference, colour selectivity and contrast sensitivity all share the same visuotopic organization. Figure 5 illustrates that the visuotopic organization of the local map has the scale of the orientation pinwheel.

Fig. 5.

Signals from the visuotopic field provide long-range contextual modulation of local map activity. Left Two extended texture elements are projected onto the retina. The grey-scale region indicates a retinal property that decreases monotically with eccentricity (i.e. a fovea-like property). Middle Long-range contextual information is projected onto a local map. Right The grey-scale region indicates populations of neurons with properties that are fovea-like; boxes indicate activated RFs of two orientation-selective neurons. Features that are spatially and temporally contiguous in the visuotopic field tend to be stored in neighbouring locations of the local map

In the section devoted to orientation, Eq. 3 expressed the remapping of contextual inputs, Θ, into the orientation pinwheel. Because orientation was the only relevant feature, only the polar dimension had to be considered. We need to generalize this equation, in order to account for properties that change in the radial dimension. This enables us to encode contextual features based on position in the visuotopic field as well as orientation. The generalization made is analogous to that from Eq. 1 to 2 and is described in Eq. 4:

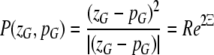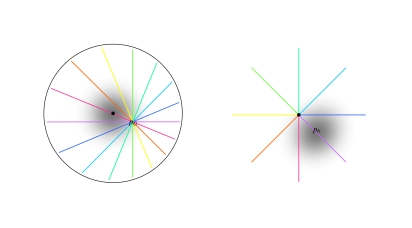
where P(z_G,p_G) denotes the mapping of visuotopic coordinates onto the complex coordinates of the local map. The point z_G denotes a location within the local map and p_G is the position of the local map in the visuotopic field.2 The offset z_G − p_G has the effect of translating all points in the field by p_G, so that p_G becomes the new origin. The squared term therefore has the effect of doubling the angles of points in the visual field about the point p_G. In polar coordinates, the term arg(z_G − p_G) describes an orientation Ξ, relative to p_G in the visuotopic field. The meaning of Ξ is that of contextual orientation preference. The centre of the local map, p₀, will be at P(z_G,p_G) = (0,0) and so in the contextual orientation preference map, p₀ marks the singularity. The distance R = |z_G − p_G| refers to the maximum range of the visuotopic field from which P(z_G,p_G) receives input i.e. the range of its functional connectivity.

An indication of this range can readily be obtained from previous observations on the scale of context influences in V1 (Alexander and Wright 2006). These data show this range to extend over a large portion of the visuotopic field. Just as orientation selectivity is systematically related to distance from the pinwheel, here the term |z_G − p_G| implies that there are contextual properties that are systematically related to distance from the centre of the local map. The precise nature of this relationship will have to be explored empirically, for example, using optical imaging techniques to map the range of contextual integration. In the next section, we will discuss the contextual mapping of colour and low-contrast selectivity. We will argue that these can be characterized, in accordance with Eq. 4, as long-range remappings of fovea-like properties to the upper layers in V1.

Mapping of fovea-like properties to CO blobs across macaque V1

The properties of the macaque retina are relatively well understood. As in most other primates, a number of these properties vary systematically with eccentricity. For example, the density of ganglion cells declines in an exponential fashion with distance from the centre of the fovea to the periphery (measured by connection topology rather than physical proximity; Azzopardi and Cowey 1996). The density of the wavelength sensitive cones also falls monotonically with distance from the centre of the fovea. Cone density is approximately four times greater in the centre of the fovea compared to the density at an eccentricity of 6° and twenty times greater compared to the density at an eccentricity of 50° (Rolls and Cowey 1970). As well as supporting colour vision, cones imbue the fovea with greater contrast sensitivity than the periphery (Kiorpes and Kiper 1996). Visual discrimination studies indicate that colour and contrast sensitivity decrease with eccentricity (Mullen 1991; Kiorpes and Kiper 1996; Martin et al. 2001).

These same studies show that colour and contrast sensitivity in the periphery are not as poor as one would expect from cone density alone. Cone densities do not provide a complete account of colour and contrast sensitivity in the visual system, because ganglion cells summate over larger numbers of cone cells in the periphery (Goodchild et al. 1996). This observation illustrates the importance of horizontal interactions in the visual system. This is the case, as we argued, even for V1. Here we will further argue that there is a specifically important role for widespread transmission of the foveal signal into V1.

A crucial observation is the striking correspondence between the response properties of, respectively, the neurons within CO blobs and those in the foveal portion of the retina (Alexander et al. 1998). Both systems show enhanced colour selectivity and contrast sensitivity, and greater response intensity. Response intensity is defined as the chronic activity per unit area; it is observed in V1 as the CO staining density. In the retina, response intensity is observed as ganglion cell density, assuming approximately equal activity per ganglion cell. We coin the term fovea-like to describe any functional property with activity levels that decrease monotonically with eccentricity on the retina. Thus, the notion of fovea-like applies to the colour specific response, the response to low contrasts, and to response intensity.

Conversely, a correspondence exists between interblob regions and the periphery of the retina. Interblob regions have response properties reflecting the characteristics of the periphery: poor colour selectivity, poor response to low contrasts, and lower response intensity.

Our claim is that these correspondences are not coincidental. As with RF and contextual orientation preference, they reflect the remapping of foveal contextual information onto populations tuned for related RF information in the supragranular layers of V1.

In order to predict how fovea-like properties are remapped contextually onto V1, we apply Eq. 4. The centre of the fovea in the visuotopic field is denoted p_F. The centre of a CO blob, hereafter denoted p_b, can be located in the local map accordingly:

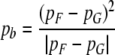The mapping is illustrated in Fig. 6. Equation 5 has two important consequences. One is that CO blob centres map in a systematic manner onto local maps: p_b, the position of the CO blob centre within the local map varies in a manner that directly reflects p_G, the position of the local map in the visuotopic field. We will deal with this issue in the next section. The second consequence is that p_b exists in each local map. This means that in every local map there is a CO blob and that the neurons in this blob receive contextual information that is fovea-like.

Fig. 6.

Visuotopic mapping of global inputs onto a local map according to Eqs. 4 and 5 (adapted from Alexander et al. 2004). Left Visuotopic coordinate system. The black dot indicates the origin, which is at the centre of the fovea. Greyscale indicates a retinal property that decreases monotically with eccentricity (i.e. a fovea-like property). The coloured lines indicate a set of rays that pass through a point in the visual field, p_G. Right The local map situated at the retinotopic coordinate p_G. The black dot indicates the origin of the coordinate system of this local map, which corresponds to the orientation singularity. The mapping given in Eq. 4 has the primary effect of doubling the angles of the rays in the visual field, so that the range 2π of stimulus orientations maps to the range π of orientation preferences. The position of the CO blob centre is indicated by p_b; the maximum of the fovea-like property in the local map

When fovea-like properties are projected onto the local map according to Eq. 4, the local map preserves the monotonicity. Response intensity is maximal at p_b and decreases monotonically with distance from p_b. The distribution of response intensity, which is a function of ganglion cell density in the retina, is mirrored in the CO staining. According to the LGM hypothesis then, the gradient of CO staining from blobs to inter-blobs expresses the monotonic decrease in activity per unit area in the local maps of V1.

Because there is a CO blob centre in every local map, and because of the fluid tiling of local maps, we should observe periodicity in fovea-like properties across the entire surface of V1, similar to that of iso-orientation domains. We expect these patterns to be particularly manifest in the macaque, which has a clear periodic organization of response properties in V1 (Bartfeld and Grinvald 1992). Indeed, the periodicity of CO blobs in the macaque is approximately 400 μm, very similar to that of iso-orientation domains (Tootell et al. 1988b).

Colour selectivity comprises another fovea-like property that is mapped onto the neighbourhood of p_b. As outlined in the introduction, colour stimuli selectivity activate CO blobs. In macaque supragranular layers, colour selective subregions have a periodicity of ~400 μm, co-axial with the CO blobs (Tootell et al. 1988b; Landisman and Ts’o 2002b).

Tootell et al. (1988b) note that within CO blobs the population response to colour gratings does not vary with eccentricity. Whereas this independence has been measured using DG labelling techniques up to 10° of eccentricity, qualitative observation (R. B. H. Tootell, personal communication) confirmed that it extends to the periphery as well. All this is exactly what we would expect from the remapping of contextual properties. Equation 5 states that fovea-like contextual properties are recapitulated within each local map.

So far, we have interpreted the mapping of fovea-like properties onto CO blob centres in Eq. 5 as a matter of functional connectivity. That is, we have related functional properties of the fovea to the functional properties at CO blob centres. The anatomical connectivity from the former to the latter is complex, having to pass polysynaptically via the LGN and Layer 4C of V1. Techniques exist, however, to study the gross connectivity patterns predicted by the proposed mapping. In terms of feed-forward anatomy, Equation 5 predicts that the fovea will connect selectively to CO blob centres in each local map.

When [³H]-proline, a trans-neuronal tracer, is injected into the eye, the tracer uptake in the retina is thought to be proportional to ganglion cell density (Adams and Horton 2003) and therefore provides a vehicle to test the proposed mapping.3 After transmission via ganglion cells, LGN and the granular layer of V1, [³H]-proline is taken up in the supra-granular layers. In Layer 3 the tracer uptake forms a banded pattern that contains the CO blobs; in Layer 2 the uptake is punctate and in register with the CO blobs (Horton and Hocking 1996). While this observation concerns the gross pattern of anatomical connectivity, we note that specific feedforward connections into CO blobs arrive via multiple routes (Shostak et al. 2002), including direct koniocellular inputs from the LGN to the supragranular layers (Lachica et al. 1992; Lachica and Casagrande 1992; Ding and Casagrande 1997). We interpret the gross pattern of [³H]-proline uptake coaxial with CO blobs as directly reflecting a mapping of ganglion cell density, via transneuronal connectivity, into the local maps. CO staining reflects the same quantity but via the functional property of response intensity. The direct relation between functional and structural connectivity is quite striking. Here, interestingly, techniques aimed at gross connectivity patterns reveal a functional architecture not readily apparent from tracing individual axons.

Figure 6 gives an overview of the mapping of fovea-like properties into the supra-granular layers for a number of interrelated measures. It describes the mapping of response intensity (as density of CO staining), functional activation by colour and low-contrast lines, as well as trans-neuronal connectivity ([³H]-proline uptake). Equations 4 and 5 give rise to some predictions based on these measures. The first prediction arises from the observation that removal of the signal from one eye causes the CO blobs it innervated to shrink and fade (Horton and Hubel 1981). If CO blobs are the recipient regions of fovea-like response properties, lesioning only the fovea of one eye should cause the CO blobs in alternate rows to fade. Use of focal retinal lesions in combination with CO staining (Horton and Hocking 1998) can therefore be used to test the proposed mapping. The fading of CO blobs should also arise outside the region of V1 that, retinotopically, corresponds to the foveal scotoma; even in the peripheral region of V1. A related anatomical prediction arises from the observation that [³H]-proline uptake is co-axial with CO blobs in Layer 2. Foveal lesioning of one eye should result in relatively lighter staining by [³H]-proline within the CO blobs located in monocular bands receiving inpus from the lesioned eye.

Counting CO blobs and orientation singularities in the macaque

Equations 4 and 5 predict a numerical relationship between CO blobs and orientation pinwheels: there should be approximately one CO blob for every orientation singularity. There are two critical local map coordinates: the CO blob centre p_b and the singularity p₀. These two sites correspond, respectively, to the fovea p_F and the position of the local map p_G in the coordinate system of the visuotopic field. Accordingly, there will be one p_b and one p₀ per local map. Such a one to one relationship between CO blob centres and singularities should be clearly in evidence in the macaque.

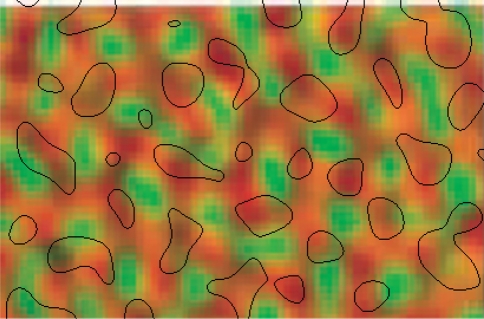
Numerical estimates of CO blobs and singularities have put their ratio at approximately 1:2 (Xu et al. 2007). However, these estimates count elongated CO regions as a single blob (Murphy et al. 1998; Fig. 1). Elongated CO regions may be comprised of two or more joined functional units. An alternative method to count CO blobs is to use local maxima in CO activity (Alexander et al. 1998). Elongated CO regions often have multiple local maxima (see Bartfeld and Grinvald 1992; Fig. 3a). This method will result in a higher CO blob count. The ratio could also be biased by overestimating the number of singularities. In the introduction we discussed how ‘border’ singularities can arise as a function of the pinwheel tiling pattern, even when ‘true’ singularities are assumed to exist only at the centres of orientation pinwheels (see Fig. 1). In the Bartfeld and Grinvald (1992) data, several singularities lie on ocular dominance borders. The absence of methods to exclude these ‘border’ singularities may lead to overestimation of their number, and hence underestimation of the ratio. As a result, the true ratio of CO blob centres to singularities will be much closer to unity. This is tentatively illustrated in Fig. 7, which demarcates local map tiles, CO-blob centres, and singularities in data from Bartfeld and Grinvald (1992).

Spatial relationships between CO blobs and orientation maps in the macaque

Equations 4 and 5 further predict a specific spatial organization of different response properties. There are two substantive predictions which can be tested by experiment. The first, orientation prediction, is regarding the orientation preferences within CO blobs: outside the foveal region of V1, orientation preferences of the CO blob centres will be systematically biased depending on the polar angle of the site of imaging. The orientation preference at the CO blob centre, arg(p_b − p₀), changes proportionally to arg(p_F − p_G), the polar angle of the retinotopic coordinates of the imaging site in V1. The second, singularity prediction, is about the relationship between CO blobs and singularities: CO blob centres and singularities will be found to coincide in the foveal region of V1 but not outside the foveal region. |p_b − p₀|, the distance between the singularity and the CO blob centre in the local map, increases with |p_F − p_G|, the distance from the imaging site to the foveal region of V1. These two predictions are illustrated in Fig. 8. They can readily be understood, considering that Eq. 4 is just a mapping of the visuotopic field centered on p_G. As p_G varies in the visuotopic field, the position of p₀ also varies relative to the other local map coordinates; as the angle and distance between p_G and p_F vary, the angle and distance between p₀ and p_b also vary. Thus, as we vary the retinotopic coordinates of the site of imaging relative to the centre of the fovea, the relationship between the orientation singularity and the CO blob centre will vary.

Fig. 8.

LGM Orientation and singularity predictions for macaque V1. The transformation of visual field coordinates (left) to local map coordinates (right) is given by Eq. 4. The small images in-between show the retinotopic map of V1. Upper half The red dot in the retinotopic map of V1 indicates a site of imaging near the horizontal meridian in the parafoveal/peripheral region. Here, the prediction is that singularities will tend not to coincide with CO blobs centres and that the orientation preference in the CO blob centres will change systematically depending on the polar angle of the imaging site. In this case, a horizontal line passes through the site of imaging, p_G, and through the fovea (left-hand side of figure). This means that horizontal orientation preferences and fovea-like properties will be co-axial in the local map (right-hand side of figure). Lower half The red dot on the retinotopic map of V1 indicates a site of imaging in the foveal region. Imaging the foveal region of V1 will show singularities and CO blobs tending to coincide. In this case, all lines that pass through the site of imaging, p_G, also pass through the fovea (left-hand side of figure). This means that singularities and fovea-like properties will be co-axial in the local map (right-hand side of figure)

The orientation prediction can be tested by measurement of population activity in response to wide-field oriented stimuli. Vanduffel et al. (2002) used a double-label DG technique to measure the organization of orientation preference over the entire area of macaque V1. The use of two labels enabled both vertical and horizontal orientation preference patches to be localized within the same animal. Importantly, Vanduffel et al. (2002) used full field gratings, so the activity measured at a given point in V1 is potentially a function of the influence of the stimulus over a large extent of the visual field. In addition, CO staining was undertaken. Figure 3 in Vanduffel et al. (2002) shows a patch of CO blobs located at ~6° eccentricity on the horizontal meridian and the DG labeling of orientation preferences taken from the same region. We simply aligned these two images in order to test the orientation prediction. Figure 9 shows that CO blobs on the horizontal meridian have a very strong tendency to coincide with regions of horizontal orientation preference; 28/33 CO regions had a majority of area devoted to horizontal orientation preference.

Fig. 9.

Superimposed images of CO blobs and orientation preferences from the horizontal meridian in V1, at about 6° eccentricity; adapted from Vanduffel et al. (2002). The majority of CO blobs (black boundaries) overlie regions of horizontal orientation preference (orange) and stay away from regions of vertical orientation preference (green)

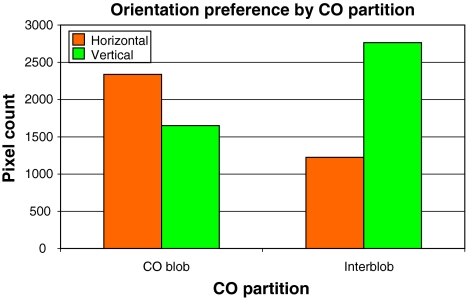
We divided the CO map into CO and non-CO regions of equal area, and compared for both the uptake for horizontal and vertical orientation labels (Fig. 10). The figure clearly shows that opposite orientation preferences are found inside and outside of blob regions.

Fig. 10.

Numerical analysis of the Vanduffel et al. (2002) data. The map of CO staining was partitioned into two equally sized regions: high versus low CO. There is a strong preference in high-CO regions for horizontal orientations and for vertical orientations in low-CO regions

The Vanduffel et al. (2002) data therefore confirm that outside the foveal region of V1, CO blobs will show a systematic bias in orientation preference for large contextual-type stimuli. Static, sign reversing, square-wave gratings produce a bias towards a horizontal orientation preference within CO blobs along the horizontal meridian (see Fig. 8, upper), and the opposite bias outside the blobs. Unfortunately, Vanduffel et al. (2002) paper does not contain the data to test the obverse prediction: a bias towards vertical orientations within CO blobs along the vertical meridian.

The orientation prediction is consistent with the radial bias effect measured using fMRI in macaques (Sasaki et al. 2006). Full-field, horizontally oriented gratings produce a greater relative BOLD response along the horizontal meridian in V1. Likewise, there is higher activity along the vertical meridian in response to full-field vertical gratings. The analogous result also applies to diagonally oriented gratings. Conventional assumptions about the early visual system cannot explain this interaction between orientation and retinotopy (Sasaki et al. 2006).

This result is readily explicable within the LGM hypothesis. Neurons within CO blobs have higher rates of activity (Wong-Riley 1979; Humphrey and Hendrickson 1983) and denser vascularisation than interblob regions (Zheng et al. 1991). We may therefore assume that there is a greater-amplitude BOLD response within CO blobs compared to interblobs. Equation 4 states that CO blob centres respond to stimuli of orientation equal to arg(p_F − p_G), the polar angle of the imaging site. CO blobs will preferentially be activated where arg(p_F − p_G) is aligned with the stimulus orientation. Consequently, the BOLD response to full-field gratings will be greater where arg(p_F − p_G) is aligned with the stimulus orientation. The orientation prediction therefore explains the observed interactions between orientation and retinotopy seen in the radial bias effect. The Sasaki et al. (2006) results therefore generalize Vanduffel et al. (2002) data concerning the activations of CO blobs by horizontal gratings along the horizontal meridian.

The radial bias effect was confirmed in human psychophysical experiments using contrast sensitivity thresholds. Small, peripherally located gratings were used to test the observer’s ability to detect radially or tangentially oriented stimuli (Sasaki et al. 2006). The relationships between contrast sensitivity and CO blobs (Tootell et al. 1988a; Edwards et al. 1995) have already been noted, adding support to our interpretation of the radial bias effect. Although less pronounced, the effect has also been observed in visual acuity experiments (Westheimer 2003). A further prediction would be that the physiological correlates of the radial bias effect should be enhanced in fMRI when colour or low-contrast luminance gratings are used, compared to high-contrast luminance gratings.

Let us now turn to the singularity prediction. Vanduffel et al. (2002) reported that the relationship between CO blobs and orientation selectivity changes as a function of eccentricity. In the foveal region of V1, orientation patches activated in response to either horizontal or vertical gratings tended to be coaxial; with increasing eccentricity, they became more separated, and in the parafovea/periphery they were completely interdigitated. In addition, the orientation patches had consistently lower uptake of label within the foveal region, while the patches became more clearly defined progressively with eccentricity. Vanduffel et al. (2002) concluded that the combination of lower metabolic response to the oriented stimuli, and the coaxial horizontal and vertical patches, show that activated orientation columns were less orientation specific in the foveal region of V1. In the foveal region, these weak orientation patches coincided with CO blobs. Outside the foveal region, CO blobs were coaxial with patches of strong orientation selectivity.

The singularity prediction is that singularities and CO blobs will be coaxial in the foveal region and separated in the periphery. Now consider the poor resolution of the orientation map as obtained by DG labelling techniques. At least we can still expect that singularities will appear as overlapping orientation patches. Due to the convergence of iso-orientation lines at the singularity, columnar-scale measures of the singularity would appear as overlapping orientation patches. However, the orientation response will be weak, because singularities have been shown to coincide with regions of low orientation response at the population scale (Blasdel 1992; Swindale et al. 2003). Iso-orientation regions outside the pinwheel will appear as strong but interdigitated orientation patches. The Vanduffel et al. (2002) results are therefore consistent with the singularity prediction.

Further evidence for this prediction comes from anatomical studies using large injections of HRP tracer. Tracer lacunae have been suggested as markers for the position of singularities (Lund et al. 2003). Rockland and Lund (1983) have demonstrated that tracer lacunae and CO blobs are not co-axial in the parafovea. An addition prediction from Eqs. 4 and 5 is that tracer lacunae and CO blobs will be co-axial in the foveal region of V1. Large injections of tracer into foveal V1 in the macaque or squirrel monkey could readily be used to confirm this prediction.

Generally, methods available to image the whole V1 (such as DG and fMRI) are limited by poor spatial resolution. Optical imaging at present offers the best resolution, but is limited in the macaque (due to the folding of the cortex) to the vertical meridian of the parafoveal region. The application of high-resolution fMRI in combination with Fourier domain signal processing techniques (Fukuda et al. 2006; Moon et al. 2007) may allow for non-invasive imaging of orientation preference maps. Likewise we might be able to localize ‘functional’ CO blobs using differential selectivity for colour and low contrast.

Mechanisms of horizontal integration into V1

Functional connectivity

Our predictions regarding CO blobs require that visual information propagates from the fovea to each and every CO blob, that is, to even the most peripheral regions of V1. Isolated local stimuli may fail to show this effect in the laboratory but global spatio-temporal information is abundantly present in the visual field under naturalistic viewing conditions (Vinje and Gallant 2000; Alexander and Wright 2006; Yen et al. 2007).

The maximum range of excitatory contextual modulation measurable in monkey V1 is consistent with widespread horizontal integration of visual information (Alexander and Wright 2006). Several experimental paradigms show contextual modulation ‘tuning curves’ that do not decline over the range of distances tested experimentally (Lee et al. 1998; Kinoshita and Komatsu 2001; Khayat et al. 2004a). The anatomical routes by which these long-range contextual interactions arise are numerous. Horizontal interactions begin at the retina (Kruger et al. 1975; Berry et al. 1999) and are further extended by ongoing feedback from V1 to LGN (Marrocco et al. 1982; Briggs and Usrey 2007).

CO blobs receive feedforward inputs both from the magnocellular and parvocellular recipient layers of V1 as well as from the koniocellular layers of LGN (Lachica et al. 1992; Lachica and Casagrande 1992; Ding and Casagrande 1997). Within V1, long-range intrinsic connections extend for 3 mm within the supragranular layers (Stettler et al. 2002), and 6 mm within the infra-granular layers (Rockland and Knutson 2001). Within Layer 4B the horizontal fibres are heavily myelinated, as are many of the horizontal fibres within the infra-granular layers (Peters and Sethares 1996). This means there is fast horizontal communication within these layers. CO blobs receive inputs from all layers in V1 with the exception of Layer 1 (Shostak et al. 2002). V1 receives feedback from at least nine extra-striate areas (Rockland et al. 1994; Rockland and Vanhoesen 1994). Incoming feedback connections often terminate in patches, coaxial with the ones of the long-range intrinsic connections in the supra-granular layers of V1 (Lund et al. 2003; Angelucci et al. 2002; c.f. Stettler et al. 2002).

Functional connectivity can be measured by assessing the extent of spatio-temporal dynamics of neuronal activity. Spatio-temporal waves have been measured in macaque V1 extending over 8 mm, which was the maximum extent of the recording array (Eckhorn et al. 2001). Similar wave phenomena have been measured in cat (Benucci et al. 2007; Nauhaus et al. 2009), the rabbit (Freeman and Barrie 2000) and the rat (Xu et al. 2007). In these latter two cases, the measurement arrays allowed the detection spatio-temporal waves that had a spatial extent greater than the entirety of V1. In macaque V1, spatio-temporal waves have a modal velocity of 0.4 m/s (Eckhorn et al. 2001); in the cat the velocity is of the same order (Benucci et al. 2007; Nauhaus et al. 2009).

Regarding the range of functional connectivity, measurement of spatio-temporal waves in V1 under wide-field stimulation, and quantifying the longer latency components of the response, leads to contrasting conclusions compared to measuring stimulus-locked responses to focal stimuli on a blank background, and quantifying the initial impulse response. This is not surprising, since the goals of the two types of experiments are often-times quite different. These latter methods, however, have been predominant in V1 experimentation. This may lead to an underestimation of the extent of spatial integration in the neuronal population response (Alexander and Wright 2006). Nauhaus et al. (2009) have shown that the spatial extent of spatio-temporal waves in cat V1 depends on the contrast of the stimulus, with low-contrast gratings resulting in greater propagation distances. It is our expectation that analogous results showing long-range spatio-temporal dynamics in V1 will be found for naturalistic viewing conditions.

Wide-field naturalistic or isolated local stimuli are not the only alternatives; functional connectivity can also be assessed using particular global configurations comprised of local stimulus components. Small grating patches (1.2° × 1.2° visual angle) organized in a square with 30° of diagonal separation were used to induce the radial bias effect (Sasaki et al. 2006); see Fig. 10a. The effect depends on the global configuration of the stimulus, that is, activation is higher for radially aligned components. Related observations have been made for radially aligned grating patches separated up to 12°; in this case using single cell measurements in the cat (Mizobe et al. 2001); see Fig. 10b. The radial bias effect is found across multiple visual areas, including V2, V3, V4 and MT; this is of interest because it demonstrates the importance of extra-striate interactions for long-range contextual modulation in V1. In another fMRI experiment, human subjects were trained on an illusory contour discrimination task (Maertens and Pollmann 2005) using Kanizsa squares with stimulus components encompassing 3.24° × 3.24° of visual angle and 20° apart diagonally; see Fig. 10c. Here, interestingly, the effect of the training was only detected in V1. These results illustrate that the type of global interactions predicted by Eq. 4 can be measured at the population level using focal stimulus components arranged in appropriate global visual field configurations (Fig. 11).

Fig. 11.

Global configurations of local stimulus components. a Radial bias effect: grating patches placed in the periphery of the visual field elicit a larger BOLD response when they are radially oriented compared to when they are tangentially oriented (Sasaki et al. 2006). In this case, the top-right and bottom-left patches elicit a greater response because the gratings within each patch are oriented diagonally top-right to bottom-left. The BOLD response is smaller where the global orientation of the patches does not agree with the local grating orientation, such as the top-left and bottom-right patches in this figure. b Radially aligned grating patches: an excitatory contextual response is more likely to be elicited in cat V1 neurons when the distant Gabor patches are aligned in a radial fashion with the RF patch (Mizobe et al. 2001). c Illusory contours: when subjects are trained to discriminate variants of Kanizsa squares, V1’s BOLD response increases as a result of the training (Maertens and Pollmann 2005)

Motion in the visual field

The LGM hypothesis implies that horizontal diffusion of signal enables every local map in V1 to access information from wide regions of the visual field. Horizontal diffusion allows activation of remote areas with close temporal contiguity. This may be useful for perceiving motion in the visual field, including that resulting from body, head and eye movements. Because the visual environment changes in a predictable way under motion of various kinds (Young 2000; Guo et al. 2007), the information elicited at one point in the visual field is therefore potentially relevant to the activation of any retinotopic point in V1. The present discussion will focus on motion due to saccades because of their ubiquitousness and rapidity.

Even if horizontal propagation of signal in the visual system were absent, saccades consistently bring together pre-saccadic and post-saccadic elements of the visual scene to the same retinotopic location. V1 is able to form short-term memories of aspects of the visual scene (Super et al. 2001; Harrison and Tong 2009) and these memories survive the ‘saccadic gap’ (Khayat et al. 2004b). For example, optical imaging of V1 with voltage sensitive dyes shows that pre-saccadic activation by a focal grating stimulus is sustained for 100 + ms post-saccade (Slovin et al. 2002; Fig. 10b). The saccade will usually bring a different stimulus feature ‘onto’ the retinotopic location. This is sufficient for coincident activation of widely separated visual features at single locations within the upper layers of V1, even if there were no horizontal diffusion of signal.

However, there is evidence that horizontal diffusion is a highly active process, particularly prior to saccades. From ~100 ms prior to saccade, there is a widespread increase in neuronal activity in V1, and this increase is greatest at the target location of the saccade (Super et al. 2004). This prior activation may constitute the projection of an ‘efferent copy’ of the present activity in V1. There is a very close relationship between the notion of mapping, as expressed in Eq. 4, and that of efferent copy, as expressed here. Similar predictive activation has been measured for moving stimuli: line segments travelling toward the RF of V1 neurons (Guo et al. 2007).

Curve tracing experiments, in which the monkey is required to make two saccadic motions along a line, show pre-saccadic increases in activation at RFs along the curve (Khayat et al. 2004a), similar to that found for texture elements (Super et al. 2004). Activation is increased along the entire length of the curve to which the monkey attends, from RFs near the initial fixation point to ones near the planned saccade destination (Roelfsema et al. 1998). This effect arises over distances measured up to 30 mm in V1 (as estimated in Alexander and Wright 2006). After the saccade, the increased activation over the attended curve is quickly re-established; this, even though its retinotopic position has been shifted substantially (Khayat et al. 2004a). Taken together, these experiments suggest that activity from the entirety of the attended curve (Khayat et al. 2004b) is projected to contextually relevant sites up to at least 30 mm distant in the upper layers of V1, as the LGM hypothesis requires.

Discussion

Evidence and predictions

We reviewed the evidence concerning the population mapping of long-range contextual effects onto V1. We related these effects to the mapping of RF properties: orientation preference, selectivity for colour, and low-contrast selectivity. The relevant observations were population measures of neuronal responses; the smallest being in the order of ~100 μm, encompassing some thousands of V1 neurons. We discussed results from optical imaging techniques and measures of metabolic activity, such as CO staining and DG uptake, and gross anatomical structures at the columnar scale, as studied with bulk injections of HRP and [³H]-proline tracer. Some relevant effects occur at the centimetre scale as measured by fMRI.4 To interpret these phenomena, we introduced the LGM hypothesis, which is based on the relational concept of the visuotopic field; the visual field as it strikes the retina. Our review provided us with evidence for predictions concerning the organization of the population response. The evidence allowed us to relate phenomena at the scale of 100 + μm to that of the orientation pinwheel (~400 μm), and beyond that to patterns at the scale of centimetres that encompasses V1.

We previously described how orientation pinwheels can be considered as the basic units, or tiles, of the orientation preference map (Alexander et al. 2004) and how net-excitatory contextual modulation of orientation preference and other response properties can occur over large distances in the visual field (Alexander and Wright 2006). We now reviewed results showing that contextual orientation preferences are mapped onto orientation preference pinwheels. This mapping has been demonstrated with context-only stimulation (Fiorani et al. 1992; Toth et al. 1996; Sugita 1999) and second-order edges (Sheth et al. 1996; Zhou and Baker 1996; Lee et al. 1998; Ramsden et al. 2001; Zhan and Baker 2006, 2008; Schmid 2008). Consistent with these results are maps of orientation preference in response to non-orthogonal motion in the ferret (Basole et al. 2003) and length summation measurements in the tree shrew (Bosking et al. 1997; Chisum et al. 2003).

We started from a formal description of the mapping of RF orientation preference onto orientation pinwheels (Eq. 1), and proposed an analogous mapping of contextual orientations (Eq. 3). The mapping recapitulates the organization of these inputs in the visual field. The LGM hypothesis extends this observation to include a second dimension in the mapping (Eq. 4). The two-dimensional representation allows additional contextual response properties to be incorporated, such as colour and low contrast selectivity (Alexander et al. 1998). We proposed as a key assumption that CO blobs act as centres for the contextual remapping of colour and low contrast selectivity, just like orientation pinwheels remap contextual orientations. While this proposal is novel, it leads to a consistent reinterpretation of existing data on CO blobs and a number of strong, testable predictions.

The first two predictions concern the physiology of CO blobs. We saw that CO blobs are selectively activated by low-contrast oriented gratings (Tootell et al. 1988a), even when presented in a context-only fashion. The uniformity of the population colour response mapping to CO blobs in the upper layers of V1, independent of eccentricity (Tootell et al. 1988b), also suggested contextual remapping. Equation 4 states that the contextual remapping, called local map, preserves relative areas in the visuotopic field. In conjunction with Eq. 5, this means that ganglion cell density in the retina and CO staining in the upper layers of V1 can be considered as expressing a related property—chronic, overall activity, which we called response intensity. It has a gross anatomical correlate: [³H]-proline uptake in the upper layers. As a consequence, a foveal scotoma in one eye will (1) selectively dim CO blobs within ocular dominance bands corresponding to that eye and will (2) decrease the transmission of [³H]-proline, injected intra-ocularly, to those same CO blobs.

Contextual maps of orientation preference are proposed to interact with the contextual mapping of fovea-like properties. It follows from Eqs. 4 and 5 that the distance between CO blob centres and singularities will increase with the eccentricity of the imaging site. In support of this prediction, Vanduffel et al. (2002) found systematic changes in the relationship between orientation preference patches and CO blobs as a function of eccentricity. Moreover, tracer lacunae and CO blobs do not coincide in the parafovea (Rockland and Lund 1983). We predict that (3) CO blobs and tracer lacunae will be co-axial in the foveal region of monkey V1.

Equations 4 and 5 state that, outside the foveal region of V1, the orientation preference within CO blobs will be systematically related to the retinotopic polar angle of the imaging site. By re-analysing data from Vanduffel et al. (2002), we demonstrated that, under conditions of sustained stimulation with wide-field oriented gratings, the orientation preference within CO blobs along the horizontal meridian is strongly biased to the horizontal. We predict that (4) the same relationship will exist for all retinotopic polar angles in V1. Selective activation of CO blobs vs. interblobs can account for the elevated BOLD response to radially oriented stimulus components. This effect, the radial bias effect (Sasaki et al. 2006), is consistent with our prediction. Moreover, we predict that (5) the radial bias effect should be greater for stimuli with fovea-like properties, such as colour and low-contrast gratings.

Relationship to models of RF organization

An early model describing how classical RF interactions lead to smooth transitions between neighbouring neurons for orientation preference is found in Linsker (1986). Organization of orientation preference is seeded by feed-forward inputs and arises from local interactions through self-organization. This model, like most others since (e.g. Obermayer et al. 1990; Swindale and Bauer 1998), considers localized RF properties to be the driving force in the formation of cortical maps. Recent modelling has also included effects from neighbouring extra-RF regions (Schwabe et al. 2006; Wielaard and Sajda 2006). Here, we made a case for long-range contextual influences on the organization of V1, and their relationship to a number of RF response properties.

In the introduction we noted that neighbouring neurons tend to have similar response properties. In addition, there tends to be systematic relationships between the periodicities with which these are mapped tangentially to the cortical surface. If these periodicities scale by appropriate factors, different combinations of features will have a localized representation in V1. To arrive at an optimally homogeneous spatial distribution of these localized feature combination across V1, Swindale et al. (2000) proposed a mechanism that seeks for the best compromise between two opposing requirements: the need to maintain continuity of response properties within the cortical sheet, versus completeness, or the need to ensure that all combinations of the features represented are distributed uniformly over visual space (Swindale 2004; Carreira-Perpinan et al. 2005).

Under the LGM hypothesis, continuity and completeness follow directly from the properties of the visuotopic field. Each local map stores a range of contextual response properties, such as orientation preference, colour and low contrast selectivity. The maps have a spatial organization that recapitulates the visuotopic field. Continuity in the visuotopic field is assured due to local spatial correlations of features in the visual field and continuity on the retina, and is preserved by the local maps. Completeness arises through the remapping of multiple response properties from the visuotopic field onto the local map; features that tend to coincide visuotopically will give rise to coinciding response properties in the local map (see Fig. 5). A mathematical treatment of these issues is presented in Wright et al. (2006). The local maps, rather than co-localizing all possible feature combinations, co-localize only ecologically relevant combinations (Brunswik 1956). When, for instance, a horizontally elongated object passes through the fovea, its colour information is available along the horizontal meridian. As a consequence, colour selectivity and horizontal orientation preference tend to be co-localized on the horizontal meridian in V1 (Vanduffel et al. 2002).

Properties such as orientation preference, velocity of motion and line length can be unified into a single property: spatio-temporal orientation energy (Basole et al. 2003, 2006; Mante and Carandini 2005). These authors have proposed that this property is mapped into the upper layers of V1. This concept fits nicely with the LGM hypothesis if we consider spatio-temporal orientation energy, rather than a property of the stimulus, as a property of the visuotopic field. We would then expect the maximum range of spatial integration of this property to be large, not only in the ferret but also in the monkey and the cat. In addition, as this property depends on organization of the visuotopic field, it will be tied to the mapping of CO blobs and fovea-like properties such as colour and low contrasts. This proposal is underdetermined by the currently available data.

Implications for V1 function

The proposed role of CO blobs under the LGM hypothesis is to boost the signal to noise (S/N) ratio within the primary visual cortex for properties that are associated with the response characteristics of the fovea. This mechanism facilitates detection of colour information in the periphery of V1, by dispersal of high S/N colour information from the fovea. This may explain the compelling nature of colour perception in the periphery, despite the sparseness of colour selective cones.

More generally, every local map in V1 potentially has access to response properties projected from wide regions of the visual field, not just foveal properties. This means that properties characteristic of the retinal periphery, such as sensitivity to high temporal frequencies, enhance the S/N during foveal detection. This may relate to our ability to foveally detect fast-moving features. Overall, the LGM hypothesis offers an explanation for the cohesiveness of our visual world in face of the large, exponential, variation in the distribution of receptor properties over the extent of the retina.

Under the LGM hypothesis, neurons embedded within local maps can discover those global contexts that are predictively related to their own activity (Alexander et al. 2004) and can then use those predictive contexts to boost S/N locally (Guo et al. 2007). These predictive processes occur within the overarching, ongoing dynamics of the visual system allowing it to capitalize on the highly redundant nature of the visual field (Young 2000). The scope of contextual influence may vary, depending on the task-relevance of the currently available contextual information (van Leeuwen 1995, 1998). The relevance of contextual information is by no means limited to the visuotopic field, and can encompass non-visual contexts.

The resulting theoretical framework for V1 is consonant with that proposed by Lee et al. (1998). Rather than merely a way-station for local processing of visual information, V1 is involved in integrating global visual information with spatial precision. However, the LGM hypothesis does not require V1 to take on functions normally associated with higher visual areas, like face or object recognition. Thus in our understanding, even though V1 is liable to influences of attention (Roelfsema et al. 1998; Khayat et al. 2004a), long and short term memory (Super et al. 2001; Maertens and Pollmann 2005; Harrison and Tong 2009), prediction (Guo et al. 2007; Plomp et al. 2009) and long-range integration (Alexander and Wright 2006), it essentially remains a low-level representation, specialized for oriented edges, textures and texture boundaries (see Figs. 2, 10).

The notion that response properties in the upper layers of V1 recapitulate global visual contexts has strong implications for our understanding of V1’s function. The mapping of contextual properties shares the same organization as RF properties at the population scale. The proposed organization of RF properties only makes sense when considered in the light of the visuotopic organization of context. As the contextual information that individual neurons receive is determined by their location in the map, so are their RF properties. The underlying implication is that RF tuning is also a function of the population organization of global visual context. Contextual modulation in V1 cannot be regarded as mere modulation of the primary activity. The existence of such an organization of RF properties would provide a strong case for the centrality of global context to the function of V1.