Encoding of speed and direction of movement in the human supplementary motor area

Abstract

Object

The supplementary motor area (SMA) plays an important role in planning, initiation, and execution of motor acts. Patients with SMA lesions are impaired in various kinematic parameters, such as velocity and duration of movement. However, the relationships between neuronal activity and these parameters in the human brain have not been fully characterized. This is a study of single-neuron activity during a continuous volitional motor task, with the goal of clarifying these relationships for SMA neurons and other frontal lobe regions in humans.

Methods

The participants were 7 patients undergoing evaluation for epilepsy surgery requiring implantation of intracranial depth electrodes. Single-unit recordings were conducted while the patients played a computer game involving movement of a cursor in a simple maze.

Results

In the SMA proper, most of the recorded units exhibited a monotonic relationship between the unit firing rate and hand motion speed. The vast majority of SMA proper units with this property showed an inverse relation, that is, firing rate decrease with speed increase. In addition, most of the SMA proper units were selective to the direction of hand motion. These relationships were far less frequent in the pre-SMA, anterior cingulate gyrus, and orbitofrontal cortex.

Conclusions

The findings suggest that the SMA proper takes part in the control of kinematic parameters of end-effector motion, and thus lend support to the idea of connecting neuroprosthetic devices to the human SMA.

Almost 60 years ago, Penfield and Welch⁶² defined the human SMA. This area is known to be involved in planning, initiation, and execution of movements because patients with bilateral SMA lesions suffer from akinesia and reduced spontaneous motor activity,³⁹ and its electrical stimulation elicits the “urge” to move.^25,26,47 Investigators using fMR imaging studies have associated SMA activation with the intention to move and with the planning of movements.^29,40,41 Electrophysiological studies in monkeys^2,16,60,89 as well as magnetoencephalography and fMR imaging studies in humans^32,45 have found movement-related SMA activation ~ 60 msec prior to that of the M1. In monkeys, the SMA is known to be active during the preparatory period before movement,^{12,13,16,38,51,68,79,80,88} and the neurons active during this period have been found to project to M1.^1,90

The SMA has been subdivided into rostral (pre-SMA) and caudal (SMA proper) regions based on anatomical and physiological criteria.^{33,48,50,64,81,97} Its organization is somatotopic.^26,55,102 Whereas the premovement activation of the pre-SMA is earlier than that of the SMA proper,^{3,18,40,41,68} the SMA proper cells are more active during the action itself;^31,81 see also survey papers.^64,88,91

Multiple lines of evidence link the SMA proper to movement-related parameters. Patients who underwent unilateral cortical resections of all or part of the SMA were impaired in scaling the velocity of hand movement,⁷ and they exhibited the SMA syndrome,⁷⁰ which is manifested in global akinesia, abnormalities in alternating movements of the hands with slight motor perseveration and grasp reflex,^39,104 initial paralysis/paresis or neglect of the contralateral extremities, paucity of spontaneous movement, hesitancy in activating volitional movements, apraxia,⁷⁰ and hemiparesis.^10,104 The EEG recordings demonstrated that SMA activity correlates with the rate of torque development, force/torque level, elbow-flexion force, rate of rising of force, and muscle electromyogram signals.^16,21,69,83 Single-cell activity in the monkey SMA proper is influenced by hand position,⁴⁴ movement direction, ^2,16,44 shift in movement direction,⁵² and target location.^16,43 The rate of repetitive finger movements was found to be linearly related to the blood oxygen level–dependent fMR imaging signal and inversely proportional to scalp EEG power and cortical potentials in the SMA proper ^{11,19,36,67,74,75,87,94}

Despite evidence of coding for the aforementioned kinematic parameters, and in contrast with M1, where a mapping between neuronal firing rates and movement speed and direction has been established,^{4,14,15,28,34,57,82} there is still no clear model of the relationship between firing rates in the SMA and kinematic parameters of hand movements. The goal in this paper is to elucidate the relationship between SMA firing rates and hand motion speed and direction.

The evidence of firing at an early stage of the motor control loop, combined with relationships to kinematic parameters, makes the SMA a potential site for implantation of a BCI (also called a brain-machine interface or neuroprosthesis).^{9,22,46,54,63,76,101} Nevertheless, the vast majority of single-unit neuroprosthetic studies have focused only on M1.^{14,22,30,42,54,57,61,76,78,92,98} A better understanding of the neural underpinning of movement preparation in the human SMA may establish the basis for the development of a BCI guided by SMA neuronal activity.

Methods

We recorded from a total of 589 units (284 single units and 305 multiunits) in the frontal lobe: the SMA proper (80 units); pre-SMA (86); dACC (221); vACC (192); and OFC (10). The units were recorded from 7 patients during 20 sessions (see below, in Patients and Electrophysiological Studies and The Task). Each session was held on a different day. Within each session, activations of between 3 and 61 frontal units were recorded (mean 29.45 ± 19.08 units; values expressed as the mean ± SD). In each session, we recorded between 0.19 and 1.27 units per microwire (mean 0.74 ± 0.31 units). The average number of units recorded from simultaneously on a single microwire by region was as follows: SMA proper, 1.67; pre-SMA, 0.57; dACC, 1.06; vACC, 0.63; and OFC, 1.25. Units recorded from in different sessions are treated as different in this study. The average firing rate was 4 Hz (SMA proper, 3.8 Hz; pre-SMA, 5.6 Hz; dACC, 3.5 Hz; vACC, 3.8 Hz; and OFC, 7.9 Hz).

Patients and Electrophysiological Studies

The participants in this study were 7 patients between the ages of 15 and 38 years (mean age 24.4 ± 7.7 years), including 2 right-handed females, 2 left-handed females, 2 right-handed males, and 1 left-handed male with pharmacologically resistant epilepsy. Because noninvasive monitoring did not yield concordant data corresponding to a single resectable focus, the patients underwent implantation of chronic depth electrodes that remained in place for 1–2 weeks to determine the seizure focus for potential surgical treatment.^3,24,27,100 Between 9 and 12 electrodes were implanted in each patient (surgeries were performed by I.F.). The electrodes were implanted based on clinical criteria. Each of these clinical electrodes terminated with a set of 9 40-μm platinum-iridium microwires. Each patient had between 16 and 48 microwires (excluding reference microwires) in frontal lobe regions (mean 36 ± 13.11 microwires). The total number of microwires by region was as follows: SMA proper, 24; pre-SMA, 64; dACC, 56; vACC, 96; and OFC, 8. All SMA electrodes were placed in the mesial SMA; none of them were located in the posterior part of this structure. Electrodes in other lobes were excluded from the present research. Signals from these microwires were recorded at ~ 28 kHz and bandpass filtered in the range of 0.3–3 kHz by using a 64-channel acquisition system (Neuralynx). Spikes of individual cells were isolated based on their wavelet coefficients and the distribution of interspike intervals by using the method suggested by Quian-Quiroga et al.⁶⁵ (original code courtesy of those authors). This method was used in multiple research studies.^58,66

The classification between a single unit and a multiunit was done visually based on the following: 1) the spike shape and its variance; 2) the ratio between the spike peak value and the noise level; 3) the interspike interval distribution of each cluster; and 4) the presence of a refractory period for the single units (that is, < 1% of the spikes within a < 2.5-msec interspike interval).

The MR imaging scans obtained following placement of electrodes or postplacement CT scans that were coregistered to preoperative MR images were used to verify the anatomical location of the electrodes. We adopted the definition of the vertical anterior commissure plane as the anatomical border between the pre-SMA and SMA proper,^5,6,97,105 and the coronal plane 1 slice forward from the slice in which the 2 sides of the anterior corpus callosum are no longer connected through the genu was adopted as the anatomical border between the dACC and vACC.⁵³ Participation in this study was completely voluntary, and all patients provided informed consent. All studies conformed with the guidelines of the Medical Institutional Review Board at the University of California Los Angeles.

The Task

The participants played a computer game in which they moved a cursor in a simple 2D maze between 4 fixed-location virtual stones to discover which stone concealed a virtual treasure (Fig. 1). The maze “corridors” were parallel to the x and y axes (that is, parallel to the edges of the screen). Upon discovery, the virtual treasure was relocated beneath a randomly selected stone, and the player had to return to the center and repeat the task. This particular task was chosen to capture the most elementary directions of movement used in navigation, for potential use in future BCIs.

Fig. 1.

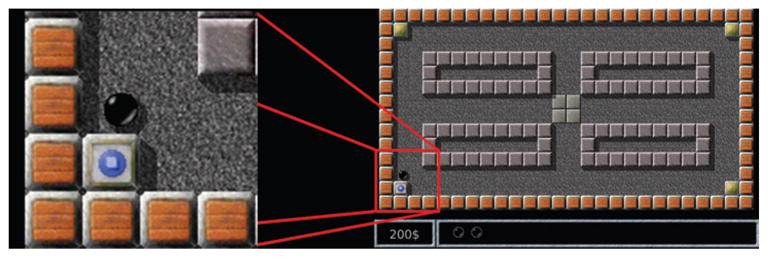
The maze game. The player used a ball-shaped cursor to touch a stone and find a virtual treasure (marked by the blue color in the lower left corner and enlarged panel). The other stones are closed (marked by the gold color at the other corners).

The patients repeated the task (that is, they discovered the virtual treasure) between 43 and 192 times per session (mean 109.8 ± 33.5 times). Each session took between 10.16 and 29.71 minutes (mean 18.18 ± 4.77 minutes), excluding break times. Each patient repeated this paradigm 1–5 times (that is, in 1–5 different sessions) on different days (mean 2.86 ± 1.77 sessions).

The first patient moved a ball-shaped cursor (3.7-mm radius) by using a computer mouse (optical wheel mouse, Microsoft Corp.). The other patients used a digitizer tablet with a hand-held stylus (Graphire3 6 × 8 tablet, Wacom Technology Co.; active area 208.8 × 150.8 mm² [width × height], report rate 100 Hz).

Control for Vision

In 7 of the 20 sessions, patients were asked, in addition to playing the aforementioned game, also to watch the screen while another individual played the same computer game. An investigator monitored their attentiveness to the task. This is a control that we use to verify that neural activities during the patient’s game are related to hand movements, rather than visual responses to the moving cursor or eye movements. In this control experiment, patients watched the discovery of the virtual treasure between 64 and 96 times per session (mean 77.7 ± 17.1 times). Each session took between 6.37 and 10.97 minutes (mean 8.75 ± 1.68 minutes), excluding break times. Each patient repeated this control 0–2 times (that is, in 0–2 different sessions; mean 1 ± 0.82 sessions). In these control sessions, we recorded from a total of 155 units (SMA proper, 8; pre-SMA, 17; dACC, 62; vACC, 65; and OFC, 3). These are included in the aforementioned 589 units.

Data Analysis

Kinematic Parameters

We interpolated the position measurements to an accurate 10-msec resolution by using a cubic smoothing spline (Spline Toolbox, Math-works). The spline was also used analytically to calculate the time derivatives (that is, velocity) from which speed and the angle of the velocity vector were calculated. The smoothing parameter was manually selected to produce smooth derivatives with only negligible smoothing of the position function (this procedure was suggested by Shoham et al.⁸²).

Motion Speed

We grouped the 10-msec time bins in which no motion took place (that is, speed = 0) and the time bins with motion (speed > 0). We split the with-motion group into 100 equal-sized groups, each of which contains 1 percentile of the distribution of speeds. We thus divided the data into a total of 101 distinct groups (for example, Fig. 2A and B).

Fig. 2.

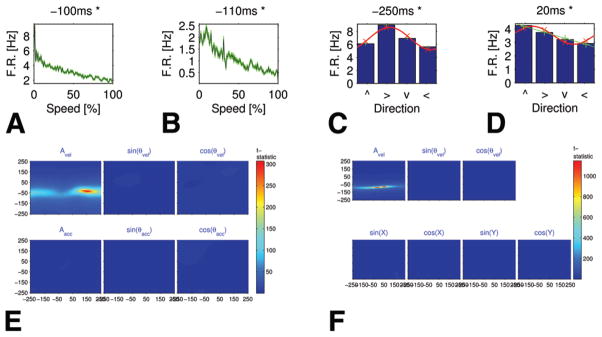
Tuning curves for speed and direction, and PCC in the SMA proper. A and B: Speed tuning curves showing a decreasing monotonic relationship between the firing rates (F.R., in Hz) and speed percentiles (Case 2). Each graph refers to a different unit (A: multiunit, B: single unit). The background (green) area around each curve represents the standard error. The leftmost point in each plot (marked 0) describes the firing rate during rest (speed = 0), whereas points 1–100 are the average firing rate during percentiles of in-motion speed. Both units had a significant monotonic relationship. Above each graph is its time lag in milliseconds (negative values indicate that firing precedes motion). The decrease in firing rate with motion speed is appreciable. C and D: Bar graphs showing selectivity to direction of motion in 2 single neurons (Case 6): firing rate versus the direction of movement (indicated as the up, right, down, and left arrows on the x axis). Because cosine tuning curves are very common, especially in M1 (see Georgopoulos et al.), we fit each graph with a cosine function (red line). In C, the cosine tuning curve fits well (R² = 0.91, MSRE = 0.06). In D, R² is relatively low for the cosine model (R² = 0.84, MSRE = 0.06); the linear model (green line) provides a better explanation for the data (R² = 0.985, MSRE = 0.02). E and F: Graphs showing the t-statistic of the PCCMs between firing rate and velocity independent of linear correlation with acceleration (in E) or position (in F) at multiple time lags. The PCCMs are as follows: upper rows, speed, sin(θ_v), and cos(θ_v); lower rows, magnitude of the acceleration vector, sin(θ_a), and cos(θ_a) in panel E and sin(kx), cos(kx), sin(ky), and cos(ky) in panel F (see Appendix 3 for an explanation of the position representation). Both panels E and F (upper left) show strong stripes for the matrices related to speed, which indicates a high correlation with speed that is independent of acceleration and position.

In 2D analyses, grouping was performed according to 2 parameters. First, grouping was performed with respect to 1 of the parameters, in a manner similar to the 1D analysis. Then, each group was divided into subgroups with respect to the second parameter, again in the same manner. For Cartesian graphs we used velocity in the x and in the y direction, each of which resulted in 25 groups (total, 625 groups). In each axis, the first 12 groups referred to negative velocity, the next group referred to exactly zero velocity, and the other 12 groups referred to positive velocity (Fig. 3E). For polar graphs (Fig. 3F), the x axis is speed whereas the y is direction, which was divided into 4 bins (see below).

Fig. 3.

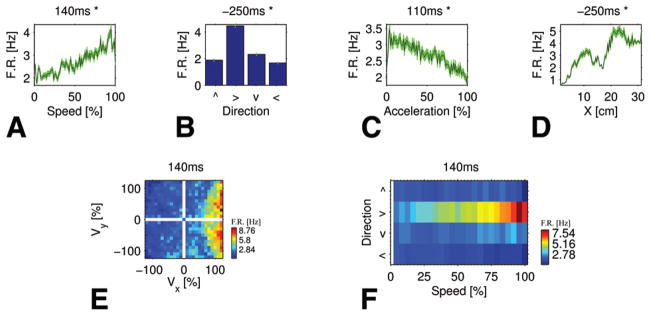
A single unit in the SMA proper (Case 2) related to multiple kinematic parameters: speed, direction, magnitude of the acceleration vector, and position in the x direction. The firing rate increases with speed (A) and x position (D), but decreases with acceleration (C). Movement to the right gains higher firing rates (B), which is consistent with an increase in firing rate along the positive x axis (D). The effective field in Cartesian velocity space (E) demonstrates the interaction between speed and direction: high firing rates are obtained at high speeds, but only when moving in the “right” direction. The gradual increase in firing rate with increase in speed is best viewed in polar coordinates (F) on the second row (that is, only for movement in the “right” direction).

The 2D graphs are analogous to receptive fields of the visual system: they represent a region in [velocity] space that an organism may move or reach toward in relation to activity in a particular neuron. In the motor system, they are called “effective” fields.⁴⁹

Motion Direction

As mentioned earlier (in The Task section), the task involved motion in a maze with corridors parallel to the x and y axes of the screen. Consequently, most of the directions of motion (defined as the angle of the velocity vector) were concentrated around the following angles: 0, 90, 180, and 270° from the positive x axis. We therefore grouped the aforementioned 10-msec time bins according to their direction into the following 4 groups: [−45°, 45°); [45°, 135°); [135°, 225°); and [225°, 315°). We will call these groups “right,” “up,” “left,” and “down,” respectively. In the direction analysis, only in-motion time bins (that is, speed > 0) were included, because during rest (speed = 0) the direction is undefined.

The polar 2-way analyses were performed in a manner similar to that for velocity in the x and y directions, but with respect to speed and direction. Thus, the data (excluding rest periods) were split into 10 groups of speed, each of which was then split into 4 groups of direction (total 40 groups).

Processing of Neural Activity

We computed the neuronal firing rates at the same 10-msec bins as speed and direction. Only neurons with a firing rate ≥ 0.5 Hz were considered for the analysis. The binned firing rate function was then smoothed by convolution with a Gaussian kernel (SD 50 msec; based on Stark et al.⁸⁴).

The normalized firing rate, defined as the z score of the raw firing rate computed over the last 60 seconds, was also computed. Because results with respect to raw and normalized firing rates are qualitatively similar, we have omitted the latter for brevity.

To investigate the relationship between firing rate and kinematic parameters, the firing rates were attributed (with a time lag; see Appendix 1) to the groups described in Kinematic Parameters. For each unit (and time lag), the average and standard error of the firing rate of each group were computed. Thus, we could plot the graphs of the average firing rate versus the 101 groups of speed. We will call these graphs “speed tuning curves,” because they show the average firing rate for each range of speeds.¹ In the 2-way analyses, similar computations were performed for the velocity.

A similar procedure was applied to the 4 groups of the direction of velocity. A cosine tuning curve was fit to the graph of average firing rate versus the 4 directions (nonlinear least squares regression). To evaluate the fitness of the cosine model, we computed the coefficient of determination (R²) and the square root of the MSRE, defined as follows:

$$\text{MSRE}=\surd \mathrm{\sum }{[({\text{y}}_{\text{i}}-{\widehat{\text{y}}}_{\text{i}})÷{\text{y}}_{\text{i}}]}^2,$$

where y₁ is the average firing rate at the ith direction, and ŷ₁ is the value of the cosine model for that direction.

Other Parameters

Acceleration

The same method was used to compute the tuning curves with respect to the norm of the acceleration vector. The correlation between speed and acceleration will be addressed using the PCC method (see below in Partial Cross-Correlation).

Position

We computed the tuning curves of the firing rate with respect to the screen position in the x and y directions in 2 ways (see Partial Cross-Correlation for the PCC method). The first is similar to the one used for speed or acceleration. The second divided each of the axes into 101 fixed-size bins. Results with both methods were similar, but the latter method seems more appropriate and we shall therefore provide its results, because position (unlike speed or acceleration) has the same range for all subjects. We once again selected a time lag that is optimal for a monotonic relationship between the firing rate and the x position, and similarly for the y position. This criterion is aimed to check whether the x or y coordinates are encoded by single units or by multiunit activity. Note that this relationship is different from the one checked using the PCC method (see Partial Cross-Correlation) of a cosine tuning curve around a single location.

Goal

We distinguished 5 fixed-location goals: the 4 virtual stones described in The Task (Goals 1–4), and the center of the screen (Goal 0). We grouped all time intervals when the player moved toward the same goal, starting either at the center of the screen or from the last virtual stone visited. Using these 5 groups, we defined the optimal time lag and the significance criterion the same way it was defined for direction (Appendices 1 and 2).

Partial Cross-Correlation

To verify further the relationship between the firing rate and end-effector speed, we used the PCC analysis suggested by Stark et al.⁸⁴ Their method estimates linear correlations between neural activity and a given feature that are not affected by linear correlations with other features at multiple time delays. We used the method in 2 ways: first, to estimate linear correlation between the firing rate and velocity that is independent of linear correlations with acceleration; and second, to estimate linear correlation between the firing rate and velocity independent of position. The model for position as well as the time lag computation and significance criteria are defined in Appendix 3.

Results

Motion Speed

Tuning Curves and Effective Fields

We found single cells and multiunits whose average firing rate relates monotonically to motion speed of the end effector (hand) of the test subject. This relationship occurred in 41 (51.3%) of 80 of the recorded SMA proper units, whereas it occurred in only 6 (7%) of 86 in the pre-SMA, in 19 (8.6%) of 221 in dACC, in 16 (8.3%) of 192 in vACC, and in 2 (20%) of 10 in OFC (Fig. 4A). In most (58 [69.1%] of 84) of the units showing this relationship, the firing rate decreased with an increase in motion speed (SMA proper, 35 [85.4%] of 41; pre-SMA, 4 [66.7%] of 6; dACC, 12 [63.2%] of 19; vACC, 5 [31.3%] of 16; and OFC, 2 [100%] of 2).

Fig. 4.

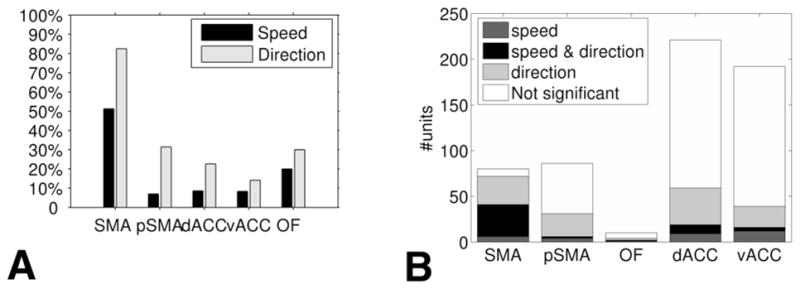
Division of the responsive units by brain regions. A: Percentages of units monotonically related to speed and units selective to direction in each recorded frontal lobe region. B: Units selective to both speed and direction. The bars present the division of recorded units in each brain region into those monotonically related to speed, selective to direction, and speed-direction units. OF = OFC; pSMA = pre-SMA.

Figure 2A and B presents the speed tuning curves of 2 SMA proper units that maintain a significant inverse relationship between their firing rate and hand speed (see Methods). These units showed a marked decrease between maximal firing rates obtained at low speeds and the firing rates at maximal speeds. For instance, in Fig. 2A the firing rate drops by a factor of 5.7, from 9.6 to 1.7 Hz, a change of 7.9 Hz. Note that in the SMA proper and dACC, approximately one-third of the “monotonic” units had a negative optimal time lag (that is, the units fired before the related speed; Table 1). In the vACC the percentage was lower.

TABLE 1.

Statistics of the time lags between firing rate and hand motion speed in 7 patients undergoing evaluation for epilepsy surgery^*

Region	% Pos	% Neg	% Zero	Mean ± SD
SMA (41)	65.9 (27)	31.7 (13)	2.4 (1)	66.59 ± 161.15
pre-SMA (6)	50.0 (3)	50.0 (3)	0.0 (0)	−3.33 ± 224.02
dACC (19)	63.2 (12)	36.8 (7)	0.0 (0)	53.16 ± 161.49
vACC (16)	75.0 (12)	25.0 (4)	0.0 (0)	95.00 ± 186.33
OFC (2)	50.0 (1)	50.0 (1)	0.0 (0)	−5.00 ± 21.21

^*Columns 2–4 present the percentage and number of units (in parentheses) with positive, negative, and zero time lags, respectively. Column 5 shows the average time lag in each region (in millseconds) ± the SD.

The PCC Method

We further examined the relationship between the firing rate and speed by another method, the PCC method. Tables 2 and 3 show the amounts and percentages of units with significant relationships to the various kinematic parameters. The linear correlation between firing rate and speed is significant for 18 (22.5%) of 80 of the SMA proper units and is independent of the linear correlation of firing rate and acceleration. For 20 (25%) of 80 of the SMA proper units, significance is obtained independently of position. Further investigation of the significant units reveals that 17 (21.3%) of 80 of the SMA proper units had a significant correlation to speed that was independent of linear correlations to both position and acceleration. All but 1 of these units (16 [94.1%] of 17) had a significant monotonic relationship to speed according to the tuning curve criteria (16 [20%] of 80). Of the units that were significant according to both methods (PCC and tuning curves), 15 (93.8%) of 16 had an inverse relationship between firing rate and speed (that is, the firing rate decreases as a function of speed). The 3 methods (tuning curves, PCC of velocity independent of acceleration, and PCC of velocity independent of position) fully agreed (16 [100%] of 16) on the type of the relationship (direct or inverse).

TABLE 2.

Significant units according to PCC of the firing rate versus velocity and acceleration^*

Region	Speed	θv	Accel	θa
SMA (80)	22.5 (18)	13.8 (11)	3.8 (3)	1.3 (1)
pre-SMA (86)	1.2 (1)	3.5 (3)	0.0 (0)	3.5 (3)
dACC (221)	1.8 (4)	2.3 (5)	3.2 (7)	0.9 (2)
vACC (192)	4.2 (8)	1.6 (3)	0.5 (1)	2.1 (4)
OFC (10)	0.0 (0)	0.0 (0)	0.0 (0)	0.0 (0)

^*Columns 2–5 show the percentage of significant units (numbers of units are in parentheses) of different kinematic parameters. Abbreviations: Accel = magnitude of acceleration vector; θ_a = direction of acceleration vector; θ_v = direction of velocity vector.

TABLE 3.

Significant units according to PCC of the firing rate versus velocity and position^*

Region	Speed	θv	cos(kx)	sin(kx)	cos(ky)	sin(ky)
SMA (80)	25.0 (20)	17.5 (14)	2.5 (2)	5.0 (4)	1.2 (1)	0.0 (0)
pre-SMA (86)	2.3 (2)	2.3 (2)	1.2 (1)	3.5 (3)	0.0 (0)	0.0 (0)
dACC (221)	4.1 (9)	3.2 (7)	1.8 (4)	4.1 (9)	0.5 (1)	2.7 (6)
vACC (192)	4.2 (8)	3.6 (7)	2.6 (5)	2.1 (4)	3.6 (7)	1.0 (2)
OFC (10)	0.0 (0)	0.0 (0)	0.0 (0)	0.0 (0)	0.0 (0)	0.0 (0)

^*Columns 2–7 show the percentage of significant units (numbers of units are in parentheses) of different kinematic parameters. Abbreviations: cos(kx), sin(kx), cos(ky), and sin(ky) = components of position (see Methods).

Figure 2E and F displays the t-statistic of the PCCMs for the unit presented in Fig. 2A. The figure describes the linear correlation with speed independently of the linear correlation with acceleration (Fig. 2E) and with position (Fig. 2F). In both parts of the figure, the PCCM of speed shows high horizontal stripes, whereas the rest of the PCCMs obtain far lower values. As described by Stark et al.,⁸⁴ this indicates that the unit correlates with speed but is independent of correlations with acceleration and position at multiple time delays.

When examining the “control for vision” sessions (see Control for Vision in Methods) by using the tuning curves method, only 1 dACC unit (1 [1.6%] of 62) showed a monotonic relationship between its firing rate and hand motion speed. In all other regions, no unit (0 [0%] of 93) showed this relationship. Using the PCC method, only 1 vACC unit (1 [1.5%] of 65) showed a significant relationship to speed independently of the relationship to acceleration (all other regions: 0 [0%] of 90). No units (0 [0%] of 155) showed a significant relationship to speed independently of the relationship to position.

Motion Direction

In addition to units whose activity is related to speed, we observed single cells and multiunits whose average firing rate had a significant relationship to the direction of motion. In the SMA proper, 66 (82.5%) of 80 of the units were direction-selective (as defined in the Methods section). In the other regions the average percentage was much lower: 107 (21%) of 509 (pre-SMA, 27 [31.4%] of 86; dACC, 50 [22.6%] of 221; vACC, 27 [14.1%] of 192; and OFC, 3 [30%] of 10; see Fig. 4A).

Figure 2C and D presents relationships between the firing rate and the direction of motion in 2 single units. Although a common model of firing rate (especially in M1²⁸) is the cosine function (Fig. 2C), the figure demonstrates that SMA proper neurons may deviate from this model (Fig. 2D). In the SMA proper, most of the direction-selective units (63.6%) had a negative time lag (Table 4), whereas in the pre-SMA, dACC, and vACC, the numbers of units with positive and negative time lags were close to one another.

TABLE 4.

Statistics of the time lags between firing rate and the direction of hand motion^*

Region	% Pos	% Neg	% Zero	Mean ± SD
SMA (66)	33.3 (22)	63.6 (42)	3.0 (2)	−70.00 ± 179.51
pre-SMA (27)	44.4 (12)	55.6 (15)	0.0 (0)	−17.41 ± 181.31
dACC (50)	48.0 (24)	48.0 (24)	4.0 (2)	−7.20 ± 169.83
vACC (27)	55.6 (15)	44.4 (12)	0.0 (0)	0.00 ± 175.19
OFC (3)	66.7 (2)	0.0 (0)	33.3 (1)	126.67 ± 113.72

^*This table is organized in the same manner as Table 1.

According to the PCC method, the linear correlation between firing rate and the direction of movement (θ_v) is significant independently of the correlation with acceleration or position in 11 (13.8%) of 80 or 14 (17.5%) of 80 of the SMA proper units, respectively (Tables 2 and 3). Ten of these units (10 [12.5%] of 80) are significant with respect to θ_v independently of both acceleration and position.

Part of the direction-selective units responded during the “control for vision” sessions according to the tuning curves method, as follows: SMA, 2 (25%) of 8; pre-SMA, 2 (11.8%) of 17; dACC, 6 (9.7%) of 62; vACC, 13 (20%) of 65; and OFC, 2 (66.7%) of 3. The time lag of all responsive units during these sessions was positive (25 [100%] of 25). When using the PCC method, no responses to direction independently of acceleration or position were found (0 [0%] of 155 each).

Speed and Direction

The previous sections dealt with units related to speed and units selective to direction. In this section we explore units whose firing rate can be related to both speed and direction, maybe at different time lags. Figure 4B presents the division of units according to their selectivity properties in each of the aforementioned regions. The SMA proper had the largest amount of speed-direction units (35 units), which is also the highest percentage taken of the total number of units in each region (35 [43.8%] of 80), of the number of units related to speed (35 [85.4%] of 41), and of the number of units related to direction (35 [53%] of 66). The percentage of speed-direction units within the total units in the SMA proper (35 [43.8%] of 80) matches a random mixture of properties in this population (P_speed = 41/80 = 0.5125; P_direction = 66/80 = 0.8250; therefore, assuming independence: P_{speed∩direction} = P_speedP_direction = 42.28%). In addition, the percentage of speed-direction units with an inverse relation to speed (29 [82.9%] of 35) matches their percentage among all speed-related units (35 [85.4%] of 41; see above). Of the SMA proper’s speed-direction combined units, 14 (40%) of 35 were single cells. This implies that in the SMA proper, the same single neuron can encode both speed and direction.

The PCC method found 3 units in the SMA proper related to both speed and direction independent of position (3 [3.8%] of 80). This percentage also matches random mixtures of properties in the population (P_speed = 20/80 = 0.25; P_direction = 14/80 = 0.175; P_{speed∩direction} = P_speedP_direction = 4.375%). No SMA proper units showed a relationship to both speed and direction independent of acceleration (0 [0%] of 80). This percentage is lower than expected by random property mixture (P_speed = 18/80 = 0.225; P_direction = 11/80 = 0.138; P_{speed∩direction} = P_speedP_direction = 3.11%), and may be due to the lower sample size.

Figure 3A, B, E, and F presents a single unit whose firing rate interacts with both speed and direction. The effective field in polar coordinates (Fig. 3F) shows that the firing rate varies monotonically with speed when the movement is rightward. Movement in other directions yields low firing rates independently of the speed.

As we saw in the previous examples, the time lag with respect to speed may differ from the time lag with respect to direction. In the SMA proper, most of the speed-direction units fired first for direction and only then for speed (26 [74.3%] of 35). The dACC showed a similar pattern (6 [60%] of 10). In the pre-SMA, vACC, and OFC, the number of speed-direction units was too low to include in this analysis (≤ 4 units in each region).

Acceleration, Position, and Goal

Acceleration

The percentage of units with a monotonic relationship between their firing rates and the magnitude of the acceleration vector was relatively low in all regions according to the tuning curves method (pre-SMA, 9 [10.47%] of 86; OFC, 1 [10%] of 10; SMA proper, 6 [7.5%] of 80; vACC, 13 [6.8%] of 192; and dACC, 9 [4.1%] of 221). The PCC method found that only 3 (3.8%) of 80 of the SMA proper units were significantly correlated with acceleration independently of motion speed (0% in the pre-SMA and OFC; Table 2). No significant responses to acceleration were found in the “control for vision” sessions (0 [0%] of 155) according to both tuning curves and PCC.

Position

Only 1 SMA proper unit exhibited a significant monotonic relationship to the x position (SMA, 1 [1.25%] of 80 [Fig. 3]; other regions, 0%), and none to the y position (all regions, 0 [0%] of 589). When looking for encoding of specific locations, similar to “place cells,” by using the PCC method, the percentages of significant units were low in all regions (≤ 5% of the examined population; see Table 3). In the “control for vision” sessions, no significant visual responses to position were found, except for 1 SMA proper unit (1 [12.5%] of 8) whose tuning curve showed a monotonic relationship to the x position (not the unit of Fig. 3).

Goal

In the SMA proper, 33 (41.3%) of 80 of the units responded to goal (pre-SMA, 4 [4.7%] of 86; dACC, 29 [13.1%] of 221; vACC, 14 [7.3%] of 192; OFC, 0 [0%] of 10). However, 30 [90.9%] of 33 of these units were also responsive to direction, which may reflect the fact that movement to a certain fixed-position goal enforces certain directions of movement. No significant responses to goal were found in the “control for vision” sessions (0 [0%] of 155).

Discussion

Motion Speed

In this study we have demonstrated that the human SMA proper encodes for hand motion speed and direction. Moreover, the firing rate of single units and multiunits in the SMA proper relates monotonically to hand motion speed. Other kinematic parameters, such as magnitude of the acceleration vector or hand position, were also encoded in the SMA proper, but in a much smaller percentage of the cells. The percentage of units demonstrating these relationships was much greater in the SMA proper than in all other frontal regions (pre-SMA, dACC, vACC, and OFC), for all types of relationships examined, except for the magnitude of the acceleration vector, for which the pre-SMA obtained the highest percentage.

These findings elucidate clinical studies in patients who had undergone unilateral cortical resections that included all or part of 1 SMA. These patients, when requested to change movement amplitude, scaled velocity to a much lower degree than did control volunteers, and they compensated for this by scaling the movement duration.⁷ In such patients, the SMA syndrome (see Introduction) usually emerges postoperatively,^10,39,70,104 and is also in concordance with our findings. Although most of these neurological disorders resolve completely within 2 months after surgery,²³ the permanent sequelae may include disturbance of fine motor function at high speed¹⁰⁴ or bilateral impairment of movement speed.⁷⁰

Our results extend observations in nonhuman primates, which reconstructed velocity based on SMA activity.^14,42 The results also explain multiple pieces of evidence in the literature for a relationship between movement frequency (for a cyclic movement) and neural response,^{11,19,36,67,73–75,87,99} because a higher movement frequency implies a higher movement speed. The results of fMR imaging studies are unclear because some enable investigators to discriminate between responses to different frequencies,^67,87 whereas others do not.^{11,19,73–75,99}

In most of the SMA proper units showing a monotonic relationship to speed, the relationship was an inverse one; that is, the firing rate decreased with an increase in motion speed. Based on this relationship, patients with increasing degrees of paresis, which lead to lower speeds, are expected to show higher activation of their SMA proper. This explains, at the single-cell level, why significant increases in fMR imaging signal with increasing degrees of paresis were found in the SMA of patients with mass lesions within or near the central region who performed a self-paced finger-thumb opposition task.³⁵ The inverse relationship also suggests that inhibition of a motor plan would activate the SMA proper. This sheds more light on clinical studies in patients with microlesions in the SMA proper, which showed that the SMA mediates automatic suppression for motor plans,^71,72,86 and fMR imaging studies with similar conclusions.^93,95 Apparently opposite results were reported by Xue et al.,¹⁰³ who found the pre-SMA, but not SMA proper, to be involved in motor inhibition, and van Mier et al.,⁹⁶ who found an increase in SMA regional cerebral blood flow with a decrease in the number of stops of a hand moving in a maze (that is, higher activation with higher speed). This apparent contradiction is resolved by the type of motor inhibition used. The latter 2 studies used an external cue (“beep” or bumping into a maze wall) to initiate motor inhibition, whereas in the present study we used a volitional process. A significant inverse relationship between cortical potentials in the SMA proper (recorded by subdural electrodes) and movement frequency³⁶ matches our observations.

The relationship between firing rate and hand motion speed in the SMA proper was established by 2 methods: tuning curves and PcC.⁸⁴ The gaps between the methods stem from differences in their goals. Whereas PCC estimates linear correlations, the tuning curves method singles out units with a monotonic relationship, which is not necessarily linear. Moreover, PCC compensates for inter-dependencies between speed and other kinematic parameters, whereas tuning curves do not. For units associated with speed by both methods, there were no discrepancies as to the type of relationship (direct or inverse). The use of the PCC method rules out the option that correlation with speed is due to the correlation between firing rate and position or acceleration.

Another noteworthy observation is that approximately one-third of the “monotonic” units fired before the related movement (a negative time lag). In these units, the neural signal may be harnessed for the control of an external device.

Motion Direction

We found SMA proper units selective to the direction of hand motion. This validates in humans earlier results from electrophysiological studies in monkeys.^2,16,44 Of note is the fact that in 63.6% of these units the correlation between firing rate and direction emerged prior to movement.

Some of the units (25 [16.1%] of 155) showed directional selectivity also during the “control for vision” sessions. The percentage of such units was higher in the SMA proper. These findings suggest that visual feedback to the SMA proper may be primarily in the form of information about motion direction rather than speed.

Motion Speed and Direction

In the SMA proper, both the tuning curves and PCC methods found single units and multiunits that were related to both speed and direction, maybe at different time lags. In this manner, these units encode the information of the velocity vector of the moving hand. The percentage of speed-direction units matches a random mixture of these 2 properties in the neural population (except when computed independently of acceleration, which may be a result of the low sample size). In addition, the percentage of units with an inverse relationship between firing rate and speed is similar in the population of speed-direction units and in the population of all speed-related units. It therefore seems that reduction in firing rate with an increase in speed (seen in most neurons) is independent of their selectivity to direction.

Acceleration

A small percentage of the SMA proper units were associated with hand acceleration (magnitude of the acceleration vector). Because acceleration and force are linearly related at biological speeds, our findings support the conclusions in electrophysiological studies in monkeys, in which SMA neurons exhibited activation patterns similar to those of muscles during flexion and extension tasks,^2,16 and in fMR imaging⁹⁹ and PET²⁰ studies, which showed high correlations between regional cerebral blood flow and different degrees of repetitively exerted force peaks. The small number of acceleration-related units in our research may be due to measurement of end-effector acceleration, not muscle forces.

Goal

Although SMA proper units selective to goal are consistent with reports of single-neuron studies in monkeys,^2,17,43 it is important to note that > 90% of these units were also direction selective. To distinguish between goal and direction, a different paradigm needs to be used.

The SMA Proper Versus Pre-SMA

Our results lend support to the concept of distinct specialized regions within the human SMA: the SMA proper and the pre-SMA. Although differences in single-neuron activity have been shown in both nonhuman primates^{31,51,59,79–81} and humans,³ these differences do not refer to kinematic parameters. In the current study we found that far more SMA proper than pre-SMA units expressed a relationship to the kinematic parameters of speed and direction.

Potential for BCI

Most animal neuroprosthetic devices and even the few that have been reported in humans are based on activity in M1. The activity in the SMA is associated with early movement, and specifically with motion planning. This makes the SMA activity a more natural guide for a BCI. Indeed, in our data we see the relationship between the kinematic parameters of speed and direction and neuronal activity emerging prior to the movement itself. Much more research is needed to see how these results can be used in future neuroprostheses.

Conclusions

This is the first study of the human SMA at the single-neuron level in which its relationship to kinematic parameters of motion is explored. The study shows a direct encoding of speed and direction of motion in the human SMA proper. A high percentage of the SMA proper units showed a monotonic relationship of the firing rate and hand motion speed. This relationship was more prominent in the SMA proper than in the neighboring pre-SMA, dACC, and vACC. This relationship was an inverse one in most of the SMA proper units related to speed; that is, the firing rate decreases with an increase in motion speed. This relationship indicates that the SMA proper is involved not only in movement initiation, but also in control of the speed profile of hand movements. This conclusion is further supported by clinical studies, which showed that unilateral resection of the SMA proper affects the speed profile of hand movements,⁷ and a permanent sequela of the surgery is impairment of movement speed.^70,104 The results agree with and extend existing observations in monkeys and provide support at the single-unit level for fMR imaging, PET, and EEG studies in humans. Our results also suggest that the involvement of the pre-SMA in the control of the speed profile is much smaller than that of the SMA proper.

The aforementioned relationships to speed and direction are apparent prior to actual movement in a portion of the SMA proper units, making it a good candidate for use in a BCI. The activity prior to movement can serve as a natural signal for guiding neuroprosthetic devices, because the temporal relationships between intention and end-effector activity mimic that of the brain. In neuroprosthetics, the end effector essentially replaces a bodily end effector, so if the relationship is maintained, the activation of the device is expected to be natural to the user.

Abbreviations in this paper

BCI

brain-computer interface

dACC

dorsal aspect of anterior cingulate cortex

EEG

electroencephalographic

fMR

functional MR

MSRE

mean square relative error

M1

primary motor cortex

OFC

orbitofrontal cortex

PCC

partial cross-correlation

PCCM

PCC matrix

SMA

supplementary motor area

vACC

ventral aspect of anterior cingulate cortex

Appendix 1

Time Lag

Time lags between neuronal firing and movement events at related kinematic variables (for example, speed and direction) were introduced during the association of the two. In our study, negative time lags mean that the firing preceded the related kinematic event. Although the literature demonstrates that SMA neurons are active as early as 1600 msec before a new movement sequence is initiated,³⁷,⁷⁹ we limited the range of time lags considered in our research to [−250, +250] msec (in steps of 1 bin size = 10 msec), which is consistent with previous studies,⁴,⁵⁶,⁷⁷,⁸⁴,⁸⁵ to avoid association of the firing with multiple movements. The autocorrelogram of the acceleration function had its first nontrivial peak at ~ 250 msec (the autocorrelograms of position, velocity, and direction peaked later). The average duration of a single movement (from one side of a corridor to the other, for full- or half-length maze corridors) was 1076 ± 892 msec; the average for full-length corridors was 1940 ± 1285 msec; and the average for half-length corridors was 806 ± 470 msec (values are given as the mean ± SD).

The optimal time lags between the firing and instance of speed or direction were determined for each recorded unit as follows:

Optimal Time Lag for Speed

The optimal time lag for speed is defined as the time lag (within the aforementioned range) with the maximal correlation coefficient (absolute value) between the average firing rates and the group index. We used the Spearman correlation, because we look for a monotonic relationship between the firing rate and speed, but not necessarily a linear correlation (such as the Pearson correlation).

Optimal Time Lag for Direction

We analyzed the variance of the firing rate in the aforementioned 4 groups of directions. The optimal time lag was defined as the one whose analysis of variance yielded the minimal probability value; that is, the one having the greatest probability that the means of the 4 groups are unequal.

Appendix 2

Significance Criteria

Speed

The response of a neuron to speed is considered significant if the following 2 conditions hold: 1) The probability value is < 0.01 for testing the hypothesis of no correlation against the alternative that there is nonzero correlation. The probability values are computed using algorithm AS 89.⁸ We applied the Bonferroni correction, due to multiple comparisons when considering multiple time lags (51). This correction is very conservative. 2) The absolute value of the Spearman correlation coefficient is > 0.8.

Direction

The response of a neuron to direction is considered significant (in which case the neuron will be called a direction-selective neuron) if the probability value obtained for the optimal time lag was < 0.01. We applied the Bonferroni correction, due to multiple comparisons when considering multiple time lags (51).

Appendix 3

Partial Cross-Correlation

Formula for PCC Independent of Position

The PCC between firing rate and velocity independent of position is based on the following model:⁸⁵

$$\begin{array}{l}F(t)=b_0+b_{1}cos\mathit{kx}(t+{\tau }_{\mathit{pos}})+b_{2}sin\mathit{kx}(t+{\tau }_{\mathit{pos}})+b_{3}cos\mathit{ky}\\ (t+{\tau }_{\text{pos}})+b_{4}sin\mathit{ky}(t+{\tau }_{\mathit{pos}})+b_5\left|\right|\overrightarrow{v}(t+{\tau }_{\mathit{vel}})\left|\right|+b_{6}cos{\theta }_{\mathit{vel}}(t+{\tau }_{\mathit{vel}})+\\ b_{7}sin{\theta }_{\mathit{vel}}(t+{\tau }_{\mathit{vel}})\end{array}$$

where (x,y), v⃗(t), and θ_vel(t) are the 2D position, velocity, and direction of the velocity function, respectively. k = 2π/10 is constant.

Time Lag and Significance

We used time lags between −250 and +250 msec in steps of 10 msec (see Appendix 1). To identify horizontal/vertical stripes in the PCCM, as was done manually in the original paper,⁸⁴ we defined the optimal time lag as the time lag of the PCCM row/column with the minimal product of probability values. The relationship to a kinematic parameter at the optimal time lag is considered significant if ≥ 50% of the entries in the optimal row/column are significant. That is, each of them has a probability value < 0.05 following Bonferroni correction, which is very conservative for our case (factor of 51). In the PCC model, the directions of the velocity vector (θ_v) and of the acceleration vector (θ_a) are split to their cosine and sine components. Therefore, we say that the relationship to θ_v is significant if the relationship to cos θ_v or sin θ_v is significant, and similarly for θ_a.