Monte Carlo calculated absorbed-dose energy dependence of EBT and EBT2 film

Abstract

Purpose: The absorbed-dose energy dependence of GAFCHROMIC EBT and EBT2 film irradiated in photon beams is studied to understand the shape of the curves and the physics behind them.

Methods: The absorbed-dose energy dependence is calculated using the EGSnrc-based EGS_chamber and DOSRZnrc codes by calculating the ratio of dose to water to dose to active film layers at photon energies ranging from 3 keV to 18 MeV. These data are compared to the mass energy absorption coefficient ratios and the restricted stopping power ratios of water to active film materials as well as to previous experimental results.

Results: In the photon energy range of 100 keV to 18 MeV the absorbed-dose energy dependence is found to be energy independent within ±0.6%. However, below 100 keV, the absorbed-dose energy dependence of EBT varies by approximately 10% due to changes in mass energy absorption coefficient ratios of water to film materials, as well as an increase in the number of electrons being created and scattered in the central surface layer of the film. Results are found to disagree with previous experimental studies suggesting the possibility of an intrinsic energy dependence at lower photon energies. For EBT2 film the absorbed-dose energy dependence at low photon energies varies by 50% or 10% depending on the manufacturing lot due to changes in the ratio of mass energy absorption coefficients of the active emulsion layers to water.

Conclusions: Caution is recommended when using GAFCHROMIC EBT∕EBT2 films at photon energies below 100 keV. It is recommended that the effective atomic number of future films be produced as close to that of water and that thicker active layers are advantageous.

INTRODUCTION

Since its creation, GAFCHROMIC EBT film was widely adopted in radiation dosimetry and was increasingly being employed for low-energy measurements.^{1, 2, 3} There have been several studies of the absorbed-dose sensitivity of EBT film as a function of photon beam quality^{4, 5, 6, 7} with various results. In this paper, we perform a detailed Monte Carlo analysis of the absorbed-dose energy dependence of GAFCHROMIC EBT and EBT2 film to understand its variation with energy and the physics behind this variation with particular focus on the low-energy range. These results cannot be applied directly since the overall variation with energy of the absorbed-dose sensitivity requires additional information about the intrinsic energy dependence of the film and also since commercially available films are in a state of flux. However, we believe the current study provides valuable insight into the characteristics of these types of films, which may prove useful for future developments.

The energy dependence of the absorbed-dose sensitivity of a detector is composed of two parts: The intrinsic energy dependence (or intrinsic beam quality dependence) and the absorbed-dose energy dependence.⁸ The intrinsic energy dependence k_bq(Q) is the ratio of the dose to the sensitive element of the detector at a given beam quality D_det(Q) to the detector reading at the same beam quality M_det(Q), i.e.,

$$D_{\text{det}}\left(Q\right)=k_{\text{bq}}\left(Q\right)M_{\text{det}}\left(Q\right).$$ (1)

The absorbed-dose energy dependence f(Q) is the ratio of the dose to the medium at the point of measurement of the detector in the absence of the detector, D_med(Q), to the dose to the sensitive material of the detector, D_det(Q), i.e.,

$$D_{\text{med}}\left(Q\right)=f\left(Q\right)D_{\text{det}}\left(Q\right).$$ (2)

In general, Monte Carlo simulation calculates only the absorbed-dose energy dependence of a detector. Although this quantity is generally studied as a function of beam quality or energy, it can also vary with location in a given beam quality (e.g., in the buildup region versus past dose maximum).

The overall energy dependence of the reading of a detector (often referred to as the energy response) is the product of the intrinsic energy dependence and the absorbed-dose energy dependence. In general terms, the absorbed-dose sensitivity of a detector S_AD,med is a function of beam quality but can also be a function of dose, dose rate, and geometry,

$$S_{\text{AD},\text{med}}\left(D,\dot{D},Q,\theta ,\varphi \right)=M_{\text{det}}\left(D,\dot{D},Q,\theta ,\varphi \right)∕D_{\text{med}}\left(Q\right),$$ (3)

where θ and ϕ are geometric factors and $\dot{D}$ is the dose rate. It is the variation in the absorbed-dose sensitivity (or corresponding air kerma sensitivity) which is needed to accurately use any detector in a beam quality which is different from the quality it was calibrated in. When the dose, dose rate, and geometric factors are held constant, the absorbed-dose sensitivity can be related to the total energy dependence

$$S_{\text{AD},\text{med}}\left(Q\right)=\frac{1}{f\left(Q\right)\cdot k_{\text{bq}}\left(Q\right)}.$$ (4)

For a photon detector, that is, a detector which responds only to the photons in its environment, the ratio of dose to the medium to dose to the detector is equal to the ratio of mass energy absorption coefficients of the medium to the detector if there is charged particle equilibrium in the undisturbed medium and the sensitive material of the detector which also implies negligible photon attenuation in the detector,⁹ i.e.,

$$\frac{D_{\text{med}}}{{\overline{D}}_{\text{det}}}=\frac{{\left(\frac{{\overline{\mu }}_{\text{en}}}{\rho }\right)}_{\text{med}}}{{\left(\frac{{\overline{\mu }}_{\text{en}}}{\rho }\right)}_{\text{det}}}.$$ (5)

When the detector only responds to electrons from its environment, the detector is an electron detector and the ratio of dose to medium of interest to dose to detector medium is given by the ratio of restricted mass collision stopping power of medium to detector,⁹ i.e.,

$$\frac{D_{\text{med}}}{{\overline{D}}_{\text{det}}}={\left(\frac{{\overline{L}}_{\text{col}}}{\rho }\right)}_{\text{det}}^{\text{med}}.$$ (6)

Depending on the beam quality involved, GAFCHROMIC EBT and EBT2 film can be either a photon detector, an electron detector, or a hybrid of the two.

METHODS

Film material

GAFCHROMIC EBT film, which was produced by International Specialty Products (ISP, Wayne, NJ) but no longer sold, is composed of five layers. The outer layers are made of clear polyester with a thickness of 97 μm. The inner layers of the film are composed of two layers of active emulsion with thicknesses of 17 μm surrounding a so-called surface layer with a thickness of 6 μm. EBT2 film is also composed of five layers. From top to bottom, they are the polyester overlaminate with a thickness of 50 μm, the adhesive layer with a thickness of 25 μm, the topcoat (called surface in EBT) with a thickness of 5 μm, the active layer with a thickness of 30 μm, and the polyester substrate with a thickness of 175 μm. Schematic diagrams of these film structures can be seen in Fig. 1 and the composition, effective atomic number, and density of the layers of both films can be found in Table 1. For this study, two lots of EBT2 film were considered. These lots have significant differences in the high-Z components of their active layers.

Figure 1.

Structure of (a) EBT (Ref. ¹⁸) and (b) EBT2 film (Ref. ²⁰).

Table 1.

Composition of GAFCHROMIC EBT (Ref. ¹⁸) and EBT2 films (Ref. ²⁰). Effective atomic number calculated using Eq. A4 from McCullough and Holmes (Ref. ¹⁹). Water included for comparison purposes. The composition of lot 020609, in mass percent, is the same as that currently provided by ISP for the EBT2 active layer, in atomic percent (http://www.gafchromic.com, accessed 4 November 2009).

Layer	Composition (Mass %)								Zeff	Density (g∕cm3)
	C	H	O	N	Li	Cl	K	Br
EBT
Active	57.4	9.4	16.4	13.2	0.8	2.9	⋯	⋯	7.05	1.1
Surface	32.3	6.5	20.5	21.6	2.3	16.8	⋯	⋯	9.90	1.2
Clear Polyester	62.5	4.2	33.3	⋯	⋯	⋯	⋯	⋯	6.64	1.35
EBT2
Active (lot 020609)	57.8	9.6	27.8	0.2	0.9	1.7	0.6	1.3	9.18	1.2
Active (lot 031109)	59.7	9.5	26.1	0.2	0.9	2.3	1.3	⋯	7.44	1.2
Adhesive	65.6	9.4	24.9	⋯	⋯	⋯	⋯	⋯	6.26	1.2
Surface	47.2	8.8	38.2	⋯	1.0	4.9	⋯	⋯	7.82	1.2
Polyester	62.5	4.2	33.3	⋯	⋯	⋯	⋯	⋯	6.64	1.35
Water
Water	⋯	11.2	88.8	⋯	⋯	⋯	⋯	⋯	7.42	0.998

Simulations

The EGSnrc user-code EGS_CHAMBER^{10, 11} was used to simulate the dose deposition in water and the dose deposition in the active layer of the film for monoenergetic incident photon energies from 3 keV to 18 MeV. A cylindrical water phantom with a radius of 20 cm and a thickness of 30 cm was modeled. The photon source was a circular parallel beam with a radius of 5 cm and the dose scoring volume consisted of the combination of both active layers for EBT and, for EBT2, the single active layer, within a radius of 3 cm. For dose to water simulations, the materials of the film were replaced with water, while the scoring volumes remained the same. The film comprised the entire radius of the water cylinder. To ensure full buildup and reasonable dose at the depth of the film, the upper surface of the film was placed at 0.05 cm depth in the water for energies of 3–9 keV, 1 cm depth for energies of 10–100 keV, and 10 cm depth for energies above 100 keV. At 10 and 200 keV, calculations were done at both the shallower and deeper depths, and the results were the same within the precision of the calculation (0.2%).

For EBT, the dose deposition in water and dose deposition in film were also simulated using the DOSRZnrc user-code to investigate the percentage of dose based on the last region from which electrons enter a particular region of interest versus those originating and staying in that region. This was performed for photon energies of 10, 50, and 200 keV.

In addition to the monoenergetic photon simulations, a variety of spectra¹² ranging from 40 to 100 kVp were used for EBT simulations. The mean energies of these spectra were calculated weighted by photon fluence and the effective energies were determined using HVL calculations.

Several simulations were performed to investigate the effect of nonequilibrium conditions on the absorbed-dose energy dependence of EBT2. To investigate the build-up region, a Varian 6 MV spectrum¹³ was used and the surface of the EBT2 film was set to depths of 1 mm, 3 mm, 1 cm, and 10 cm with the other geometry parameters remaining the same as for the full build-up absorbed-dose energy dependence calculations. To investigate lateral disequilibrium effects, the same Varian 6 MV spectrum was used and the surface of the film was set to a depth of 10 cm. The radii of the beam and the scoring region were both set to 0.5 cm to simulate a narrow beam.

In these simulations electron and photon cutoff energies of 1 keV were used and photon cross sections from the XCOM (Ref. ¹⁴) database were used. Rayleigh scattering, bound Compton scattering, photoelectric absorption, and fluorescent emission of K-shell and L-shell x rays were all modeled. Mass energy absorption coefficients were calculated using the EGSnrc user-code g and stopping power ratios were calculated using the EGSnrc user-code SPRRZnrc.^{15, 16}

RESULTS AND DISCUSSION

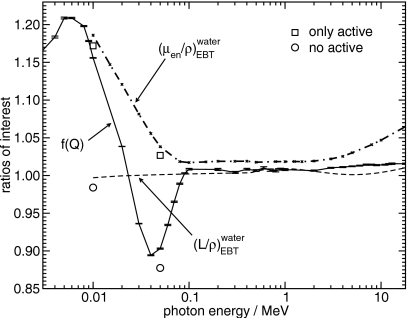
The calculated absorbed-dose energy dependence of GAFCHROMIC EBT film can be seen in Fig. 2. For the range of approximately 100 keV–18 MeV, the absorbed-dose energy dependence is reasonably constant and, as expected, approximately follows the restricted stopping power ratio of water to the EBT active layer material since it is acting like an electron detector. In this range, the absorbed-dose energy dependence is constant within ±0.6%.

Figure 2.

Absorbed-dose energy dependence of EBT film for photon energies from 3 keV to 18 MeV as well as the mass energy absorption coefficient ratio and restricted stopping power ratio of water to the EBT active material. Also included is the absorbed-dose energy dependence at 10 and 50 keV for a hypothetical film where the only film layers that are not water are the active layers (only active) and a hypothetical film that is normal except that the active layers are made of water (no active). The uncertainties for “only active” and “no active” are smaller than the symbols.

Below the energy of 100 keV the absorbed-dose energy dependence is no longer constant. To first order, one would expect that, since the photon fluences are not significantly attenuated in the detector, the low-energy behavior of the film would be determined by the ratio of mass energy absorption coefficients of water to the EBT active layer material. Figure 2 shows that this is confirmed at 10 and 50 keV within 1.2% by the absorbed-dose energy dependence of a hypothetical film where the only layers that are not composed of water are the active layers (denoted “only active”). However, the real behavior of the film differs greatly from this, particularly in the range of 10–100 keV. By investigating the absorbed-dose energy dependence of another hypothetical film that is normal except that the active layers are composed of water (denoted “no active”), one can see that the absorbed-dose energy dependence is affected by the composition and geometries of the polyester and surface layers.

Surprisingly, as is illustrated in Fig. 3, the majority of the behavior of the absorbed-dose energy dependence of EBT in the photon energy range of 10–100 keV is a result of the so-called surface layer which is the central substrate. By calculating the absorbed-dose energy dependence of a hypothetical film where the only layer that is not composed of water is the surface layer (denoted “only surface”) one obtains a value that differs from the value for the real film by approximately 1.8%. In contrast, the absorbed-dose energy dependence of another hypothetical film that is normal except that the surface layer is composed of water (denoted by “no surface”) differs from that of the actual film by 17%. By increasing the surface layer thickness by 33% from 6 to 8 μm, the absorbed-dose energy dependence decreases on the order of 3%–4%. This variation with surface layer thickness does not occur outside the region from 10 to 100 keV.

Figure 3.

The absorbed-dose energy dependence of a normal EBT film (with a surface layer thickness of 6 μm) as well as a modified film where the surface layer thickness is 8 μm. Also included is the absorbed-dose energy dependence at 50 keV of a hypothetical film, where the only layer that is not composed of water is the surface layer (only surface), a hypothetical film that is normal except that the surface layer is composed of water (no surface) as well as only active and no active from Fig. 2. The uncertainties for the hypothetical film data points are smaller than the symbols.

Table 2 presents the percentage of dose in various layers of film based on the region from which the electrons enter the region of interest for a hypothetical film, where the only layer that is not water is the surface layer and another film composed entirely of water. For the upper active layer at 50 keV, the percentage of dose due to electrons from the surface layer is (22.6%±0.2%), whereas in the absence of the surface layer material it is (12.89%±0.06%). A further simulation with ECUT set to 1 MeV for the upper active layer, i.e., no electrons would escape the upper active layer, showed no decrease in the absolute dose contributed by electrons entering from the surface layer. This indicates that the approximately 12% increase in dose in the upper active layer in the presence of the surface layer material is due to an increased number of electrons being generated in the surface layer (as opposed to electrons from the upper active layer being backscattered by the surface layer). For the lower active layer, at 50 keV the percentage of dose delivered by electrons from the surface layer is (46.5%±0.2%), whereas in the absence of the surface layer material it is (33.0%±0.1%). As before, the increased photon cross section and hence increased number of electrons generated in the surface layer increase the dose by 26% in the active layer. For 10 keV photons, these large differences do not occur since a much larger fraction of the dose is from electrons originating within the active regions. For the incident photon energy of 200 keV, the dose to the surface layer is slightly lower than the dose to the water layer since the cross sections are mostly due to Compton interactions and depend only on electron mass density. Hence, there is little difference in the dose to the active layers in the presence of the surface layer.

Table 2.

The breakdown of the dose to various layers of EBT film based on what percentage of electrons entered from above or below or stayed entirely within the layer of interest. The total dose to the layer per unit fluence incident on the phantom (in Gy cm²) is also included. The only layer that is not water is the surface layer. Data from a simulation where all layers are water are also included. Data are shown with the absolute one standard deviation uncertainty in brackets.

Layer		Surface only	All water
10 keV
Active (upper)	Total dose	5.51E−14 (2E−16)	5.48E−14 (2E−16)
	% above	9.81 (0.05)	9.88 (0.05)
	% below	0.83 (0.01)	0.54 (0.01)
	% within	89.36 (0.05)	89.58 (0.05)
Surface	Total dose	1.30E−13 (4E−16)	5.45E−14 (2E−16)
	% above	8.54 (0.05)	18.78 (0.2)
	% below	0.78 (0.01)	1.33 (0.04)
	% within	90.69 (0.05)	80.0 (0.2)
Active (lower)	Total dose	5.59E−14 (2E−16)	5.44E−14 (2E−16)
	% above	12.65 (0.06)	9.89 (0.05)
	% below	0.51 (0.01)	0.53 (0.01)
	% within	86.84 (0.06)	89.58 (0.05)
50 keV
Active (upper)	Total dose	5.54E−13 (2E−15)	4.95E−13 (1E−15)
	% above	29.6 (0.2)	33.1 (0.1)
	% below	22.6 (0.2)	12.89 (0.06)
	% within	47.7 (0.3)	54.0 (0.1)
Surface	Total dose	6.60E−13 (3E−15)	4.92E−13 (1E−15)
	% above	31.3 (0.2)	40.8 (0.2)
	% below	18.2 (0.2)	21.9 (0.1)
	% within	50.5 (0.3)	37.3 (0.2)
Active (lower)	Total dose	6.22E−13 (2E−15)	4.93E−13 (1E−15)
	% above	46.5 (0.2)	33.0 (0.1)
	% below	10.7 (0.1)	12.84 (0.06)
	% within	42.8 (0.3)	54.1 (0.1)
200 keV
Active (upper)	Total dose	1.117E−12 (5E−15)	1.101E−12 (4E−15)
	% above	52.4 (0.6)	53.1 (0.3)
	% below	13.4 (0.2)	12.7 (0.1)
	% within	34.2 (0.4)	34.2 (0.4)
Surface	Total dose	1.050E−12 (5E−15)	1.103E−12 (6E−15)
	% above	59.2 (0.4)	60.3 (0.4)
	% below	20.3 (0.2)	21.4 (0.2)
	% within	20.4 (0.4)	18.3 (0.4)
Active (lower)	Total dose	1.103E−12 (4E−15)	1.107E−12 (4E−15)
	% above	53.6 (0.3)	53.4 (0.3)
	% below	12.7 (0.1)	12.6 (0.1)
	% within	33.7 (0.4)	34.0 (0.4)

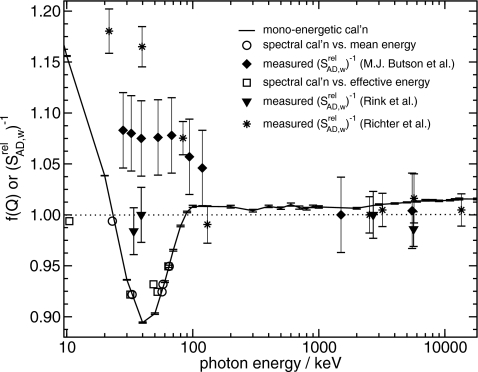
Three previous experimental studies on the energy dependence of the absorbed-dose sensitivity of EBT are shown together with the results of this study in Fig. 4. Butson et al.,⁴ Rink et al.,⁵ and Richter et al.⁷ reported the relative absorbed-dose sensitivity i.e., the absorbed-dose sensitivity [Eq. 3] at each beam quality divided by the absorbed-dose sensitivity at a reference beam quality of 6 MV beams, whereas the results of this study are expressed as the absorbed-dose energy dependence. The experimental results are shown as the inverse of the relative absorbed-dose sensitivity in Fig. 4. If one assumes that the absorbed-dose energy dependence at 6 MV is unity and that k_bq(Q), the intrinsic energy dependence is constant for all energies, then the inverse of the relative absorbed-dose sensitivity with reference to 6 MV is equal to the absorbed-dose energy dependence.

Figure 4.

The absorbed-dose energy dependence of EBT film calculated for monoenergetic photons and for spectra versus either the photon fluence weighted mean energy or the effective energy based on HVL calculations (uncertainties for spectral calculations smaller than symbols). For comparison, the inverse of the relative absorbed-dose sensitivities relative to 6 MV beams from Butson et al. (Ref. ⁴), Rink et al. (Ref. ⁵), and Richter et al. (Ref. ⁷) are shown where the effective energies of their spectra were determined using HVL measurements [or with an equation in the case of the two high photon energy data points from Richter et al. (Ref. ⁷)]. The uncertainties for the spectral calculation data points are smaller than the symbols.

Rink et al.⁵ hypothesized that the differences between their results and those of Butson et al.⁴ could possibly be attributed to the difference between real-time measurements and those obtained 24 h after irradiation compounded with the effect of the low-dose rates of orthovoltage exposures. In addition, Butson et al.⁴ used the original IAEA TRS-277 Code of Practice for their x-ray dosimetry whereas TRS-277 was revised in 1997.¹⁷ The changes for x-ray dosimetry due to the use of more accurate perturbation corrections were up to 7% in a direction to move Butson et al.'s results closer to ours and those of Rink et al.⁵ The results of Richter et al.⁷ were found with the use of a flatbed scanner. Additionally, they measured the relative absorbed-dose sensitivity for doses of 10, 6, 2, and 0.5 Gy (only the 10 Gy points are shown in Fig. 4 for clarity). At low photon energies, they found that the relative absorbed-dose sensitivity for smaller doses was even farther from unity. Nevertheless, the results of all three studies disagree with our calculated values of f(Q). One possible reason for the differences between our results and experimental results would be the existence of an intrinsic energy dependence, i.e., a variation in response per unit dose to the active material. The dose dependence of the relative absorbed-dose sensitivity found by Richter et al.⁷ indicates that there must be an intrinsic energy dependence which varies with dose. Hence, the Monte Carlo calculated absorbed-dose energy dependence cannot be compared to measured relative absorbed-dose sensitivity because such calculations are incapable of accounting for the intrinsic energy dependence. Variation in film compositions may also provide an additional explanation of differing results since, as shown in Fig. 3, one would expect the absorbed-dose energy dependence to be greater than unity if there were a water equivalent surface layer.

EBT2

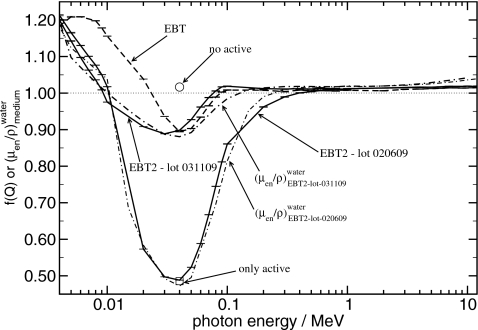
Figure 5 shows the absorbed-dose energy dependence of both lots of EBT2 as well as the mass energy absorption coefficient ratios of water to the active layer materials. The absorbed-dose energy dependence of EBT film is also included for comparison.

Figure 5.

The absorbed-dose energy dependence of EBT and both lots of EBT2 as well as the mass energy absorption coefficient ratio of the active layers of both EBT2 lots to water. Also included is the absorbed-dose energy dependence at 50 keV for a hypothetical film, where the only film layer that is not water is the active layer of lot 020609 (only active) and a hypothetical film that is normal except that the active layer is made of water (no active). The uncertainties for only active and no active are smaller than the symbols.

In contrast to EBT, the decrease in absorbed-dose energy dependence between 10 and 90–200 keV is almost entirely due to the interactions in the much thicker active layer. At 40 keV, for lot 031109, 88% of the dose comes from electrons created within the active layer. For lot 020609, 80% of the dose comes from electrons created within the active layer. For both lots, the shape of the absorbed-dose energy dependence curve as a function of energy very closely follows the mass energy absorption coefficient ratios of water to the active layers. This is confirmed in Fig. 5 by the absorbed-dose energy dependence of one hypothetical film for lot 020609, where the only layer that is not composed of water is the active layer and a second hypothetical film that is normal except that the active layer is composed of water. The value of f(Q) for the film with only the active layer present follows the behavior of the actual film, whereas the value of f(Q) for the film with the active layer set to water is very close to unity.

The behavior of EBT2 can be explained by the thicker single active layer with a higher proportion of high atomic number elements in the active layers compared to EBT. Lot 020609, having a higher effective atomic number than lot 031109, changes more drastically.

For the build-up region calculations with EBT2 using the 6 MV spectrum, the absorbed-dose energy dependence was found to vary from a low at 1 mm depth of 1.000 (±0.001), to a peak of 1.017 (±0.001) at 10 mm depth, and decreases again to 1.012 (±0.001) at 10 cm depth. The maximum variation from the value at 10 cm depth is 1.2%. This apparently occurs because of a higher proportion of low-energy electrons being preferentially created at the surface of the water as the low-energy photons interact close to the surface more frequently than the higher-energy photons. For the narrow (0.5 cm radius) beam, the absorbed-dose energy dependence was found to differ by only 0.4% (±0.2%) compared to that in a 5 cm radius beam.

CONCLUSIONS

The calculated absorbed-dose energy dependence f(Q) of GAFCHROMIC EBT film in monoenergetic photon beams was found to be reasonably constant (±0.6%) from 100 keV to 18 MeV. However, the absorbed-dose energy dependence was found to vary for photon energies from 3 to 100 keV due to the mass energy absorption coefficient ratio of water to the EBT active material below 10 keV and due to an increase in photon interactions in the surface layer between 10 and 100 keV. Although the intrinsic energy dependence of GAFCHROMIC EBT and EBT2 film cannot be determined through Monte Carlo dose calculations, the significant difference between our calculated values of f(Q) and the measured values of ${\left(S_{\text{AD},w}^{\text{rel}}\right)}^{-1}$ suggest that for low-energy photons there is a significant intrinsic energy dependence, k_bq(Q). The observed variation in measured relative absorbed-dose sensitivity with dose⁷ and time to reading⁵ further supports the hypothesis of a non-negligible intrinsic energy dependence.

We recommend that all film components be fully modeled when performing Monte Carlo dose calculations as the effects and interplay of all the film layers have been shown to have an effect at low energies.

Further investigation is required to fully characterize the response of EBT2 film in realistic nonequilibrium conditions, including the effect of electron contamination in the build-up region. Our results suggest that electron disequilibrium arising from dose build-up creates a small but clear change (up to 1.2%) in the absorbed-dose energy dependence, while that arising from a narrow beam geometry does not.

For future films, the effective atomic number of the active layer of the film should be as close as reasonable to that of water to avoid drastic changes in the absorbed-dose sensitivity at lower energies. Furthermore, a thicker active layer will reduce the effect of differences between the mass energy absorption coefficients of the other film layers and water.