A pseudoinverse deformation vector field generator and its applications

Abstract

Purpose: To present, implement, and test a self-consistent pseudoinverse displacement vector field (PIDVF) generator, which preserves the location of information mapped back-and-forth between image sets.

Methods: The algorithm is an iterative scheme based on nearest neighbor interpolation and a subsequent iterative search. Performance of the algorithm is benchmarked using a lung 4DCT data set with six CT images from different breathing phases and eight CT images for a single prostrate patient acquired on different days. A diffeomorphic deformable image registration is used to validate our PIDVFs. Additionally, the PIDVF is used to measure the self-consistency of two nondiffeomorphic algorithms which do not use a self-consistency constraint: The ITK Demons algorithm for the lung patient images and an in-house B-Spline algorithm for the prostate patient images. Both Demons and B-Spline have been QAed through contour comparison. Self-consistency is determined by using a DIR to generate a displacement vector field (DVF) between reference image R and study image S (DVF_R–S). The same DIR is used to generate DVF_S–R. Additionally, our PIDVF generator is used to create PIDVF_S–R. Back-and-forth mapping of a set of points (used as surrogates of contours) using DVF_R–S and DVF_S–R is compared to back-and-forth mapping performed with DVF_R–S and PIDVF_S–R. The Euclidean distances between the original unmapped points and the mapped points are used as a self-consistency measure.

Results: Test results demonstrate that the consistency error observed in back-and-forth mappings can be reduced two to nine times in point mapping and 1.5 to three times in dose mapping when the PIDVF is used in place of the B-Spline algorithm. These self-consistency improvements are not affected by the exchanging of R and S. It is also demonstrated that differences between DVF_S–R and PIDVF_S–R can be used as a criteria to check the quality of the DVF.

Conclusions: Use of DVF and its PIDVF will improve the self-consistency of points, contour, and dose mappings in image guided adaptive therapy.

INTRODUCTION

The development of intensity-modulated radiation therapy (IMRT) has provided the potential of delivering highly conformal dose distributions to the target volume while sparing normal tissues and organs. However, full realization of IMRT’s advantages is limited by target and normal tissue positioning uncertainties, including interfraction and intrafraction setup variations, internal organ motion, and tissue deformation.^{1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13} In this study, for simplicity, intrafraction tissue deformations for lung and interfraction tissue deformations for prostate treatment plans are used to demonstrate the concepts and techniques developed. Studies on prostate motion have shown that both the position and the shape of the prostate vary throughout the course of treatment (fraction).^{2, 3, 4, 5, 10, 14, 15, 16} Recent developments of on-board imaging guidance systems provide real-time information on the patient and target positions, and thus provide the opportunity to realign the planned dose distribution to the actual position of the tumor.^{17, 18, 19, 20, 21, 22, 23} Clinical studies using adaptive treatment planning (ATP) for prostate cancer have demonstrated the clinical feasibility of position correcting schemes as well as an improvement in dose coverage.²⁴

Recently, online reoptimization for adaptive radiation therapy²⁴ has gained some interest. However, positioning correction alone cannot correct the changes in the target shape. Treatment plan adjustment approaches could potentially correct for both position changes and organ deformations. In order to facilitate replanning∕reoptimizing in adaptive radiation therapy, contours need to be mapped from a reference image R to the study (time of treatment or 4D phase) image S. Similarly, the dose already delivered to the patient but accumulated on R needs to be mapped to S to adjust the treatment plan for the remaining fractions. The contour and dose mapping processes utilize the results from deformable image registration (DIR), which provides a nonrigid map of information contained in R to its location in S. DIR algorithms are used to generate a displacement vector field (DVF) which can be viewed as a map of points’ coordinates between R and S. Throughout this paper, DVF_R–S is used to denote a DVF which maps the points from R to S, while DVF_S–R denotes a map from S to R. Although it is often customary to have R be a reference image, such as from an initial treatment planning study or reference phase of a 4DCT, and S for a study image, in some instances, their roles may be reversed.

When DVF_R–S and DVF_S–R are used in IGRT or ATP to map contours (or dose) back-and-forth between R and S to replan∕reoptimize the treatment, a desirable property is that this back-and-forth mapping be self-consistent. For example, assume information is mapped from R to S then back to R. A natural requirement for this back-and-forth mapping is that the original contour in R (or dose distribution) and the contour (or dose distribution) mapped back from the study image should be the same. If the back-and-forth mapping lacks self-consistency, then after mapping the contour or dose distribution back-and-forth, the contour or dose distribution will be distorted on the image. Clinically, if a contour is mapped to S for dose planning and delivery, when the delivered dose is mapped back to R, lack of self-consistency can result in misalignment of the dose and the associated contours. This might give the wrong dose volume information or dose volume histogram, which are used to evaluate and optimize the treatment planning. Note that even though self-consistency is a desirable property, satisfying this condition does not mean the DVF is accurate. More discussion about self-consistency and accuracy is given in Sec. 4.

To avoid the perils of inconsistent registrations, Christensen et al.,²⁵ Joshi,²⁶ and Yang et al.²⁷ developed inverse consistent deformable image registration algorithms. These algorithms strive to achieve the desirable properties that the deformation field be smooth and invertible, so that every point in one image has a corresponding point in the other. Such smooth, invertible transformations are called diffeomorphisms. The aforementioned DIR algorithms simultaneously generate the forward field DVF_R–S=f and reverse field DVF_S–R=h such that both f and h are smooth andf=h⁻¹ holds. As a result, self-consistency is automatically achieved for these DIR algorithms. While self-consistency is a desirable property, there are several image registration algorithms which neither automatically generate the reverse field nor have proven to generate invertible DVFs.^{28, 29, 30} For these algorithms, the prevailing approach takes the negative of the forward deformation as the inverse deformation. This method is oversimplified and can cause large errors for large deformations or deformations that are composites of several deformations. Hence, it is desirable that to have an algorithm that can produce inverse field for the deformation field generated by both diffeomorphic and nondiffeomorphic DIR algorithms. This paper presents a pseudoinverse DVF (PIDVF) generator to fill this need.

The concept of developing an inverse for an arbitrary deformation field is not new. In addition to being implicitly included in the above mentioned diffeomorphic algorithms, Chen et al.³¹ presented an approach to invert a deformation field based on a fixed-point theory. One limitation reported by Chen is that their method will fail to converge and fail to produce an inverse if too many voxels in the forward field have nonpositive Jacobian values.

The PIDVF developed in this paper has two important properties related to prior works. (1) PIDVF exists for an arbitrary deformation field. (2) If the forward field f is invertible (f⁻¹ exists) and f⁻¹ is smooth, then when the inverse computing error ε (defined later) approaches zero, the PIDVF will approach the true inverse field, namely, f⁻¹.

The purposes of this paper are: First, to present an algorithm which can be used to generate a PIDVF with a small inverse computing error and to describe a method which can be used to compare the self-consistency between two fields which are inverses of one another; second, to show that the PIDVF can improve self-consistency in points (contour) mapping when the Insight Segmentation and Registration Toolkit (ITK) Demons is used with lung images and a B-Spline is used with prostate images; third, using a diffeomorphic DIR to show that the PIDVF will converge to the true inverse when inverse computing errors tends to zero.

MATERIALS AND METHODS

Patient data and DIR algorithms

A 4DCT data set with six CT images from different breathing phases for a lung patient and eight image CT sets acquired on different days for a single prostate patient are used in this study. The lung images have 104 0.25 cm slices with 0.097 cm pixel dimensions. A physician manually contoured each image set. For the prostate data set, the original images were acquired at various resolutions and scan lengths. The images are resampled to a uniform resolution and scan length, as required by the DIR algorithm used. After processing, each image has 78 0.30 cm slices with 0.082 cm pixel dimensions. A physician contoured these images for treatment planning using the structures indicated in Ref. 30. A six field 18 MV IMRT treatment was planned on the reference image R=I₀ using the PINNACLE³ treatment planning system (Philips Medical Systems, Fitchburg WI) for the prostate patient. The beam angles used are 180°, 230°, 280°, 330°, 30°, 80°, and 130° and the dose grid resolution is 0.2×0.2×0.2 cm³. Other than providing a clinically relevant dose distribution, with nearly homogenous dose in the target surrounded by gradients near the target edge and critical structures, the details of the dose planning are unimportant to this study.

Three DIR algorithms are used in this study—Christiansen’s small deformation, inverse consistent, linear elastic (SICLE) image registration algorithm,^{25, 32} the Demons algorithm implemented in ITK,³³ and a previously described in-house B-Spline DIR algorithm.³⁰ The SICLE is used with both the lung images and the prostate images. The Demons algorithm is used to register the lung images and the B-Spline was used on the prostate images. The quality of DVFs produced by SICLE and Demons are evaluated via visual comparison of the contours (see Fig. 1 for details) mapped by the DVF with the physician-drawn contours. The B-Spline algorithm³⁰ was previously benchmarked by contour comparison. Namely, contours autogenerated by the DIR algorithm’s DVF were shown to reproduce physician-drawn contour to within 0.2 cm.³⁰ Generally, the registrations created the DVF_R–S. For the B-Spline and Demons algorithm, DVF_S–R are generated by reversing the roles of R and S for each image pair and rerunning the image registration algorithm. For the SICLE algorithm, DVF_S–R is generated simultaneously with the DVF_R–S.

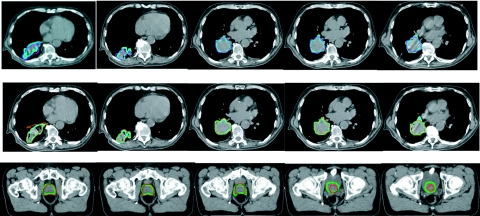
Figure 1.

The first row compares the physician-drawn contour (in thick blue lines) and the contours (in thin purple lines) mapped by the ITK DVF. The second row compares the physician-drawn contour (in thick blue lines) and the contours (in thin orange lines) mapped by the SICLE DVF generated on lung images. The last row compares physician-drawn contour (in thick green lines) and the contours (in thin red lines) mapped by the SICLE DVF generated on prostate images.

When generating DVFs, we found the DVF quality is sensitive to parameters such as CT thresholds, optimization threshold σ, the number of iterations, etc. For example, when SICLE is used to register the lung images, one can get better results for the ribs if the CT threshold is set between 0 and 1300 instead of 0 and 800. Similarly, when the same DIR is used on prostate images, the CT thresholds between 800 and 1100 produce better registrations than at other thresholds. Finding the optimal parameters for each DIR algorithm and each site is beyond the scope of this study. When different parameters are used within a given algorithm, both the DVF and the DVFs’ PIDVF will differ. However, the general properties of the PIDVF will remain similar. Only DVFs which are QAed via the aforementioned contour comparisons are used in this study.

The B-Spline DVF in Ref. 30 is generated (and evaluated) only within a selected region of interest, corresponding to slices in the range (x-slice, y-slice, and z-slice): (150, 324), (150, 299), and (40, 59), which correspond to tissues surrounding the high dose region of interest (ROI) area which contains the prostate. The DVF therefore consists of 525 000 vectors. The displacement vectors outside these areas are set to be zeros and are not utilized in this study.

Definition of PIDVF and PIDVF generator algorithm

In the following discussion, the deformation is formulated on the continuum and is discretized for implementation. Let R and S be two image domains and f:R→S be the DVF_R–S from R to S. f can be viewed as a continuous function. In real applications, it can be viewed as a map of points’ coordinates between R and S. For any point x∊R, f(x)=y is the location of the corresponding point in S. We use f:x→y to denote it. Assume g_ε is a function which will map S back to R. We say g_ε:y→x is the PIDVF of f, if for any point y^′∊S, |f(g_ε(y^′))−y^′|≤ε holds. Note that the above definition does not require g_ε be an inverse function of f, which is used as a constraint for DIR algorithms in Ref. 25. In our formulation, this constraint is relaxed. In the following, f⁻¹ is used to denote the inverse function of f when f is invertible. Two important properties of the PIDVF are formally given in the following with the detailed proofs in the Appendix0.

• PROPERTY 1: If the forward mapping f is between two finite domains R and S, then there exists an ε≥0 such that g_ε exists.

• PROPERTY 2: If f⁻¹ exists and is smooth throughout S, then for an arbitrary point y in S, |g_ε(y)−f⁻¹(y)| tends to 0 as ε→0.

Property 1 guarantees that a PIDVF exists for an arbitrary deformation field. Since both R and S represent finite domains, if ε is allowed to be large, one can always find an ε to make g_ε exist. ε is called the inverse computing error. Obviously, we would like to find a g_ε with ε as small as possible. However, even when ε is not small, the evaluation of ε is useful as a measure of the quality of the PIDVF. Property 2 provides a mechanism for checking our PIDVF generator—Via generating PIDVFs for diffeomorphic DIRs and showing that when ε→0, g_ε approach f⁻¹ for these cases.

An algorithm to generate the PIDVF is described in detail in the Appendix0. Note that in our implementation, the forward mappings are discretized so that the two images R and S are viewed as two sets of 3D grid points. The basic flow of the algorithm is as follows. First, grid points are mapped from R to S according to the DVF_R–S. The values of the inverse mapping PIDVF_S–R are initially assigned to be the negative of the DVF_R–S mapping via nearest neighbor interpolation. Since the image voxel size is small, some of these grid points in S are mapped back to R with small inverse computing errors. The algorithm identifies points in S, which can be mapped back to R with small inverse computing errors (δ<ε), and are also close to points with computing errors δ>ε. These identified points (with small inverse computing errors) are called active grid points. By systematically searching around the points in R which are mapped to the active points in S, the algorithm tries to reduce the inverse computing errors for those points in S that previously had δ>ε. Note that the PIDVF is similar in concept to the inverse computed on-the-fly by diffeomorphic DIR algorithms.²⁵ Differences between the PIDVF and the algorithm used in Ref. 25 can be found in Sec. 4.

Tests

The PIDVF algorithm is first tested on concocted displacement vector fields to conceptually test the algorithm and its implementation. Six concocted 4×4×4 DVFs are generated. (1) DVF with all components 0 cm; (2) DVF with x and y components 0 cm, but z component a constant (0.2 cm); (3) DVF with y and z components 0 cm but x component a constant (0.2 cm); (4) DVF with x and z components 0 cm but y component a constant (0.2 cm); (5) DVF with x, y, and z components being constants (0.2 cm); and (6) DVF with x, y, and z components being variables (the corresponding indices times 0.1). The PIDVFs for each concocted DVF are generated (with inverse computing error set to 0.01 cm and verified to be the inverse of the supplied DVF.

Difference between DVF_S–R and PIDVF_S–R

The PIDVF algorithm is used to generate PIDVFs for the DVFs generated by the SICLE algorithm on both the lung and prostate data sets, the DVFs generated by the ITK Demons on the lung data sets, and the DVFs generated by the B-Spline DIR algorithm³⁰ on the prostate data sets. To demonstrate that the PIDVF generator functions when the forward DVF has nonpositive Jacobian values, the number of voxels with nonpositive Jacobian values for the forward DVF is reported. In computing the PIDVF, the maximum allowed inverse computing error ε is set to 0.01 cm. This number was chosen to obtain a balance between accuracy and running time.

For a DVF_R–S, to quantify the differences between the exchange of image sets to obtain DVF_S–R and the PIDVF_S–R method to determine the inverse, the difference between PIDVFs and DVFs is examined. For an arbitrary image voxel i in S, (x_pi,y_pi,z_pi) is the pseudoinverse DVF vector (an element of PIDVF_S–R, as appropriate) and (x_di,y_di,z_di) is the reverse DVF vector (an element of DVF_S–R), the difference between the two vectors is $\sqrt{{\left(x_{p_i}-x_{d_i}\right)}^2+{\left(y_{p_i}-y_{d_i}\right)}^2+{\left(z_{p_i}-z_{d_i}\right)}^2}$. The difference is computed for each image voxel and the average and maximum differences are found.

Point mapping consistency

Contour mapping consists of transferring a connected set of points on one image to another image by the application of a DVF. The locations of exact points on a physician-drawn contour are instance-specific—Even if the same physician redraws the same contour on a given image sets, the points on the two contours drawn do not exactly overlay. In this study, instead of quantifying deviations in physician-drawn contours, deviations in points that can be mapped by the DVF are measured, thus allowing quantification of errors for an arbitrary series of contours. By connecting a series of these points, the error in a contour mapping could be determined.

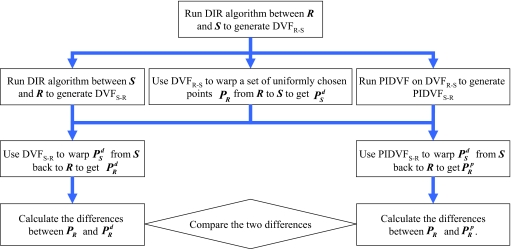
The scheme shown in Fig. 2 is used to compare the self-consistency of the DVF and PIDVF for mapping points. For this test, both the lung and prostate images are used. A set of points (in our study, each voxel in R contains at least one point) are uniformly chosen from the reference image R and are mapped to S by using DVF_R–S. The points are mapped back to R by using DVF_S–R or the PIDVF_S–R. Let p₁ be the coordinate of an arbitrarily chosen point in R and p₃ be the coordinate after the back-and-forth mapping. The Euclidean distance Δd=|p₁−p₃| is defined as the consistency error, which is used to quantitatively measure the self-consistency between forward and reverse fields. With P_R being the original point locations, $P_R^D$ being the back-and-forth mapped points (using DVF_R–S and DVF_S–R methods), and $P_R^P$ being the points mapped back using the PIDVF, the consistency errors between the points in P_R and the points in $P_R^D$ give the inconsistency of the DVF-based inverse mapping, and the consistency errors between the points in P_R and the points in $P_R^P$ give the inconsistency of the PIDVF mapping. The maximum average of the consistency errors are calculated and compared.

Figure 2.

Scheme used to compare self-consistency between DVF and PIDVF in mapping point.

Dose mapping consistency

In dose mapping, dose recorded (delivered) on R (or S) needs to be mapped to its physical location on S (or R) via the DVF to do replanning (or to accumulate the total treatment dose delivered). In this study, the trilinear method is used to map the dose.³⁴ To map a dose distribution from R to S, the dose grid points P_S on S are first mapped to P_R according to DVF_S–R. The dose values of those points in P_R are obtained by trilinear interpolation of the dose in R. These values are assigned as the dose to the points in P_S. Even though the trilinear method has been shown to be inaccurate in some special circumstances of voxel merging and splitting,³⁵ it is used in this study since it is the standard dose interpolation method.

Dose mapping quality is related to DVF errors, dose mapping methods, boundary conditions, dose gradients, and dose grid resolution. A comprehensive study of these dependencies is beyond the scope of this paper. The prostate patient and the B-Spline DIR are used to investigate if the PIDVF improves self-consistency in back-and-forth dose mapping for DVFs generated by nondiffeomorphic DIR algorithm.

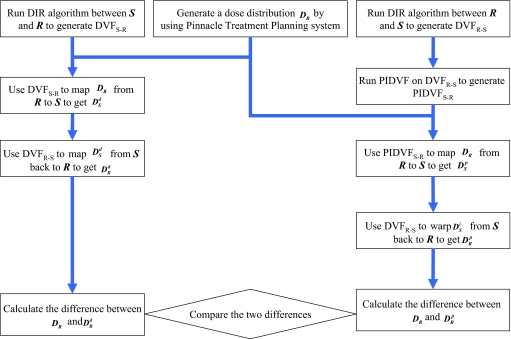
The scheme shown in Fig. 3 is used to compare the self-consistency between DVFs and PIDVFs in dose mapping. The dose on R is mapped to S using DVF_S–R and PIDVF_S–R, then mapped back to R by using DVF_R–S. The original dose distribution on image R is compared to the back-and-forth mapped dose with the difference between them quantifying the effect of inconsistencies in the dose mapping. For clarity, the dose mapped by DVF only is called DVF-only mapping and the mapping done by DVF and PIDVF is called DVF-with-PIDVF mapping. The maximum and average dose differences are compared.

Figure 3.

Scheme used to compare self-consistency between DVF and PIDVF in mapping dose.

Effect of exchanging reference and study images

As pointed out in Ref. 36, the DVFs resulting from image registrations can depend on which image is the reference and which is the study image. A desired property of mapping points, contours, or dose is that the self-consistency does not depend on which image is reference and which image is study. Motivated by this, the R and S are exchanged and the self-consistency tests shown in Figs. 23 are performed again. In particular, points and doses are mapped back-and-forth by using DVF_S–R and DVF_R–S and DVF_S–R and PIDVF_R–S, where PIDVF_R–S is the pseudoinverse of DVF_S–R.

RESULTS

Difference between DVF_S–R and PIDVF_S–R

For the eight prostate CT (denoted by I₀,…,I₇) images, PIDVFs are created for the B-Spline and the SICLE DIR results. A summary of the number of nonpositive Jacobian values for the forward registration and summary statistics of the difference between the PIDVF and the reverse field are given in Table 1. The B-Spline algorithm has a few voxels with nonpositive Jacobians, and SICLE has none, as expected. All of the PIDVF elements report an inverse computing error less than the tolerance value 0.01 cm. Differences between PIDVF and the reverse field are greater for the B-Spline DVFs than they are with SICLE. This is in agreement with Property 2 since, with SICLE, the forward DVF is invertible and smooth. Hence, the SICLE PIDVF is close to the SICLE computed inversely.

Table 1.

Differences between reverse field and the PIDVFs for registrations performed on the eight prostate image sets (I₀,I₁,…,I₇). For the B-Spline DVFs, the reverse field is generated by running the DIR algorithm with reference and study images exchanged. SICLE autogenerates the reverse field. No points had inverse computing errors greater than 0.01 cm for these PIDVFs. The number of nonpositive Jacobians for the DVFs is also listed for each registration.

R and S	B-Spline DVF			SICLE DVFs
	No. of nonpositive Jacobians	Maximum difference (cm)	Average difference (cm)	No. of nonpositive Jacobians	Maximum difference (cm)	Average difference (cm)
I0 and I1	103	2.69	0.053	0	0.74	0.0068
I0 and I2	52	1.14	0.044	0	0.87	0.0069
I0 and I3	23	1.14	0.032	0	0.45	0.0075
I0 and I4	9	1.17	0.034	0	0.27	0.0081
I0 and I5	8	0.77	0.029	0	0.039	0.0022
I0 and I6	201	0.81	0.037	0	0.076	0.0082
I0 and I7	8	0.97	0.026	0	0.591	0.0052

For the lung PIDVFs generated for the ITK Demons DVFs, multiple points have inverse computing errors greater than 0.01 cm. For the PIDVFs generated for the SICLE DVFs, all the inverse computing errors are less than 0.01 cm. The maximum inverse computing errors and the number of points with inverse computing errors greater than the 0.01 cm are listed in Table 2 together with the number of nonpositive Jacobians in the DVFs. For the Demons DVFs, even though many elements have nonpositive Jacobians, the maximum inverse computing error observed is 0.043 cm.

Table 2.

The maximum inverse computing error (ICE) and the number of points (out of 27 262 976 points) with inverse computing errors greater than the error tolerance set in the PIDVF algorithm (0.01 cm) for the DVFs between the six lung images (Phase 0, Phase 1, … Phase 5) generated by the DIR implemented in ITK and the DIR in Ref. 25. The maximum and average differences are evaluated between DVF_S–R and PIDVF_S–R. For the ITK Demons DVFs, the reverse field (DVF_S–R) is generated by running the DIR algorithm with reference and study images exchanged. SICLE autogenerates the reverse field. The number of DVF_R–S elements with nonpositive Jacobians is also listed for each registration.

R and S	ITK Demons DVFs					SICLE DVFs
	No. of nonpositive Jacobians	Max. ICE (cm)	No. of points with ICE>0.01 cm	Max. difference (cm)	Ave. difference (cm)	No. of nonpositive Jacobians	Max. ICE (cm)	No. of points with ICE>0.01 cm	Max. difference (cm)	Ave. difference (cm)
Phases 0 and 1	575 314	0.034	61	2.03	0.064	0	0.01	0	0.169	0.0024
Phases 0 and 2	657 154	0.032	95	2.90	0.12	0	0.01	0	0.28	0.0027
Phases 0 and 3	668 586	0.043	121	3.11	0.13	0	0.01	0	0.995	0.0498
Phases 0 and 4	670 976	0.035	127	3.29	0.14	0	0.01	0	0.322	0.0029
Phases 0 and 5	671 638	0.029	119	3.16	0.14	0	0.01	0	0.26	0.0029

The difference between PIDVF and the reverse fields generated by SICLE and Demons for the lung images are also compared in Table 2. The average differences for SICLE are ∼30 times lower than that for ITK Demons. For ITK Demons DVFs, generation of the reverse field by exchanging the reference and study images is about ten times slower than by using the PIDVF algorithm. One may also notice the maximum difference between SICLE reverse fields and the PIDVF shown in Tables 1, 2 are greater than 0.01 cm. To understand the cause of this, we looked at the location of the maximum difference, and found that in all cases, except when image I₀ and I₅ from the prostate patient are used as inputs, the maximum differences occur at the image edge. This may be caused by the fact that not enough information is available at the boundary of the image. In the interest of making this paper short and focused, the detailed results are omitted here.

Point and dose mapping consistency

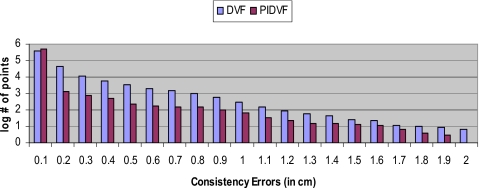
A comparison of the B-Spline DIR consistency errors for back-and-forth point mapping for one pair of prostate images (with I₀ being R and I₁ being S) is shown in Fig. 4. Table 3 lists the statistics of the consistency errors observed for other image pairs. When mapping points back-and-forth, the DVF-with-PIDVF method is more self-consistent than the DVF-only method. The reason why some points have consistency errors greater than 2ε for the DVF-with-PIDVF method is explained in Sec. 4. From Table 3, we find that the average consistency error for the DVF-with-PIDVF point mapping is ∼2 to ∼9 times less than that for the B-Spline DVF-only method. The consistency error in points mapping for the prostate images with SICLE is also shown in Table 3 (in columns denoted by S). The maximum errors are small and similar for both DVF-with-PIDVF methods. The average errors for the PIDVF method are about half of the DVF method; however, both errors are sufficiently small. For the dose mapping, the statistics of the differences between the original dose distribution and the back-and-forth mapped dose distribution are shown in Table 4. When B-Spline is used to generate the DVFs between I₀ and I₁, the largest difference in the DVF_S–R with DVF_R–S mapping is 951 out of 7000 cGy, while in DVF_S–R with PIDVF_R–S mapping, it is 254 cGy. The average difference in the DVF_S–R with DVF_R–S mapping is 35 cGy, and it is 15 cGy in the DVF_S–R with PIDVF_R–S mapping. SICLE back-and-forth dose mapping consistency errors are also shown in Table 4 (in columns denoted by S).

Figure 4.

Comparison of the consistency errors between DVF-only method and DVF-with-PIDVF method in mapping points. The x-axis is consistency errors (in cm) and y-axis is the logarithm of number of points with the consistency error.

Table 3.

Point mapping consistency errors for DVF_R–S with DVF_S–R, DVF_R–S with PIDVF_S–R, and PIDVF_R–S with DVF_S–R methods. The B-Spline (in the column denoted by B) and SICLE (in the column denoted by S) are used to generate DVFs on a set of images from a prostate patient (I₀, I₁,…,I₇ are used to denote prostate images). PIDVF_S–R is the pseudoinverse of DVF_R–S and PIDVF_R–S is the pseudoinverse of DVF_S–R.

R and S	Consistency errors by DVFR–S with DVFS–R (cm)				Consistency errors by DVFR–S with PIDVFS–R (cm)				Consistency errors by PIDVFR–S with DVFS–R (cm)
	Maximum		Average		Maximum		Average		Maximum		Average
	B	S	B	S	B	S	B	S	B	S	B	S
I0 and I1	1.94	0.54	0.06	0.005	1.92	0.54	0.006	0.002	0.02	0.01	0.0008	0.0007
I0 and I2	1.20	0.55	0.05	0.005	1.20	0.57	0.007	0.002	0.01	0.01	0.0009	0.0009
I0 and I3	0.88	0.25	0.04	0.006	0.74	0.23	0.005	0.002	0.01	0.01	0.0007	0.0007
I0 and I4	0.96	0.18	0.04	0.003	0.75	0.18	0.004	0.002	0.01	0.01	0.0007	0.0007
I0 and I5	0.66	0.05	0.04	0.001	0.66	0.02	0.008	0.001	0.01	0.01	0.001	0.0006
I0 and I6	1.05	0.7	0.05	0.005	1.05	0.75	0.01	0.003	0.01	0.01	0.002	0.0007
I0 and I7	0.95	0.42	0.03	0.004	0.75	0.32	0.003	0.002	0.01	0.01	0.0008	0.0008

Table 4.

B-Spline (B column) and SICLE (S column) back-and-forth dose mapping self-consistency comparison for DVF_R–S with DVF_S–R, DVF_R–S with PIDVF_S–R, and PIDVF_R–S with DVF_S–R mappings. The DVFs are generated for a set of prostate images (I₀,I₁,…,I₇). The PIDVF approach has 1.5–2.5 times smaller deviations for B-Spline and similar performance for SICLE.

R and S	Statistics of dose differences by DVFS–R with DVFR–S (cGy)				Statistics of dose differences by PIDVFS–R with DVFR–S (cGy)				Statistics of dose differences by DVFS–R with PIDVFR–S (cGy)
	Maximum		Average		Maximum		Average		Maximum		Average
	B	S	B	S	B	S	B	S	B	S	B	S
I0 and I1	952.0	200.6	35.6	17.8	254.1	213.2	15.6	15.5	223.1	208.1	14.6	17.5
I0 and I2	1055.5	187.9	42.7	14.5	168.4	184.9	20.4	17.1	149.1	186.1	20.4	18.5
I0 and I3	540.9	243.7	27.3	16.8	117.6	212.7	16.8	13.1	163.2	200.5	17.2	14.6
I0 and I4	719.9	197.5	32.0	16.6	178.8	198.2	18.3	15.8	153.7	187.4	17.8	15.9
I0 and I5	374.9	191.2	26.9	15.1	139.7	191.6	19.8	14.4	188.8	190.8	19.9	14.6
I0 and I6	349.3	268.8	25.0	16.5	343.7	268.5	14.6	18.1	262.3	255.6	14.4	15.4
I0 and I7	364.3	157.7	21.9	16.7	180.7	157.1	14.4	18.4	114.8	165.9	14.6	16.2

For the lung patient, the consistency errors are shown in Table 5. The DVFs are generated by the Demons in ITK (denoted by I) and SICLE (denoted by S), respectively. In Table 5, the points mapped by using DVF and its PIDVF are more consistent than the DVF and its reverse DVF method for the nondiffeomorphic ITK Demons. For SICLE, the PIDVF is almost the same as the reverse field generated by the DIR.

Table 5.

Point mapping consistency errors for DVF_R–S with DVF_S–R, DVF_R–S with PIDVF_S–R, and PIDVF_R–S with DVF_S–R methods. The DVFs are generated by the Demons in ITK (I column) and SICLE (S column) on the images from a lung patient.

R and S	Consistency errors by DVFR–S with DVFS–R (cm)				Consistency errors by DVFR–S with PIDVFS–R (cm)				Consistency errors by PIDVFR–S with DVFS–R (cm)
	Maximum		Average		Maximum		Average		Maximum		Average
	I	S	I	S	I	S	I	S	I	S	I	S
Phase 0 and 1	2.01	0.03	0.07	0.0005	0.71	0.03	0.009	0.0002	0.68	0.03	0.007	0.0002
Phase 0 and 2	2.87	0.04	0.12	0.001	0.84	0.03	0.01	0.002	0.76	0.03	0.009	0.001
Phase 0 and 3	3.11	0.99	0.14	0.05	0.90	0.03	0.01	0.002	0.91	0.03	0.01	0.002
Phase 0 and 4	3.30	0.06	0.14	0.001	1.02	0.06	0.01	0.002	0.96	0.05	0.01	0.001
Phase 0 and 5	3.16	0.06	0.14	0.001	0.80	0.06	0.01	0.002	0.74	0.03	0.01	0.002

DISCUSSION

The PIDVF generator described here finds a self-consistent inverse to a pre-existing DVF and is useful for DIR algorithms that do not autogenerate a self-consistent inverse. It generates a PIDVF even when the initial DVF has nonpositive Jacobian values. In this work, the PIDVF concept is applied to DVFs generated by a previously benchmarked B-Spline registration algorithm,³⁰ the ITK Demons algorithm, and the SICLE algorithm.²⁵ While the maximum allowed inverse computing error may need to be adjusted for different DIRs, the PIDVF concept can be applied to DVFs generated by any DIR algorithm. The forward and reverse fields generated by diffeomorphic SICLE are used to validate our PIDVF generator. The comparison between the reverse field generated by SICLE and PIDVF are used to verify Property 2 which is proven in the Appendix0.

The potential clinical impacts of the PIDVF concept are threefold. First, although a DVF itself might not perfectly map information from one image to another, its PIDVF will still give self-consistent results when mapping points, contours, dose, or other planning information back-and-forth between image sets. In adaptive therapy, when mapping contours and dose from a reference image set out to a “time of treatment” image set, mapping the per-treatment dose back to the reference image set with the PIDVF assures that the per-treatment dose resides within the reference image contour. Second, the existence of a PIDVF and subsequent comparison with the reverse DVF generated by switching the roles of R and S can test the quality of the DVF. However, similar to the previously developed unbalanced energy concept,³⁷ passing this test is only a necessary but not sufficient condition for evaluating the correctness of DVFs. For example, consider DVF_R–S and DVF_S–R with all vectors being zeros. These DVFs are meaningless when the deformation is not zero. However, these DVFs will be perfectly self-consistent since it does not move the information at all. Similarly, the PIDVF_S–R vectors will also be zeros and there are no differences between PIDVF and DVF. Hence, the difference between PIDVF and the reverse DVF alone are not sufficient condition for evaluating the correctness of DVFs. Third, the PIDVF together with the method described in Sec. 3B, can be used as a tool to detect the irregularities in the forward DVFs (between R and S). The consistency errors in point mapping can be considered to be a lower bound of DVF errors, since the correct DVFs should be self-consistent.

We use an example to show how the PIDVF and the method described in the point mapping section can be used to detect irregularities in the forward DVFs. For simplicity, assume the reference image consists of n points. Assume DVF_R–S maps all the points (x₁,…,x_n)∊R on to one point y∊S. That is the forward mapping f:x_l→y, l=1,…,n. Then according to the definition of PIDVF, g_ε with ε=0 exists. That is g₀:y→x_k where k is an arbitrary integer between 1 and n. Note that in this special case, the PIDVF is not unique. Now, a set of points are uniformly chosen from (in our experiment, at least one point is chosen from each voxel in reference image) R. Without loss of generality, assume x₁,…,x_n are chosen. If the forward DVF is used to map points from R to S, then all the points will be mapped to y. When g₀ is used to map them back to R, each point will be mapped to x_k. The consistency error for x_k is zero and nonzero for all other points. If such irregularities exist in the forward fields, the PIDVF together with the method can detect the location of such irregularities.

As shown in Tables 3, 4, the fact that the average distance and dose discrepancies obtained when using PIDVF_S–R with DVF_S–R are similar to those for DVF_S–R with PIDVF_R–S indicates that the self-consistency accuracy is not dependent on which image is chosen as the reference and study images during the image registration. In all cases, the self-consistency is improved if the DVF and its PIDVF are used to map points or dose back-and-forth. In Table 3, one may notice that the maximum and average distance deviations for the PIDVF_S–R with DVF_S–R are much smaller than the values in for the DVF_S–R with PIDVF_R–S. This is due to the points close to the edge of ROI. If DVF_R–S is used to map points, then some points close to the edge are mapped out of the ROI. Since the components of PIDVF_S–R and DVF_S–R are set to zeros, these points will not be mapped back to the ROI. This can cause large consistency errors. These consistency errors might be reduced by expanding the ROI used to generate the DVFs. Due to the limit of space, only QAed DVFs are used in this study and expanding the ROI to avoid the boundary condition is left for our future study.

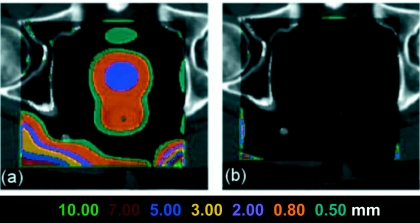
Figure 5 shows the spatial locations of the consistency errors. Since the PIDVF_R–S is self-consistent with DVF_S–R and the components of DVF_S–R out of the ROI are zeros, PIDVF_S–R will not map the edge points out of ROI, hence, those points will stay in ROI and will be mapped back. As a result, the maximum and average discrepancies are much smaller.

Figure 5.

(a) Consistency error distribution when points are mapped by DVF only for the B-Spline algorithm on the prostate images. (b) Consistency error distribution when points are mapped by DVF and PIDVF. In this mapping, errors are only at the DVF box edges.

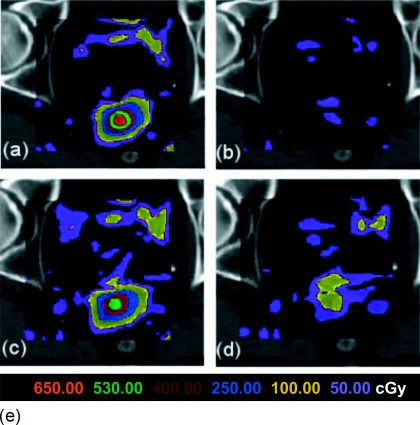
By comparing Tables 3, 4, one can see that the improvement in self-consistency in points and dose mapping are different. For example, when mapping points back-and-forth, the average distance consistency error can be reduced by three to nine times if PIDVF is used (as shown in Table 3). When dose is mapped back-and-forth, the improvement is only 1.5–2.5 times. The dose consistency error is less due to the low dose gradient in the discrepant regions and interpolation blurring. If the point-based mapping is off by some distance (e.g., even several cm), but the dose at the offset point is the same as the true point (e.g., the dose gradient is zero), then the dose consistency error will be zero. The boundary conditions also affect the dose mapping accuracy. Figure 6 shows the distribution of the dose inconsistency in dose mapping. Due to space limitations, dose mapping errors and inconsistency will be further studied in our future work.

Figure 6.

The dose mapping inconsistency for the B-Spline DVF for a prostate image displayed on a single transverse slice. (a) and (b) show the dose consistency errors for DVF-only and PIDVF-with-DVF, respectively, for a 2×2×2 mm³ dose grid resolution. (d) and (e) show the DVF-only and PIDVF-with-DVF dose consistency errors when the dose grid resolution is 4×4×4 mm³.

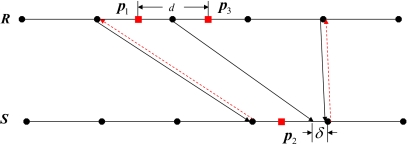
When mapping points back-and-forth, there are consistency errors greater than 2ε (0.02 cm), where ε is the maximum mapping error of PIDVF. There are two sources for such consistency errors. The first source comes from the points located at the edge of the region of interest. For example, Fig. 5b shows the consistency error in points mapping on one slice of R with I₀ being R and I₁ being S. Near the image boundary, insufficient information exists to accurately interpolate the DVF, and hence large consistency errors result. The second source of large consistency error is due to the interpolation error which is related to the resolution and magnitude of the DVF. A one-dimensional example is used to illustrate the source of this consistency error (Fig. 7). Let p₁ be a point in R, and p₂ be the point after mapping p₁ to S by using DVF_R–S (shown in solid black lines). The PIDVF_S–R (shown in dashed red lines) is used to map p₂ back to R, yielding p₃. d is the consistency error in this back-and-forth mapping. Here, when δ→0, d approaches the voxel size. Note that if the PIDVF_S–R is evaluated and stored at additional points in the image space of S (e.g., at an increased resolution), then d is reduced since the interpolating points are more closely spaced, thereby reducing the interpolation error. The standard PIDVF algorithm can be used to determine the PIDVF at the additional points. We have implemented this approach, tested it for mapping points, and found that it improved the self-consistency of the back-and-forth point mapping. Details of the implementation and testing are omitted here in the interest of space.

Figure 7.

An example of how the finite DVF resolution can contribute to consistency errors. DVF_R–S is shown in black lines and PIDVF_S–R (shown in red dashed lines). δ is a small distance in comparison with the DVF voxel resolution. By interpolation of DVF_R–S, p₁ in R is mapped to p₂ in S. By interpolation of PIDVF_S–R, p₂ in S is mapped back to p₃ in R. d is the consistency error which is due to the interpolation of the finite resolution DVF.

The PIDVF method described in this paper and the Appendix0 is different from the inverting method in Ref. 25. The inverting algorithm used in Ref. 25 can be described as the following: For each point q in S, the algorithm first picks a point p in R and calculates the inverse computing error |f(p)−q|. Points p=p+(q−f(p))∕2 are then iteratively picked and the inverse computing error is recalculated until the inverse computing error is smaller than a threshold or the maximum number of loops is reached. Note that Ref. 25 assumes that the forward field f is continuously differentiable and has positive Jacobian throughout R, thus f⁻¹ exists and is smooth. This implies the inverse computing error can be made arbitrarily small. When the algorithm in Ref. 25 encounters a point which does not converge, it stops. In contrast, the algorithm presented in this paper (and detailed in the Appendix0) only assumes the forward field is finite. The PIDVF algorithm first finds a PIDVF value with finite error at each point, and then iterates around each point to identify locations which reduce the inverse computing error at each point. The algorithm is described in further detail in the Appendix0. At completion, the algorithm reports not only the PIDVF, but also the inverse computing error at each point. The PIDVF algorithm described in this paper can generate reverse fields with small inverse computing error for DVFs generated by both B-Spline and ITK Demons algorithms. This is not assured for the algorithm in Ref. 25. To demonstrate this, an in-house implementation of the algorithm in Ref. 25 is developed. In testing with SICLE forward DVFs, the reverse DVF is quickly computed with a maximum computing error of less than 0.01 cm. However, when the ITK Demon lung DVF between Phases 0 and 4 is input into our in-house implementation of the algorithm in Ref. 25, 35 110 points have a inverse computing error greater than 0.01 cm and the maximum inverse computing error is 0.9 cm. When our PIDVF generator is used with the same inputs, only 127 points have an inverse computing error greater than 0.01 cm, and the maximum inverse computing error is reduced to 0.035 cm—A substantial improvement over our implementation of the method in Ref. 25 for this test.

An incidental finding during our back-and-forth dose mapping tests is that the dose consistency error is proportional to the dose voxel size, due to interpolation error. Figure 6 shows the improvement in self-consistency when a 2×2×2 mm³ dose voxel size is used compared to a 4×4×4 mm³ voxel size. The improvement suggests that in order to improve the self-consistency of mapping dose back-and-forth, it is not sufficient to improve the self-consistency of DVFs and PIDVFs alone. Instead, dose voxel resolution and dose mapping algorithms should also be improved. In the past few years, various methods have been introduced to incorporate organ motion into dose calculations quantitatively.^{38, 39} Assessment of dose reconstruction errors⁴⁰ has also been reported. Self-consistency should not only be a constraint for DVFs, it should also be a requirement for dose mapping algorithms. By using DVF and its PIDVF with small inverse computing errors, one can be assured that the DVF and PIDVF are consistent, so one can focus on the self-consistency of dose mapping methods.

CONCLUSION

In IGRT and ATP, points, contours, dose, and other relevant treatment information may need to be mapped back-and-forth between reference image and study images. Inconsistent forward and backward mappings may result in dose being mapped out of contours. Motivated by this, the PIDVF concept is developed in this paper. We have demonstrated that it is possible to generate a PIDVF with a small inconsistency error. Our PIDVF generator algorithm is just an example implementation and alternative algorithms to generate PIDVFs may exist. Our algorithm can be easily parallelized. The difference between the DVF generated by reversing the roles of R and S in image registration and PIDVF could be used as a metric to measure the goodness of the DVFs. As shown in our testing results, if a DVF and its PIDVF is used to map information back-and-forth, then the self-consistency is improved as compared with mapping by using the DVF only. Moreover, when using DVF with its PIDVF, the improvement in self-consistency does not depend on which image is reference and which image is study, which is a desirable property in clinical application. The PIDVF algorithm is available upon request from the first author.

APPENDIX: PIDVF GENERATOR AND ITS PROPERTIES

PIDVF generator

In describing the PIDVF generator, the DVF generated by the B-Spline DIR in Ref. 30 is used as an example. However, the DVF generated by an arbitrary deformable image registration algorithm could have been used. The input to the algorithm is a DVF between R and S, DVF_R–S. The output of the algorithm is a pseudoinverse DVF PIDVF_S–R, which is self-consistent with the DVF_R–S.

The reference and study images can be viewed as two 3D grids. The DVF_R–S can be viewed as a map from the grid points of R to the points in S. By interpolation of DVF_R–S, the mapping of an arbitrary point p in R is mapped to the point q in S. Finding the PIDVF at each grid point q in S consists of finding the point p in R, such that p is mapped to within ε of q according to the forward DVF_R–S. The PIDVF for q is then g_ε:q→p.

In the description of the algorithm, g(q) is used to denote the mapping of q to R, e(q) denotes the inverse computing error and f(p) is the point where p is mapped into S. Initially, e(q) is set to infinity for every grid point in S.

The algorithm has two main steps, each consisting of several subroutines. The first step consists of finding a finite pseudoinverse mapping for each point, the second step in reducing the mapping error for point with errors greater than the tolerance threshold. Pseudocode for the algorithm is shown in Fig. 8.

Figure 8.

Pseudocode for the inverse DVF algorithm. See text for explanation of the steps.

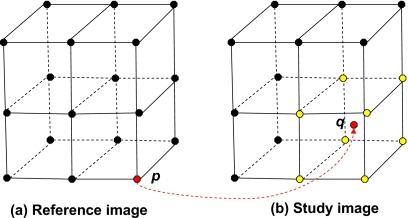
The first step consists of the following: Each grid point p in R is mapped to a point f(p) in S. The set of grid points q in S which surround f(p) are chosen and mapped back to p with the negative of the forward transformation (see Fig. 9). The PIDVF and error in each mapping e(q) equal to the distance between f(p) and the chosen grid point is updated if e(q) is reduced by the mapping. The maximum distance surrounding f(p) for these assignments is user adjustable. For the B-Spline test case, the distance is set to be the largest diagonal distance in one 0.08×0.08×0.3 cm³ voxel, ∼0.32 cm. Note that the maximum inverse computing error for these points is then 0.32 cm. At this point, it is possible that some points in S have unassigned initial PIDVF(q) and e(q) values. Each point q in S with unassigned PIDVF and e(q) values is assigned by choosing the nearest neighbor q^′ of q with finite e(q^′) and setting g(q) to g(q^′) and computing e(q). At the completion of this first step, all the points in S are mapped back to R with a finite inverse computing error.

Figure 9.

Demonstration of the selection of points to assign initial reverse mappings to. Assume the grid point p in the reference image R is mapped to q in the study image S. The yellow points in S are grid points for the voxel, which contain q. In our first step, the grid points in yellow are mapped back to p.

The second step focused on reducing the inverse computing error for points with e(q)>ε as follows, with ε being a user-specified tolerance value. In this work, ε=0.01 cm. First, for each point q in S with e(q)>ε, a box centered at g(q) is constructed with size equal to e(q). The eight corners of the box are mapped to S and the reverse mapping of q is updated if e(q) can be reduced. The box size is iteratively halved six times in search of locations with smaller computing errors. Next, several rounds of a systematic search are performed to reduce e(q) for the remaining points with e(q)>ε as follows. The search first identifies a set of active grid points. A grid point q in S is an active grid point if e(q)<ε and a grid point in N₁[q] has an inverse computing error greater than ε, where N₁[q] is a set of grid points in S directly adjacent to q. For the previously stated voxel size, this corresponds with a distance of at most $\sqrt{{0.08}^2+{0.08}^2+{0.3}^2}=0.32\text{cm}$ from q. For each identified active grid point q in S, a box centered at g(q) is constructed in R. For each grid point p of the constructed box, the inverse computing errors for the grid points surrounding f(p) are recalculated and points with reduced computing errors in that search space are identified and assigned, thereby reducing the errors for some points. The spacing of the box around p is iteratively reduced in the search for a point with reduced mapping error. The systematic search described above, beginning with the reidentification of active grid points, is repeated several times until the inverse computing error is less than ε or the maximum number of iterations is reached. The maximum number of iterations can be chosen to balance the tradeoff between inverse computing error and running time.

PIDVF properties

The two properties of PIDVF are given as two lemmas. Their proofs are given below.

Lemma 1. If the forward mappingf is between two finite domains RandS, then there exists an ε≥0, such thatg_ε exists, i.e., |f(g_ε(y^′))−y^′|≤ε for any y^′∊S.

Proof.Assume the largest distances between any two points inR is d₁ and the largest distances between any two points in Sisd₂, let ε=d=max{d₁,d₂}. SinceR and S are finite, d must exist. Now, for any given point y in S, supposeg_d:y→xforx in R. Assume in the forward mappingf:x→z, wherex is a point in Randz is point in S. By the choice ofd, |y−z|≤d=ε holds. Hence, g_d is well-defined.

Lemma 2. Iff⁻¹ exists and is smooth in S, then for an arbitrary point y in S, |g_ε(y)−f⁻¹(y)| tends to 0 when ε approaches zero,

Proof. The proof is by contradiction. Assume that there isy₀ such that |g_ε(y₀)−f⁻¹(y₀)| does not approach zero as ε tends to 0. According to the definition of g_ε, suppose g_ε(y₀)=x^′, then |f(x^′)−y₀|≤ε holds. Since f is invertible, there exists exactly one x such that f⁻¹(y₀)=x. Since |g_ε(y₀)−f⁻¹(y₀)| does not tend to zero, it implies that there exists a sequence of {ε_i},ε_i→0, such that

$$\left|{\mathit{g}}_{{\epsilon }_i}\left(y_0\right)-{\mathit{f}}^{-1}\left(y_0\right)\right|\ge C$$ (A.1)

for some constantC. Note that f⁻¹ is a continuous smooth function. When |f(g_εi(y₀))−y₀|<ε_i→0, |f⁻¹(f(g_εi(y₀)))−f⁻¹(y₀)|<ε_i→0, which contradicts Eq. A.1.