Abstract
Purpose: The authors propose the framework for an individualized adaptive computer-aided educational system in mammography that is based on user modeling. The underlying hypothesis is that user models can be developed to capture the individual error making patterns of radiologists-in-training. In this pilot study, the authors test the above hypothesis for the task of breast cancer diagnosis in mammograms.
Methods: The concept of a user model was formalized as the function that relates image features to the likelihood∕extent of the diagnostic error made by a radiologist-in-training and therefore to the level of difficulty that a case will pose to the radiologist-in-training (or “user”). Then, machine learning algorithms were implemented to build such user models. Specifically, the authors explored k-nearest neighbor, artificial neural networks, and multiple regression for the task of building the model using observer data collected from ten Radiology residents at Duke University Medical Center for the problem of breast mass diagnosis in mammograms. For each resident, a user-specific model was constructed that predicts the user’s expected level of difficulty for each presented case based on two BI-RADS image features. In the experiments, leave-one-out data handling scheme was applied to assign each case to a low-predicted-difficulty or a high-predicted-difficulty group for each resident based on each of the three user models. To evaluate whether the user model is useful in predicting difficulty, the authors performed statistical tests using the generalized estimating equations approach to determine whether the mean actual error is the same or not between the low-predicted-difficulty group and the high-predicted-difficulty group.
Results: When the results for all observers were pulled together, the actual errors made by residents were statistically significantly higher for cases in the high-predicted-difficulty group than for cases in the low-predicted-difficulty group for all modeling algorithms (p≤0.002 for all methods). This indicates that the user models were able to accurately predict difficulty level of the analyzed cases. Furthermore, the authors determined that among the two BI-RADS features that were used in this study, mass margin was the most useful in predicting individual user errors.
Conclusions: The pilot study shows promise for developing individual user models that can accurately predict the level of difficulty that each case will pose to the radiologist-in-training. These models could allow for constructing adaptive computer-aided educational systems in mammography.
Keywords: computer-aided education, mammography, user models, machine learning
INTRODUCTION
Mammography: Clinical challenges and training
Although there currently exist several imaging modalities for breast cancer detection, mammography is the only widely accepted screening modality. It has been estimated1 that in years 1975–2000, screening mammography accompanied with adjuvant therapy reduced the rate of death from breast cancer by 30%. However, there remains room for improvement in mammographic interpretation. An important issue to address is the notable variability among radiologists with respect to diagnostic accuracy in mammographic interpretation.2 In particular, dedicated training, not simply clinical practice, has been identified as a critical factor in improving radiologists’ performance. A study by Linver et al.3 showed that dedicated training in mammography improved radiologist cancer detection rate from 80% to 87% while keeping the positive predictive value approximately the same. Leung et al.4 showed that radiologists specialized in breast imaging (i.e., ones that have received additional training) perform better than general radiologists. Specifically, they showed a slight improvement in the number of detected cancers (from 2.0 to 2.5 cancers per 1000 cases) in the screening setting and a significant improvement (from 16.1 cancers to 20.0 cancers per 1000 cases) in the diagnostic setting. These results clearly suggest that additional training improves radiologists’ diagnostic performance. Therefore, any efforts to improve on the training process of radiologists could increase the overall benefit of mammography in breast cancer care.
Currently, training in mammography is performed mostly by interaction with expert mammographers and supervised interpretation of mammographic images during the residency years of a radiologist-in-training. This type of apprentice training accounts for most of the mammography education during residency. There are at least three months of training in mammography required during the four years of residency. If a Radiology resident decides to specialize in breast imaging, he∕she undertakes an additional six to 12 months of subsequent training. Such hands on training is of great importance. However, in the era of sophisticated computer aids and in the advent of web-driven virtual communities, many Radiology residents and fellows gain interest in new online tools that can help them reach excellence in performing image-based diagnostic tasks. There already exist multiple services that facilitate training in radiology. Potentially, the largest one is the web page of Radiological Association of Northern America (RSNA, http://www.rsna.org). It offers a variety of training materials including dedicated presentations on various topics. Uhrad.com offers viewing of multiple radiological cases with a detailed description (only a few cases are available in mammography). A similar service is provided by MedPix (http://rad.usuhs.edu/medpix/). Radiopaedia (http://radiopaedia.org/) serves as an online encyclopedia with a limited number of images to view. Other services have the form of online networking sites or virtual communities. An example is Radiopolis (http://www.radiopolis.com/), a large radiology online community. In radRounds (http://www.radrounds.com), the users view and share cases and discuss various issues with other specialists. As of September 9, 2009 the radRounds network had 3099 members and it is growing.
The computerized tools enable users to access multiple cases more easily, share difficult cases that they encounter in their practice, and discuss interesting findings. However, the computer tools currently available online suffer from the same drawback. All follow the one size fits all static training paradigm. These training tools present the same content to all users, disregarding their individual needs. The purpose of this paper is to address the limitations of this status quo and propose the paradigm of individualized training in which the individual needs of each user are identified using machine learning and an optimal training plan is constructed to meet those needs.
Study hypothesis and overview of the proposed adaptive training in mammography
Given that there is well established variability among radiologists in the diagnostic interpretation of mammograms,2, 5 the study hypothesis is that there are identifiable patterns in each radiologist’s diagnostic interpretation process and, therefore, in error making. In other words, we hypothesize that diagnostic errors made by radiologists are not entirely random but can be explained by properties of the interpreted case. We formalize the concept of user model for radiologists-in-training and propose a methodology of constructing such models using modern machine learning and classical statistical tools. We investigate whether user models can in fact be effectively developed to capture the error making patterns of individual radiologists in the context of the diagnostic assessment of masses in mammograms.
If successful, the proposed concept of user modeling can be the foundation of an adaptive computer-assisted training system for mammography. A diagram outlining such system is presented in Fig. 1. The training consists of four stages: (1) Acquiring knowledge about radiologist-in-training through examination; (2) building the user model; (3) constructing a training protocol based on the user model; and (4) actual training. All stages are fully automated and additionally, stages 2 and 3 do not require any human-computer interaction. Such adaptive computer-aided system addresses directly the particular challenges a radiologist-in-training faces when learning to perform a diagnostic task. To develop an adaptive system at its full capacity, each of the stages described above must be investigated thoroughly, both from a theoretical as well as a practical point of view. The core of the system is the second stage; constructing a machine learning-based “user model” of a radiologist-in-training. In this pilot study we systematically approach this issue.
Figure 1.
An overview of the proposed intelligent training system for mammography.
Related work
Adapting computer tools and interfaces to the needs of their users has been an increasingly popular research topic6, 7, 8 as computer software becomes indispensable in many domains of our life. The cornerstone of this research is the assumption that different users have different needs and that automatic customization of software to meet the specific user needs results in user-friendly as well as more effective software. The research on human-computer interaction has also been extended to computerized educational systems9 and education in medicine.10 To our knowledge, there is only one very recent attempt to construct an educational system that accounts for differences between radiologists in their interpretation of mammograms.11, 12 In that research, however, the authors focus mostly on developing related ontology for the training systems but they do not approach in depth the topic of accurate learning-based user modeling.
Research on individualized adaptive computer-aided education in radiology is interdisciplinary and of high complexity. It involves topics in computer science (specifically pattern recognition and machine learning), human factor engineering, radiology itself, and even psychology. Because of the high complexity of the problem, it has to be approached very carefully and systematically in its multiple aspects. Our study is a step in this direction.
Please note that a limited scope of the underlying concept was initially presented in Mazurowski et al..13 In this article we extend the pilot study by including more data as well as more elaborate data analysis.
METHODS
In this section we propose a framework for constructing user models that attempt to capture the error patterns of individual radiologists when diagnosing breast masses in mammograms and our methodology of testing whether accurate models can in fact be developed.
The diagnostic problem and the database
The hypothesis that individual error making patterns can be captured in formal user models was tested for the problem of determining the malignancy status of breast masses based on their mammographic appearance (Fig. 2). This is a binary problem with two possible alternatives: Malignant and benign. The actual clinical task for the radiologist is to decide whether a perceived mass looks suspicious enough to require further work-up (i.e., biopsy, short-term follow-up, or no further action). It has been shown that 70%–85% of breast masses that are referred to biopsy turn out to be benign.14 Another study shows the positive predictive value of the decision to biopsy to vary, reportedly between 6% and 92% across radiologists.15 Therefore, it is important to make mammography interpretation accurate and remove observer variability.
Figure 2.
An example mammographic region of interest depicting a mass.
For this study we used radiologists’ data previously collected at Duke University Medical Center. Specifically, interpretation of 30 mammographic cases depicting masses by ten Radiology residents were used. All were third or fourth year residents with a minimum of four weeks of prior experience in breast imaging. Malignancy status of all the masses was determined by a biopsy. The residents were asked to provide an assessment of the likelihood of the malignancy for each of the masses using a 0–100 probabilistic scale range.
To test whether certain image properties can be used to model the error making patterns of residents, we focused initially on two properties: Breast parenchyma density and mass margin. Selection of these features is intuitive. First, the margin characteristics of a breast mass are known to be highly correlated with its malignancy status.16 Second, it is also known that dense breast parenchyma makes mammographic diagnosis particularly challenging. Therefore, if indeed certain image properties are somehow related to the error making patterns of individual radiologists, then parenchyma density and mass margin should be among the key ones.
To measure the above image properties we relied on the Breast Imaging Reporting and Data System (BI-RADS) lexicon that is published by the American College of Radiology17 and is typically used by the radiologists for mammographic reporting. According to this lexicon, the BI-RADS descriptor of parenchyma density takes integer values from 1(=fatty) to 4(=dense). The BI-RADS descriptor of mass margin can take five possible nominal values: Circumscribed, microlobulated, obscured, indistinct (ill-defined), and spiculated, which are ordered according to the lexicon (the order shown above, with spiculated being assigned the highest number). Therefore, each nominal value can be assigned an integer value from 1 to 5 (the higher the value, the higher the probability of cancer) to be used in numerical analysis.
BI-RADS reporting can be subjective and some variability among radiologists has been reported when using the lexicon.5 Consequently, it is difficult to provide a unique and reliable assessment of the BI-RADS properties for a given case. Since the proposed user modeling requires robust and reliable assessment of image properties, we asked seven experienced, board-certified, fellowship-trained radiologists, and an average of 8.6 years in postfellowship clinical experience to read the same cases and report their BI-RADS findings. Then, for each case, we used the average assessment among the seven experienced radiologists as the unique assessment for the given image property. Note that since the average rating among the seven experts was used as the gold standard, the two BI-RADS features often were assigned noninteger values. The noninteger values do not have exact meaning according to the BI-RADS lexicon. However, they are still meaningful and highly appropriate in our analysis. For example, if the value of the mass margin feature is 1.29 (as determined by averaging the BI-RADS recordings among the seven experts), it means that most of the expert radiologists considered the margin circumscribed. However, the decision was not unanimous, which is a good indicator that the mass margin features were ambiguous and that there were some expert radiologists who assigned a “higher” value of this feature.
Definition of user diagnostic error
In our preliminary experiments, we evaluated how the two BI-RADS features (i.e., parenchyma density and mass margin) relate to an error in a radiologist’s decision. We define the error as the absolute value of the difference between the radiologist assessment and the actual probability of this particular case being malignant or benign (100% or 0%, respectively). For example, if for a given mass the radiologist’s assessment is that there is 60% probability of the mass being malignant and the biopsy shows that the mass is benign, the radiologist’s error is 60%. On the other hand, if the radiologist’s assessment is 95% and the mass is in fact malignant, such situation results in a minimal error of 5%. There are multiple ways of defining the error and its likelihood. In this pilot study, we used the above definition for simplicity.
User modeling
Given the definition of the extent of error, we define our problem as a function approximation (also known as regression) problem. An approximation problem18 is one where a function must be found that fits best a given set of examples. In our experiments, the approximated function is a radiologist-in-training error function. This function is constructed separately for each radiologist-in-training. We will denote this function as Ei(X). This function is the user model. The arguments X=(x1,x2) of the function are the two BI-RADS features. Therefore, the function Ei(X) is constructed by an approximation algorithm to predict the extent of error for a given case based on the two BI-RADS features. We used three approaches to the approximation task: k-nearest neighbor approximation with kernel (k-NN), artificial neural networks (ANN), and multiple regression (MR). A short introduction to each approach follows.
The k-nearest neighbor approximation with kernel relies on a simple assumption that the approximated function is smooth and two points close in the feature space also have a similar function value. To determine the value of the function in a point X, k nearest points to X (called nearest neighbors) in terms of Euclidean distance in feature space are considered. The approximated value E(X) is a weighted average of the nearest neighbors’ corresponding function values. In this study we used a Gaussian kernel to weight the neighbors. Therefore, the neighbors more distanced from X have a lower importance in determining E(X). In our experiments we used k=20. The value of k was determined empirically.
The ANN used in this study are feedforward networks. In ANN training, the collected examples (i.e., observer readings) are used to update weights between neurons. During the ANN training, the error between the estimated value of the function and its true value for the training examples is minimized. In our study, the backpropagation method with momentum (a variation in gradient descent method) was utilized.19 After training, the constructed neural network was used to find the corresponding function value for any point in the feature space. The neural network employed in our study had two inputs (each corresponding to a BIRADS feature), one hidden layer with five neurons and an output layer with a single neuron.
Multiple regression is a simple and popular statistical method designed to find a relation between a dependent variable and multiple independent variables.20 The approximating function in this study is a second order polynomial of the two BI-RADS features (without the interaction). The multiple regression algorithm finds the polynomial coefficients such that the approximating function fits best the training data.
Experimental design
The question that we addressed in the pilot study is the following: “Are there patterns in error making by radiologists-in-training that can be captured by machine learning-based or classical statistical models?” To answer this question, we constructed an individual error function Ei(X) for each Radiology resident i by approximating the errors made by him∕her on the study database.
To evaluate how accurate is the constructed function Ei(X) in predicting the extent of error made by the resident for unknown cases, we performed a leave-one-out cross validation experiment. For each resident and each approximation method, we excluded one case at a time, calculated the approximating function Ei(X) using the remaining cases and tested the accuracy of prediction on the excluded case. The procedure was repeated for all cases. Then, we stratified the cases into two groups according to the value assigned by Ei(X). The cases that had a predicted value lower than the mean of Ei(X) among all predicted values for that resident were assigned to the “low-predicted-difficulty” group and those above the average were assigned to the “high-predicted-difficulty” group. We called the groups high-predicted-difficulty and low-predicted-difficulty since the predicted error value aims at predicting the resident’s perceived difficulty level of the query case. We applied an individualized threshold between the two groups since we believe that the concept of case difficulty in the context of adaptive training should be relative to the user. For example, if a radiologist-in-training tends to make unusually high errors for most of the cases, if a global threshold that is based on the entire group of radiologists-in-training is used, then most or all cases will be classified as difficult for that radiologist-in-training, which would be of very little help when constructing an adaptive training system. Note also that assigning a case to either of the groups does not mean that the corresponding decision was right or wrong but only that the case seems more or less difficult given the overall performance of the trainee (i.e., errors for all cases).
Given the above stratification scheme for each resident and each approximation method, we examined the actual errors in both the low-predicted-difficulty and high-predicted-difficulty groups. Note that a successful user model [i.e., function Ei(X)] should show the following trend: Unknown cases that are stratified as low-predicted-difficulty by the constructed user model are cases for which the particular radiologist-in-training shows, in fact, lower diagnostic error than for those stratified as high-predicted-difficulty. Thus we performed a statistical test to determine whether the mean actual error is the same or not between the low-predicted-difficulty group and the high-predicted-difficulty group for each resident for three different approximation approaches. To account for the clustering effect due to the fact that same cases are used for all ten residents, we used generalized estimating equations (GEE) approach21 that takes into account correlation of errors made by the ten residents in the same case. The independent working correlation is used in the GEE approach and the empirical standard error is used for adjustment of clustering effect in inference.
Finally, to evaluate, which of the two features used in this proof-of-concept study is the more important one, we repeated the leave-one-out experiments described above for models that use only mass margin and for models that use only parenchyma density as an image feature. The constructed individual models had the same form of a function Ei(X), where X=x1 or X=x2.
RESULTS
Evaluation of the user models
In this main experiment, we evaluated models using the two features chosen for this pilot study. Based on the leave-one-out experiment and the stratifcation scheme described in Sec. 2D, for each method, the group effect was pooled together across the ten residents in the GEE model with only resident and group (low-predicted-difficulty vs high-predicted-difficulty) main effects. The interaction of resident and group is not significant in all three methods, possibly due to low power. We found that the adjusted group error difference (high-predicted-difficulty group minus low-predicted-difficulty group) was 22.4(p<0.001), 16.2(p=0.002), and 17.4(p=0.002) for the k-NN, ANN, and MR approaches, respectively. Therefore, all methods are capable of distinguishing between cases that will pose low difficulty and those that will pose high difficulty to the radiologist-in-training.
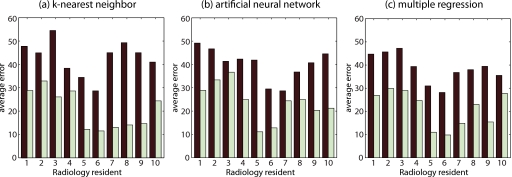
Furthermore, we performed an exploratory statistical analysis of the effectiveness of each method for each radiologist-in-training separately. The difference between the two groups can be seen in Fig. 3, which presents the average error in both groups for each resident and each method. We found that there are significant group differences at 0.05 level for all residents except for residents 2, 4, and 5 in the k-NN approach; for residents 2, 3, 7, and 8 in the ANN approach; and for residents 2, 4, 5, 8, and 10 in the MR approach.
Figure 3.
The average extent of the diagnostic errors on a scale from 0% to 100% made by each one of the ten residents. These errors are grouped based on the difficulty of the study cases as predicted by each approximation method (high-predicted-difficulty shown by the dark bar and low-predicted-difficulty shown by the light bar).
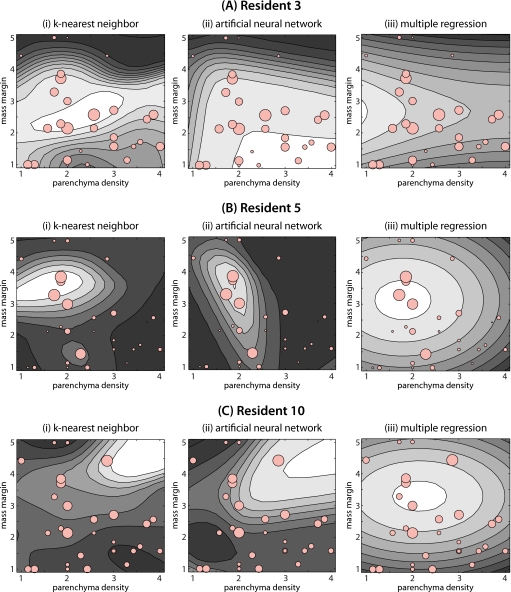
For illustration purposes, Fig. 4 shows the extent of error for three of the residents as a function of the two image properties, modeled using the three different approximation methods employed in this study. The actual observations are shown with light red circles. The size of the circle represents the extent of error. The approximating functions Ei(X) for the three approximation methods investigated in this study are shown with the contour plots. Brighter areas indicate higher values of Ei(X). By looking at the errors for resident 3 [Fig. 4a] and resident 5 [Fig. 4b], rather clear but different error making patterns can be discovered. Generally, resident 3 tends to make larger errors for masses with microlobulated and obscured margin. k-NN was effective at capturing this regularity while ANN was not as successful (see Fig. 3). Resident 5 on the other hand tends to make errors for masses that appear in breast of parenchymal density 2. ANN captured this regularity better than two other methods. Resident 10 does not have a simple and easy to describe error making pattern (at least in terms of the two analyzed features), however, some regularity was captured by k-NN and ANN methods (see Fig. 3) especially when multiple regression is used. Although there are differences among models using the three different approximation methods for each resident, they often show consistent trends.
Figure 4.
Contour plots showing the users models developed by each approximation method for three different residents. Note that the models are functions of the two BI-RADS features (parenchyma density and mass margin). For mass margin the numbers represent: 1: Circumscribed, 2: Microlobulated, 3: Obscured, 4: Indistinct (ill-defined), and 5: Spiculated. For each contour plot, brighter regions indicate areas of higher predicted error. Circles show the actual errors made by the corresponding resident. The size of each circle is directly proportional to the actual error made by the resident.
Significance of mass margin and breast parenchyma density
We also evaluated which one of the two features chosen for this pilot study is better related to the error. We observed that if the models are constructed using only mass margin as the feature, the accuracy of the models is generally comparable or even better than the accuracy of the models based on both features. Specifically, we observed that when the group effect is polled together among all residents, the adjusted group error difference (high-predicted-difficulty group minus low-predicted-difficulty group) was 22.6(p<0.001), 23.5(p<0.001), and 19.2(p<0.001) for the k-NN, ANN, and MR approaches, respectively. This means that when only mass margin is used, the models are capable of distinguishing between cases that will pose low difficulty and those that will pose high difficulty to the radiologists-in-training with similar accuracy as the models based on two features for k-NN and MR methods and a notably better accuracy than the models based on two features for ANN. The same leave-one-out experiments conducted for models that are based on parenchyma density only showed that this feature on its own is not a good predictor of individual case difficulties. Therefore, we conclude that it is the mass margin that is the dominating feature among the two BI-RADS features analyzed in this study.
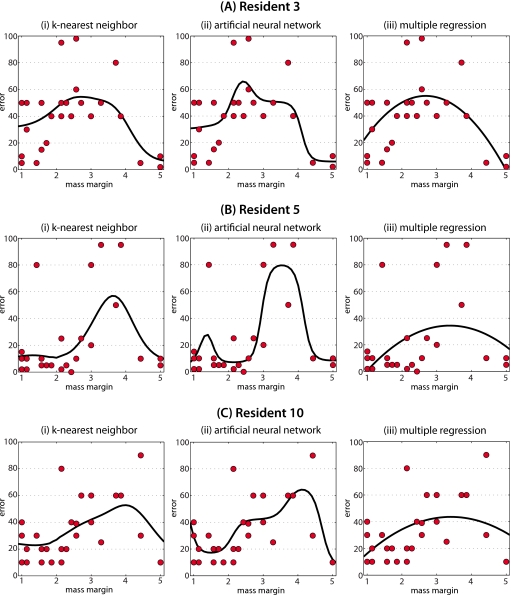
Similarly as for the models based on two features, for illustration purposes, in Fig. 5 we present the extent of error for three of the residents as a function of mass margin only, modeled using the three different approximation methods employed in this study. The actual errors are shown with circles. The approximating functions Ei(X) for the three approximation methods investigated in this study are shown with the thick black lines. A similar common pattern can be observed between the residents 3, 5, and 10: The error tends to be lower for the extreme values of margin (circumscribed and spiculated) and higher for the intermediate values. However, notable differences between the radiologists-in-training can also be observed. For example, the errors made by resident 5 are lower than the errors made by resident 3 especially for cases with mass margin 1 and 2 (circumscribed and microlobulated). Also, it is rather clear that for residents 5 and 10 the errors are made for cases with mass margin 3 and 4 (obscured and indistinct), whereas resident 3 makes the highest errors for margin 2, 3, and 4. Those differences suggest that an error making pattern is a combination of global patterns observed in the entire group of trainees and individual pattern observed for each trainee.
Figure 5.
Plots showing the users models developed by each approximation method for three different residents when on mass margin is used as the image feature. The predicted error is indicated by black lines. Circles show the actual errors made by the corresponding resident.
CONCLUSIONS AND DISCUSSION
In this paper, we proposed the concept of exploiting user models as the foundation for building adaptive computer-aided training systems in mammography. We discussed the overall framework of individualized training and then performed a pilot study as a proof-of-concept. Specifically, we tested the hypothesis that a machine learning-based user model can be constructed to capture regularities in error making of radiologists-in-training. We formally defined the user model and presented methodology on how it can be constructed. Our pilot study suggests that, in fact, radiologists-in-training do not make errors in a random manner but there exist error making patterns that can be captured by machine learning-based models.
The user models used in the study were relating image features to the extent of the diagnostic error made by a radiologist-in-training. For the exploratory analysis, we used two BI-RADS features: Mass margin and parenchyma density. The analysis showed that models based on these features are capable of predicting the extent of error for particular cases individually for each radiologist-in-training. We also showed that among the two BI-RADS features investigated in this study, mass margin is the dominating feature among the two BI-RADS features analyzed in this study. Note, however, that this conclusion does not mean that mass margin is sufficient to predict individual case difficulty level for all radiologists-in-training; rather, that mass margin is a strong predictive feature and further analysis is granted to establish whether additional features can improve the prediction accuracy. The two main reasons are the following. First, only two features were thoroughly evaluated in this study. Multiple additional features, both man-extracted (such as BI-RADS) and computer-extracted, can be found to be useful. Such analysis is beyond the scope of this proof-of-concept study in which we tested the hypothesis that error making patterns exist, and that they can be captured by machine learning algorithms. Second, even though adding parenchyma density as a feature in our models did not improve the performance of the models in general, when all observers are pooled together, it did help in some scenarios. Specifically, the improvement in model performance was observed in ten out 30 scenarios (i.e., observer-method combinations). As a performance measure, we used the difference between average actual error in high-predicted-difficulty group and average error in low-predicted-difficulty group for a particular radiologist-in-training. This last result suggests the optimal combination of features used in the model may also be individual (i.e., user-dependent). These issues will be studied in our future research.
The presented study has some limitations. First, the study was based on a relatively small number of cases, which can lead to overtraining issues with machine learning algorithms. To mitigate this limitation, we narrowed the modeling task to only two image properties (i.e., features). We also used appropriate crossvalidation to avoid a positive bias of our results. Future studies will focus on expanding the case base as well as including more image features. Second, our user models were based on BI-RADS features which suffer from interobserver and intraobserver variability. Although we attempted to reduce the potential impact of this source of variability by using the average assessment of multiple expert radiologists, it is possible that computer-extracted image features may be better suited to this task. Finally, in this study, we used only one simple definition of diagnostic error. Other definitions such as a likelihood of error, or definitions that differentiate types of errors (false positive and false negative) could provide more insight into the nature of error making by radiologists-in-training. However, more elaborate definitions of errors require larger case bases for robust user modeling. The simple definition of error used in our study was sufficient to confirm that there are error making patterns in mammographic interpretation that can be captured by machine learning-based models. More complex definitions of errors will be utilized in the future studies. Overall, regardless of the limitations of this pilot study, we observed consistent trends that support our hypothesis.
Given efficient algorithms to develop user models, we propose their application in adaptive computer-aided training systems. Such systems will require multiple well documented mammographic cases. If BI-RADS features are used for creating user models, then each case will have to be assessed by multiple experienced radiologists. This will require significant amount of time but it is feasible. In our future studies we will evaluate if we can develop computer-based features that can replace BI-RADS features for the modeling purpose. Furthermore, given the definition of error presented in this paper, each abnormal case will have to have associated pathology results (malignant vs benign). A database containing large number of cases with pathology results is actually available online.24, 25
We believe that research on educational systems in mammography has high clinical significance. Individualized adaptive computer-aided training systems can notably improve the efficiency of radiology education in time (faster training) and diagnostic performance of the trainees (higher diagnostic accuracy). Ensuring the highest quality of training in mammography is crucial as increasingly fewer radiologists want to specialize in interpreting mammograms22, 23 and need for such experts is very high. Thus, the long term benefit is better breast cancer care for all women. Furthermore, even though the hypothesis of this study was evaluated on the particular problem of breast mass diagnosis in mammography, the research findings can be potentially translated into other clinical tasks (detection, diagnosis, etc.) as well as other imaging modalities such as CT or MRI of various organs. We believe that the concept and initial results presented in this paper are a step toward laying a foundation for a new, more efficient, and more effective paradigm of training support in radiology.
ACKNOWLEDGMENTS
This work was supported in part by Grant No. R01 CA101911 from the National Cancer Institute.
References
- The Cancer Intervention and Surveillance Modeling Network Collaboration, Berry D. A., Cronin K. A., Plevritis S. K., Fryback D. G., Clarke L., Zelen M., Mandelblatt J. S., Yakovlev A. Y., Habbema J. D. F., and Feuer E. J., “Effect of screening and adjuvant therapy on mortality from breast cancer,” N. Engl. J. Med. 353, 1784–1792 (2005). 10.1056/NEJMoa050518 [DOI] [PubMed] [Google Scholar]
- Elmore J. G., Wells C. K., Lee C. H., Howard D. H., and Feinstein A. R., “Variability in radiologists’ interpretations of mammograms,” N. Engl. J. Med. 331, 1493–1499 (1994). 10.1056/NEJM199412013312206 [DOI] [PubMed] [Google Scholar]
- Linver M. N., Paster S. B., Rosenberg R. D., Key C. R., Stidley C. A., and King W. V., “Improvement in mammography interpretation skills in a community radiology practice after dedicated teaching courses: 2-year medical audit of 38,633 cases,” Radiology 184, 39–43 (1992). [DOI] [PubMed] [Google Scholar]
- Leung J. W. T., Margolin F. R., Dee K. E., Jacobs R. P., Denny S. R., and Schrumpf J. D., “Performance parameters for screening and diagnostic mammography in a community practice: Are there differences between specialists and general radiologists?,” AJR, Am. J. Roentgenol. 188, 236–241 (2007). 10.2214/AJR.05.1581 [DOI] [PubMed] [Google Scholar]
- Lazarus E., Mainiero M. B., Schepps B., Koelliker S. L., and Livingston L. S., “Bi-rads lexicon for us and mammography: Interobserver variability and positive predictive value,” Radiology 239, 385–391 (2006). 10.1148/radiol.2392042127 [DOI] [PubMed] [Google Scholar]
- Rich E., “Users are individuals: Individualizing user models,” Int. J. Man-Mach. Stud. 18, 199–214 (1983). 10.1016/S0020-7373(83)80007-8 [DOI] [Google Scholar]
- Fischer G., “User modeling in humancomputer interaction,” User Model. User-Adapt. Interact. 11, 65–86 (2001). 10.1023/A:1011145532042 [DOI] [Google Scholar]
- Webb G. I., Pazzani M. J., and Billsus D., “Machine learning for user modeling,” User Model. User-Adapt. Interact. 11, 19–29 (2001). 10.1023/A:1011117102175 [DOI] [Google Scholar]
- Yudelson M. V., Medvedeva O. P., and Crowley R. S., “A multifactor approach to student model evaluation,” User Model. User-Adapt. Interact. 18, 349–382 (2008). 10.1007/s11257-007-9046-5 [DOI] [Google Scholar]
- Suebnukarn S. and Haddawy P., “A bayesian approach to generating tutorial hints in a collaborative medical problem-based learning system,” Artif. Intell. Med. 38, 5–24 (2006). 10.1016/j.artmed.2005.04.003 [DOI] [PubMed] [Google Scholar]
- Sun S., Taylor P., Wilkinson L., and Khoo L., “An ontology to support adaptive training for breast radiologists,” in Proceedings of the International Workshop on Digital Mammography, 2008, pp. 257–264 (unpublished).
- Sun S., Taylor P., Wilkinson L., and Khoo L., “Individualised training to address variability of radiologists performance,” in Proceedings of the SPIE Medical Imaging, 2008, Vol. 69170G (unpublished).
- Mazurowski M. A., Lo J. Y., and Tourassi G. D., User modeling for improved computer-aided training in radiology: Initial experience, Proceedings of SPIE, Medical Imaging 2010: Image Perception, Observer Performance, and Technology Assessment (accepted).
- Kopans D. B., “The positive predictive value of mammography,” AJR, Am. J. Roentgenol. 158, 521–526 (1992). [DOI] [PubMed] [Google Scholar]
- Sickles E. A., Miglioretti D. L., Ballard-Barbash R., Geller B. M., Leung J. W. T., Rosenberg R. D., Smith-Bindman R., and Yankaskas B. C., “Performance benchmarks for diagnostic mammography,” Radiology 235, 775–790 (2005). 10.1148/radiol.2353040738 [DOI] [PubMed] [Google Scholar]
- Sickles E. A., “Mammographic features of 300 consecutive nonpalpable breast cancers,” AJR, Am. J. Roentgenol. 146, 661–663 (1986). [DOI] [PubMed] [Google Scholar]
- Breast Imaging Reporting and Data System, Breast Imaging Atlas (American College of Radiology, 1998).
- Poggio T. and Girosi F., “Networks for approximation and learning,” Proc. IEEE 78, 1481–1497 (1990). 10.1109/5.58326 [DOI] [Google Scholar]
- Zurada J. M., Introduction to Artificial Neural Systems (West Publishing, St. Paul, 1992). [Google Scholar]
- Rosner B., Fundamentals of Biostatistics, 6th ed. (Duxbury, 2006). [Google Scholar]
- Diggle P., Heagerty P., and Liang K., Analysis of Longitudinal Data (Oxford University Press, New York, 2002). [Google Scholar]
- Lewis R. S., Sunshine J. H., and Bhargavan M., “A portrait of breast imaging specialists and of the interpretation of mammography in the United States,” AJR, Am. J. Roentgenol. 187, W456–W468 (2006). 10.2214/AJR.05.1858 [DOI] [PubMed] [Google Scholar]
- Atlas S. W., “Embracing subspecialization: The key to the survival of radiology,” J. Am. Coll. Radiol. 4, 752–753 (2007). 10.1016/j.jacr.2007.04.003 [DOI] [PubMed] [Google Scholar]
- Heath M., Bowyer K., Kopans D., Kegelmeyer W. P., Moore R., Chang K., and MunishKumaran S., “Current status of the digital database for screening mammography,” Digital Mammography: Proceedings of the Fourth International Workshop on Digital Mammography (Kluwer Academic, Dordrecht, 1998), pp. 457–460.
- Heath M., Bowyer K., Kopans D., Moore R., and Kegelmeyer W. P., “The digital database for screening mammography,” in Proceedings of the Fifth International Workshop on Digital Mammography, 2001, pp. 212–218 (unpublished).