Abstract
Purpose: The use of positron emission tomography (PET) imaging has proved beneficial in the staging and diagnosis of several cancer disease sites. Additional applications of PET imaging in treatment planning and the evaluation of treatment response are limited by the relatively low spatial resolution of PET images. Including point spread function (PSF) information in the system matrix (SM) of iterative reconstruction techniques has been shown to produce improved spatial resolution in PET images.
Methods: In this study, the authors sampled the spatially variant PSF at over 6000 locations in the field of view for a General Electric Discovery ST PET∕CT (General Electric Healthcare, Waukesha, WI) scanner in 2D acquisition mode. The authors developed PSF blurred SMs based on different combinations of the radial, depth, and azimuthal spatial dependencies to test the overall spatial dependence of the PSF on image quality. The PSF blurred SMs were included in a LOR-OSEM reconstruction algorithm and used for image reconstruction of geometric phantoms. The authors also examined the effect of sampling density on PSF characterization to design a more efficient sampling scheme.
Results: The authors found that depth dependent change in the amplitude of the detector response was the most important factor affecting image quality. A SM created from a PSF that introduced r (perpendicular to the LOR), d (parallel to the LOR), or r and d dependent blurring across the radial lines of response led to visually identifiable improvements in spatial resolution and contrast in reconstructed images compared to images reconstructed with a purely geometric SM with no PSF blurring. Images reconstructed using a SM with r and d dependent blurring across the radial lines of response showed improved spatial resolution and contrast-noise ratios compared to images reconstructed with a SM that had only r dependent blurring. Additionally, the authors determined that the PSF could be adequately characterized with roughly 85% fewer samples through the use of a better optimized sampling scheme.
Conclusions: PET image reconstruction using a SM made from an accurately characterized PSF that accounts for r and d dependencies results in improved spatial resolution and contrast-noise relations, which may aid in lesion boundary detection for treatment planning or quantitative assessment of treatment response.
Keywords: PET, point spread function, spatial resolution, LOR-OSEM
INTRODUCTION
Positron emission tomography (PET) is a noninvasive functional imaging technique that has shown great value in the clinical evaluation of oncology patients. The use of PET coupled with computed tomography (CT) has been shown to have a beneficial impact on the diagnosis and staging∕restaging of a wide range of disease sites.1 Currently, PET∕CT is commonly used in the staging∕restaging of lung cancer,2 colorectal cancer,3 and lymphomas.4
Recently, application of PET∕CT to the areas of radiation treatment planning and treatment evaluation has shown promise. The inclusion of PET in treatment planning has been found to reduce interobserver variability in target delineation compared to CT alone,5, 6, 7 minimize dose to organs outside the target volume,8, 9, 10 reduce the failure rate in treatment of mediastinal nodes,11 and limit the possibility of geometrical misses.12 The functional information provided by PET scans allows biological subvolumes of interest, such as hypoxic or rapidly proliferating regions, to be identified and possibly targeted for treatment with escalated dose.9, 13, 14, 15, 16 Also, some initial success in evaluating patient response to radiation and∕or chemotherapy using fluorodeoxyglucose-PET has been reported for lymphoma, breast cancer, lung cancer, esophageal cancer, and colorectal cancer (see Ref. 17 and references within).
While the use of PET∕CT has shown early promise in radiation treatment planning and treatment evaluation, it is currently underutilized in both of these areas, primarily due to poor spatial resolution18 and the resulting partial volume effects.19 Limited spatial resolution and partial volume effects make it difficult to accurately image the activity distribution over the field of view (FOV). These effects are particularly problematic when using PET imaging to evaluate small volumes of activity. Also, spatial resolution of PET images sometimes shows a radial dependence, which could lead to nonuniform activity measurement across the FOV.
The spatial resolution of a reconstructed PET image depends on several factors: (1) The size of the detectors; (2) acolinearity of the annihilation photons (the effects of which are accentuated with increasing bore diameters); (3) intercrystal scatter and crystal penetration; and (4) positron range.18, 20, 21 These factors may be addressed using an iterative reconstruction algorithm based on Poisson statistics, such as ordered subset expectation maximization (OSEM),22 that models these effects in the system matrix (SM). The SM defines the operational relationship between image space and projection space.
Over the years, PET spatial resolution has been improved by using increasingly complex SMs. The simplest SM implementation describes only the geometry of the system. Geometric SMs have been based on line integrals,23 detector tube-voxel intersections,24, 25 and depth dependent geometric sensitivity calculations based on the solid angle.26, 27 More complex analytical SMs have been developed that include the effects of photon pair acolinearity, intercrystal scatter, crystal penetration, and positron travel.28, 29, 30, 31, 32, 33, 34 Monte Carlo derived SMs35, 36, 37, 38, 39 offer an improvement over the analytical SMs, but are highly dependent on an accurate physical model of the scanner and the relevant physical phenomena.
A more accurate system model can be achieved by making empirical measurements of the spatially variant point spread function (PSF) using an uncollimated point source positioned throughout the scanner FOV. Recent works have shown that including empirically measured PSF information in the system model leads to improved resolution of the reconstructed images.40, 41, 42, 43, 44, 45 To investigate the benefit of PSF based SMs for a PET∕CT scanner dedicated for radiation treatment simulation, we have made the most extensive set of PSF measurements, to our knowledge, reported in the literature. These measurements were used to evaluate the effects of depth, radial, and azimuthal position, as well as sampling density, on the PSF for the General Electric Discovery ST (DST) PET∕CT (General Electric Healthcare, Waukesha, WI) operated in 2D high sensitivity acquisition mode. The goals of this work are to accurately characterize the PSF as a function of point source position over the FOV, investigate image reconstruction fidelity as a function of SM parameters, and determine the most efficient PSF sampling scheme (i.e., determine the fewest number of measurements that can be used to adequately characterize the PSF over the entire FOV).
MATERIALS AND METHODS
Description of the General Electric Discovery ST PET∕CT scanner
In this work we characterized the spatially variant PSF for the DST in 2D high sensitivity acquisition mode. In 2D acquisition mode, the DST has 0.8 mm thick by 54 mm long tungsten septa that define the detector planes. List mode data are sorted into 249 lines of response (LOR)×210 azimuthal angles×47slices. The DST has a uniform crystal ring diameter of 886 mm over the axial FOV. In the azimuthal direction, the ring is composed of 70 blocks of six uniformly spaced detectors and interblock gaps. In the axial direction, the scanner has four blocks of uniformly spaced detectors with interblock gaps. The detector configuration of the DST yields C70h symmetry about the center of the scanner, which means that every sixth projection in the azimuthal direction will share the same, nonuniform LOR radial spacing and that there is a mirror plane between the second and third block of detectors axially (see Table 1).
Table 1.
Characteristics of the GE Discovery ST PET scanner.
| Detector material | BGO |
|---|---|
| Crystal size (mm) | 6.3×6.3×30 |
| Block size (number of crystals) | 6×6 |
| Crystals per ring | 420 |
| Detector ring diameter | 886 |
| Transaxial FOV (mm) | 700 |
| Axial FOV (mm) | 157 |
| Number of image planes | 47 |
Each axial plane, denoted by ξ, represents projections of LOR described by a radial index s and an azimuthal index φ. This parametrization of the LOR is described in Fig. 1. The data are grouped axially with a span of 11, which means that even ξ between 6 and 42 are composed of LOR from six different detector ring pairs (±1, ±3, and ±5 ring differences) and odd ξ between 5 and 43 consist of LOR from five different ring pairs (0, ±2, and ±4 ring differences). Slices near the axial edges are constructed from fewer ring pairs due to system geometry. Planes ξ=1 and 47 are composed of LOR from one direct ring pair each, ξ=2 and 46 are composed of two ring pairs each, ξ=3 and 45 are composed of three ring pairs each, and ξ=4 and 44 are composed of four ring pairs each.
Figure 1.
A schematic representation of a transaxial slice. The LOR are parametrized by an angle index φ, a radial index s, and into slices ξ. The solid line represents the LOR through the center of the scanner FOV, while the dashed line represents an LOR at (s,φ,ξ).
PSF Acquisition and analysis
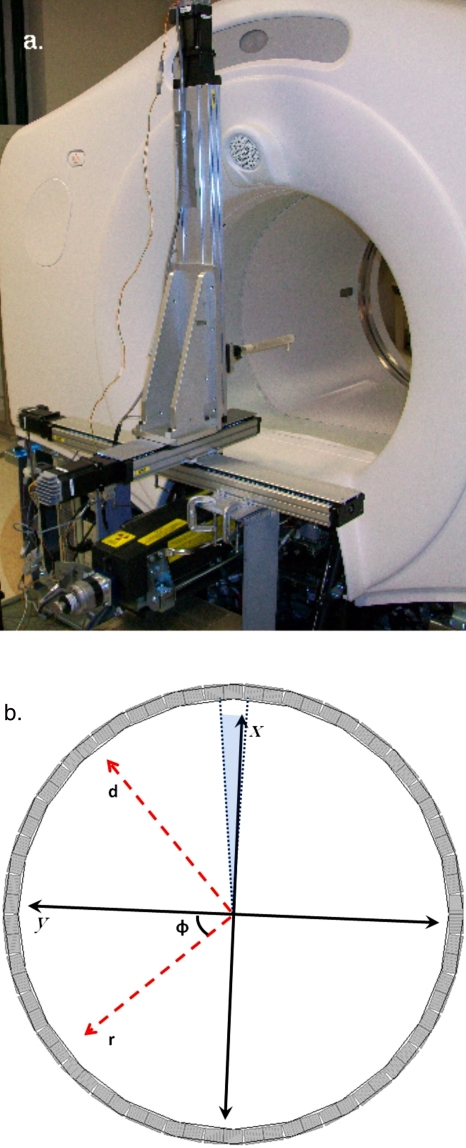
The PSF data were acquired using a 68Ge point source with a 0.5 mm diameter and an activity of ∼1 mCi. The point source was moved throughout the FOV by a high accuracy and precision 3D linear positioning robot (Parker Hannifin Corp., Rohnert Park, CA) [Fig. 2a] that allowed for a minimum step of 0.01 mm along each axis. The robot was fixed to the DST frame and then shimmed, leveled, and marked for future repositioning. The orientation of the positioning robot was verified prior to each data acquisition run by scanning the point source in axial slices separated by 100 mm to ensure that the point source appeared in the same location in each of the ξ sinograms. Data acquisition in each slice began with the point source at the center of the FOV. From the center of the FOV the point source was moved to predetermined sample positions in 100 s intervals. Data were acquired for the first 90 s, while the remaining 10 s were used to reposition the point source. The 90 s acquisition time yielded roughly 8×106 counts with a live time of >97% at all sample positions in the FOV.
Figure 2.
(a) An image of the 3D linear positioning robot mounted to the base of the DST. (b) A schematic representation of the point source position parametrization. The position of the point source was described by an azimuthal index φ, a radial location r (which runs in the same direction as the s index), a location d (distance perpendicular to r), and an axial location z (not shown, would be into the plane of the paper). The center of the axial FOV is located at z=0.
Scanner symmetry was exploited to reduce the number of individual PSF measurements needed to create a model for the system. The point source was moved over a 5 mm grid that covered the area subtended by one block and one interblock gap in a transaxial slice for ξ=24–47. This gave 264 sample locations per slice for a total of 6336 sample points. The axial location of the point source is described by z, where z=0 is the center of the axial FOV. For each φ the point source position within the axial plane is described by a radial coordinate r and a depth coordinate d, where r runs along the same axis as s and d is perpendicular to s. This parametrization scheme is shown schematically in Fig. 2b. A computerized, automated system drove the positioning robot in synchrony with a standard GE dynamic acquisition protocol using the 90 s∕10 s acquire∕pause scheme. Each of the 24 z acquisitions required slightly more than 7 h to complete and filled ∼1.3 GB of disk space. After each set of 264 points was acquired it was sent via FTP to an offline workstation for analysis. The total data set was acquired over four separate sessions, with six z locations sampled per session.
The PSF measurements were corrected for detector sensitivity using the standard GE method and for decay of the sample from the time of the first sample acquisition session. The measurements were treated as ideal points, so scatter, random, and attenuation correction were not performed (deadtime was <3% at all points and was neglected). Each projection, indexed by s, d, z, φ, and ξ, was characterized with two half Gaussians by the equation
| (1) |
where A is the amplitude, r is the radial location in mm, r0 is the location of the center of the Gaussian in mm, and σ is the standard deviation. Figure 3 shows an example of the Gaussian fit applied to several points. For each projection, A, r0, σR, and σL were stored, where σR and σL are standard deviations for the right and left half Gaussians, respectively.
Figure 3.
Projections of point source centered at ξ=24 at (a) r=0, d=0, (b) r=250 mm, d=0 mm, and (c) r=0 mm, d=250 mm. These plots are representative of the behavior of the detector response as a function of r and d. The amplitude falls off sharply as d increases, while the amplitude shows only a slight decrease with increasing r. The width of the Gaussians increases with increasing r due to parallax error at larger r, while the width of the Gaussians shows a much weaker response as a function of d.
The samples collected at each z location were used to create plots of the fit parameters A, r0, σR, and σL as functions of r and d for each of the six φ symmetry groups (i.e., grouped by which part of the detector block r=0 was aligned with) for each ξ sinogram, yielding a total of 6×47 plots for each of the individual z sample locations. Each of the plots was fit using a least square method with a polynomial of the form
| (2) |
where a, b, c, e, f, g, h, and k are variable fit parameters. The fits for the σR and σL parameters were not constrained to be equal at r=0, d=0 in the fitting process. However the fits of σR and σL at r=0, d=0 agreed to within 0.95±0.3 averaged over all φ symmetry groups and slices. Examples of the plots and fits for A, r0, σR, and σL are shown in Fig. 4.
Figure 4.
Representative plots of the fit parameters for ξ=24 produced by points in the z=0 axial plane for φ=3 (the middle of a block). The fits found using Eq. 2 are plotted on top of the parameters found from Eq. 1 as a function of r and d, for (a) r0, (b) A, (c) σR, and (d) σL. In (a), r0 is not equal to the r position of the point source due to nonzero depth of photon interaction in the detectors, which moves the effective center of the response to lower r.
Optimization of the PSF acquisition process
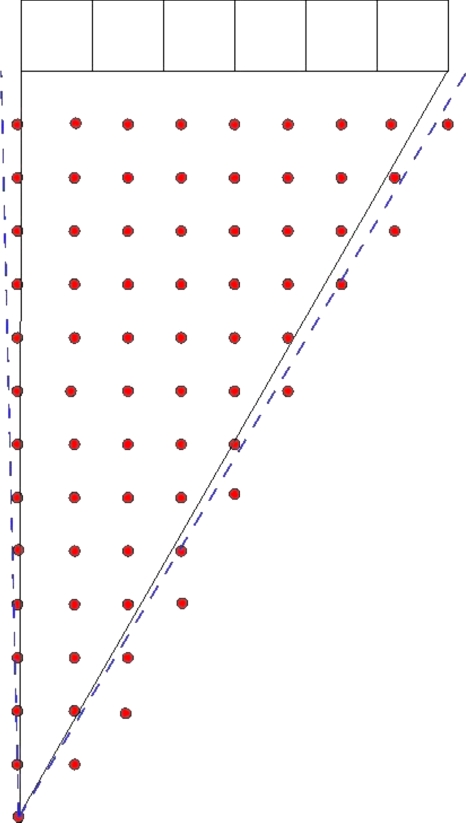
The effects of sampling density on the A, σR, and σL components of the PSF [Eqs. 1, 2] were evaluated by systematically reducing the number of sample points used to generate the A, σR, and σL fits, and then comparing the resulting fits from reduced data sets to fits of full data sets using visual inspection and absolute differences of the different fits. Figure 5 shows a schematic representation of the sampling scheme at a single z location. For a given z, the point source was positioned over a square grid pattern that covered the area subtended by a single block of detectors, with each row and column of the sample grid spaced by 5 mm. The fits produced by this complete data set were compared to fits produced by data sets where the row, column, or both row and column (giving a larger square grid) spacing was increased by an increment of 5 mm, e.g., in one case the rows were spaced by either 5, 10, 15, or 20 mm, while the columns were held at 5 mm spacing. The fits produced by the complete data set were assumed to be the most accurate model. The graphed fits found from the reduced data sets were qualitatively compared to the complete set by visual inspection over the region r=0–350 mm andd=0–350 mm. The fits were quantitatively compared by graphical subtraction to yield absolute difference plots.
Figure 5.
(NOT TO SCALE) A schematic representation of the in-plane sampling scheme. The rows and columns of points represent sampling locations, the boxes at the top of the picture represent a block of six detectors, and the dashed lines represent inter-block gaps. The rows and columns are separated by 5 mm gaps. This pattern yielded 264 samples over the ∼350 cm2 area in the plane. This pattern was repeated at the center of the ξ planes in the positive z half of the scanner (24 planes spaced ∼3.2 mm apart).
Axial responses were compared to determine if measurements in one axial plane can be used to describe the PSF in other planes, thus reducing the total number of measurements needed.
Description of the PSF blurred system matrix and image reconstruction
The effect of the PSF blurred SM on image reconstruction was evaluated using a LOR-OSEM reconstruction algorithm that reconstructs directly from nonuniformly spaced LOR with scatter, random, attenuation, deadtime, and detector sensitivity corrections included within the projection steps to preserve the Poisson statistics of the data.46 The LOR-OSEM algorithm was implemented with 21 subsets of ten angles, with matching forward and backward rotation projectors based on the three pass method of shears47, 48 driving the reconstruction. Attenuation correction from CT images,49 scatter correction using a single scatter algorithm,50 random correction from singles rates,51 detector efficiency correction, and block deadtime correction were included within the iterative loop. The PSF blurred SM was applied to the data set at the forward and back projection in each step. The algorithm was coded in MATLAB 2008B (Mathworks Inc., Natick, MA) with mex files based on C code used to speed up the projection steps.
All images were reconstructed to 256×256×47 voxels (giving a voxel size of 2.73×2.73×3.27 mm3). The PSF blurred SM gave the detector response over nonuniform LOR for each voxels’ center point with positive r and d. The point response was taken to represent a total voxel response. The amplitude of each voxel response was normalized to the maximum voxel value within the slice. The blurred SMs were stored as six (one for each φ symmetry group) 770 048×11 703 sparse arrays (128×128×24 voxels representing the positive r and d values by 249×47 LOR seen in a projection). Each PSF blurred SM occupied just under 300 MB of memory stored as a sparse array of doubles in MATLAB, with all contributions <2% of the maximum value set to zero. Symmetry arguments were used to generate the PSF for voxels not directly stored in the memory. The base LOR-OSEM implementation using a SM with no PSF blurring took ∼90 s per iteration, while the versions with PSF blurred SMs took ∼240 s per iteration running on a single core of a Linux workstation with a quad core 3.0 GHz Intel Xeon processor. Computation time does not include the time needed to calculate the correction factors, which was done independently before the reconstruction. This code was not optimized for speed, and many speed improvements, particularly parallelization, are available to reduce reconstruction time.
Six different sets of PSF blurred SMs were created, expressing different combinations of dependencies, to evaluate the importance of the r, d, and φ dependence of the PSF function. The PSF blurred SMs dependencies were (φ,r,d), (φ,r), (φ,d), (r,d), (r), and (d), where r and d were set to zero and φ was set to the middle of the block for the cases not explicitly listed. In all cases, A and r0 expressed both r and d dependence to allow the σ spatial dependence to be evaluated. Four different geometric phantoms were scanned and reconstructed using LOR-OSEM with the geometric SM and with LOR-OSEM plus each of these PSF blurred SMs. Resolution and overall image fidelity for all techniques were compared to any advantages for using a fully 3D spatially variant PSF blurred SM to reconstruct a 2D PET acquisition.
Phantom measurements
Four different phantoms were scanned to evaluate the merits of the PSF blurred SMs described above. The first phantom was created from individual point source measurements. A grid of points separated by 10 mm covering the area corresponding to one block in the ξ=24 slice was corrected for detector sensitivity and then reconstructed using each technique. Next, the Flangeless Deluxe ECT Phantom (Data Spectrum Corp., Chapel Hill, NC) was scanned with three different configurations to represent a wide range of activity distributions: (1) The cylindrical phantom with six hot spheres with activities between 0.30 and 0.55 mCi, placed in the FOV center, scanned for 20 min, and reconstructed using LOR-OSEM and the six PSF blurred SMs; (2) the phantom with six cold spheres and 5.5 mCi background, placed in the FOV center, scanned for 20 min, and reconstructed using each of the PSF blurred SMs; and (3) the phantom containing a grid of cold rods and six cold spheres with 2.2 mCi background, placed with its central axis 170 mm off axis from the FOV center, scanned for 25 min, and reconstructed using each of the PSF blurred SMs. Reconstructed images were analyzed for spatial resolution using intensity profiles through spheres or rods and contrast to noise ratios were determined using standard deviations of background compared to means of regions of interest.
RESULTS AND DISCUSSION
Optimization of the PSF acquisition process
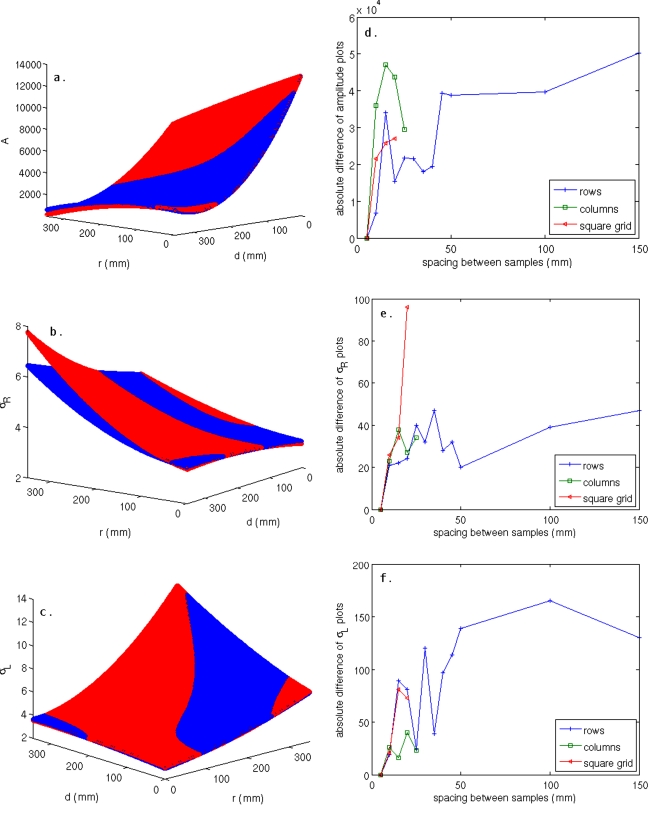
The PSF’s dependence on in-plane sampling density was evaluated with the point source located axially at the center of ξ=24, ξ=25, and ξ=45, which represent three different geometric sampling situations (ξ=24 is composed of LOR from six ring pairs, ξ=25 is composed of LOR from five ring pairs, and ξ=45 is composed of LOR from three ring pairs). The three cases showed similar behavior as the sampling density was varied—For this reason only the ξ=25 is examined in detail. The full data set was reduced by looking only at points with increased spacing between the rows, the columns, or both the rows and columns of samples. The reduced sample sets were fit in the same manner as the complete sample set, and were then plotted over the positive r and d values on the same graph as the full data set. The first visually identifiable deviations of the reduced data set from the full data set occurred when either the row or the column spacing was increased to 15 mm between samples with the other dimension held fixed at 5 mm, or when both the row and column spacing was increased to 10 mm.
Figures 6a, 6b, 6c show surface fits for the case when the row spacing was 15 mm and the column spacing was 5 mm. A slight deviation of the reduced data set from the full data set is seen in the A plot [Fig. 6a], while a more severe deviation can be identified in the σR plot along the direction of increasing r [Fig. 6b]. Figures 6d, 6e, 6f show difference plots, as a function of sample spacing, for the fits shown in Figs. 6a, 6b, 6c. The magnitude of the difference increases sharply for spacing between 5 and 15 mm for each of the data reduction schema, then oscillates at higher spacing, indicating random changes in the fit model with decreasing sample density. This agrees well with the visual inspection of the data that showed very good agreement for models produced with uniform 5 mm spacing and those produced with either the rows or columns at 5 mm spacing and the other dimension at 10 mm spacing, and a breakdown of the fitting process when the spacing exceeded 10 mm along a dimension.
Figure 6.
Plots of the fits produced by the full data set overlaid with plots produced from a coarser data set with 5 mm column spacing and 15 mm row spacing over the range r=0–350 mm and d=0–350 mm for a point centered in the ξ=25 plane for (a) A, (b) σR, and (c) σL. Disagreement between the data sets shown is most evident in σR along the direction of increasing r. The absolute difference of the plots (a)–(c) is shown for (d) A, (e) σR, and (f) σL. In all cases, a large increase in the difference of the plots occurs as the spacing increases from 10 to 15 mm, and the differences oscillate with random changes in the fits as the sampling density decreases. This agrees with visual inspection of the plots that shows a noticeable change in the fits as the spacing goes from 10 to 15 mm.
The dependence on axial sampling density was evaluated by comparing A, σR, and σL fits, created using the full data set, for each of the ξ using the techniques described above. We found that fits for points centered in ξ=12, 24, and 36 were in good agreement with one and other. These ξ represent the situation where the sample is composed of LOR from six ring pairs and ξ is centered at an axial interblock gap. The fits to the other even ξ between ξ=5 and ξ=43 (composed of LOR from six ring pairs, not centered at an interblock gap) were found to agree well with each other. Similarly, fits at ξ=11, 13, 23, 25, 35, and 37, which represent samples composed of LOR from five ring pairs centered at either the first or sixth axial detector on a block, are consistent with each other. The fits for the other odd ξ between ξ=5 and ξ=43 (composed of LOR from five ring pairs, not centered at the first or sixth detector) were in good agreement. Fits from the edge slices (ξ<5 and ξ>43) were found to be independent of the other slices. In general, the shape of the amplitude response changed more strongly than the σ at different ξ. The differences between the even and odd ξ planes and the differences between the slices at the axial edge of the scanner and those away from the edge were more pronounced than the differences between ξ centered at the edge of a block and ξ centered at the middle of a block.
These findings indicate that similar surface fits could be produced with far fewer PSF sample points. The in-plane results show that increasing the row spacing to 10 mm while leaving the column spacing at 5 mm (gives 132 sample points), or increasing the column spacing to 10 mm while leaving the row spacing at 5 mm (149 points) yields fits comparable to those found using uniform 5 mm spacing. We found that axial interblock gaps, as well as geometric sampling limitations at the edge of the scanner, had a noticeable effect on the detector response. However, we still could have reduced the axial sampling to one even plane at the center of the block, one odd plane at the center of the block, one odd plane at the edge of the block, one even plane in the interblock gap, plus the four edge planes (eight axial samples) and achieved similar results to what we found with 24 axial samples. In practice, a sample scheme that uses ∼140 samples evenly distributed over the roughly 350 cm2 sampling area (∼0.4 point∕cm2) should give suitable measurements to reproduce our results found with 264 samples. For example, a sample set of 132 in-plane points, obtained by a row spacing of 10 mm, a column spacing of 5 mm, and eight axial samples using the scheme described above, gives a total of 1056 points. This ∼85% reduction in sample size gives a savings in acquisition time of nearly 150 h and a savings in data storage of over 25 GB. However, reducing the number of points sampled may lead to increased uncertainty in the fitting process, as well as an increased chance that bad detectors or mispositioning errors will affect the results, which should be considered when designing a sampling scheme.
PSF acquisition and analysis
The detector response at three different point source locations was shown in Fig. 3. These plots are representative of two trends observed in the PSF. One trend is that σ values increase with r. This broadening of the Gaussian at higher r values is a result of the parallax effect,51 in which LOR at higher r values encounter less perpendicular detector surface area per LOR. The other trend is a rapid decrease in A with increasing depth. This is an interesting observation that is contrary to other studies, which found that A remained relatively constant as a function of d for 2D acquisition on a Siemens HiRez scanner (Siemens Medical Solutions, Knoxville, TN) with a similar span but with no septa.42, 43
This drop in A with increasing d is a geometric effect directly related to the presence of the inter-ring septa. Figure 7 shows a schematic representation of a scanner cross section with and without septa present. It can be easily recognized that the annihilation photons created by a point source located at d=0 in the axial center of an odd ξ plane will have access to the entire areas of the detector faces in each of the contributing ring pairs, while in the case where the septa are present, the annihilation photons see a limited section of the detector faces. In fact, at d=0, a pair of annihilation photons subtends roughly the same solid angle with and without the septa present. However, as the point source is moved to increasing d, the septa increasingly limit the axial acceptance of the nondirect ring pairs as seen by the annihilation photons, decreasing the total solid angle sampled by the detectors [the septa have minimal effect on the direct ring pairs with increasing d, as can be seen by comparing Figs. 7a, 7b].
Figure 7.
(NOT TO SCALE) A schematic representation of the cross section of the scanner (a) without septa present and (b) with septa present. The black circle at the center of the image represents a point source centered in an odd ξ plane (composed of 0, ±2, and ±4 ring pairs). The shaded areas represent the solid angles made by the annihilation photons with respect to detectors in the direct ring pair, the ±2 ring pairs, and the ±4 ring pairs. The solid angle seen without septa is larger than the angle subtended with septa present. (c) Geometric sensitivity of the detector pair, normalized to the geometric sensitivity at d=0, plotted as a function of d with septa present and without septa present. The geometric sensitivity decreases much faster with the septa present than without, which accounts for the low amplitude at larger d observed in our measurements.
Figure 7c shows a plot of the geometric sensitivity calculated from solid angles of interaction (geometric sensitivity is proportional to the smaller of the solid angles that the annihilation photons make with the detectors in a coincidence pair26) with the detectors in the coincidence pair for a point source located at the center of an odd ξ plane (composed of LOR from five ring pairs) as a function of d for the case with and without septa present. With no septa present, the solid angle subtended by the annihilation photons shows about a 60% decrease in geometric sensitivity from d=0 to d=300 mm. With the septa present, the geometric sensitivity decreases much more rapidly as a function of d. The geometric sensitivity derived from solid angle interactions for the case with no septa showed a larger variation with d than what has been observed by others.42, 43 This is because our calculation of the solid angle used a true point source and did not account for effects of intercrystal scatter and penetration, photon pair acolinearity, and positron travel, which are present in the physical measurement and would change the angular relationship of the source and the detector pairs.
Axial blur of the point source measurements is represented in Fig. 8. At the center of the transaxial FOV (r=0, d=0, and z centered in ξ), the response is centered at ξ with symmetric blur into the two neighboring ξ planes. At larger r, values the axial blur is similar to the blur at the center [Fig. 8a]. However, at large d values, the axial blur increases to involve up to nine axial slices. The axial detector response showed an even-odd effect, as described in the section on sampling density. The increase in axial blurring as a function of d is a geometric effect based on the nonzero span of the 2D acquisition. Figure 8b shows a schematic representation of the situation. At the center of the scanner, photon annihilation pairs are only geometrically aligned with the detectors in ring pairs associated with ξ plane where the point source is centered axially, as the point source moves away from the center of the scanner the annihilation photons are able to interact with detectors in ring pairs associated with neighboring ξ planes.
Figure 8.
(a) The left pane shows plots of the measured axial response of a point source centered in ξ=24. The right pane shows plots of the measured axial response of a point source centered in ξ=25. (b) (not to scale) A schematic representation of the cross section of the scanner with septa present. The dashed lines represent the geometric tubes of interaction for the individual detector pairs for ξ centered at crystal number 3. The point source located at the center of ξ−2 (the center of crystal 2) will not contribute to ξ when it is located at d=0, but will move into the volume that is sampled by ξ at larger d values.
Another feature of interest shown in Fig. 8 is that the axial responses at large d are centered in the ξ planes, where the point source is located when the source is in odd ξ planes and the response is maximum in ξ planes that neighbor the plane of the point source when the source is centered in even ξ planes. This effect is due to the finite size of the point source, the nonzero span, and septa. Earlier we explained that the geometric sensitivities of the oblique components of both the even and odd ξ planes fall off rapidly at larger d, and that the zero ring difference components of the odd ξ planes vary much more slowly with increasing d than the oblique components. As a result of this, the geometric sensitivities of the even ξ planes, which are composed entirely of nonzero ring difference components, will be lower at high d values than the geometric sensitivities of the neighboring odd ξ planes. So for a finite point source centered in an even plane (with overlap into the neighboring odd planes), the sensitivity in the central even plane will fall off more rapidly with increasing d than the sensitivity of the neighboring odd planes, which creates the situation where the response is higher in the neighboring odd ξ planes than in the center even plane.
Phantom measurements
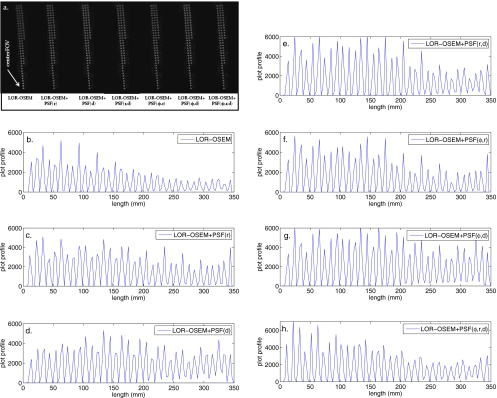
Four different phantoms were imaged and reconstructed to test the effect of the PSF blurred SMs in the reconstruction process. The point source phantom was reconstructed with 50 iterations of LOR-OSEM and each of the LOR-OSEM+PSF algorithms. The LOR-OSEM algorithm converged after about ten iterations, while the LOR-OSEM+PSF algorithms continued to converge to ∼35 iterations. The reconstructed images of the point source phantom and profiles through the longest radial line of points are shown in Fig. 9. The addition of any PSF blurred SM offers slight improvements of resolution and contrast for the reconstructed points at s<∼150 mm, and a large improvement in contrast and resolution at s>150. All of the images reconstructed with PSF blurred SMs showed improved contrast and resolution over the FOV as compared to the images reconstructed with the geometric SM. The reconstructed images produced using the PSF blurred SMs were all of similar quality.
Figure 9.
(a) Reconstructions of the 10×10 mm2 point phantom located at z=0 after 50 iterations. The longest line of points runs from the center of the FOV to a radial position of 300 mm. (b)–(h) Profiles through the longest line of point sources for each of the reconstruction techniques.
The phantoms containing the hot and cold spheres were reconstructed with 50 iterations using each of the PSF blurred SMs and evaluated without any postprocessing. The cold spheres showed slower convergence than the hot phantom, so it was used to evaluate the contrast-noise relation as a function of iteration number. To evaluate the contrast-noise relation, a 65 mm diameter circular region of interest (ROI) was drawn in the background region over the ten slices closest to the 15.9 mm diameter cold sphere, and a second 10 mm ROI was drawn in the center of the 15.9 mm cold sphere. The standard deviation (STD) of the background ROI divided by the mean of the background ROI at the final iteration was plotted versus the mean of the cold sphere ROI divided by the mean of the background ROI at the final iteration as a function of iteration number in Fig. 10. A curve closest to the origin indicates the most favorable contrast to the noise relationship. Figure 10 shows that the plots for from images reconstructed PSF blurred SMs with (r), (r,d), (φ,r), and (φ,r,d) dependence are nearly coincident, and that the plots of the images reconstructed with (d) and (φ,d) dependent SMs are nearly identical to each other. All of the PSF blurred SMs produced images with favorable contrast-noise ratios compared to the geometric SM after each iteration. The optimal contrast-noise trade-off occurred at around 20 iterations for the images reconstructed with the PSF blurred SMs. At 20 iterations, all the images reconstructed with the PSF blurred SMs gave nearly identical contrast-noise ratios, and at higher iteration numbers, the (r), (r,d), (φ,r), and (φ,r,d) dependent SMs performed better than the (d) and (φ,d) dependent SMs. The inset of Fig. 10 shows an image reconstructed with LOR-OSEM+PSF(φ,r,d) after 15 iterations. Gibbs ringing artifacts37, 42 can be observed near the phantom circumference, and appear after about five iterations at high gradient edges for all reconstruction techniques.
Figure 10.
Standard deviation of the 65 mm diameter background ROI averaged over the ten slices surrounding the 15.9 mm cold sphere divided by the mean of the background ROI at the last iteration plotted versus the mean of the 15.9 mm diameter cold sphere divided by the mean of the background ROI at the last iteration as a function of iteration number. A curve closest to the origin represents the most desirable contrast-noise characteristics. The iteration number is increasing from 1 to 50 from right to left. (inset) A reconstruction of the cold sphere phantom. The larger circle represents the background ROI within the transaxial slice. The smaller circle represents the 10 mm ROI covering the 15.9 mm cold sphere.
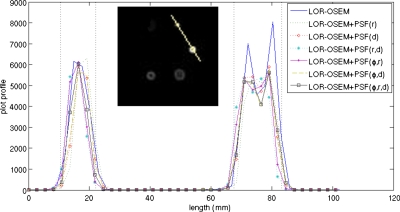
Figure 11 shows a profile through the 12.7 and 15.9 mm diameter cold spheres after 15 iterations for each of the reconstruction techniques. Both the LOR-OSEM and the LOR-OSEM+PSF reconstructions showed similar resolution characteristics in this evaluation. The images reconstructed with PSF blurred SMs gave a full width at half maximum (FWHM) of 14.5±2.5 mm for the 12.7 mm cold sphere and a FWHM of 14.5±2.5 mm for the 15.9 mm cold sphere, while the images reconstructed with LOR-OSEM gave a FWHM of 15.5±2.5 mm for the 12.7 mm cold sphere and a FWHM of 14.5±2.5 mm for the 15.9 mm cold sphere.
Figure 11.
Profiles through the centers of 12.7 and 15.9 mm diameter cold spheres after 15 iterations. The dashed lines represent the physical diameters of the cold spheres. (inset) A reconstruction of the cold sphere phantom. The line represents the line along which the profiles were measured.
Profiles through the 12.7 and 15.9 mm diameter hot spheres are shown after five iterations in Fig. 12. Again, all of the SMs produced images with similar resolution properties. Images reconstructed with LOR-OSEM+PSF(φ,r,d) gave a FWHM of 11.7±1.0 for the 15.9 mm hot sphere and a FWHM of 7.2±1.0 for the 12.7 mm hot sphere, which was typical for images reconstructed with PSF blurred SMs. Images reconstructed with LOR-OSEM gave a FWHM of 13.9±1.1 for the 15.9 mm hot sphere and a FWHM of 7.0±1.0 for the 12.7 mm hot sphere. The measured FWHMs are lower than the expected values in all cases. However, the slopes of the profile lines are very steep and a measurement at the base of each profile gives diameters of ∼13 and ∼16 mm for the 12.7 and 15.9 mm sphere, respectively, which indicates that this might be a better representation of the data than the FWHM in this case.
Figure 12.
Profiles through the centers of 12.7 and 15.9 mm diameter hot spheres after five iterations. The dashed lines represent the physical inner diameters of the hot spheres. (inset) A reconstruction of the hot sphere phantom. The line represents the line along which the profiles were measured.
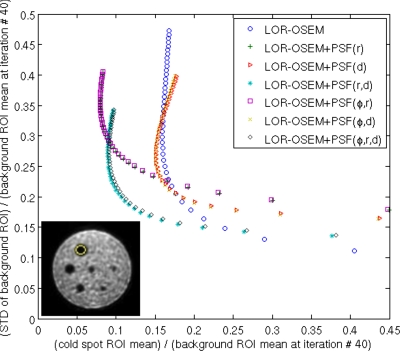
The phantom with the cold rods and spheres located off the central axis of the scanner was reconstructed using 40 iterations of each of the SMs and analyzed with no postprocessing. The contrast-noise properties were evaluated using the cold spheres in the phantom, in the same manner as described above, in order to test the effect of the radial position. In this case, a 65 mm diameter ROI was placed in the center of five slices that did not contain any rods or spheres to determine the background STD, and a 20 mm diameter ROI was placed over the 31.8 mm sphere to determine the cold sphere ROI. Figure 13 shows the STD of the background ROI divided by the mean of the background ROI at the final iteration versus the mean of the cold sphere ROI divided by the mean of the background ROI at the final iteration as a function of iteration number for reconstructions with each of the SMs. Plots of the images reconstructed with (r) and (φ,r) dependent SMs were nearly coincident; plots of images reconstructed with (d) and (φ,d) dependent SMs were nearly coincident, as were images reconstructed with (r,d), and (φ,r,d) dependent SMs. After six iterations all of the images reconstructed with PSF blurred SMs had better contrast-noise ratios than images reconstructed with the geometric SM. However, a marked separation could be observed between the results produced by the different PSF blurred SMs. After two iterations the images reconstructed with (r,d) and (φ,r,d) dependent SMs clearly offered favorable contrast-noise ratios compared to images reconstructed with the other SMs, with an optimum contrast-noise ratio occurring between ten and 20 iterations. The difference in the contrast-noise appears to be negligible between images reconstructed with the φ dependent SMs and the rotation independent SMs.
Figure 13.
A 65 mm diameter background ROI was placed over 5 slices free of rods and spheres. The STD of the background ROI divided by the mean of the background ROI at the last iteration plotted versus the mean of the 31.8 mm diameter cold sphere divided by the mean of the background ROI at the last iteration as a function of iteration number is shown. A curve closest to the origin represents the most desirable contrast-noise characteristics. The iteration number is increasing from 1 to 40 from right to left. (inset) A reconstruction after 15 iterations. The small circle shows the 20 mm ROI covering the 31.8 mm cold sphere.
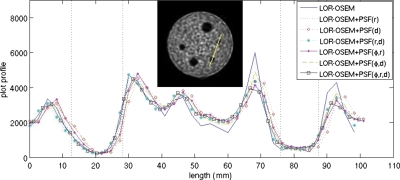
Figure 14 shows a slice containing the grids of cold rods reconstructed with 15 iterations for each of the SMs. The 7.9, 9.5, 11.1, and 12.7 mm rods are clearly distinguishable on all of the LOR-OSEM+PSF reconstructed images, with the 6.4 mm rods visible but blurred. In the images reconstructed with LOR-OSEM, only the 11.1 and 12.7 mm rods are clearly visible, with the 9.5 mm rods present but blurred. Visual evaluation of the images shows that the rods near the top of the images are more clearly formed in the images reconstructed with the (r), (φ,r), (r,d), and (φ,r,d) dependent SMs than in the images reconstructed with the (d) or (φ,d) dependent SMs. As in the other cases, any φ dependence is not observed.
Figure 14.
Reconstruction of the cold rod grid phantom located 170 mm off the central axis of the scanner after 15 iterations. The rods’ diameters are, from largest to smallest, 12.7, 11.1, 9.5, 7.9, 6.4, and 4.8 mm. The four largest rods can clearly be discerned on all of the images except the LOR-OSEM.
Figure 15 shows a profile through a line of 7.9 mm rods. Again, no φ dependence was observable. Plots of profiles from images reconstructed with (r) and (φ,r) dependent SMs were nearly coincident; plots from images reconstructed with (d) and (φ,d) dependent SMs were nearly coincident, as were the plots from images reconstructed with (r,d) and (φ,r,d) dependent SMs. Each of the plots shows similar latitude between the peaks and valleys.
Figure 15.
Profiles through the row of 7.9 mm diameter rods after 15 iterations. (inset) A reconstruction after 15 iterations. The line represents the line along which the profiles were measured.
CONCLUSION
As expected, the addition of a PSF blurred SMs leads to improved and more uniform spatial resolution and contrast-noise properties over the entire FOV in reconstructed images compared to images reconstructed using a geometrically derived SM. In a 2D acquisition with septa present, the depth dependence of the amplitude of the detector response is the most important factor affecting reconstructed image quality. PSF blurred SMs derived from σ dependent on r produced higher fidelity reconstructed images than those derived from σ dependent on d alone, while SMs derived from fully r and d dependent σ led to improved spatial resolution and contrast-noise ratios, compared to SMs derived from σ dependent on r or d alone. The σ(r) effects on the SM are most evident at larger radial values where parallax errors become more prominent. Any φ dependence for σ components is weak, with negligible effect. Results are highly dependent on the system acquisition geometry. For example, geometries with no septa present or with smaller spans will show smaller changes in sensitivity at large d positions.
In terms of PSF characterization, we found that a coarser PSF sampling density of about 0.5 points∕cm2 could be used, compared to the original 5 mm grid with 4 points∕cm2, resulting in a 20% savings in computational resources. This coarser sampling pattern can be obtained with one point every 2 cm2 within a transaxial plane, such as a square grid or a spoke pattern of radial lines covering the area subtended by one block of detectors. By exploiting axial symmetries, the number of axial planes sampled could have been reduced from 24 to eight planes, giving a total savings of time and computational burden of roughly 85%.
Positron emission tomography with 2D acquisition is widely used in many clinics. Algorithms containing PSF blurred SMs can easily be added to existing scanners with minimum effort. Optimization and parallelization of these more complete algorithms will reduce the reconstruction time to clinically acceptable levels. Inclusion of PSF blurred SMs in the PET image reconstruction process, with improved spatial resolution and contrast-noise ratios, would be very beneficial for PET imaging for (a) large patients that occupy most of the FOV and (b) small or distal tumors that require tumor volume delineation and quantification, as is relevant for radiation treatment planning and evaluation of treatment response. Further investigation of PSF blurred SMs is warranted for these indications for clinical PET imaging and as an aid to the design of future PET scanners.
ACKNOWLEDGMENTS
The authors would like to thank S. Wollenweber and S. Kohlmyer at General Electric Medical Systems for help in understanding data formats and geometry for the GE DST scanner. This work was supported by the TRADONC Program, Wake Forest University, School of Medicine (Grant No. NCI T-32 CA113267).
References
- Gambhir S. S., Czernin J., Schwimmer J., Silverman D. H., Coleman R. E., and Phelps M. E., “A tabulated summary of the FDG PET literature,” J. Nucl. Med. 42, 1S–93S (2001). [PubMed] [Google Scholar]
- Baum R. P., Hellwig D., and Mezzetti M., “Position of nuclear medicine modalities in the diagnostic workup of cancer patients: Lung cancer,” Q. J. Nucl. Med. Mol. Imaging 48, 119–142 (2004). [PubMed] [Google Scholar]
- von Schulthess G. K., Steinert H. C., and Hany T. F., “Integrated PET∕CT: Current applications and future directions,” Radiology 238, 405–422 (2006). 10.1148/radiol.2382041977 [DOI] [PubMed] [Google Scholar]
- Kirby A. M. and Mikhaeel N. G., “The role of FDG PET in the management of lymphoma: What is the evidence base?,” Nucl. Med. Commun. 28, 335–354 (2007). 10.1097/MNM.0b013e3280895e23 [DOI] [PubMed] [Google Scholar]
- Ashamalla H., Rafla S., Parikh K., Mokhtar B., Goswami G., Kambam S., Abdel-Dayem H., Guirguis A., Ross P., and Evola A., “The contribution of integrated PET∕CT to the evolving definition of treatment volumes in radiation treatment planning in lung cancer,” Int. J. Radiat. Oncol., Biol., Phys. 63, 1016–1023 (2005). 10.1016/j.ijrobp.2005.04.021 [DOI] [PubMed] [Google Scholar]
- Fox J. L., Rengan R., O’Meara W., Yorke E., Erdi Y., Nehmeh S., Leibel S. A., and Rosenzweig K. E., “Does registration of PET and planning CT images decrease interobserver and intraobserver variation in delineating tumor volumes for non-small-cell lung cancer?,” Int. J. Radiat. Oncol., Biol., Phys. 62, 70–75 (2005). 10.1016/j.ijrobp.2004.09.020 [DOI] [PubMed] [Google Scholar]
- Steenbakkers R. J., Duppen J. C., Fitton I., Deurloo K. E., Zijp L. J., Comans E. F., Uitterhoeve A. L., Rodrigus P. T., Kramer G. W., Bussink J., De Jaeger K., Belderbos J. S., Nowak P. J., van Herk M., and Rasch C. R., “Reduction of observer variation using matched CT-PET for lung cancer delineation: A three-dimensional analysis,” Int. J. Radiat. Oncol., Biol., Phys. 64, 435–448 (2006). 10.1016/j.ijrobp.2005.06.034 [DOI] [PubMed] [Google Scholar]
- Ciernik I. F., Dizendorf E., Baumert B. G., Reiner B., Burger C., Davis J. B., Lutolf U. M., Steinert H. C., and Schulthess G. K. V., “Radiation treatment planning with a integrated positron emission and computer tomography (PET∕CT): A feasibility study,” Int. J. Radiat. Oncol., Biol., Phys. 57, 853–863 (2003). 10.1016/S0360-3016(03)00346-8 [DOI] [PubMed] [Google Scholar]
- Schwartz D. L., Ford E. C., Rajendran J., Yueh B., Coltrera M. D., Virgin J., Anzai Y., Haynor D., Lewellen B., Mattes D., Kinahan P., Meyer J., Phillips M., Leblanc M., Krohn K., Eary J., and Laramore G. E., “FDG-PET∕CT-guided intensity modulated head and neck radiotherapy: A pilot investigation,” Head Neck 27, 478–487 (2005). 10.1002/hed.20177 [DOI] [PubMed] [Google Scholar]
- van Baardwijk A., Baumert B. G., Bosmans G., van Kroonenburgh M., Stroobants S., Gregoire V., Lambin P., and De Ruysscher D., “The current status of FDG-PET in tumour volume definition in radiotherapy treatment planning,” Cancer Treat. Rev. 32, 245–260 (2006). 10.1016/j.ctrv.2006.02.002 [DOI] [PubMed] [Google Scholar]
- De Ruysscher D., Wanders S., van Haren E., Hochstenbag M., Geeraedts W., Utama I., Simons J., Dohmen J., Rhami A., Buell U., Thimister P., Snoep G., Boersma L., Verschueren T., van Baardwijk A., Minken A., Bentzen S. M., and Lambin P., “Selective mediastinal node irradiation based on FDG-PET scan data in patients with non-small-cell lung cancer: A prospective clinical study,” Int. J. Radiat. Oncol., Biol., Phys. 62, 988–994 (2005). 10.1016/j.ijrobp.2004.12.019 [DOI] [PubMed] [Google Scholar]
- Erdi Y. E., Rosenzweig K., Erdi A. K., Macapinlac H. A., Hu Y. C., Braban L. E., Humm J. L., Squire O. D., Chui C. S., Larson S. M., and Yorke E. D., “Radiotherapy treatment planning for patients with non-small cell lung cancer using positron emission tomography (PET),” Radiother. Oncol. 62, 51–60 (2002). 10.1016/S0167-8140(01)00470-4 [DOI] [PubMed] [Google Scholar]
- Bentzen S. M., “Radiation therapy: Intensity modulated, image guided, biologically optimized, and evidence based,” Radiother. Oncol. 77, 227–230 (2005). 10.1016/j.radonc.2005.11.001 [DOI] [PubMed] [Google Scholar]
- Bradley J., Thorstad W. L., Mutic S., Miller T. R., Dehdashti F., Siegal B. A., Bosch W., and Bertrand R. J., “Impact of FDG-PET on radiation therapy volume delineation in non-small cell lung cancer,” Int. J. Radiat. Oncol., Biol., Phys. 59, 78–86 (2004). 10.1016/j.ijrobp.2003.10.044 [DOI] [PubMed] [Google Scholar]
- Ling C. C., Humm J., Larson S., Amols H., Fuks Z., Leibel S., and Koutcher J. A., “Towards multidimensional radiotherapy (MD-CRT): Biological imaging and biological conformality,” Int. J. Radiat. Oncol., Biol., Phys. 47, 551–560 (2000). 10.1016/S0360-3016(00)00467-3 [DOI] [PubMed] [Google Scholar]
- Tanderup K., Olsen D. R., and Grau C., “Dose painting: Art of science?,” Radiother. Oncol. 79, 245–248 (2006). 10.1016/j.radonc.2006.05.002 [DOI] [PubMed] [Google Scholar]
- Ben-Haim S. and Ell P., “18F-FDG PET and PET∕CT in the evaluation of cancer treatment response,” J. Nucl. Med. 50, 88–99 (2009). 10.2967/jnumed.108.054205 [DOI] [PubMed] [Google Scholar]
- Mawlawi O. and Townsend D. W., “Multimodality imaging: An update on PET∕CT technology,” Eur. J. Nucl. Med. Mol. Imaging 36, 15–29 (2009). 10.1007/s00259-008-1016-6 [DOI] [PubMed] [Google Scholar]
- Kirov A. S., Piao J. Z., and Schmidtlein C. R., “Partial volume effect correction in PET using regularized iterative deconvolution with variance control based on local topology,” Phys. Med. Biol. 53, 2577–2591 (2008). 10.1088/0031-9155/53/10/009 [DOI] [PubMed] [Google Scholar]
- Nestle U., Weber W., Hentschel M., and Grosu A. -L., “Biological imaging in radiation therapy: Role of positron emission tomography,” Phys. Med. Biol. 54, R1–R25 (2009). 10.1088/0031-9155/54/1/R01 [DOI] [PubMed] [Google Scholar]
- Pan T. and Mawlawi O., “PET∕CT in radiation oncology,” Med. Phys. 35, 4955–4966 (2008). 10.1118/1.2986145 [DOI] [PubMed] [Google Scholar]
- Hudson H. M. and Larkin R. S., “Accelerated image reconstruction using ordered subsets of projection data,” IEEE Trans. Med. Imaging 13, 601–609 (1994). 10.1109/42.363108 [DOI] [PubMed] [Google Scholar]
- Joseph P. M., “An improved algorithm for reprojecting rays through pixel images,” IEEE Trans. Med. Imaging 1, 192–196 (1982). 10.1109/TMI.1982.4307572 [DOI] [PubMed] [Google Scholar]
- Johnson C. A., Yan Y., Carson R. E., Martino R. L., and Daube-Witherspoon M. E., “A system for the 3D reconstruction of retracted-septa PET using the EM algorithm,” IEEE Trans. Nucl. Sci. 42, 1223–1227 (1995). 10.1109/23.467875 [DOI] [Google Scholar]
- Ollinger J. M. and Goggin A. S., “Maximum likelihood reconstruction in fully 3D PET via the SAGE algorithm,” in Proceedings of the IEEE Nuclear Science Symposium and Medical Imaging Conference, Anaheim, CA, 1996, pp. 1594–1598 (unpublished).
- Chen C. M., Lee S. -Y., and Cho Z. H., “Parallelization of the EM algorithm for 3-D PET image reconstruction,” IEEE Trans. Nucl. Sci. 10, 513–522 (1991). [DOI] [PubMed] [Google Scholar]
- Terstegge A., Weber S., Herzog H., Muller-Gartner H. W., and Halling H., “High resolution and better quantification by tube of response modeling in 3D PET reconstruction,” in Proceedings of the IEEE Nuclear Science Symposium and Medical Imaging Conference, Anaheim, CA, 1996, pp. 1603–1607 (unpublished).
- Lecomte R., Schmitt D., and Lamoureux G., “Geometry study of a high resolution PET detection system using small detectors,” IEEE Trans. Nucl. Sci. 31, 556–561 (1984). 10.1109/TNS.1984.4333318 [DOI] [Google Scholar]
- Liang Z., “Detector response restoration in image reconstruction of high resolution positron emission tomography,” IEEE Trans. Med. Imaging 13, 314–321 (1994). 10.1109/42.293924 [DOI] [PubMed] [Google Scholar]
- Rahmim A., Tang J., Lodge M. A., Lashkari S., Ay M. R., Lautamaki R., Tsui B. M. W., and Bengel F. M., “Analytic system matrix resolution modeling in PET: An application to Rb-82 cardiac imaging,” Phys. Med. Biol. 53, 5947–5965 (2008). 10.1088/0031-9155/53/21/004 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schmitt D., Karuta B., Carrier C., and Lecomte R., “Fast point spread function computation from aperture functions in high-resolution positron emission tomography,” IEEE Trans. Med. Imaging 7, 2–12 (1988). 10.1109/42.3923 [DOI] [PubMed] [Google Scholar]
- Selivanov V. V., Picard Y., Cadorette J., Rodrigue S., and Lecomte R., “Detector response models for statistical iterative image reconstruction in high resolution PET,” IEEE Trans. Nucl. Sci. 47, 1168–1175 (2000). 10.1109/23.856565 [DOI] [Google Scholar]
- Strul D., Slates R. B., Dahlbom M., Cherry S. R., and Marsden P. K., “An improved analytical detector response function model for multilayer small-diameter PET scanners,” Phys. Med. Biol. 48, 979–994 (2003). 10.1088/0031-9155/48/8/302 [DOI] [PubMed] [Google Scholar]
- Yamaya T., Hagiwara N., Obi T., Yamaguchi M., Ohyama N., Kitamura K., Hasegawa T., Haneishi H., Yoshida E., Inadama N., and Murayama H., “Transaxial system models for the jPET-D4 image reconstruction,” Phys. Med. Biol. 50, 5339–5355 (2005). 10.1088/0031-9155/50/22/009 [DOI] [PubMed] [Google Scholar]
- Alessio A. M., Kinahan P. E., and Lewellen T. K., “Modeling and incorporation of system response functions in 3-D whole body PET,” IEEE Trans. Med. Imaging 25, 828–837 (2006). 10.1109/TMI.2006.873222 [DOI] [PubMed] [Google Scholar]
- Mumcuoglu E. U., Leahy R. M., Cherry S. R., and Hoffman E., “Accurate geometric and physical response modeling for statistical image reconstruction in high resolution PET,” in Proceedings of the IEEE Nuclear Science Symposium Medical Imaging Conference, 1996, Vol. 3, pp. 1569–1573 (unpublished).
- Qi J., Leahy R. M., Cherry S. R., Chatziioannou A., and Farquhar T. H., “High-resolution 3D Bayesian image reconstruction using the microPET small-animal scanner,” Phys. Med. Biol. 43, 1001–1013 (1998). 10.1088/0031-9155/43/4/027 [DOI] [PubMed] [Google Scholar]
- Rafecas M., Mosler B., Dietz M., Pogl M., Stamatakis A., McElroy D. P., and Ziegler S. I., “Use of Monte Carlo-based probability matrix for 3-D iterative reconstruction of MADPET-II data,” IEEE Trans. Nucl. Sci. 51, 2597–2605 (2004). 10.1109/TNS.2004.834827 [DOI] [Google Scholar]
- Veklerov E., Llacer J., and Hoffman E. J., “MLE reconstruction of a brain phantom using a Monte Carlo transition matrix and a statistical stopping rule,” IEEE Trans. Nucl. Sci. 35, 603–607 (1988). 10.1109/23.12795 [DOI] [Google Scholar]
- Alessio A. M. and Kinahan P. E., “3D whole-body PET image reconstruction,” in Proceedings of the IEEE International Symposium on Biomedical Imaging, Paris, 2008. (unpublished). [DOI] [PMC free article] [PubMed]
- De Bernardi E., Mazzoli M., Zito F., and Baselli G., “Resolution recovery in PET during AWOSEM reconstruction: A performance evaluation study,” IEEE Trans. Nucl. Sci. 54, 1626–1638 (2007). 10.1109/TNS.2007.905167 [DOI] [Google Scholar]
- Panin V. Y., Kehren F., Michel C., and Casey M., “Fully 3-D PET reconstruction with system matrix derived from point source measurements,” IEEE Trans. Med. Imaging 25, 907–921 (2006). 10.1109/TMI.2006.876171 [DOI] [PubMed] [Google Scholar]
- Panin V. Y., Kehren F., Rothfuss H., Hu D., Michel C., and Casey M. E., “PET reconstruction with a system matrix derived from point source measurements,” IEEE Trans. Nucl. Sci. 53, 152–159 (2006). 10.1109/TNS.2005.862979 [DOI] [PubMed] [Google Scholar]
- Fin L., Bailly P., Daouk J., and Meyer M. -E., “A practical way to improve contrast-to-noise ratio and quantitation for statistical-based iterative reconstruction in whole-body PET imaging,” Med. Phys. 36, 3072–3079 (2009). 10.1118/1.3152116 [DOI] [PubMed] [Google Scholar]
- Tohme M. S. and Qi J., “Iterative image reconstruction for positron emission tomography based on a detector response function estimated from point source measurements,” Phys. Med. Biol. 54, 3709–3725 (2009). 10.1088/0031-9155/54/12/007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kadrmas D. J., “LOR-OSEM: Statistical PET reconstruction from raw line-of-response histograms,” Phys. Med. Biol. 49, 4731–4744 (2004). 10.1088/0031-9155/49/20/005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Di Bella E. V. R., Barclay A. B., Eisner R. L., and Schaffer R. W., “A comparison of rotation-based methods for iterative reconstruction algorithms,” IEEE Trans. Nucl. Sci. 43, 3370–3376 (1996). 10.1109/23.552756 [DOI] [Google Scholar]
- Paeth A., “A fast algorithm for general raster rotation,” Proceedings on Graphics Interface, 1986, pp. 77–81 (unpublished).
- Burger C., Goerres G., Schoenes S., Buck A., Lonn A. H. R., and Von Schulthess G. K., “PET attenuation coefficients from CT images: Experimental evaluation of the transformation of CT into PET 511-keV attenuation coefficients,” Eur. J. Nucl. Med. 29, 922–927 (2002). 10.1007/s00259-002-0796-3 [DOI] [PubMed] [Google Scholar]
- Accorsi R., Adam E., Werner M. E., and Karp J. S., “Optimization of a fully 3D single scatter simulation algorithm for 3D PET,” Phys. Med. Biol. 49, 2577–2598 (2004). 10.1088/0031-9155/49/12/008 [DOI] [PubMed] [Google Scholar]
- Valk P. E., Bailey D. L., Townsend D. W., and Maisey M. N., Positron Emission Tomography: Basic Science and Clinical Practice (Springer, London, 2004). [Google Scholar]