Neuromechanical simulation of the locust jump

Abstract

The neural circuitry and biomechanics of kicking in locusts have been studied to understand their roles in the control of both kicking and jumping. It has been hypothesized that the same neural circuit and biomechanics governed both behaviors but this hypothesis was not testable with current technology. We built a neuromechanical model to test this and to gain a better understanding of the role of the semi-lunar process (SLP) in jump dynamics. The jumping and kicking behaviors of the model were tested by comparing them with a variety of published data, and were found to reproduce the results from live animals. This confirmed that the kick neural circuitry can produce the jump behavior. The SLP is a set of highly sclerotized bands of cuticle that can be bent to store energy for use during kicking and jumping. It has not been possible to directly test the effects of the SLP on jump performance because it is an integral part of the joint, and attempts to remove its influence prevent the locust from being able to jump. Simulations demonstrated that the SLP can significantly increase jump distance, power, total energy and duration of the jump impulse. In addition, the geometry of the joint enables the SLP force to assist leg flexion when the leg is flexed, and to assist extension once the leg has begun to extend.

INTRODUCTION

The ability to escape predators is of great evolutionary importance. Many animals, including the locust, have evolved to specialize in jumping as a method of escape and locomotion. The locust jump is mediated by neural and biomechanical mechanisms that first prepare the animal for the jump by storing mechanical energy in the legs, and then release it suddenly to catapault the animal into the air. Because of the impossibility of making the necessary measurements during a jump, the mechanisms have primarily been studied during a different behavior, the kick, when the locust body is held stationary (Heitler, 1988; Heitler and Burrows, 1977a; Heitler and Burrows, 1977b). The kick and the jump both involve rapid extension of the leg, but because the kick is unloaded, it occurs much more rapidly than the jump. Despite this difference, the similar neuromuscular activity before and during both behaviors has led to the suggestion that the kick and jump motor programs are the same (Heitler and Burrows, 1977a).

The locust kick/jump motor program consists of three phases (Burrows, 1995; Heitler and Burrows, 1977a). The first phase is cocking the leg. The locust prepares for a jump by activating the flexor tibia muscle to bring the tibia into a fully flexed position. The second phase is a period of co-contraction where both the extensor and flexor tibia muscles are active. The extensor tibia muscle slowly contracts and stores energy in the extensor apodeme, in the semi-lunar process (SLP) and in the leg cuticle. As tension builds in the flexor tibia, its distal tendon passes over a cuticular invagination in the ventral aspect of the distal ventral femur called Heitler's lump (Bennet-Clark, 1975). This enables the flexor tibia tendon to attach to the tibia at an angle of nearly 90 deg. when the tibia is fully flexed, thereby maximizing its mechanical effectiveness in maintaining tibial flexion against the increasing tension in the much larger extensor tibia muscle (Heitler, 1974). The lump also acts as a catch or lock on the tendon that helps keep the tibia flexed while the flexor muscle has tension. In the third phase, the jump is triggered when both the flexor muscle and its motor neurons are inhibited. When the flexor tension drops below a threshold, the tendon slips off the catch and the tibia is rapidly extended to produce the jump (Heitler, 1974).

Technical limitations have prevented a clear understanding of the role of the SLP in the kick and jump. The SLP is a highly sclerotized portion of cuticle at the femoral–tibia joint of the metathoracic leg. In preparation for a kick or jump, the SLP bends like an archery bow during a slow contraction of the powerful extensor muscle to store energy that is later released rapidly to power the kick or jump (Bennet-Clark, 1975). The function of the SLP has been inferred from its movement during kicks as recorded by high-speed video and from calculations of the energy stored in the extensor apodeme, the SLP and the femur cuticle (Bennet-Clark, 1975; Burrows and Morris, 2001). The energy stored in the SLP and the timing of its release appear to be important for jump performance. High-speed video of locusts kicks show that the SLP does not begin unfurling until the tibia has rotated by more than 30 deg. (Burrows and Morris, 2001). The reason for this delay and the role it may play in the jump dynamics are unknown. Damage to the SLP, which is an integral part of the leg joint, makes the locust unable to jump, and so makes comparisons of the jump performance of animals with and without a functional SLP almost impossible.

The emerging field of neuromechanical simulation can help address these issues (Pearson et al., 2006). We have used a new neuromechanical simulator, AnimatLab (www.animatlab.com), to build and test a model of the locust based on current descriptions of the neural and biomechanical processes that govern the jump. The model locust was then situated in a physically realistic environment within AnimatLab to study both the ability of the kick motor program to produce a realistic jump and the effects of the SLP on jumping behavior.

MATERIALS AND METHODS

Animals

Adult locusts, Schistocerca americana L., were obtained from a breeding colony at Agnes Scott College, Decatur, GA, USA, kept caged in small groups at 27°C under a 12 h:12 h L:D cycle, and fed fresh organic lettuce and 2/1 mixture of fresh wheat germ and powdered milk. Individuals were taken from the cage to a video-recording room and placed on a jumping platform. The platform contained a heating element that could adjust the local temperature and was covered by very fine sandpaper to allow the locust a slip-free surface for jumping. A 25 cm × 30 cm yellow wooden target was placed 30 cm from the platform, and jumps to the target were induced by either gentle touches of the abdomen by a hand-held wand or by raising the temperature of the platform. Animals were retrieved after the jump and returned to the platform for another attempt. Jumps were evoked at about 5 min intervals; individuals were returned to their cage after 10 jumps. Locust jumps were recorded at 500 frames s⁻¹ and a resolution of 512 pixels × 240 pixels by two Photron PIC R2 Fastcam video cameras (San Diego, CA, USA) with an exposure time of 0.5 ms.

Locust model

To distinguish references to the model and its parts from references to the locust, the model part names have been given the italicized names of the corresponding locust body parts whereas references to the locust and its body parts are made in normal font.

The 3-D graphical model of the locust body was developed from a 3-D polygon mesh that was purchased online (www.turbosquid.com) and then separated into individual body segments using the graphics program Blender (www.blender.org). A polygon mesh is a set of vertices and triangular faces that define the volume for that segment. The dimensions of each segment were re-scaled to match published anatomical measurements (Bennet-Clark, 1975; Heitler, 1974). All segments were assumed to have a uniform density, and the distribution of mass throughout the mesh volume determined the moment of inertia for that segment. The model has a body length of 48 mm and a total mass of 2.5 g, with metathoracic femur and tibia lengths of 26 mm (Bennet-Clark, 1975). Individual body and limb segments were connected with either static or planar hinge joints in AnimatLab to assemble the locust body model. Angular limits on the hinge joints were set to restrict the movement of each joint to the normal range of the corresponding animal's joint. To ensure that the center of mass (COM) of the whole locust was located appropriately, small weighted masses were placed along the body axis of the thorax and abdominal segments to adjust the distribution of mass within the body (Bennet-Clark, 1975). The COM was then determined by pinning the body to a hinge joint and allowing it to rotate freely. Mass was re-distributed until the locust balanced both vertically and horizontally at the desired location. The locust model used for these simulations can be found at www.animatlab.com/locust.

Biomechanics

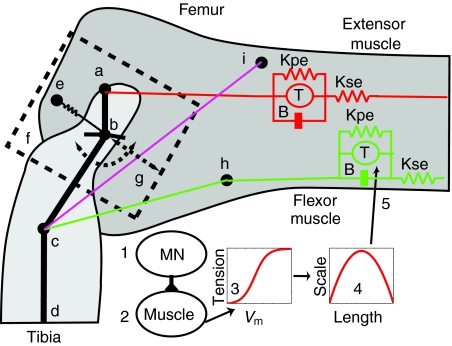
The geometry and biomechanical properties of the femur–tibia joint of the metathoracic leg play a crucial role in the energy storage for the jump (Fig. 1). The tibia extensor muscle/apodeme is shown as a red line that attaches to the tibia (Fig. 1a) whereas the tibia flexor muscle/apodeme is shown in green. It wraps over Heitler's lump (Fig. 1h) and attaches to the tibia (Fig. 1c). The femur was connected to a small block of mass 1.6 mg that represented the SLP (Fig. 1f) (Bennet-Clark, 1975). A sliding prismatic joint connected the SLP to the femur (Fig. 1g). During normal co-contraction, the distal end of the SLP (where the tibia attaches) moves 0.3 mm ventrally and 0.4 mm proximally (Burrows and Morris, 2001). The slider joint was oriented to allow the SLP mass to move in the same direction (Fig. 1b–g). A spring attached the SLP mass to the femur and was oriented along the direction of movement of the slider joint (Fig. 1e). The stiffness of the semi-lunar spring was calculated from a stress–strain curve obtained for the SLP (Bennet-Clark, 1975). Straining the process parallel to the extensor apodeme by 0.4 mm required approximately 14.2 N of force (Bennet-Clark, 1975). However, the SLP moves both proximally and ventrally, and this amount of proximal strain corresponds to 0.3 mm of ventral strain, for 0.5 mm of total strain. From this strain, we calculated the stiffness of the SLP as 28.4 kN m⁻¹. The semi-lunar spring constant was set to this value.

Fig. 1.

Model of the femur–tibia (FT) joint of the metathoracic leg. (a) Extensor apodeme attachment point on the tibia. (b) FT hinge joint and connection of semi-lunar process (SLP) spring. (c) Flexor apodeme attachment point on the tibia. (d) A more distal point on the tibia. (e) The SLP spring is attached between the femur and the tibia. (f) The SLP mass moves along the slider joint (g) oriented between the points b and g that is at an inclination of 36.9 deg. (h) Heitler's lump. The flexor muscle wraps over this lump to alter its orientation with respect to the tibia as the leg is moved. (i) The tendon lock is modeled as a spring located between points c and i (magenta line). It is only enabled when the tibia is fully flexed and flexor muscle has a tension greater than 0.15 N (Bennet-Clark, 1975; Heitler, 1974). The distance between a,b is 0.76 mm, b,c is 1.64 mm. The angle a,b,c is 144 deg. and b,c,d is 143 deg. (Heitler, 1974). The muscle model is shown for the flexor and extensor muscles. This consists of a spring (Kpe), in parallel with a tension generator (T), and a dashpot (B), in series with another spring (Kse). (1) The muscle is activated by firing of a motor neuron (MN). (2) This depolarizes the muscle membrane. (3) Changes in the membrane voltage (V_m) are converted to a tension value using a sigmoidal function. (4) The tension value is scaled based on the muscle length. (5) The scaled tension is applied to the muscle by the force generator to produce a contraction. Tibia extensor muscle/apodeme is shown as a red line, and the tibia flexor muscle/apodeme is shown in green.

The tibia was connected to the SLP mass by a hinge joint that allowed the tibia to rotate between 5 deg. and 160 deg. (Fig. 1b). The femur–tibia hinge joint is connected to the SLP mass, so that during co-contraction and tibial extension, the hinge joint will move along the slider with the SLP mass to approximate the joint movement observed in the locust (Burrows and Morris, 2001). The distances and angles that define the relationships between the extensor attachment, femur–tibia hinge joint and flexor attachment were set to published measured values (the distance between a,b is 0.76 mm and between b,c is 1.64 mm. The angle a,b,c is 144 deg. and the angle b,c,d is 143 deg.) (Heitler, 1974).

Muscle is represented in AnimatLab by a linear Hill muscle model (Hill, 1970; McMahon, 1984; Shadmehr and Wise, 2005a; Shadmehr and Wise, 2005b). Each muscle model consists of a serial spring (Kse) in series with the parallel combination of a parallel spring (Kpe), a dashpot (B) and a force actuator (T). Muscle model properties are determined by the resting muscle length, the spring and dashpot constants, the stimulus–tension curve and the length–tension curve. The stimulus–tension curve is a sigmoidal function that relates the force level of the actuator to muscle membrane depolarization. The length–tension curve is an inverse parabola that determines the percentage of actuator force that is applied at a given muscle length.

Only two muscles for each of the rear legs are modeled in this simulation, the flexor tibiae and extensor tibiae. The maximum force that can be produced by the extensor is 15 N, which is achieved upon depolarization after a latency of 300–800 ms (Bennet-Clark, 1975). The serial spring constant of the extensor was calculated using the Young's modulus of 18.9 kN mm⁻² found for the extensor apodeme by Bennet-Clark (Bennet-Clark, 1975). The average size of the apodeme test pieces was 3 mm long × 0.25 mm wide × 40 μm thick, and so they have an area of 0.01 mm², and a length of 3 mm. These values allowed us to calculate the spring constant as 63 kN m⁻¹ from Young's modulus using the equation K=YA/L, where Y is the modulus, A is the area and L is the length. In the absence of published measurements that would allow calculation of the parallel spring constant, we used a value of 20 N m⁻¹ because it produced a small but noticeable tension when the extensor muscle was stretched. The damping coefficient of the extensor muscle was set by hand to 700 Ns m⁻¹ to produce a rise time to peak tension of approximately 400 ms. The stimulus–tension curve and the response properties of the non-spiking neuron that represents the muscle membrane were configured to reproduce the twitch response of the extensor muscle to a single FETi spike at a femur–tibia angle of 90 deg. (Heitler, 1988). The length–tension curve was also reproduced from muscle twitch values that were taken at various femur–tibia angles by stimulation of the muscle (Bennet-Clark, 1975). Stimulation of the extensor muscle produced twitch responses very similar to those recorded from extensor muscle in response to a FETi spike. The resulting length–tension curve of the extensor muscle reached the maximum at the fully flexed position and was reduced as the leg extended.

Recordings from the flexor muscle showed that it produces a maximum tension of around 0.75 N in response to tetanizing stimulation, and that it reached maximum tension 35–40 ms after a latency of 15 ms (Bennet-Clark, 1975). The following parameter values enabled the flexor muscle model to reproduce the recorded peak tension and tension time course; the serial spring constant, K_se, was 100 N m⁻¹, the parallel spring constant K_pe was 20 N m⁻¹ and the damping coefficient, B, was 10 Ns m⁻¹. The stimulus–tension curve was configured to produce the desired maximum tension. As with the extensor model, the flexor length–tension curve was near its maximum value when the leg was fully flexed and near its minimum value when the leg was extended.

The tendon on the flexor muscle of the locust contains a pocket. When the tibia is fully flexed and the flexor has a tension greater than 0.15 N, this pocket is caught on Heitler's lump, which helps keep the tendon locked in place (Bennet-Clark, 1975; Heitler, 1974). This tendon lock property plays an important role in the jump after co-contraction when the flexor muscle and motor neurons are being inhibited. The lock helps keep the tibia fully flexed even while the flexor tension is dropping. This prevents premature extension of the tibia and initiates the jump once the flexor tension drops below a threshold value for maintaining the lock. In the model, the tendon lock was represented by a spring that connects the flexor attachment to a point on the femur (Fig. 1, magenta line between points c and i). The spring was disabled and produced no tension unless the tibia was fully flexed and the flexor tension was greater than 0.15 N.

Neural model

A conductance-based integrate-and-fire neuron model was used in this simulation. Neurons were modeled as single equipotential compartments, each characterized by a set of user-specifiable parameters, including membrane time-constant, size (i.e. input conductance), membrane voltage, current noise, initial spike threshold, spike-frequency accommodation, spike after-hyperpolarization conductance and calcium conductances with activation and inactivation variables (MacGregor and Lewis, 1977).

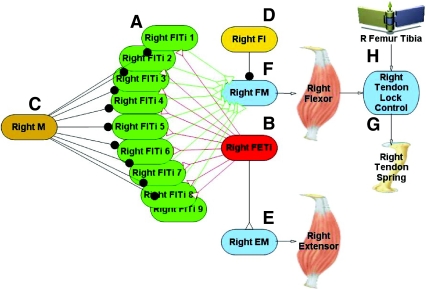
The neural network used to generate both the kick and jump motor programs was designed to apply the correct motor signals in a sequence and duration that mimics the motor program seen during kicking in locusts (Heitler and Burrows, 1977a; Heitler and Burrows, 1977b). Initial flexion of the tibia begins when the nine fast flexor tibia motor neurons are stimulated to fire (Fig. 2A, green FLTi neurons) (Burrows, 1995; Burrows, 1996). These neurons synapse onto the flexor muscle membrane (Fig. 2F, light blue FM node) causing muscle depolarization and flexor muscle contraction. The fast extensor of the tibia motor neuron (Fig. 2B, red FETi neuron) synapses onto the extensor muscle membrane (Fig. 2E, light blue EM node) causing it to contract. A central excitatory synapse connects the FETi neuron to the fast flexor motor neurons (B to A) (Burrows, 1996; Heitler and Burrows, 1977b). There are also two inhibitory interneurons that are involved in triggering the jump. The multimodal ‘M’ interneuron (Fig. 2C, gold M neuron) inhibits the excitatory flexor motor neurons, while the inhibitory flexor inhibitor motor neuron (Fig. 2D, yellow FI neuron) synapses onto the flexor muscle and inhibits it directly (Burrows, 1995; Pearson et al., 1980). The tendon lock control node (Fig. 2G, light blue) is responsible for enabling the tendon lock spring when the tibia is sufficiently flexed and the flexor has a tension above the lock threshold. The network that governs the right metathoracic leg is shown in Fig. 2; an identical network governs the left metathoracic leg.

Fig. 2.

Neural network model to produce the kick and jump motor programs. Network shown is for the right leg. (A) Nine fast flexor tibia motor neurons (green FlTi). FlTis synapse onto the flexor muscle membrane (light blue FM). (B) A single fast extensor tibia motor neuron (red FETi). FETi synapses onto the extensor muscle membrane (light blue EM). (C) The multimodal interneuron (gold M) inhibits the FlTis. (D) The flexor inhibitor (yellow FI) inhibits the flexor muscle. (E) Depolarization of the extensor muscle membrane causes the extensor muscle to contract. (F) Depolarization of the flexor muscle membrane causes the flexor muscle to contract. (G) The tendon lock control node (light blue) controls when the tendon lock spring is enabled based on the rotation of the tibia and the tension in the flexor muscle. (H) When the jump is triggered the femur–tibia joint rotates rapidly to produce the kick or jump.

Neurons were configured to reproduce the observed firing frequencies during the kick. Peak FETi neuron firing ranged between 60 Hz and 100 Hz (Heitler and Burrows, 1977a), while the FLTi neurons fired around 60 Hz (Heitler and Burrows, 1977A). The central excitatory synapse connecting the FETi to the FLTi neurons was configured by reproducing an experiment in which the FETi was stimulated to fire at roughly 10 Hz while the synaptic response of the FLTi was monitored (Heitler and Burrows, 1977b). The first FETi spike produced a 20 mV EPSP (excitatory postsynaptic potential) in all of the FLTi motorneurons; the EPSPs decayed in approximately 100 ms (Burrows, 1996; Heitler and Burrows, 1977b). Responses to subsequent spikes were reduced by synaptic depression in a manner similar to that observed experimentally (Heitler and Burrows, 1977b).

All neurons had a random tonic noise of 0.3 mV added to their membrane potentials at each time step. The pseudo-random number generator that controlled the noise was initialized using a random seed value at the beginning of each simulation. This caused each simulation with a different seed to produce slightly different results because changes in the neuron voltages led to alterations in the timing of the motor program and the rise and fall times of the tension in each of the muscles.

Procedures for simulation of experiments

During the kick simulations, the locust was suspended above the ground and rotated so that its ventral surface was uppermost, and pinned in place so it could not fall. All leg joints except the femur–tibia and tibia–tarsus joints of the metathoracic legs were locked to prevent rotation. The kick motor program caused the tibia to flex initially and then kick out at high speed. This allowed us to measure the movement of the SLP and tibial rotation. SLP torque relative to the extensor attachment was calculated by recording the coordinates of the femur–tibia joint, extensor attachment and the SLP force vector. These values were used to calculate the moment arm of the SLP force vector relative to the extensor attachment, and this was used to calculate the torque applied by the SLP. Kick velocity was measured as the peak velocity between the beginning of the kick and end of the kick when the tibia had fully rotated by 160 deg. Kick duration was the time from the beginning of the kick until full rotation of the tibia.

The same stimulus pattern that was used for kicks was applied to produce the motor pattern for the jump. Simulations of the locust jump began with the locust held 4.5 cm above the ground, and then dropped to the ground. Initially, only the femur–tibia joints of the rear legs were free to rotate. All of the other joints were locked and unmoving, and the rear legs were held up in the air to allow the tibia to rotate freely without interference with the ground. Once the tibia was fully flexed, the metathoracic coax–femur joint was adjusted to fix the angle of the leg with respect to the ground and ensure a take-off angle of approximately 55 deg. This angle was chosen because it produced jumps that minimized tumbling during take-off. The joints for all of the other legs remained locked throughout the jump motor program in order to maintain a stable and consistent posture, and the posture of the front legs was adjusted to fix the initial body pitch of the animal at 2 deg. The locks on the joints of the front and middle legs were disabled when the jump was triggered. This allowed all the legs to move freely throughout the take-off and ballistic phase of the jump. The SLP was disabled for tests by locking the SLP sliding prismatic joint to prevent it from moving and by disabling the SLP spring to prevent it from generating tension. Extensor tension was controlled by varying the firing frequency of the FETi motor neurons.

Predicted jump distance was calculated using the equation:

$$d=\frac{2\cdot E\cdot \text{sin}\left(2\cdot \theta \right)}{m\cdot \mathbf{g}},$$ (1)

where d is distance, E is energy, θ is the average take-off angle for all simulated jumps, m is the mass and g is gravity (Bennet-Clark, 1975). The power of the jump was calculated as the dot product of the force acting on the body during the jump impulse and the velocity of the body (Bennet-Clark, 1975). The energy of the jump was calculated by integrating the power curve over the time period of the impulse. The beginning of a jump or kick was always measured from when the tendon lock was disengaged. Jump duration was the time from the beginning until either the body or one of the rear legs first touched the ground. Jump distance was measured as the difference between the positions of the locust at the end and at the beginning of the jump. Jump impulse duration was the time from the beginning of the jump until one of the legs lost contact with the ground. Jump velocity and acceleration was the peak of those values obtained during the jump impulse. All data analysis was performed in Matlab (Matlab R2007a, Mathworks Inc., Natick, MA, USA), and statistical comparisons were made using its Anova1 one-way analysis of variance function.

The influence of SLP flexion torque on the flexor muscle was determined by comparing the tension level at which the extensor muscle was able to overcome the tension in the flexor when the SLP spring was intact and when it was disabled. The extensor tension was set to 5 N, and the tendon lock was disabled for both tests. The first test was performed with the SLP intact whereas in the second test the SLP spring was disabled. Once the extensor reached the 5 N tension level the flexor was inhibited and its tension dropped until it reached a point where the extensor muscle was able to overcome it and extend the leg.

RESULTS

Motor program and jumping

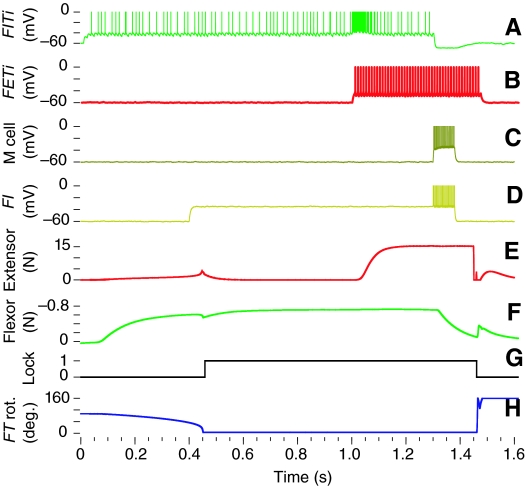
The simulated motor program and patterns of muscle activity responsible for the kick are shown in Fig. 3. The kick motor program began by stimulating the nine FlTi motorneurons on the right and left side (Fig. 2) to fire at about 60 Hz, which produced tension in the flexor muscles that caused the left and right tibiae to become fully flexed (Fig. 3A,F). A train of current stimuli applied to the FETi motorneurons on both sides began the co-contraction phase (Fig. 3B,E). Each current stimulus evoked a corresponding spike in FETi. In addition to driving the extensor muscle, the FETi excited the FlTis on the same side (Heitler, 1988) to enable the flexor muscle to keep the tibia flexed despite the mounting extensor tension. The kick was triggered by stimulation of the FI (Fig. 3D) and M inhibitory neurons (Fig. 3C) with an applied current for 80 ms, which caused them to fire at approximately 200 Hz. The FI neuron inhibited the flexor muscle, causing the flexor tension to decline rapidly. Simultaneously, the M neuron inhibited the FlTis to remove the drive on the flexor muscle. Rapid inhibition of the FlTis and the flexor muscle triggered the kick by reducing the flexor tension below the level needed to maintain the tendon lock (Fig. 3F,G) (Heitler and Burrows, 1977a; Pearson et al., 1980). With the flexor tendon lock disabled, the tibia began to extend very rapidly, completing extension in 4 ms, the same time course that was recorded with high-speed videography (Burrows and Morris, 2001).

Fig. 3.

Neural output of the jump motor network. The nine flexor motor neurons were stimulated to fire (A) during the cocking phase, which increased tension in the flexor muscle (F) and rotated the tibia into a fully flexed position (H). The extensor motor neuron FETi (B) began firing to produce co-contraction and increase flexor frequency through the central excitatory synaptic connection from FETi to FLTi. The inhibitory interneurons M (C) and flexor inhibitor (FI) (D) then began firing once the extensor had reached the desired tension level (E). This caused the tension in the flexor (F) to fall below the tendon lock threshold (G), which disabled the tendon spring. The unopposed tension produced a rapid extension of the tibia (H). Each chart corresponds to the output from a labeled element from Fig. 2.

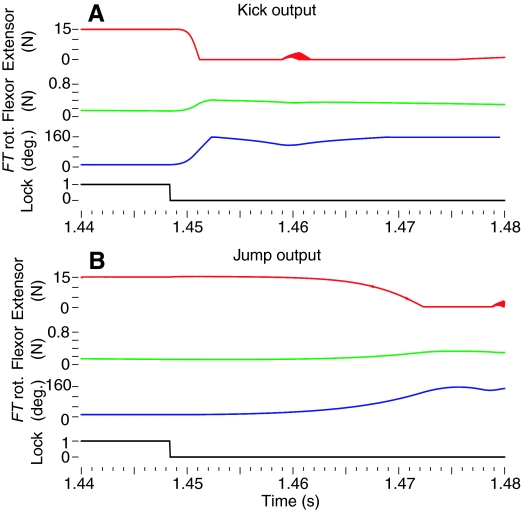
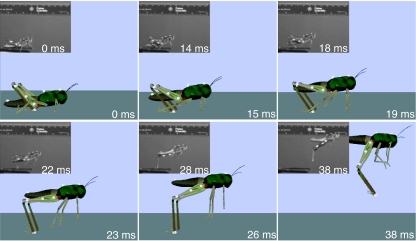
To test the hypothesis that the same neural circuitry and motor program could produce both the kick and the jump, we used the model of the kick circuit and motor program to evoke a simulated jump. An expanded view of the data for both the kick and jump are shown in Fig. 4. Although the same motor program controlled both simulated behaviors, the unloaded leg extended in less than 5 ms to produce the kick (Fig. 4A) whereas the load imposed by the body caused the leg to extend much more gradually to produce the jump (Fig. 4B). Comparison of the simulated movements of the locust with a series of frames taken of a locust's jump (S. americana) by a high-speed camera operating at 500 frames s⁻¹ (see Materials and methods; Fig. 5) shows that the simulation has captured the most salient features of the resulting jump behavior. In this, as in most of our recorded locust jumps, the animal's legs left the ground at about 30 ms after the start of the jump, and the head and thorax maintained their orientation during the 45 ms that the animal remained in view (Fig. 5, inset). Simulated locust jumps displayed most of these behaviors. The locust shown jumping in Fig. 5 displays the same series of leg movements at the same times as the locust shown in the inset, although its body has begun to rotate forward by the final frame of the simulation.

Fig. 4.

Expanded view of jump or kick data. Kick data from Fig. 3 is expanded and compared with data from a jump. The output of the motor program was the same for both the kick and the jump, and so was omitted here. Each chart shows the tension in the extensor and flexor muscle of the left metathoracic leg, the rotation of the femur–tibia (FT) joint and the status of the tendon lock. (A) To produce a kick, the tibia began to rotate very rapidly after the tendon lock was disabled, and completed full extension in 4.1 ms. (B) The jump used the same motor program but the leg rotated more slowly because the tibia was loaded, and so reached its maximum value after 28.35 ms. The colored plot lines have the same colors as the corresponding lines for plots of the same variables in Fig. 3.

Fig. 5.

Screenshots of the simulated and real locust jumping. Images of a real locust jump are in the insets. The simulated locust produces a jump very similar to those recorded from live locusts. Live locust images are sequential frames taken using a high-speed camera at 500 frames s⁻¹.

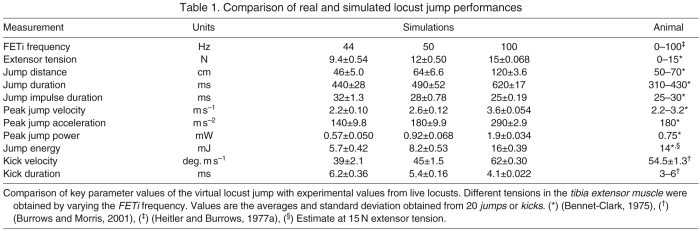
Published measurements of locust (Schistocerca gregaria) jump behavior (Table 1) provide benchmarks with which to compare the model locust jump behavior. Model locust jumps were performed with randomly seeded noise added to the membrane potentials of all of the model neurons and muscles, while all of the other model parameters were kept constant. Randomly seeded membrane potential noise ensured that the locust behaved slightly differently for each jump simulated under a given set of parameter values due solely to the randomness in the neurons and their effect on the biomechanics. This provided a method to measure the variance of the behavior when all of the other initial conditions were identical. By varying the FETi firing frequency extensor tension it was possible to encompass the entire range of behavioral data that was observed in the live animals. Several indicators of jump performance were obtained and compared with the published benchmark values for live locusts (Table 1), and were found to be essentially the same. FETi frequencies between 44 Hz and 100 Hz produced extensor tensions from 9.4 N to 15 N that led to jumps between 46 cm and 120 cm long (Table 1; Fig. 6A circles, R²=0.96). The simulations most closely matched the live data when the FETi frequency was set to 50 Hz, which evoked extensor tensions of 12 N and jumps 64 cm long. Energy for the jump also varied linearly and provided a very good match to the predicted distance for that energy level and take-off angle (Fig. 6B, R²=0.98). These similarities demonstrate that the jump performance of the locust using the kick motor program closely matched that of the live locusts.

Table 1.

Comparison of real and simulated locust jump performances

Fig. 6.

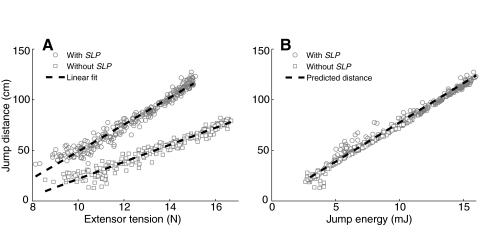
Jumping performance. (A) Jumps were performed with and without the semi-lunar process (SLP) for a variety of different extensor tension values. Extensor tension was altered by varying the time between FETi spikes between 10 ms and 23 ms at 1 ms intervals. Twenty jumps were performed at each time interval. Jump distance varied linearly with extensor tension for both cases (R²=0.96 with SLP, R²=0.95 without SLP). Without the SLP the jump distance was reduced by 45% at 15 N, and this reduction increased to 55% at 10 N. (B) Jump distance also varied linearly with the jump energy, and matched the predicted jump distance (R²=0.98). This is consistent with the hypothesized relationship between jump energy and distance (Bennet-Clark, 1975).

Role of the SLP

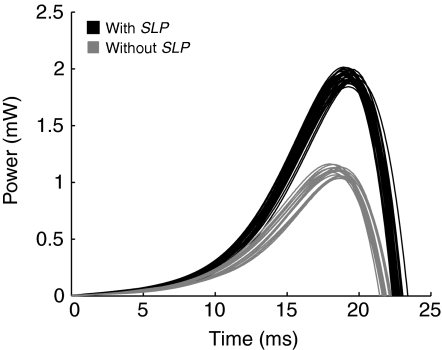
The contribution of the SLP to the locust jump was analyzed by comparing jumps made with the SLP intact with jumps made with it disabled. Without the SLP, the jump distance remained proportional to extensor tension but the slope of the regression line was reduced by 40% and the projected X-intercept (the minimal extensor tension needed to produce a jump) was greater (Fig. 6A squares, R²=0.95). The difference in slope indicates that the SLP increases the effect of a change in extensor tension on the distance jumped. The difference in X-intercept provides a measurement of how energy storage by the SLP reduces the minimal extensor tension needed to make a jump. The difference between the two regression lines was used to determine the contribution of the SLP to jump distance for different extensor tensions. When the SLP was disabled the jump distance was reduced by 45% at 15 N and by 55% at 10 N. The peak power of the jump impulse when the SLP was intact was significantly higher than when the SLP was disabled (1.94±0.05 mW with, 1.10±0.04 mW without, P<10⁻³⁰; Fig. 7). A higher peak power also resulted in a significant increase in the total energy for the jump (15.3±0.4 mJ with, 8.58±0.4 mJ without, P<10⁻³⁰). In addition, when the SLP was disabled, the power ended significantly sooner than it did when the SLP was intact (24.7±0.3 ms with, 24.1±0.3 ms without, P<10⁻¹⁰).

Fig. 7.

Jump power with and without semi-lunar process (SLP). Only extensor tensions within 0.25 N of 15 N were used. Jump power with the SLP intact (black) and with the SLP disabled (gray). There is a significant difference in the magnitude of the peak power (1.94±0.05 mW with, 1.10±0.04 mW without, P<10⁻³⁰), the total energy during the jump impulse (15.3±0.4 mJ with, 8.58±0.4 mJ without, P<10⁻³⁰) and the duration of the impulse (24.7±0.3 ms with, 24.1±0.3 ms without, P<10⁻¹⁰).

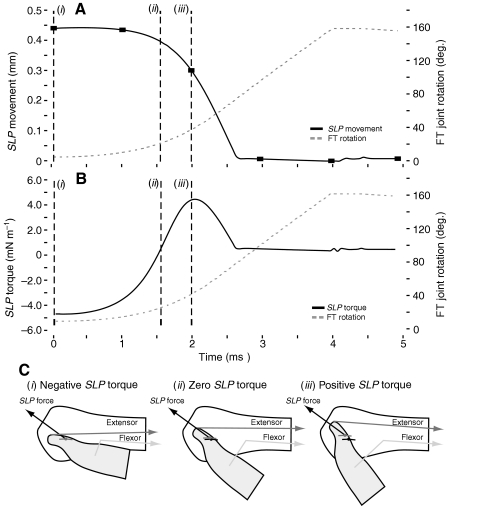
High-speed video of locust kicks have shown that the SLP does not unfurl until after the tibia has extended by more than 30 deg. (Burrows and Morris, 2001). To analyze this result through simulations, the locust kick was reproduced by the locust. Fig. 8A shows how the strain of the SLP and the FT joint rotation both vary with time during the jump. The filled black squares mark the values of the SLP strain at 1 ms intervals as they would be recorded by a high-speed video camera operating at 1000 frames s⁻¹, like those reported in fig. 3B of Burrows and Morris (Burrows and Morris, 2001). A significant unfurling of the SLP would first be detected 2 ms after start of the jump when photographed at 1000 frames s⁻¹ (Fig. 8A,B, broken line i), when the FT rotation has reached 38.1 deg.

Fig. 8.

Semi-lunar process (SLP) movement and torque during a kick. Prior to the kick, the tibia was flexed, the extensor tension was 15 N, SLP torque was −4.7 mN m⁻¹, and the SLP strain was nearly 4.5 mm. (A) The femur–tibia (FT) joint rotated with a maximum velocity of 63 deg. m s⁻¹ and reached full extension of 160 deg. in 4 ms (broken gray line, right axis). The SLP strain decreased quickly during the kick (black line, left axis). The filled black squares represent the SLP positions at 1 ms time intervals when a high-speed camera at 1000 frames s⁻¹ would take images [compare with fig. 3B of Burrows and Morris (Burrows and Morris, 2001)]. The beginning of the kick is shown with the broken vertical line (i). The first point where a noticeable decrease in the SLP would be visible at 1000 frames s⁻¹ is shown with the broken vertical line (iii), which corresponds to a FT rotation of 38.12 deg. (B) SLP torque around the extensor attachment point (black line, left axis) was initially negative, which helped to maintain leg flexion. Significant SLP movement and leg extension occurred after the torque became positive, at broken vertical line (ii). (C) Negative SLP torque occurred when the force applied by the SLP caused torques that retarded tibia rotation (i), while positive torque enhanced tibia rotation. Positive torque only occurred after the leg had rotated enough to move the extensor attachment point to the opposite side of the SLP force vector (iii). Light gray hinge joint is the position of the FT joint at that time, while the black hinge is the position of the FT joint at the beginning of the kick. Figures in part C are for illustrative purposes only and are not drawn to scale.

To understand what caused this delay it is useful to look at the SLP torque generated by the SLP force relative to the extensor attachment (Fig. 8B). The force of the SLP is applied at the FT joint, and so produced no direct torque around that joint, but it did produce a torque on the tibia around the extensor attachment. The SLP torque has a dual role: it acts to keep the leg flexed until leg extension begins, when it changes sign and accelerates leg extension. This sign reversal results from changes in the configuration of the FT joint during leg extension (Fig. 8; Movie 1 in supplementary material). The time needed for the sign reversal accounts for the delay.

The change in the sign of the SLP torque resulted from the change in position of the extensor attachment relative to the SLP force vector. At the beginning of the kick, with the tibia still flexed, the SLP force vector was directed above the extensor attachment, and so the SLP torque was negative, and acted to keep the leg flexed (Fig. 8B,Ci). Moreover, the tension in the extensor apodeme kept the SLP strained. When the negative torque produced by the flexor muscle on the FT joint was removed by inhibition, the positive torque exerted by the extensor muscle on the FT joint began to extend the leg. Both the initial rotation of the leg and the shortening of the extensor apodeme reduced the force applied to the SLP, which began to reduce its strain (Fig. 8A, between i and ii). The extensor attachment was pulled through the SLP force vector, causing the negative (flexion) SLP torque to decrease and change to a positive (extension) torque (Fig. 8C ii and iii). At the time of this cross-over (Fig. 8A, broken line ii), the strain in the SLP had decreased by less than 10%. After the SLP torque became positive, it enhanced the femoral–tibia joint rotation, and the extensor tension could no longer maintain the SLP strain, which then rapidly decreased (Fig. 8Aiii–Ciii).

The negative SLP torque at the beginning of the jump assists the flexor muscle in maintaining the flexed position of the tibia. To determine the amount of assistance provided by the SLP, we compared the amount of flexor tension required to keep the leg flexed when the SLP spring was intact and when it was disabled. With the SLP spring intact, the flexor muscle held the tibia fully flexed until the flexor tension dropped to 0.26 N. When the SLP spring was disabled, the minimum flexor tension required to keep the leg from extending was 0.56 N. When the SLP spring was present it required 54% less tension in the flexor muscle to keep the leg from extending when the tibia lock was not active.

DISCUSSION

Motor program and jumping

The neural control and biomechanics of locust kicking have been well described because the kick can be evoked while the locust is dissected and restrained; thus, allowing simultaneous muscle electromyograms (EMGs) and intracellular recordings from central neurons. Although it is currently not possible to make these recordings in a jumping locust, the similarities between the kick and jump have led to the assumption that the same motor program may produce both behaviors. A computational neuromechanical model of the locust has allowed us to determine whether the neural circuit, the motor program and the biomechanical configuration of the locust legs are sufficient to account for the jump as well as the kick. Our results demonstrate that the kick motor program is capable of reproducing the full range of jump behaviors that have been described in the literature, and that the control of the key variable of extensor tension gives the locust the ability to alter important jump characteristics like jump distance and take-off velocity. Furthermore, we were also able to verify that the jump energy and take-off angle are good predictors of the final jump distance when the locust takes off with minimal tumbling. These results strongly support the hypothesis that the kick motor program is used for both kicking and jumping.

Role of the SLP

The jump is an important behavior of locusts for both locomotion and escape from predators. The SLP is an evolutionary adaptation that has been thought to allow locusts to jump significantly farther than they could without it. However, because of the biomechanics of the metathoracic FT joint, direct tests of the effects of the SLP on jump performance of live locusts are difficult or impossible. The neuromechanical model of a locust presented here has allowed us to identify the contributions that the SLP makes to the jump. The simulations indicate that the SLP can help keep the leg flexed until the rotation of the tibia changes the sign of the SLP torque to favor extension. The SLP then approximately doubles the power of the jump.

The primary role of the flexor muscle of the metathorcic leg during jumping and kicking is to keep the tibia in a fully flexed position while co-contraction is occurring. The flexor muscle must be big enough to carry out this role but any excess volume devoted to the flexor muscle is wasteful and that volume would be better used by the extensor muscle to provide more power for the jump. We found that the SLP helps to maintain leg flexion during co-contraction, and so provides flexion torque that the flexor muscle would otherwise have to provide. When the SLP spring was disabled, any flexion torque that it generated was removed, and 54% more flexor tension was required to keep the tibia from extending. We suggest that the presence of the SLP enables the flexor muscle to be smaller than would be otherwise necessary, and that the savings in tibial volume may permit a relatively larger extensor muscle and more powerful jump.

High-speed video of locust kicking has shown that unfurling of the SLP is delayed until after the tibia had rotated by greater than 30 deg. (Burrows and Morris, 2001). The locust model helps to explain why there is such a delay in unfurling the SLP, and how this affects the jump abilities of locust. As shown in Fig. 8, the delay appears to depend on the movement of the extensor tibiae attachment point through the SLP force vector during the initial period of leg extension, changing an SLP torque that produced flexion to one that promotes leg extension. Finally, the simulations show that the SLP enables the locust to jump more than 45% farther than without it, depending on the force applied by the extensor tibia.

Storing energy by cuticle deformation or strain in apodemes are common methods of overcoming the limitations of skeletal muscle that are required for arthropods to make quick movements like jumping and snapping (Gronenberg, 1996). Some of these animals have evolved elaborate specializations to allow them to perform these rapid movements. The rabbit flea Spilopsyllus cuniculus stores energy for its jump in a resilin pad in the internal skeleton of its thorax but is released when the force vector passes over the leg joint and is redirected from leg flexion to leg extension, like the locust SLP (Bennet-Clark and Lucey, 1967). The froghopper Philaenus spumarius stores energy for the jump by bending a bow-like cuticle formation in the pleural arch. A friction-locking system prevents the legs from moving until tension in the depressors exceeds the holding force of the lock (Burrows, 2003; Burrows, 2006; Burrows et al., 2008). Both the trap-jaw ant Odontomachus bauri and the snapping shrimp Alpheus californiensis store energy for the rapid closing of their mandible or claw in the apodeme of the muscle and by deformation of the cuticle of the exoskeleton (Gronenberg, 1995a; Gronenberg, 1995b; Ritzmann, 1973). The shrimp Alpheus heterochelis has a mechanism similar to the flea where the locking of the closer occurs when the force vector is brought above the pivot point, and release occurs when an accessory closer muscle pulls it back down to generate a large closing torque (Ritzmann, 1974).

While all of these mechanisms are similar, there is a difference that appears to be unique to the SLP mechanism of the locust. Energy from the jump primarily comes from the apodeme of the extensor and the SLP. In the locust the SLP and apodeme produce forces that act at different sites and in different directions, and this is a key feature for causing the delay in unfurling the SLP. The energy storage mechanisms used by the flea (Bennet-Clark and Lucey, 1967) and the shrimp (Ritzmann, 1974) both have similarities and differences with the system described here. They are similar in that the movement of the force vector causes a reversal in the direction of a torque. In the shrimp this occurs when the closer muscle is pulled from one side of the joint to the other. In the locust this happens when the extensor apodeme is pulled through the SLP force vector. The difference is because the shrimp and flea use a small accessory muscle to pull the main contractile muscle over a joint, whereas in the locust it is the biomechanics of the movement of the joint that causes the SLP torque reversal.

Conclusion

This work demonstrates the utility of neuromechanical simulation for analysis of the interaction of neural mechanisms of control with biomechanical processes that mediate and constrain the animal's movement. Neuromechanical simulation enables the operation of neural circuits that have been described in dissected, restrained and anesthetized animals to be understood in something like their natural context, where the consequences of their activity for movement become readily apparent.

One area of future study that these simulations identified is the role of tumbling during the jump. The take-off angle can be controlled by the orientation of the rear legs (Sutton and Burrows, 2008). We have noted in simulations that a change in orientation can produce a take-off angle where the thrust vector is not aligned with the locust's COM. On those occasions, the locust displayed tumbling behavior during the jump that was qualitatively different from that of live animals jumping with similar take-off angles. We believe that locusts may have several mechanisms for preventing unwanted tumbling at different take-off angles, including the setting the initial body elevation, changing the body posture during take-off and controlling the transfer of momentum between the legs and body. The locust model may prove useful in studying those mechanisms and their importance.

A second area is the role of reafference in the control of the jump. The direction and distance of a jump are controlled by the initial posture of the animal and the tension in the extensor tendon (Santer et al., 2005; Sutton and Burrows, 2008). Several sets of proprioceptors that provide sensory information useful for this control have been identified, and the roles that some play during kicking have been described (Burrows and Pfluger, 1988; Heitler, 1977; Heitler, 1995). However, it is unclear how the reafferent responses or their uses might be modified for jumping, when both the load conditions and the constraints imposed by the initial setup are different. Given the great difficulties in addressing these questions experimentally, simulations of reafferent responses under the closed-loop conditions that lead to the jump may prove helpful.