FR3D: finding local and composite recurrent structural motifs in RNA 3D structures

Abstract

New methods are described for finding recurrent three-dimensional (3D) motifs in RNA atomic-resolution structures. Recurrent RNA 3D motifs are sets of RNA nucleotides with similar spatial arrangements. They can be local or composite. Local motifs comprise nucleotides that occur in the same hairpin or internal loop. Composite motifs comprise nucleotides belonging to three or more different RNA strand segments or molecules. We use a base-centered approach to construct efficient, yet exhaustive search procedures using geometric, symbolic, or mixed representations of RNA structure that we implement in a suite of MATLAB programs, “Find RNA 3D” (FR3D). The first modules of FR3D preprocess structure files to classify base-pair and -stacking interactions. Each base is represented geometrically by the position of its glycosidic nitrogen in 3D space and by the rotation matrix that describes its orientation with respect to a common frame. Base-pairing and base-stacking interactions are calculated from the base geometries and are represented symbolically according to the Leontis/Westhof basepairing classification, extended to include base-stacking. These data are stored and used to organize motif searches. For geometric searches, the user supplies the 3D structure of a query motif which FR3D uses to find and score geometrically similar candidate motifs, without regard to the sequential position of their nucleotides in the RNA chain or the identity of their bases. To score and rank candidate motifs, FR3D calculates a geometric discrepancy by rigidly rotating candidates to align optimally with the query motif and then comparing the relative orientations of the corresponding bases in the query and candidate motifs. Given the growing size of the RNA structure database, it is impossible to explicitly compute the discrepancy for all conceivable candidate motifs, even for motifs with less than ten nucleotides. The screening algorithm that we describe finds all candidate motifs whose geometric discrepancy with respect to the query motif falls below a user-specified cutoff discrepancy. This technique can be applied to RMSD searches. Candidate motifs identified geometrically may be further screened symbolically to identify those that contain particular basepair types or base-stacking arrangements or that conform to sequence continuity or nucleotide identity constraints. Purely symbolic searches for motifs containing user-defined sequence, continuity and interaction constraints have also been implemented. We demonstrate that FR3D finds all occurrences, both local and composite and with nucleotide substitutions, of sarcin/ricin and kink-turn motifs in the 23S and 5S ribosomal RNA 3D structures of the H. marismortui 50S ribosomal subunit and assigns the lowest discrepancy scores to bona fide examples of these motifs. The search algorithms have been optimized for speed to allow users to search the non-redundant RNA 3D structure database on a personal computer in a matter of minutes.

1 Introduction

The database of atomic-resolution RNA 3D structures is growing rapidly [6,7,11,21] and now includes ribozymes [1,14,25], ribosomal subunits [3,16,44] and intact 70S ribosomes [42]. The number, size, and complexity of these structures make manual analyses to find and classify recurrent RNA 3D motifs difficult and time-consuming. Systematic and exhaustive RNA motif identification and classification is crucial for integration of RNA structural and sequence data. As new experimental structures become available they must be systematically searched for new motifs as well as for new examples of known motifs. Data integration will make possible more powerful RNA sequence searching in genomes, more accurate alignment of homologous RNA sequences and more realistic modeling of RNA 3D structures, and will thus increase knowledge of RNA structure, function and evolution [28].

RNA molecules form compact 3D structures by hierarchical folding of the RNA chain. RNA secondary structure comprises the double helices made of contiguous Watson–Crick basepairs, which contribute most of the free energy of stabilization and serve as structurally well-defined struts connecting the other elements of the 3D structure. These elements appear in RNA secondary structures as single-stranded hairpin, internal, and multi-helix (junction) “loops,” but in fact most of their nucleotides form non-Watson–Crick basepairs that stack in characteristic ways to form modular motifs. RNA bases can pair in 12 geometrically distinct ways, depending on which of their three edges interact (Watson–Crick, Hoogsteen, or Sugar) and the relative orientations of their glycosidic bonds (cis or trans) [32]. The Watson–Crick basepairs belong to the cis Watson–Crick/Watson–Crick geometric family. The Watson–Crick edges of bases forming non-Watson–Crick basepairs are available to form tertiary interactions that stabilize the compact folding of the biologically active structures of RNA molecules. In addition, unpaired bases extruded from motifs may intercalate to form tertiary basepairs or stacking interactions that also stabilize tertiary interactions with other RNA regions, distant in the secondary structure.

RNA motifs are called recurrent when they occur independently in different, non-homologous places of the same or different RNA molecules while sharing a similar 3D structure. Many of the motifs composing hairpin, internal and junction “loops” and the RNA tertiary interactions they form recur in RNA 3D structure and so a general approach to 3D motif searching must handle all these cases. Recurrent motifs usually share a core of base-paired and -stacked nucleotides arranged in the same way while differing from each other in the identity of the nucleotides forming each basepair and the number of unpaired bases bulged out or extruded from the motif. By comparing all available examples of recurrent motifs, we can better understand the natural variability within each motif family.

Recurrent motifs can be local or composite. Local motifs are composed of nucleotides that belong to the same hairpin (terminal) or internal loop. Terminal loops occur at the ends of individual helices while internal loops are flanked by two helices. Composite motifs are composed of nucleotides from disparate and discontinuous stretches of polynucleotide sequence. The same recurrent motif can occur in local and composite versions. For example, composite instances of sarcin motifs [31] and kink-turn motifs [34] have been identified in the structures of the 5S, 16S, and 23S ribosomal RNAs (rRNA). The internal loop in Helix 95 of 23S rRNA is a local example of the sarcin/ricin motif. A composite version of this motif occurs in the multi-helix junction in Domain 2 of 23S rRNA (Helices 35, 37, 39, 40 and 45) [31]. Composite motifs are easy to overlook in visual analyses and are generally missed by computational approaches that analyze the conformations of successive nucleotides in the RNA chain [18,43]. Thus, none of the composite kink-turn motifs were identified in the original paper [26]. Recurrent motifs play similar roles in different RNA molecules or domains. Some play architectural roles, for example forming bends, kinks or branch points, while others serve as anchors for tertiary interactions that compact and stabilize the folded 3D structure of the molecule [12]. Still others mediate RNA–protein or RNA–ligand inter-molecular interactions.

A variety of approaches for motif search and classification have been reported and recently reviewed [29,33]. Yang et al. introduced three programs, BPViewer, RNA-View, and RNAMLView, to aid in the classification and visualization of RNA structure [45]. These programs automatically produce 2D symbolic representations of RNA 3D structures that can then be searched manually for recurrent motifs. BPViewer provides a web interface for displaying three-dimensional coordinates of base pairs. A web server, RNAview, automatically identifies and classifies the base pairs in an RNA 3D structure. RNAView produces secondary structure (2D) diagrams annotated with symbols representing each type of non-Watson-Crick basepair and stores them in Postscript, VRML or RNAML formats. The application RNAMLview can be used to rearrange various parts of the RNAView 2D diagram to generate a standard representation (like the cloverleaf structure of tRNAs) or any layout desired by the user. The application S2S integrates the 2D and 3D representations of an RNA molecule with sequence alignments of homologous sequences [24].

Several different representations of RNA backbone conformations have been introduced to search for, analyze, and classify recurrent RNA 3D conformations [9,10,18,37,38,41,43]. In general, backbone search methods are relatively fast and can be automated to find new recurrent motifs [43]. However, such methods have limitations when searching for composite motifs or recurrent tertiary interactions. Backbone search also has difficulty assessing the similarity of motifs that differ due to inserted nucleotides in some of the motifs [23].

Huang et al. 2004 used a purely geometric approach to find and classify all four-nucleotide (tetraloop) hairpin motifs [23]. They calculate the geometric distance between two RNA fragments of the same length, superposed in 3D space, using an RMSD metric that employs 15 atoms per nucleotide, including 3 atoms in each base. The metric was applied to cluster hairpin tetraloops using UPGMA. This algorithm also compares continuous chain segments.

Major and co-workers pioneered the combined geometric and symbolic approach to analyze RNA 3D structure [13,36]. Their program MC-Annotate uses 4 × 4 homogeneous transformation matrices (HTM) to calculate the relative positions and orientations of pairs of bases in an RNA structure. By separating the translational and rotational components of the HTM they calculate a distance measure between pairs of bases that corresponds to our pairwise geometric discrepancy (see below). They use HTMs to reduce RNA structures to graphs in which each nucleotide is a node and interacting bases in the structure are connected by edges labeled by the pairwise distance measure. To find 3D motifs, they use subgraph isomorphism algorithms. This has been implemented in the program MC-Search. [20,35,39]. Note that symbolic search methods depend on consistent and precise coding of all pairwise base-base interactions. Symbolic searches cannot find motifs comprising interactions that have not already been defined and found in 3D structures during the preprocessing of structure files.

Harrison and co-workers also apply subgraph isomorphisms to search for motifs in graphs representing RNA 3D structure [17], using methods that were first developed for substructure searching libraries of small molecule structures and then applied to proteins, carbohydrates, and most recently, RNA [4]. For RNA structure searching, each base is represented by two vectors and the whole RNA structure as a labeled graph so the search problem is reduced to finding subgraph isomorphisms representing query motifs in graphs representing RNA 3D structures. This approach was applied to search for non-Watson–Crick basepairs and other small motifs in RNA structures [17]. As the Ullman algorithm used for subgraph searching scales with n factorial (n!), where n is the number of nodes in the query motif (subgraph), it is not clear how practical this approach will be for searching larger motifs representing entire hairpin or internal loops.

Recently a new computational method appeared, Alignment of RNA Tertiary Structures (ARTS), which compares and aligns pairs of 3D nucleic acid structures (RNAs or DNAs) to identify common substructures. Each nucleotide is represented by the position of its phosphate group. The program seeks the rigid transformation of one structure onto another that superimposes the largest number of phosphate groups of one structure onto the phosphate groups of the second structure, within a specified distance error [8]. ARTS can also be used to discover new motifs.

For comparison with these papers, we note that our approach is base centered. For searching, each base is represented by a single “center” point, so that we may treat base substitutions with no difficulty, and the RMS deviation of centers is a component of our measurement of discrepancy between a candidate motif and the query motif. We derive an inequality that allows us to reject candidates whose discrepancy with the query motif will be large, based on pairwise distances between centers. This leads us to a screening algorithm that bears some resemblance to subgraph isomorphism, but which differs in important ways. In particular, it is possible to incorporate symbolic criteria at the screening stage. With or without symbolic criteria, the screening algorithm runs quickly in most searches.

2 Materials and methods

The sample searches and performance trials were run on a Dell Optiplex GX280 with two Intel Pentium 4 processors running at 3.4 GHz and with 1 GB of RAM. We used MATLAB version 7.1.0.246 (R14) Service Pack 3 for program development, Canvas 8 was used for annotations of motifs, and Microsoft Excel was used for tables. Structure files were obtained in Protein Data Bank (PDB) format from the Protein Data Bank (http://www.rcsb.org/pdb/Welcome.do) [5].

3 Results

3.1 Overview of discrepancy-based geometric motif search

The goal of RNA 3D motif searching is to find and rank candidate motifs according to how closely they resemble the structure of the query motif. An objective numerical measure to compare the structures of motifs is therefore needed. This measure must maintain a delicate balance: it must be simple enough to compute or approximate quickly, while able to discriminate meaningfully between candidate motifs. We define an entirely geometric measure that we call the geometric discrepancy that takes into account the general shape of the candidate motif and the orientations of its bases. First, we determine the shift vector and rotation matrix which map the geometric centers of the bases of each candidate motif onto the corresponding base centers in the query motif with the smallest error, called the fitting error. After the rigid body operations are performed, we compute the angles of rotation needed to align each base of the candidate with the corresponding base of the query motif. The square root of the sum of the squares (RMS sum) of these angles (in radians) is called the orientation error. The geometric discrepancy is defined to be the RMS sum of the fitting and orientation errors, divided by the number of bases in the query motif. The mathematical details regarding the discrepancy are given in Sect. 3.4 below. The mathematical formula for the discrepancy for motifs with three or more nucleotides is given in Eq. (3).

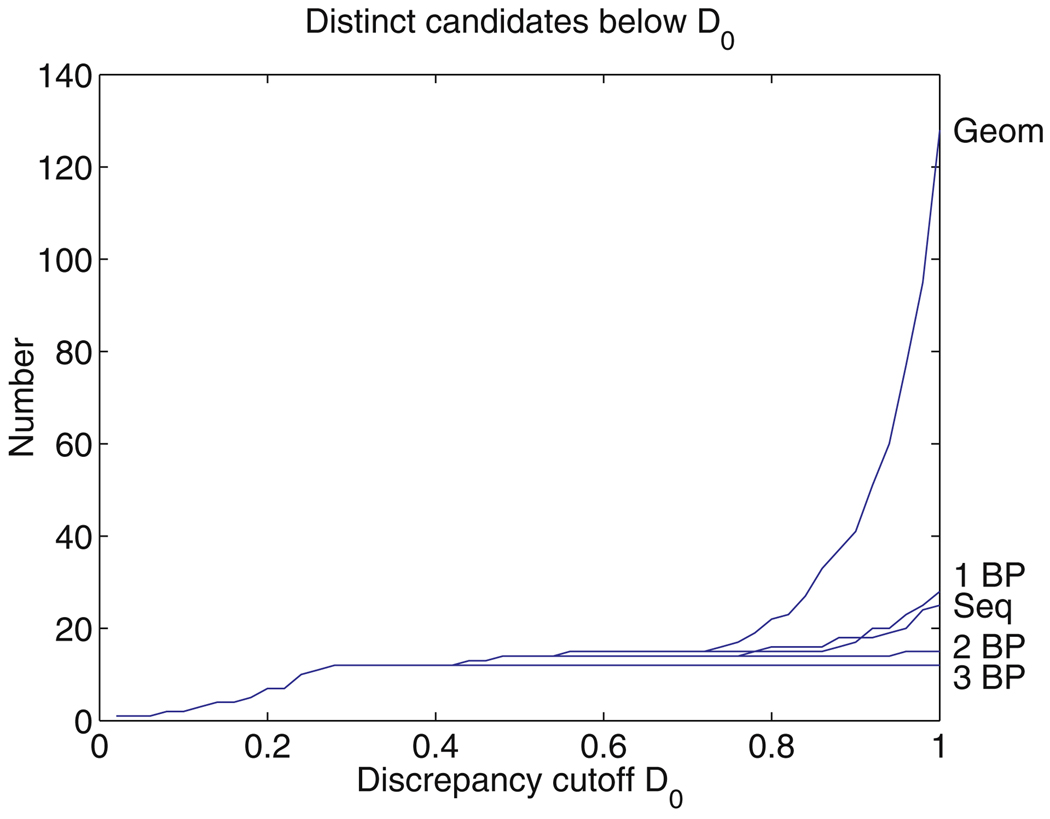
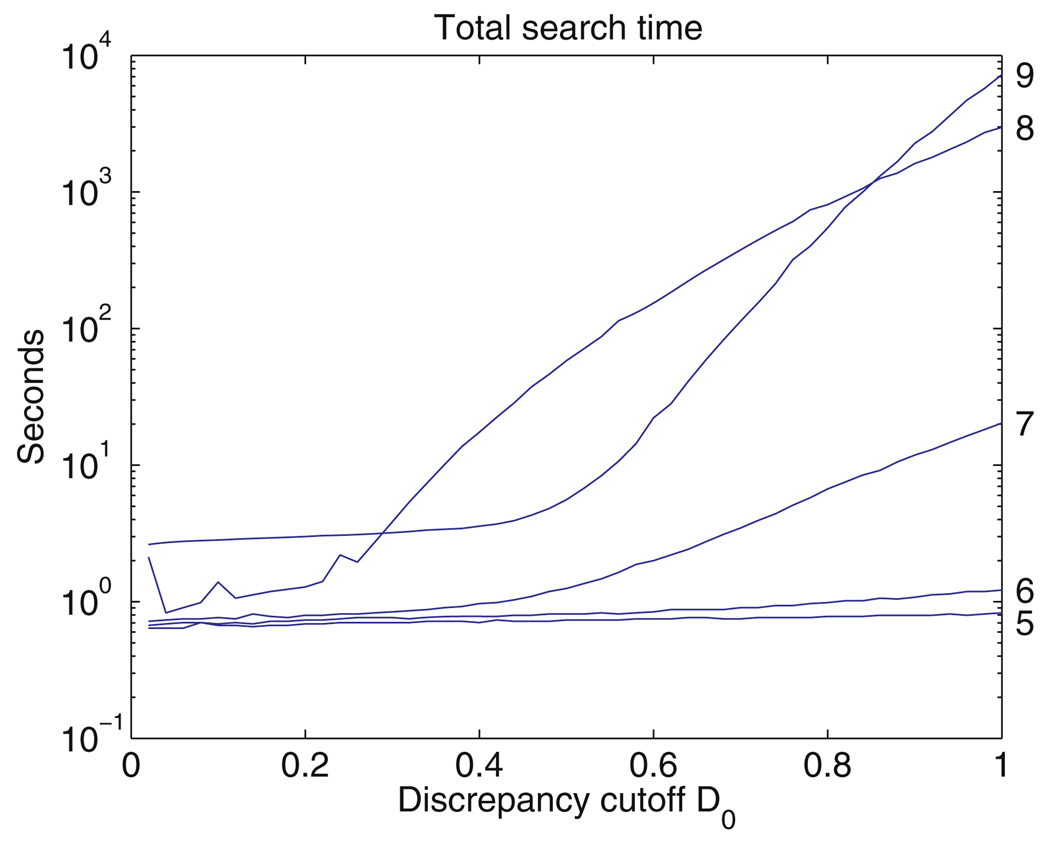
Given an RNA structure containing n nucleotides and a query motif consisting of m nucleotides, the number of candidate sets of nucleotides is roughly n^m. Unless n and m are both small, there are simply too many candidates to allow the computation of each discrepancy in order to rank all candidates. We have developed an algorithm to quickly screen out high discrepancy candidates with minimal computation. The user sets a cutoff discrepancy D₀, and the algorithm returns all candidate motifs in the RNA structures with discrepancy below this cutoff. For a query motif having four nucleotides, the screening process works this way: Each of the six distances between pairs of base centers are calculated for each conceivable candidate motif in a 3D structure file and are compared to the corresponding six distances in the query motif. If any of the six distances in a candidate is too far above or below the corresponding distance in the query motif, that candidate is rejected immediately, using an inequality that we derive below [Eq. (9)]. A reasonable cutoff discrepancy will typically leave fewer than 100,000 candidates at this stage; see Sect. 5. Further screening can be done by adding the squares of the six differences in distances; the inequality we derive shows that if this number is too large, the discrepancy will exceed the cutoff discrepancy, and the candidate will be rejected without further computation. This typically rejects 30 to 90% of the remaining candidates. In general, for a query motif with m nucleotides, there are m(m − 1)/2 distances that can be used for screening, and the process is similar. Only at this point, after the initial screening is completed, is it necessary to compute the shift vector, rotation matrix, and angles of rotation to determine the full geometric discrepancy between the remaining candidates and the query motif.

3.2 Operation of FR3D

FR3D is a suite of Matlab programs that implement the geometric search algorithm described above and provide additional features. The inputs include a query motif in the form of a list of m nucleotides from a particular RNA 3D structure file, a set of RNA 3D structure files to search, and a cutoff discrepancy D₀. The output is a list of candidate motifs from these structure files, sorted according to the geometric discrepancy between the candidate and query motifs. The m nucleotides of each candidate motif are listed in the order of the corresponding nucleotides in the query motif. Additional modules display the candidate motifs geometrically, indicate the basepairs and stacking in the motif, and perform other analyses. The programs are available at http://rna.bgsu.edu/FR3D.

Symbolic constraints can be used in FR3D to focus the search and reduce search time. The user can specify the types of basepairing (according to the Leontis/Westhof classification) or base stacking interactions between given nucleotides, to screen out candidates lacking these interactions. The user can specify upper (or lower) limits on the differences between nucleotide numbers to find (or exclude) motifs consisting of segments of sequential nucleotides. This makes searches for local motifs confined to hairpin or internal loops very fast. In addition, the user can choose to screen candidates using identity constraints (nucleotide masks) that implement abbreviations corresponding to each possible subset of the four nucleotides. Thus one can search with the sequence mask GNRA, where N = {ACGU} and R = {AG}. A complete list of these symbols is found at http://www.chem.qmul.ac.uk/iubmb/misc/naseq.html#300. Finally, one can specify what pairs of bases are to be allowed so that, for instance, only candidates with a GC or CG pair are kept.

In fact, if desired, one can use FR3D to search using only symbolic constraints, without the 3D coordinates of a query motif, by specifying the pairwise relations between its nucleotides and any sequence continuity or identity constraints. For example, one can search for Watson–Crick helices of a given length by specifying that candidate motifs consist of two equal length sequence segments forming complementary cis Watson–Crick basepairs in an anti-parallel sense with each base stacked on its immediate neighbors in the sequence. As another example, one can use symbolic search to find all motifs in which a cis Watson–Crick basepair stacks on a trans Hoogsteen/Sugar Edge (sheared) basepair.

3.3 Preparatory analysis

The FR3D program suite includes routines that read and analyze RNA 3D structure files. The results of the preparatory analysis for each structure file are automatically saved and used by subsequent modules that execute motif searches. The analysis routines read the locations of the heavy atoms of the base and backbone of each nucleotide, ignoring hydrogen atoms, if present. For each base, the Cartesian coordinates of its atoms are reduced to two descriptive geometric quantities: the geometric center of the base, which is the unweighted average of the positions of the heavy base atoms, and a 3 × 3 rotation matrix giving the orientation of the base in 3D space relative to a reference orientation.

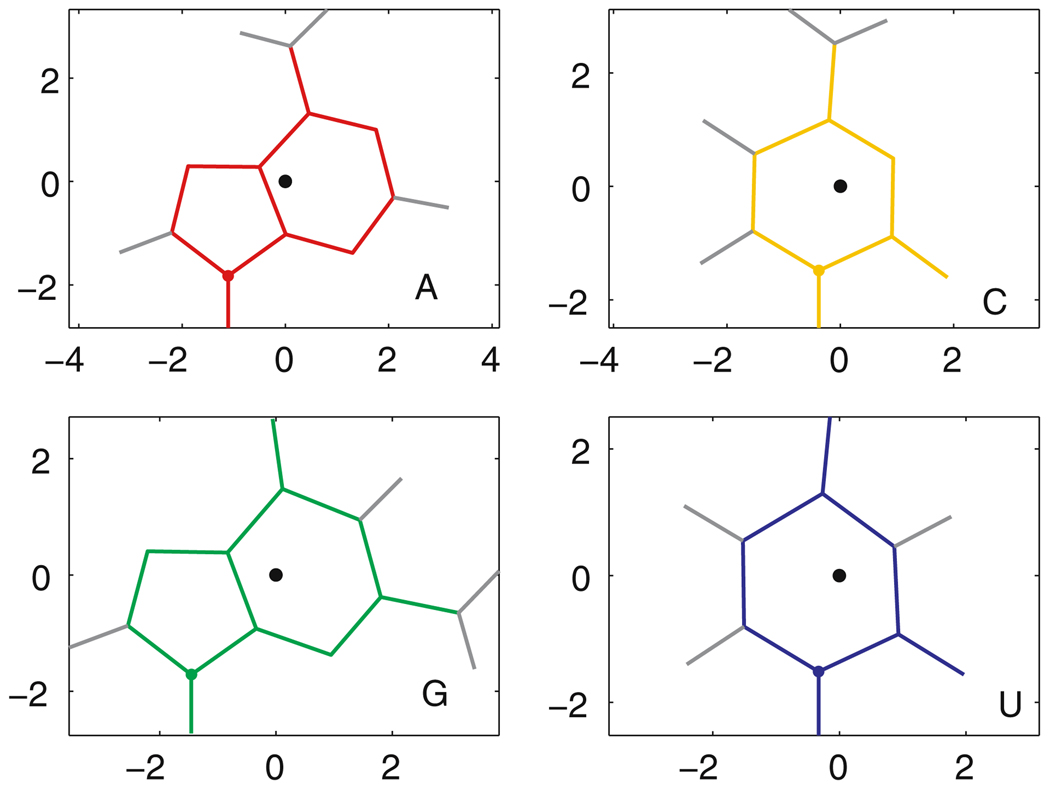
The rotation matrix is obtained as follows. Reference bases are centered at the origin of a 3D coordinate system, lying in the xy plane with the glycosidic bond parallel to the y axis and the Watson–Crick edge at the upper right. Their atom locations are taken from quantum mechanical calculations by [19] that give optimized geometries for each of the RNA bases. In Fig. 1, the reference bases are shown with the hydrogen atoms (to aid in visualization) and with their geometric centers at the origin. For each nucleotide in the 3D structure, we find the translation vector and rotation matrix which optimally and rigidly move the heavy base atoms of the corresponding reference base onto the observed locations of the base atoms of the nucleotide, according to the least-squares criterion and technique of [22], as detailed in Appendix A, with comments on how to improve its numerical stability. The fitting error is typically very small. In this way, each base in the experimental structure is replaced by an optimized standard geometry with hydrogen atoms.

Fig. 1.

Reference bases. The geometric center of each base, marked by a black dot, is used as the origin of its local coordinate system. For each base, the 3′ face is shown. Hydrogen atoms are marked with gray lines. The axes are marked in Ångstroms

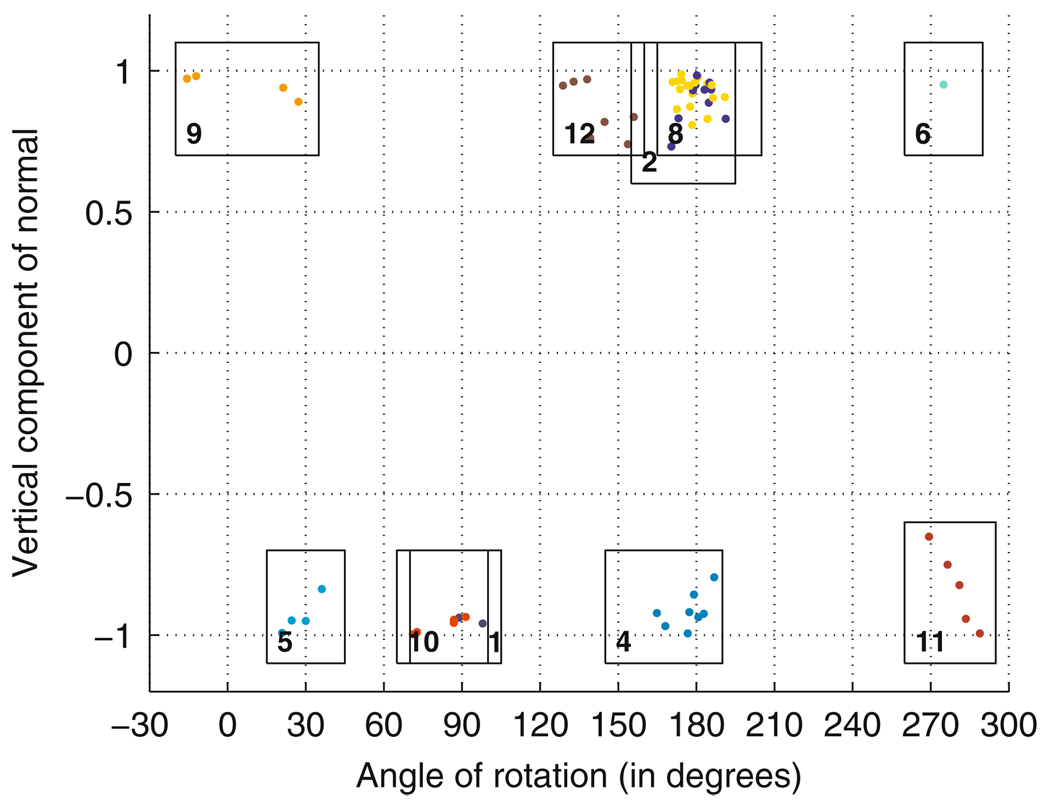
Next, pairs of nucleotides in the structure file that are close enough to interact are identified and their interactions, if any, are classified. Basepairs are classified according to the geometric categories introduced by Leontis and Westhof [32]. We illustrate by describing the classification of AA basepairs. First, we shift and rotate the pair so that the A with lower nucleotide number lies in the xy plane with its glycosidic atom at the origin, as shown in Fig. 2. The second A of each pair is represented by its glycosidic nitrogen, shown for each A as a dot in Fig. 2, and by two additional parameters which describe its orientation, shown in Fig. 3. First, mapping the reference A from Fig. 1 onto the second A gives a sense of the relative orientation of the second A; the unit vector in the positive z direction in the reference frame becomes a normal vector for the second A. We consider the vertical component of this normal vector; as Fig. 3 shows, the normal vector is usually nearly straight up or straight down. Second, we consider the angle of rotation to rotate the reference A to align with the second A; if the normal vector of the second A points downward, we first flip the reference A about the y axis, then rotate. The resulting angle of rotation is displayed in Fig. 3.

Fig. 2.

Relative location in 65 AA basepairs extracted from PDB files 1s72 and 1j5e by the classification module. Each pair is rigidly translated and rotated so that the first A coincides with the A at the origin; the glycosidic nitrogen of the second A is shown as a colored dot. Each of the basepairing categories is colored with a different color. Boxes indicate cutoffs for each category. The axes are marked in Ångstroms

Fig. 3.

Relative orientation of 65 AA basepairs from PDB files 1s72 and 1j5e. The normal vector indicates whether the two A’s share the same or opposite orientation in the plane of the pair. The angle of rotation (in degrees) is measured after the bases have been given the correct orientation. Boxes indicate cutoffs for each category

The dots in Fig. 2 and Fig. 3 represent 65 AA basepairs from the PDB files 1s72 (Haloarcula marismortui (H.m.) 50S ribosomal subunit) and 1j5e (Thermus thermophilus 30S ribosomal subunit) colored according to the 12 basepairing categories of [30]. To be classified into a certain category, the glycosidic nitrogen of the second A must fall inside the specified box in Fig. 2 and the normal vector and angle of rotation must fall inside the corresponding box in Fig. 3. Note that, while boxes 11 and 12 overlap in Fig. 2, they are quite distinct in Fig. 3, so the classification regions, in fact, do not overlap. Categories 11 and 12 are interactions between the Sugar edges of the A’s; but there is a 180 degree flip that distinguishes them. Note that categories 3 and 7 do not occur for AA basepairs. Additional parameters that are used but not shown are the z component of the glycosidic nitrogen of the second A and a parameter that measures the degree to which the interacting edges of the two A’s tilt toward each other or fail to meet. Finally, once a preliminary classification is made, we check the lengths and angles of hydrogen bonds that should be present. Hydrogen bond lengths greater than 4 Ångstroms, or bond angles less than 110 degrees together with interacting edges which fail to meet, are cause for disclassification. Hydrogen bonds involving the H2’ sugar atom are not checked because we generally do not know the location of this atom. If the pair fails to fall into any category, we place the second A at the origin and reclassify. In this way, the classification system is symmetric in the order in which the bases are encountered. For asymmetric pairs, we always place the purine at the origin; for AG pairs, we place the A at the origin.

Base stacking is treated in a similar way. We name the two faces of each base according to their orientation in a regular helix; the side that faces the 3′ end is called the 3′ face, while the other face is called the 5′ face. In Fig. 1, the 3′ face is shown. Two nucleotides are said to be stacked on one another if they lie in roughly parallel planes, with their geometric centers roughly 3 to 4.5 Ångstroms from one another, and with non-zero overlap when the convex hull of each base is projected vertically onto the convex hull of the other. We name the possible base stacking interactions according to which faces of the two nucleotides are interacting. For instance, in a regular helix, both strands have “35” stacking, while cross-strand stacking is typically “55 stacking”. We write, for example, A1 - G2 s35 to indicate that A1 and G2 are stacked on one another with the A using its 3′ face and the G using its 5′ face. We could just as well write G2 - A1 s53.

We note two points of contrast with other basepair classification schemes. First, we do not use the axis system of [2,40], which includes parameters such as buckle, propeller twist, opening, shear, stretch, and stagger. Second, our classifications are absolute, rather than indicating a continuum of degrees of agreement with one category or another [13]. Nonetheless, we obtain lists of basepairs very similar to those obtained with BPViewer and reported on the NDB website: (http://ndbserver.rutgers.edu/services/BPviewer/index.html). Initial classifications were done by expert visual analysis, and cutoffs were set quite strictly, to insure a low false positive rate. Classifications are periodically revised as new 3D structures become available. FR3D can be used to view diagrams such as those in Fig. 2 and Fig. 3.

Implementation details, such as the treatment of modified bases, NMR files, multiple chains, and numbering systems, are addressed in the FR3D documentation.

3.4 Definition of geometric discrepancy D

In this section we describe in detail how we define the geometric discrepancy D between query and candidate motifs of three or more nucleotides. (The discrepancy for motifs comprising only two nucleotides requires separate treatment and is discussed at the end of this section.) We chose this measure to identify and rank candidate motifs similar to a query motif because it is easy to calculate and provides excellent discrimination, as will be shown in Sect. 4.

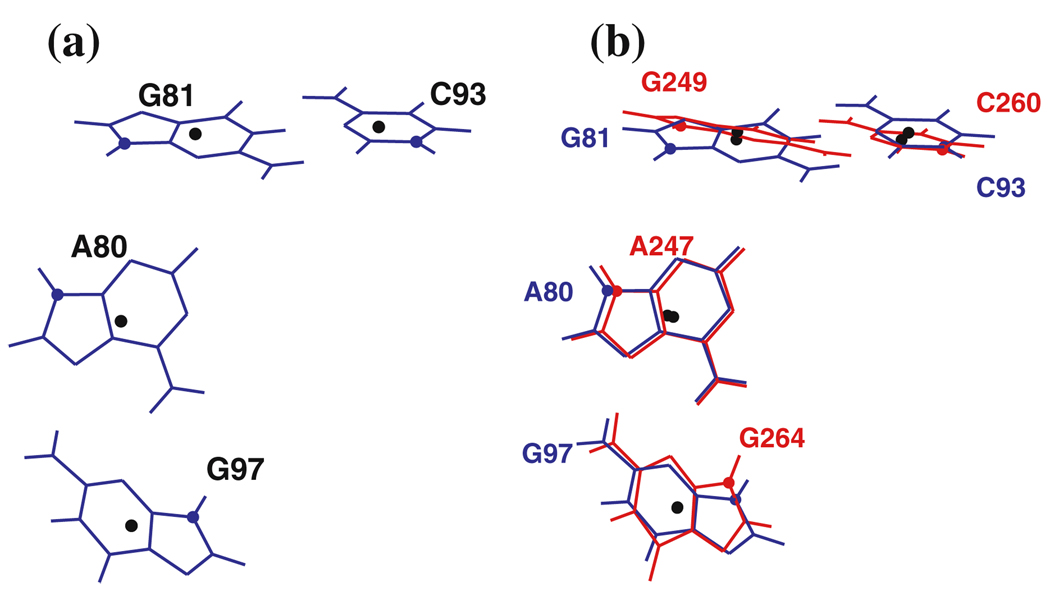
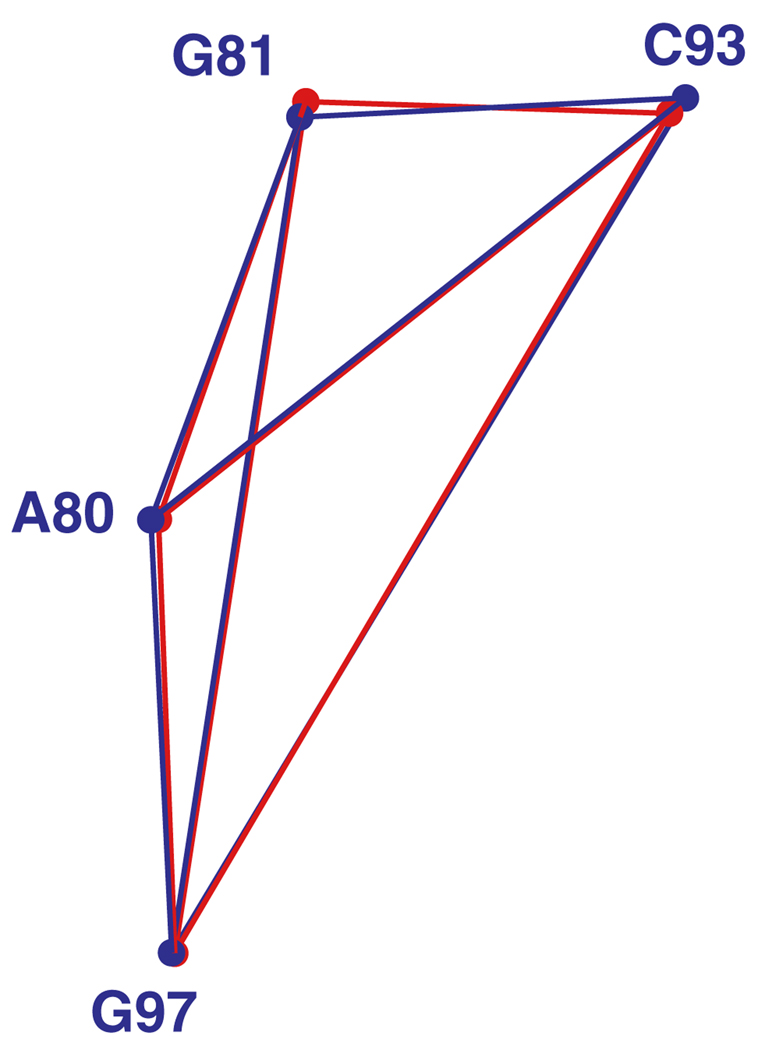
First, we translate and rotate the candidate motif onto the query motif. For nucleotide i of the query motif, i = 1,…, m, let the vector b_i be the geometric center of the heavy base atoms, as in Fig. 1. For example, four bases belonging to the 23S rRNA kink-turn in Helix 7 (Kt-7) are shown in Fig. 4a with the geometric centers marked by black dots. We take this as the query motif.

Fig. 4.

a Query motif, part of the kink-turn in Helix 7 of H. marismortui 23S rRNA (Kt-7, PDB file 1s72). The geometric center of each base is marked by a black dot. b Query motif (blue) with candidate motif (red) superimposed. The candidate motif is from Helix 15 of the same molecule

For the candidate bases, denote the geometric centers by c_i, i = 1,…, m. We seek the translation vector t and 3 × 3 rotation matrix R which are optimal in the sense that they minimize the squared error,

$$L^2=\underset{R}{\text{min}}\underset{t}{\text{min}}{\displaystyle \sum _{i=1}^m{w}_i{\Vert b_i-R(c_i-t)\Vert }^2.}$$ (1)

The minimal value L is called the fitting error. The weights w_i, i = 1,…, m, allow us to fit key bases in a motif more closely than other bases, if desired. We assume that the weights are strictly positive and sum to m. It was shown by [22] how to choose t and R to achieve the minimum in Eq. (1). The procedure is briefly explained in Appendix A. See also [15], Sect. 12.4.1. Fig. 4b shows a candidate motif fitted optimally onto the kink-turn in Fig. 4a. The fitting error, L, is the RMS sum of the distances between corresponding base centers, shown as black dots.

The second contribution to the geometric discrepancy is due to differences in orientation between the corresponding bases of the candidate and the query motifs. Consider base i of each motif. Denote by M_i the rotation matrix taking a base in standard orientation to the orientation of base i in the query motif, and by N_i the rotation matrix for base i of the candidate motif before it is rotated onto the query motif. Once the candidate is rotated onto the query motif by the rotation matrix R, the rotation matrix $M_i{N}_i^{-1}{R}^{-1}$ tells how to rotate base i of the candidate onto base i of the query motif. As the two bases need not be the same, we use standard orientations for all four bases; as in Fig. 1. Denote by α_i the angle of rotation for the rotation matrix $M_i{N}_i^{-1}{R}^{-1}$, in radians. This is a number between 0 and π. We define the orientation error A by

$$A=\sqrt{{\displaystyle \sum _{i=1}^m{v}_i^2{\alpha }_i^2.}}$$ (2)

The weights v_i are nominally 1, but they can be changed to adjust the sensitivity of the search to the orientations of particular bases. Also, they can be raised or lowered as a group to alter the relative weight given to the orientation error compared to the fitting error. In Fig. 4b, one can see that after the base centers are fitted the orientations of corresponding bases are not the same, and some bases happen to be more closely aligned than others. Note that we do not minimize the orientation error, we just measure it using (2).

The geometric discrepancy D is defined by combining the fitting and orientation errors:

$$D=\frac{1}{m}\sqrt{L^2+A^2}$$ (3)

Dividing by m allows us to interpret D as the discrepancy per nucleotide, so it has the same meaning for small and large motifs. The units for L are typically Ångstroms. We can think of A as having units of Ångstroms as well, for the number v_iα_i is the arc-length, in Ångstroms, traveled by an atom located v_i Ångstroms from the axis of rotation when base i of the candidate is rotated to align with base i of the query motif. Increasing v_i increases the distance from the axis of rotation, and so raises the importance of angle α_i in the discrepancy. Thus, combining the fitting error L and the orientation error A into the discrepancy D gives the discrepancy per nucleotide, measured in Ångstroms. We find that typical values of D for a good match to the query motif are in the range 0.2 to 0.6 Ångstroms per nucleotide. When the candidate is identical to the query motif, the discrepancy is, of course, zero, and excellent matches have discrepancy between 0 and 0.2.

It is noteworthy that the numerical value of the geometric discrepancy D is not changed by reversing the roles of the query and the candidate motifs. A proof of the symmetry property for D is provided in Appendix B.

If the query and candidate motifs had the same bases, one could fit the entire candidate motif onto the query motif and use the RMS deviation between atoms to measure the discrepancy between the two motifs. Such a discrepancy measure would have similar qualitative features to our geometric discrepancy. The discrepancy we define has the advantage that it can be used to compare motifs which are not composed of the same bases.

Finally, we note that motifs consisting of only two nucleotides (m = 2) must be evaluated in a different way because, while the candidate can be rotated onto the query motif (so that the candidate base centers lie on the line through the query motif base centers), there is no obvious additional criterion to remove all ambiguity (the candidate can still be rotated freely about the line). Instead, we define the discrepancy between the candidate and the query motif following [13]. First, we rigidly translate and rotate the candidate motif so that its base 1 aligns with base 1 of the query motif. This leaves a distance ℓ₁ between the centers of the second bases, and an angle θ₁ required to rotate base 2 of the candidate to align with base 2 of the query motif. Second, to make the discrepancy symmetric, we move the candidate again so that its second base aligns with the second base of the query motif, then calculate the distance ℓ₂ and angle θ₂ between the first nucleotides. The discrepancy is defined for the special case of two-base motifs by

$$D=\frac{1}{\sqrt{2}}\frac{1}{4}\left(\sqrt{{\ell }_1^2+v^2{\theta }_1^2}+\sqrt{{\ell }_2^2+v^2{\theta }_2^2}\right).$$ (4)

The discrepancy for two nucleotide motifs as defined in (4) is also symmetric with respect to the identification of the query and candidate motif and with respect to the order in which the nucleotides are numbered. We may interpret D to have units of Ångstroms, as explained above. The prefactor 1/4 averages the two contributions to the discrepancy and divides by the number of bases, so again we may interpret D as the discrepancy per nucleotide, in Ångstroms. The prefactor $1/\sqrt{2}$ is for convenience; as defined in Eq. (4) the discrepancy for m = 2 then satisfies inequality (9) below.

3.5 Geometric screening criterion for rapid searching

Given a query motif consisting of m nucleotides and an RNA 3D structure file of n nucleotides, there are nominally n(n − 1)(n − 2) … (n − m + 1), or roughly n^m, candidate motifs. This number is typically so large that it is impossible to examine all candidates in order to rank them according to their geometric discrepancy with the query motif. Therefore, we set a cutoff discrepancy D₀ and seek candidates whose discrepancy with respect to the query motif is below D₀. The key to rapid searching is to eliminate as many candidates with D > D₀ as possible using minimal computation. In this section, we describe the geometric screening criterion for eliminating candidates on the basis of the distances between base centers. The screening algorithm we describe in Sect 3.7 uses this screening method. It runs quickly and is guaranteed to find all candidates whose geometric discrepancy is below D₀. Moreover, it can easily be adapted to generic RMSD (root-mean-square deviation) searches.

For candidate and query motifs to be geometrically similar, the distances between base centers in the candidate must be roughly the same as the corresponding distances in the query motif. For the query motif, we compute an m × m matrix QD for which QD(i, j) is the Euclidean distance between the geometric centers of query motif bases i and j. That is, QD = [‖b_i − b_j‖], where b_i is defined above. This matrix is symmetric and equal to zero on the diagonal. For the four nucleotides of the kink-turn in Helix 7 (Kt-7) of H.m. 23S rRNA shown in Fig. 4a, the QD matrix is:

$$\mathit{\text{QD}}=\begin{array}{cc}\hfill & \begin{array}{cccc}A80\hfill & G81\hfill & C93\hfill & G97\hfill \end{array}\hfill \\ \begin{array}{c}A80\hfill \\ G81\hfill \\ C93\hfill \\ G97\hfill \end{array}\hfill & \left[\begin{array}{cccc}0.0000\hfill & 6.2582\hfill & 9.9930\hfill & 6.2553\hfill \\ 6.2582\hfill & 0.0000\hfill & 5.5964\hfill & 12.0338\hfill \\ 9.9930\hfill & 5.5964\hfill & 0.0000\hfill & 14.2647\hfill \\ 6.2553\hfill & 12.0338\hfill & 14.2647\hfill & 0.0000\hfill \end{array}\right]\hfill \end{array}$$ (5)

We have indicated outside the matrix the corresponding nucleotide numbers of four conserved nucleotides used to define the motif. The six distances we consider are shown in blue in Fig. 5.

Fig. 5.

Base centers and joining line segments for four bases belonging to the query motif from Fig. 4 (in blue) superposed on those of a candidate motif (in red). The geometric centers of the bases are indicated by dots

Consider a candidate motif and its corresponding matrix CD of distances, CD = [‖c_i − c_j‖]. The candidate from the 23S rRNA shown in red in Fig. 4 and Fig. 5 has discrepancy 0.54967 from the query motif. Its matrix CD is given by

$$\mathit{\text{CD}}=\begin{array}{cc}\hfill & \begin{array}{cccc}\hfill A247\hfill & \hfill G249\hfill & \hfill C260\hfill & \hfill G264\hfill \end{array}\hfill \\ \begin{array}{c}A247\hfill \\ G249\hfill \\ C260\hfill \\ G264\hfill \end{array}\hfill & \left[\begin{array}{cccc}\hfill 0.0000\hfill & \hfill 6.4172\hfill & \hfill 9.3606\hfill & \hfill 6.2895\hfill \\ \hfill 6.4172\hfill & \hfill 0.0000\hfill & \hfill 5.7158\hfill & \hfill 12.2578\hfill \\ \hfill 9.3606\hfill & \hfill 5.7158\hfill & \hfill 0.0000\hfill & \hfill 14.0696\hfill \\ \hfill 6.2895\hfill & \hfill 12.2578\hfill & \hfill 14.0696\hfill & \hfill 0.0000\hfill \end{array}\right]\hfill \end{array}$$ (6)

When the candidate matches the query motif exactly, the matrices CD and QD are identical. The more the candidate differs from the query motif, the more CD and QD differ. We measure the differences between the matrices by subtracting them and squaring each component, to obtain a matrix Q of squared distance differences:

$$Q=[(\Vert b_i-b_j\Vert -{\Vert c_i-c_j\Vert )}^2]$$ (7)

For the kink-turn and candidate in Fig. 5, Q is:

$$Q=\left[\begin{array}{cccc}0.0000\hfill & 0.0253\hfill & 0.3998\hfill & 0.0012\hfill \\ 0.0253\hfill & 0.0000\hfill & 0.0143\hfill & 0.0502\hfill \\ 0.3998\hfill & 0.0143\hfill & 0.0000\hfill & 0.0380\hfill \\ 0.0012\hfill & 0.0502\hfill & 0.0380\hfill & 0.0000\hfill \end{array}\right]$$ (8)

In this case all of the entries are fairly small because the candidate matches the query motif fairly well.

The entries of Q are not involved in the definition of the geometric discrepancy, nor are they as precise a geometric measure of the shape of a motif as the fitting error. However, they can be computed quickly because they depend only on pairwise distances. Moreover, in Appendix C we derive inequality (9) which relates the entries of Q to the discrepancy D:

$$D\ge \frac{L}{m}\ge \frac{1}{m}\sqrt{\frac{1}{{\displaystyle {\sum }_{i\in I}{w}_i}}\left({\displaystyle \sum _{\underset{i<j}{i,j\in I}}{w}_i{w}_j{Q}_{ij}}\right).}$$ (9)

In inequality (9), I is a subset of {1, 2,…, m} with two or more elements, meaning that we use only certain nucleotides in the sum, and w_i, i = 1,…, m are the weights used in the definition of the discrepancy.

Inequality (9) says that the larger the entries of Q, the larger the discrepancy between the candidate and the query motif. We use this observation to screen out candidates. Using the cutoff discrepancy D₀, if the squared distance differences in Q are so large that

$${\displaystyle \sum _{\underset{i<j}{i,j\in I}}{w}_i{w}_j{Q}_{ij}>m^2{D}_0^2\left({\displaystyle \sum _{i\in I}{w}_i}\right)},$$ (10)

then D > D₀ and we may reject the candidate. We call this the subset screening criterion. In particular, when I has just two elements, i and j, and Q_ij is so large that

$$Q_{ij}>\frac{m^2{D}_0^2(w_i+w_j)}{w_i{w}_j},$$ (11)

then we may reject the candidate on the basis of this pairwise criterion alone. We call this the pairwise screening criterion. In a candidate with m nucleotides, there are m(m − 1)/2 pairwise distances that can be checked and used for screening. Screening using pairwise distances alone typically reduces the number of candidates from the astronomical n^m to a few hundred thousand or less. The same screening technique could be used in other settings in which RMS deviation alone (represented here by L) is used for the discrepancy.

3.6 Data structures for screening

Well-chosen data structures allow for fast pairwise and subset screening while using minimal memory space. Suppose we wish to search for the query motif in an RNA 3D structure file with n nucleotides. For each p, q = 1,…, n, let C_pq be the Euclidean distance between the geometric centers of nucleotides p and q in the structure. Then C is an n × n matrix of distances. For each pair 1 ≤ i, j ≤ m of nucleotides in the query motif, we construct an n × n matrix S^(ij) as follows:

$$S^{(ij)}(p,q)=w_i{w}_j{(\Vert b_i-b_j\Vert -C_{pq})}^2,p,q=1,\dots ,n.$$ (12)

Entry (p, q) of S^(ij) tells how closely the distance between bases p and q in the structure matches the distance between bases i and j in the query motif. It plays the same role as w_iw_j Q_ij in (11). The entries of S^(ij) are generally greater than zero, but S^(ij)(p, q) = 0 when the distances are exactly the same, which happens when the query motif itself belongs to the structure file being searched. For technical reasons that will become clear below, we replace 0 entries by a suitably small number such as 10⁻¹⁰. Thus, S^(ij) has strictly positive entries.

Note from (11) that if $S^{(ij)}(p,q)>m^2{D}_0^2(w_i+w_j)$, then the pair (p, q) fails to meet the pairwise screening criterion for query motif nucleotides (i, j). This is the case for the vast majority of entries in S^(ij). To save storage space and help with screening, we replace these entries of S^(ij) with zeros:

$$S^{(ij)}(p,q)\leftarrow \{\begin{array}{cc}\hfill S^{(ij)}(p,q),\hfill & \text{if}{S}^{(ij)}(p,q)<m^2{D}_0^2(w_i+w_j)\hfill \\ \hfill 0,\hfill & \text{otherwise}\hfill \end{array}$$ (13)

We also replace the diagonal entries of S^(ij) with zeros to preclude a nucleotide being paired with itself. From a programming standpoint, the matrices S^(ij) are sparse; they are overwhelmingly filled with zeros. From a constructive perspective, those (p, q) pairs for which S^(ij)(p, q) > 0 are nucleotide pairs which match query motif nucleotides (i, j) closely enough that they cannot be rejected on the basis of inequality (11). We say that these pairs satisfy the pairwise constraint.

3.7 Building lists of partial candidates and the screening algorithm

In this section we describe how to construct a relatively short yet inclusive list of m-nucleotide candidate motifs from an RNA structure file. The full geometric discrepancy with the m-nucleotide query motif need only be calculated for these candidates, since these are the only candidates whose discrepancy may be below D₀.

We systematically build up the list of candidates, starting with 2-nucleotide partial candidates which match the first two nucleotides of the query motif, then 3-nucleotide partial candidates which match the first three, and so on, until we have a list of m-nucleotide candidates. When building k-nucleotide partial candidates, we retain only those partial candidates which cannot be rejected on the basis of the pairwise screening criterion (11) for 1 ≤ i < j ≤ k. Thus, we retain partial candidates whose k(k − 1)/2 pairwise distances between bases are close enough to the corresponding distances in the query motif. We say that the partial candidates satisfy the pairwise constraints. Next, we apply the subset screening criterion, Eq. (10), to reject some of these k-nucleotide partial candidates. The ones that remain are said to satisfy the subset screening constraint. Then we build k + 1-nucleotide partial candidates in the same way, and continue until we have candidates with m nucleotides. This procedure retains many candidates with D > D₀, but not so many that it is unwieldy, see Sect. 5. Once we have a list of m-nucleotide candidates, we compute the discrepancy of each with the query motif using Eq. (3) and rank them.

Here are the details. The screening algorithm starts with nucleotides 1 and 2 of the query motif. From S⁽¹²⁾ we obtain a list of (p, q) pairs for which S⁽¹²⁾ (p, q) > 0, and so (p, q) satisfy the pairwise constraint for (1, 2). If m > 2, for each (p, q) pair, we find all possible third nucleotides r for which two additional constraints are met:

$$S^{(13)}(p,q)>0\text{\hspace{1em}and\hspace{1em}}{S}^{(23)}(q,r)>0.$$ (14)

This results in a list of (p, q, r) triples from the RNA 3D structure file which satisfy all pairwise constraints for query motif nucleotides (1, 2, 3). Now we reject some of these partial candidates by applying the subset screening criterion (10) with I = {1, 2, 3}; we reject (p, q, r) triples for which

$$S^{(12)}(p,q)+S^{(13)}(p,r)+S^{(23)}(q,r)>m^2{D}_0^2(w_1+w_2+w_3),$$ (15)

because we can be certain that any m-nucleotide candidate for which (p, q, r) correspond to (1, 2, 3) will have discrepancy greater than D₀.

Generally, if (p₁,…, p_k) is a partial candidate for query motif nucleotides (1,…, k) and m > k, we retain the larger partial candidate (p₁,…, p_k, q) for (1, 2,…, k, k + 1) provided that

$$S^{(i,k+1)}(p_i,q)>0,i=1,2,\dots ,k,$$ (16)

so that all pairwise constraints between the k existing nucleotides and the one new nucleotide are met. We then use the subset screening criterion; we reject those candidates for which:

$$S^{*}+S^{(1,k+1)}(p_1,q)+\cdots +S^{(k,k+1)}(p_k,q)>m^2{D}_0^2(w_i+\cdots +w_{k+1}).$$ (17)

Here S^* is the corresponding sum for (p₁,…, p_k). Thus, when adding the next nucleotide, k pairwise constraints must be checked, and k additional terms must be summed to apply the subset screening criterion.

One could apply the subset screening criterion to every subset of {1, 2,…, k + 1}, but this would be impractical. It works well enough to apply subset screening for subsets of the form {1, 2,…, j}, j ≤ k + 1. Some candidates with large discrepancies will survive the screening process, but not so many that it is worth imposing additional subset screens during this procedure.

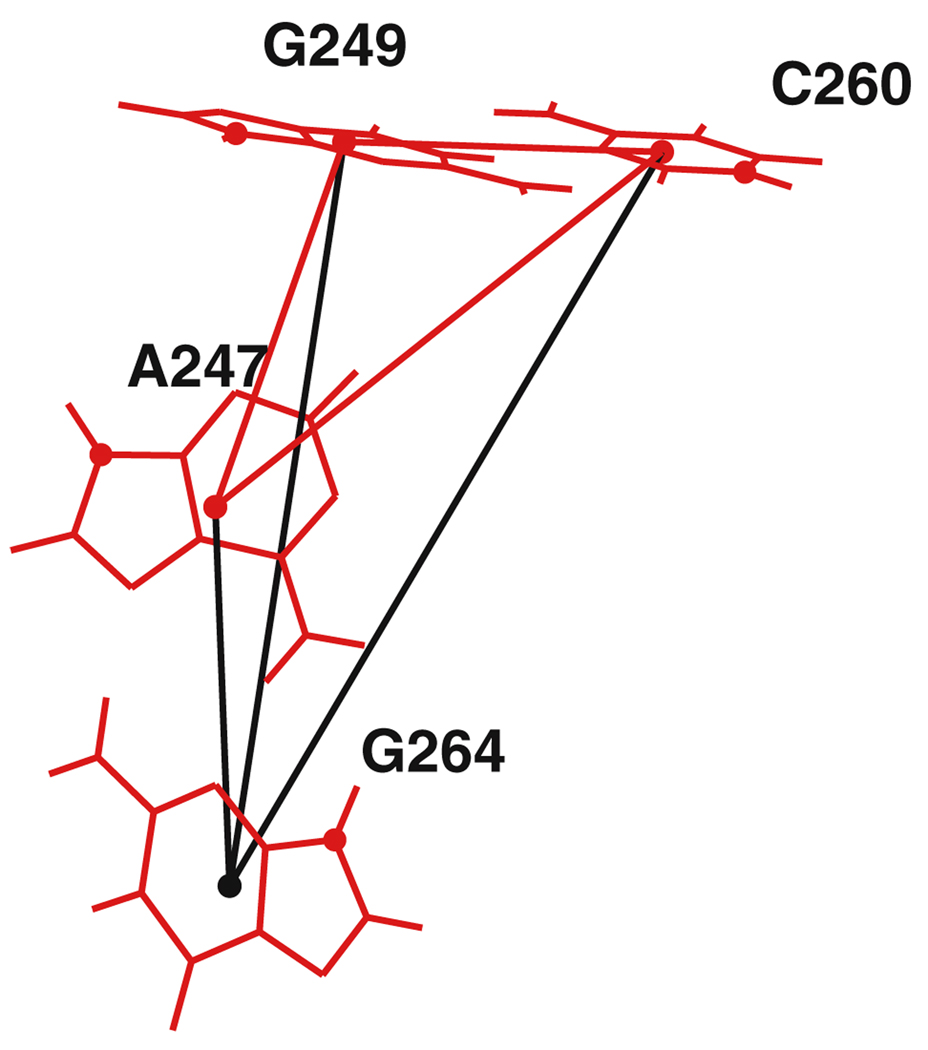
In Fig. 6, we illustrate how the candidate in Fig. 4b is found. First, nucleotides A247, G249, and C260 satisfy the three pairwise constraints on their three mutual pairwise distances (shown in red) to become a partial candidate matching A80, G81, C93. Then, one additional nucleotide is added. In this case, we find that the distances to G264 (shown in black) satisfy three additional pairwise constraints as well as the subset screening constraint, and so A247-G249-C260-G264 becomes a full candidate for the query motif A80-G81-C93-G97.

Fig. 6.

Adding a fourth nucleotide, G264, to a three-nucleotide partial candidate, A247-G249-C260, in the screening algorithm. The black lines indicate the new pair distances checked by the pairwise screening criterion

From a graph-theoretic perspective, the n nucleotides in the structure file can be thought of as vertices, and for each i, j pair with 1 ≤ i < j ≤ m, the non-zero entries of S^(ij) can be thought of as edges between those vertices. This makes for m(m − 1)/2 different edge sets on the same vertices, one for each distinct pair of nucleotides in the query motif. Full m-nucleotide candidates correspond to a set of m numbered vertices in which vertices i and j are connected by an edge from edge set S^(ij). In Sect. 3.10, we will see that symbolic constraints on a pair are imposed by removing edges from the corresponding edge set.

3.8 Exhaustive screening guarantee

Because a candidate whose discrepancy with the query motif is less than or equal to the cutoff discrepancy D₀ will satisfy all pairwise constraints and all subset constraints, it will always be retained in lists of partial candidates and will never be screened out. Thus, the list of candidates returned by the algorithm is guaranteed to include every candidate whose discrepancy with the query motif is less than the user-specified D₀. In practice, the list also contains candidates whose discrepancy with the query motif exceeds D₀, which is expected since the fitting error has not yet been completely calculated, and the orientation error has not been considered at all.

3.9 Implementation of the screening algorithm in FR3D

The order in which the nucleotides of the query motif are specified (i.e., which nucleotide is called number 1, number 2, etc.) affects the running time of the screening algorithm. After we compute the matrices S^(ij), we permute the nucleotides so that S⁽¹²⁾ is the matrix with the smallest number of non-zero entries. We permute the remaining nucleotides to minimize the number of non-zero entries in S³⁴, and so on. This appears to be the optimal ordering of the nucleotides, and results in greatly improved runtimes over other orderings. Thus, the order in which the user lists the nucleotides in the query motif does not affect the runtime or the results obtained.

When building partial candidates, we add two nucleotides simultaneously at each step until zero or one nucleotide remains to be added. This reduces the number of times we must loop through the list of partial candidates. If the partial candidate has k nucleotides, each new nucleotide must satisfy k pairwise screening constraints, plus the pairwise constraint between the two new nucleotides, for a total of 2k + 1 pairwise constraints. We apply the subset screening criterion only once, after both nucleotides have been added.

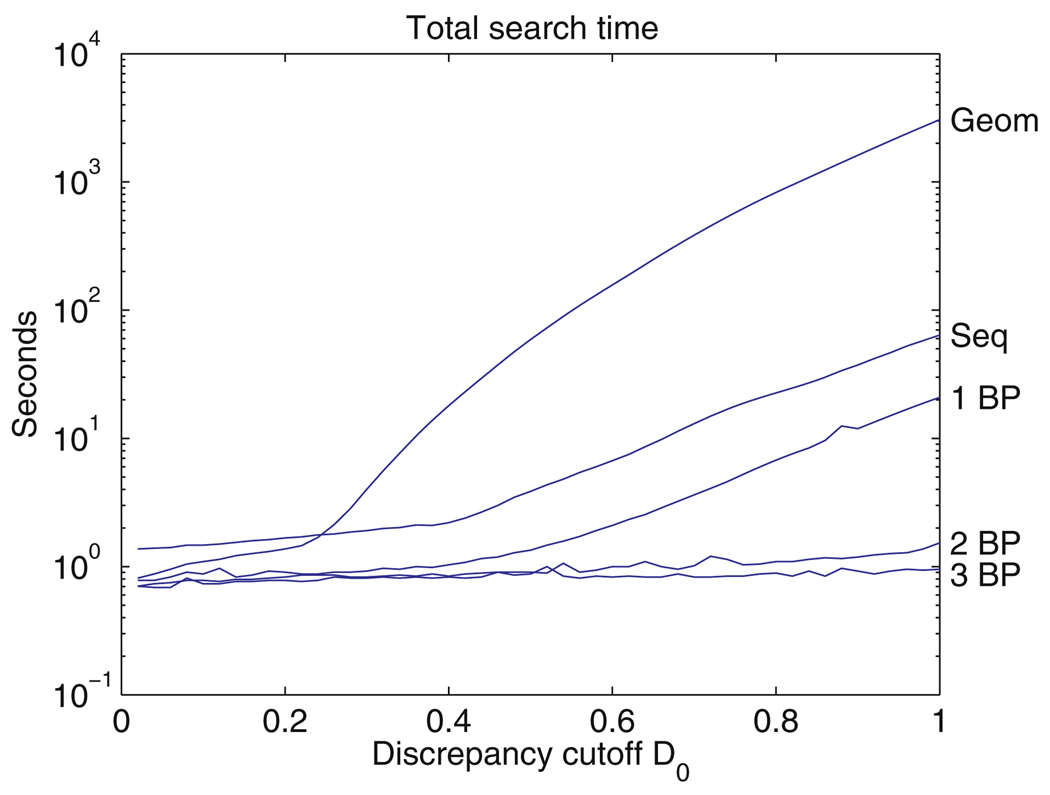
The subset screening criterion (10) can be relaxed by setting a second, larger cutoff D₁. This retains some interesting candidates whose discrepancy is between D₀ and D₁, but does not increase the number of candidates nearly as much as it would if D₀ were increased to D₁, because the pairwise screens reduce the length of the list of candidates much more effectively. In this way, FR3D can be used to quickly generate candidates with discrepancies up to D₁, but without a guarantee of finding every candidate with discrepancy between D₀ and D₁.

After a list of m-nucleotide candidates has been produced, the discrepancy from the query motif is calculated for each candidate motif, and the candidates are sorted by discrepancy. In practice, once the fitting error, L, has been calculated, it may be clear that the discrepancy will exceed D₀ (or the larger cutoff D₁ mentioned above), in which case the candidate can be rejected, saving the time of calculating the orientation errors. Similarly, after each of the first m − 1 orientation errors is computed, we check to see if the candidate can be rejected without computing the remaining orientation errors. Only a small fraction of the candidates retained by the screening process actually have discrepancy below D₀. This is because the inequality (9) is rather weak, although very useful.

Finally, the larger the query motif, the more likely FR3D is to obtain redundant candidate motifs with discrepancies below D₀ but differing from one another by just one or two nucleotides. For example, in a candidate motif having a cis WC/WC basepair, replacing one of the paired bases by a base stacked on it results in a candidate with only somewhat larger discrepancy. If desired, FR3D can exclude redundant versions of candidate motifs, keeping only those with the lowest discrepancies.

3.10 Screening with interaction, identity, and continuity constraints

Symbolic search criteria specifying base–base interactions, base identity, or chain continuity constraints can be imposed in addition to the geometric shape of the motif and usually greatly reduce the search time. Alternatively, purely symbolic searches can be carried out. For example, one may wish to find all examples of A–G trans Hoogsteen/Sugar Edge basepairs stacked on G–A trans Sugar Edge/Hoogsteen pairs separated by no more than two additional nucleotides in each chain. Examples of purely geometric, purely symbolic, and mixed searches will be provided in Sect. 4.

3.10.1 Pairwise interaction constraints

Many motifs have characteristic pairwise interactions. In a regular helix, for example, all the basepairs are cis WC/WC and are constrained by sequence to be A/U, U/A, G/C, C/G, G/U or G/U. In addition, there are stacking interactions between successive nucleotides in each strand. For each pair of nucleotides in the query motif, the user may specify one or more desired interaction categories, using the 12 geometric basepairing categories from [30] and three additional stacking categories. Basepair and stacking classification is done automatically when an RNA 3D structure file is first read by FR3D as described above. Only candidate motifs whose nucleotides engage in the specified interaction will be retained.

The interaction constraint between i and j is implemented in FR3D by setting certain entries of S^(ij) equal to 0, so that all but the specified nucleotide pairs are excluded by the pairwise screening constraint. We set to zero those entries S^(ij) (p, q) for which nucleotides (p, q) are not classified to engage in one of the specified interactions for nucleotides corresponding to i and j. This is a fast operation which dramatically reduces the number of non-zero entries in S^(ij) and the number of partial or full candidates which are retained at every step of the process.

3.10.2 Base identity and nucleotide masks

In some motifs, only certain nucleotides occur in certain positions. For instance, many hairpin loops match the pattern “GNRA” - G in the first position, any nucleotide in the second (denoted N), A or G in the third (denoted R), and A in the last. We use the standard conventions for nucleotide masks. In addition, the user may specify that only certain pairs of letters are allowed for particular pairs of nucleotides in the candidate motif; for instance, the user may specify that nucleotides 1 and 4 of a motif match the pattern ‘CG’ or ‘GC’.

We implement the nucleotide mask by setting the appropriate entries of S^(ij) equal to 0. For instance, if entry i of the nucleotide mask is “C”, then for each j and q, we set S^(ij)(p, q) = 0 whenever nucleotide p is not a C. This sets row p of S^(ij) equal to 0 all at once, and significantly reduces the number of non-zero entries in S^(ij). Similarly, if the user specifies certain allowed patterns for nucleotides i and j, we set S^(ij)(p, q) = 0 for nucleotides p and q which do not match an allowed pattern.

3.10.3 Sequence continuity constraints

In some motifs, such as regular helices, certain nucleotides are expected or required to be adjacent in the nucleotide sequence. In other cases, a variable number of unpaired (“bulged”) nucleotides occur between two target nucleotides of the query motif. The corresponding candidate nucleotides should at least be nearly adjacent in the nucleotide sequence. With composite motifs, however, base-paired or -stacked nucleotides may be separated by one or more looped out bases, entire helices or even entire domains. Some motifs of interest may even contain nucleotides from two different molecules.

FR3D allows the user to specify sequence continuity constraints in the following way. For each pair of nucleotides in the query motif, the user may set upper and/or lower limits on the difference between nucleotide numbers of the corresponding nucleotides in the candidate. Candidates whose corresponding nucleotide numbers have larger or smaller gaps than what is allowed will be rejected without further computation. Note that, because nucleotide numbers can be non-numeric and different chains may use the same nucleotide numbers, the constraint is, in fact, implemented using the position of each nucleotide in the RNA 3D structure file. Thus, nucleotides from separate chains whose nucleotide numbers happen to be very close to one another will not automatically pass this screen.

The sequence continuity constraint is implemented as follows. Suppose that, for query motif nucleotides i and j, the sequence continuity constraint limits candidates to a maximum difference of d. Then we set S^(ij)(p, q) to 0 unless |p − q| ≤ d. This sets all entries of S^(ij) to 0 except those sufficiently close to the main diagonal, again dramatically reducing the number of non-zero entries.

3.10.4 Symbolic searching using interaction constraints, nucleotide masks, and sequential constraints

Sometimes it is desired to search for motifs based only on the desired base-pairing and base-stacking pattern, with the possible addition of a nucleotide mask or sequential continuity constraint, but without a query motif or discrepancy ranking. This is useful when one wants to determine whether a particular sub-motif exists, for example, to find all motifs having basepairs of type A stacked on basepairs of type B. As mentioned above, imposing these kinds of constraints dramatically reduces the number of non-zero entries in S^(ij), and so it is plausible that, following the procedure described above for building candidate motifs, but only imposing the pairwise constraint S^(ij)(p, q) > 0, one may be able to reduce the list of conceivable candidates down to a reasonable number to examine by hand.

Recall the definition (12) of S^(ij) and its subsequent modification. A non-zero entry in S^(ij)(p, q) meant that nucleotides p and q have the right mutual distance to be able to correspond to query motif nucleotides i and j. With no query motif, this needs modification. One could reasonably make all off-diagonal entries of S^(ij) be non-zero. But even with a reasonable number of symbolic constraints, the search could return enormous numbers of candidates. We are helped by the following observation: if we are able to give an upper limit on the center to center distances in a candidate motif (we use 30 Ångstroms as the default), then we may set to zero all entries S^(ij)(p, q) for which the center to center distance between nucleotides p and q exceeds this upper limit. Once again, then, S^(ij) will be sparse, and will be made more sparse by the symbolic constraints. We may use the screening algorithm described above to build up partial and full candidates, although we do not impose the subset screening constraint, nor do we compute a discrepancy between candidates and a query motif. Thus, we are unable to sort the resulting candidate list according to similarity to a query motif. It is worth noting that if the set of constraints admits symmetries, a permutation of the nucleotides in a candidate motif may also satisfy the constraints. For example, if A1 C2 G8 U9 is a canonical helix (with AU and CG pairs), then so are U9 G8 C2 A1, C2 A1 U9 G8, and G8 U9 A1 C2, giving four ways that these nucleotides would match a canonical helix. To keep such permutations together, the candidate list is sorted first by the RNA 3D structure file the candidate came from, then by the sum of nucleotide numbers.

4 Motif search examples

We illustrate the capabilities of FR3D by presenting the results of searches for known motifs in the 50S ribosomal subunit of Haloarcula marismortui, PDB file 1s72, since we have a comprehensive catalog of known motifs [31,34]. Searches were performed using core nucleotides for each motif. Extruded unpaired bases were omitted from the query motifs since these nucleotides are less conserved among similar motifs and can generally assume a number of different orientations. The symbols used in the annotated 2D figures follow the Leontis/Westhof basepair nomenclature and classification [32].

4.1 Sarcin/Ricin search

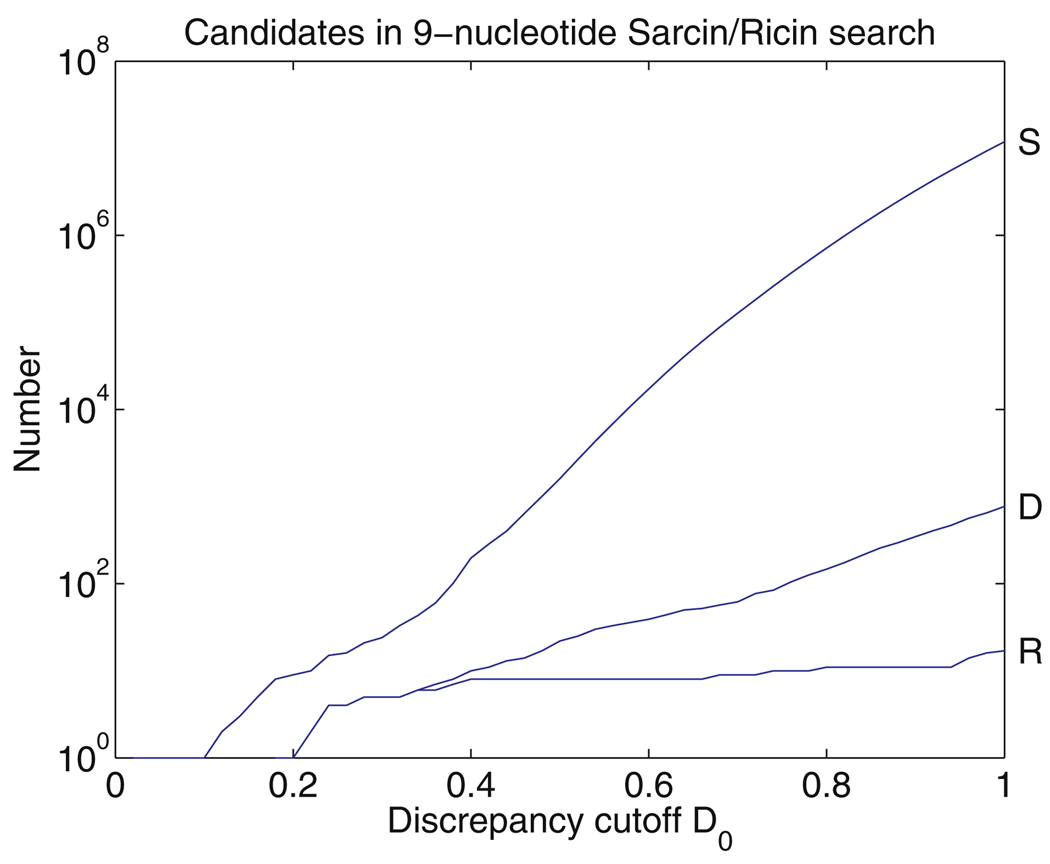
The complete sarcin/ricin motif has nine nucleotides, which make five non-canonical basepairs. There are twelve motifs in the H.m. 50S ribosomal subunit that contain at least five core nucleotides of the motif and eight instances of the complete motif. We describe three geometric and one symbolic search for the motif. The geometric searches were conducted using the parent sarcin/ricin motif from Domain VI of 23S rRNA to construct query motifs, with discrepancy cutoff D₀ set to 0.5. For the first search we used a five-nucleotide submotif as the query motif. These five nucleotides are highlighted in yellow in Fig. 7a. No symbolic constraints were used and redundant candidates were excluded, as described in Sect. 3.9. The FR3D code for the search is:

Model.Filename  =’1s72’;
Model.NTList    ={’2694’ ’2701’ ’2693’ ’2702’ ’2692’};
Model.ChainList ={’0’ ’0’ ’0’ ’0’ ’0’};   % all in the 23S
Model.DiscCutoff=0.5;

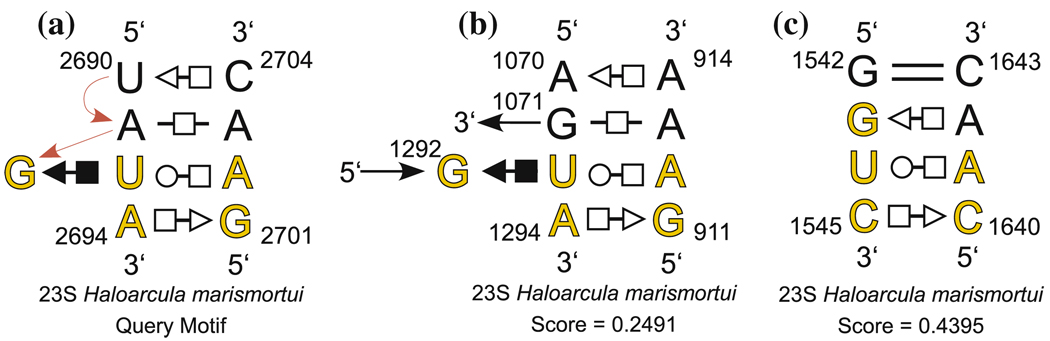
All other options are set by default, including D₁ = D₀. The search took 58.6 s. The thirteen best scoring motifs found by FR3D are listed by increasing discrepancy in Table 1. The twelve best scoring candidates correspond exactly to the twelve motifs containing the five core nucleotides of the full sarcin/ricin motif, including composite versions of the motif. The bona fide sarcin/ricin motifs, shown in yellow, have the lowest discrepancy scores (below 0.30). From the 12th candidate to the 13th, there is a considerable jump in discrepancy. The 13th candidate, while closely related, is not a bona fide sarcin/ricin motif, nor are any of the candidates further down the list (not shown). We examined candidate 13 to understand the degree to which it differs from the query motif. Its annotated secondary structure is shown in yellow in Fig. 7c. Three additional nucleotides are also shown. This candidate shares two basepairs of the type found in the sarcin/ricin motif, but G1543, which corresponds to G2692 in the query motif, is shifted slightly downward and pairs with A1642 instead of forming a cis Sugar Edge/Hoogsteen basepair with U1544.

Fig. 7.

Annotated secondary structures of query motif from PDB file 1s72 for sarcin/ricin geometric search (a) with one bona fide candidate motif (b) and the highest scoring related motif (c). Yellow letters indicate the bases of the query motif used for the geometric search reported in Table 1 and the corresponding bases of the candidate motifs

Table 1.

FR3D search results for the five-nucleotide sarcin/ricin query motif shown with yellow letters in Fig. 7a from the PDB file 1s72. The query motif is shown in the first row. Candidate motifs are listed in order of increasing discrepancy, with bases of each candidate motif placed in the same column as the corresponding bases of the query motif. Yellow background indicates bona fide sarcin/ricin motifs confirmed by visual inspection. In the last column, L represents a local motif, C represents a composite motif, and C^* represents a case where an intercalated base (A2302) comes from a third strand and forms a trans Hoogsteen/Hoogsteen basepair

		Discrepancy	Motifs found by FR3D					Type
Query Motif (Sarcin):		0.0000	A2694	G2701	U2693	A2702	G2692	L
PDB File:	1S72	0.0712	A1372	G2053	U1371	A2054	G1370	L
Number of Search Nucleotides:	5	0.1080	A 383	G 406	U 382	A 407	G 381	L
Motifs Identified:	12 (All)	0.1275	A 590	G 568	U 589	A 569	G 588	L
Basepairs Constrained:	None	0.1784	A 177	G 159	U 176	A 160	G 175	L
Guaranteed Cutoff D0:	0.5	0.1844	A 466	G 475	U 465	A 476	G 464	L
Relaxed Cutoff D1:	0.5	0.1976	A 360	G 292	U 359	A 293	G 358	L
Exclude Redundant Candidates:	Yes	0.2284	A 215	G 225	U 214	A 226	G 213	L
		0.2374	A 80	G 102	U 79	A 103	G 78	L
		0.2391	A1973	G2009	U1972	A2010	G1971	C
		0.2491	A1294	G 911	U1293	A 912	G1292	C
		0.2714	A 955	A1012	U 954	A1013	G 953	C*
Highest Scoring non-sarcin motif:		0.4395	C1545	C1640	U1544	A1641	G1543	L

To illustrate the purely symbolic search capabilities of FR3D we repeated the search for the 5-nucleotide core sarcin/ricin motif using only interaction and sequential continuity constraints, and no query motif. Using the same ordering of nucleotides as in the previous search, we specify the relationships between these five bases in FR3D as follows:

Query.Edges{1,2}   = ’tHS’;
Query.Edges{3,5}   = ’cHS’;
Query.Edges{3,4}   = ’tWH’;
Query.MaxDiff(5,3) = 2;
Query.MaxDiff(3,1) = 2;
Query.MaxDiff(4,2) = 2;

The Edges{1,2} field specifies that nucleotides 1 and 2 in the candidate should form a trans Hoogsteen/Sugar edge pair. Similarly for the other two edge specifications. The MaxDiff field specifies that, in order to be accepted as a candidate, the difference between the first and third, third and fifth, and second and fourth nucleotide numbers must be no greater than 2. The search took 6.6 s and returned the first 12 candidates listed in Table 1, with no others.

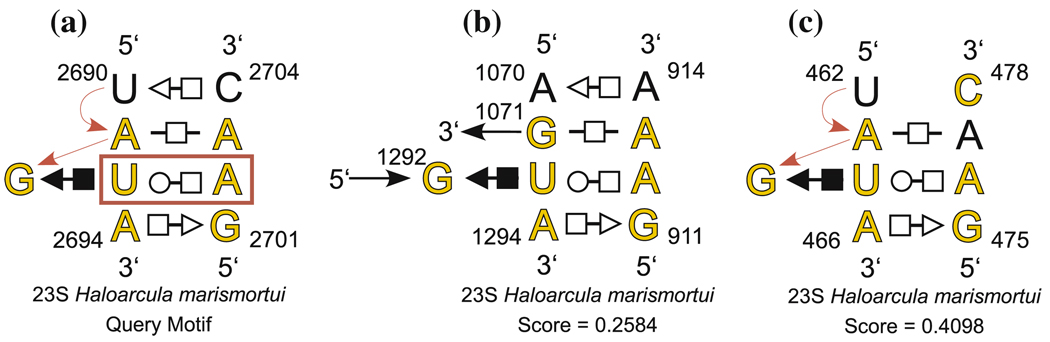
Next we provide examples of mixed geometric and symbolic searches for efficiently searching with larger query motifs. First, we used seven nucleotides from the sarcin/ricin motif to form the query motif. These nucleotides are shown in yellow in Fig. 8a. For this search the cutoffs were set as D₀ = 0.5 and D₁ = 0.5. We imposed one basepair interaction constraint corresponding to the U2693/A2702—trans Watson–Crick/Hoogsteen basepair in the query motif, but no basepair mask or sequential continuity constraint. For illustration purposes, we did not exclude redundant motifs. This search took 5.7 s.

Fig. 8.

Annotated secondary structures of query motif (a) and two candidate motifs for the seven-base sarcin/ricin motif search reported in Table 2. Yellow letters indicate the bases of the query motif used for the geometric search and the corresponding bases of the candidate motifs. The bold red box shows the constrained basepair. Candidate motifs obtained by the search include a bona fide composite sarcin/ricin motif (b) and a redundant motif (c) in which base A2703 in the query motif is mismatched to base C478 in the candidate motif. The higher-scoring version of this candidate, in which A477 is matched with A2703, had discrepancy 0.2161

All eleven motifs (shown in yellow in Table 2) which contain these seven nucleotides of the query motif were found and assigned the lowest discrepancy scores, including the composite motif shown in Fig. 8b. The last candidate in the list, shown in Fig. 8c, is a duplicate of the 7th motif in the list with a change of one nucleotide (C478 rather than A477). This type of redundancy occurs often in searches and has only a somewhat higher discrepancy (0.4098 vs. 0.2216), since all but one of the seven nucleotides are properly oriented. This candidate is excluded when we carry out a non-redundant search by setting the program parameter Query.ExcludeRedundant to 1.

Table 2.

Results from geometric search of PDB file 1s72 using the seven nucleotide sarcin/ricin query shown in Fig. 8a. The eleven highest scoring motifs are bona fide motifs (Yellow background). The last candidate motif shown (discrepancy = 0.4098) is a redundant version of the seventh candidate motif (discrepancy = 0.2161) in which C478 is matched with A2703 of the query motif instead of A 477, as shown in Fig. 8c. In the last column, L, C, and C^* have the same meanings defined in the legend to Table 1

		Discrepancy	Motifs found by FR3D							Type
Query Motif (Sarcin):		0.0000	A2694	G2701	U2693	A2702	G2692	A2691	A2703	L
PDB File:	1S72	0.0904	A1372	G2053	U1371	A2054	G1370	A1369	A2055	L
Number of Search Nucleotides:	7	0.1372	A 383	G 406	U 382	A 407	G 381	A 380	A 408	L
Motifs Identified:	11 (All)	0.2003	A 80	G 102	U 79	A 103	G 78	A 77	A 104	L
Basepairs Constrained:	1	0.2063	A 215	G 225	U 214	A 226	G 213	A 212	A 227	L
Guaranteed Cutoff D0:	0.5	0.2108	A 177	G 159	U 176	A 160	G 175	A 174	A 161	L
Relaxed Cutoff D1:	0.5	0.2161	A 466	G 475	U 465	A 476	G 464	A 463	A 477	L
Exclude Redundant Candidates:	No	0.2584	A1294	G 911	U1293	A 912	G1292	G1071	A 913	C
		0.2973	A 590	G 568	U 589	A 569	G 588	A 587	C 570	L
		0.3387	A 955	A1012	U 954	A1013	G 953	A2302	A1014	C*
		0.3572	A 360	G 292	U 359	A 293	G 358	A 357	C 294	L
		0.4098	A 466	G 475	U 465	A 476	G 464	A 463	C 478	L

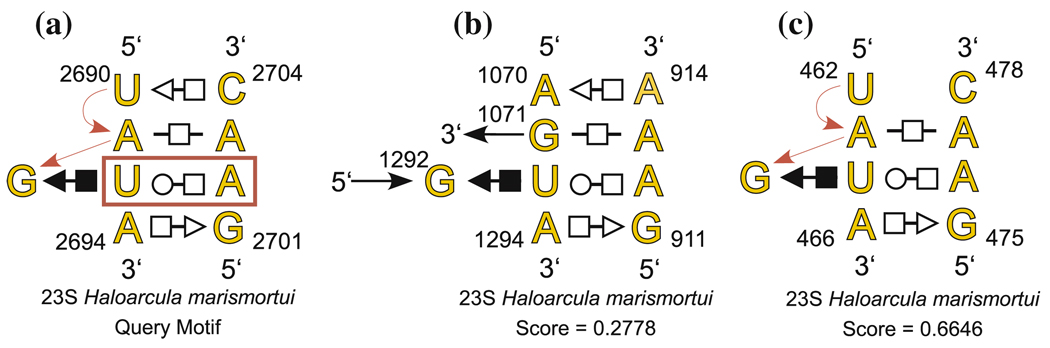
Finally, we carried out a geometric search using all nine nucleotides of the sarcin/ricin motif, shown in yellow in Fig. 9a. As in the previous search, the cutoffs D₀ and D₁ were set to 0.5 and one basepair constraint was imposed (U2693/A2702 - trans Watson–Crick/Hoogsteen). Redundant motifs were excluded. This search took 58.7 s. As shown in Table 3, the eight complete sarcin motifs that occur in the H.m. 50S subunit are the highest scoring motifs obtained by this search. To obtain additional candidates, we raised the discrepancy cutoff D₀ to 0.7, which took 2.63 hours to run. The ninth candidate obtained has a score almost double that of the eighth motif. It is one of the partial sarcin motifs having seven nucleotides and lacking the fifth non-Watson–Crick basepair of the full motif, as shown in the annotated structure in Fig. 9c. U462 and C478 do not form a basepair.

Fig. 9.

Annotated secondary structure of nine-nucleotide sarcin/Ricin query motif (a) reported in Table 3 with one bona fide composite candidate motif (b) and the highest-scoring related motif, which differs from the query motif only at nucleotides U2690 and C2704 (c). The bold red box shows the constrained basepair

Table 3.

Search results for nine-nucleotide sarcin/ricin query motif. Yellow background indicates bona fide motifs. The last entry is the incomplete motif shown in Fig. 9c, in which bases U462 and C 478 are not basepaired as in the complete nine-nucleotide motif. In the last column, L represents a local motif and C represents a composite motif

		Discrepancy	Motifs found by FR3D									Type
Query Motif (Sarcin):		0.0000	A2694	G2701	U2693	A2702	G2692	A2691	A2703	U2690	C2704	L
PDB File:	1S72	0.1631	A1372	G2053	U1371	A2054	G1370	A1369	A2055	U1368	C2056	L
Number of Search Nucleotides:	9	0.2142	A 215	G 225	U 214	A 226	G 213	A 212	A 227	U 211	C 228	L
Motifs Identified:	8 (All)	0.2217	A 80	G 102	U 79	A 103	G 78	A 77	A 104	G 76	A 105	L
Basepairs Constrained:	1	0.2293	A 177	G 159	U 176	A 160	G 175	A 174	A 161	C 173	C 162	L
Guaranteed Cutoff D0:	0.5	0.2778	A1294	G 911	U1293	A 912	G1292	G1071	A 913	A1070	A 914	C
Relaxed Cutoff D1:	0.5	0.3235	A 590	G 568	U 589	A 569	G 588	A 587	C 570	C 586	C 571	L
Exclude Redundant Candidates:	Yes	0.3644	A 360	G 292	U 359	A 293	G 358	A 357	C 294	C 356	C 295	L
		0.6646	A 466	G 475	U 465	A 476	G 464	A 463	A 477	C 461	C 478	L

4.2 Kink-turn search

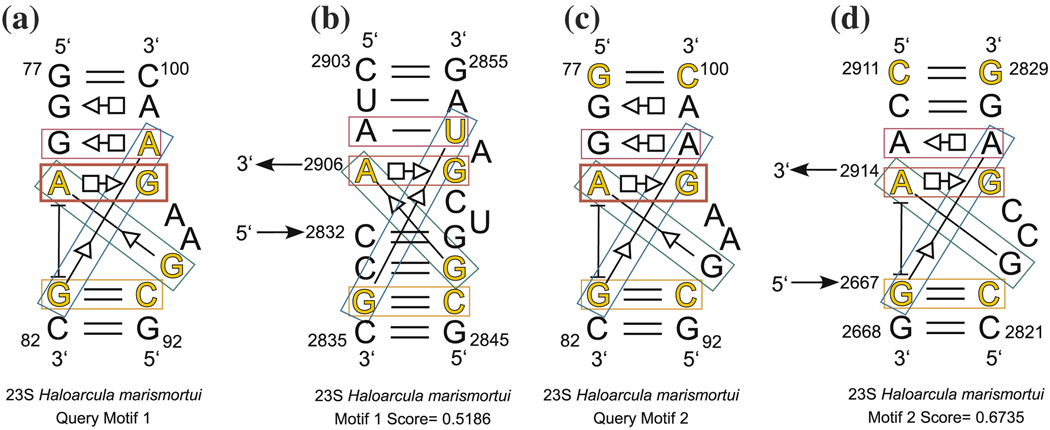
Next, we illustrate the use of different basepairs to define the query motif, by performing two six-nucleotide searches using the Kink-turn motif Kt-7 of H.m. as the query motif. The cutoffs D₀ and D₁ were set to 0.7, one basepair constraint was imposed (A80/G97 - trans Hoogsteen/Sugar Edge), and redundant candidates were excluded. The six query nucleotides for the first search are shown in yellow in Fig. 10a. These six nucleotides take part in four basepairing interactions at the heart of the kink turn.

Fig. 10.

Query motif for kink-turn search reported in Table 4 (a) and new composite kink-turn motif identified by this search (b). Query motif for kink-turn search reported in Table 5 (c), and a composite kink-turn obtained by this search (d). The bold red box shows the constrained basepair

This search took 14.3 s, and the results are shown in Table 4. The eight known kink-turns were found by this search; these are shown in yellow in Table 4. The candidate shown in blue in Table 4 is a new kink-turn, which is located within a three-way junction in Domain V. This new kink-turn is annotated and shown in Fig. 10b. It is notable that the search picks up other candidates which have exactly the same set of interactions that exist in kink-turns but which comprise tertiary contacts between structural elements distant in the secondary structure.

Table 4.

Results of FR3D kink-turn search of PDB file 1s72 using query motif shown in Fig. 10a. The candidate shown with a blue background is a new kink-turn. In addition to bona fide kink-turn motifs, the search obtains tertiary interactions that have the same core basepairs as kink turns. In the last column, L represents a local motif, C represents a composite motif, and T means the motif comprises tertiary interactions

		Query Motif 1 Search
		Discrepancy	Motifs found by FR3D						Type
Query Motif (Kink-turn):		0.0000	A 80	G 97	G 81	C 93	G 94	A 98	L
PDB File:	1S72	0.1720	A 113	G 47	A 148	U 43	G 44	A 48	C
Number of Search Nucleotides:	6	0.2196	A 939	G1031	G 940	C1026	G1027	A1032	L
Motifs Identified:	8 (All)	0.2402	A1215	G1151	G1216	C1147	C1148	A1152	L
Basepairs Constrained:	1	0.3874	A1341	G1316	C1342	G1312	A1313	A1317	L
Guaranteed Cutoff D0:	0.7	0.5186	A2906	G2851	G2834	C2846	G2847	U2853	C
Relaxed Cutoff D1:	0.7	0.5259	A2914	G2826	G2667	C2822	G2823	A2827	C
Exclude Redundant Candidates:	Yes	0.5335	A 247	G 264	G 249	C 260	A 261	U 265	L
		0.5373	A1294	G 911	U1041	C 930	C 931	A 912	T
		0.5617	A2875	G2882	G1806	C1786	C1787	A2883	T
		0.6406	A1590	G1605	C1593	G1601	C1602	A1606	L

In a second kink-turn search, we used different query nucleotides, namely, the closing Watson–Crick basepairs on either end of the kink-turn, together with one characteristic basepair within the kink-turn. These nucleotides are shown in yellow in Fig. 10c. The cutoffs D₀ and D₁ were set to 0.9, one basepair constraint was imposed (A80/G97 - trans Hoogsteen/Sugar Edge), and redundant candidates were excluded. This search strategy focuses on the overall 3D shape of the kink-turn rather than the specific interactions which form the kink-turn. This search took 154 s. The results are shown in Table 5. All known kink-turns were found, but a higher discrepancy was required, due to the greater size of the query motif and the inherent flexibility of the kink-turn motif.

Table 5.

Search results using query motif comprising closing basepairs and one central basepair of the kink-turn, shown in Fig. 10c. The candidate shown with blue background is a new kink-turn. In addition to bona fide kink-turn motifs, the search obtains tertiary interactions that have the same core basepairs as kink turns. In the last column, L represents a local motif, C represents a composite motif, and T means the motif comprises tertiary interactions

		Query Motif 2 Search
		Discrepancy	Motifs found by FR3D						Type
Query Motif (Kink-turn):		0.0000	A 80	G 97	G 81	C 93	C 100	G 77	L
PDB File:	1S72	0.2166	A 113	G 47	A 148	U 43	G 50	C 111	C
Number of Search Nucleotides:	6	0.5406	A1341	G1316	C1342	G1312	G1319	U1338	L
Motifs Identified:	8 (All)	0.5887	A1215	G1151	G1216	C1147	A1154	C1212	L
Basepairs Constrained:	1	0.6137	A 939	G1031	G 940	C1026	G1034	C 936	L
Guaranteed Cutoff D0:	0.9	0.6735	A2914	G2826	G2667	C2822	G2829	C2911	C
Relaxed Cutoff D1:	0.9	0.6814	A2875	G2882	G1806	C1786	A2885	U2872	T
Exclude Redundant Candidates:	Yes	0.6912	A 955	A1012	C 81 (5S)	G 102 (5S)	C1015	G 952	T
		0.7125	A1590	G1605	C1593	G1601	G1608	U1587	L
		0.7337	A1294	G 911	U1041	C 930	A 914	A1070	T
		0.7340	A2906	G2851	G2834	C2846	G2855	C2903	C
		0.7631	A 520	G 23	A 639	G1363	U 26	U 517	T
		0.7820	A 80 (5S)	G 102 (5S)	G 956	A1012	C 106 (5S)	G 75 (5S)	T
		0.7859	A1318	G1339	U 27	A 516	C1342	A1313	T
		0.8003	A1459	G1484	A 784	U 862	G1489	C1456	T
		0.8126	A1294	G 911	A1040	C 931	A 913	A1070	C
		0.8274	A 666	G 680	G 209	C 230	G 684	C 663	T
		0.8298	A 247	G 264	G 249	C 250	G 267	C 244	L
		0.8582	A 242	G 269	C 377	G 273	G 379	G 431	T
		0.8731	A1626	G1571	G1510	G1496	C1574	G1621	T

4.3 GNRA search

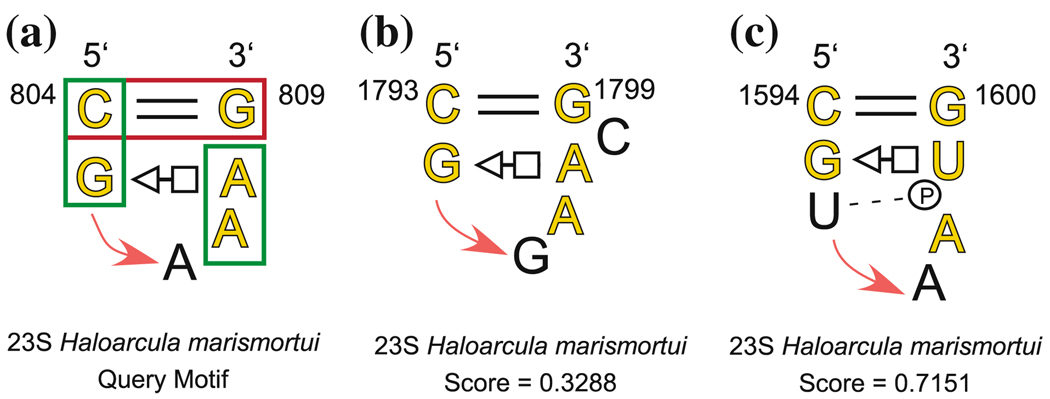
We illustrate how the geometric and symbolic search capabilities of FR3D can be used to understand and characterize an RNA motif by reviewing a search process for GNRA hairpins.

We refer to the hairpin loop annotated in panel (a) of Fig. 11. First, we used bases 804, 805, 808, and 809 as the query motif and constrained candidate motifs to have the same two basepairing interactions. This search returned some hairpins and some internal loops. To exclude the internal loops, we imposed a sequential continuity constraint to limit the difference in nucleotide numbers corresponding to 805 and 808 to at most 4. Some GNRA hairpins were missing from the list however, due to the fact that they do not have the trans Hoogsteen/Sugar edge interaction, or, in one case, the cis Waston–Crick basepair. We removed the tHS basepair constraint, weakened the cWW constraint, added a fifth nucleotide (A807) to the query motif, and used a large discrepancy cutoff to find as many GNRA hairpins as possible. We found that all of the known GNRA hairpins have “35” stacking interactions between the nucleotides corresponding to A804–G805 and to A807–A808. The final search parameters were as follows:

Query.NTList         = {’804’ ’805’ ’807’ ’808’ ’809’};
Query.ChainList      = {’0’ ’0’ ’0’ ’0’ ’0’};
Query.Edges{1,5}     = ’cWW bif’;
Query.Edges{1,2}     = ’s35’;
Query.Edges{3,4}     = ’s35’;
Query.DiscCutoff     = 0.8;
Query.MaxDiff(1,5)   = 6;
Query.MaxDiff(2,4)   = 4;
Query.ExcludeOverlap = 1;

The three interaction constraints are illustrated with boxes in panel (a) of Fig. 11. The key bif refers to the bifurcated category in [30], which is close to the cis Waston–Crick category. The two MaxDiff constraints exclude internal loops and force the hairpin to close below the basepairs illustrated in Fig. 11, rather than above. The search took 3.0 s. The results of the search are shown in Table 6; all known GNRA loops from 5S and 23S H.m. were found (highlighted in yellow) [27], and only one additional motif appeared in the list. This indicates that the search parameters accurately and succinctly describe what characterizes GNRA motifs. The one related hairpin is shown in panel (c) of Fig. 11. It has the features of the GNRA motif and should be found by our search parameters, however, it also contains a U-turn after G1595.

Fig. 11.

Query motif used for GNRA searche (a), GNRA motif with a bulged nucleotide which was correctly identified (b), related hairpin which is intermediate between GNRA and a T-loop (c). The bold red box shows the constrained basepair, and the green boxes indicate stacking constraints

Table 6.

Search results for query motif shown in Fig. 11a, from a GNRA hairpin loop in H.m. 23S rRNA, using a sequential continuity constraint, a basepair constraint, and two base stacking constraints. In the Type column, RH represents a related hairpin

		Discrepancy	Motifs found by FR3D					Type
Query Motif (GNRA):		0.0000	C 804	G 805	A 807	A 808	G 809
PDB File:	1S72	0.1408	C2695	G2696	G2698	A2699	G2700
Number of Search Nucleotides:	5	0.1568	C2248	G2249	G2251	A2252	G2253
Motifs Identified:	21 (All)	0.1687	C 89	G 90	G 92	A 93	G 94	in 5S
Basepairs Constrained:	1	0.2077	C1862	G1863	A1865	A1866	G1867
Stacking Constraints:	2	0.2405	G2876	G2877	A2879	A2880	C2881
Guaranteed Cutoff D0:	0.8	0.2562	G 690	G 691	A 693	A 694	C 695
Relaxed Cutoff D1:	0.8	0.2598	G1628	G1629	A1631	A1632	C1633
Sequential Constraint:	Yes	0.2799	G1054	G1055	A1057	A1058	C1060
Exclude Redundant Candidates:	Yes	0.3027	C 252	U 253	A 255	C 256	G 257
		0.3152	C 217	C 218	G 221	A 222	G 223
		0.3288	C1793	G1794	A1796	A1797	G1799
		0.3528	C2411	G2412	A2414	A2415	G2416
		0.3801	C2629	G2630	G2632	A2633	G2634
		0.3905	C 576	G 577	G 579	A 580	G 581
		0.4120	U 468	G 469	G 471	A 472	A 473
		0.4943	U1326	G1327	A1329	A1330	A1331
		0.5350	U 493	C 494	G 496	A 498	G 499
		0.6009	G1468	C1469	A1471	C1472	C1474
		0.6314	C1275	U1276	A1278	A1280	C1281
		0.7151	C1594	G1595	A1598	U1599	G1600	RH
		0.7350	U 733	U 734	A 736	A 737	G 738

5 Performance characteristics

The running time and memory requirements of FR3D depend strongly on the size and nature of the query motif, the number of symbolic constraints, the characteristics of the RNA 3D structure file being searched, and the discrepancy cutoffs D₀ and D₁. The theoretical worst-case operation count for evaluating each conceivable candidate motif is O(n^m) as n → ∞, where n is the number of nucleotides in the file being searched and m is the number of nucleotides in the query motif. The worst-case count with FR3D is somewhat better; there are at most n² pairs satisfying S⁽¹²⁾ > 0, and for each of these, we check n third and fourth nucleotides, and for each four-nucleotide partial candidate, we check n fifth and sixth nucleotides, and so on, leaving an operation count of order O(n^{2+⌊(m−1)/2⌋}). Fortunately, because of the screening algorithm and symbolic constraints in FR3D, in practice there are far fewer partial candidates than the theoretical worst case. Thus, actual peformance on a range of common tasks is more relevant than theoretical worst-case estimates.

We illustrate the performance of FR3D on some benchmark examples, beginning with the five-nucleotide sarcin/ricin motif search. We consider five variants of the search for the query motif. In every case, we exclude redundant candidates. The first search is a purely geometric search for the query motif shown in Fig. 7a. The second search is identical to the first except that sequential constraints are imposed so that the nucleotide numbers corresponding to G2692-U2693-A2694 differ by at most 2, and that the nucleotide numbers corresponding to G2701-A2702 differ by at most 2. The text of the search is:

Model.Filename         = ’1s72’;
Model.NTList           = {’2694’ ’2701’ ’2693’ ’2702’ ’2692’};
Model.ChainList        = {’0’ ’0’ ’0’ ’0’ ’0’};   % all in the 23S
Model.MaxDiff{1,3}     = 2;
Model.MaxDiff{2,4}     = 2;
Model.MaxDiff{3,5}     = 2;
Model.ExcludeRedundant = 1;

(We do not list the discrepancy cutoff, since that will be varied.) For the third search we add one basepair constraint, that the nucleotides corresponding to A2694-G2701 form a trans Hoogsteen/Sugar Edge pair. This adds the line Model.Edges{1,2} = ’tHS’; to the query definition script above. For the fourth search, we impose a second basepair constraint, that the nucleotides corresponding to U2693-A2702 form a trans Watson–Crick/Hoogsteen pair and for the fifth search we impose a third basepair constraint, that the nucleotides corresponding to U2693-G2692 form a cis Hoogsteen/Sugar Edge pair. We ran the five searches over a range of values for D₀ ranging from 0.02 to 1.0. We display the running time versus D₀ in Fig. 12. The purely geometric search has the longest run time, and each of the others ran faster according to the number of additional constraints imposed. In all cases, larger values of the cutoff discrepancy D₀ required longer run times. This is partly because vastly more candidates survive the screening process and must have their discrepancies computed. Even so, once the candidates are sorted by discrepancy and redundant candidates are eliminated, the total number of remaining candidates is fairly similar in the five cases, until large discrepancies of the order of 0.8 are used; see Fig. 13.

Fig. 12.

Total search time for five geometric searches as a function of discrepancy cutoff. The search labeled GEOM is purely geometric. Other searches are identical to the previous search with the exception of one added constraint as indicated: SEQ sequential constraint; 1 BP one basepair constraint; 2 BP two basepair constraints; 3 BP three basepair constraints. The PDB file 1s72 was searched. Note the logarithmic scale on the vertical axis

Fig. 13.

Number of distinct candidates satisfying the discrepancy limit for the five searches in Fig. 12. The PDB file 1s72 was searched

Next, we illustrate the effect of motif size on search time. We ran five versions of the sarcin/ricin motif, using, respectively, the first 5, 6, 7, 8, and 9 nucleotides of the 9-nucleotide sarcin/ricin search in Table 3. In every case, we imposed two interaction constraints, that the nucleotides corresponding to A2694–G2701 form a trans Hoogsteen/Sugar Edge pair and that those corresponding to U2693/A2702 form a trans Watson–Crick/Hoogsteen basepair. Total search times for a range of cutoff discrepancies are shown in Fig. 14. Clearly, larger query motifs require longer search times. Longer search times directly reflect the number of candidates which survive the screening process. Even so, the final number of candidates is not so large. Figure 15 shows the number of candidates that are produced by the screening process, the number which have discrepancy below the cutoff discrepancy, and, of these, the number of non-redundant candidates for the 9 nucleotide search. The number which survive the screening process is many times larger than the number which have discrepancy below the cutoff discrepancy; this is because the screening process only uses an approximation of the fitting error and totally neglects the orientation error. These are considered for the first time when the full discrepancy is computed. Finally, the number of non-redundant candidates is considerably smaller, and increases only slowly as the cutoff discrepancy is increased. The situation is similar with the other searches profiled in this section. Thus, increasing the cutoff discrepancy D₀ greatly increases the total search time, but does not greatly increase the number of non-redundant candidate motifs.

Fig. 14.

Search times for sarcin/ricin query motifs with 5, 6, 7, 8, and 9 nucleotides, as a function of discrepancy cutoff value. The PDB file 1s72 was a mixed geometric and symbolic search with two basepair interaction constraints

Fig. 15.

Number of candidates remaining after screening (S), after the discrepancy calculation (D), and after redundant candidates were removed (R), as a function of discrepancy cutoff value. The query motif was the nine-nucleotide sarcin/ricin motif and PDB file 1s72 was searched

6 Conclusions

The geometric discrepancy that we define is sufficiently simple to calculate and to approximate, which makes possible efficient and exhaustive screening for recurrent motifs, local and composite, in RNA 3D structures. It captures the essential features of the motifs we tested, as indicated by its success in finding all structurally similar sarcin/ricin and kink-turn motifs in the 3D structure of the H.m. 50S ribosomal subunit. Moreover, this measure is highly discriminating as shown by the lack of high scoring false positive motifs obtained in these searches. Finally, the discrepancy measure shows promise for clustering and classifying structurally related motifs.

The program FR3D can screen candidates according to basepair interactions, sequential continuity constraints, and nucleotide masks. If desired, non-geometric symbolic searches can be conducted, using only such constraints. FR3D has been optimized to run fast, and in the tradeoff between search time and number of non-redundant candidates found, shorter searches with lower discrepancies typically produce nearly the same candidate lists as much longer searches with higher discrepancy.

Appendix A: Least-squares fitting

In this appendix, we review the solution of [22] to the problem of finding a vector t and rotation matrix R which minimize the least squares error

$$E(R,t)={\displaystyle \sum _{i=1}^m{w}_i{\Vert b_i-R(c_i-t)\Vert }^2}$$ (18)

from rigidly translating and rotating vectors c₁,…, c_m onto vectors b₁,…, b_m. The constants w₁,…, w_m are strictly positive. We also indicate a variation on their solution which is more numerically stable. See also [15], Sect. 12.4.1.

Fix a rotation matrix R and differentiate E(R, t) with respect to the components of t. Setting the derivatives equal to zero immediately leads to the unique solution

$$t^{*}=\frac{{\displaystyle {\sum }_{i=1}^m{w}_i(c_i-R^{-1}{b}_i)}}{{\displaystyle {\sum }_{i=1}^m{w}_i}}.$$ (19)

This is easier to understand if we express t^* as t^* = c̄ − R⁻¹ b̄, where

$$\overline{c}=\frac{{\displaystyle {\sum }_{i=1}^m{w}_i{c}_i}}{{\displaystyle {\sum }_{i=1}^m{w}_i}}\text{\hspace{1em}\hspace{1em}and\hspace{1em}\hspace{1em}}\overline{b}=\frac{{\displaystyle {\sum }_{i=1}^m{w}_i{b}_i}}{{\displaystyle {\sum }_{i=1}^m{w}_i}}$$ (20)

are the weighted centers of mass of the two sets of vectors. Substituting this optimal value of t into the error E leaves

$$E(R,t^{*})={\displaystyle \sum _{i=1}^m{w}_i{\Vert (b_i-\overline{b})-R(c_i-\overline{c})\Vert }^2.}$$ (21)

Thus, the first step amounts to centering each set of vectors at the origin.

Squaring out the vector norm in (21) using the dot product and the fact that ‖Ra‖ = ‖a‖ leads to an equivalent optimization for R: maximize ${\displaystyle {\sum }_{i=1}^m{w}_i{(b_i-\overline{b})}^{T}R(c_i-\overline{c})}$. As explained in [22], one maximizes this sum in the following way. Define a matrix M by

$$M={\displaystyle \sum _{i=1}^m{w}_i(b_i-\overline{b}){(c_i-\overline{c})}^T,}$$ (22)

and find the eigenvalues λ₁, λ₂, λ₃ and mutually orthogonal unit eigenvectors u₁, u₂, u₃ of M^T M. Because M^T M is symmetric and positive semi-definite, we may assume that λ₁ ≥ λ₂ ≥ λ₃ ≥ 0. The optimal rotation matrix R is an orthogonal matrix with determinant 1 for which M = RS, where $S={(M^{T}M)}^{\frac{1}{2}}$. In [22], R is found by inverting S, using the formula

$$S^{-1}=\frac{1}{\sqrt{{\lambda }_1}}{u}_1{u}_1^T+\frac{1}{\sqrt{{\lambda }_2}}{u}_2{u}_2^T+\frac{1}{\sqrt{{\lambda }_3}}{u}_3{u}_3^T.$$ (23)

Unfortunately, this solution is numerically unstable when λ₃ is close to zero, and undefined when λ₃ = 0. These cases occur, respectively, when the vectors b_i lie near or on a single plane. But this is exactly the situation with base atoms in RNA, which is our first application of least squares fitting.

Our variation of the procedure is the following. Because M satisfies M = RS, we have

$$\begin{array}{cc}{Mu}_i\hfill & ={RSu}_i\hfill \\ \hfill & =R\left({\displaystyle \sum _{j=1}^3\sqrt{{\lambda }_j}{u}_j{u}_j^T}\right)u_i\hfill \\ \hfill & =R\sqrt{{\lambda }_i}{u}_i,\hfill \end{array}$$ (24)

for i = 1, 2, 3 by orthonormality. If the vectors b_i, i = 1,…, m do not all lie on the same line, and if the same is true of c_i, i = 1,…, m, then λ₁ and λ₂ will be non-zero and we may write

$${Ru}_i=\frac{1}{\sqrt{{\lambda }_i}}{Mu}_i,i=1,2.$$ (25)

Knowing how R rotates the two mutually perpendicular vectors u₁ and u₂ will suffice to determine R. Let z be a unit vector which is perpendicular to both Mu₁ and Mu₂. Define R^* by

$$R^{*}=\frac{1}{\sqrt{{\lambda }_1}}{Mu}_1{u}_1^T+\frac{1}{\sqrt{{\lambda }_2}}{Mu}_2{u}_2^T+{zu}_3^T.$$ (26)

One readily sees that $R^{*}{u}_i=\frac{1}{\sqrt{{\lambda }_i}}{Mu}_i$ for i = 1, 2, and that R^*u₃ = z. Because Mu₁ is orthogonal to Mu₂, R^* maps mutually orthogonal vectors to mutually orthogonal vectors. Moreover, one readily checks that R^*u_i has length 1 for i = 1, 2, 3. As such, the determinant of R^* will be +1 or −1. If the determinant is −1, we replace z by −z; this will change the determinant to +1, but all other properties will still be satisfied.

Appendix B: Proof of symmetry of geometric discrepancy

Here we show that the geometric discrepancy, as defined in (3), is symmetric, i.e. the same value of D is obtained for motifs of three or more nucleotides when the sense of query and candidate motif is switched. We use some results from Appendix A.

The fitting error obtained by aligning the query motif to the candidate motif is given by:

$$L^2=\underset{Q}{\text{min}}\underset{s}{\text{min}}{\displaystyle \sum _{i=1}^m{w}_i\Vert Q(b_i-s)-c_i\Vert }$$ (27)

instead of Eq. (1). Here Q is a rotation matrix and s is the shift vector. As in Appendix A, the optimal shift vector s^* would be given by s^* = b̄ − Q⁻¹ c̄. Substituting this in (27) gives

$$L^2=\underset{Q}{\text{min}}{\displaystyle \sum _{i=1}^m{w}_i\Vert Q(b_i-\overline{b})-(c_i-\overline{c})\Vert }$$ (28)

However, because Q is a rotation matrix, ‖Qa‖ = ‖a‖ = ‖Q⁻¹ a‖ for all vectors a, and we soon see that the minimum is attained precisely when Q = R⁻¹, where R is the optimal rotation matrix from Eq. (1). Thus, the fitting error L is the same as before.

For the orientation error, the matrix $N_i{M}_i^{-1}{Q}^{-1}$ rotates base i of the query motif onto base i of the candidate. The angle of rotation β_i may be calculated by

$$\begin{array}{cc}{\beta }_i\hfill & =2{\text{cos}}^{-1}\left(\frac{1}{2}\sqrt{\text{Tr}(N_i{M}_i^{-1}{Q}^{-1})+1}\right)\hfill \\ \hfill & =2{\text{cos}}^{-1}\left(\frac{1}{2}\sqrt{\text{Tr}(N_i{M}_i^{-1}R)+1}\right)\hfill \\ \hfill & =2{\text{cos}}^{-1}\left(\frac{1}{2}\sqrt{\text{Tr}(R^{-1}{M}_i{N}_i^{-1})+1}\right)\hfill \\ \hfill & =2{\text{cos}}^{-1}\left(\frac{1}{2}\sqrt{\text{Tr}(M_i{N}_i^{-1}{R}^{-1})+1}\right)\hfill \\ \hfill & ={\alpha }_i\hfill \end{array}$$ (29)

where we have used the identities Tr(A^T) = Tr(A) and Tr(AB) = Tr(BA) and the fact that the transpose of a rotation matrix is equal to its inverse. Thus, the orientation error is unchanged, and the geometric discrepancy is the same whether we align the candidate to the query motif or the query motif to the candidate.

Appendix C: Derivation of inequality (9)

Here we derive the inequality (9) relating the discrepancy D to the distance differences in the matrix Q defined in (7). Suppose there are m nucleotides. Let I be a subset of {1, 2,…, m} having two or more elements. We will give a lower bound on D in terms of a sum of the entries of Q over I × I. From the definition (3) of the discrepancy D, we see that D² ≥ L²/m². Using the optimal rotation matrix R for rotating the candidate onto the query motif and using the optimal translation vector t = c̄ − R⁻¹ b̄, we have from Eq. (1),

$$\begin{array}{cc}{L}^2\hfill & ={\displaystyle \sum _{i=1}^m{w}_i{\Vert (b_i-\overline{b})-R(c_i-\overline{c})\Vert }^2}\hfill \\ \hfill & \ge {\displaystyle \sum _{i\in I}{w}_i{\Vert (b_i-\overline{b})-R(c_i-\overline{c})\Vert }^2}\hfill \\ \hfill & ={\displaystyle \sum _{i\in I}{w}_i{\Vert b_i^{\prime }-{Rc}_i^{\prime }\Vert }^2}\hfill \end{array}$$ (30)

where we have denoted $b_i^{\prime }=b_i-\overline{b}$ and $c_i^{\prime }=c_i-\overline{c}$. We have bounded the fitting error L in terms of the fitting error of a subset of nucleotides.

To make the connection between the right side of (30) and the squared distance difference matrix Q, we introduce an intermediate sum and manipulate it two ways. On the one hand, we have:

$$\begin{array}{c}{\displaystyle \sum _{i\in I}{\displaystyle \sum _{j\in I}{w}_i{w}_j{\Vert (b_i-b_j)-R(c_i-c_j)\Vert }^2}}\hfill \\ \ge {\displaystyle \sum _{i\in I}{\displaystyle \sum _{j\in I}{w}_i{w}_j(\Vert b_i-b_j\Vert -{\Vert c_i-c_j\Vert )}^2}}\hfill \\ =2{\displaystyle \sum _{\underset{i<j}{i,j\in I}}{w}_i{w}_j{Q}_{ij},}\hfill \end{array}$$ (31)

using the “reverse triangle inequality” ‖u − v‖ ≥ |‖u‖ − ‖v‖| and the fact that ‖Ra‖ = ‖a‖ because R is a rotation matrix. On the other hand, using the facts that ‖u‖² = u·u, $b_i-b_j=b_i^{\prime }-b_j^{\prime }$, and $c_i-c_j=c_i^{\prime }-c_j^{\prime }$, we have,

$$\begin{array}{c}{\displaystyle \sum _{i\in I}{\displaystyle \sum _{j\in I}{w}_i{w}_j\Vert (b_i-b_j)-R(c_i-c_j){\Vert }^2}}\hfill \\ ={\displaystyle \sum _{i\in I}{\displaystyle \sum _{j\in I}{w}_i{w}_j\Vert (b_i^{\prime }-R{c}_i^{\prime })-(b_j^{\prime }-R{c}_j^{\prime }){\Vert }^2}}\hfill \\ ={\displaystyle \sum _{i\in I}{\displaystyle \sum _{j\in I}{w}_i{w}_j[\Vert b_i^{\prime }-R{c}_i^{\prime }{\Vert }^2-2(b_i^{\prime }-R{c}_i^{\prime })·(b_j^{\prime }-R{c}_j^{\prime })+\Vert b_j^{\prime }-R{c}_j^{\prime }{\Vert }^2]}}\hfill \\ =2\left({\displaystyle \sum _{i\in I}{w}_i\Vert b_i^{\prime }-R{c}_i^{\prime }{\Vert }^2}\right)\left({\displaystyle \sum _{j\in I}{w}_j}\right)-2\Vert {\displaystyle \sum _{i\in I}{w}_i(b_i^{\prime }-R{c}_i^{\prime })}{\Vert }^2\hfill \\ \le 2\left({\displaystyle \sum _{i\in I}{w}_i\Vert b_i^{\prime }-R{c}_i^{\prime }{\Vert }^2}\right)\left({\displaystyle \sum _{j\in I}{w}_j}\right).\hfill \end{array}$$ (32)

Combining (30), (31), and (32) gives the inequality

$$L\ge \sqrt{\frac{1}{{\displaystyle {\sum }_{i\in I}{w}_i}}\left({\displaystyle \sum _{\underset{i<j}{i,j\in I}}{w}_i{w}_j{Q}_{ij}}\right),}$$ (33)

from which (9) follows by the fact that D ≥ L/m. Because L is the weighted RMSD between the optimal fit of the c_i and the b_i, (33) could be used to screen candidates in RMSD searches.