Responses of Escherichia coli Bacteria to Two Opposing Chemoattractant Gradients Depend on the Chemoreceptor Ratio

Abstract

Escherichia coli chemotaxis has long served as a simple model of environmental signal processing, and bacterial responses to single chemical gradients are relatively well understood. Less is known about the chemotactic behavior of E. coli in multiple chemical gradients. In their native environment, cells are often exposed to multiple chemical stimuli. Using a recently developed microfluidic chemotaxis device, we exposed E. coli cells to two opposing but equally potent gradients of major attractants, methyl-aspartate and serine. The responses of E. coli cells demonstrated that chemotactic decisions depended on the ratio of the respective receptor number of Tar/Tsr. In addition, the ratio of Tar to Tsr was found to vary with cells’ growth conditions, whereby it depended on the culture density but not on the growth duration. These results provide biological insights into the decision-making processes of chemotactic bacteria that are subjected to multiple chemical stimuli and demonstrate the importance of the cellular microenvironment in determining phenotypic behavior.

In their natural environment, both prokaryotic and eukaryotic cells are exposed to multiple chemical stimuli. It is thus important to learn how cells make a decision when confronted with complex chemical stimuli. Escherichia coli bacteria have long served as a model system for chemotaxis studies due to their known and simple genetic makeup. Signaling in bacterial chemotaxis is comparatively well understood (3, 18, 19). To summarize it briefly, there are five types of chemoreceptors in E. coli, of which Tar and Tsr are the most abundant. The basic functional chemosensing unit is a ternary complex that consists of transmembrane chemoreceptors, a linker molecule, CheW, and a histidine kinase, CheA. Within each functional receptor complex, the receptors are known to function in a cooperative manner (9, 12, 16). Upon the binding of attractant molecules, this sensory complex undergoes a conformational change that suppresses the autophosphorylation activity of CheA. This response is then transmitted to the flagellar motor via a regulator protein, CheY. As a result, the run time of an E. coli bacterium is lengthened when swimming toward a high-chemoattractant-concentration region (4).

While the molecular mechanisms governing bacterial chemotaxis in a single gradient have been investigated extensively both in experiments and in theory (see reference 8 and references therein), very little is known about how bacteria behave in the presence of dual chemical gradients (1, 17). Early work by Adler and Tso explored the chemotactic responses of E. coli cells in the presence of both attractant and repellent gradients by using a microcapillary chemotaxis assay (1). Twenty years later, Strauss et al. (17) revisited the problem by using a stop-flow chamber. Both investigations concluded that bacteria sum the chemical signals to provide a coordinated output to control flagellar rotation. However, the molecular mechanisms responsible for this calculation have not yet been explored.

In this paper, we investigated the molecular mechanism that underlies the bacterial decision-making processes in two opposing attractant gradients that are sensed by the two most abundant E. coli receptors, Tar and Tsr, respectively. By varying the relative expression levels of Tar and Tsr, we demonstrated that the receptor ratio defines the attractant preference in dual gradients of their ligands. The Tar-to-Tsr ratio itself depends on the cell culture density but not on the duration of growth.

MATERIALS AND METHODS

Bacterial strains.

Escherichia coli strain RP437 (13) was used as a wild type for chemotaxis. To facilitate visualization in the microfluidic experiments, cells were transformed with plasmid pTrc-GFP (a kind gift of M. DeLisa, Cornell University), which confers ampicillin resistance and encodes green fluorescent protein (GFP) under the control of the pTrc promoter inducible by isopropyl-β-d-thiogalactopyranoside (IPTG). RP437 derivative VS154 [Δ(cheR-cheZ) Δtrg::Tn10], also transformed with pTrc-GFP, was used for receptor quantification in the immunoblot experiments. For the regulated expression of Tar in the microfluidic experiments, strain RP4532 [Δ(tar-tap)] was transformed with pVS123, which confers chloramphenicol resistance and encodes Tar under the control of a salicylate-inducible promoter (2, 6, 16), and pVS132, which is similar to pTrc-GFP except that it encodes yellow fluorescent protein (YFP) instead of GFP.

Preparation of cells.

E. coli cells were grown in tryptone broth (TB) (10.0 g/liter of Bacto tryptone powder dissolved in 10 mM phosphate buffer [pH 7.3]) supplemented with 100 μg/ml ampicillin, and 34 μg/ml chloramphenicol for RP4532, in a shaker bath at 30°C at 150 rpm. Cultures grown overnight were diluted 1:25 (corresponding to an optical density at 600 nm [OD₆₀₀] of ∼0.05) into fresh media and grown in the shaker bath until the indicated OD₆₀₀ value was reached. IPTG was added 2 h before the cell harvesting time to a final concentration of 1 mM to induce the expression of fluorescent proteins. Where indicated, salicylate was added to a final concentration of 0 to 0.5 μM. Alternatively, to reach a different cell density at the same time, cultures grown overnight were diluted into fresh media at dilution ratios ranging from 1:5 to 1:300, and cells were harvested at the same time point 4 h later. Prior to experiments, cells were washed twice with chemotaxis buffer (10 mM phosphate buffer-0.1 mM EDTA-1 μM methionine-10 mM lactic acid [pH 7.3]). For all experiments using the microfluidic device, the final cell density was ∼1.5 × 10⁸ cells/ml.

Quantitative immunoblotting.

To determine the relative levels of Tar and Tsr in bacteria grown to various OD₆₀₀ values in rich TB medium, VS154 cells from a 1.5-ml culture were precipitated, and the pellets were frozen on dry ice. To adjust samples for immunoblots to the same protein concentration, a culture with an OD₆₀₀ of 0.45 was resuspended in 125 μl of 1× Laemmli buffer, and the Laemmli buffer volume for other samples was chosen according to their initial OD₆₀₀ values. Samples were boiled for 5 min at 95°C, and 15 μl of each sample was loaded onto a 12% SDS gel. After separation by electrophoresis, the proteins were blotted onto a 0.2-μm Hybond ECL nitrocellulose membrane, by using a tank blot device (Bio-Rad), for 1 h at 100 V in transfer buffer (25 mM Tris, 96 mM glycine, 0.02% SDS, and 10% methanol). The membrane was blocked for 30 min in TBST (150 mM NaCl, 20 mM Tris-HCl [pH 7.5], 0.2% Tween 20) with 10% nonfat dry milk on a rocking platform and incubated overnight in polyclonal primary rabbit anti-Tar antibody diluted 1:10,000 in TBST with 1% nonfat dry milk. This antibody recognizes both Tar and Tsr receptors with similar specificities. The blots were washed five times (5 min each) with TBST, incubated for 30 min with IRDye 800-conjugated secondary goat anti-rabbit antibody (Rockland) diluted 1:10,000 at room temperature, and washed again as described above before the membrane was scanned with an Odyssey imager (Li-Cor). Protein bands were quantified by using ImageJ software (http://rsbweb.nih.gov/ij). To obtain the Tar/Tsr ratio, the antibody specificity was calibrated by using fluorescent protein fusions to Tar and Tsr as a reference (S. Neumann and V. Sourjik, unpublished data), and the relative intensity of receptor bands was corrected for a small difference in specificity.

Microfluidics for dual-gradient generation.

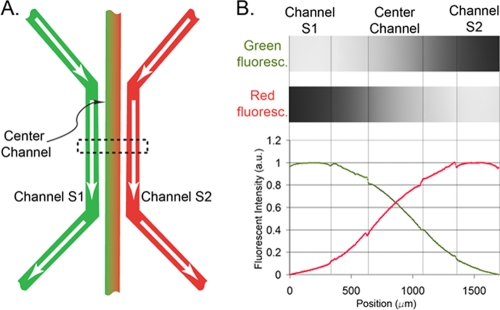
A microfluidic chemotaxis device used for this work was described previously (5, 7). Briefly, four identical microfluidic devices were patterned on an agarose gel membrane with a size of 25 mm by 75 mm by 1 mm. Each device consists of three parallel microfluidic channels, as shown in Fig. 1A. By flowing two different noninteracting chemicals through the side channels S1 and S2 and allowing the chemicals to diffuse through the agarose gel, two opposing linear gradients were established in the center channel. The establishment of the dual gradients is characterized by flowing fluorescein and rhodamine dyes of 100 μM along the two side channels, respectively. Figure 1B shows two fluorescent images of a portion of the center channel recording green and red fluorescent light emitted from the center channel, respectively. Also shown are the fluorescent intensity profiles of the dual gradients across all three channels. Note the two linear gradients crossing the center channel. Numerical calculation as well as experimental measurements (7, 8) both show that the time for the concentration gradient to reach a steady state is about 8 min using fluorescein (376 Da), and the linear gradients can be kept constant, within ±5%, as long as flows along the side channels are kept constant at a rate of ≥5 μl/min (7). The chemoattractants used in our experiments were l-serine (105 Da) and α-methyl-dl-aspartate (MeAsp) (147 Da). The molecular masses of both chemoattractants are lower than those of rhodamine B (479 Da) and fluorescein (376 Da), and they are thus expected to diffuse faster than dyes.

FIG. 1.

Dual chemical concentration gradient generated by a microfluidic chemotaxis device. (A) Three parallel channels are patterned in a 1-mm-thick agarose gel membrane. By flowing two different chemicals (e.g., green fluorescein and red rhodamine) through the side channels, the chemicals diffuse through the agarose gel barrier and establish a dual cross-concentration gradient in the center channel. (B) The top shows two micrographs of all three channels recording green and red fluorescent light when two fluorescent dyes (fluorescein and rhodamine) of 100 μM flow through the side channels. The bottom shows the corresponding scaled red and green fluorescent intensity profiles. Note the two linear intensity profiles crossing in the center channel. a.u., arbitrary units.

Data acquisition and imaging.

For each experimental run, we performed four parallel experiments using the four devices on the same chip. First, we seeded cells in four center channels by injecting the cell culture with a gel-loading pipette tip and sealed all the inlet and outlet to avoid flowthrough in the center channel. MeAsp and serine solutions were then pumped through channels S1 and S2, respectively, at a rate of 5 μl/min. Four movies of the four center channels were taken consecutively at about 20 min after the start of the flow in the side channels. A typical movie had 500 frames recorded at 10 frames per s, and each image is 410 μm by 410 μm in size. A fluorescent microscope (Olympus IX 51 microscope, 20× objective lens, and EXFO X-Cite 120 fluorescence illumination system) and a charge-coupled-device (CCD) camera (Photometrics Cascade 512B EM camera) were used for imaging.

Data analysis.

To quantify the bacterial chemotactic response, we first tracked the x_i,y_i positions of the swimming bacteria in the mid-93% portion of the center channel (an area of 380 μm by 410 μm) by using in-house particle-tracking software (available at our laboratory website [http://biofluidics.mae.cornell.edu]). Here, i is the index of the bacterium being tracked and 0,0 is defined as the left upper corner of the imaged portion of the center channel (Fig. 2). Using tracked positions, we first calculated the chemotactic migration coefficient (CMC) of the swimming bacteria in the channel (8, 11). The CMC is the average x position of all the cells being tracked with respect to the center position of the channel. Here, the CMC is calculated as follows: CMC = [mean(x_i) − x_c)/190] μm, where x_c is the x coordinate at the center of the channel and 190 μm is the half-width of the channel being monitored. Second, we computed the normalized cell density distribution, ρ(x), across the channel. For each movie series, we calculated the CMC or ρ(x) for each of the 500 images first and then obtained an average value. Third, we formed tracks using the nearest-neighbor method. For more details of this computation, please refer to work of Liao et al. (10). To improve the data quality, we removed bacterial trajectories that exhibited limited motility. Specifically, we discarded trajectories (i) whose total run time length was less than 3 s and (ii) whose absolute spatial variation, as measured by the standard deviation of the x or y coordinates of the trajectory, was less than 3 μm or whose relative variation scaled by the trajectory length was less than 0.25.

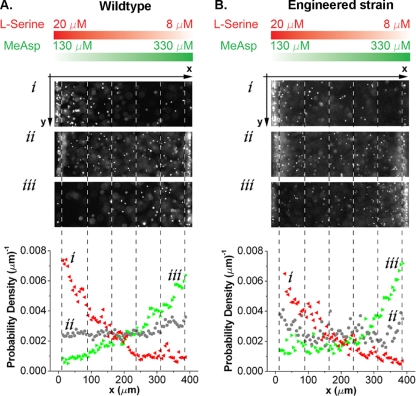
FIG. 2.

Responses of E. coli bacteria to two opposing chemoattractant gradients. The chemical concentration gradients of MeAsp (green) and serine (red) in the center channel are the same for both sets of experiments and are illustrated at the top. (A) Images of wild-type E. coli (RP437) cells, harvested at OD₆₀₀ values of 0.26 (i), 0.53 (ii), and 0.65 (iii), in the center channel and their corresponding cell density profiles. (B) Images of RP4532 [Δ(tar-tap)] cells expressing various levels of Tar from plasmid pVS123 in the presence of native Tsr and their corresponding cell density profiles. Concentrations of the chemical inducer sodium salicylate for the expression of Tar were 0.06 μM (i), 0.15 μM (ii), and 0.4 μM (iii).

RESULTS AND DISCUSSION

Generation and definition of two opposing but equally potent chemoattractant gradients.

For creating dual chemical gradients of equal potency for Tar and Tsr in opposite directions in the center channel, we flowed 500 μM MeAsp in side channel S1 and 30 μM serine in side channel S2. Rationales for choosing the above-mentioned MeAsp and serine concentrations are as follows. (i) The response of wild-type E. coli bacteria (harvested at an OD₆₀₀ of 0.5) in the center channel to a single MeAsp or serine concentration gradient peaks when these above-mentioned concentrations flow in one side channel and buffer flows in the other (8). Therefore, the use of these gradients maximizes the signal-to-noise ratio for later experiments. (ii) Wild-type E. coli bacteria (harvested at an OD₆₀₀ of ∼0.5) showed no directional preference when 500 μM MeAsp and 30 μM serine flowed along the two side channels, respectively (Fig.2Aii). Accordingly, the MeAsp concentration of 500 μM in channel S1 and the serine concentration of 30 μM in channel S2 were fixed for all the experiments reported below. Note that because the concentration of serine in the center channel is kept below 20 μM in our experiments and each experiment is carried out within 20 min, its metabolism is not expected to influence the chemotactic responses. Consistent with this, no significant increase of the swimming speed of E. coli cells was observed in the presence of 20 μM serine, suggesting that the energy state of the cells was not changed. Furthermore, any degradation of serine by cells should not significantly distort the gradient in our experimental setup because of the rapid equilibration with the serine replenishing continuously through the side channel (7).

Responses of wild-type E. coli cells to dual chemoattractant gradients depend upon the cell culture density.

E. coli bacteria harvested at different cell culture concentrations responded differently in the dual and opposing gradients. Figure 2A shows images of E. coli cells (wild-type strain RP437) exposed to two opposing gradients using bacterial cultures harvested at three different cell culture densities. We observed that bacteria harvested at higher OD₆₀₀ values (∼0.65) swam toward high concentrations of MeAsp, while the cells harvested at lower OD₆₀₀ values (∼0.26) swam toward high concentrations of serine. This behavior was very robust: it did not depend upon the sequence in which each of the two gradients was established and remained stable in time as long as the cross-gradients were maintained steadily (checked for at least 40 min). The E. coli cells’ chemotactic behavior was further quantified by evaluating the cell migration coefficient (CMC) using the cell density distribution profiles shown in Fig. 2A. The CMC is a dimensionless number that represents the center of weight of the cellular distribution in the viewing area with respect to the center of the channel (Fig. 2) (8). A CMC of 0 represents no chemotactic preference, a CMC of >0 represents net chemotaxis toward MeAsp, and a CMC of <0 represents net chemotaxis toward serine. Our experiments show that the CMC increases with the OD₆₀₀: cells prefer serine at an OD₆₀₀ below 0.4 and MeAsp otherwise (Fig. 3).

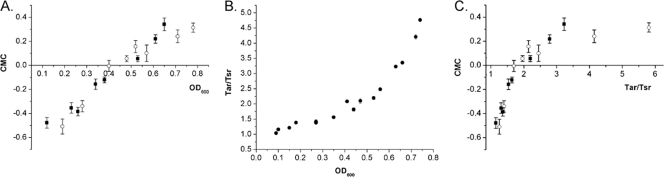
FIG. 3.

Responses of wild-type bacteria in dual chemical gradients depend on the cell culture density or the Tar/Tsr receptor ratio. (A) CMC of wild-type RP437 as a function of cell culture density. Cells were subjected to dual opposing chemical gradients as shown in Fig. 2. Positive CMC values indicate a preference for MeAsp, whereas negative CMC values correspond to a preference for serine. Solid squares represent the data points for when E. coli bacteria were subcultured with the same dilution ratio (1:25) from a culture grown overnight and then harvested at different time points. The open circles represent the data for when E. coli cells were subcultured with different dilution factors (1:5 to 1:300) from cultures grown overnight and then harvested at the same time point (in 4 h). (B) Tar/Tsr ratio as a function of cell culture density, obtained by quantitative immunoblotting using reference strain VS154 (see Materials and Methods for details). All cells in B have the same growth time of 4 h. (C) CMC as a function of the Tar/Tsr ratio.

Responses of wild-type E. coli cells to dual chemoattractant gradients depend upon the Tar/Tsr ratio.

It was reported in a recent publication by Salman and Libchaber (15) that the ratio of Tar to Tsr for cells grown in minimal medium depends on the cell culture density. Therefore, we hypothesize that the observed change of chemotactic behavior with optical density in dual gradients may follow this ratio. We measured the relative levels of Tar and Tsr at various OD₆₀₀ values in bacteria grown in rich tryptone broth (TB) medium by quantitative immunoblotting using an antibody that was raised against the signaling domain of Tar and recognizes both receptors with similar specificities (Neumann and Sourjik, unpublished). To facilitate the measurement, we used a strain (VS154) that lacks the receptor modification enzymes CheR and CheB. This ensures that all Tar and Tsr receptors are in the same modification state and therefore run as well-separated single bands in a gel. VS154 is also deleted for the minor receptor Trg to avoid a possible interfering overlap of the Trg and Tar bands. The quantification also showed that in TB medium, the ratio of Tar to Tsr increases with the OD₆₀₀ (Fig. 3B), whereby the level of Tsr per cell remains constant and the level of Tar rises with cell density. Data shown in Fig. 3C suggest that bacteria change their preference from serine to MeAsp when the ratio of Tar to Tsr exceeds 2.0. Notably, the same bias was observed at a given OD₆₀₀ (or Tar/Tsr ratio) regardless of the growth time (Fig. 3A and C). This may indicate that the relative expression levels of Tar and Tsr depend on the availability of serine and aspartate in the medium, since E. coli cells are known to preferentially consume serine before aspartate (14). Such direct or indirect temporal correlation between the relative receptor expression level and the abundance of their ligands in the medium would be physiologically meaningful, but further investigations are needed to verify this conjecture and to understand the underlying mechanism.

Responses of E. coli cells with various Tar expression levels in dual gradients.

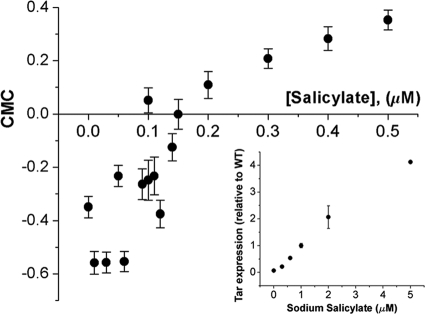
To further verify that the receptor number ratio plays a critical role in a bacterium's decision-making when in dual gradients, we used a tar mutant with the native expression of Tsr and varied the number of Tar receptors that were expressed under the control of the chemical inducer sodium salicylate. As expected, the chemical preference of E. coli changed from serine to MeAsp as the salicylate concentration increased from 0.06 μM to 0.4 μM (Fig. 2B). Accordingly, the experimental CMC value changed as a function of the salicylate concentration (Fig. 4).

FIG. 4.

Responses of the engineered strain at various Tar expression levels while the Tsr level was kept native. Shown are CMC values of strain RP4532 expressing Tar receptors from plasmid pVS123 under various levels of salicylate induction. The inset shows the expression level of Tar in the reference strain. WT, wild type.

In this paper we have demonstrated that (i) chemical preferences of E. coli bacteria in dual gradients can be correlated with the expression levels of the corresponding receptors and (ii) wild-type bacteria vary their receptor expression levels as a function of cell density but not growth time. This demonstrates that the chemoreceptor clusters in E. coli bacteria are highly dynamic entities that adjust their properties based upon environmental conditions and provides insights into the behavior of E. coli cells when multiple chemoattractant gradients are present in the environment.