An illness–death stochastic model in the analysis of longitudinal dementia data

SUMMARY

A significant source of missing data in longitudinal epidemiological studies on elderly individuals is death. Subjects in large scale community-based longitudinal dementia studies are usually evaluated for disease status in study waves, not under continuous surveillance as in traditional cohort studies. Therefore, for the deceased subjects, disease status prior to death cannot be ascertained. Statistical methods assuming deceased subjects to be missing at random may not be realistic in dementia studies and may lead to biased results. We propose a stochastic model approach to simultaneously estimate disease incidence and mortality rates. We set up a Markov chain model consisting of three states, non-diseased, diseased and dead, and estimate the transition hazard parameters using the maximum likelihood approach. Simulation results are presented indicating adequate performance of the proposed approach.

1. INTRODUCTION

As ageing of the world population progresses, dementia is emerging as one of the major public health problems. Many large community-based longitudinal dementia studies are conducted to assess the prevalence and incidence of the disease, providing valuable input for planning and allocating health care resources. These studies also provide epidemiological evidence in the search for risk factors of the disease.

Longitudinal dementia studies differ from traditional cohort studies in at least one fundamental way. Study participants in large dementia study cohorts are not under continuous surveillance for the determination of disease status. Since the onset of dementia is subtle and insidious, it requires extensive clinical evaluations to make a diagnosis. In a community-based longitudinal study, therefore, periodic evaluations of the cohort are conducted at regular intervals. During each wave of evaluations, new incident cases of dementia are detected among those who were diagnosed as non-demented in the previous wave.

For studies on elderly subjects, death is an inevitable source of missing data. A considerable number of subjects die between study waves and disease status prior to death cannot be ascertained on previously non-demented subjects. Under the assumption of missing completely at random (MCAR) [1] or missing at random (MAR) [1] for the missing data mechanism, valid inference can be derived provided appropriate likelihood or Bayesian approaches are used and all covariates contributing to the missing data process are included in the model [2]. However, in dementia cohort studies demented subjects have been found to be more likely to die than non-demented subjects [17]. Therefore, there are reasons to believe that data missing due to death are non-ignorable, meaning missingness may depend on the unobserved disease status.

Statistical inference with non-ignorable missing data has mostly relied on making assumptions about the missing data mechanism. The approaches taken can be broadly classified into the selection model approach (Diggle and Kenward [3]), and the pattern mixture model approach, as reviewed by Little [4]. The selection model approach has been applied to dementia studies with complex sampling by Gao and Hui [5]. In the selection model and pattern mixture approaches, emphasis is on the estimation of disease incidence while the missing data mechanism is treated as a nuisance process. However, in many longitudinal dementia studies, it is important to estimate simultaneously the disease incidence and mortality rates. Inferences from both the disease model and death model can be informative in determining disease genesis and population characteristics.

In this paper we propose an illness–death stochastic model approach in which both disease incidence and mortality are modelled simultaneously. The proposed illness–death model, also known as the disability model, has been studied extensively with the assumption of continuous monitoring times for both disease status and mortality. Early references include Chiang [6, 7] and Beck [8]. Chiang et al. [9] extended the early models to include baseline and time-dependent covariates of the hazard functions. Keiding [10] used the illness–death model in a general discussion of incidence and prevalence of disease under the continuous monitoring times assumption. An overview of other applications of the disability model was presented by Hougaard [11].

Additional contributions to the study of the illness–death stochastic model were made when the exact observation times are not available. Kalbfleisch and Lawless [12, 13] proposed a Markov model for the analysis of panel data. Craig and Newton [14] used a Markov chain Monte Carlo method (MCMC) to model the history of diabetic retinopathy. Recently, Hui and Gao [15] used the illness–death stochastic model assuming constant hazard functions to estimate the incidence of dementia. They used the method of moments to estimate the hazard rates. We extend the use of the illness–death stochastic models to incorporate the dependence of hazard rates on covariates. We also use the full likelihood approach to estimate the hazard rates and coefficients of the covariates. Maximum likelihood estimation allows us to incorporate multiple follow-up waves and makes the estimation of the covariate coefficients possible.

In Section 2 we introduce the illness–death stochastic model approach and describe the likelihood estimation of the parameters. In Section 3, a simulation study and its results are presented. We conclude with a discussion and proposals for future work in Section 4.

2. A STOCHASTIC MODEL APPROACH

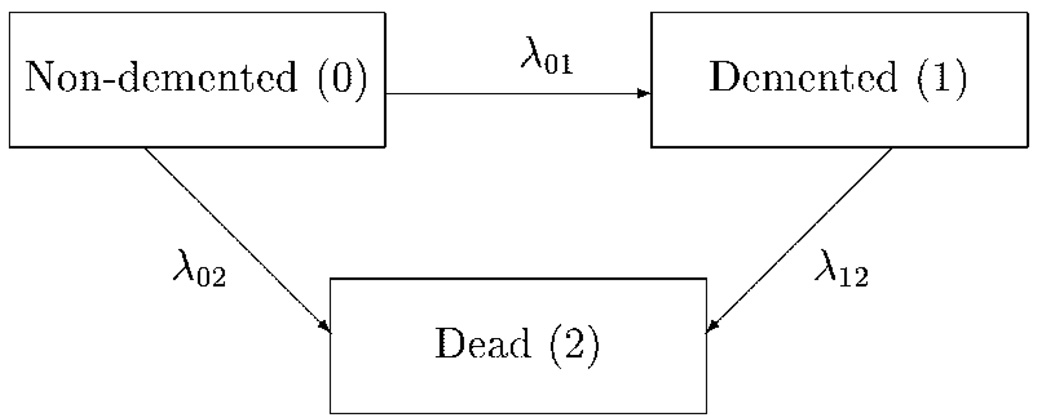
We propose to use an illness–death stochastic model to simultaneously estimate disease incidence and mortality rates. Our sample at baseline consists of subjects classified as either ‘non-demented’ or ‘demented’. At follow-up time t, the subjects will be in one of the following three states: ‘non-demented’, ‘demented’ or ‘dead’. At any possible time t a subject who was ‘non-demented’ at time T <t can be in any of the three states at time t. The two transient states of ‘non-demented’ and ‘demented’ apply only to those subjects who are alive, and the transition from ‘non-demented’ to ‘demented’ is assumed irreversible. ‘Dead’ is an absorbing state that can be reached from both ‘non-demented’ and ‘demented’ states.

At any time t, we define the state

$$S(t)=\{\begin{array}{cc}0\hfill & \text{if a subject is}‘\text{non-demented}’\hfill \\ 1\hfill & \text{if a subject is}‘\text{demented}’\hfill \\ 2\hfill & \text{if a subject is}‘\text{dead}’\hfill \end{array}$$

and the transition hazards

$${\lambda }_{\mathit{\text{jl}}}(t)=\underset{\mathrm{\Delta }t\to 0}{\text{lim}}\frac{P\{S(t+\mathrm{\Delta }t)=l|S(t)=j\}}{\mathrm{\Delta }t}$$

where j = 0, 1, l = 0, 1, 2 and j≤l.

The transition between the three stochastic states is illustrated in Figure 1.

Figure 1.

Schematic representation of the transitions between the three states.

Given the status of a subject at any time t, we can derive the probability of the subject being in any eligible state at time s>t. Define the transition probabilities as π_jl(s,t) = P{S(s) = l|S(t) = j} and the transition probability matrix as

$$\left[\begin{array}{ccc}\hfill {\pi }_{00}(s,t)\hfill & \hfill {\pi }_{01}(s,t)\hfill & \hfill {\pi }_{02}(s,t)\hfill \\ \hfill 0\hfill & \hfill {\pi }_{11}(s,t)\hfill & \hfill {\pi }_{12}(s,t)\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill \end{array}\right]$$

In this paper we consider time-homogeneous models in which λ_jl(t) is independent of t, that is, λ_jl(t) = λ_jl, for any t. We can introduce the simplified notation

$${\pi }_{\mathit{\text{jl}}}(T)={\pi }_{\mathit{\text{jl}}}(t,t+T)={\pi }_{\mathit{\text{jl}}}(0,T)$$

Under the assumption of constant hazard rates, we can use Kolmogorov backward equations [16] to derive the following expressions for the π_jl(T):

$$\begin{array}{c}{\pi }_{00}(T)=\text{exp}\{-({\lambda }_{\mathbf{★★}}+{\lambda }_{12})T\}\hfill \\ {\pi }_{01}(T)=\frac{{\lambda }_{01}}{{\lambda }_{\mathbf{★★}}}\text{exp}\{-{\lambda }_{12}T\}(1-\text{exp}\{-{\lambda }_{\mathbf{★★}}T\})\hfill \\ {\pi }_{02}(T)=1-{\pi }_{00}(T)-{\pi }_{01}(T)\hfill \\ {\pi }_{11}(T)=\text{exp}\{-{\lambda }_{12}T\}\hfill \\ {\pi }_{12}(T)=1-{\pi }_{11}(T)\hfill \end{array}$$

where λ_★★ = λ₀₁ + λ₀₂ − λ₁₂.

Our model formulation can be used for both continuous and discrete-time Markov processes. We concentrate here on the discrete case in which we observe study participants at equally spaced time points (study waves). Let k denote a time point of observation, k = 0, 1, 2,…,K; k = 0 to denote study baseline. Now define the following random variable:

$$y_i^{(k)}(\mathit{\text{jl}})=\{\begin{array}{cc}1\hfill & \text{if a subject}i\text{is in state}j\text{at time}k\text{and in state}l\text{at time}(k+1)\hfill \\ 0\hfill & \text{otherwise}\hfill \end{array}$$

for 0≤k≤K − 1.

Then the likelihood function for n subjects followed for K times is the product of a multinomial distribution under the assumption of time-independent transitional hazard rates:

$$\begin{array}{cc}L=\hfill & {\displaystyle \prod _{i=1}^n{\displaystyle \prod _{k=0}^{k-1}{\pi }_{00}{(k,k+1)}^{y_i^{(k)}(00)}{\pi }_{01}{(k,k+1)}^{y_i^{(k)}(01)}{\pi }_{02}{(k,k+1)}^{y_i^{(k)}(02)}}}\hfill \\ \hfill & \times {\pi }_{11}{(k,k+1)}^{y_i^{(k)}(11)}{\pi }_{12}{(k,k+1)}^{y_i^{(k)}(12)}\hfill \end{array}$$

Since the π_jl’s are functions of the transitional hazards, λ_jl, parameter estimates of λ_jl can be computed by using maximum likelihood methods.

In the development above we have assumed constant hazard rates. In dementia studies group specific incidence and mortality rates are often desirable. For example, the incidence rates of dementia for specific age-groups are often assumed to be constant over the study period. In situations where the time between study waves is considered short enough, the constant hazard assumption does not seem to be overwhelmingly restrictive. However, these group-specific rates do assume that subjects in the same group have the same transitional hazards, which may be a potential problem due to heterogeneity among subjects within each group. To allow heterogeneity within the groups we can make the hazard functions covariate dependent, that is

$${\lambda }_{\mathit{\text{jl}}}^{(i)}(k)=\eta (X_i^{(k)}\beta )i=1,\dots ,n,k=0,\dots ,k$$

where ${\lambda }_{\mathit{\text{jl}}}^{(i)}(k)$ is the transitional hazard function between the j and l states for the ith subject at the kth time, $X_i^{(k)}$ is a 1 × p vector of subject-specific covariates for the ith subject at the kth time, β is a p × 1 vector of coefficients and η is a link function. Many link functions may be considered, for example, the exponential link, η(x) = exp(x). For the models with covariate dependent hazards, maximum likelihood methods can also be used to derive parameter estimates of the β’s.

Note that the covariate-dependent model allows the covariates to be time-dependent. The inclusion of the covariates that define the heterogeneity within each group will, in effect, create more homogeneous subgroups.

3. SIMULATION STUDIES

In order to assess the performance of the method proposed in Section 2, we conducted a simulation study. The setting of the simulation was modelled using the design and variables from the Indianapolis Dementia Study [17]. The study sample includes 2212 African-American subjects 65 years of age or older. The Indianapolis Dementia Study is designed to have a baseline prevalence wave and two follow-up waves two years apart. The purpose of the study is to estimate incidence rates of dementia and Alzheimer’s disease in this population and elucidate potential risk factors for these diseases. The Indianapolis Dementia Study used a complex sampling design for the selection of clinical evaluation of disease status at each of the three study waves. Therefore, the number of clinically evaluated subjects at each study wave was relatively small to directly apply the approach proposed here. A probability of disease model derived from the clinical subsample of the study was used to generate baseline disease status for all 2212 subjects. In Section 3.1 we present the results of the simulations for constant age-specific hazard rates. In Section 3.2 we deal with the estimation of covariate-dependent hazard rates.

3.1. Age-specific hazard rates

Baseline disease status for all 2212 subjects was generated using a probability model from the clinical subsample of the Indianapolis Dementia Study. Using the incidence and mortality rates presented in Hendrie et al. [17], we generated the states of subjects in the two follow-up waves using the following four designs:

1. Use the age-specific incidence (λ₀₁) and state-specific mortality rates (λ₀₂, λ ₁₂) as in Hendrie et al. [17].

2. Double both the incidence and mortality rates in design 1.

3. Use the age-specific incidence rates and mortality rates for the non-demented subjects as in design 1, and make the mortality rate for demented subjects twice that of non-demented subjects.

4. Use the age-specific incidence rates and mortality rates for the non-demented as in design 1, and use the same mortality rates for demented and non-demented subjects.

The simulations were designed to vary the true hazard rates to detect the impact of the rates on the precision of estimation. Design 4 represents the situation of non-differential mortality where inference procedures assuming missing at random are expected to perform adequately.

Since the study was conducted over a 4-year span, subjects could start in a younger age-group at baseline, and move to an older age-group in the follow-up waves.

Maximum likelihood estimates of the hazard rates were calculated using the non-linear programming procedure in SAS/OR. This procedure uses a numerical algorithm to derive gradient and Hessian matrices and solves for parameter estimates iteratively using the Newton–Raphson algorithm. Various initial parameter values were used to assess if the procedure converged to a global maximum. In most simulation runs (over 99.6 per cent), the maximization procedure converged and we were able to obtain estimates of the hazard rates.

As a comparison to our proposed method we included naive estimates of the hazard rates for each simulation design. The naive rates were calculated as the number of subjects in transition divided by the total number of subjects at risk. Results from 5000 Monte Carlo simulations and each of the four designs are presented in Table I. Estimates of hazards rates for each age group, that is, 65–74, 75–84 and 85 years or older, using the illness–death (I–D) model and the naive method are included in the table. We calculated the relative bias of the estimated hazard rates by

$$\text{Relative bias}(\widehat{\lambda })=\frac{\widehat{\lambda }-\lambda }{\lambda }$$

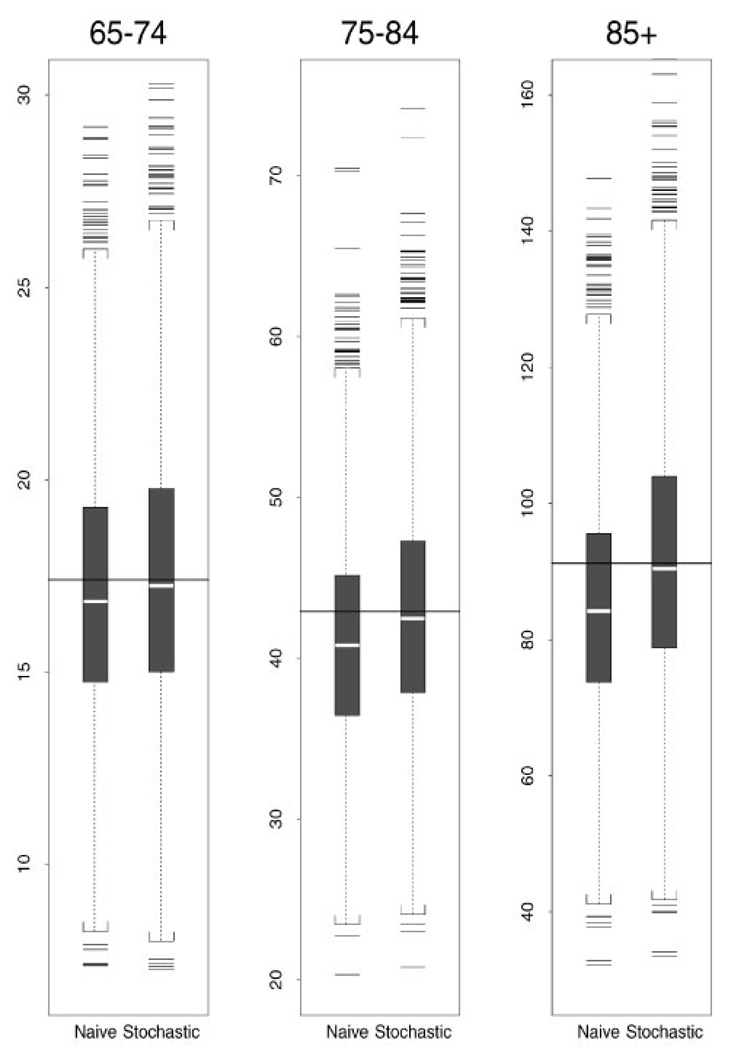
The relative bias for each rate estimate is also included in Table I. In Figure 2, box plots of the estimated incidence rates for the first design using the naive method and the stochastic model method are presented for each age group.

Table I.

Results of simulations comparing estimates of hazard rates between the illness–death (I–D) model and the naive model. Estimates of the rates (per 1000) are equal to the average of 5000 simulated values. Relative bias of the estimates, expressed as a percentage, is included in parentheses beneath the estimates.

Design	Method	65–74 Hazard rates			Age groups 75–84 Hazard rates			85 or more Hazard rates
		λ01	λ02	λ12	λ01	λ02	λ12	λ01	λ02	λ12
1	True	17.40	46.25	74.00	42.90	68.25	109.2	91.20	101.0	161.6
	I–D	17.42	46.16	76.37	42.76	68.10	110.7	91.56	101.2	163.2
		(0.14)	(−0.19)	(3.21)	(−0.34)	(−0.22)	(1.38)	(0.40)	(0.18)	(0.96)
	Naive	17.01	45.35	72.72	40.97	66.63	104.3	84.87	98.52	149.6
		(−2.25)	(−1.94)	(−1.73)	(−4.49)	(−2.37)	(−4.48)	(−6.94)	(−2.46)	(−7.40)
	True	34.80	92.50	148.0	85.80	136.5	218.4	182.4	202.0	323.2
2	I–D	34.88	92.32	151.8	85.75	136.3	220.8	183.5	202.5	326.5
		(0.23)	(−0.19)	(2.56)	(−0.06)	(−0.11)	(1.12)	(0.62)	(0.26)	(1.03)
	Naive	30.32	89.09	139.7	68.66	130.4	197.3	128.3	191.4	277.0
		(−12.9)	(−3.69)	(−5.62)	(−20.0)	(−4.47)	(−9.64)	(−29.7)	(−5.22)	(−14.3)
3	True	17.40	46.25	92.50	42.90	68.25	136.5	91.20	101.0	202.0
	I–D	17.43	46.11	95.36	42.76	68.18	138.4	91.87	100.8	204.5
		(0.18)	(−0.31)	(3.09)	(−0.32)	(−0.10)	(1.37)	(0.73)	(−0.19)	(1.23)
	Naive	16.86	45.45	89.94	40.44	67.24	128.6	83.51	99.80	183.8
		(−3.12)	(−1.72)	(−2.76)	(−5.73)	(−1.48)	(−5.76)	(−8.44)	(−1.19)	(−9.00)
	True	17.40	46.25	46.25	42.90	68.25	68.25	91.20	101.0	101.0
4	I–D	17.47	46.19	47.60	42.84	68.01	68.70	91.53	101.0	102.6
		(0.42)	(−0.13)	(2.92)	(−0.15)	(−0.36)	(0.66)	(0.36)	(−0.05)	(1.61)
	Naive	17.30	45.14	45.97	41.89	65.73	66.09	87.23	95.93	96.96
		(−0.57)	(−2.40)	(−0.61)	(−2.35)	(−3.69)	(−3.17)	(−4.35)	(−5.02)	(−4.00)

Figure 2.

Incidence estimates (per 1000) from design 1 for three age groups. Solid line indicates the true value and white strip indicates the median of estimated values.

For the first design, naive estimates of incidence rates (λ̂₀₁) are between 2.2 per cent and 6.9 per cent lower than the true value, whereas stochastic model estimates are within 0.5 per cent of the true value. Results of simulations with designs 2 and 3 indicate an increased bias in naive estimates ranging from 3.1 per cent to 30 per cent when the incidence rates increase. The stochastic model estimates are within 0.8 per cent of the true value in designs 2 and 3. When the mortality rates are assumed the same for the ‘non-demented’ and ‘demented’ subjects (design 4), the naive estimates differ by no more than 4.4 per cent from the true value, and the stochastic model estimates are within 0.5 per cent of the true value. It is worth noticing that the naive estimator always underestimates the true incidence rates.

3.2. Covariate dependent hazard rates

In the second set of simulations, we generated baseline disease status for all study subjects (n = 2212) using the same probabilistic model as in Section 3.1 and we modelled the hazard rates to be covariate dependent. Three covariates from the Indianapolis data were used: age of the subjects at each study wave, a binary indicator for sex and a three-level categorical variable indicating a subject’s general cognitive functioning at study baseline screening phase (good, intermediate and poor). Epidemiological studies have shown that age and sex are risk factors for dementia [18]. The instrument used to evaluate cognitive functioning was shown to be a good predictor of dementia status [19].

The model we used to generate the subject specific transition hazard rate from the ‘non-demented’ to ‘demented’ state (incidence model) was

$$\begin{array}{cc}\text{Logit}({\lambda }_{01})=\hfill & -7+0.064*(\text{Age})-0.5*\mathrm{I}(\text{Sex}=‘\text{Female}’)\hfill \\ \hfill & +0.5*\mathrm{I}(\text{Group}=‘\text{Intermediate}’)+1.0*\mathrm{I}(\text{Group}=‘\text{Poor}’)\hfill \end{array}$$

The model for the transition hazard rate to the absorbing ‘dead’ state was set to be

$$\begin{array}{cc}\text{Logit}({\lambda }_{j2})=\hfill & -4+0.0425*(\text{Age})-0.6*\mathrm{I}(\text{Sex}=‘\text{Female}’)\hfill \\ \hfill & +0.5*\mathrm{I}(\text{Status}=‘\text{Demented}’)\hfill \end{array}$$

where j = 0, 1.

The parameter specifications were based on the results from simple logistic regression models from the clinically evaluated subsamples in the Indianapolis Dementia Study.

We ran 1000 Monte Carlo simulations with the coefficients specified in the incidence and death models. In most simulation runs (99.5 per cent), the maximization procedure converged and we were able to obtain parameter estimates. As a comparison to our incidence model using stochastic model approach, we fitted a logistic regression model ignoring the deceased subjects in the analysis, the so-called naive model. We define the relative bias of the parameter estimates as

$$\text{Relative bias}(\widehat{\beta })=\frac{\widehat{\beta }-\beta }{\beta }$$

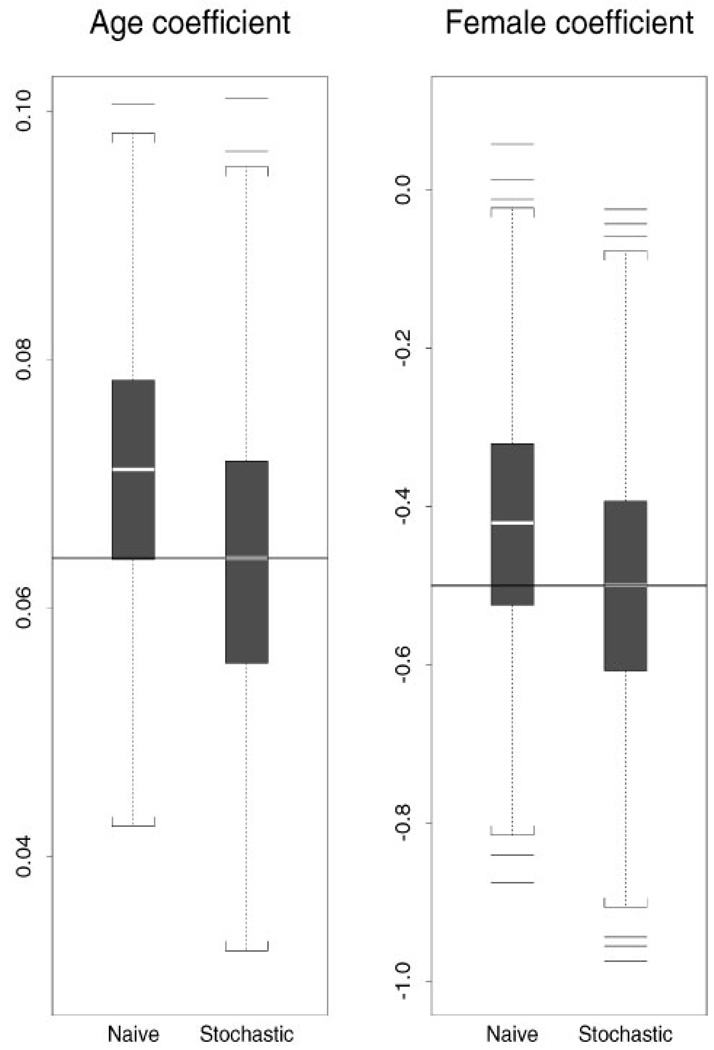
Parameter estimates using the stochastic model approach and using the naive model are presented in Table II for the incidence model and in Table III for the death model. In Figure 3 box plots of the parameter estimates for two covariates (age and sex indicator) in the incidence model are presented. Results are based on 995 simulations (five simulation runs did not converge).

Table II.

Parameter estimates for the incidence model from the simulation. Relative bias of the estimates, expressed as a percentage, is included in parentheses is beneath the estimates.

Method	Coefficients for the incidence model
	Intercept	Age	Female	Intermediate	Poor
True	−7.0	0.064	−0.5	0.5	1.0
I–D Model	−6.997	0.0639	−0.501	0.486	0.996
	(−0.04)	(−0.14)	(0.11)	(−2.74)	(−0.38)
Naive	−7.084	0.0711	−0.422	0.538	0.835
	(1.19)	(11.1)	(−15.6)	(7.6)	(−16.5)

Table III.

Parameter estimates for the death model from the simulations. Relative bias of the estimates, expressed as a percentage, is included in parentheses is beneath the estimates.

Method	Coefficients for the death model
	Intercept	Age	Female	Demented
True	−4.0	0.0425	−0.6	0.75
I–D Model	−4.02	0.0427	−0.599	0.762
	(0.50)	(0.52)	(−0.08)	(1.58)

Figure 3.

Parameter estimates for the coefficients of age and sex in the incidence model using the stochastic model approach and the naive method. The solid line indicates the true value and the white strip indicates the median of coefficient estimates.

The absolute value of the maximum relative bias for the stochastic model approach is under 3 per cent, while the absolute value of relative bias for the naive estimates is in the range of 7.6 per cent to 16.5 per cent.

4. DISCUSSION

In this paper we proposed using the stochastic model method for dealing with non-ignorable missing data in longitudinal dementia studies. This method simultaneously estimates transition hazards to multiple states that are of interest in longitudinal dementia studies. The use of maximum likelihood estimation extends the work of Hui and Gao [15] by allowing the hazard rates to be covariate dependent. Performance of the illness–death stochastic model approach was evaluated through a Monte Carlo simulation study. The simulation results indicate adequate performance of the stochastic model approach.

Each of the three major approaches for dealing with non-ignorable missing data, namely, the selection model approach, the pattern mixture approach and the stochastic model approach, makes inferences by using different assumptions of the missing data mechanism. Since the assumptions underlying non-ignorable missing data are untestable [4], direct comparisons among the three methods are difficult, if not impossible. When analysing data with non-ignorable missing values, one has to consider whether the assumptions underlying each approach are plausible for the situation at hand in deciding which approach to take.

Our future research plan includes the extension of the proposed method to data collected using complex sampling designs and the application of the method to the Indianapolis Dementia Study data.