Abstract
The assumption that different genetic elements can make separate contributions to the same quantitative trait was originally made in order to reconcile biometry and Mendelism and ever since has been used in population genetics, specifically for the trait of fitness. Here we show that sex is responsible for the existence of separate genetic effects on fitness and, more generally, for the existence of a hierarchy of genetic evolutionary modules. Using the tools developed in the process, we also demonstrate that in terms of their fitness effects, separation and fusion of genes are associated with the increase and decrease of the recombination rate between them, respectively. Implications for sex and evolution theory are discussed.
Keywords: recombination, epistasis, additive effects, fitness, genetic architecture
Sex has been called “the queen of problems in evolutionary biology” largely because its functional significance has not been determined (1). In a recent paper, a new approach to this problem was proposed: mixability theory (2). It was shown formally that sex enables selection for alleles that perform well across different genetic contexts (henceforth, “selection for mixability”). Furthermore, it was argued qualitatively that selection for mixability is responsible for the existence of separate, identifiable contributions by genes to fitness (2). Separate contributions to fitness are a defining characteristic of evolutionary modules—modules that serve different adaptive functions and that are expected to reduce evolutionary tradeoffs between adaptations (3, 4). Thus, a connection was hypothesized between sex, separate contributions to fitness, and genetic modularity (2, 5), the last of which has become widely appreciated for its importance to evolution as a result of the genomic era (3, 6).
In this article, two major limitations of mixability theory are overcome. First, although mixability theory has so far considered only the gene as a potential evolutionary module (2), the study of genetic modularity is concerned largely with the existence of sets of closely interacting (but not necessarily linked) genes, with weak interactions between these sets (3, 6). Here, we show that sex causes the existence of evolutionary modules consisting of such sets of genes. In addition, we show that the modularity characteristics of strong interactions within sets, weak interactions between sets, and multiple use of lower-level modules in higher-level modules (3, 6) arise together in evolutionary modules directly from the interaction of sex and natural selection.
Second, the argument that sex causes separate genetic effects on fitness (2) followed qualitatively from the results of mixability theory and, due to its importance, warrants a rigorous demonstration. Here, such a demonstration is provided.
The implications of the argument on separate effects relate to the foundations of evolutionary theory. For evolution to have occurred by small, cumulative steps, Darwin proposed that natural selection acted on continuous variation. But as inheritance turned out to be based on discrete elements, a seeming contradiction emerged between Darwin’s reliance on continuous (“quantitative”) traits and the discrete nature of inheritance (see biometry-Mendelism debate, ref. 7). This contradiction was resolved by making the assumption that different genes could make separate, small contributions to the same quantitative trait (8); because, as Fisher showed (8), these separate effects allowed the trait to vary continuously in the population. The assumption of the existence of such separate effects has become a cornerstone of the modern evolutionary synthesis (7) and has been commonly applied in population genetics, specifically for the trait of fitness.
In the context of sex, it is after this assumption of separate effects had been made that ideas were proposed for how sex might be beneficial. The Fisher/Muller hypothesis (9, 10) as well as Muller’s ratchet (11) and the deterministic mutation hypothesis (12) are ideas of this kind, and they require separate effects on fitness (the beneficial and deleterious mutations they invoke can exist only when alleles maintain their respective effects on fitness to some degree in different individuals). However, if sex causes separate effects on fitness in the first place, then it needs to be treated as a part of the foundations of the modern synthesis.
The present results are made possible by a sequence of measures of the evolutionary dynamics in population genetic models. These measures focus on the evolutionary transient (2), which has rarely been analyzed for reasons of mathematical tractability. They show that sex enables selection for mixability of both single alleles as well as sets of alleles at different loci, and that at the same time genes and sets of (not necessarily linked) genes acquire separate effects on fitness. No contradiction exists between separate effects and genetic interaction or “epistasis”: What is a separate effect of a set of genes is at the same time a tight interaction of the genes within the set. Finally, these measures make it possible to demonstrate the fusion and separation of genes in terms of their fitness effects with the decrease and increase of the recombination rate between them, respectively. Implications of this result for understanding genetic interactions will also be discussed.
Separate Effects and Modularity
In what follows, we will use the terms “locus” and “gene” interchangeably. Consider a population of haploid genotypes made up of alleles at three loci. The fitnesses of the three-locus haplotypes may be represented as
where wijk is the fitness of the haploid genotype with alleles i, j and k at the first, second, and third loci respectively, and the s terms are the separate selection coefficients associated with alleles or interactions of alleles, with superscripts indicating the loci (labeled 1, 2, and 3) that each term refers to and subscripts indicating the respective alleles at those loci. Thus, s2j, for example, represents the effect on fitness of allele j at locus 2, whereas s23jk is the effect on fitness of the interaction between alleles j and k at loci 2 and 3, respectively. Notice, however, that this system of equations, viewed as equations with the s terms as unknowns and the wijk left-hand sides as given quantities, is severely underdetermined: We can always take s123ijk = wijk – 1, and all other s terms equal to zero. Thus, this system becomes meaningful only when the s123ijk are very small in absolute value — small corrections to an otherwise accurate inference of fitness effects. We will see that sex acts to establish this “meaningfulness” of fitness effects.
Notice that the important aspect of Eq. 1 for our purposes is not additivity per se but separability. Although models with additive and multiplicative effects can yield quantitatively different results, similar principles to the ones explored here may be expected to apply to analogous equations written with multiplication or another associative operation as an aggregator. We use additivity here to facilitate the handling of the multiplicity of levels.
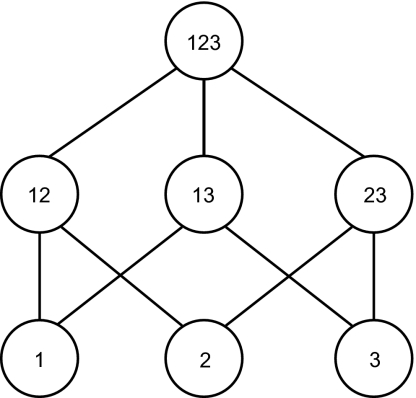
We now notice that, when such systems of equations become meaningful: (i) s terms come to represent genes and sets of genes that have relatively context-insensitive effects on fitness, because the same terms can be used in the description of different fitnesses (e.g., wijl includes the same s1i, s2j and s12ij, as wijk). This point further implies that these genes and sets of genes operate semi-independently of each other to produce their respective context-insensitive effects. (ii) Strong interactions within a set of genes and weak interactions between sets are implied by the facts that each s term is a potentially complex function of its alleles, whereas different s terms are added to each other regardless of the particular identities of the alleles involved in each. (iii) The genes and sets of genes thus represented can be embedded in a hierarchy of modules, with repeated use of lower-level modules in higher-level modules (Fig. 1). (iv) The effect of a gene substitution on fitness is local; e.g., a change in locus 1 from allele i to allele i′ entails an effect on fitness limited to the modules that gene 1 participates in (e.g., s1, s12, and s123). Because points (i)–(iv) describe characteristics of genetic evolutionary modules (3, 4), a connection is established between separate fitness effects and genetic evolutionary modularity. Eq. 1 can be generalized to include sets of many genes.
Fig. 1.
A hierarchy of genetic modules in a three-locus haploid model. The bottom nodes represent genes 1, 2, and 3 and are the first-level modules. The center nodes represent the interactions of genes 1 and 2, 1 and 3, and 2 and 3 (denoted 12, 13, and 23, respectively) and are the second-level modules. The top node represents the interaction of all three genes and is the third-level module. Notice that a correspondence can be drawn between the s terms in Eq. 1 and the modules in Fig. 1 based on the former’s superscripts and the latter’s labels, and that in such a hierarchy of modules, lower-level modules are multiply used in higher-level modules.
Model and Conceptualization
We use a classical population genetic framework (13) to model the discrete time evolutionary dynamics of a large panmictic population without mutation. We consider haplotypes ijk···, with allele i at the first locus, allele j at the second locus, allele k at the third locus, etc., and their frequencies at generation t, Pijk···, t. Each genotype, namely a haplotype ijk··· in the haploid case, or an unordered pair of haplotypes {ijk···;lmn···} in the diploid case, has a certain fitness value wijk··· or wijk···/lmn···, respectively. To represent selection, we multiply the frequency of each genotype by its fitness and normalize. To represent sex, i.e., genetic mixing due to recombination or segregation, we assume that each pair of parental haplotypes generates a recombinant offspring haplotype with the appropriate probability as determined by the laws of inheritance (Methods).
To gain a geometric intuition into the system, consider the space of haplotypes, which in the three-locus case becomes a 3D space with points representing combinations of alleles at three genes, lines parallel to the axes representing combinations of alleles at two genes, and planes parallel to the axes representing single alleles. Now, the mating between two haplotypes can be conceptualized as a transfer of frequencies from these haplotypes to the other points in the Cartesian closure that these two haplotypes define. For example, the mating between ijk and lmk transfers frequencies from Pijk,t and Plmk,t to Pimk,t+1 and Pljk,t+1; and the mating between ijk and lmn transfers frequencies from Pijk,t and Plmn,t to Pijn,t+1, Pimk,t+1, Pimn,t+1, Pljk,t+1, Pljn,t+1, and Plmk,t+1. Taking all matings together, we see that sex tends to homogenize the frequencies within each plane parallel to the axes, each line parallel to an axis, and other such entities in higher-dimensional systems, to the degree that all such entities can be homogenized simultaneously. This process, which we call “rebalancing” (2), changes the multigenerational growth-rate of the sum total of the frequencies within a given entity from being determined largely by the maximal fitness value in that entity toward being determined by the various fitness values in it. Thus, sex enables haplotypes made up of combinations of alleles at different loci (including the single locus case, ref. 2) to compete with each other based on how well they perform across different genetic contexts, whereas in asexual populations only whole genotypes can be meaningfully said to be competing with each other. In population genetic terms, rebalancing reduces linkage disequilibrium, which has the effect of favoring mixability. This geometric view amounts to a generalization of the concept of rebalancing in mixability theory (2).
Mixability Measures and Results
Key to our methodology is decomposing the classical population mean fitness measure into a new sequence of measures, M1,t, M2,t, …, Mm,t. The first measure in the sequence, M1,t, is analogous to the mixability measure 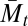 (2), and the last, Mm,t, is identical to the population mean fitness,
(2), and the last, Mm,t, is identical to the population mean fitness, 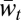 . Thus, this sequence explores the large middle area between
. Thus, this sequence explores the large middle area between 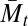 and
and 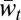 left unexplored in ref. 2.
left unexplored in ref. 2.
For haploids, the measures are calculated as follows. Given all n fitness values wijk··· for a system of m loci, we find single-superscript parameters s1i, s2j, s3k… that minimize the error in the prediction of wijk··· in the form: wijk··· = s∅ + s1i + s2j + s3k…, where 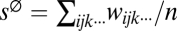 . These parameters are ones that minimize
. These parameters are ones that minimize 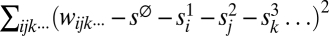 . Having fixed those, we find two-superscript parameters s12ij, s13ik, s23jk… that minimize the error further, i.e., that minimize
. Having fixed those, we find two-superscript parameters s12ij, s13ik, s23jk… that minimize the error further, i.e., that minimize 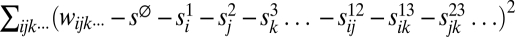 ; and so on for s terms with 3, 4, …, m superscripts. (Strictly speaking, one could use
; and so on for s terms with 3, 4, …, m superscripts. (Strictly speaking, one could use 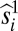 ,
, 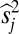 , etc. to distinguish between the variables and the optimizing solutions; in what follows, the s terms will refer to these optimizing solutions.) At generation t, we then calculate, for the level of single alleles, the measure:
, etc. to distinguish between the variables and the optimizing solutions; in what follows, the s terms will refer to these optimizing solutions.) At generation t, we then calculate, for the level of single alleles, the measure:
for the level of pairs of alleles, the measure:
and so on for M1,t, M2,t, …, Mm,t, adding s terms of one more superscript at each level. Finally, we obtain the difference measures: Δ1,t = M1,t – s∅, Δ2,t = M2,t – M1,t, …, Δm,t = Mm,t – Mm–1,t.
For diploids, we assume for now no position effects (SI Text) and allow each set of alleles represented by an s term to include alleles from either haplotype (SI Text). The resulting measures are similar in essence to the ones above.
Mℓ,t and Δℓ,t show the extent to which, in a sexual population, there is selection for sets of alleles representing haplotypes of up to size ℓ (Mℓ,t) and of size ℓ (Δℓ,t), including ℓ = 1, that have high s terms (in diploids, these sets may also include two alleles from the same locus; see SI Text). These sets of alleles are ones that both perform well across different genetic contexts and for which it is meaningful to impute separate effects on fitness, as follows from the definition of the s terms. If Δℓ,t is more often larger in sexual than in asexual populations, then the s terms of level ℓ are more appropriate for describing fitnesses in sexual than in asexual populations, subject to the considerations below.
First, selection for mixability is inherently multigenerational and dependent on the existence of variation (2) and, therefore, as explained in (2) for 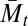 and extended here to Mℓ,t, Mℓ,t functions best during the evolutionary transient. Therefore, we expect that, where Mℓ,t is more often larger with sex than with asex, this difference would be observed most clearly during the evolutionary transient.
and extended here to Mℓ,t, Mℓ,t functions best during the evolutionary transient. Therefore, we expect that, where Mℓ,t is more often larger with sex than with asex, this difference would be observed most clearly during the evolutionary transient.
Second, as ℓ increases, Mℓ,t comes to approximate more closely 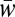 , which corresponds to the level which we know a priori to be the only level selected in asexual populations and which is selected more strongly there than in sexual populations (2). Thus, although we expect M1,t to be more often larger with sex than with asex during the evolutionary transient, at some ℓ we expect this relationship to reverse so that Mℓ,t will be more often larger with asex than with sex. We expect a similar reversal for Δℓ,t.
, which corresponds to the level which we know a priori to be the only level selected in asexual populations and which is selected more strongly there than in sexual populations (2). Thus, although we expect M1,t to be more often larger with sex than with asex during the evolutionary transient, at some ℓ we expect this relationship to reverse so that Mℓ,t will be more often larger with asex than with sex. We expect a similar reversal for Δℓ,t.
Third, since this reversal occurs because Mℓ,t approaches Mm,t (as ℓ approaches m), we expect that by increasing the number of loci and/or increasing the number of alleles per locus, thereby making the approximation of Mm,t by Mℓ,t improve more slowly in ℓ, the reversal would occur at higher ℓ.
To test our predictions, we calculated Mℓ,t and Δℓ,t for several combinations of locus number and allele number per locus under both haploidy and diploidy. If aL is the case of L loci and a alleles per locus, we considered the cases 23, 33, 43, 53, 63, 24, 34, 44, 25, and 26 for haploidy and 22, 32, 42, 52, 62, 72, 23, 33, 43, and 53 for diploidy. In each case, we ran a computer program that performed the equivalent of iterating Eq. 4 for 300 generations for both a recombination rate r = 0 (asex) and free recombination between any two loci, 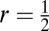 (sex), 30 separate times or “trials” in the haploid case and 100 separate trials in the diploid case. At each trial we started both the sexual and asexual populations with the same random set of fitness values drawn independently from a uniform distribution on the interval [0.5,1.5] and the same initial genotypic frequencies drawn independently from a uniform distribution and normalized (the frequencies and fitnesses differed across trials). We then calculated Mℓ,t and Δℓ,t for each population at each generation. To summarize the results across trials, we calculated for each case: (i) the average Mℓ,t across trials (〈Msexℓ,t〉 and 〈Masexℓ,t〉), (ii) the percentage of trials in which the sexual population had a higher Mℓ,t than the asexual population (%Msexℓ,t > Masexℓ,t), (iii) the percentage of trials in which the sexual population had a higher Δℓ,t than the asexual population (%Δsexℓ,t > Δasexℓ,t), and (iv) the percentage of trials in which the peak of the Δℓ,t curve, Kℓ, was higher in the sexual than in the asexual population (%Ksexℓ > Kasexℓ) and vice versa (%Ksexℓ < Kasexℓ).
(sex), 30 separate times or “trials” in the haploid case and 100 separate trials in the diploid case. At each trial we started both the sexual and asexual populations with the same random set of fitness values drawn independently from a uniform distribution on the interval [0.5,1.5] and the same initial genotypic frequencies drawn independently from a uniform distribution and normalized (the frequencies and fitnesses differed across trials). We then calculated Mℓ,t and Δℓ,t for each population at each generation. To summarize the results across trials, we calculated for each case: (i) the average Mℓ,t across trials (〈Msexℓ,t〉 and 〈Masexℓ,t〉), (ii) the percentage of trials in which the sexual population had a higher Mℓ,t than the asexual population (%Msexℓ,t > Masexℓ,t), (iii) the percentage of trials in which the sexual population had a higher Δℓ,t than the asexual population (%Δsexℓ,t > Δasexℓ,t), and (iv) the percentage of trials in which the peak of the Δℓ,t curve, Kℓ, was higher in the sexual than in the asexual population (%Ksexℓ > Kasexℓ) and vice versa (%Ksexℓ < Kasexℓ).
As an example, Fig. 2 shows these measures for the haploid three-locus case with five alleles per locus. We see that M1,t and M2,t are more often larger with sex than with asex—a difference which peaks during the evolutionary transient—whereas M3,t (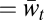 ) is more often larger with asex (Fig. 2A). These relationships are seen also in the across-trial averages (Fig. 2B). The extension of mixability theory from single alleles to sets of alleles of size ≥ 1 is seen here in the fact that Δ2,t is also more often larger with sex than with asex during the transient (Fig. 2C). Thus, in this case, sex selects more efficiently than asex not only for single alleles that have high s terms but also for pairs of alleles at different loci that have high s terms. Comparing how often the peak of Δℓ,t was larger with sex than with asex and vice versa clearly shows the advantage to sex in the lower levels and the advantage to asex in the highest level (Fig. 2D).
) is more often larger with asex (Fig. 2A). These relationships are seen also in the across-trial averages (Fig. 2B). The extension of mixability theory from single alleles to sets of alleles of size ≥ 1 is seen here in the fact that Δ2,t is also more often larger with sex than with asex during the transient (Fig. 2C). Thus, in this case, sex selects more efficiently than asex not only for single alleles that have high s terms but also for pairs of alleles at different loci that have high s terms. Comparing how often the peak of Δℓ,t was larger with sex than with asex and vice versa clearly shows the advantage to sex in the lower levels and the advantage to asex in the highest level (Fig. 2D).
Fig. 2.
Across-trial summary measures for the haploid three-locus case with five alleles per locus. For ℓ = 1 (solid), ℓ = 2 (dashed), and ℓ = 3 (dot-dash), the graphs show: (A) %Msexℓ,t > Masexℓ,t, (B) 〈Msexℓ,t〉 (gray) and 〈Masexℓ,t〉(black). (C) %Δsexℓ,t > Δasexℓ,t. (D) %Ksexℓ> Kasexℓ(gray) and %Ksexℓ< Kasexℓ (black).
Fig. 3 shows this peak comparison for all conditions studied and therefore shows all of the main results together. Although asex has an advantage in one or more of the higher levels (with an exception to be discussed), sex has an advantage in one or more of the lower levels. Furthermore, the number of levels in which sex has an advantage increases with the number of alleles and/or with the number of loci. Thus, all predictions mentioned above—the better applicability of the measures during the evolutionary transient, the existence of a reversal point, and the relation of this reversal point to the gene and allele numbers—are confirmed.
Fig. 3.
Comparisons of the peaks of Δsexℓ,t and Δasexℓ,t for all conditions studied. Each graph gives the percentage of times in which the peak of the Δℓ,t curve, Kℓ, was higher with sex than with asex (gray bars) and vice versa (black bars) for the stated number of loci, number of alleles per loci, and ploidy (diploid in rows 1 and 2 and haploid in rows 3–6). The number of loci increases from top to bottom in each of the diploid and haploid cases and the number of alleles increases from left to right.
Importantly, the reversal from advantage of sex in lower levels to advantage of asex in higher levels does not mean that higher levels are not selected for mixability by sex nor that they are selected for mixability by asex. This reversal is due to the approximation of 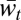 by Mℓ,t, where
by Mℓ,t, where 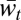 is the measure that is actively increased with asex. Moreover, for large enough ℓ, this approximation can be closer in the asexual population, in which case an advantage of sex can be seen in Δℓ,t (Fig. 3; six-locus haploid case) that is not accompanied by an advantage in Mℓ,t and is therefore another artifact of the comparison method. Thus, our comparison of sex and asex confirms the prediction that sex selects for mixability on multiple levels by revealing that selection at lower levels and, at the same time, that comparison shows sex to be the cause of the appropriateness of separate effect terms. However, it is not designed to compare the strength of the selection for mixability between levels.
is the measure that is actively increased with asex. Moreover, for large enough ℓ, this approximation can be closer in the asexual population, in which case an advantage of sex can be seen in Δℓ,t (Fig. 3; six-locus haploid case) that is not accompanied by an advantage in Mℓ,t and is therefore another artifact of the comparison method. Thus, our comparison of sex and asex confirms the prediction that sex selects for mixability on multiple levels by revealing that selection at lower levels and, at the same time, that comparison shows sex to be the cause of the appropriateness of separate effect terms. However, it is not designed to compare the strength of the selection for mixability between levels.
On this important point we propose a qualitative argument. In the geometric space of haplotypes described in Model and Conceptualization, with free recombination between any two loci, higher-level entities (i.e., larger sets of genes) are more homogeneously rebalanced than lower-level entities, because for example, more transfers occur between two points that are on the same line (e.g., ijk, ljk) than between two points that are on the same plane but not on the same line (e.g., ijk, lmk). At the same time, higher-level entities experience more exchange of frequencies per genotype between the genotypes within them and the genotypes outside of them, which weakens the feedback between the fitnesses within the entity and the evolutionary change of the sum total of the frequencies in that entity. These trends represent opposing influences on the strength of the selection for mixability and suggest that it is not the lowest-level entities (genes) but rather middle-level entities (sets of genes) that are most strongly selected for mixability and that acquire the strongest separate effects on fitness—a conjecture that cannot be examined by the present comparison of sex and asex and that will require new methodology to be examined. In agreement with it, though, a verbal argument by Schlosser (14) that is based on opposing trends and that is akin to our analysis suggests that middle-level units are the best-delimited units of evolution (14).
Importantly, our iterations started with random genotypic fitnesses and frequencies. Hence, there was no justification for the use of separate effect terms in describing genotypic fitnesses initially. The appropriateness of these terms emerged a posteriori from the interaction of sex and natural selection, as indicated by the increase in the Δℓ,t measures at low ℓ. Thus, our results establish formally that sex causes the existence of separate effects on fitness at multiple levels.
Two remarks are useful. First, although it is the erasure of initially meaningless small s terms that shows the emergence of separate genetic effects here, once separate effects are assumed to exist they can be recalculated by weighing the genotypic fitnesses by genotypic frequencies, which would then allow the s terms to be both positive and negative. Second, because the genes in our models are symmetric, our models give equal representation to all possible modules (sets of closely interacting genes) and, thus, do not address the sparsity of gene interaction networks. They address the existence of a hierarchy of genetic evolutionary modules.
Fusion and Separation Measures and Results
If sex entails separate fitness effects on genes, then the lack of recombination between two adjacent loci would mean that, as far as fitness is concerned, these two loci should be considered as one. In this sense, the decrease and increase of recombination rates can make one gene from two and two genes from one. This point can be demonstrated by varying the recombination rate between 0.5 and 0 in the haploid three-locus model or in the diploid two-locus model and observing its effect on components of the Δ measures. In the haploid three-locus model, we break Δ1 into its components: 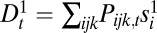 ,
, 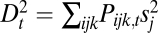 and
and 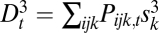 , and Δ2 into its components:
, and Δ2 into its components: 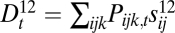 ,
, 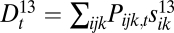 and
and 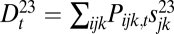 . We expect that, if the recombination rate r2 between loci 2 and 3 is fixed at
. We expect that, if the recombination rate r2 between loci 2 and 3 is fixed at 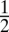 , and the recombination rate r1 between loci 1 and 2 is decreased, then loci 1 and 2 will fuse in terms of fitness effects, which would be observed as a decrease in D1 and D2 relative to D3, along with an increase in D12 relative to D13 and D23 (Fig. S1).
, and the recombination rate r1 between loci 1 and 2 is decreased, then loci 1 and 2 will fuse in terms of fitness effects, which would be observed as a decrease in D1 and D2 relative to D3, along with an increase in D12 relative to D13 and D23 (Fig. S1).
In the diploid two-locus model, we now allow for position effects (where wij/kl = wkl/ij, but wij/kl = wil/kj need not apply) and distinguish in the second level between three types of pairs of alleles: cis, trans, and within-locus, as follows (see SI Text for the second-level entities without this distinction). For genotype ij/kl, the cis fitness contribution terms are s12cij and s12ckl; the trans terms are s12til and s12tkj, and the within-locus terms are s11ik and s22jl (repetition of superscripts means that the respective alleles belong the the same locus; SI Text). After fixing the first-level terms, we take these second level terms to minimize 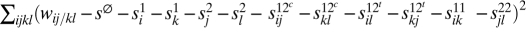 , and then calculate the following components of the Δ2 measure:
, and then calculate the following components of the Δ2 measure: 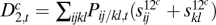 ,
, 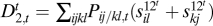 and
and 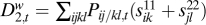 . We expect that, as the recombination rate r between the two loci is decreased, these loci will fuse in terms of their fitness effects and, therefore, Δ1 will decrease, while D2c will increase relative to D2t and D2w (Fig. S2). These trends mean fusion, while the opposite trends for increasing r1 or r mean separation.
. We expect that, as the recombination rate r between the two loci is decreased, these loci will fuse in terms of their fitness effects and, therefore, Δ1 will decrease, while D2c will increase relative to D2t and D2w (Fig. S2). These trends mean fusion, while the opposite trends for increasing r1 or r mean separation.
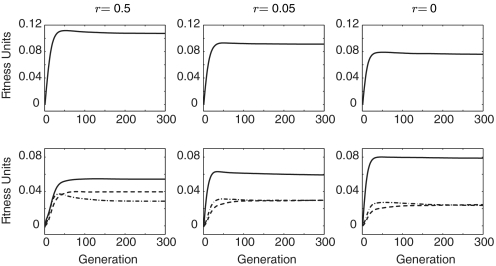
Fig. S3 and Fig. 4 confirm these trends for the haploid 3-locus model with 4 alleles per locus and the diploid two-locus model with three alleles per locus, respectively. We observed these trends at various strengths also for 2, 3, …, 6 alleles per locus. Thus, fitness effects fuse with decreasing recombination rates and separate with increasing recombination rates. In fact, at r1 or r = 0 the two fused loci are better understood as a single locus with the number of alleles being the product of the number of alleles in the two original loci (15), with corresponding s terms.
Fig. 4.
Varying r in the diploid two-locus model with three alleles per locus. (Upper) The across-trial averages 〈Δsex1〉 for r = 0.5 (Left), r = 0.05 (Center), and r = 0 (Right). (Lower) The across-trial averages 〈Dc2〉 (solid), 〈Dt2〉 (dashed) and 〈Dw2〉 (dot-dash) for the same values of r. Results are based on 500 trials. With decreasing r, Δ1 decreases, and D2c increases relative to D2t and D2w.
Discussion
In evolutionary theory, genes are depicted both as units of recombination and as units that contribute to phenotypes and, ultimately, to the fitness, of their carriers. Here, we saw that these two meanings of a gene are intimately interrelated: that it is due to recombination that the fitness of an organism can be meaningfully decomposed into separate genetic effects.
The assumption that different genes make separate contributions to fitness is normally made a priori in population genetics. Particularly in the context of sex, the Fisher/Muller hypothesis (9, 10) as well as Muller’s ratchet (11) and the deterministic mutation hypothesis (12) rely on this assumption, as said. Here, we did not make this assumption a priori. Instead, we found that separate genetic effects on fitness emerged a posteriori from the interaction of sex and natural selection.
Notably, the existence of such effects is an important consequence of sex. The reconciliation of evolution and genetics relies on it (7) and, similarly, if only the interaction of all alleles together determined fitness, then small genetic changes would affect the whole organism profoundly, preventing evolution. It is not necessary to ask, then, how mixability supports the Fisher/Muller hypothesis, the deterministic mutation hypothesis, or other hypotheses that rely on separate effects.
Evidence relating sex to separate genetic effects of single loci was mentioned in ref. 2. In particular, bacteriophage T4 populations selected for drug resistance evolved stronger single-locus separate effects on fitness and weaker whole-genotype epistasis at higher recombination rates (16). In light of mixability theory, however, evidence of this kind requires more attention. Furthermore, the present analysis suggests that experiments could be conducted to see whether not only single loci but also pairs or even larger sets of loci up to some size may develop stronger, higher-level separate effects at higher recombination rates.
The present results substantially extend the connection between sex and genetic modularity recently proposed (2, 5). Although it has been suggested that sex endows single loci with relatively context insensitive effects on fitness (2) (a characteristic of evolutionary modules; refs. 3 and 4), here we found sex to be a cause of the existence of a hierarchy of genetic evolutionary modules. Importantly, a “module” here includes not only the elementary module that is a gene or a block of absolutely linked genes but also a set of closely interacting but not necessarily linked genes.
Semi-independent operation, repeated use, and tight internal interactions are often-cited characteristics of modules (3, 6). We saw that, in genetic evolutionary modules, they arise together directly from the interaction of sex and natural selection. For example, in a four-locus haploid system, module 12 (consisting of genes 1 and 2) has its own separate effect, s12, and therefore operates independently of other modules, but it also participates in the next-level modules s123, s124, and is therefore repeatedly used, and it consists of a tight interaction between genes 1 and 2. Thus, these different aspects of a genetic evolutionary module are inherently related to each other.
In addition to the above, we saw that the lower the recombination rate between sequences the more they are able to fuse and act as one. Thus, as will be explained shortly, our findings connect two general observations. First, the sexual recombination apparatus is such that the rate of recombination between two points increases with the distance between those points. Second, the meaning of genes comes from the context of the genetic apparatus in its entirety (including transcription, translation, and regulation machinery), which entails that bases that together constitute a coding or regulatory region of a gene are near each other on the genome, whereas sequences that are far apart interact indirectly through the products they produce. In this comparison of local and global interactions, the genes are composed of local interactions, and modules of unlinked genes consist of global interactions.
According to our theory, these observations are related as follows. The lower the recombination rate between sequences, the more these sequences fuse, meaning that the interactions between them become local—of the nature of interactions within a gene—and that they interact with the rest of the organism as one, as through a common product; whereas at high recombination rates, a hierarchy of modules emerges, where each sequence has its own identity and is able to serve in several modules. Thus, a deep consistency exists between the physical nature of sexual recombination and the physical nature of genes and their mechanisms of action: Sexual recombination seems to be causally related to both the nature of local interactions and the nature of global interactions in the genome. Of course, asexual forms pose no contradiction to this consistency if they inherited their genetic systems from sexual ancestors.
Sex and natural selection were often thought of in two steps, where, first, natural selection was formalized in terms of the increase in population mean fitness and, second, sex was assumed to be an adaptation that facilitated that increase. Thus, the breaking down of highly favorable gene combinations by sex (17) has been perceived as a problem (18). However, our models reveal that, when sex and natural selection interact, they are particularly efficient in increasing mixability. Furthermore, the breaking down of highly favorable combinations of genes is part of the rebalancing mechanism, and is therefore necessary for the generation of mixability (see also ref. 2). And mixability has implications for separate effects and modularity.
If sex is tied to the nature of genes, then one may reconsider the question of the origin of sex. Although it is common to imagine evolution as an originally asexual process that became sexual at some point, it is possible that sex had existed in a primitive sense of mixing before the emergence of genes as we know them, and that the interaction of sex and natural selection played a role in the shaping of the genetic architecture.
Methods
Let N = {1, 2, …, m} be the set of loci. Each haplotype h has, at each locus i ∈ N, an allele hi from the set Ai of alleles that belong to that locus. Thus, if h = ijk··· defined in the text, then h1 = i, h2 = j, h3 = k, etc. Let I ⊆ N be a set of loci, 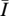 be the set of all other loci (the complement of I in N), and X(I) be the probability of inheriting the alleles in loci I from one parent and the alleles in loci
be the set of all other loci (the complement of I in N), and X(I) be the probability of inheriting the alleles in loci I from one parent and the alleles in loci 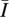 from the other parent. For example, in a two-locus case with free recombination, N = {1, 2} and
from the other parent. For example, in a two-locus case with free recombination, N = {1, 2} and 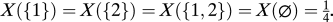 . Finally, let FIh be the set of all haplotypes that have the same alleles as haplotype h at loci I; i.e., FIh = {f:fi = hi ∀i ∈ I}. The haplotype frequencies at generation t + 1 in terms of the frequencies at generation t can be written as:
. Finally, let FIh be the set of all haplotypes that have the same alleles as haplotype h at loci I; i.e., FIh = {f:fi = hi ∀i ∈ I}. The haplotype frequencies at generation t + 1 in terms of the frequencies at generation t can be written as:
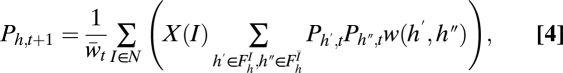 |
where w(h′, h″) = w′hw″h for haploidy and w(h′, h″) = wh′/h″ for diploidy, and 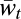 is the sum of the numerators of the right-hand sides of Eqs. 4 over all h. This equation accords with Geiringer (13), except that it includes selection in addition to recombination. As an example, in the haploid three-locus case with free recombination between any two loci, Eq. 4 takes the specific form:
is the sum of the numerators of the right-hand sides of Eqs. 4 over all h. This equation accords with Geiringer (13), except that it includes selection in addition to recombination. As an example, in the haploid three-locus case with free recombination between any two loci, Eq. 4 takes the specific form:
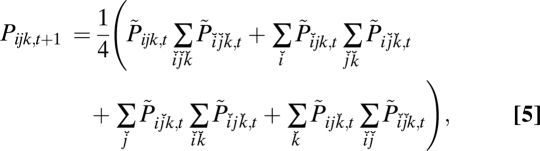 |
where 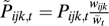 , and
, and 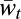 is the sum of the numerators of the right-hand sides of Eq. 5 for all ijk. This equation can be compared to the asexual three-locus haploid case, where
is the sum of the numerators of the right-hand sides of Eq. 5 for all ijk. This equation can be compared to the asexual three-locus haploid case, where 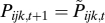 .
.
Supplementary Material
Acknowledgments
We thank Leiguang Ren for technical assistance and two anonymous referees for excellent comments on a previous version of this manuscript. AL acknowledges financial support from the Miller Institute for Basic Research in Science. Research was supported in part by National Science Foundation Grants CCF-0635319 (to C.P.) and CCF-0646682 (to N.P.) and National Institutes of Health Grant GM28016 (to M.W.F.).
Footnotes
The authors declare no conflict of interest.
This article contains supporting information online at www.pnas.org/cgi/content/full/0910734106/DCSupplemental.
References
- 1.Bell G. The Masterpiece of Nature: the Evolution and Genetics of Sexuality. Berkeley: Univ California Press; 1982. [Google Scholar]
- 2.Livnat A, Papadimitriou C, Dushoff J, Feldman MW. A mixability theory for the role of sex in evolution. Proc Natl Acad Sci USA. 2008;105:19803–19808. doi: 10.1073/pnas.0803596105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Schlosser G, Wagner GP. In: Modularity in Development and Evolution. Schlosser G, Wagner GP, editors. Chicago: The Univ Chicago Press; 2004. pp. 1–11. [Google Scholar]
- 4.Schlosser G. In: Modularity in Development and Evolution. Schlosser G, Wagner GP, editors. Chicago: The Univ Chicago Press; 2004. pp. 519–582. [Google Scholar]
- 5.Misevic D, Ofria C, Lenski RE. Sexual reproduction reshapes the genetic architecture of digital organisms. Proc R Soc Lond B Biol Sci. 2006;273:457–464. doi: 10.1098/rspb.2005.3338. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Kirschner MW, Gerhart JC. The Plausibility of Life. New Haven: Yale Univ Press; 2005. [Google Scholar]
- 7.Provine WB. The Origins of Theoretical Population Genetics. Chicago: The Univ Chicago Press; 1971. [Google Scholar]
- 8.Fisher RA. The correlation between relatives on the supposition of Mendelian inheritence. Trans R Soc Edinb. 1918;52:399–433. [Google Scholar]
- 9.Fisher RA. The Genetical Theory of Natural Selection. Oxford: Clarendon; 1930. [Google Scholar]
- 10.Muller HJ. Some genetic aspects of sex. Am Nat. 1932;66:118–138. [Google Scholar]
- 11.Muller HJ. The relation of recombination to mutational advance. Mutat Res. 1964;1:2–9. doi: 10.1016/0027-5107(64)90047-8. [DOI] [PubMed] [Google Scholar]
- 12.Kondrashov AS. Selection against harmful mutations in large sexual and asexual populations. Genet Res. 1982;40:325–332. doi: 10.1017/s0016672300019194. [DOI] [PubMed] [Google Scholar]
- 13.Geiringer H. On the probability theory of linkage in Mendelian heredity. Ann Math Stat. 1944;15:25–57. [Google Scholar]
- 14.Schlosser G. Modularity and the units of evolution. Theory Biosci. 2002;121:1–80. [Google Scholar]
- 15.Karlin S, Feldman MW. Linkage and selection: Two locus symmetric viability model. Theor Popul Biol. 1970;1:39–71. doi: 10.1016/0040-5809(70)90041-9. [DOI] [PubMed] [Google Scholar]
- 16.Malmberg RL. The evolution of epistasis and the advantage of recombination in populations of bacteriophage T4. Genetics. 1977;86:607–621. doi: 10.1093/genetics/86.3.607. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Eshel I, Feldman MW. On the evolutionary effect of recombination. Theor Popul Biol. 1970;1:88–100. doi: 10.1016/0040-5809(70)90043-2. [DOI] [PubMed] [Google Scholar]
- 18.Barton NH, Charlesworth B. Why sex and recombination? Science. 1998;281:1986–1990. [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.